Distributed Antenna in Drone Swarms: A Feasibility Study
Abstract
1. Introduction
2. Materials and Methods
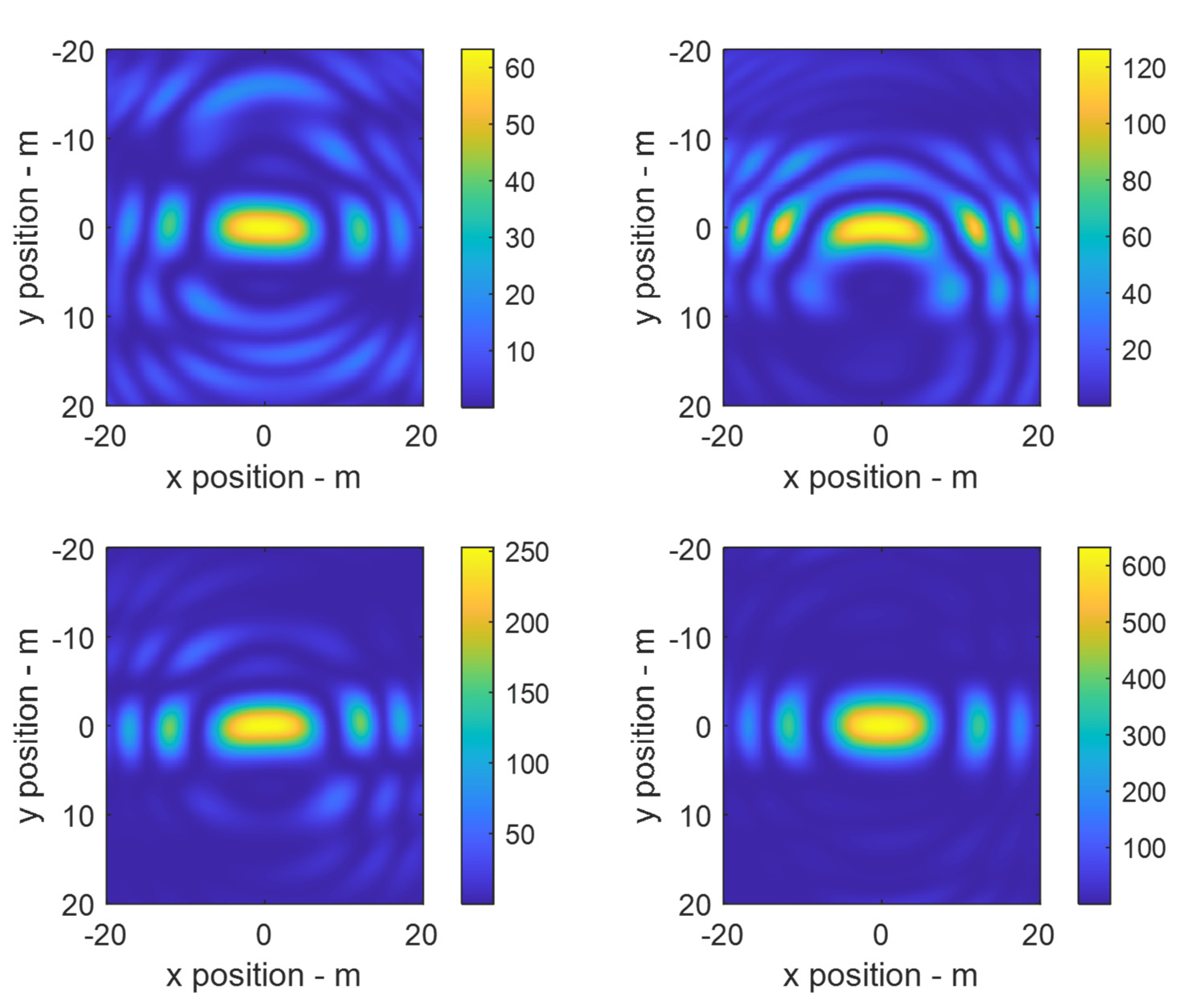
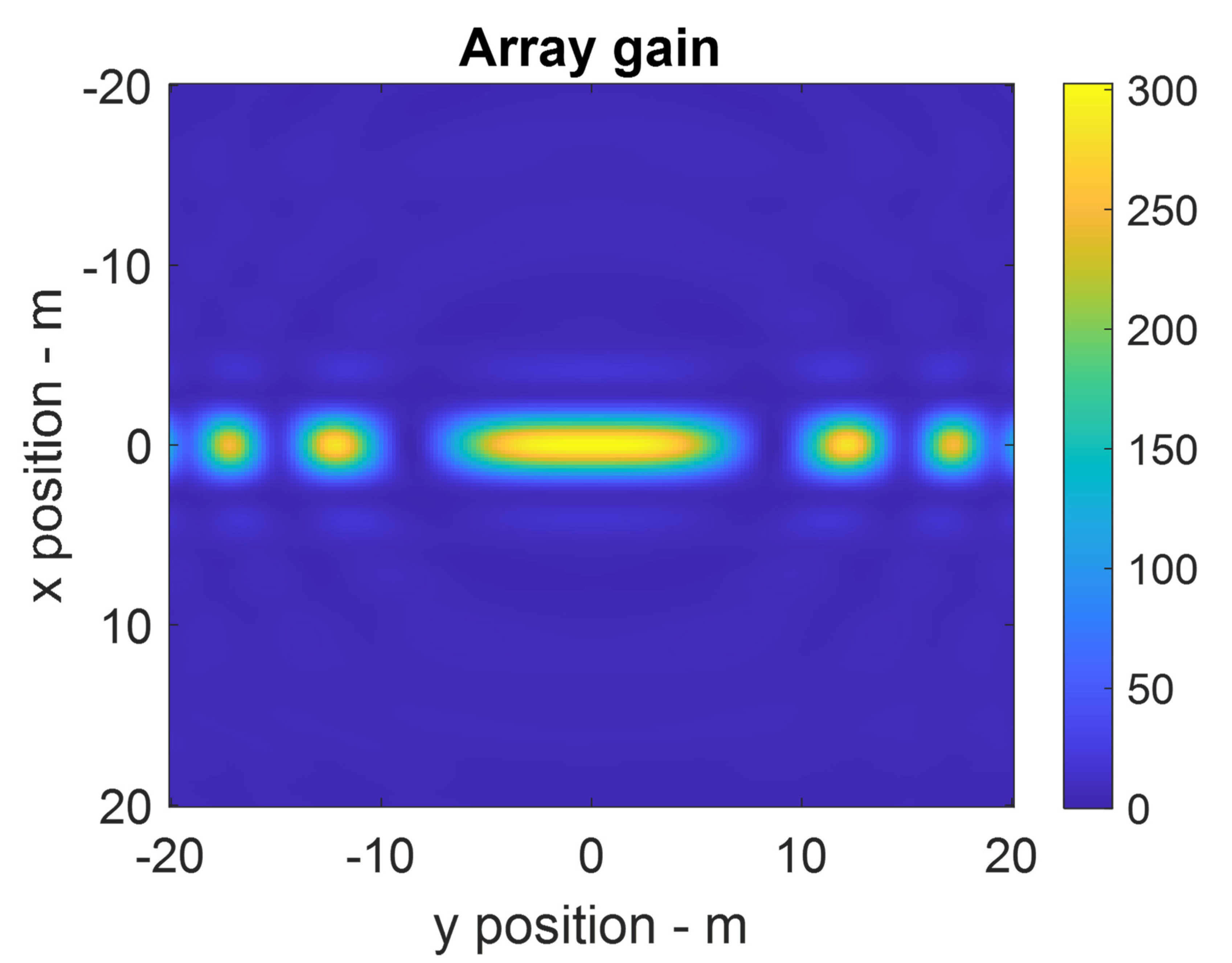
3. Results
4. Discussion
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chapman, A. It’s okay to call them drones. J. Unmanned Veh. Syst. 2014, 2, iii–v. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A Review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for Remote Sensing Applications—A review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Benarbia, T.; Kyamakya, K. A literature review of drone-based package delivery logistics systems and their implementation feasibility. Sustainability 2021, 14, 360. [Google Scholar] [CrossRef]
- Hildmann, H.; Kovacs, E. Review: Using unmanned aerial vehicles (uavs) as mobile sensing platforms (msps) for disaster response, Civil Security and Public Safety. Drones 2019, 3, 59. [Google Scholar] [CrossRef]
- Amponis, G.; Lagkas, T.; Zevgara, M.; Katsikas, G.; Xirofotos, T.; Moscholios, I.; Sarigiannidis, P. Drones in B5G/6G networks as flying base stations. Drones 2022, 6, 39. [Google Scholar] [CrossRef]
- Castrillo, V.U.; Manco, A.; Pascarella, D.; Gigante, G. A review of Counter-UAS Technologies for cooperative defensive teams of drones. Drones 2022, 6, 65. [Google Scholar] [CrossRef]
- Roldán-Gómez, J.J.; González-Gironda, E.; Barrientos, A. A survey on robotic technologies for Forest Firefighting: Applying drone swarms to improve firefighters’ efficiency and safety. Appl. Sci. 2021, 11, 363. [Google Scholar] [CrossRef]
- Asaamoning, G.; Mendes, P.; Rosário, D.; Cerqueira, E. Drone swarms as networked control systems by integration of networking and computing. Sensors 2021, 21, 2642. [Google Scholar] [CrossRef]
- Hildmann, H.; Kovacs, E.; Saffre, F.; Isakovic, A.F. Nature-inspired drone swarming for real-time aerial data-collection under dynamic operational constraints. Drones 2019, 3, 71. [Google Scholar] [CrossRef]
- Huang, J.; Tian, G.; Zhang, J.; Chen, Y. On unmanned aerial vehicles light show systems: Algorithms, software and hardware. Appl. Sci. 2021, 11, 7687. [Google Scholar] [CrossRef]
- Parker, D.; Zimmermann, D.C. Phased arrays—Part 1: Theory and architectures. IEEE Trans. Microw. Theory Tech. 2002, 50, 678–687. [Google Scholar] [CrossRef]
- Mayo, R.; Harmer, S. A cost-effective modular phased array. In Proceedings of the 2013 IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 15–18 October 2013. [Google Scholar]
- Weedon, W.H. Phased array digital beamforming hardware development at Applied Radar. In Proceedings of the 2010 IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 12–15 October 2010. [Google Scholar]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting ris-aided hybrid satellite-terrestrial relay networks: Joint Beamforming Design and optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- An, K.; Lin, M.; Ouyang, J.; Zhu, W.-P. Secure transmission in Cognitive Satellite Terrestrial Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3025–3037. [Google Scholar] [CrossRef]
- An, K.; Liang, T.; Zheng, G.; Yan, X.; Li, Y.; Chatzinotas, S. Performance limits of cognitive-uplink FSS and terrestrial FS for ka-band. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2604–2611. [Google Scholar] [CrossRef]
- Robinson, L.A.; Weir, W.B.; Young, L. An RF time-domain reflectometer not in Real time (short papers). IEEE Trans. Microw. Theory Tech. 1972, 20, 855–857. [Google Scholar] [CrossRef]
- Brookner, E. Phased-array and radar breakthroughs. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007. [Google Scholar]
- Naqvi, A.; Lim, S. Review of recent phased arrays for millimeter-wave wireless communication. Sensors 2018, 18, 3194. [Google Scholar] [CrossRef]
- Hall, T.; Lie, D.; Nguyen, T.; Mayeda, J.; Lie, P.; Lopez, J.; Banister, R. Non-contact sensor for long-term continuous vital signs monitoring: A review on Intelligent phased-array doppler sensor design. Sensors 2017, 17, 2632. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory Analysis and Design; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Alexeff, I.; Anderson, T.; Farshi, E.; Karnam, N.; Pulasani, N.R. Recent results for plasma antennas. Phys. Plasmas 2008, 15, 057104. [Google Scholar] [CrossRef]
- Chandra, R.S.; Breheny, S.H.; D’Andrea, R. Antenna Array synthesis with clusters of unmanned aerial vehicles. Automatica 2008, 44, 1976–1984. [Google Scholar] [CrossRef]
- Tanmay, R.G. Evaluation of Coordinated Drone Swarm Operation as a Synthetic Aperture Antenna: A Simulation-Based Study. MPhil Thesis, Tampere University, Tampere, Finland, 2019. [Google Scholar]
- Dill, S.; Schreiber, E.; Engel, M.; Heinzel, A.; Peichl, M. A drone carried multichannel Synthetic Aperture Radar for advanced buried object detection. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Ren, H.; Sun, Z.; Yang, J.; Xiao, Y.; An, H.; Li, Z.; Wu, J. Swarm UAV SAR for 3-D Imaging: System Analysis and sensing matrix design. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5238316. [Google Scholar] [CrossRef]
- Beauchamp, R.M.; Arumugam, D.D.; Burgin, M.S.; Bush, J.D.; Khazendar, A.; Gim, Y.; Almorqi, S.; Almalki, M.; Almutairi, Y.A.; Alsama, A.A.; et al. Can airborne ground penetrating radars explore groundwater in hyper-arid regions? IEEE Access 2018, 6, 27736–27759. [Google Scholar] [CrossRef]
- Edemsky, D.; Popov, A.; Prokopovich, I.; Garbatsevich, V. Airborne ground penetrating radar, field test. Remote Sens. 2021, 13, 667. [Google Scholar] [CrossRef]
- Utsi, E.C. Ground Penetrating Radar: Theory and Practice; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Šipoš, D.; Gleich, D. A lightweight and low-power UAV-borne ground penetrating radar design for landmine detection. Sensors 2020, 20, 2234. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Fernandez, M.; Lopez, Y.A.; Andres, F.L.-H. Airborne multi-channel ground penetrating radar for improvised explosive devices and landmine detection. IEEE Access 2020, 8, 165927–165943. [Google Scholar] [CrossRef]
- Čeru, T.; Dolenec, M.; Gosar, A. Application of ground penetrating radar supported by mineralogical-geochemical methods for mapping unroofed cave sediments. Remote Sens. 2018, 10, 639. [Google Scholar] [CrossRef]
- Poisel, R. Antenna Systems and Electronic Warfare Applications; Artech House: Boston, MA, USA, 2012. [Google Scholar]
- Guccione, P.; Monti Guarnieri, A.; Rocca, F.; Giudici, D.; Gebert, N. Along-track multistatic synthetic aperture radar formations of Minisatellites. Remote Sens. 2020, 12, 124. [Google Scholar] [CrossRef]
- GPS World. Skytraq Offers Multi-Band GNSS Receiver with 1-cm Position Accuracy. Available online: https://www.gpsworld.com/skytraq-offers-multi-band-gnss-receiver-with-1-cm-position-accuracy/ (accessed on 19 December 2022).
- Campion, M.; Ranganathan, P.; Faruque, S. UAV swarm communication and Control Architectures: A Review. J. Unmanned Veh. Syst. 2019, 7, 93–106. [Google Scholar] [CrossRef]
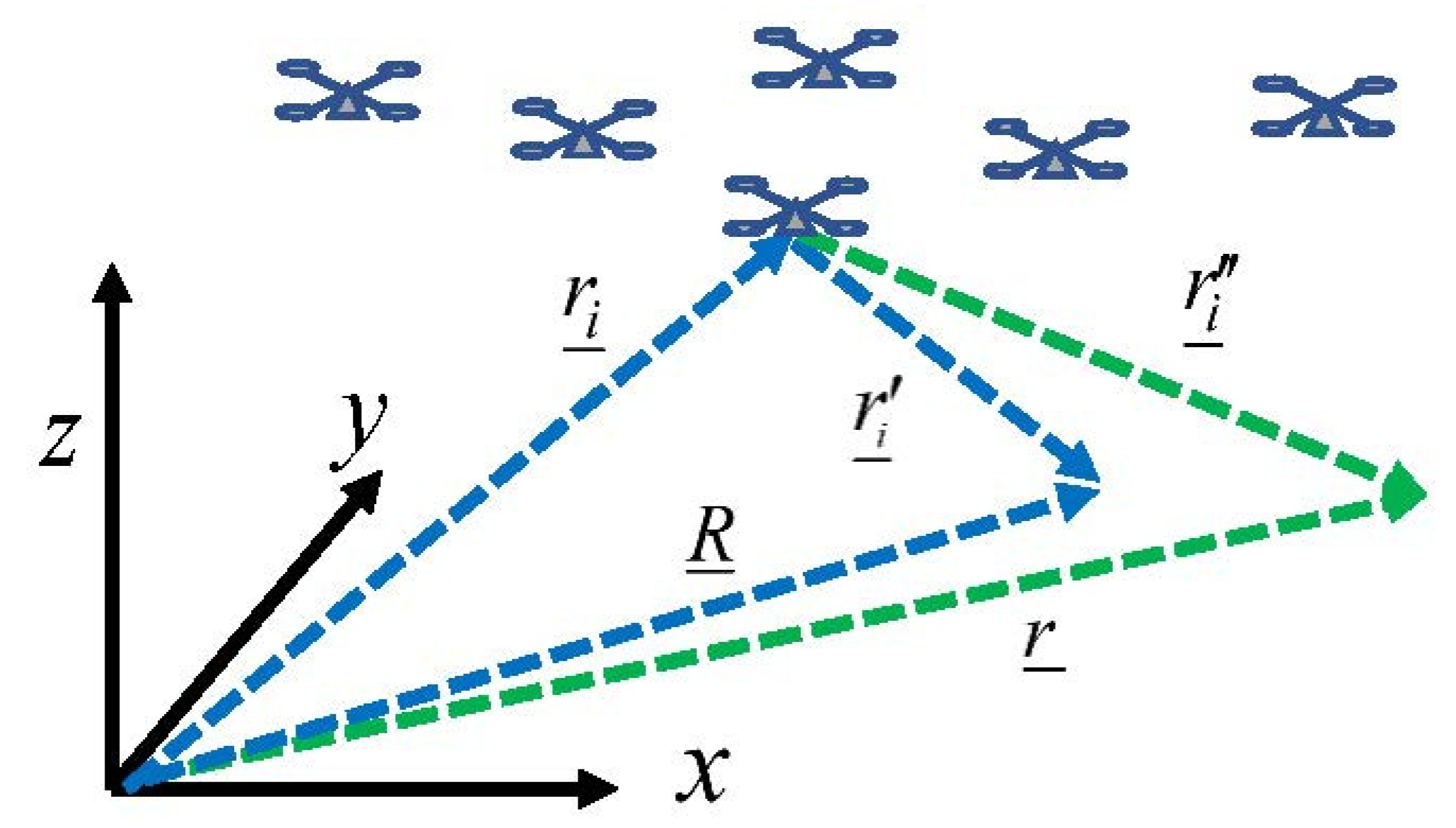

| Symbol | Quantity | Unit | Implemented in Model as |
|---|---|---|---|
| Position of ith drone | m | Input | |
| Vector displacement of steering position from ith drone | m | Calculated | |
| Vector displacement of general position from ith drone | m | Calculated | |
| Steering position | m | Input | |
| General position | m | Input | |
| Electric field | Vm−1 | Calculated | |
| Speed of light | ms−1 | Input | |
| Permeability of free space | Hm−1 | Input | |
| Wavenumber of jth frequency step | m−1 | Calculated | |
| Power fed into the ith antenna element at the jth wavenumber | W | Calculated | |
| Gain of the ith antenna element at the jth wavenumber | - | Calculated | |
| Phase shift applied to the ith antenna element at the jth wavenumber. | Radians | Calculated | |
| Individual antenna side length | m | Input | |
| Angle between ith drone and vertical | Radians | Calculated | |
| Intensity ofjth frequency step | Wm−2 | Calculated | |
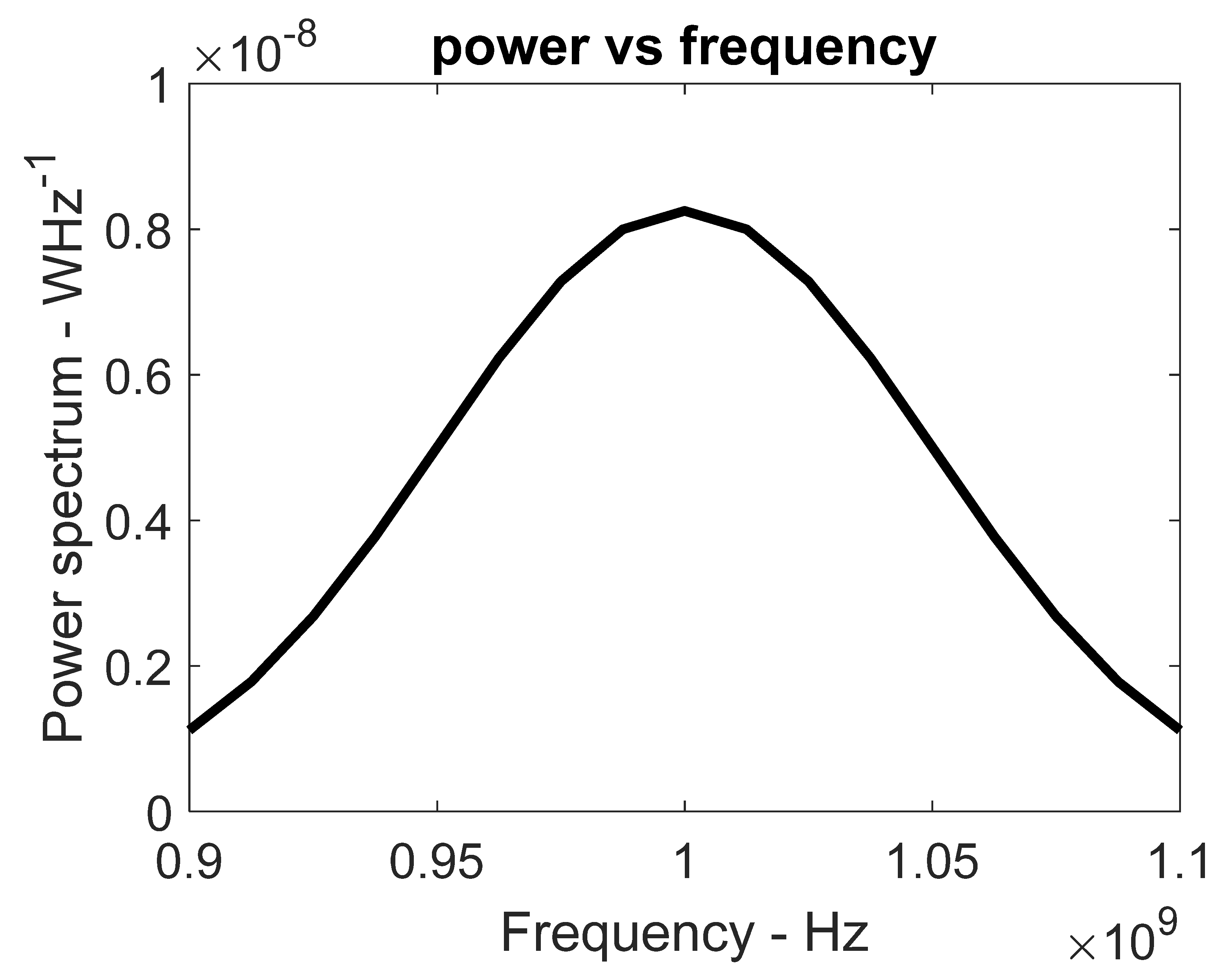
| Frequency of jth frequency step | Hz | Calculated | |
| Centre frequency | Hz | Input | |
| Bandwidth | Hz | Input | |
| Max power per element | W | Input | |
| Mean phase of radiation from ith drone at jth frequency step | Radians | Calculated | |
| Standard deviation of phase at jth frequency step | Radians | Input | |
| Array gain at jth frequency step | - | Calculated | |
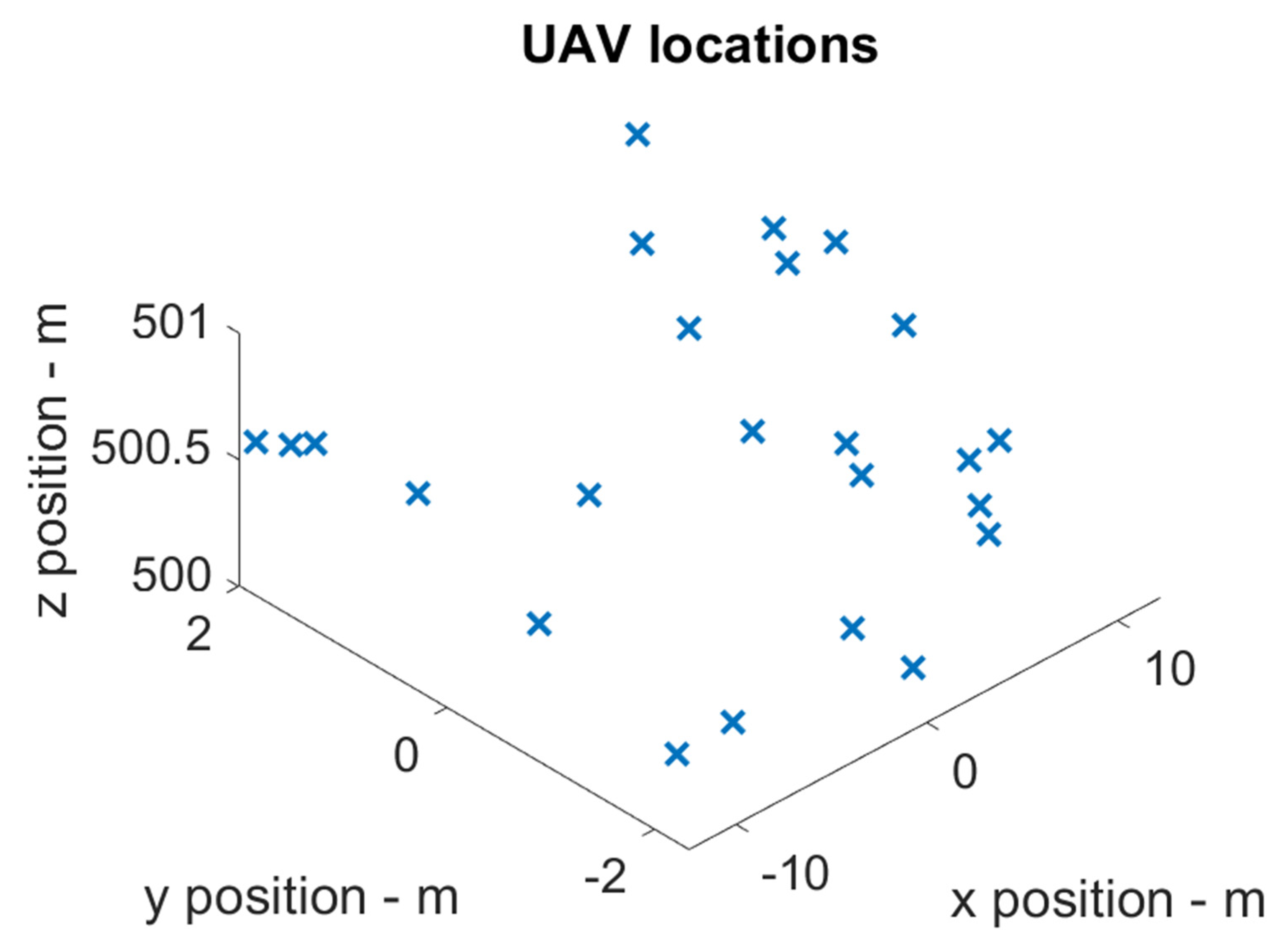
| Standard deviation in position | m | Input | |
| Standard deviation in timing | s | Input |
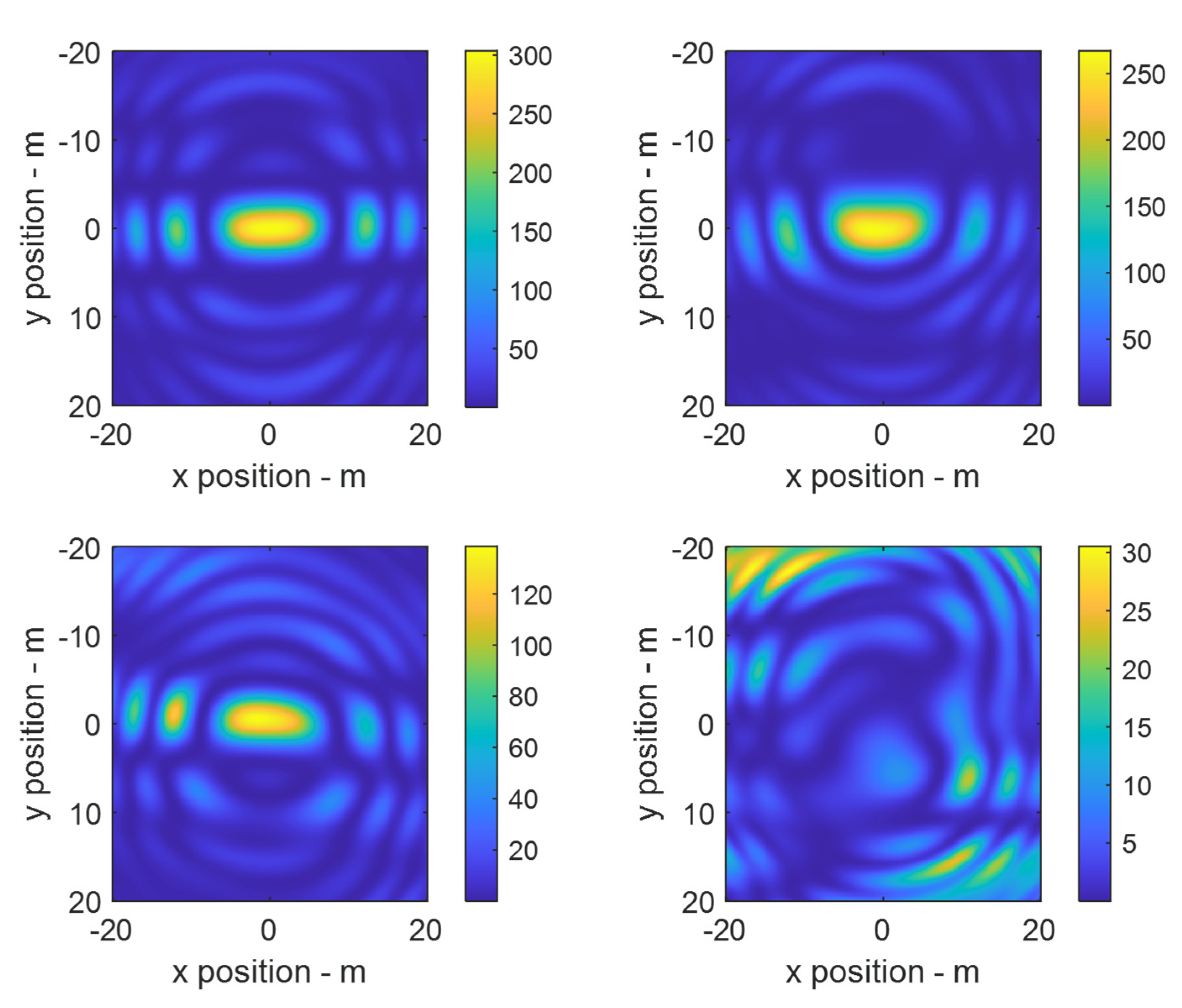
| Number of Drones | Mean Maximum Gain | −3 dB Mean Beam Size at 500 Meters m | Field Region at 500 m | Drone Position Uncertainty m | Distribution |
|---|---|---|---|---|---|
| 24 | 302 | Width 2.34 Length 11.4 | Near | 0 | Cuboid 50 × 5 × 1 m |
| 24 | 112 | Width 2.60 Length 11.8 | Near | 0.05 | Cuboid 50 × 5 × 1 m |
| 24 | 302 | Width 4.91 Length 4.98 | Near | 0 | Cuboid 25 × 25 × 1 m |
| 24 | 109 | Width 4.75 Length 5.06 | Near | 0.05 | Cuboid 25 × 25 × 1 m |
| 24 | 303 | Width 9.79 Length 9.95 | Far | 0 | Cuboid 10 × 10 × 1 m |
| 24 | 109 | Width 9.70 Length 9.56 | Far | 0.05 | Cuboid 10 × 10 × 1 m |
| 24 | 296 | Width 1.23 Length 1.25 | Near | 0 | Cuboid 100 × 100 × 1 m |
| 24 | 105 | Width 1.26 Length 1.27 | Near | 0.05 | Cuboid 100 × 100 × 1 m |
| 24 | 109 | Width 5.30 Length 11.32 | Far | 0.05 | The line y = x, distributed between values −10 < x < 10 and −10 < y < 10 m |
| 24 | 110 | Width 6.42 Length 6.38 | Far | 0.05 | The surface of a spherical cap, with radius of 500 m and with x and y distributed between −10 and 10 m |
| Number of Drones | Mean Maximum Gain dB | −3 dB Mean Beam Size at 500 Meters m | Field Region at 500 m | Drone Position Uncertainty m | Distribution |
|---|---|---|---|---|---|
| 5 | 56 | Length 1.67 Width 1.60 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
| 10 | 105 | Length 1.37 Width 1.42 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
| 25 | 262 | Width 1.28 Length 1.30 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
| 50 | 521 | Width 1.29 Length 1.29 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
| 100 | 1040 | Width 1.29 Length 1.29 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
| 250 | 2580 | Width 1.28 Length 1.28 | Near | 0.02 | Cuboid 100 × 100 × 1 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harmer, S.W.; De Novi, G. Distributed Antenna in Drone Swarms: A Feasibility Study. Drones 2023, 7, 126. https://doi.org/10.3390/drones7020126
Harmer SW, De Novi G. Distributed Antenna in Drone Swarms: A Feasibility Study. Drones. 2023; 7(2):126. https://doi.org/10.3390/drones7020126
Chicago/Turabian StyleHarmer, Stuart William, and Gianluca De Novi. 2023. "Distributed Antenna in Drone Swarms: A Feasibility Study" Drones 7, no. 2: 126. https://doi.org/10.3390/drones7020126
APA StyleHarmer, S. W., & De Novi, G. (2023). Distributed Antenna in Drone Swarms: A Feasibility Study. Drones, 7(2), 126. https://doi.org/10.3390/drones7020126






