Safeguarding UAV Networks against Active Eavesdropping: An Elevation Angle-Distance Trade-Off for Secrecy Enhancement

Abstract

Because of their low expense and ease of rapid deployment, unmanned aerial vehicles (UAVs) are frequently applied in wireless networks. Although the wireless channel is able to broadcast, legitimate communications between UAVs and ground nodes are incredibly susceptible to severe security threats, such as malicious jamming and eavesdropping. Compared with the traditional line-of-sight channel (LC) model, the probabilistic LC (PrLC) model can better describe the practical channel conditions of UAV-to-ground transmission in city areas. Therefore, this paper considers the UAV-enabled networks under the PrLC model in complex city environments. Specifically, when the UAV transmits classified messages to legitimate ground nodes, multiple active eavesdroppers simultaneously eavesdrop on the transmitted confidential information to interfere with the signal and limit the legal transmission. We jointly optimize the communication connection, the three-dimensional (3D) UAV trajectory, and the transmit power of the UAV to increase the average secrecy rate for the worst condition. Because the problem is non-convex, the best solution is formidable to get, this paper designs an iterative algorithm and use the successive convex approximation (SCA) technique to solve it. Compared to other benchmarks, our proposed algorithm, as demonstrated by numerical results, can effectively balance the elevation angle-distance trade-off to improve secrecy rate performance.

1. Introduction

The development of information technology has reached a new peak with the explosive growth of wireless networks. Although the Fifth Generation (5G) mobile communication networks have been gradually commercialized, 5G networks still suffer an enormous communication burden due to the need for ultra-reliable, low-latency communication, and the rising demand for ubiquitous wireless services [1,2]. To tackle such difficulties, industry and academia have prioritized research on Sixth Generation (6G) networks. In typical 6G network application scenarios, such as emergency communication, traffic control, monitoring, search and rescue, the unmanned aerial vehicles (UAVs) can use their flexibility to expand the communication coverage, reduce the path loss of signal transmission, improve communication quality, reduce transmission delay, and so on [3,4,5,6,7,8]. Thus, UAV-enabled communications will play an importance role of assistance in the future 6G networks. However, the line-of-sight channel (LC) link and broadcast characteristics of wireless communications make UAV communications in 6G networks particularly susceptible to serious security threats such as intentional jamming and eavesdropping. Therefore, studying how to solve the security issues of UAV networks has turned into a challenging and thorny problem in industry and academia.

UAVs can provide superiority conditions for legitimate nodes over malignant ground nodes using their adjustable flying trajectories. Several works have studied various UAV-enabled secure communication systems. These studies mainly fall into two categories: one against passive eavesdroppers [9,10,11,12,13,14,15,16,17] and the other against active eavesdroppers [18,19,20,21,22,23]. Especially for the first category, the UAV trajectory, power control, and time allocation can be combined to improve the secrecy rates in UAV networks. However, full-duplex technology has become a viable strategy for improving future communication systems’ spectrum efficiency. Therefore, active eavesdroppers can further threaten the UAV communication systems by employing the full-duplex technology. Specifically, the active eavesdroppers not only wiretap the confidential information between legitimate ground nodes and the UAV, but also transmit jamming signals to the legitimate nodes. As a result, the research of secure UAV-enabled communication when active eavesdroppers are present is particularly important. In [18], the authors investigated the secure UAV communication involving uplink and downlink transmission. The average secrecy rate was improved by jointly optimizing the UAV trajectory, the power allocation of the UAV, and legitimate ground nodes. The literature [19] proposed a secure UAV communication scheme based on artificial noise beamforming, in which the full-duplex relay UAVs send jamming signals to confuse active eavesdropping nodes. The authors designed an algorithm based on reinforcement learning to find the best UAV trajectory and appropriate allocation to ensure secure transmission. The authors in [20] investigated the wireless surveillance problem in UAV relay systems, by optimizing the interference power allocation of the legal monitor, the average effective eavesdropping rate is maximized, and the proposed active eavesdropping method significantly improved the eavesdropping rate. The literature [21] studied the UAV-assisted secure communication system, in which the source communicates with a legitimate UAV while a full-duplex active eavesdropper interferes. In order to minimize the mixed outage probability, the authors jointly designed the power distribution ratio of the transmit signal and the UAV altitude. To decrease the power consumption of the UAV, the literature [22] proposed a UAV secure communication system model based on an energy harvesting scheme. By analyzing the secrecy performance under the full-duplex active eavesdropping, it obtained the optimal coding rate through the derived transmission outage probability expression. The literature [23] discussed the secrecy performance of communication systems in which the UAVs send friendly interference signals to prevent full-duplex active eavesdropping with the help of caching. The authors designed an algorithm based on alternating optimization (AO) and successive convex approximation (SCA) to minimize the sum of intercept probability and maximum outage probability for all users.

Although the above literatures optimize the UAV trajectory air-ground channel modeling design for secure UAV communication with active eavesdropping nodes, most of them adopted the Rician fading channel model or LC. Firstly, there are two practical limits to adopting the LC: (i) The critical impacts of LC and non-LC (NLC) conditions related to air-to-ground transmission in city environments are not fully captured by LC [24]; (ii) Since the elevation between the ground node and the UAV is closely related to the flight path of the UAV, the elevation angle-distance trade-off can not be described accurately [25]. Secondly, in urban or suburban environments where the UAV flies at high elevations and small-scale fading can dominate channel states, the Ricia fading channel model is more applicable [26]. In contrast, the PrLC model completely ponders the probability of LC and NLC conditions. When a UAV performs its mission in city areas, sometimes random buildings may block the communications. In this instance, through the 3D UAV trajectory design, the PrLC model can represent more significant shadowing effects.

Inspired by them, we ponder a UAV downlink secure communication system based on the PrLC model, in which the UAV sends classified messages to the legitimate ground nodes under the environment with multiple active eavesdroppers. By concurrently optimizing the communication connection, the 3D UAV trajectory, and the UAV’s transmit power, this paper intends to improve the worst-case average max-min secrecy rate for avoiding against severe threats from the active eavesdroppers. However, obtaining the optimal solution is difficult because it is a non-convex problem, and its secrecy rate expression is complex. Firstly, we approximate the secrecy rate to solve such a problem efficiently without losing the secrecy performance. Secondly, we divided the original problem into four subproblems based on the block coordinate descent (BCD) technique, i.e., the communication connection, the UAV’s transmit power, horizontal trajectory, and altitude optimization. By introducing the SCA technique and slack variables, the non-convex subproblems are converted into convex ones that can be well addressed. Numerical results prove that our proposed algorithm performs better than other benchmark algorithms in improving secrecy rate performance, which highlights the importance of using 3D trajectories using a more precise PrLC model in city environments.

2. System Model

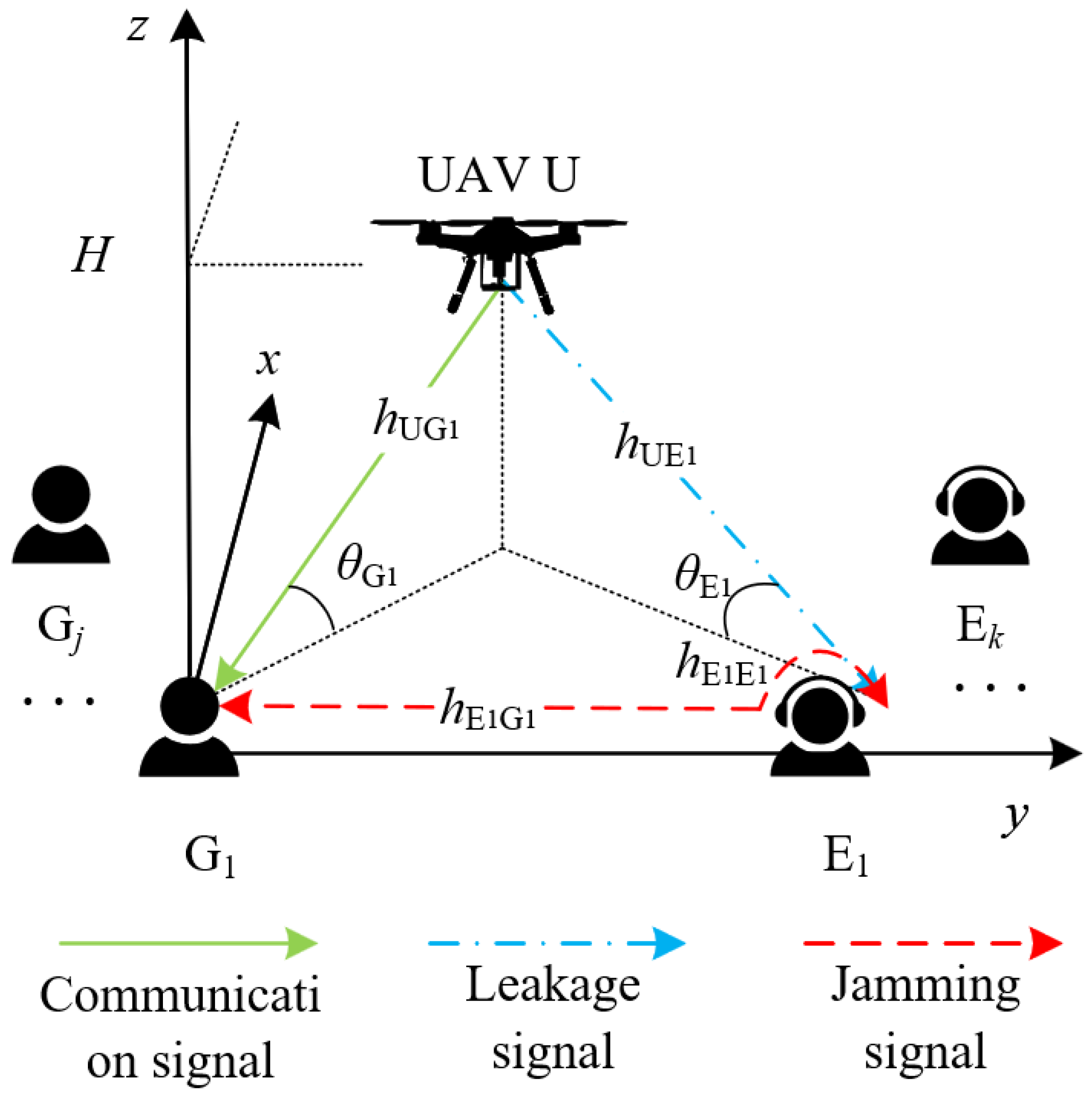
We consider a secure UAV network against active eavesdropping in this paper, as shown in Figure 1. Specifically, a UAV sends classified messages to ground nodes denoted by $({\mathrm{G}}_j,j\in \{1,\dots ,J\})$, while multiple active eavesdroppers denoted by $({\mathrm{E}}_k,k\in \{1,\dots ,K\})$ not only wiretap their transmission but also send jamming signals to interfere with the legitimate receivers.

In this paper, the location of each node is represented by a three-dimensional Cartesian coordinate system, in which the horizontal coordinate of ${\mathrm{G}}_j$ and ${\mathrm{E}}_k$ are represented by ${\mathbf{w}}_{{\mathrm{G}}_j}=(x_{{\mathrm{G}}_j},y_{{\mathrm{G}}_j})$ and ${\mathbf{w}}_{{\mathrm{E}}_k}=(x_{{\mathrm{E}}_k},y_{{\mathrm{E}}_k})$, respectively. In practical applications, the locations of the active eavesdroppers can be accurately determined by using existing technologies, such as the global positioning system (GPS) and optoelectronic devices [27,28,29], so we assume that ${\mathbf{w}}_{{\mathrm{E}}_k}$ is known in advance.

Furthermore, we suppose that the UAV flies horizontally from its original position to its final location, which is represented by $({\mathbf{q}}_I,z_I)=(x_I,y_I,z_I)$ and $({\mathbf{q}}_F,z_F)=(x_F,y_F,z_F)$, respectively, $z_I$ and $z_F$ are the fixed altitude. In order to solve this problem flexibly, we divide the limited flying time T of the UAV into N equal-length time slots, each of which is indicated as ${\delta }_t$. Therefore, when ${\delta }_t$ is sufficiently small, the continuous 3D UAV trajectory is approximated by ${\left\{\left(\mathbf{q}\right[n],z[n\left]\right)\right\}}_{n=0}^N$, $\mathbf{q}\left[n\right]=\left(x\right[n],y[n\left]\right)$ and $z\left[n\right]$ represent the horizontal and vertical coordinates of the UAV at time slot n, respectively.

Let binary variables $s_i\left[n\right]\in \{0,1\}$ for $i\in \left\{{\mathrm{G}}_j,{\mathrm{E}}_k\right\}$ represent the channel condition in time slot n, where $s_i\left[n\right]=0$ is the LC conditions and $s_i\left[n\right]=1$ is NLC condition. This paper adopts the PrLC model [30], for which the UAV-to-${\mathrm{G}}_j$ channel or the UAV-to-${\mathrm{E}}_k$ channel can be described by LC or NLC condition. Thus, in the nth time slot, the LC probability for ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ is given by

$$P_i^{\mathrm{L}}\left[n\right]=\frac{1}{1+{\eta }_{1}exp\left(-{\eta }_2\left({\theta }_i\left[n\right]-{\eta }_1\right)\right)},i\in \left\{{\mathrm{G}}_j,{\mathrm{E}}_k\right\}$$

(1)

where ${\eta }_1>0$ and ${\eta }_2>0$ are constants specified by the actual area, and the elevation angle from the UAV to ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ is denoted as

$${\theta }_i\left[n\right]=\frac{180}{\pi }arctan\left(\frac{z\left[n\right]}{∥\mathbf{q}\left[n\right]-{\mathbf{w}}_i∥}\right)$$

(2)

Then, the NLC probability between the UAV and ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ is denoted as $P_i^{\mathrm{N}}\left[n\right]=1-P_i^{\mathrm{L}}\left[n\right]=\frac{1}{1+\frac{1}{{\eta }_1}exp\left({\eta }_2\left({\theta }_i\left[n\right]-{\eta }_1\right)\right)}$.

Thus, the power gain of the UAV and ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ is denoted as

$$h_{\mathrm{U}i}\left[n\right]=s_i\left[n\right]h_{\mathrm{U}i}^{\mathrm{L}}\left[n\right]+\left(1-s_i\left[n\right]\right)h_{\mathrm{Ui}}^{\mathrm{N}}\left[n\right]$$

(3)

where $h_{\mathrm{U}i}^{\mathrm{L}}\left[n\right]={\rho }_0{d}_{\mathrm{U}i}^{-{\beta }_{\mathrm{L}}}\left[n\right]$ and $h_{\mathrm{U}i}^{\mathrm{N}}\left[n\right]=\alpha {\rho }_0{d}_{\mathrm{U}i}^{-{\beta }_{\mathrm{N}}}\left[n\right]$, ${\beta }_{\mathrm{L}}$ and ${\beta }_{\mathrm{N}}$ are the path loss exponents, $\alpha$ is the signal attenuation factor. Furthermore, the length between the UAV and ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ in nth is expressed as $d_{\mathrm{U}i}\left[n\right]=\sqrt{{∥\mathbf{q}\left[n\right]-{\mathbf{w}}_i∥}^2+{z\left[n\right]}^2}$.

The channel between ${\mathrm{E}}_k$ and ${\mathrm{G}}_j$ is described by the Rayleigh channel, and its power gain is expressed as

$$h_{{\mathrm{E}}_k{\mathrm{G}}_j}={\rho }_0{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }{\zeta }_{{\mathrm{E}}_k{\mathrm{G}}_j}$$

(4)

where $\kappa$ denotes the path loss exponent, $d_{{\mathrm{E}}_k{\mathrm{G}}_j}=∥{\mathbf{w}}_{{\mathrm{E}}_k}-{\mathbf{w}}_{{\mathrm{G}}_j}∥$ is the distance between ${\mathrm{E}}_k$ and ${\mathrm{G}}_j$, and ${\zeta }_{{\mathrm{E}}_k{\mathrm{G}}_j}$ denotes a random variable with a zero-mean and unit-variance circularly symmetric complex Gaussian (CSCG) random variable.

Because of the limitation of airborne energy, the UAV’s transmit power $p_{\mathrm{U}}\left[n\right]$ should be constrained by the average power and peak power, which are described by $\overline{p}$ and $\tilde{p}$, i.e.,

$$\frac{1}{N}\sum _{n=1}^N{p}_{\mathrm{U}}\left[n\right]\le \overline{p},0\le p_{\mathrm{U}}\left[n\right]\le \tilde{p}$$

(5)

Suppose that UAV U serves the ground nodes in Time Division Multiple Access (TDMA) mode. Let ${\lambda }_j\left[n\right]\in \{0,1\}$ denotes the scheduling constraint between the UAV and ${\mathrm{G}}_j$ in the nth, and ${\lambda }_j\left[n\right]=0$ represents that the UAV does not communicate with ${\mathrm{G}}_j$; or else ${\lambda }_j\left[n\right]=1$. Therefore, the average achievable secrecy rate in bps/Hz of ${\mathrm{G}}_j$ over N time slots can be denoted as [31,32]

$$R_j^{\sec }=\frac{1}{N}\sum _{n=1}^N\left({\lambda }_j\left[n\right]{\left[R_{{\mathrm{G}}_j}\left[n\right]-\underset{k\in K}{max}{R}_{{\mathrm{E}}_k}\left[n\right]\right]}^{+}\right)$$

(6)

where, ${\left[A\right]}^{+}=max(A,0)$,

$$R_{{\mathrm{G}}_j}\left[n\right]=\mathbb{E}\left[{log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{{\mathrm{UG}}_j}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{h}_{{\mathrm{E}}_k{\mathrm{G}}_j}+{\sigma }^2}\right)\right]$$

(7)

$$R_{{\mathrm{E}}_k}\left[n\right]={log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{\mathrm{U}{\mathrm{E}}_k}\left[n\right]}{p_{{\mathrm{E}}_k}{h}_{{\mathrm{E}}_k{\mathrm{E}}_k}+{\sigma }^2}\right)$$

(8)

where $\mathbb{E}\left[x\right]$ is the expectation operator about ${\zeta }_{{\mathrm{E}}_k{\mathrm{G}}_j}$, $p_{{\mathrm{E}}_k}$ represents the maximum jamming power of ${\mathrm{E}}_k$, and $h_{{\mathrm{E}}_{\mathrm{k}}{\mathrm{E}}_{\mathrm{k}}}$ is the self-interference between ${\mathrm{E}}_k$’s receiving antenna and its transmitting antenna. Since we assume that the distance between the eavesdroppers is great, only the self-interference of the eavesdroppers exists, without the interference from other eavesdroppers, which thus can be ignored.

We notice that $R_{{\mathrm{G}}_j}\left[n\right]$ is convex with respect to (w.r.t.) ${\zeta }_{{\mathrm{E}}_k{\mathrm{G}}_j}$ in $h_{{\mathrm{E}}_k{\mathrm{G}}_j}$. Therefore, based on Jensen’s inequality, the lower bound of $R_{{\mathrm{G}}_j}\left[n\right]$ is expressed as

$$\begin{array}{cc}\hfill R_{{\mathrm{G}}_j}\left[n\right]& =\mathbb{E}\left[{log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{{\mathrm{UG}}_j}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{h}_{{\mathrm{E}}_k{\mathrm{G}}_j}+{\sigma }^2}\right)\right]\hfill \\ & \ge {log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{{\mathrm{UG}}_j}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{\rho }_0{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }\mathbb{E}\left[{\zeta }_{{\mathrm{E}}_k{\mathrm{G}}_j}\right]+{\sigma }^2}\right)\hfill \\ & ={log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{{\mathrm{UG}}_j}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{\rho }_0{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }+{\sigma }^2}\right)\hfill \end{array}$$

(9)

Since this paper considers the worst-case secrecy rate performance, we assume that during the UAV’s mission, the active eavesdropping node ${\mathrm{E}}_k$ transmits with its maximum power while being able to eliminate its self-interference $h_{{\mathrm{E}}_k{\mathrm{E}}_k}$ completely. Therefore, $R_{{\mathrm{E}}_k}\left[n\right]$ can be upper-bounded by

$$\begin{array}{cc}\hfill R_{{\mathrm{E}}_k}\left[n\right]& ={log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{\mathrm{U}{\mathrm{E}}_k}\left[n\right]}{p_{{\mathrm{E}}_k}{h}_{{\mathrm{E}}_k{\mathrm{E}}_k}+{\sigma }^2}\right)\hfill \\ & \le {log}_2\left(1+\frac{p_{\mathrm{U}}\left[n\right]h_{\mathrm{U}{\mathrm{E}}_k}\left[n\right]}{{\sigma }^2}\right)\hfill \end{array}$$

(10)

Therefore, according to [24], using the total probability theorem, the expected achievable rate of ${\mathrm{G}}_j$ or ${\mathrm{E}}_k$ at slot n is denoted as

$$\mathbb{E}\left[R_i\left[n\right]\right]=P_i^{\mathrm{L}}\left[n\right]R_i^{\mathrm{L}}\left[n\right]+P_i^{\mathrm{N}}\left[n\right]R_i^{\mathrm{N}}\left[n\right],i\in \left\{{\mathrm{G}}_j,{\mathrm{E}}_k\right\}$$

(11)

where $R_{{\mathrm{G}}_j}^{\mathrm{L}}\left[n\right]={log}_2\left(1+\frac{{\rho }_0{p}_{\mathrm{U}}\left[n\right]d_{{\mathrm{UG}}_j}^{-{\beta }_{\mathrm{L}}}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{\rho }_0{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }+{\sigma }^2}\right)$ and $R_{{\mathrm{G}}_j}^{\mathrm{N}}\left[n\right]={log}_2\left(1+\frac{\alpha {\rho }_0{p}_{\mathrm{U}}\left[n\right]d_{{\mathrm{UG}}_j}^{-{\beta }_{\mathrm{N}}}\left[n\right]}{{\sum }_{k=1}^K{p}_{{\mathrm{E}}_k}{\rho }_0{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }+{\sigma }^2}\right)$ denote the reachable rates conditioned on the LC and NLC conditions from the UAV to ${\mathrm{G}}_j$, respectively.

Furthermore, $R_{{\mathrm{E}}_k}^{\mathrm{L}}\left[n\right]={log}_2\left(1+\frac{{\rho }_0{p}_{\mathrm{U}}\left[n\right]d_{\mathrm{U}{\mathrm{E}}_k}^{-{\beta }_{\mathrm{N}}}\left[n\right]}{{\sigma }^2}\right)$ and $R_{{\mathrm{E}}_k}^{\mathrm{N}}\left[n\right]={log}_2\left(1+\frac{\alpha {\rho }_0{p}_{\mathrm{U}}\left[n\right]d_{\mathrm{U}{\mathrm{E}}_k}^{-{\beta }_{\mathrm{N}}}\left[n\right]}{{\sigma }^2}\right)$ indicate the reachable rate of UAV to ${\mathrm{E}}_k$ under the LC and NLC conditions.

For ease of solution, we approximate the anticipated rate in (11) as

$$\mathbb{E}\left[R_i\left[n\right]\right]\approx P_i^{\mathrm{L}}\left[n\right]R_i^{\mathrm{L}}\left[n\right]\triangleq {\overline{R}}_i\left[n\right],i\in \left\{{\mathrm{G}}_j,{\mathrm{E}}_k\right\}$$

(12)

To demonstrate the accuracy of the approximate result ${\overline{R}}_i\left[n\right]$ in (12), we suppose that the UAV remains level during the flight from $\mathrm{G}$ to $\mathrm{E}$, where $\mathrm{G}$ locates at ${\mathbf{w}}_{\mathrm{G}}=\left(0,0\right)$ m and $\mathrm{E}$’s horizontal coordinate is ${\mathbf{w}}_{\mathrm{E}}=\left(150,0\right)$ m. Furthermore, the simulation parameters set as $z=100$ m, $\alpha =-20$ dB, ${\beta }_{\mathrm{L}}=2.2$, ${\beta }_{\mathrm{N}}=3.2$, $p_U=0.1$ W, $p_{{\mathrm{E}}_k}=0.1$ W, ${\eta }_1=11.95$, ${\eta }_2=0.14$, $\kappa =3$, ${\sigma }^2=-110$ dBm and ${\rho }_0=-60$ dB. As shown in Figure 2, we provide an illustrative result, the values of the NLC terms $P_{\mathrm{G}}^{\mathrm{N}}\left[n\right]R_{\mathrm{G}}^{\mathrm{N}}\left[n\right]$ and $P_{\mathrm{E}}^{\mathrm{N}}\left[n\right]R_{\mathrm{E}}^{\mathrm{N}}\left[n\right]$ in the $\mathbb{E}\left[R_i\left[n\right]\right]$ expression in (11) are both close to zero. Therefore, the rate expression can be calculated without affecting the accuracy of the rate expression.

3. Problem Formulation

Let $\mathbf{A}\triangleq \left\{{\lambda }_j\left[n\right]\right\}$, $\mathbf{P}\triangleq \left\{p_{\mathrm{U}}\left[n\right]\right\}$, $\mathbf{Q}\triangleq \left\{\mathbf{q}\left[n\right]\right\}$ and $\mathbf{Z}\triangleq \left\{z\left[n\right]\right\}$ express the communication connection, the UAV’s transmit power, horizontal trajectory and altitude, respectively, where $j\in \{1,\cdots ,J\}$, $n\in \mathcal{N},\mathcal{N}\triangleq \{1,\dots ,N\}$. By jointly designing $\mathbf{A}$, $\mathbf{P}$, $\mathbf{Q}$ and $\mathbf{Z}$, we aim to maximize the average secrecy rate. Thus, the optimization problem is generally expressed as follows

$$\begin{array}{cc}\hfill \underset{\mathbf{A},\mathbf{P},\mathbf{Q},\mathbf{Z},\chi }{max}& \chi \hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \frac{1}{N}\sum _{n=1}^N\left({\lambda }_j\left[n\right]\left({\overline{R}}_{{\mathrm{G}}_j}\left[n\right]-{\overline{R}}_{\mathrm{E}}\left[n\right]\right)\right)\ge \chi \hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\parallel \mathbf{q}[n+1]-\mathbf{q}\left[n\right]\parallel }^2\le D_{xy}^2,n=0,\cdots ,N-1\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & (\mathbf{q}\left[0\right],z\left[0\right])=\left({\mathbf{q}}_I,z_I\right),(\mathbf{q}\left[N\right],z\left[N\right])=\left({\mathbf{q}}_F,z_F\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {(z[n+1]-z\left[n\right])}^2\le D_z^2,n=0,\cdots ,N-1\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & H_{min}\le z\left[n\right]\le H_{max},\forall n\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\lambda }_j\left[n\right]\in \{0,1\},\forall j,n\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \sum _{j=1}^J{\lambda }_j\left[n\right]\le 1\hfill \\ & \left(5\right)\hfill \end{array}$$

(20)

where we let ${max}_{k\in K}{\overline{R}}_{{\mathrm{E}}_k}\left[n\right]\triangleq {\overline{R}}_{\mathrm{E}}\left[n\right]$, ${\overline{R}}_{\mathrm{E}}\left[n\right]$ represents the maximum achievable rate of the eavesdroppers at the nth time slot. Among them, (15)–(18) are the movement constraints of the UAV. $V_{xy}^{max}$ and $V_z^{max}$ represent the maximum horizontal and vertical flight speeds in meters per second (m/s). $H_{min}$ and $H_{max}$ are the minimum and maximum altitudes that the UAV can reach. Thus, in each time slot n, the farthest horizontal and vertical distance that the UAV flies can be denoted as $D_{xy}=V_{xy}^{max}{\delta }_t$ and $D_z=V_z^{max}{\delta }_t$, respectively.

Since the secrecy rate in practice will not be negative, by allocating $p_{\mathrm{U}}\left[n\right]=0$, the best result of (6) can be at least zero. Thus, we can drop the operation ${\left[A\right]}^{+}$. However, problem (13) remains intractable for the following three main reasons: (1) The interference and wiretapping caused by the multiple active eavesdroppers; (2) The probability in (12) is higly related to the UAV’s 3D trajectory; (3) It is challenging to settle the mixed-integer optimization problem caused by binary variable constraints (19) and (20).

Thus, this paper design an efficient iterative algorithm to settle (13) alternately in the next section.

4. Optimization Algorithm Design

With the BCD and SCA techniques, this paper design an efficient algorithm to solve problem (13). Specifically, this paper divide (13) into four sub-problems, and iteratively optimize the variables of the communication connection $\mathbf{A}$, the UAV’s transmit power $\mathbf{P}$, its horizontal trajectory $\mathbf{Q}$, and the altitude $\mathbf{Z}$ of the UAV until it converges.

4.1. Communication Scheduling Optimization

Problem (13) can be expressed as follows by giving any appropriate $\mathbf{P}$, $\mathbf{Q}$ and $\mathbf{Z}$

$$\begin{array}{ccc}\hfill \underset{\mathbf{A},\chi }{max}& \chi \hfill & \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& 0\le {\lambda }_j\left[n\right]\le 1\hfill & \\ & \left(14\right),\left(20\right)\hfill & \hfill \end{array}$$

(22)

Since (21) has been transformed into a convex problem, it is settled by using the CVX toolbox [33].

4.2. Optimization of the UAV’s Transmit Power

By giving any appropriate $\mathbf{A}$, $\mathbf{Q}$ and $\mathbf{Z}$, problem (13) can be denoted as follows

$$\begin{array}{ccc}\hfill \underset{\mathbf{P},\chi }{max}& \chi \hfill & \\ \hfill \mathrm{s}.\mathrm{t}.& \left(5\right),\left(14\right)\hfill & \hfill \end{array}$$

(23)

We set $a\left[n\right]=\frac{{\gamma }_0{d}_{{\mathrm{UG}}_j}^{-{\beta }_{\mathrm{L}}}\left[n\right]}{{\sum }_{k=1}^K{\gamma }_0{p}_{{\mathrm{E}}_k}{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }+1}$, $b\left[n\right]={\gamma }_0{d}_{\mathrm{U}\mathrm{E}}^{-{\beta }_{\mathrm{L}}}\left[n\right]$ to deal with the non-convex constraint (14), where $\gamma =\frac{{\rho }_0}{{\delta }^2}$. Therefore, problem (23) can be definited as

$$\begin{array}{ccc}\hfill \underset{\mathbf{P},\chi }{max}& \chi \hfill & \end{array}$$

(24)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& \frac{1}{N}\sum _{n=1}^N\left[{\lambda }_j\left[n\right]\left(P_{{\mathrm{G}}_j}^{\mathrm{L}}\left[n\right]{log}_2\left(1+a\left[n\right]p_{\mathrm{U}}\left[n\right]\right)-P_{\mathrm{E}}^{\mathrm{L}}\left[n\right]{log}_2\left(1+b\left[n\right]p_{\mathrm{U}}\left[n\right]\right)\right)\right]\ge \chi \hfill & \\ & \left(5\right)\hfill & \hfill \end{array}$$

(25)

Because of the non-convex constraint (25), (24) is still non-convex. However, it is observed that ${log}_2\left(1+b\left[n\right]p_{\mathrm{U}}\left[n\right]\right)$ in (25) is concave w.r.t. $p_{\mathrm{U}}\left[n\right]$, so the first-order Taylor expansion can be used for the local point ${\mathbf{P}}^f\triangleq \left\{p^f\left[n\right]],n\in \mathcal{N}\right\}$ in the fth iteration to obtain its upper bound, i.e.,

$${log}_2\left(1+b\left[n\right]p_{\mathrm{U}}\left[n\right]\right)\le A^f\left[n\right]$$

(26)

where $A^f\left[n\right]={log}_2\left(1+b\left[n\right]p_{\mathrm{U}}^f\left[n\right]\right)+\frac{b\left[n\right]\left(p_{\mathrm{U}}\left[n\right]-p_{\mathrm{U}}^f\left[n\right]\right)}{ln2\left(1+b\left[n\right]p_{\mathrm{U}}^f\left[n\right]\right)}$.

Using (26) to replace (25), problem (24) can be reconstructed as

$$\begin{array}{ccc}\hfill \underset{\mathbf{P},\chi }{max}& \chi \hfill & \end{array}$$

(27)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& \frac{1}{N}\sum _{n=1}^N\left[{\lambda }_j\left[n\right]\left(P_{{\mathrm{G}}_j}^{\mathrm{L}}\left[n\right]{log}_2\left(1+a\left[n\right]p_{\mathrm{U}}\left[n\right]\right)-P_{\mathrm{E}}^{\mathrm{L}}\left[n\right]A^f\left[n\right]\right)\right]\ge \chi \hfill & \\ & \left(5\right)\hfill & \hfill \end{array}$$

(28)

which has been converted into a convex optimization problem that can be successfully settled by applying the interior point method [34].

4.3. Optimization of the UAV’s Horizontal Trajectory

By giving any appropriate $\mathbf{A}$, $\mathbf{P}$, $\mathbf{Z}$, problem (13) can be denoted as follows

$$\begin{array}{ccc}\hfill \underset{\mathbf{Q},\chi }{max}& \chi \hfill & \\ \hfill \mathrm{s}.\mathrm{t}.& \left(14\right),\left(15\right),\left(16\right)\hfill & \hfill \end{array}$$

(29)

By using slack variables ${\mathbf{u}}_j\triangleq \left\{u_j\left[n\right]\right\}$, ${\mathbf{l}}_j\triangleq \left\{l_j\left[n\right]\right\}$, $\mathbf{t}\triangleq \left\{t\left[n\right]\right\}$ and $\mathbf{m}\triangleq \left\{m\left[n\right]\right\}$, where $n\in \mathcal{N}$, problem (29) can be reconstructed as

$$\begin{array}{ccc}\hfill \underset{\mathbf{Q},{\mathbf{u}}_j,{\mathbf{l}}_j,\mathbf{t},\mathbf{m},\mathbf{\tau },\mathbf{\theta },\chi }{max}& \chi \hfill & \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& \frac{1}{N}\sum _{n=1}^N\left[{\lambda }_j\left[n\right]\left(\frac{1}{u_j\left[n\right]}{log}_2\left(1+\frac{c\left[n\right]}{l_j^{{\beta }_L/2}\left[n\right]}\right)-\tau \left[n\right]\right)\right]\ge \chi \hfill & \end{array}$$

(31)

$$\begin{array}{ccc}\hfill & \tau \left[n\right]\ge \frac{1}{t\left[n\right]}{log}_2\left(1+\frac{d\left[n\right]}{m^{{\beta }_L/2}\left[n\right]}\right)\hfill & \end{array}$$

(32)

$$\begin{array}{ccc}\hfill & u_j\left[n\right]\ge 1+{\eta }_{1}exp\left[-{\eta }_2\left({\theta }_{{\mathrm{G}}_j}\left[n\right]-{\eta }_1\right)\right]\hfill & \end{array}$$

(33)

$$\begin{array}{ccc}\hfill & l_j\left[n\right]\ge {∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥}^2+z^2\left[n\right]\hfill & \end{array}$$

(34)

$$\begin{array}{ccc}\hfill & t\left[n\right]\le 1+{\eta }_{1}exp\left[-{\eta }_2\left({\theta }_{\mathrm{E}}\left[n\right]-{\eta }_1\right)\right]\hfill & \end{array}$$

(35)

$$\begin{array}{ccc}\hfill & m\left[n\right]\ge {∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{\mathrm{E}}∥}^2+z^2\left[n\right]\hfill & \end{array}$$

(36)

$$\begin{array}{ccc}\hfill & {\theta }_{{\mathrm{G}}_j}\left[n\right]\le \frac{180}{\pi }arctan\left(\frac{z\left[n\right]}{∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥}\right)\hfill & \end{array}$$

(37)

$$\begin{array}{ccc}\hfill & {\theta }_{\mathrm{E}}\left[n\right]\ge \frac{180}{\pi }arctan\left(\frac{z\left[n\right]}{∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{\mathrm{E}}∥}\right)\hfill & \\ & \left(15\right),\left(16\right)\hfill & \hfill \end{array}$$

(38)

where $c\left[n\right]=\frac{{\gamma }_0{p}_{\mathrm{U}}\left[n\right]}{{\sum }_{k=1}^K{\gamma }_0{p}_{{\mathrm{E}}_k}{d}_{{\mathrm{E}}_k{\mathrm{G}}_j}^{-\kappa }+1}$ and $d\left[n\right]={\gamma }_0{p}_{\mathrm{U}}\left[n\right]$. Furthermore, $\mathbf{\tau }\triangleq \left\{\tau \left[n\right]\right\}$ and $\theta \triangleq \left\{{\theta }_{{\mathrm{G}}_j}\left[n\right],{\theta }_{\mathrm{E}}\left[n\right]\right\}$ are slack variables, where $n\in \mathcal{N}$.

Due to non-convex constraints (31), (32), (35)–(37), it is difficult to find the best result of problem (30).

Though the constraint (31) is non-convex, $\frac{1}{u_j\left[n\right]}{log}_2\left(1+\frac{c\left[n\right]}{l_j^{{\beta }_{\mathrm{L}}/2}\left[n\right]}\right)$ is jointly convex w.r.t. both $u_j\left[n\right]$ and $l_j\left[n\right]$. Therefore, in the fth iteration, the first-order Taylor expansion for the given local points ${\mathbf{u}}_j^f=\left\{u_j^f\left[n\right]\right\}$ and ${\mathbf{l}}_j^f=\left\{l_j^f\left[n\right]\right\}$, where $n\in \mathcal{N}$, can be expressed as

$$\begin{array}{cc}\hfill \frac{1}{u_j\left[n\right]}{log}_2\left(1+\frac{c\left[n\right]}{l_j^{{\beta }_{\mathrm{L}}/2}\left[n\right]}\right)& \ge \frac{1}{u_j^f\left[n\right]}{log}_2\left(1+\frac{c\left[n\right]}{{\left(l_j^f\right)}^{{\beta }_{\mathrm{L}}/2}\left[n\right]}\right)\hfill \\ \hfill & -B_j^f\left[n\right]-C_j^f\left[n\right]\hfill \\ \hfill & \triangleq R_j^{\mathrm{tb}}\left[n\right]\hfill \end{array}$$

(39)

where

$B_j^f\left[n\right]=\frac{1}{{\left(u_j^f\left[n\right]\right)}^2}{log}_2\left(1+\frac{c\left[n\right]}{{\left(u_j^f\right)}^{{\beta }_L/2}\left[n\right]}\right)\left(u_j\left[n\right]-u_j^l\left[n\right]\right)$,

$C_j^f\left[n\right]=\frac{c\left[n\right]{\beta }_L}{2ln2u_j^f\left[n\right]\left(c\left[n\right]+{\left(l_j^f\right)}^{{\beta }_L/2}\left[n\right]\right)l_j^f\left[n\right]}\left(l_j\left[n\right]-l_j^f\left[n\right]\right)$.

For the non-convex constraint (32), we take the logarithm to decouple the optimization variables. Then, by giving slack variables $\upsilon \triangleq \left\{\upsilon \left[n\right]\right\}$ and $\omega \triangleq \left\{\omega \left[n\right]\right\}$, where $n\in \mathcal{N}$, we can get

$$ln\tau \left[n\right]\ge ln\upsilon \left[n\right]-lnt\left[n\right]$$

(40)

$$\upsilon \left[n\right]\ge {log}_2\left(1+exp\omega \left[n\right]\right)$$

(41)

$$m^{{\beta }_L/2}\left[n\right]\ge \frac{d\left[n\right]}{exp\omega \left[n\right]}$$

(42)

Although the constraints (35)–(37), (40) and (42) are non-convex, we can observe that $exp\left(-{\eta }_2{\theta }_{\mathrm{E}}\left[n\right]\right))$ in (35) is convex w.r.t. ${\theta }_{\mathrm{E}}\left[n\right]$, ${∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{\mathrm{E}}∥}^2$ in (36) is convex w.r.t. $\mathbf{q}\left[n\right]$, and the right-hand side of (37) is convex w.r.t. $∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥$, $ln\upsilon \left[n\right]$ in (40) is concave w.r.t. $\upsilon \left[n\right]$, and the left-hand side of (42) is convex w.r.t. $m\left[n\right]$. Therefore, the first-order Taylor formula can be expanded at local points ${\theta }_{\mathrm{E}}^f=\left\{{\theta }_{\mathrm{E}}^f\left[n\right]\right\}$, ${\upsilon }^f=\left\{{\upsilon }^f\left[n\right]\right\}$, ${\mathbf{m}}^f=\left\{m^f\left[n\right]\right\}$ and ${\mathbf{Q}}^f=\left\{{\mathbf{q}}^f\left[n\right]\right\}$ in the fth iteration, where $n\in \mathcal{N}$, i.e.,

$$t\left[n\right]\le 1+{\eta }_{1}exp\left({\eta }_1{\eta }_2\right)D^f\left[n\right]$$

(43)

$$m\left[n\right]\le z^2\left[n\right]+{∥{\mathbf{q}}^f\left[n\right]-{\mathbf{w}}_{\mathrm{E}}∥}^2+2{\left({\mathbf{q}}^f\left[n\right]-{\mathbf{w}}_{\mathrm{E}}\right)}^T\left(\mathbf{q}\left[n\right]-{\mathbf{q}}^f\left[n\right]\right)$$

(44)

$${\theta }_{{\mathrm{G}}_j}\left[n\right]\le \frac{180}{\pi }\left(E_j^f\left[n\right]-F_j^f\left[n\right]\left(∥\mathbf{q}\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥-∥{\mathbf{q}}^f\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥\right)\right)$$

(45)

$$ln\tau \left[n\right]\ge ln{\upsilon }^f+\frac{1}{{\upsilon }^f\left[n\right]}\left(\upsilon \left[n\right]-{\upsilon }^f\left[n\right]\right)-lnt\left[n\right]$$

(46)

$${\left(m^f\left[n\right]\right)}^{{\beta }_{\mathrm{L}}/2}+\frac{{\beta }_{\mathrm{L}}}{2}{\left(m^f\left[n\right]\right)}^{{\beta }_{\mathrm{L}}/2-1}\left(m\left[n\right]-m^f\left[n\right]\right)\ge \frac{d\left[n\right]}{exp\left(\omega \right[n\left]\right)}$$

(47)

where

$D^f\left[n\right]=exp(-{\eta }_2{\theta }_{\mathrm{E}}^f\left[n\right])-{\eta }_{2}exp(-{\eta }_2{\theta }_{\mathrm{E}}^f\left[n\right])({\theta }_{\mathrm{E}}\left[n\right]-{\theta }_{\mathrm{E}}^f\left[n\right])$,

$E_j^f\left[n\right]=arctan\left(\frac{z\left[n\right]}{∥{\mathbf{q}}^f\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥}\right)$, $F_j^f\left[n\right]=\frac{z\left[n\right]}{{∥{\mathbf{q}}^f\left[n\right]-{\mathbf{w}}_{{\mathrm{G}}_j}∥}^2+z^2\left[n\right]}$.

With (39), (41), and (43)–(47), problem (30) can be transformed into the convex optimization formula as follows

$$\begin{array}{ccc}\hfill \underset{\mathbf{Q},{\mathbf{l}}_j,{\mathbf{u}}_j,\mathbf{t},\mathbf{m},\mathbf{\theta },\mathbf{\tau },\mathbf{\upsilon },\mathbf{\omega },\chi }{max}& \chi \hfill & \end{array}$$

(48)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& \frac{1}{N}\sum _{n=1}^N\left[{\lambda }_j\left[n\right]\left(R_j^{lb}\left[n\right]-\tau \left[n\right]\right)\right]\ge \chi \hfill & \\ & \left(15\right),\left(16\right),\left(33\right),\left(34\right),\left(38\right),\left(41\right),\left(43\right)–\left(47\right)\hfill & \hfill \end{array}$$

(49)

By applying the interior point method, the above problems can be easily worked out. Therefore, the solution $\mathbf{Q}$ obtained from this sub-problem as a given variable in the sub-problem of vertical trajectory optimization for UAV in the next subsection.

4.4. Optimization of the UAV’s Vertical Trajectory

Problem (13) can be denoted as follows by giving any appropriate $\mathbf{A}$, $\mathbf{P}$ and $\mathbf{Q}$

$$\begin{array}{ccc}\hfill \underset{\mathbf{Z},\chi }{max}& \chi \hfill & \\ \hfill \mathrm{s}.\mathrm{t}.& \left(14\right),\left(17\right),\left(18\right)\hfill & \hfill \end{array}$$

(50)

For the optimization variable $\mathbf{Z}$, following the procedure for solving problem (29), problem (50) can be solved similarly. The same convex constraints (33), (34), (37), (41), (43), (46), (47), and (49) can be obtained by introducing similar slack variables and approximating them using the SCA technique. Furthermore, since the right-hand sides of the non-convex conditions (36) and (38) are convex and concave w.r.t optimization variable $\mathbf{Z}$, respectively, they can also be converted to convex constraints by using SCA techniques. Together with (17) and (18), problem (50) can be reformulated into a convex optimization problem.

In conclusion, by resolving four sub-problems (21), (27), (48) and (50) until the algorithm converges to a prespecified accuracy $ϵ$, the suboptimal solution to (13) can be found. Algorithm 1 summarizes the process of obtaining the sub-optimal solution.

Algorithm 1 Algorithm to solve problem (13)

1: Initialize variable ${\mathbf{A}}^0$, ${\mathbf{P}}^0$, ${\mathbf{Q}}^0$, ${\mathbf{Z}}^0$, let the number of iterations; 2: repeat: 3:     Given ${\mathbf{P}}^f$, ${\mathbf{Q}}^f$, ${\mathbf{Z}}^f$, solve the problem (21), get ${\mathbf{A}}^{f+1}$ as the optimal solution; 4:     Given ${\mathbf{A}}^{f+1}$, ${\mathbf{Q}}^f$, ${\mathbf{Z}}^f$, solve the problem (27), get ${\mathbf{P}}^{f+1}$ as the optimal solution; 5:     Given ${\mathbf{A}}^{f+1}$, ${\mathbf{P}}^{f+1}$, ${\mathbf{Z}}^f$, solve the problem (48), get ${\mathbf{Q}}^{f+1}$ as the optimal solution; 6:     Given ${\mathbf{A}}^{f+1}$, ${\mathbf{P}}^{f+1}$, ${\mathbf{Q}}^{f+1}$, solve the problem (50), get ${\mathbf{Z}}^{f+1}$ as the optimal solution; 7:     number of update iterations $f=f+1$; 8: until: convergence to a given accuracy $ϵ$.

5. Numerical Results

In this part, three benchmark strategies are analyzed and compared to verify our proposed algorithm’s effectiveness under the PrLC model represented by TP-PrLC:

• 3D UAV trajectory design without power control based on the PrLC model (represented as TNP-PrLC);
• A joint majorization strategy of UAV horizontal trajectory and power control based on the PrLC model, in which the UAV altitude is fixed as the lowest altitude (represented as HTP-PrLC);
• A joint development strategy of UAV 3D trajectory and communication resources based on the LC model (represented as TP-LC).

Specifically, in the TNP-PrLC strategy, the UAV’s transmit power is fixed to be its average power rate, i.e., $p_{\mathrm{U}}\left[n\right]=\overline{p}$. The solutions to the communication connection and 3D UAV trajectory are obtained by solving problems (21), (48), (50) alternatively. While in the HTP-PrLC strategy, the UAV altitude is fixed to the minimum height, i.e., $z=50$ m. By solving problems (21), (27) and (48) alternately in an iterative manner, we can obtain the optimized communication connection and horizontal trajectory of the UAV.

Table 1. Simulation parameters.

Parameters	Definitions	Values
${\mathbf{w}}_{\mathrm{G}}$, ${\mathbf{w}}_{{\mathrm{G}}_1}$, ${\mathbf{w}}_{{\mathrm{G}}_2}$	The horizontal coordinates of $\mathrm{G}$, ${\mathrm{G}}_1$, ${\mathrm{G}}_2$	(0,0), (−200,−50), (400,0) m
${\mathbf{w}}_{\mathrm{E}}$, ${\mathbf{w}}_{{\mathrm{E}}_1}$, ${\mathbf{w}}_{{\mathrm{E}}_2}$	The horizontal coordinates of $\mathrm{E}$, ${\mathrm{E}}_1$, ${\mathrm{E}}_2$	(200,−100), (0,50), (200,100) m
${\mathbf{q}}_I$, ${\mathbf{q}}_F$	The original and final horizontal positions of UAV U	(−600,−300), (600,−300) m
$z_I$, $z_F$	The original and final altitudes of UAV U	50 m
$V_{xy}^{max}$, $V_z^{max}$	The maximum horizontal and vertical speed of UAV U	10, 5 m/s
$H_{min}$, $H_{max}$	The lowest or highest altitude of UAV U	50, 150 m
$p_{\mathrm{E}}$	The jamming power of $\mathrm{E}$	0, 0.02, 0.04 W
${\delta }_t$	Time slot length	1 s
${\rho }_0$	Channel power gain at reference distance	−60 dB
${\sigma }^2$	AWGN power	−110 dBm
${\beta }_L$, ${\beta }_N$, $\kappa$	path loss exponent	2.2, 3.2, 3
${\eta }_1$, ${\eta }_2$	Environmental parameters	11.95, 0.14
$\overline{p}$, $\tilde{p}$	Average and peak power of UAV U	10, 16 dBm
$\alpha$	Signal attenuation factor	−20 dB
$ϵ$	Precision	${10}^{-4}$

shows the simulation parameters.

Next, the numerical results are divided into two subsections. We analyze the different case of a single ground node and eavesdropper, as well as that with more practical multiple ground nodes and eavesdroppers.

5.1. Single Ground Node and Active Eavesdropper Instance

The convergence performance of Algorithm 1 is verified in Figure 3, where $p_{\mathrm{E}}$ = 0.02 W. As the number of iterations increases, the average achievable rate will also increase. For different time T, about ten iterations, it will be convergent. As T increases, the average achievable rate increases significantly. This is because as T increases, the UAV has more time to hover at the optimal position, so as to strike a balance between mitigating the malicious interference as well as eavesdropping caused by the active eavesdropper and increasing the achievable rate at the ground node.

Figure 4a presents the horizontal trajectories of the UAV with different strategies when T = 160 s and $p_{\mathrm{E}}$ = 0.02 W. In the TP-LC strategy, the UAV first flies to the left of $\mathrm{G}$ along an approximately straight path. However, the UAV under the PrLC model flies directly to the top of $\mathrm{G}$. This is because the PrLC model has an additional elevation-distance trade-off compared to the LC model. Therefore, the UAV can achieve a better balance between minimizing the message leakage rate to $\mathrm{E}$ and maximizing the achievable rate to $\mathrm{G}$. During the return journey, to reduce the message leakage of the UAV, almost benchmarks follow a larger arc trajectory to move away from $\mathrm{E}$. However, the UAV in the TP-LC strategy can only trade off the information achievable rate and information leakage rate by adjusting the distance, so it can only shorten the distance with $\mathrm{G}$ along an approximately straight line to the destination. In the TNP-PrLC strategy, because of the lack of power control, the UAV can only move away along a larger arc trajectory to move away from $\mathrm{E}$ to reduce unnecessary information leakage.

Figure 4b presents the 3D trajectories of the UAV with different strategies. The UAV in the TP-PrLC strategy first climbs to the highest altitude to rise its elevation angle to $\mathrm{G}$, resulting in a higher LC probability, and flies at $H_{max}$ towards $\mathrm{G}$. Then, when almost reaching $\mathrm{G}$, the UAV descends rapidly to reduce path loss while still insisting a high LC probability. However, in order to attain best channel quality, in the TP-LC strategy, the UAV needs to rely on shorter distances to $\mathrm{G}$. Therefore, the UAV remains at its lowest altitude and flies towards $\mathrm{G}$. During the return journey, the UAV in the TP-PrLC strategy adopts a flight trend of first ascending and then descending to adjust its elevation angle to achieve the optimal secrecy rate balance. In contrast, in the TP-LC strategy, the UAV perform its mission by climbing to the highest altitude to increase the distance from $\mathrm{E}$ while not getting too far from $\mathrm{G}$.

Figure 5 presents the 3D trajectories of the UAV with different jamming powers in the TP-PrLC strategy when T = 160 s. It can be seen that the UAV of all strategies follows the same 3D trajectory. This is because the malicious interference generated by $\mathrm{E}$ mainly affects the information reception of the legitimate node $\mathrm{G}$ but cannot interfere with the information transmission of the UAV. Therefore, in the UAV downlink information transmission, the change in interference power does not result in a change in the optimized UAV trajectory.

Figure 6 presents the relationship between the average secrecy rates of different strategies with different T and $p_{\mathrm{E}}$. It can be seen that the TP-PrLC strategy achieves the best average secrecy rate; however, the TP-LC strategy has the worst performance. This verifies the accuracy of PrLC model compared with LC model for the representation of the path loss and shadow fading in city areas. In contrast, since the TNP-PrLC strategy cannot further adjust the secrecy rate through power control, it cannot effectively combat the threats of the active eavesdropper, which results in worse performance. Due to the lack of additional gain obtained by altitude optimization, the secrecy rate of the HTP-PrLC strategy is lower than that of the TP-PrLC strategy. Furthermore, as $p_{\mathrm{E}}$ increased, the gaps between all strategies increased with T. This shows that in complex city environments, jointly designing the 3D trajectory and the UAV’s power control can significantly reduce the adverse impact of the active eavesdropper.

5.2. Multiple Ground Nodes and Active Eavesdroppers Instance

We consider two legitimate ground nodes in this subsection, ${\mathrm{G}}_1$ and ${\mathrm{G}}_2$, and two active eavesdroppers, ${\mathrm{E}}_1$ and ${\mathrm{E}}_2$. Specifically, Figure 7 reveals the 3D trajectory of the UAV with different strategies when T = 160 s and $p_{\mathrm{E}}$ = 0.02 W; Figure 8 illustrates the transmit power of various strategies with $p_{\mathrm{E}}$ = 0.02 W; Figure 9 demonstrates the average secrecy rate with $p_{\mathrm{E}}$ = 0.02 W.

Figure 7a presents the horizontal trajectories for different strategies when T = 160 s and $p_{\mathrm{E}}$ = 0.02 W. It can be noted that the UAVs of all strategies fly from ${\mathbf{q}}_I$ to ${\mathrm{G}}_1$, and from ${\mathrm{G}}_2$ to ${\mathbf{q}}_F$, at their maximum flying speeds to complete their missions as soon as possible. However, when the UAVs fly from ${\mathrm{G}}_1$ to ${\mathrm{G}}_2$, their trajectories show obvious differences. Specifically, in the TP-PrLC and HTP-PrLC strategies, the UAV trajectory takes an arcing flight, making the elevation angles between the UAV and ${\mathrm{G}}_1$ and ${\mathrm{G}}_2$ much more extensive than those with ${\mathrm{E}}_1$ and ${\mathrm{E}}_2$, thereby obtaining a higher LC probability. In contrast, the UAV trajectory in the TP-LC strategy is closer to both legitimate and illegitimate nodes, because it can only trade-off the secrecy rate by adjusting its distance to these nodes. In the TNP-PrLC strategy, because lack of power control, the UAV can only fly farther to escape the active eavesdroppers obtaining more information.

Figure 7b presents the UAV 3D trajectories with different strategies when T = 160 s and $p_{\mathrm{E}}$ = 0.02 W. During the flight of the UAV from ${\mathbf{q}}_I$ to ${\mathrm{G}}_1$, the UAVs in both of the TP-PrLC and TNP-PrLC strategies first rise then descend, since the higher LC probabilities with ${\mathrm{G}}_1$ and ${\mathrm{G}}_2$ can be obtained. However, the UAVs in both strategies transmit at lower power to avoid leaking more information to ${\mathrm{E}}_1$ and ${\mathrm{E}}_2$. During the flight towards ${\mathbf{q}}_F$, the UAVs still have higher LC probabilities with the gournd nodes, compared to the active eavesdrop nodes. Therefore, the UAVs are able to send messages at higher powers which can be verified in Figure 8. For the flight from ${\mathrm{G}}_1$ to ${\mathrm{G}}_2$, compared to other bechmark strategies that the UAVs fly at their lowest altitude to achieve better secrecy perofrmance, the UAV in the TP-LC strategy ascends to enlarge the distance with the active eavesdroppers, but it cannot fly too high due to the guarantee of less pathloss.

Figure 8 presents the schematic of the UAV’s transmit power change with time T under different strategies when $p_{\mathrm{E}}$ = 0.02 W. It is worth noting that the UAV under the PrLC model can stay longer at the hovering position above ${\mathrm{G}}_1$ and ${\mathrm{G}}_2$ to transmit information with the highest possible transmit power, which can greatly balance the trade-off between elevation and distance. However, since in the TP-LC strategy, the UAV can only avoid the threats from the active eavesdroppers by adjusting the distance, it cannot stay at the hovering location for too long. It can transmit at a certain power to increase the secrecy rate as much as possible. Moreover, when the UAV approaches ${\mathrm{G}}_2$, compared with the TP-PrLC strategy, the UAV in the HTP-PrLC, can only increase its transmit power to enhance the achievable rates at ${\mathrm{G}}_2$.

Figure 9 plots the comparison of the relation between average secrecy rate and time T of different strategies when $p_{\mathrm{E}}$ = 0.02 W. It can also be seen that compared with the single legitimate ground node and active eavesdropper case, applying the PrLC model for creating the UAV’s 3D trajectory and power control can provide a more significant secrecy rate improvement in the more practical multiple ground nodes and eavesdroppers case. This confirms that the PrLC model can more accurately describe the channel condition between the UAVs and multiple ground nodes in city environments.

6. Conclusions

In order to deal with the threat of active eavesdropping in typical communication scenarios, this paper consider the UAV security communication system against active eavesdropping based on PrLC model. Specifically, the UAV sends classified messages to legitimate nodes, while the active eavesdroppers wiretap the information between legitimate ground nodes and the UAV and transmit jamming signals to reduce the legitimate transmission. By jointly designing the communication connection, the UAV’s transmission power, and its 3D trajectory, the objective was to increase the average secrecy rate in the worst scenario. Although the problem is non-convex, it is hard to find the optimal solution, this paper propose an efficient algorithm to get the suboptimal solution using the BCD and SCA techniques. The numerical results indicate that our algorithm is more effective at balancing the elevation angle-distance trade-off, and improving the average secrecy rate. In particular, the proposed algorithm is more effective in increasing the average secrecy rate as $p_{\mathrm{E}}$ increases. In the multiple legitimate ground nodes and active evasdroppers scenario, applying the PrLC model can provide greater benefits to secrecy performance.