Abstract
Free-space optical (FSO) communication is expected to play an indispensable role with high data rates and low system complexity in beyond fifth-generation (B5G) networks. However, infrequent adverse weather conditions can incapacitate its performance. The combination of FSO and radio frequency (RF) has emerged as an effective alternative for meeting the growing need for high data rates in wireless communication networks. Unmanned aerial vehicles (UAVs) are also anticipated to play an instrumental role in B5G networks due to their flexible movement and deployment. In this paper, a UAV-aided hybrid FSO/RF backhauling system using a matching game theory (GT) and reinforcement learning (RL) framework is investigated. We deploy a UAV to provide a user offloading service to an already existing ground base station (GBS), which is facing a reduced backhaul capacity due to weather attenuation (e.g., fog). It is considered that the GBS has a pre-installed FSO backhaul connection to a macro-base station (MBS). However, during adverse weather conditions, the FSO backhaul is severely affected, compromising the reliability of the FSO link. With the reduced FSO backhaul capacity, the GBS needs an additional backhaul link to support its backhaul data transmission to the destination MBS. As a result, instead of building an expensive permanent parallel RF link for the rare foggy situation, a UAV can be hired to serve a portion of the users, thereby reducing the GBS load. The users perform a matching game-based procedure to select the base station (BS) of their choice to maximize their utility. The UAV is deployed at an optimal altitude, and the bandwidth partition between the GBS and the UAV is optimized to maximize the system throughput using RL. Real weather data from the cities of Edinburgh and London in the U.K. are used to evaluate the performance of the system. The numerical results show the superiority and effectiveness of the proposed scheme compared to conventional methods.
1. Introduction
Data rates on the order of terabits per second are expected as wireless technology evolves beyond fifth-generation (B5G) networks. To properly evaluate the B5G wireless networks, new technical requirements, dynamic communication scenarios, and performance indicators are introduced [1]. Unmanned aerial vehicles (UAVs) have been widely proposed to support existing networks in providing wireless communication services anywhere and at any time to enable flexible movement, powerful computing, etc. [2]. In addition to the rising demand for UAVs, relay stations and small cells are expected to be widely deployed to improve mobile data coverage, necessitating high-speed backhauling. To address these issues, free-space optical (FSO) communication has been identified as a promising wireless technology for high-capacity, cost-effective, and energy-efficient communication networks with data rates comparable to optical fiber links [3,4]. The FSO link’s wireless functionality offers a suitable communication system for both dense urban and rural locations as well as areas prone to fiber cut failures. In fact, FSO systems are expected to be critical in emerging network architectures such as cell-free technology [5].
However, practical FSO systems face some limitations and challenges, such as pointing and misalignment loss due to building sways, turbulence-induced intensity fluctuation (also known as scintillation), and adverse weather conditions such as fog and snow [6,7]. In particular, FSO links can be severely hampered by a fog event, which is a relatively long-lasting yet infrequent phenomenon. In contrast, fog has practically a nominal impact on radio frequency (RF) systems; therefore, one possible solution is to build hybrid FSO/RF links [8]. However, given the increasing demand for FSO links and the massive expansion of cell sites, it is reasonable to assume that not all FSO links can have parallel RF transmission links for various reasons such as the high link expense. Moreover, adverse weather conditions such as fog are not frequent in many geographical areas. For example, official weather data from the Meteorological Office of the United Kingdom show that the city of Edinburgh experienced only 86 h of fog events (visibility < 1 km) from January 2016 to June 2017, which is only almost 0.65% of the specified duration [6]. To this end, temporary solutions can be envisaged rather than permanent, expensive RF links.
Motivated by the growing demand for UAV deployment as relays, we propose a UAV-aided user offloading scheme using matching game theory (GT) and reinforcement learning (RL), in particular Q-learning. This approach can enhance the throughput of a ground base station (GBS) to the macro-base station (MBS) supported by a fog-troubled FSO backhaul link. The UAV can establish a temporary RF backhaul link (e.g., millimeter wave) with the MBS in adverse weather conditions. The UAV relay offloads users from the coverage area of the GBS. The FSO channel condition determines the optimal placement of the UAV, which defines the coverage ratio of the GBS and UAV to maximize the end-to-end network throughput. As the adverse weather event passes, the UAV may be withdrawn and the GBS can resume regular operation without a UAV relay. We refer to our proposed scheme as capacity-aware UAV deployment and resource allocation (CURE) and its suboptimal version as cell-edge-based UAV deployment (CUDE). We also compare the performance of the proposed scheme with the state-of-the-art schemes, which include GBS-only (GBSO), e.g., traditional FSO backhauling without UAV, and Cell association with range expansion (CARE).
Related Work and Contribution
The emergence of UAV technologies has created new potential for a wide range of applications [9]. Under many network scenarios, UAVs are becoming more popular for user offloading. For instance, the authors of [10] evaluated the impact of UAV altitude and transmit power, as well as the offload portion, on the user’s downlink sum rate, assuming that UAV to user links are line-of-sight (LoS) channels. To provide downlink data offloading in some areas of a BS, the work in [11] temporarily deployed UAVs. The method utilizes contract theory to model the situation, where the BS manager must develop an optimal contract to maximize its own revenue. By jointly optimizing the UAV’s trajectory, bandwidth allocation, and user partitioning, Lyu et al. [12] proposed an aerial mobile BS to offload data traffic for cell-edge users. In [13], the heterogeneous UAV-enabled data offloading is modeled in an innovative framework to dynamically estimate user status information and determine the UAV scheduling strategy, whose purpose is to lower the user data queue length while extending the working time of the UAV.
Machine learning (ML)-based optimization solutions are increasingly considered in the context of UAV-assisted networks. For instance, reference [14] discussed various ML methods for developing UAV-assisted radio access networks, with a special emphasis on supervised ML and RL procedures with high-speed backhaul links (e.g., FSO). Fan et al. [15] investigated the UAV-enabled traffic offloading problem under a mixed user traffic scenario, where delay-sensitive user traffic and delay-insensitive user traffic are jointly considered, and a deep neural network-powered genetic algorithm is used to obtain the optimal association between the UAVs and the ground systems. The authors of [16] used a multiarmed bandit-based offload path selection scheme to address the issue of decentralized data offloading in an edge UAV swarm. This is to reduce the complexities of a single UAV repeatedly producing and processing large amounts of application-specific data. In UAV networks, a combination of ML and GT is also regarded as a promising technique. For example, Gao et al. [17] proposed a game-based multi-agent deep deterministic policy gradient approach for optimizing the trajectory of multiple UAVs while taking into account users’ offloading delay, energy efficiency, and the use of an obstacle avoidance system. The work in [18] adopted a novel game-theoretic and RL framework for computational offloading in a multi-service provider mobile edge computing network. Li et al. [19] investigated a joint optimization of beamforming and beam-steering in multi-UAV millimeter wave networks considering LoS communication for UAVs, where beamforming and beam-steering optimizations were carried out using an ML-inspired algorithm and a mean field GT scheme, respectively.
Several studies have considered UAVs for offloading, capacity enhancement, and relaying services. However, only a few studies have addressed both UAV-assisted networks and FSO backhauling to provide network service. The study in [20] investigated the 3D deployment and resource allocation of a UAV in a hotspot area to maximize access link throughput given constraints on user quality-of-service (QoS), FSO backhaul link capacity, and total bandwidth and power. However, the backhaul constraint is eased by assuming an ideal, high-capacity FSO backhaul. To maximize the network throughput, the authors of [21] considered the association between aerial and terrestrial terminals, transmit power, and the deployment of multiple UAVs, wherein backhaul-to-relay and relay-to-user communications employed FSO and RF links, respectively. In [22], a hovering UAV-based serial FSO decode-and-forward relaying system that considers various types of channel impairments is investigated to improve system performance by optimizing the beam width, field of view, and UAVs’ locations. Ajam et al. [23] proposed a UAV-aided communication system with RF access links to mobile users and an FSO backhaul link to analyze the end-to-end system performance of a network in terms of the ergodic sum rate by optimizing the placement of UAV that serve as buffer-aided and non-buffer-aided relays. By jointly designing the FSO and RF links and the UAV altitude, the study in [24] maximized the system-level energy efficiency, which is equivalently expressed as the ratio of the UAV’s multicasting rate over the optics BS transmit power, subject to the UAV’s sustainable operation and reliable backhauling constraints. The work in [25] investigated the 3D location of the drone BS, user association, and bandwidth allocation policy between the MBS and the drone BS in order to minimize the total average latency ratio of all users while maintaining each user’s QoS requirement. However, these studies have not taken into account the weather’s impact on FSO backhaul, which is crucial in the FSO link availability and consequently impacts the UAV deployment.
This work can be considered as one of the pioneering studies toward hybrid FSO/RF networks under the umbrella of B5G networks, which are envisioned to integrate a combination of FSO, UAVs, and high-speed RF (e.g., millimeter wave) technology for diverse scenarios. The main contributions of this study are stated below.
Contributions: The main contributions of this study are stated below.
- We investigate a scenario where a UAV provides user offloading service to a GBS, which has an FSO backhaul connection to the MBS. Specifically, the objective is to maximize the network’s overall end-to-end throughput with the aid of a UAV when the GBS’s FSO backhaul link is not reliable due to adverse weather conditions. We propose an FSO backhaul-aware matching GT and RL-based solution for optimal user association and overall network throughput maximization. The users decide for themselves which BS (GBS or UAV) they would like to be associated with to increase their utility (data rate).
- The paper proposes a two-layer system, where a matching GT technique is employed at the lower layer to associate users with the GBS or UAV that maximizes their utility. The system is then trained using RL to optimize the UAV’s altitude and bandwidth partitioning based on the weather conditions. The proposed scheme does not require users to be aware of other players’ actions, which can greatly reduce the communications overhead. In addition, once the training is completed, the system can quickly obtain optimal parameters (altitude and bandwidth partition) for any random user distribution.
- Lastly, the proposed hybrid network framework is evaluated under different weather conditions including realistic weather statistics from the cities of Edinburgh and London in the UK. The results clearly indicate the supremacy of the proposed approach over GBS-only and two other benchmark user association schemes.
We organize the rest of this article as follows. The system model of the proposed UAV-aided hybrid FSO/RF network is presented in Section 2. The problem formulation and resource allocation using a matching GT and RL framework are detailed in Section 3. The complexity and convergence analysis of the proposed scheme are also given in Section 3. Some numerical results are presented in Section 4, and results based on practical weather measurements are also discussed in Section 4. Finally, the paper is concluded in Section 5.
2. System Model
The schematic of the proposed system for high-speed wireless backhauling of a GBS is shown in Figure 1. We assume that a preinstalled FSO link exists between the GBS and the MBS. In the context of B5G, the GBS could be in the same coverage area as MBS, e.g., heterogeneous network or in a remote location, e.g., relay station. FSO-based wireless backhauling solutions are very reliable and offer high achievable data rates in more frequent normal weather conditions. So, in addition to the existing FSO link, installing a parallel high-speed RF link between GBS and MBS just for occasional use in adverse weather events is redundant, expensive (e.g., RF licensing costs), and difficult to maintain considering the large number of anticipated BSs in B5G. When the FSO backhaul capacity drops below a minimal threshold because of the adverse weather conditions, e.g., fog events, the GBS would like to maximize the utilization of its licensed sub-6 GHz spectrum W in the downlink. It takes advantage of the UAV’s services to help some users by letting the UAV use some portion of W, which should be efficiently shared between the two BSs. In addition, the UAV can establish a temporary LoS link for backhaul with any nearby node, including the MBS. Owing to its higher capacity and active beam steering, millimeter wave backhauling outperforms sub-6 GHz backhauling across the RF spectrum [26]. Hence, it is assumed that the UAV establishes a backhaul link to the MBS using an ideal high-speed directional millimeter wave link.
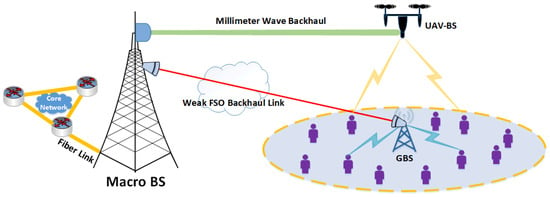
Figure 1.
The proposed system model for UAV-aided user offloading in adverse weather conditions.
Due to the increased density of BS nodes in B5G, it is impractical to equip every GBS node with an expensive and difficult-to-maintain parallel high-speed RF backhaul. As a result, it is anticipated that a UAV is equipped with a high-performance millimeter-wave transceiver designed to operate in the scenarios such as depicted in Figure 1. Millimeter-wave communications using the large bandwidth over 28 GHz is promising for high-rate UAV transmissions [27]. It is also worth pointing out that instead of the MBS, the UAV can also establish a backhaul connection with any nearby RF node, which might not have an LoS connection possibility with the GBS. Note that this assumption is justified because the foggy conditions have a negligible impact on RF signals. Hence, the system could now be referred to as a hybrid FSO/RF backhauling system, since both FSO and RF technologies are used at the backhaul links, i.e., FSO backhaul for the GBS and millimeter wave backhaul for the UAV. As the fog event passes, the UAV may be withdrawn because the FSO backhaul link of the GBS can resume regular operation. Furthermore, we assume that in the downlink, both BSs use omnidirectional antennas. Next, a brief description of the channel models is provided.
2.1. FSO Channel Model
Given that the FSO link employs intensity modulation direct detection (IM/DD), the received electrical signal expression can be written as
where is the responsivity of the photodetector, refers to the average channel gain, denotes the random turbulence-induced intensity fading, is the transmitted optical intensity, is the received electrical signal and is zero-mean real Gaussian noise with variance . Note that we use the subscript ‘o’ to denote the optical link. The signal-independent Gaussian noise in (1) arises from thermal noise as well as the shot noise induced by the ambient light. The average gain could be expressed as [6,28]
where the first and second terms are the geometric loss due to the divergence of the transmitted beam and the atmospheric loss due to scattering and absorption, respectively. The receiver aperture diameter is denoted by d, is the beam divergence angle, is the distance between the source and the destination, and is a weather-dependent attenuation coefficient determined based on the Beer–Lambert law. The relationship between and the visibility V in km can be expressed as [29], where is the weather condition-based size distribution of the scattering particles. It can be expressed as a function of the visibility distance as [30]
The log-normal distribution and the Gamma–Gamma distribution are two common methods for modeling the turbulence-induced intensity fluctuation . We use the Gamma–Gamma distribution, which can characterize the intensity function under a variety of turbulence situations as [6,31]
where denotes the Gamma function, and is the modified Bessel function of the second type. The parameters and are defined as [32]
where , and . Note that is the turbulence refraction structure parameter. The achievable rate (channel capacity lower bound) conditioned on the random channel gain for the IM/DD FSO channel described in (1) can be stated as [6,33]
where is the optical bandwidth, e is the base of natural logarithm and represents the optical transmission power of the FSO node (e.g., MBS).
Strong atmospheric turbulence is highly unlikely during a fog event due to their inverse correlation [34], but it cannot be totally ignored. It is worth noting that due to a very small coherence time (i.e., rapid changes), UAV deployment and resource allocation are unable to respond to channel capacity fluctuations caused by scintillation. To cope with this problem and to encounter the impact of turbulence on the proposed system, we use a sliding window averaging strategy [6,35] to smooth out the rapid FSO link capacity fluctuations. Note that a window with a longer interval than the scintillation coherence time (which is on the order of milliseconds) should be used so that the average FSO link capacity can accurately reflect long-term weather conditions. The average FSO link capacity is measured over the window interval, which is estimated as , where denotes the ensemble expectation. The GBS can monitor the condition of the FSO link and calculate every window interval. When falls below a certain threshold, , the services of a UAV may be required to offload some users—in the worst case, all users due to the total non-functionality of the FSO link. To ensure that the GBS can respond quickly to changing weather conditions, the window interval should be significantly shorter than the time-scale of the weather changes, which is on the order of hours.
2.2. RF Channel Model
2.2.1. Air to Ground Channel
The wireless air-to-ground (AtG) channel between a UAV and a ground user is primarily composed of two components: the LoS component and the non-LoS (NLoS) component. The probability of establishing an LoS link between a user and the UAV with an elevation angle of (in degrees) is given by [10]
where and are constant parameters which depend on the carrier frequency and the communication environment. In addition, is the elevation angle between the kth user and the UAV with , the total distance between kth user and the UAV, which has an altitude . Then, the average path loss (PL) can be expressed as [36,37]
where is the carrier frequency, c denotes the speed of light and is the PL exponent. The PL values of the LoS and NLoS components are represented by and , respectively. In addition, and denote the additional PL, which depends on the type of communication environment.
2.2.2. Ground-to-Ground Channel
The GBS-to-user channels are only considered NLoS because the elevation angle between them is small. In effect, there is a high probability of NLoS links, which defines the PL as [11]
where is the GBS to user distance, and denotes the altitude of the GBS.
2.3. Cell-Edge-Based UAV Altitude
In a traditional UAV deployment technique [38,39,40,41], the edge user (cell-edge) is considered while positioning the UAV to enhance the QoS of the farthest users. At an optimal elevation angle , the coverage radius is maximized for a predefined PL value. Equivalently, there is an optimal altitude at which the PL at the cell-edge is minimized for a given radius. Let denote the optimal altitude that minimizes the PL at the cell-edge and be the coverage radius of the area in Figure 1. Hence, by taking the partial derivative of (7), an equation of the critical point could be developed as [41]
where and is the elevation angle of an edge user. Therefore, cell-edge-based optimal UAV altitude can be obtained from (9), which is widely adopted to determine the optimal altitude in UAV networks. It is worth noting that the UAV altitude obtained from (9) serves as a benchmark for the proposed model and a backhaul-aware UAV altitude optimization is performed in Section 3.2.
2.4. User Distribution and Cell Association
We assume that K users are uniformly and independently distributed in the coverage area using a homogeneous Poisson point process, which is obtained through a spatial point process. Let denote the set of users and be the set of two BSs (UAV and GBS). We employ a widely used cell association strategy known as reference signal received power (RSRP) [42] for the initial user association because of the flexibility it provides to users. The policy allows the kth user to be associated with the BS m that has the strongest RSRP as
In addition, it is considered that the users can only be associated with one BS. To this end, a user association matrix can be developed as
It is important to note that for the proposed model, an initial user association policy is given in (10) and a backhaul-aware optimal policy is devised in Section 3.1.
3. Problem Formulation and Resource Allocation
In this paper, we assume that bandwidth W is shared between the two BSs based on a bandwidth allocation factor that can be adjusted to efficiently manage the bandwidth partition. Hence, is the bandwidth used by the UAV and is allocated to the GBS. Consider that both GBS and UAV broadcast at fixed transmit powers of and , respectively. Thus, the data rate achieved by the kth user associated with the GBS can be calculated as
where is the user-load for the GBS and denotes the power of additive white Gaussian noise (AWGN). However, an unreliable backhaul can limit the user data rate and also incur delay. The rate constraint directly impacts the network throughput, whereas the delay constraint is critical for control signalling deadlines [43]. In this paper, we only consider the backhaul rate limitation which is caused by the weather attenuation. As a result, when the total access link throughput exceeds the FSO backhaul capacity, the user rate in (12) cannot be guaranteed. To this end, the effective throughput of the kth user could be expressed as
Note that the fog-based attenuation is negligible for RF below 100 GHz frequencies [44]; hence it is assumed that the UAV can establish a reliable millimeter wave (e.g., 28 GHz) backhaul with capacity which is always sufficient to support the UAV’s access link throughput, i.e., . Then, the data rate of the kth user offloaded to the UAV could be calculated as follows
where denotes the number of users offloaded to the UAV. Once the user association is completed, the sum throughput of UAV and GBS are, respectively, given as and .
The proposed backhaul-aware system’s goal is to maximize the total end-to-end throughput by optimizing the user’s BS selection, the bandwidth partition between BSs, and the altitude of the UAV. More formally, the following optimization problem is formulated
where constraints (15) and (16) ensure that each user must connect to only one BS. The constraints (17) and (18) represent the range of values for the bandwidth partition factor and UAV altitude , respectively. The value of could be regarded as equivalent to in (9) because the UAV cannot provide better service above this altitude. Note that the association matrix can be influenced by UAV altitude and bandwidth partition, while the optimal value of would be different at different altitudes and vice versa. Hence, problem is intractable owing to the interactions and coupled relationship between user association, UAV deployment, and bandwidth partition.
One efficient approach to solve is to employ a hierarchical framework that combines GT and RL. The proposed framework decouples into two-layer hierarchical sub-problems. Firstly, problem (lower layer) presented in Section 3.1 deals with the backhaul-aware user association between the GBS and the UAV for a predefined and . This problem is solved by adopting a matching GT approach to provide an optimal user association in which users select the BS that offers a better utility (rate). Next, the second sub-problem (upper layer) presented in Section 3.2 leverages RL to obtain the UAV altitude and bandwidth partition that maximize the total system throughput according to the prevailing weather conditions. In essence, the objective of is to acquire an optimal combination of bandwidth partition and UAV altitude denoted as and , respectively. is iteratively solved by calling for each combination of and until the convergence is reached (total network throughput is maximized), which occurs at the optimum combination and . It is worth noting that the values of these optimal combinations could be different for different weather-dependent attenuation coefficients , hence making the RL process even more crucial, as will be shown and discussed in Section 4. Figure 2 depicts a visual representation of the hierarchical structure for solving employing the matching GT and RL in Section 3.1 and Section 3.2, respectively.
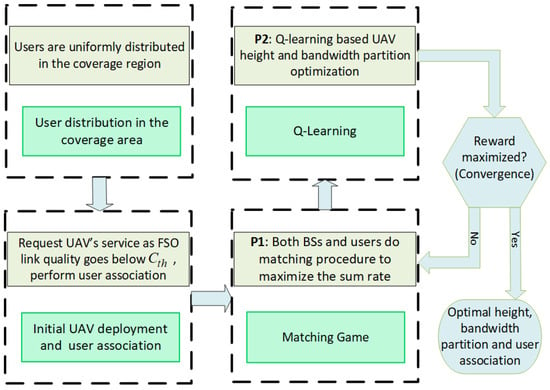
Figure 2.
The framework for solving the problem of optimal user association, UAV deployment, and bandwidth partition.
3.1. Matching Game Formulation
The potential to model individual, independent decision makers with interactional strategies makes GT particularly appealing for analyzing wireless network performance. In contrast to conventional methods, GT can be used to construct robust and efficient distributed algorithms to address technical problems in UAV-assisted networks. Distributed solutions based on GT can help to reduce communication signal overhead [45]. In particular, the matching GT [46] can be used to provide solutions for combinatorial problems of matching players in two disjoint sets to investigate how different types of rational and selfish players form dynamic and thus useful relationships.
It is worth noting that the proposed model completely matches a user association problem in which each user would like to be associated with the BS that maximizes its throughput. However, one can see from (13) and (14) that the achievable user rates also depend on the existing user load on the BSs. Thus, a coupled relationship between the entities needs to be solved. To obtain a tractable solution, the BS-user association problem could be modeled as a one-to-many matching game. To this end, the goal of the first sub-problem is to maximize the end-to-end sum rate of both BSs by optimizing users’ BS selection with fixed values of and . The first sub-problem is formulated as follows
Note that the objective in could be achieved by developing a user association matrix where each user is allowed to be associated with the BS that offers a higher transmission rate. The weather attenuation condition can also affect user association and achievable user throughput, and the matching GT could provide an adaptive solution that responds to the prevailing weather.
In this game, we have two disjoint sets of players, the set of users and the set of BSs . Note that each user could be associated with one BS at a time. To this end, the matching cell association problem is determined by the tuple , where and define the preference list of users’ and BSs, respectively. Note that ≻ denotes the preference notation and is the quota vector of the BSs. One can note that in adverse weather, all users might want to switch to the UAV. In favorable weather, the opposite could happen. Hence, limiting the number of user associations with the BSs could be counterproductive. Thus, it is assumed that the quota vector can house up to K users for both BSs. In the matching GT, if a particular user is matched to a BS, it can be also interpreted as the BS being matched to that user [47]. The matching is mathematically defined as follows.
Definition 1.
A utility matching function represents the BS–user association problem which can be expressed as a function from the set into the set such that
- and ;
- , ;
- if and only if .
where is the matching outcome and denotes its cardinality.
Definition 2.
A matching with link is considered to be stable if there exists no matching such that the kth user favors BS m to (or vice versa), or BS m prefers user to k, . In addition, a matching could be blocked by the BS (i.e., the user is not permitted to change BS) for a BS–user pair if and .
Hence, an outcome of a stable matching is a bilateral assignment to all players. An iterative matching permits the kth user to iterate its matching if and only if it is beneficial in terms of the attained utility . Specifically, the users build their preferences relation based on the achievable throughput using both BSs. For any kth user and the two BSs , , two possible matches exist, , , . To this end, we have the following properties:
where indicates that the user prefers BS m as opposed to BS due to a higher achievable throughput (utility) with BS m. In addition, for BS m and any two users , , two possible matches exist, , , , and we have the following properties:
One can note from (20) and (21) that the matching preferences of the players are related to their utilities, which are governed by the achievable data rates defined in (13) and (14).
Iterative Matching Game Procedure
Algorithm 1 outlines the proposed iterative matching procedure, which involves iterative matching until network-wide stability is attained. All users are initially assumed to be associated with the BS with the highest RSRP. Each user creates a list of preferred BSs and requests to be associated with their preferred BS. Both BSs also construct their preference lists depending on the total rate they offer to the associated users. Each BS also gives a ranking score to the users based on their preference list. Note that the user preference relations are interdependent, as they are influenced by the existing matching (i.e., the individual user data rate could change with a change in user load on the BS). This type of matching is categorized as matching with peer effects [48]. Users would only seek a change in serving BS if the other BS provided a better data rate. Additionally, the BS agent approves the request if the requesting user increases the BS’s overall ranking; otherwise, it rejects it. Usually, a user would not request a change of BS which needs to be blocked, as under the proposed scheme, increasing the user’s data rate also increases the BS rate and the ranking score. The blocking mechanism would only be activated if an abnormal request is received. The procedure is iteratively updated, and the algorithm returns a stable matching when no user would like to change its association. It is worth emphasizing that an outcome of Algorithm 1 could vary if the weather condition changes i.e., change in .
| Algorithm 1:Optimal User Association Using Iterative Matching Game |
 |
Note that Algorithm 1 is guaranteed to converge to a final matching for the given weather attenuation from any initial user association. There are only two BSs; we can determine a fixed number of user transfers in the network, and each user only intends to change BS if it improves its data rate. That is, with the specified parameters and , it is clear that in a network with a fixed number of users and BSs, user gain is always limited, meaning users could only conduct a finite number of transfers to maximize their gain. The number of transfers are mainly dictated by the weather attenuation coefficient . Hence, the while loop of Algorithm 1 is guaranteed to terminate after a certain number of steps when no user could improve their data rate. The convergence ensures the stability of the association, as no user would have a desire to deviate from their final BS–user association.
3.2. Resource Optimization Using Reinforcement Learning
Note that Algorithm 1 solves P1 to maximize the network sum throughput using the matching GT method and produces and , the end-to-end network throughput of the GBS and the UAV, respectively. This is achieved by supplying a fixed combination of bandwidth partition factor , and the UAV altitude as the optimization problem involving these parameters becomes intractable due to coupled relationships. However, it is crucial to determine the optimal values of both and , as both parameters could significantly impact not only the user association but also the individual user rates and total network throughput. We need to iteratively invoke Algorithm 1 to optimize the sum of and . Since a nearly optimal solution necessitates a large number of iterations, we exploit RL to obtain a joint optimization of and by periodically invoking Algorithm 1 to optimize the sum of and . To this end, the optimization problem P2 is presented as
In RL, an agent continuously interacts with the environment, taking various actions in response to new conditions (states) presented by the environment. The agent obtains a reward from the environment after completing an action. The reward can be positive if the action was desirable or negative (e.g., a penalty) if the action was unfavorable. One of the most popular RL methods is Q-learning [49] in which the agent learns the action–value function Q, which represents the expected reward against a state–action pair . It is considered that the UAV agent takes both actions (modifying the UAV altitude and bandwidth partition). This assumption simplifies the model because the UAV must act according to weather attenuation and the GBS and UAV need minimal communication. For instance, the UAV would share the bandwidth partition parameter while the GBS only needs to share its total end-to-end throughput values in return after each iteration. To this end, the state–action value function of the UAV agent could be iteratively updated as
where and represent the learning rate and discount factor, respectively. In this paper, UAV functions as an agent for the Q-learning model, which is composed of four components: states, actions, rewards, and the Q-value. The objective of Q-learning is to develop a policy that maximizes observed rewards over the duration of the agent’s interactions. Note that we employ Q-learning because we could formulate the problem with a finite state and action space and because it is an efficient algorithm for this type of problem. If the state space was large, we could have used other RL methods such as deep Q-network (DQN), which approximates Q-values for state–action pairs using a deep neural network (DNN). Figure 3 depicts the working principle of RL in the proposed framework.
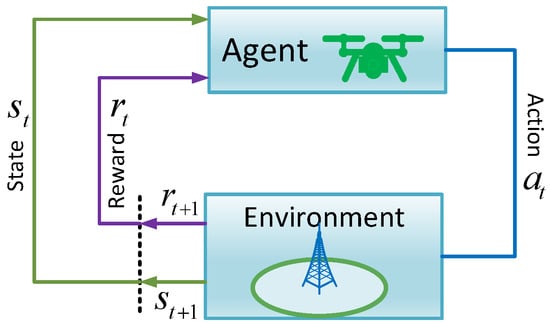
Figure 3.
The working principle of reinforcement learning.
3.2.1. State Representation
The UAV agent employs a state model comprised of , where is the altitude of UAV and denotes the bandwidth partition between the UAV and GBS. The state for a UAV deployment can be denoted as , .
3.2.2. Action Space
The agent carries out an action at each step, which comprises a combination of altitude (increase or decrease) and bandwidth partition (increase or decrease) based on the decision policy , which is determined in the Q-table, .
3.2.3. State Transition Model
A transition from to having reward at action is characterized by the conditional transition probability . By exploiting Q-learning, we aim to maximize the long-term reward for the given weather attenuation condition, which can be stated as
where is the discount factor and the reward is calculated based on the objective function in as explained below.
3.2.4. Rewards
Without loss of generality, the reward function is formulated by the total network throughput for the given weather attenuation. If the action that the UAV carries out at current time t can improve , then the UAV receives a positive reward. The UAV agent receives a negative reward otherwise. Hence, the reward function can be stated as [50]
Algorithm 2 outlines the complete RL approach for solving P2. The plot in Figure 4 depicts the algorithm’s convergence for the use-case of 0.8 km. It is worth noting that the algorithm converges in approximately 1800 episodes, each of which has 250 steps.
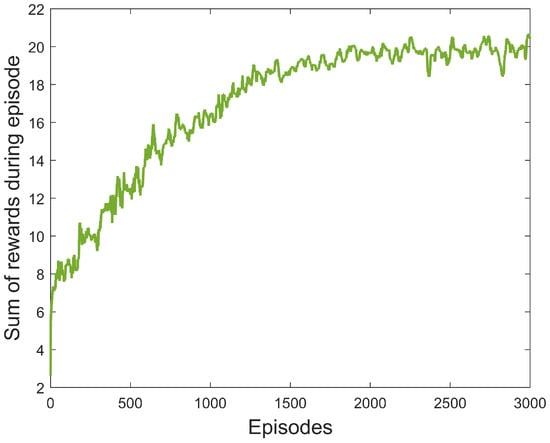
Figure 4.
Convergence of the Q-Learning algorithm; based on our experiments, it converges within around 1800 episodes.
Remark 1.
It is also worth noting that the system is trained for random user distributions with uniform statistics, while the convergence for a more predictable user distribution is expected to be substantially faster. After training, the model can quickly determine optimal values and for any user distribution. (The non-uniform and clustered user distribution will be considered in future work.)
| Algorithm 2:Q-Learning Algorithm for UAV Deployment and Resource Partition Optimization |
 |
3.3. Additional Performance Metric
The main goal of the proposed scheme is to maximize the end-to-end system throughput and allow users to associate with the preferable BS. However, we could also consider other important metrics to evaluate and compare the performance of the systems. To this end, we employ Jain’s fairness index, which is an important measure of fairness, and it is defined as [51,52]
where represents the data rate of the kth user, irrespective of its associated BS. In comparison to other measures, Jain’s index has a fairness criterion that considers all system users, not only the users that are allocated minimal resources. Note that lies in the range where 1 corresponds to the fairest allocation; i.e., every user receives the same data rate.
3.4. Complexity and Convergence Analysis
The computational complexity of the Q-learning algorithm scales linearly with the number of states and the number of actions [53]. The complexity of the proposed Algorithm 2 is the same as Q-learning, which is . Since our action-space consists of only four actions, the complexity could be reduced to only . Note that we can obtain a tradeoff between the accuracy and model complexity when the discretization of state-space is appropriately chosen. The complexity of the matching GT-based Algorithm 1 depends on the number of user association transfers . Therefore, the complexity of the proposed framework is . Moreover, studies have proved that both Q-learning [53] and the matching game [47] are guaranteed to converge if sufficient iterations are provided.
4. Numerical Results and Discussion
In this section, we present some simulation results for our proposed system as an application of user offloading during the adverse weather conditions as plotted in Figure 1. Unless otherwise stated, the values of the system parameters used for the numerical simulations are listed in Table 1. The AWGN noise power is assumed to be = −90 dBm [10,54]. In addition, a moderate turbulence condition with [55] is considered. The minimum threshold capacity of the FSO link corresponds to the weather-attenuation coefficient 10 dB/km.

Table 1.
Simulation parameters.
Note that CUDE is a suboptimal CURE scheme with lower complexity. That is, the UAV deployment (i.e., altitude) under the CUDE scheme is based on (9), while the bandwidth partitioning factor is optimized to maximize the total network throughput, and it follows the same matching GT procedure as the CURE scheme. The benchmark CARE model uses a bias parameter for cell range expansion (CRE) [56] to encourage user association with the UAV. The CRE technique virtually increases the user’s received power by adding a bias value to balance the user load and improve the system’s performance. Otherwise, almost all users would like to be associated with the GBS under the maximum RSRP policy since the transmit power of UAV is practically lower than that of GBS. It is worth noting that the CARE scheme does not consider the backhaul condition, and it employs an equal bandwidth (i.e., ) allocation policy to all users.
Firstly, we plot the individual BS throughput and user association probability as a function of weather attenuation coefficient for the proposed CURE scheme in Figure 5. Note that user association probability could be defined as the ratio of the number of users connected to a specific BS to the total number of users. One can see that both individual BS throughput and user association probability are an increasing and decreasing function of the weather attenuation coefficient for the UAV and GBS, respectively. That is, as increases, the capacity of the FSO backhaul diminishes, causing an increasing number of users to migrate from the GBS to the UAV, which illustrates the importance of UAV deployment during an infrequent foggy weather situation. In addition, Figure 6 shows the optimal UAV altitude and bandwidth allocation factor against an increasing weather attenuation coefficient . As the weather deteriorates, the UAV is assigned more bandwidth resources so that it could offload more users and increase total system throughput; also, as the FSO backhaul becomes less reliable, the UAV’s altitude is increased to cover the entire cell. As the optimal value of both parameters varies, it emphasizes the need for optimizing these parameters with regard to a particular weather attenuation condition.
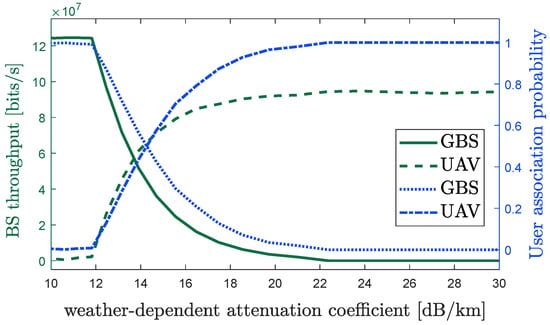
Figure 5.
Individual BS throughput and user association probability as a function of increasing weather-attenuation coefficient for CURE model.
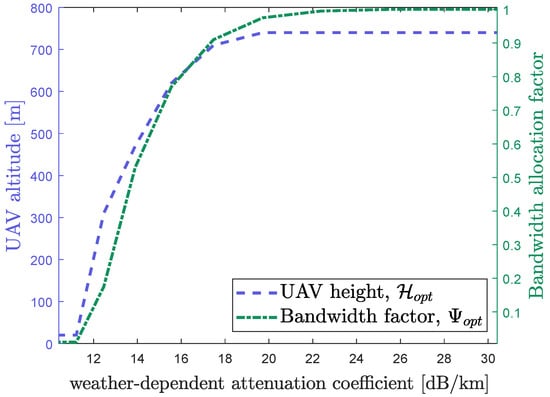
Figure 6.
Optimal UAV altitude and bandwidth partition between two BSs as a function of increasing weather-attenuation coefficient for the proposed CURE model.
We illustrate the user association between the GBS and the UAV for the proposed CURE scheme under three low-visibility conditions for the conventional case in Figure 7 wherein the transmit power of GBS is higher than the UAV i.e., . The users associated with the GBS and the UAV are represented by the blue and orange dots (100 trials), respectively. Under a low visibility situation in Figure 7a,b, the UAV tends to cover the majority of users in the middle of the coverage region, whereas the GBS covers some users closer to the origin and at the edges. This is particularly interesting because due to the relatively high weather attenuation at visibility km, the GBS backhaul cannot support many users which are offloaded to the UAV. More interestingly, since the UAV’s access link is weaker than that of the GBS (due to its lower transmit power) despite a better UAV–user LoS channel, it hovers at an intermediate altitude to cover users in the middle of the cell. In fact, this inhibits the use of exclusive inner and outer ring coverage (e.g., [10]) for the GBS and UAV, respectively, when the GBS backhaul is not reliable. However, as the visibility increases further in Figure 7c to 0.9 km, the GBS backhaul is relatively more reliable, but it is not entirely capable of supporting all access traffic. Thus, the UAV is pushed to cover users in the center rather than at the edges due to the UAV’s limited transmit power, and it also hovers at a low altitude (e.g., 184 m).
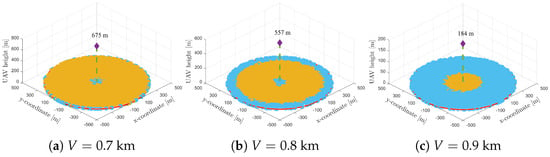
Figure 7.
Three–dimensional (3D) coverage map and UAV altitude for three low-visibility regimes when ; the blue and orange dots represent users associated with the GBS and UAV, respectively.
On the other hand, when the transmit power of both the BSs is comparable in Figure 8 (equal in this case, ), the GBS’s coverage shrinks to a small region close to the origin. Note that this situation is not practical because UAVs have limited power and their transmit power is usually not comparable to that of a GBS; rather, these results are plotted to show how the system behaves when both BSs have comparable transmit powers. One can note that in all three visibility scenarios presented in Figure 8, the UAV covers most of the cell (outer region) because it has a better channel and same transmit power level that offers an advantage; therefore, more users would like to be associated with the UAV. However, the UAV would tend to fly at a higher altitude to cover the entire cell, which allows the users closer to the origin to prefer GBS compared to the UAV. As visibility improves, the altitude of the UAV increases because the GBS with a more reliable backhaul can support more users closer to the origin, and the UAV serves the majority of the users away from the origin to maximize total network throughput.
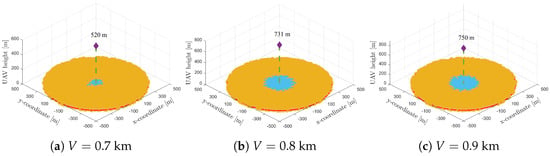
Figure 8.
Three–dimensional (3D) coverage map and UAV altitude for three low visibility regimes when ; the blue and orange dots represent users associated with the GBS and UAV, respectively.
The results in Figure 9 show the superior system throughput performance of the proposed CURE scheme over the conventional user association methods. It is evident that the proposed suboptimal CUDE model exhibits closer performance to the CURE scheme compared to the other benchmark cases. However, the performance limitation is caused by the traditional UAV placement method (edge user-based UAV deployment) despite the implementation of a backhaul-aware user association policy. One can note that the CARE scheme’s performance, in both cases of 5 dB and 10 dB of added power for CRE, deteriorates as the weather attenuation increases. This is because the user association disregards the FSO link reliability and only cares about access link conditions. As expected, the performance of GBSO increasingly deteriorates as the weather attenuation increases, because the FSO backhaul becomes more unreliable as increases. The proposed CURE scheme achieves the best total system throughput performance and offers users the flexibility to choose their preferred BS to enhance their user experience. However, it is worth assessing the impact of this objective on the fairness of the users. To do this, we employ the widely used Jain’s fairness index , as outlined in (26). The results in Figure 10 clearly illustrate that the proposed CURE scheme offers good fairness results to the users, while the fixed altitude case of the proposed model (i.e., CUDE, which is also backhaul-aware but with a fixed UAV altitude) leads in terms of fairness performance. It is worth noting here that the Jain’s fairness index evaluates the disparity of the data rates within an individual scheme. That is, if a scheme has very low system throughput (e.g., GBSO in Figure 9), it can still be very fair if all the users have comparable data rates. The GBSO scheme is a classic illustration of this situation, as shown in Figure 10.
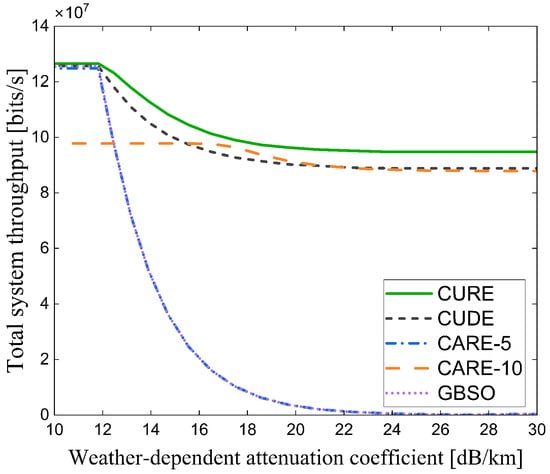
Figure 9.
Total system throughput of all the models versus the weather-dependent attenuation coefficient of the FSO link.
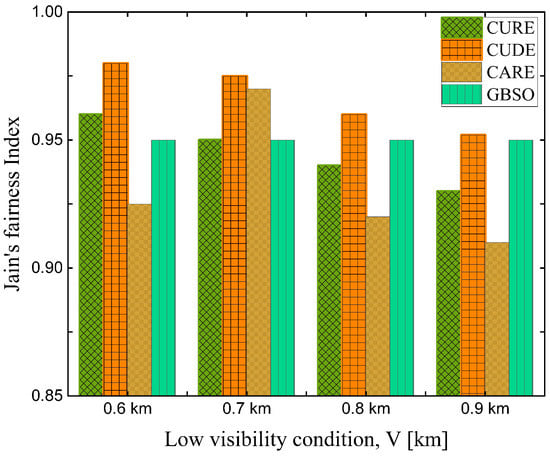
Figure 10.
Fairness performance of all the schemes under four low-visibility conditions.
We now evaluate how our system would perform in a realistic channel model that uses climate data from the cities of Edinburgh and London. Figure 11 plots the histogram of hourly visibility for Edinburgh and London as reported by the United Kingdom Meteorological Office for January 2019 to June 2020, totaling = 13,106 h (Edinburgh), = 13,128 h (London). As can be seen, the probability of fog events (visibility < 1 km) which can severely deteriorate the FSO link’s performance is very small. Because FSO links function well most of the time, fixed hybrid FSO/RF links with permanent or backup RF links are not necessarily the most cost-effective and practical solution all the time [6]. To this end, it encourages researchers to come up with short-term solutions such as the one proposed here. These approaches might play a significant role in B5G networks where UAVs can offload traffic from the BS during rare low-visibility situations.
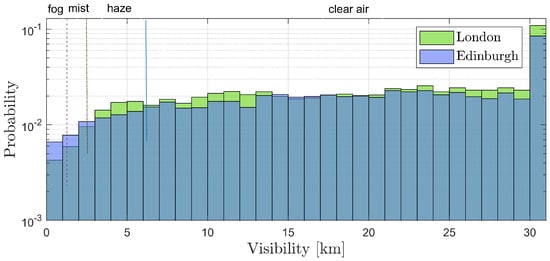
Figure 11.
Hourly visibility histogram for Edinburgh and London from January 2019 to June 2020.
We use fog events to simulate the total system throughput using the hourly visibility data, with low visibility hours of 87 and 56 for Edinburgh and London, respectively. Figure 12 demonstrates that the proposed CURE scheme outperforms the other systems, including the GBSO, CUDE, and CARE scheme during the fog events in both cities. When visibility is near 1 km, the CUDE and CARE schemes rarely perform comparably to the proposed CURE scheme. On the other hand, the CURE scheme performs well throughout the fog events in both London and Edinburgh, even when the counterpart models perform poorly. For example, during fog hour 26 and 30 in Edinburgh and London, respectively, the GBSO’s throughput is almost zero, while the CURE scheme still offers better throughput compared to the CUDE and CARE scheme in both Edinburgh and London.
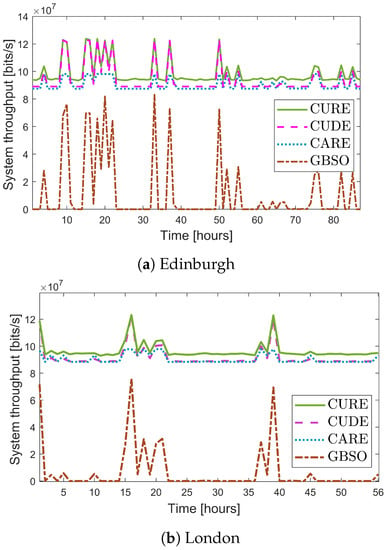
Figure 12.
The end-to-end system throughput of the proposed and benchmark schemes versus the fog hours in Edinburgh and London from January 2019 to June 2020.
5. Conclusions
A novel hybrid FSO/RF system based on the matching game theory and RL is proposed in this study with the use of UAV-assisted user offloading. Originally, only the GBS is serving the coverage area, and no UAV is assumed to be involved. However, when the infrequent adverse weather strikes to impair the FSO link’s availability, the GBS can be augmented by a UAV. It helps to establish a dual-hop RF link to maintain its throughput to the MBS by using a portion of the RF spectrum from the GBS node. The problem is solved using a layered framework, where the user association is performed using a matching-game while the UAV’s altitude optimization and bandwidth resource sharing with the GBS are optimized using RL. Numerical simulations demonstrate that the proposed approach can considerably increase the system’s total throughput under the adverse weather conditions when compared to the FSO-only and other benchmark schemes. A realistic channel based on Edinburgh and London weather records was used to evaluate the proposed system’s performance; the proposed system showed a significant increase in throughput which can increase the network availability over the other schemes. With the expected exponential growth of FSO nodes in B5G networks, the findings of this study motivate the development of temporary and practical UAV-assisted FSO backhaul solutions. These condition-aware hybrid FSO/RF systems will optimize the network performance during rare weather situations, which considerably hamper the FSO link’s capacity.
Author Contributions
Conceptualization, M.N., S.H. and M.S.; Methodology, M.N., S.H. and M.S.; Validation, S.H. and M.S.; Investigation, M.N.; Writing—original draft, M.N.; Writing—review and editing, M.N., S.H., J.T. and M.S.; Visualization, M.N.; Supervision, J.T. and M.S.; Project administration, M.N. and S.H.; Funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Majid Safari was supported by the Engineering and Physical Sciences Research Council (EPSRC) through the Terabit Bidirectional Multi-User Optical Wireless System (TOWS) for 6G LiFi under Program EP/S016570/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the Meteorological Office of the United Kingdom for supplying measured hourly temperature and visibility data for January 2019 to June 2020 from the Edinburgh Gogarbank and the London Heathrow weather stations.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AWGN | additive white Gaussian noise |
| B5G | beyond fifth-generation |
| BS | base station |
| CRE | cell range expansion |
| FSO | free-space optical |
| GBS | ground base station |
| GBSO | GBS only |
| GT | game theory |
| IM/DD | intensity modulation direct detection |
| MBS | macro base station |
| ML | machine learning |
| QoS | quality of service |
| RF | radio frequency |
| RL | reinforcement learning |
| RSRP | reference signal received power |
| UAVs | unmanned aerial vehicles |
References
- Jiang, W.; Han, B.; Habibi, M.A.; Schotten, H.D. The Road Towards 6G: A Comprehensive Survey. IEEE Open J. Commun. Soc. 2021, 2, 334–366. [Google Scholar] [CrossRef]
- Ullah, Z.; Al-Turjman, F.; Mostarda, L. Cognition in UAV-Aided 5G and Beyond Communications: A Survey. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 872–891. [Google Scholar] [CrossRef]
- Dang, S.; Amin, O.; Shihada, B.; Alouini, M.S. What should 6G be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef]
- Bekkali, A.; Fujita, H.; Hattori, M. New Generation Free-Space Optical Communication Systems With Advanced Optical Beam Stabilizer. J. Light. Technol. 2022, 40, 1509–1518. [Google Scholar] [CrossRef]
- Agheli, P.; Emadi, M.J.; Beyranvand, H. Cognitive RF-FSO Fronthaul Assignment in Cell-Free and User-Centric mMIMO Networks. IEEE Trans. Mob. Comput. 2021. [Google Scholar] [CrossRef]
- Huang, S.; Shah-Mansouri, V.; Safari, M. Game-Theoretic Spectrum Trading in RF Relay-Assisted Free-Space Optical Communications. IEEE Trans. Wirel. Commun. 2019, 18, 4803–4815. [Google Scholar] [CrossRef]
- Yahia, O.B.; Erdogan, E.; Kurt, G.K.; Altunbas, I.; Yanikomeroglu, H. A Weather-Dependent Hybrid RF/FSO Satellite Communication for Improved Power Efficiency. IEEE Wirel. Commun. Lett. 2022, 11, 573–577. [Google Scholar] [CrossRef]
- Hassan, M.Z.; Hossain, M.J.; Cheng, J.; Leung, V.C.M. Hybrid RF/FSO Backhaul Networks With Statistical-QoS-Aware Buffer-Aided Relaying. IEEE Trans. Wirel. Commun. 2020, 19, 1464–1483. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, H.; Shu, L.; Liu, Y. UAV-Assisted Sleep Scheduling Algorithm for Energy-Efficient Data Collection in Agricultural Internet of Things. IEEE Internet Things J. 2022, 9, 11043–11056. [Google Scholar] [CrossRef]
- Ali, M.A.; Jamalipour, A. UAV-Aided Cellular Operation by User Offloading. IEEE Internet Things J. 2021, 8, 9855–9864. [Google Scholar] [CrossRef]
- Hu, Z.; Zheng, Z.; Song, L.; Wang, T.; Li, X. UAV offloading: Spectrum trading contract design for UAV-assisted cellular networks. IEEE Trans. Wirel. Commun. 2018, 17, 6093–6107. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R. UAV-Aided Offloading for Cellular Hotspot. IEEE Trans. Wirel. Commun. 2018, 17, 3988–4001. [Google Scholar] [CrossRef]
- Yan, H.; Bao, W.; Zhu, X.; Wang, J.; Liu, L. Data Offloading Enabled by Heterogeneous UAVs for IoT Applications under Uncertain Environments. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- Kouhdaragh, V.; Verde, F.; Gelli, G.; Abouei, J. On the application of machine learning to the design of UAV-based 5G radio access networks. Electronics 2020, 9, 689. [Google Scholar] [CrossRef]
- Fan, B.; Jiang, L.; Chen, Y.; Zhang, Y.; Wu, Y. UAV Assisted Traffic Offloading in Air Ground Integrated Networks With Mixed User Traffic. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12601–12611. [Google Scholar] [CrossRef]
- Mukherjee, A.; Misra, S.; Chandra, V.S.P.; Obaidat, M.S. Resource-Optimized Multiarmed Bandit-Based Offload Path Selection in Edge UAV Swarms. IEEE Internet Things J. 2019, 6, 4889–4896. [Google Scholar] [CrossRef]
- Gao, A.; Wang, Q.; Liang, W.; Ding, Z. Game Combined Multi-Agent Reinforcement Learning Approach for UAV Assisted Offloading. IEEE Trans. Veh. Technol. 2021, 70, 12888–12901. [Google Scholar] [CrossRef]
- Asheralieva, A.; Niyato, D. Hierarchical Game-Theoretic and Reinforcement Learning Framework for Computational Offloading in UAV-Enabled Mobile Edge Computing Networks With Multiple Service Providers. IEEE Internet Things J. 2019, 6, 8753–8769. [Google Scholar] [CrossRef]
- Li, L.; Ren, H.; Cheng, Q.; Xue, K.; Chen, W.; Debbah, M.; Han, Z. Millimeter-Wave Networking in the Sky: A Machine Learning and Mean Field Game Approach for Joint Beamforming and Beam-Steering. IEEE Trans. Wirel. Commun. 2020, 19, 6393–6408. [Google Scholar] [CrossRef]
- Zhang, S.; Ansari, N. 3D Drone Base Station Placement and Resource Allocation With FSO-Based Backhaul in Hotspots. IEEE Trans. Veh. Technol. 2020, 69, 3322–3329. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, K.H.; Ko, Y.C.; Alouini, M.S. Spectral-Efficient Network Design for High-Altitude Platform Station Networks With Mixed RF/FSO System. IEEE Trans. Wirel. Commun. 2022, 21, 7072–7087. [Google Scholar] [CrossRef]
- Wang, J.Y.; Ma, Y.; Lu, R.R.; Wang, J.B.; Lin, M.; Cheng, J. Hovering UAV-Based FSO Communications: Channel Modelling, Performance Analysis, and Parameter Optimization. IEEE J. Sel. Areas Commun. 2021, 39, 2946–2959. [Google Scholar] [CrossRef]
- Ajam, H.; Najafi, M.; Jamali, V.; Schober, R. Ergodic Sum Rate Analysis of UAV-Based Relay Networks With Mixed RF-FSO Channels. IEEE Open J. Commun. Soc. 2020, 1, 164–178. [Google Scholar] [CrossRef]
- Che, Y.L.; Long, W.; Luo, S.; Wu, K.; Zhang, R. Energy-Efficient UAV Multicasting With Simultaneous FSO Backhaul and Power Transfer. IEEE Wirel. Commun. Lett. 2021, 10, 1537–1541. [Google Scholar] [CrossRef]
- Zhang, S.; Ansari, N. Latency Aware 3D Placement and User Association in Drone-Assisted Heterogeneous Networks With FSO-Based Backhaul. IEEE Trans. Veh. Technol. 2021, 70, 11991–12000. [Google Scholar] [CrossRef]
- Kouzayha, N.; Elsawy, H.; Dahrouj, H.; Alshaikh, K.; Al-Naffouri, T.Y.; Alouini, M.S. Analysis of Large Scale Aerial Terrestrial Networks with mmWave Backhauling. IEEE Trans. Wirel. Commun. 2021, 20, 8362–8380. [Google Scholar] [CrossRef]
- Zeng, Y.; Lyu, J.; Zhang, R. Cellular-Connected UAV: Potential, Challenges, and Promising Technologies. IEEE Wirel. Commun. 2019, 26, 120–127. [Google Scholar] [CrossRef]
- Jamali, V.; Michalopoulos, D.S.; Uysal, M.; Schober, R. Link allocation for multiuser systems with hybrid RF/FSO backhaul: Delay-limited and delay-tolerant designs. IEEE Trans. Wirel. Commun. 2016, 15, 3281–3295. [Google Scholar] [CrossRef]
- Kim, I.I.; Koontz, J.; Hakakha, H.; Adhikari, P.; Stieger, R.; Moursund, C.; Barclay, M.; Stanford, A.; Ruigrok, R.; Schuster, J.J.; et al. Measurement of scintillation and link margin for the TerraLink laser communication system. Proc. SPIE 1998, 3232, 100–118. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Tsiftsis, T.A.; Tombras, G.S. Performance analysis of free-space optical communication systems over atmospheric turbulence channels. IET Commun. 2009, 3, 1402–1409. [Google Scholar] [CrossRef]
- Al-Habash, A.; Andrews, L.C.; Phillips, R.L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- He, B.; Schober, R. Bit-interleaved coded modulation for hybrid RF/FSO systems. IEEE Trans. Commun. 2009, 57, 3753–3763. [Google Scholar] [CrossRef]
- Lapidoth, A.; Moser, S.M.; Wigger, M.A. On the capacity of free-space optical intensity channels. IEEE Trans. Inf. Theory 2009, 55, 4449–4461. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage Capacity Optimization for Free-Space Optical Links With Pointing Errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Izadpanah, H.; ElBatt, T.; Kukshya, V.; Dolezal, F.; Ryu, B. High-availability free space optical and RF hybrid wireless networks. IEEE Wirel. Commun. 2003, 10, 45–53. [Google Scholar] [CrossRef]
- Nafees, M.; Thompson, J.; Safari, M. Multi-Tier Variable Height UAV Networks: User Coverage and Throughput Optimization. IEEE Access 2021, 9, 119684–119699. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Unmanned Aerial Vehicles (UAVs) for Energy-Efficient Internet of Things Communications. IEEE Trans. Wirel. Commun. 2017, 16, 7574–7589. [Google Scholar] [CrossRef]
- Khuwaja, A.A.; Zheng, G.; Chen, Y.; Feng, W. Optimum Deployment of Multiple UAVs for Coverage Area Maximization in the Presence of Co-Channel Interference. IEEE Access 2019, 7, 85203–85212. [Google Scholar] [CrossRef]
- Namvar, N.; Homaifar, A.; Karimoddini, A.; Maham, B. Heterogeneous UAV Cells: An Effective Resource Allocation Scheme for Maximum Coverage Performance. IEEE Access 2019, 7, 164708–164719. [Google Scholar] [CrossRef]
- Azari, M.M.; Rosas, F.; Chen, K.; Pollin, S. Ultra Reliable UAV Communication Using Altitude and Cooperation Diversity. IEEE Trans. Commun. 2018, 66, 330–344. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Qian, C.; Zhang, W.; Zhou, W. Performance Evaluation of Reference Signal Received Power Strength Based Idle Users’ Cell Selection in 3GPP LTE. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Ghimire, J.; Rosenberg, C. Revisiting Scheduling in Heterogeneous Networks When the Backhaul Is Limited. IEEE J. Sel. Areas Commun. 2015, 33, 2039–2051. [Google Scholar] [CrossRef]
- Nadeem, F.; Kvicera, V.; Awan, M.S.; Leitgeb, E.; Muhammad, S.S.; Kandus, G. Weather effects on hybrid FSO/RF communication link. IEEE J. Sel. Areas Commun. 2009, 27, 1687–1697. [Google Scholar] [CrossRef]
- Mkiramweni, M.E.; Yang, C.; Li, J.; Zhang, W. A Survey of Game Theory in Unmanned Aerial Vehicles Communications. IEEE Commun. Surv. Tutorials 2019, 21, 3386–3416. [Google Scholar] [CrossRef]
- LeAnh, T.; Tran, N.H.; Saad, W.; Le, L.B.; Niyato, D.; Ho, T.M.; Hong, C.S. Matching Theory for Distributed User Association and Resource Allocation in Cognitive Femtocell Networks. IEEE Trans. Veh. Technol. 2017, 66, 8413–8428. [Google Scholar] [CrossRef]
- Sekander, S.; Tabassum, H.; Hossain, E. Decoupled Uplink-Downlink User Association in Multi-Tier Full-Duplex Cellular Networks: A Two-Sided Matching Game. IEEE Trans. Mob. Comput. 2017, 16, 2778–2791. [Google Scholar] [CrossRef]
- Gu, Y.; Saad, W.; Bennis, M.; Debbah, M.; Han, Z. Matching theory for future wireless networks: Fundamentals and applications. IEEE Commun. Mag. 2015, 53, 52–59. [Google Scholar] [CrossRef]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y. Reinforcement Learning in Multiple-UAV Networks: Deployment and Movement Design. IEEE Trans. Veh. Technol. 2019, 68, 8036–8049. [Google Scholar] [CrossRef]
- Jain, R.K.; Chiu, D.M.W.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984; Volume 21. [Google Scholar]
- Sediq, A.B.; Gohary, R.H.; Schoenen, R.; Yanikomeroglu, H. Optimal Tradeoff Between Sum-Rate Efficiency and Jain’s Fairness Index in Resource Allocation. IEEE Trans. Wirel. Commun. 2013, 12, 3496–3509. [Google Scholar] [CrossRef]
- Valente Klaine, P.; Jaber, M.; Souza, R.D.; Imran, M.A. Backhaul Aware User-Specific Cell Association Using Q-Learning. IEEE Trans. Wirel. Commun. 2019, 18, 3528–3541. [Google Scholar] [CrossRef]
- Zeng, F.; Hu, Z.; Xiao, Z.; Jiang, H.; Zhou, S.; Liu, W.; Liu, D. Resource Allocation and Trajectory Optimization for QoE Provisioning in Energy-Efficient UAV-Enabled Wireless Networks. IEEE Trans. Veh. Technol. 2020, 69, 7634–7647. [Google Scholar] [CrossRef]
- Shakir, W.M.R. Performance evaluation of a selection combining scheme for the hybrid FSO/RF system. IEEE Photon. J. 2017, 10, 7901110. [Google Scholar] [CrossRef]
- Muhammad, F.; Abbas, Z.H.; Li, F.Y. Cell Association With Load Balancing in Nonuniform Heterogeneous Cellular Networks: Coverage Probability and Rate Analysis. IEEE Trans. Veh. Technol. 2017, 66, 5241–5255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).