A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments
Abstract
:1. Introduction
- •
- This study proposes a multi-sensor fusion scheme for UAV navigation and landing on a randomly moving non-cooperative UGV in GPS-denied environments.
- •
- In contrast to considering only distance measurement information at two time instants, this study selects measurements at multiple time instants to estimate the relative position and considers the case of measurement noise.
- •
- During the landing process, a landing controller based on position compensation is designed based on the fusion of distance measurement, vision and IMU positioning information.
- •
- Finally, the feasibility of the proposed scheme is verified and validated using a numerical simulation and a real experiment.
2. Problem Formulation
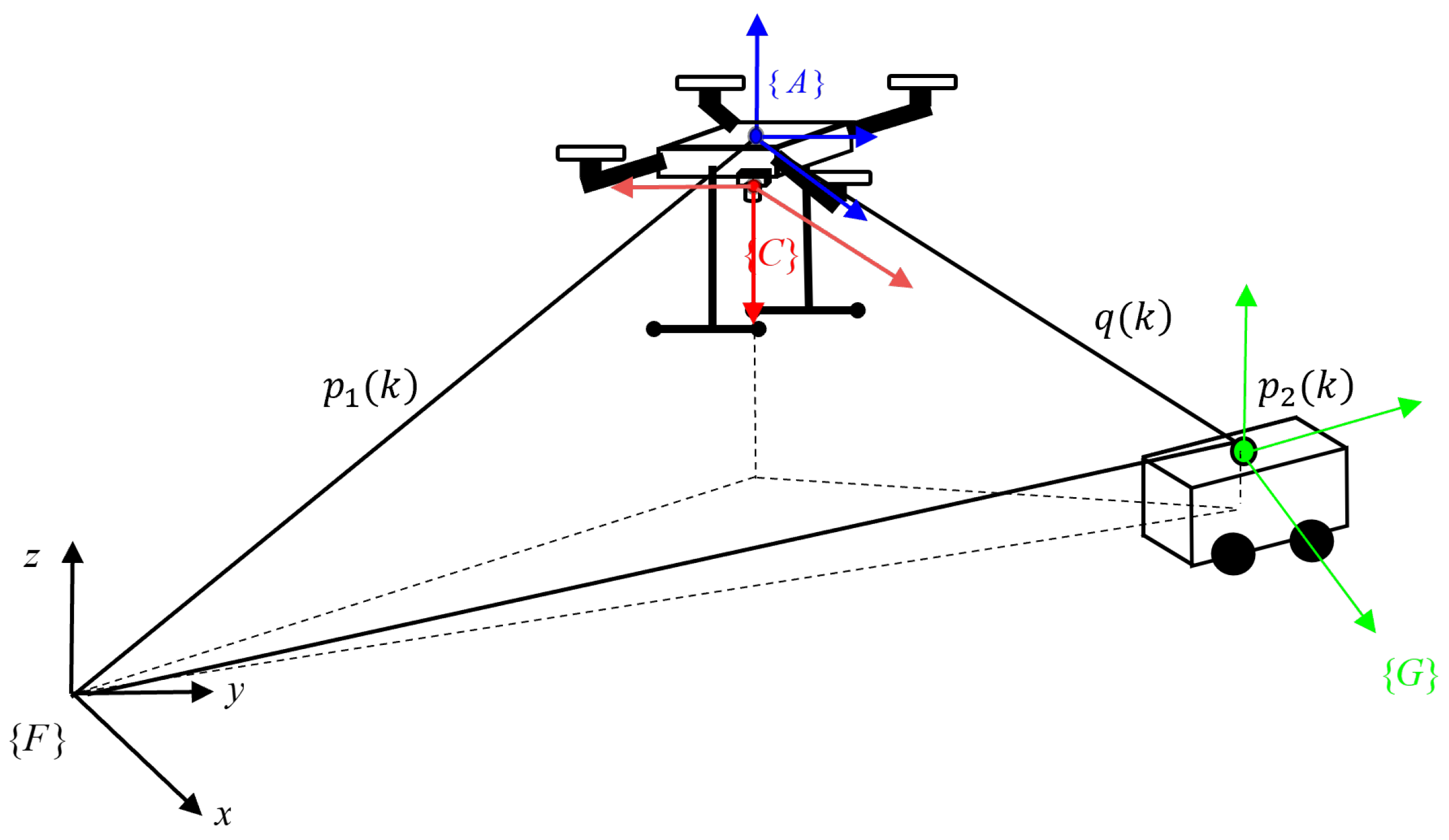
2.1. UAV and UGV Models
2.2. Relative Attitude Relationship of Two Vehicles
2.3. Control Objectives
3. Navigation Control Design
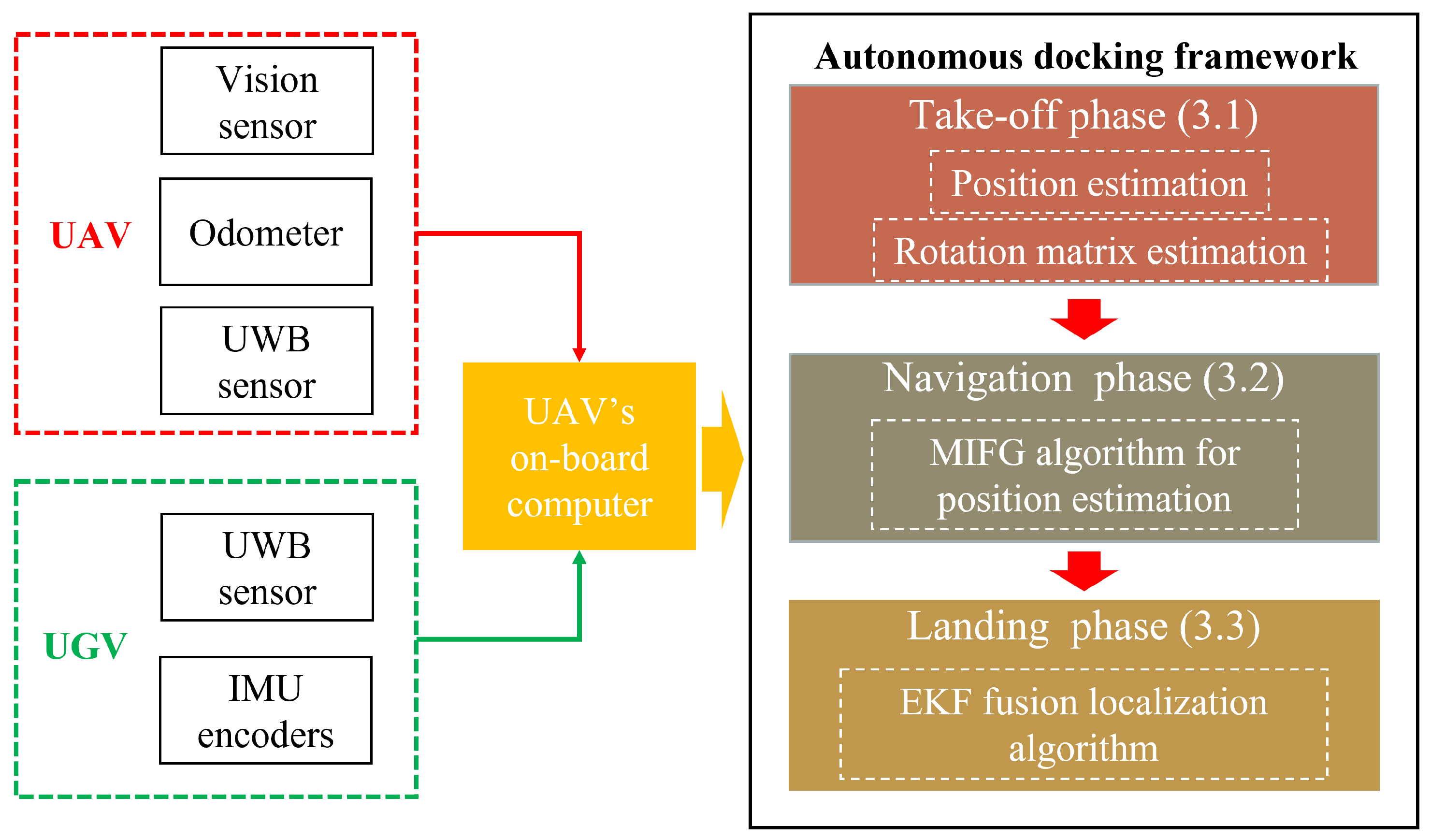
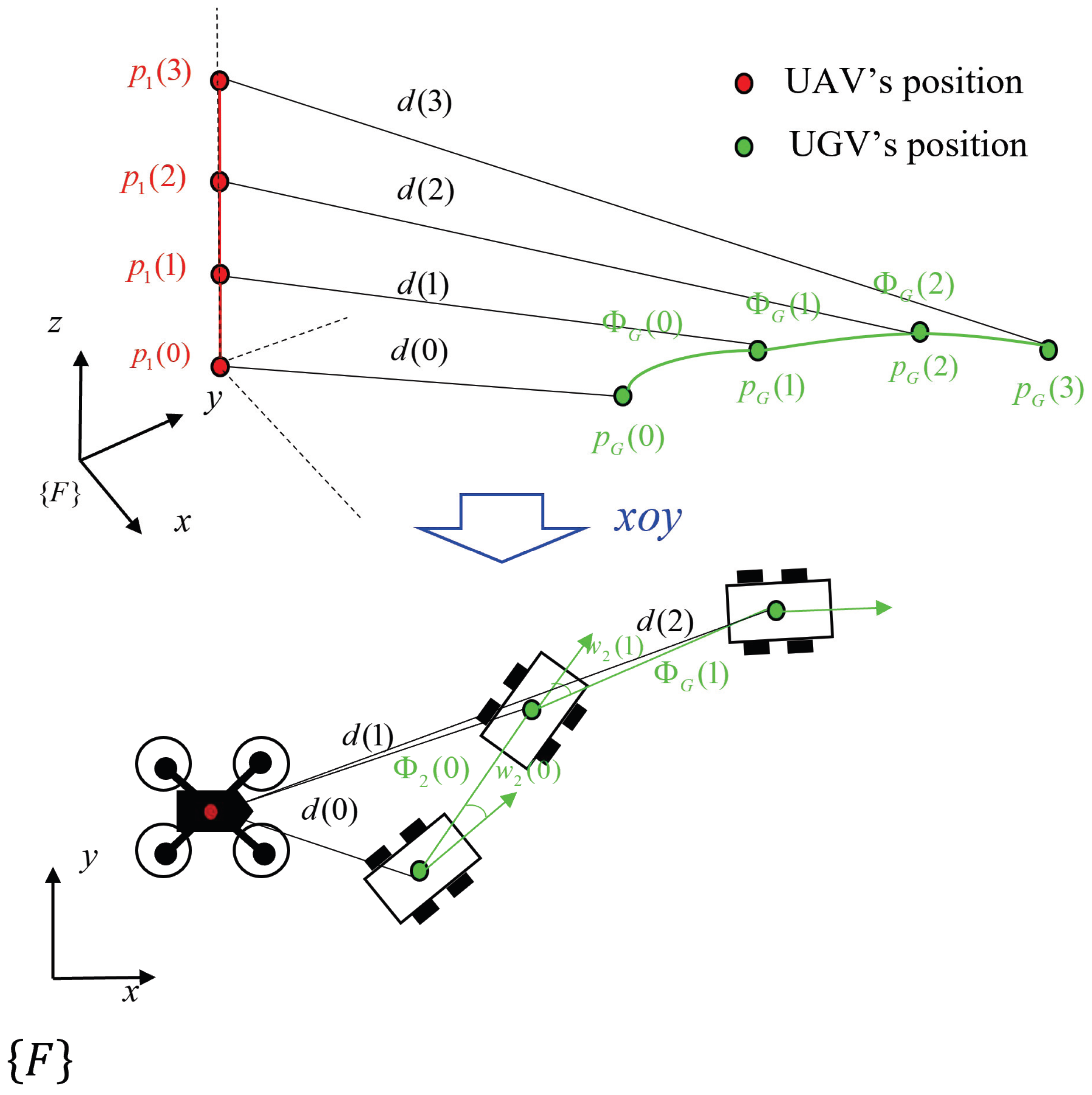
3.1. Take-Off Positioning Phase
3.2. Navigation Control Algorithm
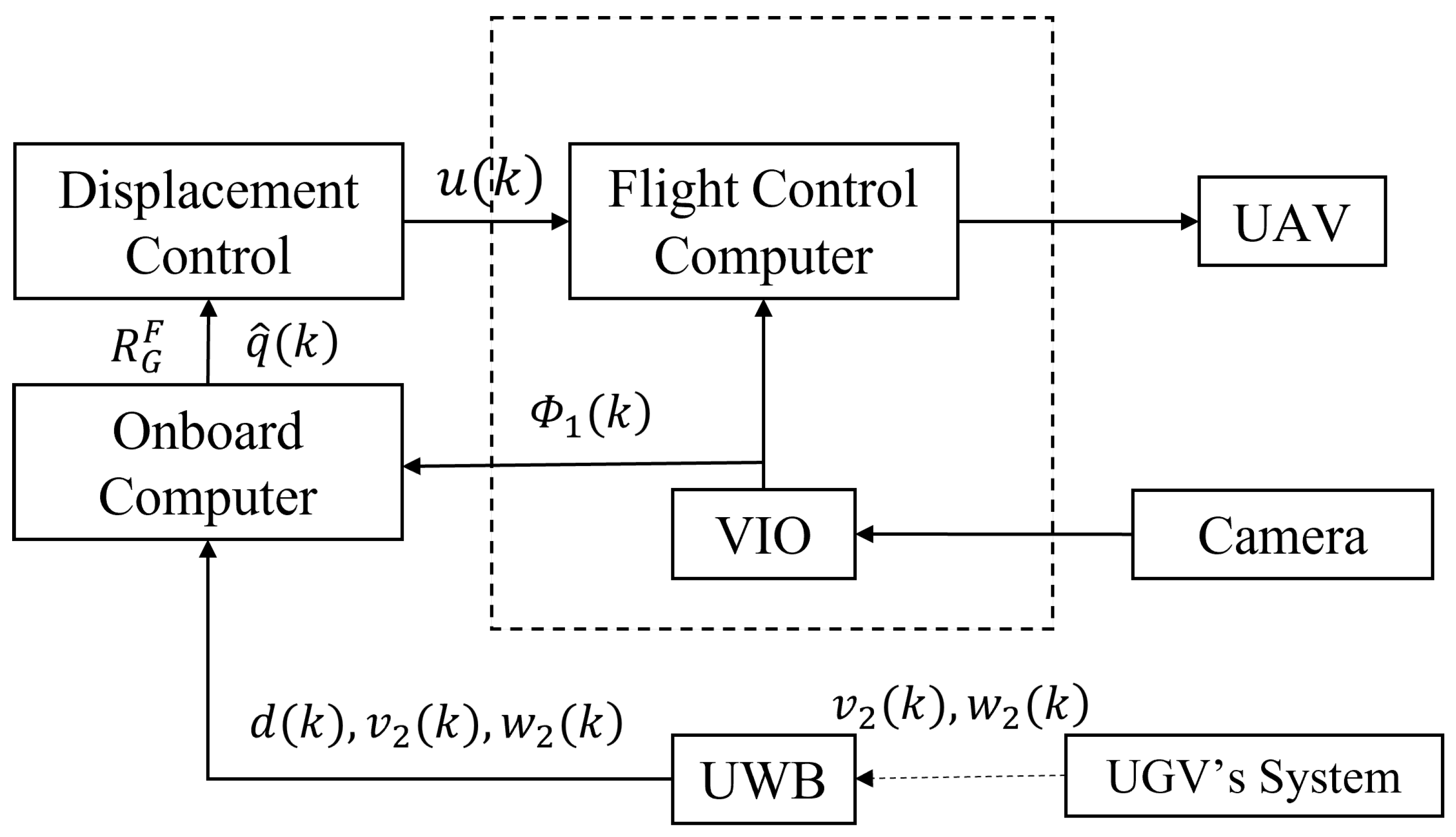
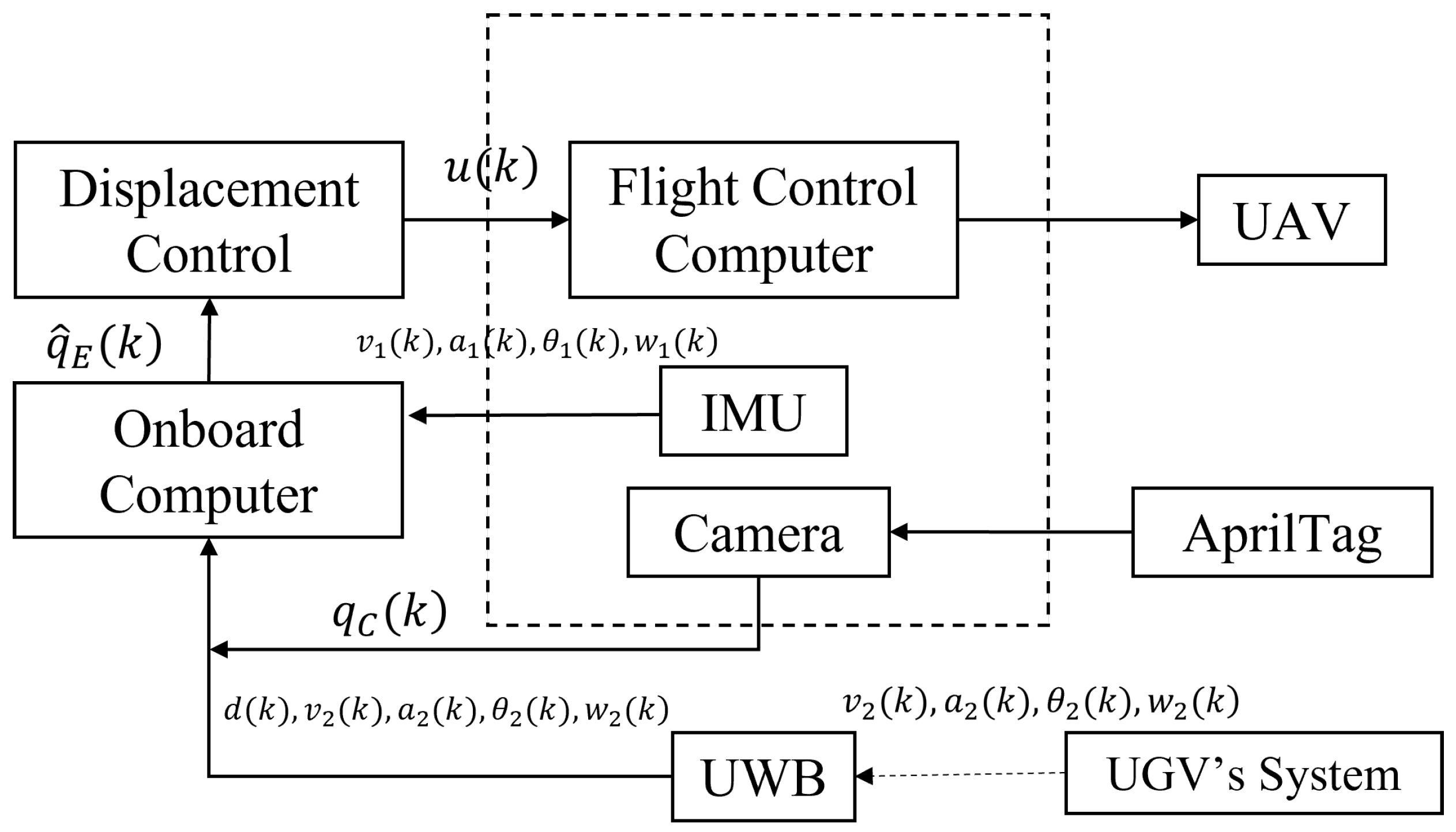
3.3. Multi-Sensor Fusion Landing Scheme
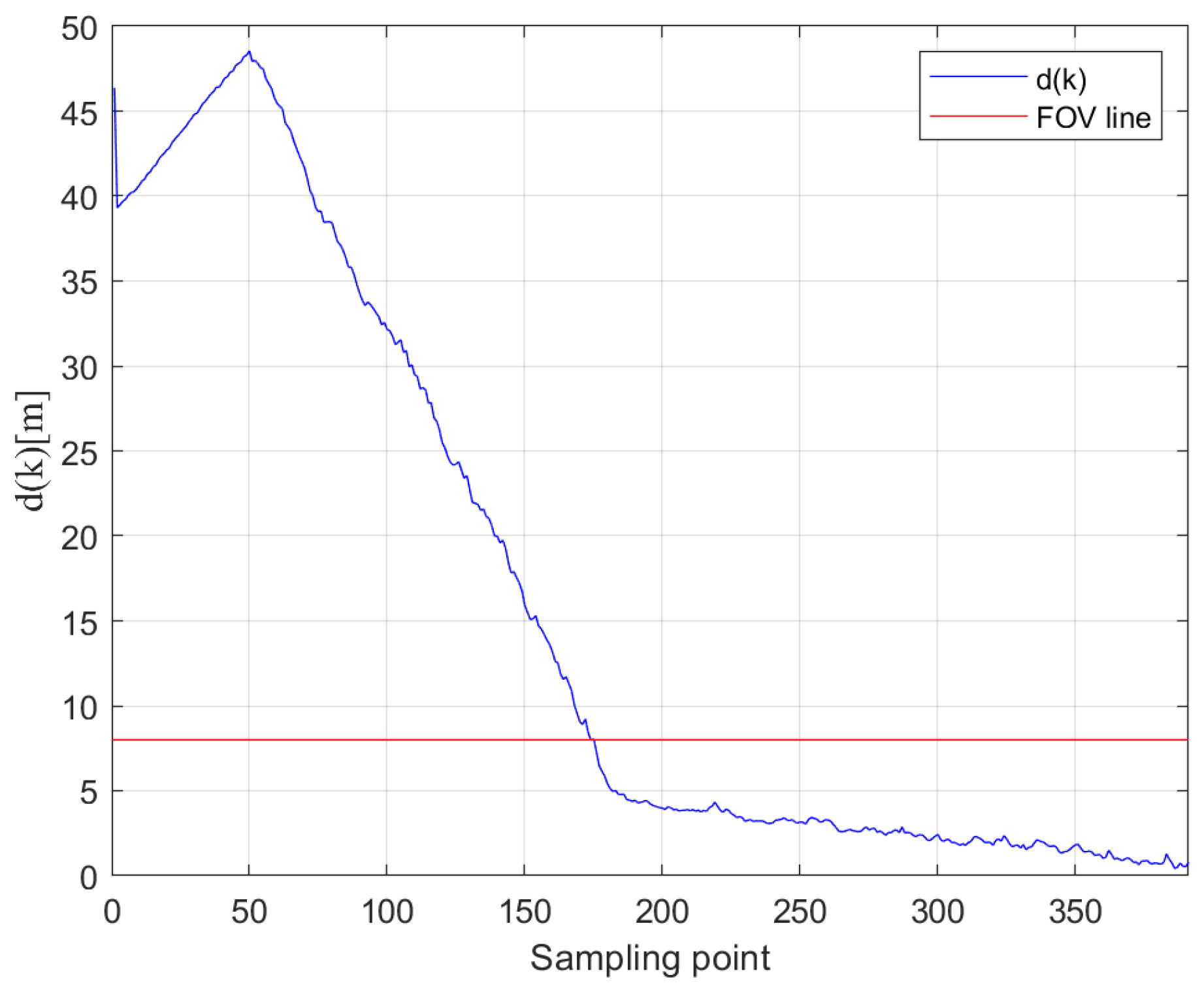
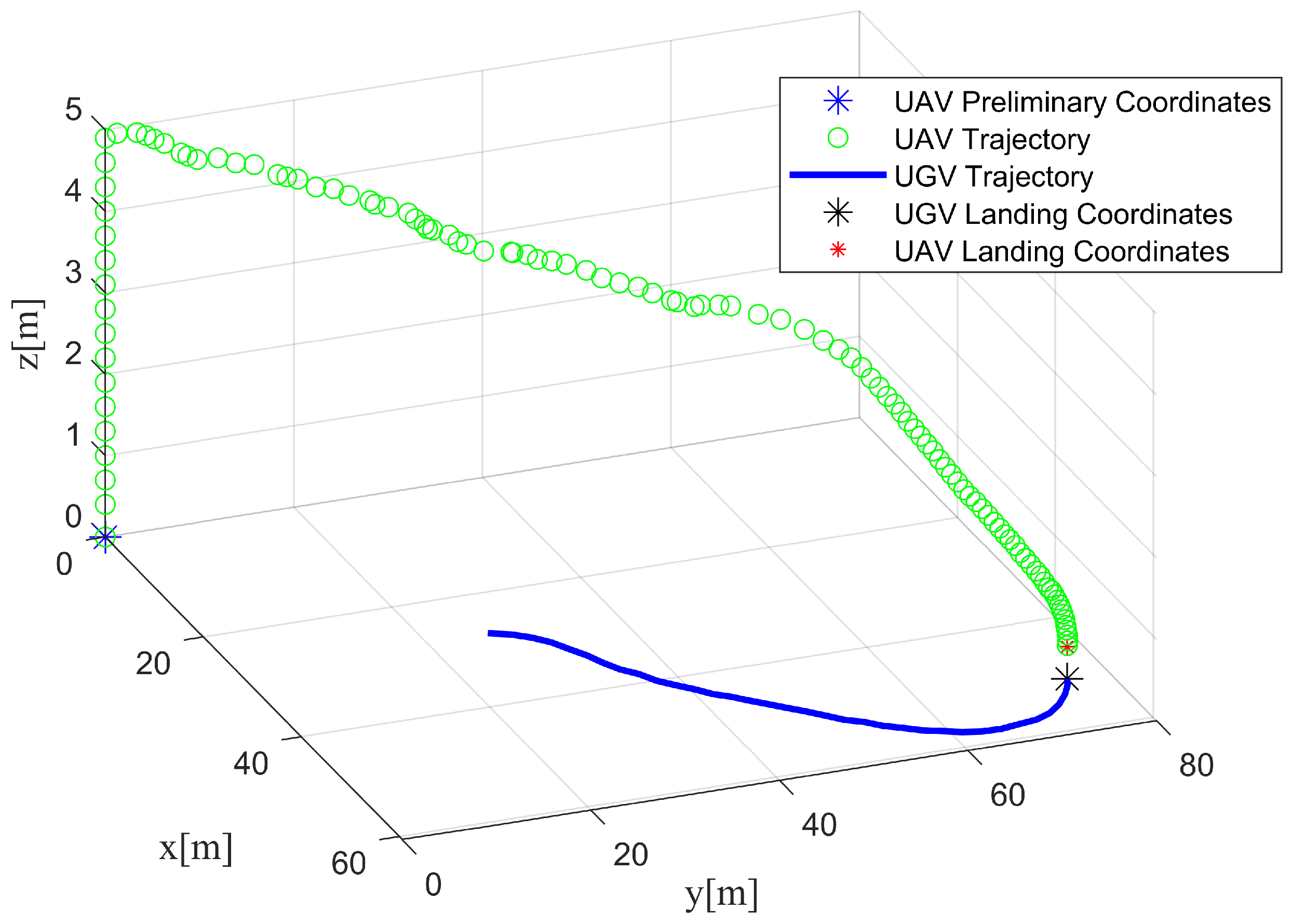
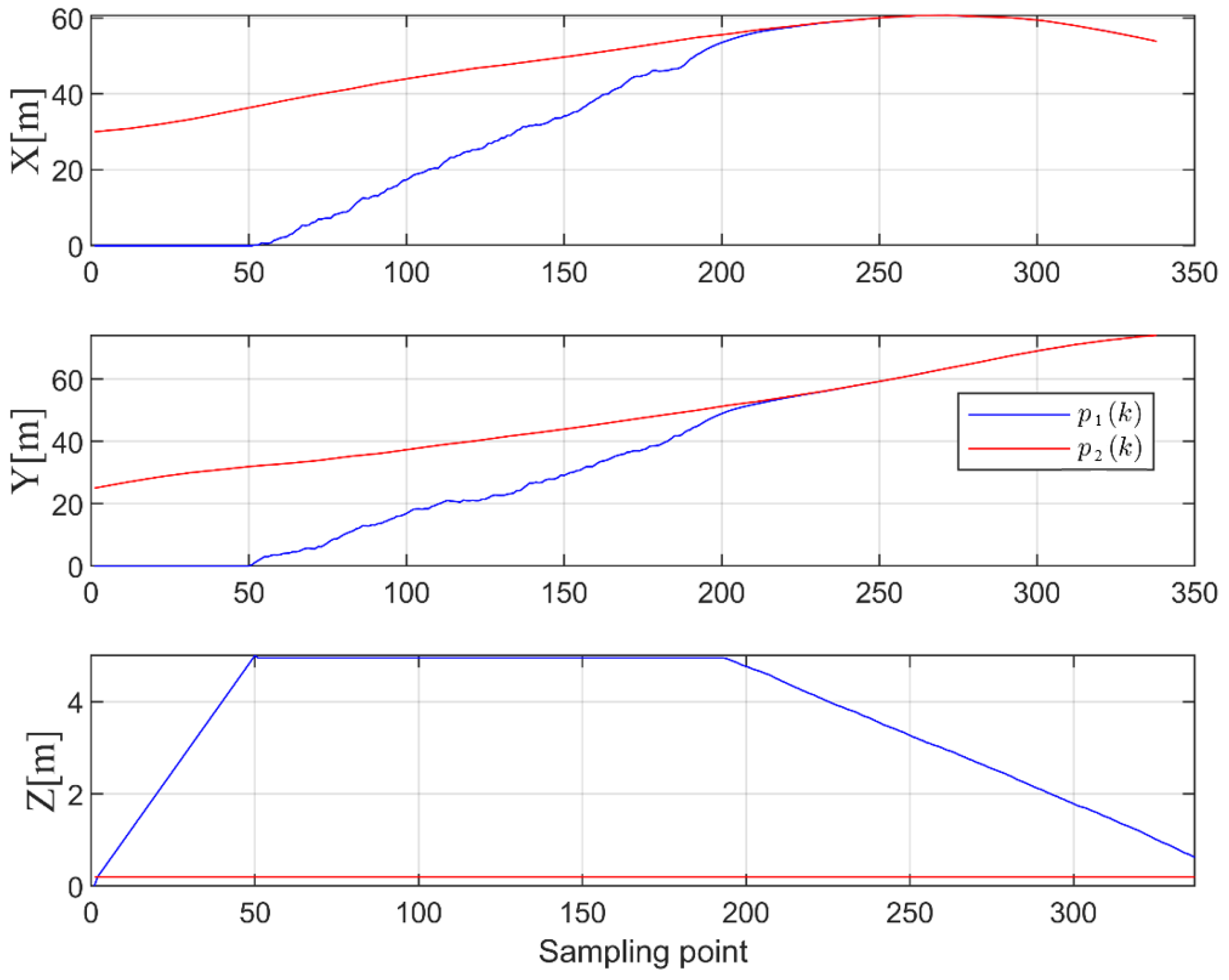
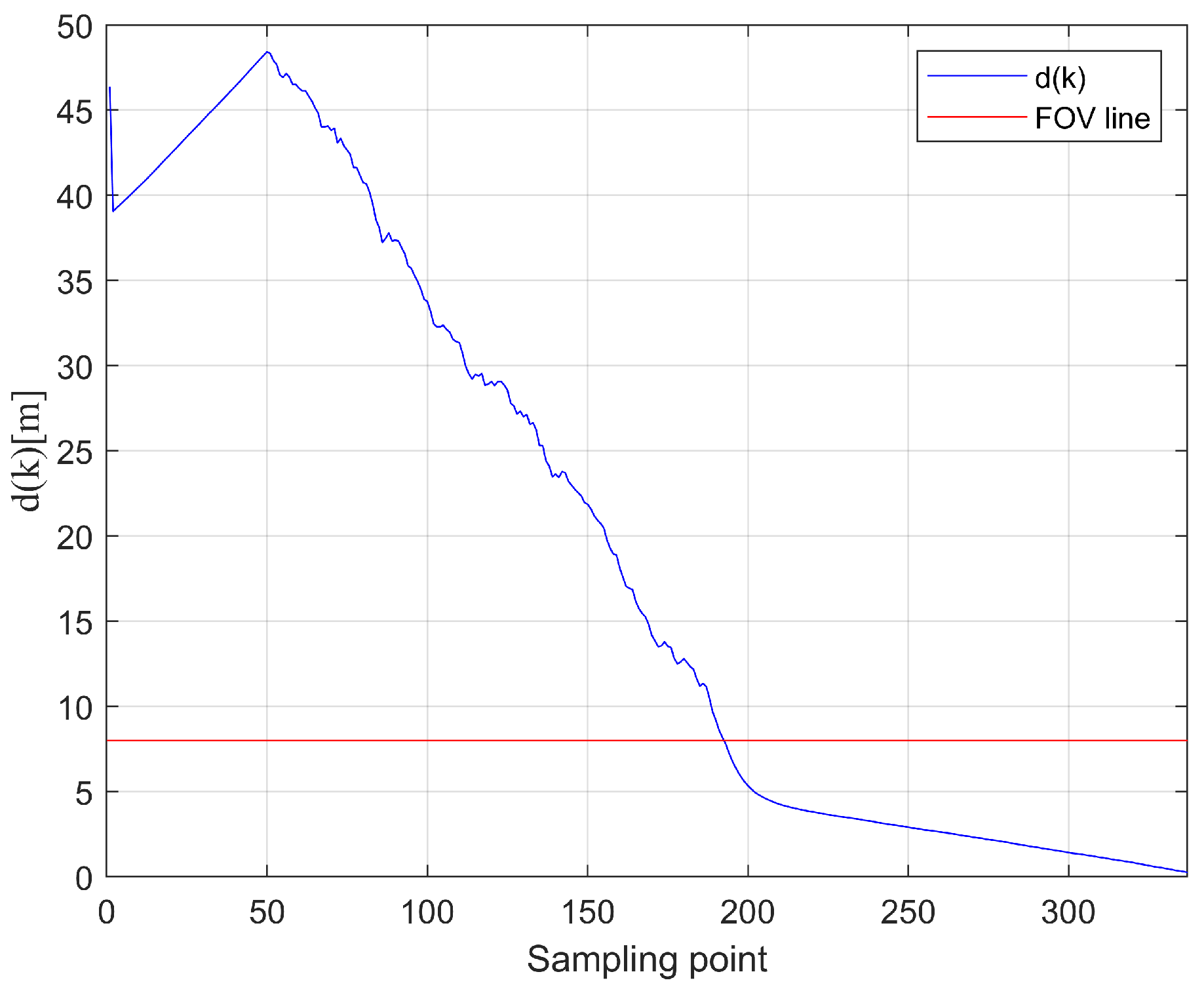
4. Experiments
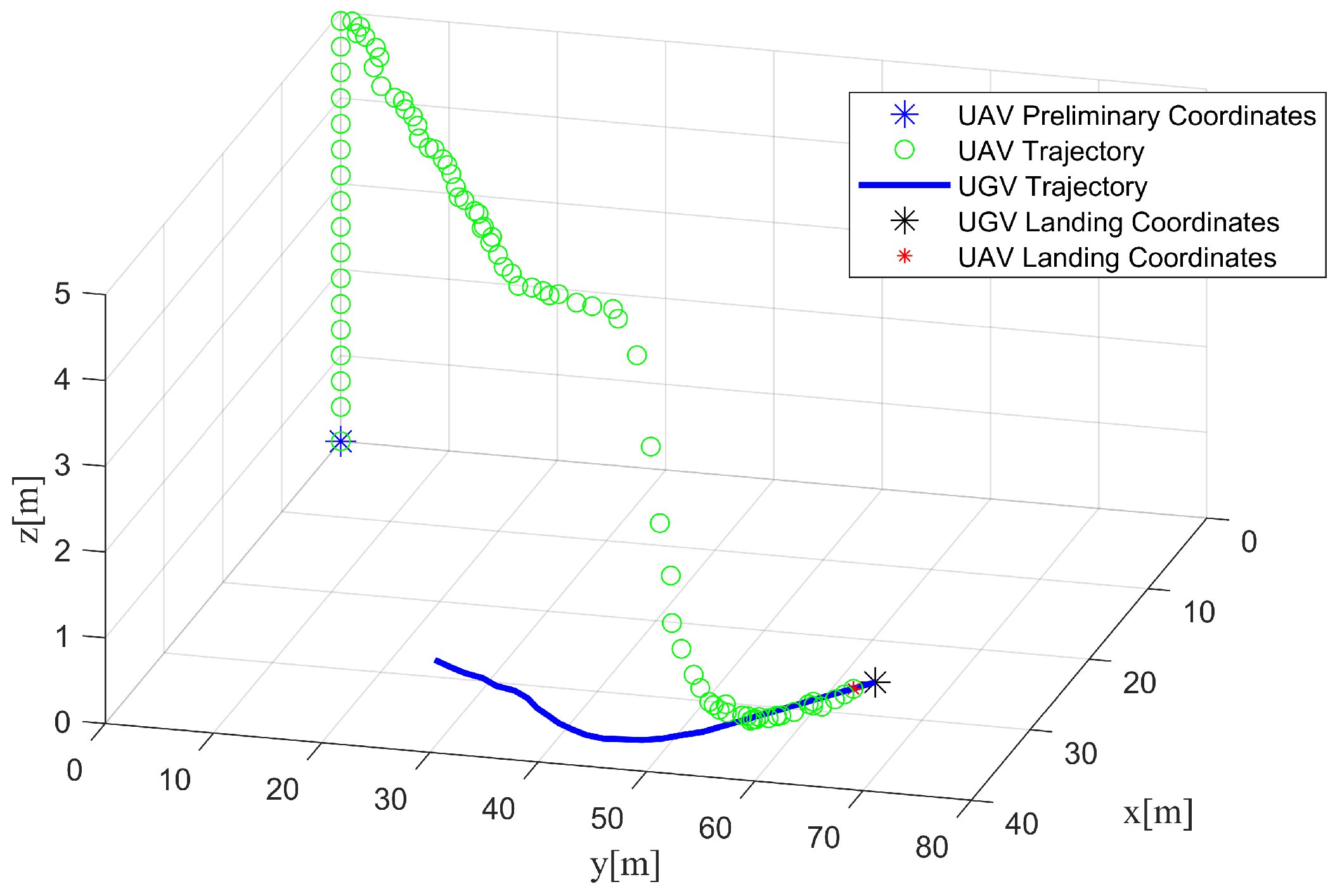
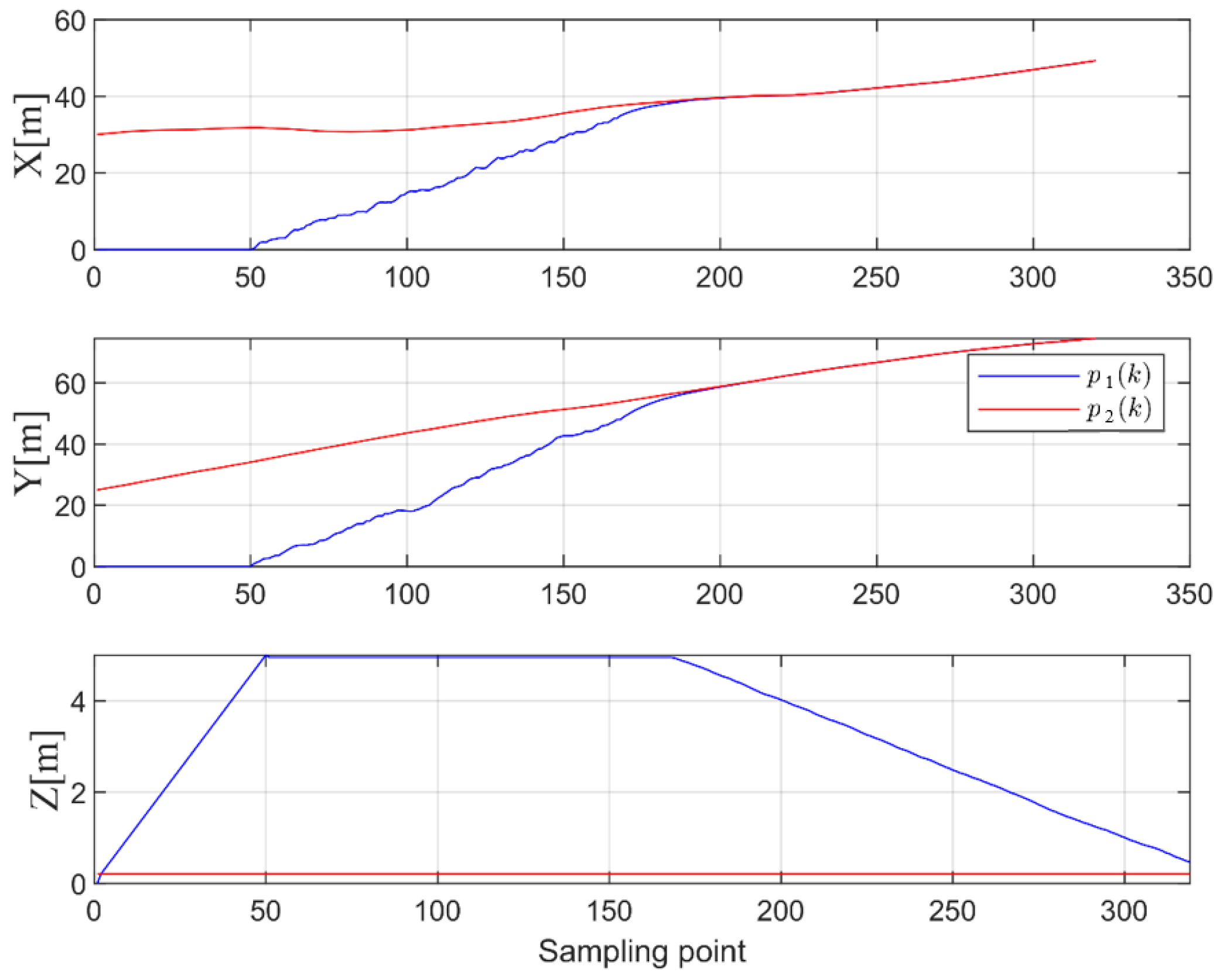
4.1. Simulation
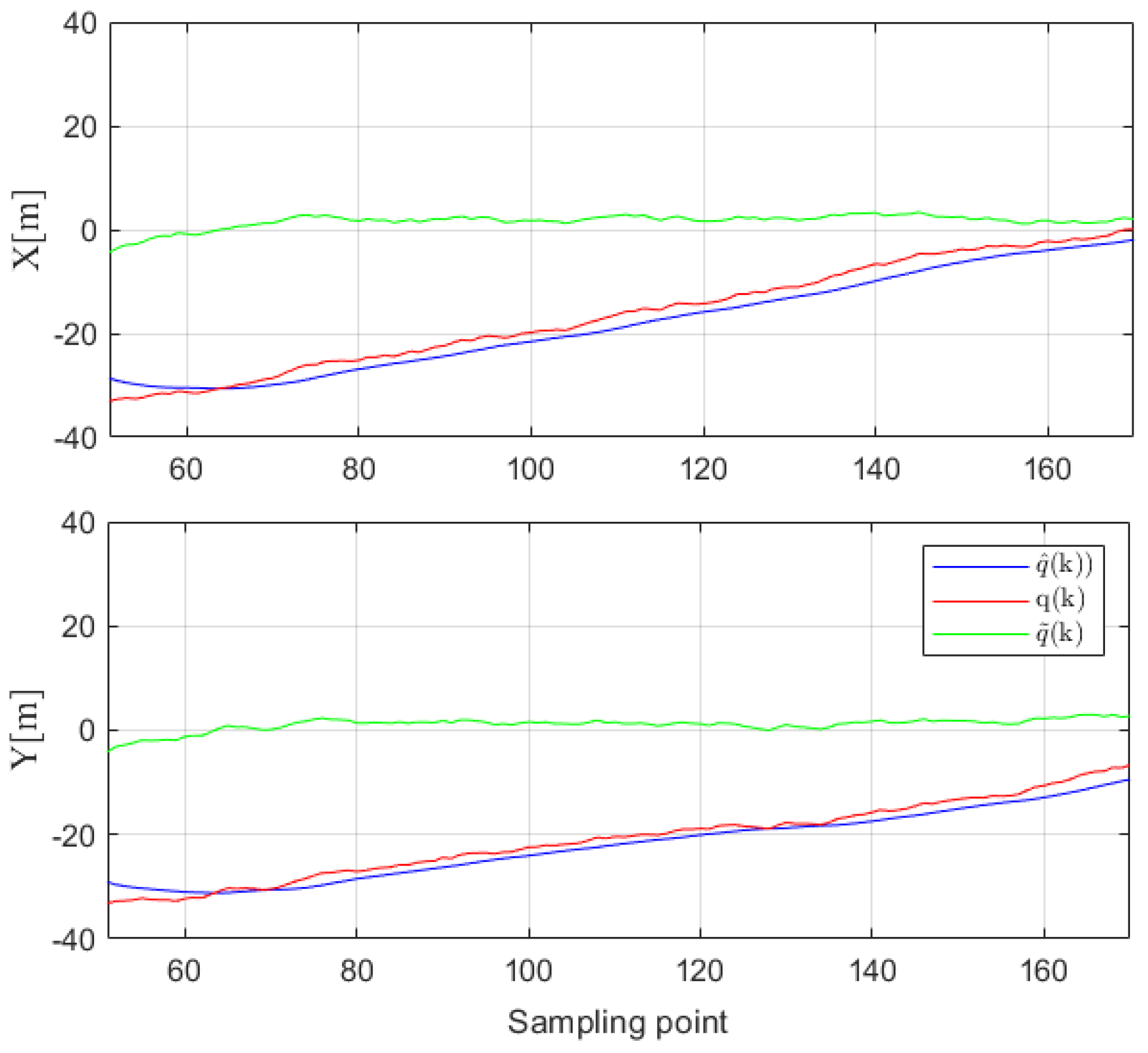
4.2. Real Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Lemma 1
Appendix A.2. Theorem 1
References
- Huzaefa, F.; Liu, Y.C. Force distribution and estimation for cooperative transportation control on multiple unmanned ground vehicles. IEEE Trans. Cybern. 2021, 53, 1335–1347. [Google Scholar] [CrossRef] [PubMed]
- Chae, H.; Park, G.; Lee, J.; Kim, K.; Kim, T.; Kim, H.S.; Seo, T. Façade cleaning robot with manipulating and sensing devices equipped on a gondola. IEEE/ASME Trans. Mechatron. 2021, 26, 1719–1727. [Google Scholar] [CrossRef]
- Chernik, C.; Tajvar, P.; Tumova, J. Robust Feedback Motion Primitives for Exploration of Unknown Terrains. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 8173–8179. [Google Scholar]
- Pradhan, M.; Noll, J. Security, privacy, and dependability evaluation in verification and validation life cycles for military IoT systems. IEEE Commun. Mag. 2020, 58, 14–20. [Google Scholar] [CrossRef]
- Li, B.; Huang, J.; Bai, S.; Gan, Z.; Liang, S.; Evgeny, N.; Yao, S. Autonomous air combat decision-making of UAV based on parallel self-play reinforcement learning. CAAI Trans. Intell. Technol. 2023, 8, 64–81. [Google Scholar] [CrossRef]
- Shao, Z.; Cheng, G.; Ma, J.; Wang, Z.; Wang, J.; Li, D. Real-time and accurate UAV pedestrian detection for social distancing monitoring in COVID-19 pandemic. IEEE Trans. Multimed. 2021, 24, 2069–2083. [Google Scholar] [CrossRef] [PubMed]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [Google Scholar] [CrossRef]
- Gyagenda, N.; Hatilima, J.V.; Roth, H.; Zhmud, V. A review of GNSS-independent UAV navigation techniques. Robot. Auton. Syst. 2022, 152, 104069. [Google Scholar]
- Guo, Y.; Wu, M.; Tang, K.; Tie, J.; Li, X. Covert spoofing algorithm of UAV based on GPS/INS-integrated navigation. IEEE Trans. Veh. Technol. 2019, 68, 6557–6564. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Zhang, N.; Benslimane, A. Learning in the air: Secure federated learning for UAV-assisted crowdsensing. IEEE Trans. Netw. Sci. Eng. 2020, 8, 1055–1069. [Google Scholar] [CrossRef]
- Queralta, J.P.; Almansa, C.M.; Schiano, F.; Floreano, D.; Westerlund, T. UWB-based system for UAV localization in GNSS-denied environments: Characterization and dataset. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; pp. 4521–4528. [Google Scholar]
- Yang, X.; Lin, D.; Zhang, F.; Song, T.; Jiang, T. High accuracy active stand-off target geolocation using UAV platform. In Proceedings of the IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Kallwies, J.; Forkel, B.; Wuensche, H.J. Determining and improving the localization accuracy of AprilTag detection. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8288–8294. [Google Scholar]
- Fang, Q.; Xu, X.; Wang, X.; Zeng, Y. Target-driven visual navigation in indoor scenes using reinforcement learning and imitation learning. CAAI Trans. Intell. Technol. 2022, 7, 167–176. [Google Scholar] [CrossRef]
- Vandendaele, B.; Fournier, R.A.; Vepakomma, U.; Pelletier, G.; Lejeune, P.; Martin-Ducup, O. Estimation of northern hardwood forest inventory attributes using UAV laser scanning (ULS): Transferability of laser scanning methods and comparison of automated approaches at the tree-and stand-level. Remote Sens. 2021, 13, 2796. [Google Scholar] [CrossRef]
- Stuckey, H.; Al-Radaideh, A.; Escamilla, L.; Sun, L.; Carrillo, L.G.; Tang, W. An Optical Spatial Localization System for Tracking Unmanned Aerial Vehicles Using a Single Dynamic Vision Sensor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3093–3100. [Google Scholar]
- Wang, J.; Olson, E. AprilTag 2: Efficient and robust fiducial detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 4193–4198. [Google Scholar]
- Chen, D.; Weng, J.; Huang, F.; Zhou, J.; Mao, Y.; Liu, X. Heuristic Monte Carlo Algorithm for Unmanned Ground Vehicles Realtime Localization and Mapping. IEEE Trans. Veh. Technol. 2020, 69, 10642–10655. [Google Scholar] [CrossRef]
- Jiang, X.; Li, N.; Guo, Y.; Yu, D.; Yang, S. Localization of Multiple RF Sources Based on Bayesian Compressive Sensing Using a Limited Number of UAVs With Airborne RSS Sensor. IEEE Sens. J. 2021, 21, 7067–7079. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, L.; You, T.; Ning, X. An adaptive clustering-based algorithm for automatic path planning of heterogeneous UAVs. IEEE Trans. Intell. Transp. Syst. 2021, 23, 16842–16853. [Google Scholar] [CrossRef]
- Uluskan, S. Noncausal trajectory optimization for real-time range-only target localization by multiple UAVs. Aerosp. Sci. Technol. 2020, 99, 105558. [Google Scholar] [CrossRef]
- Miki, T.; Khrapchenkov, P.; Hori, K. UAV/UGV autonomous cooperation: UAV assists UGV to climb a cliff by attaching a tether. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8041–8047. [Google Scholar]
- Cantieri, A.; Ferraz, M.; Szekir, G.; Antônio Teixeira, M.; Lima, J.; Schneider Oliveira, A.; Aurélio Wehrmeister, M. Cooperative UAV–UGV autonomous power pylon inspection: An investigation of cooperative outdoor vehicle positioning architecture. Sensors 2020, 20, 6384. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, R.; Yin, K.; Wang, Z.; Gui, M.; Chen, S. Intelligent Collaborative Localization Among Air-Ground Robots for Industrial Environment Perception. IEEE Trans. Ind. Electron. 2019, 66, 9673–9681. [Google Scholar] [CrossRef]
- Shah Alam, M.; Oluoch, J. A survey of safe landing zone detection techniques for autonomous unmanned aerial vehicles (UAVs). Expert Syst. Appl. 2021, 179, 115091. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, W.; Han, H.; Ban, J. A visual/inertial integrated landing guidance method for UAV landing on the ship. Aerosp. Sci. Technol. 2019, 85, 474–480. [Google Scholar] [CrossRef]
- Xia, K.; Shin, M.; Chung, W.; Kim, M.; Lee, S.; Son, H. Landing a quadrotor UAV on a moving platform with sway motion using robust control. Control Eng. Pract. 2022, 128, 105288. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Nguyen, T.H.; Cao, M.; Qiu, Z.; Xie, L. Integrated UWB-vision approach for autonomous docking of UAVs in GPS-denied environments. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9603–9609. [Google Scholar]
- Nguyen, T.M.; Qiu, Z.; Cao, M.; Nguyen, T.H.; Xie, L. Single landmark distance-based navigation. IEEE Trans. Control Syst. Technol. 2019, 28, 2021–2028. [Google Scholar] [CrossRef]
- Cheng, C.; Li, X.; Xie, L.; Li, L. Autonomous dynamic docking of UAV based on UWB-vision in GPS-denied environment. J. Frankl. Inst. 2022, 359, 2788–2809. [Google Scholar] [CrossRef]
- Spica, R.; Cristofalo, E.; Wang, Z.; Montijano, E.; Schwager, M. A real-time game theoretic planner for autonomous two-player drone racing. IEEE Trans. Robot. 2020, 36, 1389–1403. [Google Scholar] [CrossRef]
- Li, J.; Ran, M.; Wang, H.; Xie, L. MPC-based Unified Trajectory Planning and Tracking Control Approach for Automated Guided Vehicles. In Proceedings of the IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; pp. 374–380. [Google Scholar]
- Ren, H.; Chen, S.; Yang, L.; Zhao, Y. Optimal path planning and speed control integration strategy for UGVs in static and dynamic environments. IEEE Trans. Veh. Technol. 2020, 69, 10619–10629. [Google Scholar] [CrossRef]
- Cao, M.; Yu, C.; Anderson, B.D. Formation control using range-only measurements. Automatica 2011, 47, 776–781. [Google Scholar] [CrossRef]
- Lisus, D.; Cossette, C.C.; Shalaby, M.; Forbes, J.R. Heading Estimation Using Ultra-Wideband Received Signal Strength and Gaussian Processes. IEEE Robot. Autom. Lett. 2021, 6, 8387–8393. [Google Scholar] [CrossRef]
- Maaref, M.; Khalife, J.; Kassas, Z.M. Aerial Vehicle Protection Level Reduction by Fusing GNSS and Terrestrial Signals of Opportunity. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5976–5993. [Google Scholar] [CrossRef]
- Chen, S.; Ma, D.; Yao, Y.; Wang, X.; Li, C. Cooperative polynomial guidance law with collision avoidance and flight path angle coordination. Aerosp. Sci. Technol. 2022, 130, 107809. [Google Scholar] [CrossRef]
- Jia, J.; Guo, K.; Yu, X.; Guo, L.; Xie, L. Agile Flight Control Under Multiple Disturbances for Quadrotor: Algorithms and Evaluation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3049–3062. [Google Scholar] [CrossRef]
- Yu, J.; Shi, Z.; Dong, X.; Li, Q.; Lv, J.; Ren, Z. Impact Time Consensus Cooperative Guidance Against the Maneuvering Target: Theory and Experiment. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4590–4603. [Google Scholar] [CrossRef]
- Jepsen, J.H.; Terkildsen, K.H.; Hasan, A.; Jensen, K.; Schultz, U.P. UAVAT framework: UAV auto test framework for experimental validation of multirotor sUAS using a motion capture system. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 619–629. [Google Scholar]
- Nguyen, T.M.; Zaini, A.H.; Wang, C.; Guo, K.; Xie, L. Robust target-relative localization with ultra-wideband ranging and communication. In Proceedings of the IEEE international conference on robotics and automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2312–2319. [Google Scholar]
- Simanek, J.; Reinstein, M.; Kubelka, V. Evaluation of the EKF-Based Estimation Architectures for Data Fusion in Mobile Robots. IEEE/ASME Trans. Mechatronics 2015, 20, 985–990. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, M.; Wang, C.; Luo, L.; Li, J.; Lian, G.; Zou, X. Recognition and localization methods for vision-based fruit picking robots: A review. Front. Plant Sci. 2020, 11, 510. [Google Scholar] [CrossRef] [PubMed]






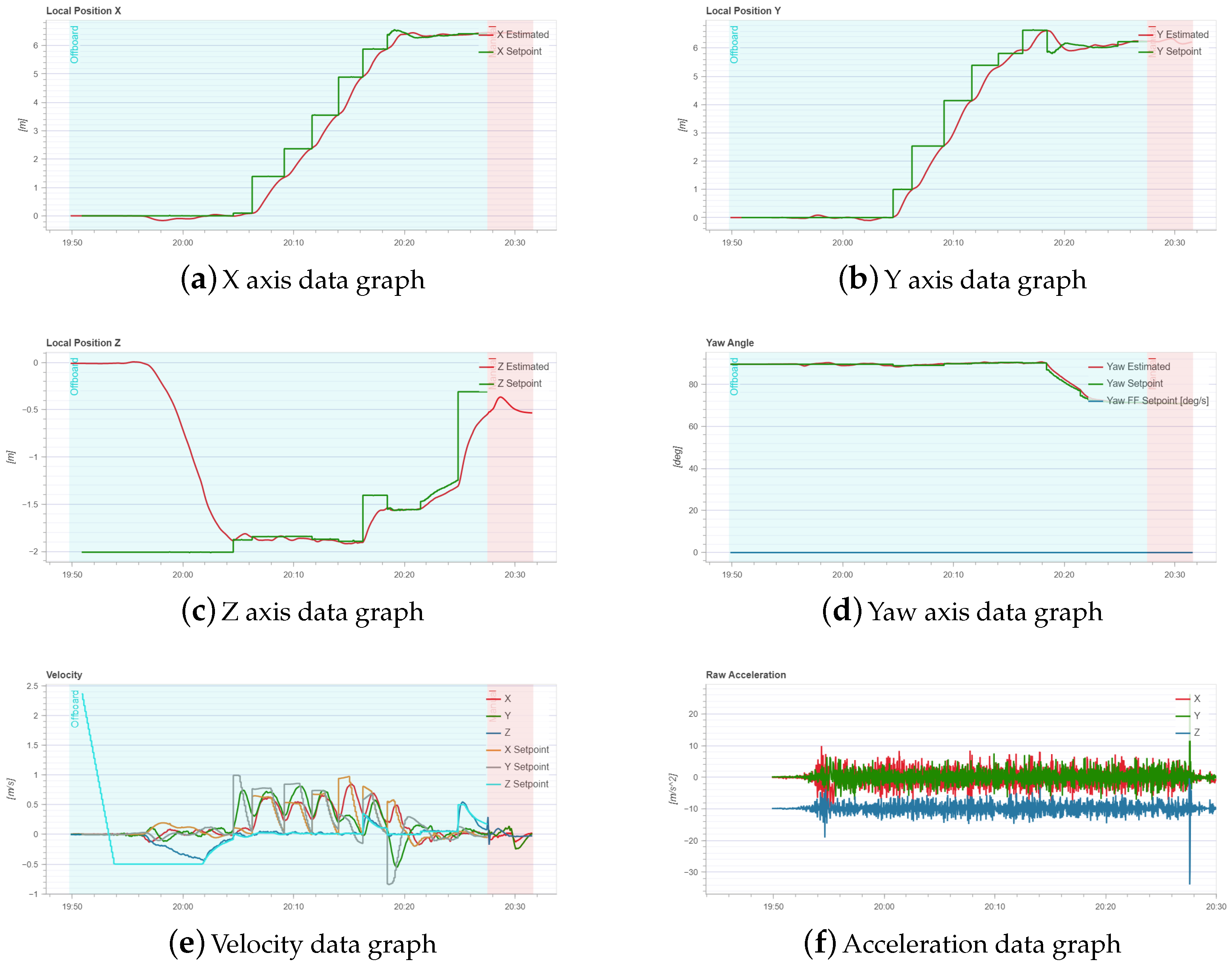
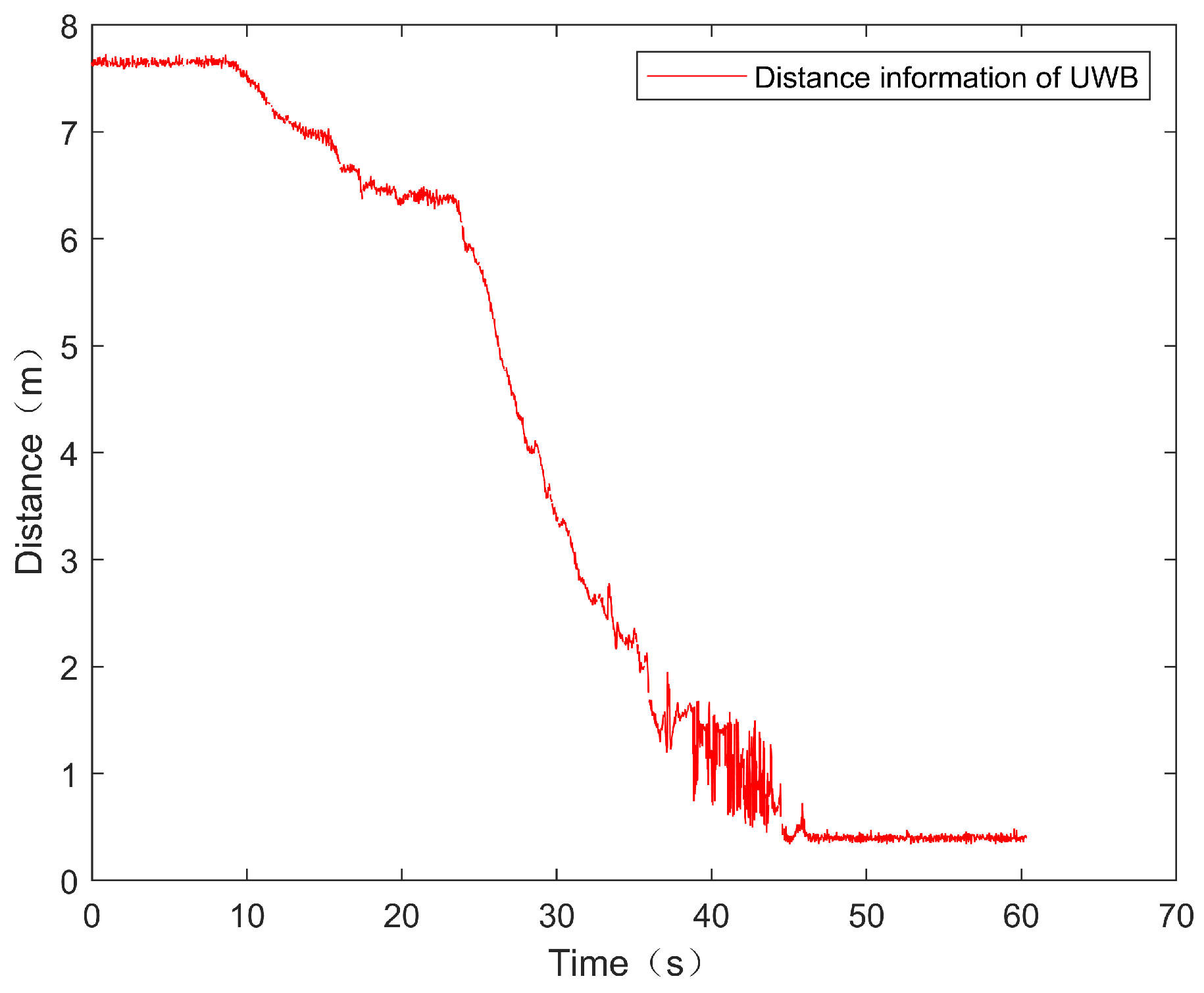
| Type | ||||||
|---|---|---|---|---|---|---|
| MIFG | 0.4088 | 0.6554 | ∖ | 0.3276 | 0.3104 | ∖ |
| FFLS | 0.6321 | 0.7905 | ∖ | 0.3989 | 0.4254 | ∖ |
| Type | ||||||
|---|---|---|---|---|---|---|
| UWB | 0.4122 | 0.6902 | ∖ | 0.3127 | 0.3250 | ∖ |
| Visual | 0.0321 | 0.0200 | 0.0199 | 0.0168 | 0.0201 | 0.0223 |
| Fusion | 0.0153 | 0.0160 | 0.0191 | 0.0130 | 0.0109 | 0.0143 |
| Type | ||||||
|---|---|---|---|---|---|---|
| MIFG | 0.5152 | 0.5854 | ∖ | 0.5152 | 0.5847 | ∖ |
| FFLS | 0.7622 | 0.8005 | ∖ | 0.5809 | 0.6003 | ∖ |
| Type | ||||||
|---|---|---|---|---|---|---|
| UWB | 0.5833 | 0.5962 | ∖ | 0.5232 | 0.5155 | ∖ |
| Visual | 0.0522 | 0.0378 | 0.0269 | 0.0232 | 0.0276 | 0.0288 |
| Fusion | 0.0198 | 0.0188 | 0.0221 | 0.0200 | 0.0189 | 0.0182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Li, X.; Xie, L.; Li, L. A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments. Drones 2023, 7, 613. https://doi.org/10.3390/drones7100613
Cheng C, Li X, Xie L, Li L. A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments. Drones. 2023; 7(10):613. https://doi.org/10.3390/drones7100613
Chicago/Turabian StyleCheng, Cheng, Xiuxian Li, Lihua Xie, and Li Li. 2023. "A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments" Drones 7, no. 10: 613. https://doi.org/10.3390/drones7100613
APA StyleCheng, C., Li, X., Xie, L., & Li, L. (2023). A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments. Drones, 7(10), 613. https://doi.org/10.3390/drones7100613






