Onboard Distributed Trajectory Planning through Intelligent Search for Multi-UAV Cooperative Flight

Abstract

Trajectory planning and obstacle avoidance play essential roles in the cooperative flight of multiple unmanned aerial vehicles (UAVs). In this paper, a unified framework for onboard distributed trajectory planning is proposed, which takes full advantage of intelligent discrete and continuous search algorithms. Firstly, the Monte Carlo tree search (MCTS) is used as the task allocation algorithm to solve the cooperative obstacle avoidance problem. Taking the task allocation decisions as the constraint, knowledge-based particle swarm optimization (Know-PSO) is used as the optimization algorithm to solve the onboard distributed cooperative trajectory planning problem. Simulation results demonstrate that the proposed intelligent MCTS-PSO search framework is effective and flexible for multiple UAVs to conduct the cooperative trajectory planning and obstacle avoidance. Further, it has been applied in practical experiments and achieved promising results.

1. Introduction

Unmanned aerial vehicles (UAVs) have been extensively used in many areas, such as surveying [1,2,3,4], military surveillance [5,6,7,8], disaster rescue [9,10], etc. Although a single UAV can conduct the above-mentioned tasks, some disadvantages, including energy and others, have placed severe limitations on its applications. That is the reason why cooperative multiple UAVs have been further developed and utilized, which can overcome the disadvantages of single UAVs and accomplish tasks more robustly and intelligently with less time consumption [11].

Trajectory planning plays an essential role in the cooperative flight of multiple UAVs, which can be seen as continuous search algorithms mathematically. Commonly with some environmental constraints and UAVs’ own constraints, the trajectories that minimize the cost function are seen as the best ones. Trajectory planning has been widely researched for many years, and two classes of trajectory planning methods have been developed. The first one is those traditional algorithms, including dynamic planning, the Voronoi diagram [12,13], the Dijkstra algorithm [14,15], and the A* algorithm [16]. The other class is swarm intelligence algorithms, such as the artificial bee colony (ABC) algorithm [17], the ant colony optimization (ACO) algorithm [18], and especially, the particle swarm optimization (PSO) algorithm [19,20,21]. In the literature [22], the trajectories of multiple UAVs were firstly given out by an offline simulation software program and saved in a text file. Then, the trajectories of all UAVs were transferred into the ground station software and displayed on a map. Finally, the trajectories were downloaded to the UAVs through the ground stations, and the UAVs completed the flight. The offline operation as in the literature [22] is now the mainstream execution style for cooperative trajectory planning.

Obstacle avoidance plays another essential role in the cooperative flight of multiple UAVs, for which the artificial potential field (APF) method is widely used [23,24]. To some extent, cooperative obstacle avoidance of multiple UAVs can be seen as a task allocation problem [25], in which multiple UAVs have to choose one side or the other to pass through the threat area. The Hungarian algorithm [22] and the auction algorithm [26,27] are two mainstream algorithms for the task allocation of multiple UAVs. In the literature [28], a two-step auction mechanism was first proposed to select the optimal action. Then, an obstacle avoidance mechanism was designed by defining several heuristic rules. Finally, a reverse auction mechanism was developed to balance the workload between multiple UAVs.

Although a large amount of effort has been devoted to addressing the trajectory planning and task allocation problems for multiple UAVs, there is still some room for further improvement. For instance, traditional task allocation algorithms often require that the input dimension must be equal to the output dimension, namely, the allocation matrix has identical row and column numbers, which severely restricts the application for more general task allocation problems. In addition, the efficiency and effectiveness of trajectory planning algorithms for multiple UAVs are not satisfactory in some circumstances. Meanwhile, the trajectory planning and task allocation for multiple UAVs are conducted offline in some literature, which cannot meet the requirements in complex and intense environments, where multiple UAVs must respond to commands rationally and quickly.

Taking the abovementioned issues into consideration, a unified framework for onboard distributed trajectory planning is proposed in this paper, which takes full advantage of intelligent discrete and continuous search algorithms. The main contributions of this paper are as follows:

(1)

The Monte Carlo tree search (MCTS) is used as a task allocation algorithm to conduct obstacle avoidance, which does not require the equality of the row and column numbers of the allocation matrix. Further, the obstacle avoidance for multiple UAVs takes the energy constraint into account.

(2)

Knowledge-based particle swarm optimization (Know-PSO) is used as the optimization algorithm to solve the onboard distributed cooperative trajectory planning problem, in which the motion energies of a few good particles are used to improve the velocities of those bad particles, and the information of the individual worst particles and global worst particle are also used. Furthermore, the interaction among multiple UAVs is utilized to avoid conflicts.

(3)

The decisions of MCTS are taken as constraints for Know-PSO to form a unified framework for onboard distributed trajectory planning.

(4)

The method proposed in this paper has been verified by actual flights and achieved good practical results.

The remainder of this paper is organized as follows: Section 2 formulates the trajectory planning and obstacle avoidance problem. Section 3 presents the proposed intelligent MCTS-PSO search framework. In Section 4, a series of simulations and actual experiments were conducted to evaluate the performance of MCTS-PSO. Finally, Section 5 concludes the paper and presents the future direction for the next work.

2. Mathematical Model

Cooperative trajectory planning driven by obstacle avoidance for multiple UAVs can be presented in the following mathematical models:

(1)

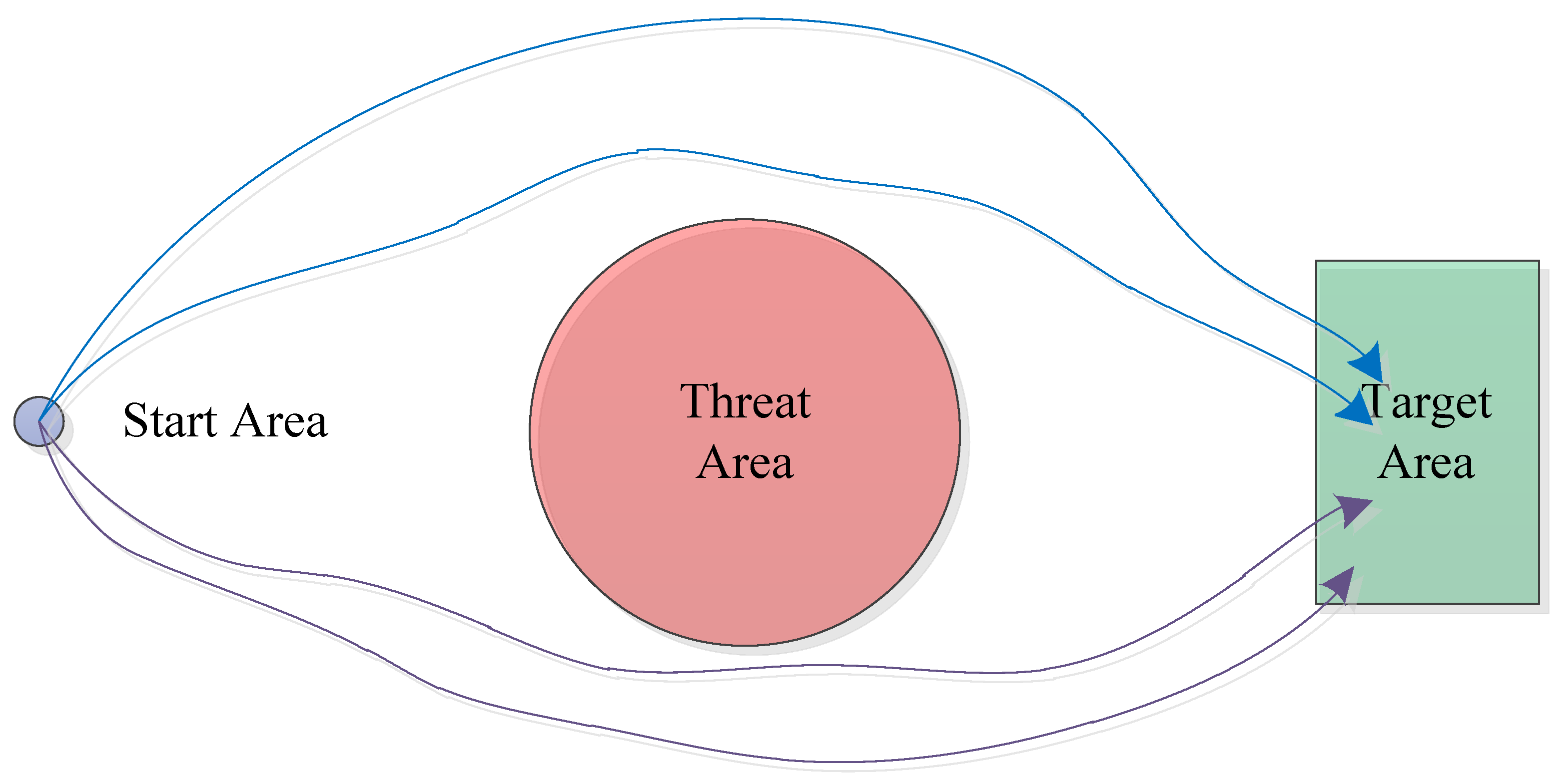
Task allocation to obstacle avoidance: As shown in Figure 1, m UAVs are configured to go to the target area to conduct some important operations, in which the threat area must be avoided. Regarding each UAV, there are two choices for it to avoid the threat area, going through one side of the threat area or the other. Consequently, the cooperative obstacle avoidance problem can be translated into the task allocation problem, for which there are m decisions that have to be made. Generally, suppose there are n choices for each UAV, then the mathematical model for task allocation is as below:

$$\begin{array}{l}\max {\displaystyle \sum _{j=1}^n{w}_j[1-{\displaystyle \prod _{i=1}^m{(1-e_{ij})}^{x_{ij}}}]}\\ s.t.\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{x}_{ij}=1, i=1,2,\dots ,m}\\ x_{ij}=0 or 1, i=1,2,\dots ,m,j=1,2,\dots n\end{array}\end{array}$$

(1)

where w_j is the threat value of j choice, e_ij is the capacity evaluation of the i UAV to pass through the j choice and can be seen as the energy constraints, x_ij is the final decision, whether the i UAV passes through the j choice or not. The MCTS is used to solve the model to obtain x_ij. All x_ij compose the task allocation matrix, which is a 0–1 matrix and has m rows and n columns. Each row has only one, which means that the corresponding UAV can only make one choice.

(2)

Cooperative trajectory planning driven by obstacle avoidance: The goal of cooperative trajectory planning is to minimize the total distances of m UAVs from the start area to the target area; in the meantime, m UAVs must avoid the threat area and not collide with each other. The mathematical model is as below:

$$\begin{array}{l}\min {\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{l}_{ij}}}{x}_{ij}\\ s.t. \{\begin{array}{l}d{m}_{i,k}>d_s, i,k=1,2,\dots ,m,i\ne k\\ x_{ij}=0 or 1, i=1,2,\dots ,m,j=1,2,\dots n\end{array}\end{array}$$

(2)

where l_ij is the length of a trajectory that the i UAV pass through the j choice, dm_i,k is the margin distance between trajectories of two different UAVs, and d_s is the safe distance between two adjacent UAVs. x_ij is the final decision, whether the i UAV passes through the j choice or not as in formula (1), which is solved by the MCTS method.

3. MCTS-PSO Framework for Onboard Distributed Trajectory Planning

In this section, we elaborate on the cooperative trajectory planning driven by obstacle avoidance, which can be conducted in an onboard distributed mode. Firstly, MCTS is used as a task allocation algorithm to conduct obstacle avoidance, taking the energy constraint into consideration; secondly, the decisions of MCTS are taken as constraints for Know-PSO to conduct onboard distributed trajectory planning for multiple UAVs. The schematic diagram of the MCTS-PSO framework is shown in Figure 2, and the Pseudo-code of the MCTS-PSO Algorithm 1 is:

Algorithm 1: MCTS-PSO framework

Input: UAVs number m,    choices number n,    start position Ps and target position Pt,    Threat area center Pc and radius r,    the safe distance ds,  Output: best trajectories  1: for $i\leftarrow 1$ to m do  2: for $j\leftarrow 1$ to n do  3: Evaluate the threat values wj;  4: Evaluate the capacity values eij;  5: end for  6: end for  7: Use MCTS to solve formula (1) to get decisions xij;  8: Use Know-PSO to generate a trajectory for one UAV i;  9: for $k\leftarrow 1$ to m do 10: if k == i 11: continue; 12: else 13: Use Know-PSO to generate a trajectory for UAV k with ds; 14: Check whether dmi,k is larger than ds or not; 15: end if 16: end for 17: Return m best trajectories;

The resulting m best trajectories obtained after the above steps is the optimal solution for onboard distributed cooperative trajectory planning; end

3.1. MCTS Task Allocation for Multiple UAVs

Task allocation plays an essential role in the cooperative flight of multiple UAVs. In this paper, MCTS, as an intelligent discrete search algorithm, is used to conduct task allocation. MCTS does not require the equality of the row and column numbers of the allocation matrix, beyond the traditional mainstream Hungarian algorithm and auction algorithm. The flow chart of MCTS task allocation is shown in Figure 3, whose specific steps are presented as follows:

• Step 1: Input UAV number, choices number, threat values, UAV capacities, and iteration number. The UAV capacities can be seen as the energy constraints:

  $$e_{ij}=\frac{1}{\alpha \ast dist(UA{V}_i,choic{e}_j)}$$

  (3)

  where α is the energy coefficient.
• Step 2: Construct a new search tree and initialize the root node.
• Step 3: Iterate the search tree until the iteration number:

    (1)

  Select the best child layer by layer to find a leaf node;

    (2)

  Expand the tree from the leaf node;

    (3)

  Conduct the default policy;

    (4)

  Back up the score and update nodes’ attributes.

• Step 4: Update the allocation matrix.
• Step 5: Repeat steps 2–4 for all UAVs.

The resulting 0–1 matrix obtained after the above steps is the optimal solution for multiple UAV task allocation problems.

Pseudo-code of the MCTS task allocation Algorithm 2 is:

Algorithm 2: MCTS task allocation

Input: UAVs number m,    choices number n,    threat values w,    capacities e,    IterNum,  Output: Allocation matrix AlloMx  1: for $i\leftarrow 1$ to m do  2: Create a new tree with root node and initialize root:  3: $root.N\leftarrow 0$, $root.Q\leftarrow 0$;  4: for $j\leftarrow 1$ to IterNum do  5: node $p\leftarrow root$;  6: $AlloMx\_copy\leftarrow AlloMx$;  7: $i\_temp\leftarrow i$;  8: while(True)  9: if p is leaf  10: break;  11: end if  12: find the best child of p and its index ind;  13: $p\leftarrow best child of p$;  14: $AlloMx\_copy[i\_temp][ind]\leftarrow 1$;  15: $i\_temp\leftarrow i\_temp+1$;  16: end while  17: if $i\_temp~=m$  18: Expand the node p;  19: end if  20: Conduct the default policy for $AlloMx\_copy$ and get the score;  21: Back up the score;  22: end for  23: find the best child of root and its index $ind\_best$;  24: $AlloMx[i][ind\_best]\leftarrow 1$;  25: end for  26: Return AlloMx;

The resulting 0–1 matrix obtained after the above steps is the optimal solution for task allocation;     end

3.2. Onboard Distributed Cooperative Trajectory Planning for Multiple UAVs

Trajectory planning plays another essential role in the cooperative flight of multiple UAVs. PSO, as an intelligent continuous search algorithm, has been widely used to conduct trajectory planning. Nevertheless, the standard PSO algorithm has some limitations such as premature convergence. In this paper, knowledge-based particle swarm optimization (Know-PSO) is proposed as the optimization algorithm to solve the onboard distributed cooperative trajectory planning problem, in which the motion energies of a few good particles are used to improve the velocities of those bad particles, and the information of the individual worst particles and global worst particle is also used. Furthermore, the interaction among multiple UAVs is utilized to avoid conflicts.

The well-known standard PSO algorithm is

$$\{\begin{array}{l}{V}_i^{k+1}=\omega V_i^k+c_1{r}_1(p_{best,i}^k-x_i^k)+c_2{r}_2(g_{best}^k-x_i^k)\\ x_i^{k+1}=x_i^k+V_i^{k+1}\end{array}$$

(4)

Practically, it has been found that the information of individual worst particles and global worst particle are also beneficial, which are introduced as

$$\{\begin{array}{l}{V}_i^{k+1}=\omega V_i^k+c_1{r}_1(p_{best,i}^k-x_i^k)+c_2{r}_2(g_{best}^k-x_i^k)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-c_3{r}_3(p_{worst,i}^k-x_i^k)-c_4{r}_4(g_{worst}^k-x_i^k)\\ x_i^{k+1}=x_i^k+V_i^{k+1}\end{array}$$

(5)

Further, the motion energies of a few good particles are used to improve the velocities of those bad particles, which is defined as

$$E^{k,m_1}={\displaystyle \sum _{i=1}^{m_1}{(V_i^k)}^T(V_i^k)}$$

(6)

The energy loss is

$$\Delta E^{k,m_1}=E^{k,m_1}-E^{k-1,m_1}$$

(7)

Consequently, the updated equation for bad particles is

$$\{\begin{array}{l}{V}_i^{k+1}=\omega V_i^k+c_1{r}_1(p_{best,i}^k-x_i^k)+c_2{r}_2(g_{best}^k-x_i^k)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-c_3{r}_3(p_{worst,i}^k-x_i^k)-c_4{r}_4(g_{worst}^k-x_i^k)+\Delta E^{k,m_1}/m_1\\ x_i^{k+1}=x_i^k+V_i^{k+1}\end{array}$$

(8)

The decisions of MCTS are taken as constraints for Know-PSO to form a unified framework for onboard distributed trajectory planning. Specifically,

$$cost(x_{ij})=\{\begin{array}{ll}0,& x_{ij}=1\\ 1000,& x_{ij}\ne 0\end{array}$$

(9)

The flow chart of Know-PSO for onboard distributed cooperative trajectory planning is shown in Figure 4, whose specific steps are presented as follows:

Step 1:

Input particle number, point number, start position and target position, threat area center and radius, task allocation matrix, iteration number, UAV number, the safe distance, and the max velocity.

Step 2:

Initialize the particles and best values.

Step 3:

Iterate the particles until the iteration number:

(1)

Compute the cost of particles;

(2)

Update the best values;

(3)

Update the velocities;

(4)

Update the particles.

Step 4:

Generate one best trajectory.

Step 5:

Repeat steps 2–4 for all UAVs considering the safe distance between them.

The resulting best trajectories obtained after the above steps is the optimal solution for onboard distributed cooperative trajectory planning.

Pseudo-code of the cooperative trajectory planning Algorithm 3 is:

Algorithm 3: Onboard distributed cooperative trajectory planning

Input: particle number mp,    point number n,    start position PS and target position Pt,    Threat area center Pc and radius r,    AlloMx,    IterNum,    UAVs number m,    the safe distance ds,    Vmax,  Output: best trajectories  1: $particles\leftarrow rand(mp,n)$;  2: $particlesBest\leftarrow zeros(mp,n)$;  3: $globalBest\leftarrow zeros(1,n)$;  4: $particlesV\leftarrow rand(mp,n)\ast 2V_{max}-V_{max}$  5: for $iter\leftarrow 1$ to IterNum do  6: for $i\leftarrow 1$ to mp do  7: Compute the $cost$ of $particles[i,:]$ with decision AlloMx and Pc, r;  8: if cost is descending  9: $particlesBest[i,:]\leftarrow particles[i,:]$;  10: $globalBest\leftarrow particles[i,:]$;  11: end if  12: for $j\leftarrow 1$ to n do  13: Update $particlesV[i,j]$ according Formulas (5) and (8);  14: Adjust $particlesV[i,j]$ into $[-V_{max},V_{max}]$;  15: $particles[i,j]\leftarrow particles[i,j]+particlesV[i,j]$;  16: end for  17: end for  18: end for  19: Here, we got the best trajectory for one UAV.  20: for $i\leftarrow 2$ to m do  21: Repeat 1~21 considering the safe distance ds;  22: end for  23: Return m best trajectories;

The resulting m best trajectories obtained after the above steps is the optimal solution for onboard distributed cooperative trajectory planning;     end

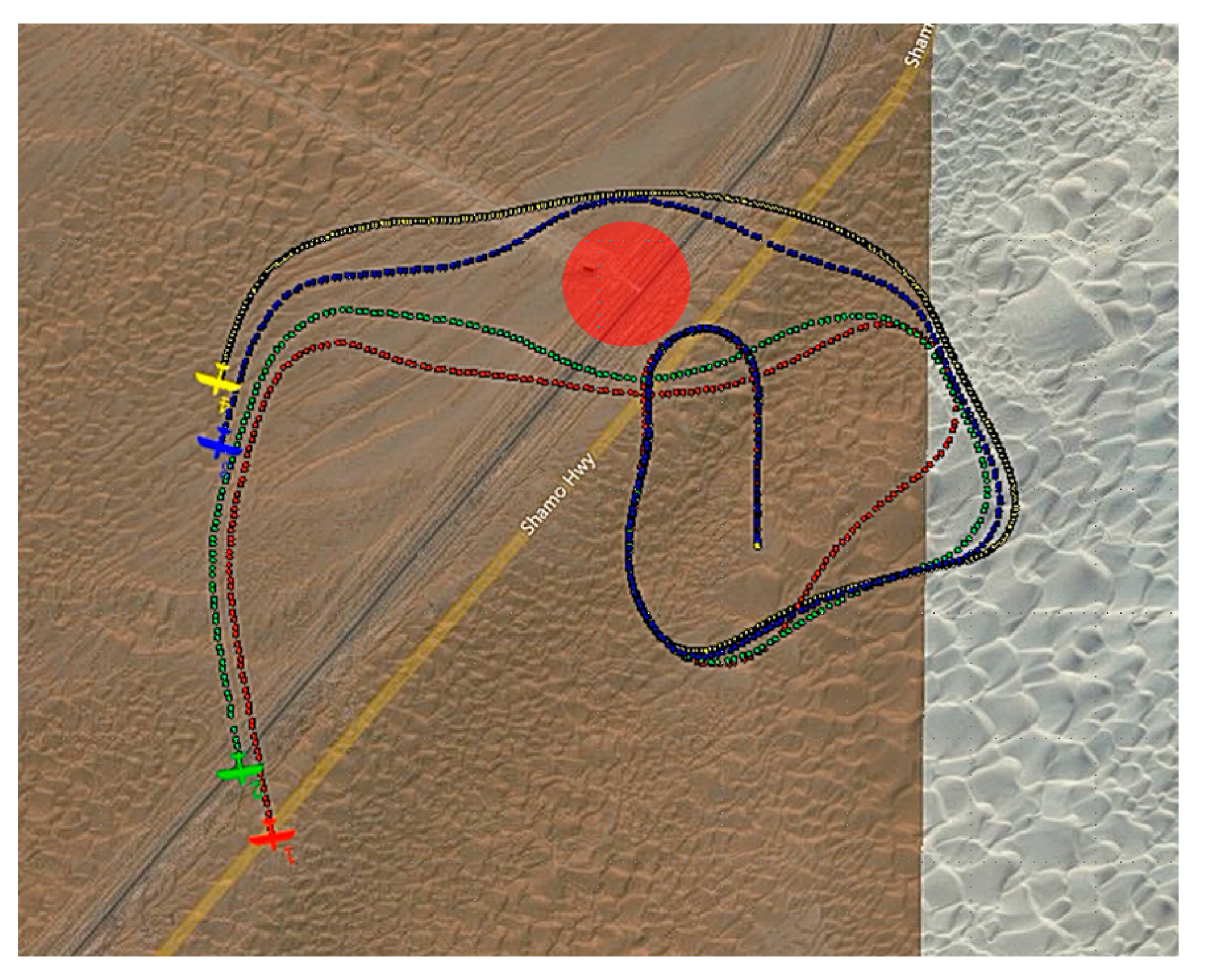
4. Experiments and Analysis

This section demonstrates the performance of the MCTS-PSO framework by conducting a series of experiments.

A cooperative processor was deployed for each UAV. The processor had a four-core CPU, whose main frequency was 1.5G Hz and AI computational power was 20 TOPS(int8).

The experiments were all conducted in open environments, including plains and mountainous areas. The environmental temperature was generally higher than −20 °C.

Wind has a very important influence on flight in open environments. According to all experiments, UAVs could be controlled stably if the wind velocity was smaller than 15 m/s; otherwise, there would be some accidents.

Firstly, a flight of two drones was conducted, whose trajectories were shown in Figure 5, of which the red circle was a threat area. It can be seen that the two drones avoided the threat area successfully and passed it by one side, respectively. The task allocation matrix of them was shown in

Table 1. Task allocation matrix for two drones in Figure 5.

	Top Channel	Bottom Channel
UAV1	1	0
UAV2	0	1

.

Secondly, a flight of three drones was conducted, whose trajectories were shown in Figure 6, of which the red circle was a threat area. It can be seen that the three drones avoided the threat area successfully. The task allocation matrix of them was shown in

Table 2. Task allocation matrix for three drones in Figure 6.

	Top Channel	Bottom Channel
UAV1	1	0
UAV2	0	1
UAV3	0	1

.

Thirdly, a flight of four drones was conducted in another environment, whose trajectories were shown in Figure 7, of which the red circle was a threat area. It can be seen that the four drones avoided the threat area successfully. The task allocation matrix of them was shown in

Table 3. Task allocation matrix for four drones in Figure 7.

	Top Channel	Bottom Channel
UAV1	1	0
UAV2	1	0
UAV3	0	1
UAV4	0	1

.

It was shown in these experiments, when the number of UAVs changed, the trajectories were slightly adjusted automatically. For example, comparing Figure 5 and Figure 6, when the green UAV joined in, the trajectory of the yellow UAV was automatically adjusted to leave some space for the green one. This reflected the intelligent onboard adjustment ability of the algorithm.

Cooperative flight in an open environment was shown in Figure 8, in which five quadcopters were used. It must be noted that the MCTS-PSO framework can also be applied to other kinds of UAVs, such as fixed-wing UAVs.

The further computational time of the proposed distributed framework and common centralized framework were shown in

Table 4. Computational time.

	Distributed Framework	Centralized Framework
2 UAVs	0.72s	2.2s
3 UAVs	0.73s	3.1s
4 UAVs	0.73s	4.2s

.

It is quite clear that the proposed distributed framework was more efficient than a common centralized framework, especially when there were more UAVs, because each UAV planned its trajectory using its own processor.

The distance between the start area and the target area was about 1.4 Km. Note that the start area was where the proposed distributed framework conducted cooperative trajectory planning, not the location where the UAVs were launched. The total distances were shown in

Table 5. Total distances.

	Total Distances
2 UAVs	3.2 Km
3 UAVs	4.9 Km
4 UAVs	6.6 Km

.

In open environments, other factors could also influence the real flight trajectories, such as maneuverability, wind, etc. Moreover, PSO variants could not always generate the best trajectories. These were the reasons why the trajectories in Figure 5, Figure 6 and Figure 7 were not very close to the threat area.

Generally, the effectiveness, scalability, and adaptability of our framework were verified through the quantitative experiments with different UAV numbers. Moreover, it realized the avoidance of conflicts between multiple UAVs. All experiments demonstrated that the MCTS-PSO framework could be applied in dynamic and complex environments.

5. Conclusions

In this paper, the unified MCTS-PSO framework for onboard distributed trajectory planning is proposed, which takes full advantage of intelligent discrete and continuous search algorithms. The effectiveness, scalability, and adaptability of our framework have been verified through a series of experiments with different UAV numbers. Moreover, the proposed framework can also be applied in other similar swarm systems.

In future work, large-scale UAVs will be tested with the MCTS-PSO framework. Further, other intelligent algorithms such as multi-agent reinforcement learning will be introduced into the framework. In addition, we would like to evaluate our framework in intense confrontation applications.