Persistent Charging System for Crazyflie Platform

Abstract

Nowadays, quadcopters are used widely in different applications, but their flight time is limited during operation. In this paper, a precision landing method based on a Kalman filter is proposed for an autonomous indoor persistent drone system that aims to increase the flight time of quadcopters. First, a local positioning system is used for tracking performance. Second, instead of using this local positioning system during the landing phase, a multi-ranger sensor is proposed to increase the accuracy of horizontal errors. Next, based on the relative position provided by the multi-ranger sensor, a Kalman filter technique is applied to estimate the relative velocity of the system, which is then applied to control the position of the quadcopter during the landing phase. Finally, a charging state machine law is proposed to charge the battery of three quadcopters sequentially. The experimental results demonstrate that the proposed concept based on a multi-ranger sensor can enhance the accuracy of the landing phase in comparison with the conventional method.

1. Introduction

Quadcopters are unmanned aerial vehicles (UAVs) that have been studied and utilized in a variety of applications owing to their advantages, such as simple structure, small size, low cost, and agility. Consequently, quadcopters are more popular than other types of UAV systems. Therefore, they have been tested and commercialized for several applications, including formation flight [1,2], transportation [3,4], fault-tolerant control [5,6], precision landing [7,8,9,10], and search and rescue [11,12]. Normally, a quadcopter is lifted by four propellers through navigation and flight control systems to operate hovering and maneuverability for both indoor and outdoor tasks. However, one of the main issues of quadcopters is their short operation time. This is because quadcopters frequently generate their total force from the propellers to achieve the desired positions, and this requires high power consumption. Therefore, there is an essential need to charge the battery of UAVs autonomously for long-time operation. One of the main problems in autonomous drone-charging systems is to accomplish a precise landing phase. This task would be useful for coastal surveillance that requires the quadcopter UAVs to return to a home position for battery charging. Moreover, marine applications could be used to transport quadcopter UAVs to desired locations and to allow them to charge periodically after finishing their operations. The main issue of this task is the limited accuracy of navigation systems. Due to the drawback of low-cost navigation systems, the research topic of landing approach of the quadcopter on a stationary target is more and more crucial for many precise applications.

Several studies focused on the development of new strategies to address autonomous recharging [13,14] with the aim of increasing the flight time and endurance during missions. In [15], researchers presented a mobile vehicle that had the capability of recharging automatically on a static station and then resuming its original mission. In [16], a persistent mission based on a contact charging method was studied for UAVs. In [17], a drone-charging station was implemented using RTK-GPS, which is a more accurate positioning system than conventional GPS. An autonomous landing scheme based on an infrared beam was proposed in [18]. However, most of the above-mentioned methods are difficult to incorporate in practical solutions because of the precise positioning system and mechanical design required.

Another solution using vision techniques was recently investigated to increase the accuracy of drone charging. In [19,20,21], vision-based landing techniques with robust controllers were proposed to land quadcopters in a precise manner; these controllers include a model-predictive controller, neural network controller, and backstepping controller. In [22], a landing task was proposed for an aerial vehicle using optical flow and adaptive control law. Another development of the landing method was proposed in [23] based on the orientation estimation from a camera. These studies elaborated on landing on a charging pad, but they require high computation for filtering data from vision sensor.

Compared with contract-based charging, wireless charging was investigated in many low-power applications, such as smartphones, cleaning robots, mobile robots, and other electronic devices. The principle of wireless operation based on magnetic resonant induction [24,25,26,27] was applied to drone-charging systems. The goal of wireless communication is to develop a battery charging system for UAVs with a considerable improvement in reliability [28]. In [29], a drone was proposed to land on a ground vehicle for charging through such ground vehicle and a robot arm. In [30], a persistent charging strategy was proposed for drones via wireless communication. Most of the aforementioned studies demonstrated significant results through simulations or experiments, but they did not present a persistent charging scheme for a group of quadcopters. This was the motivation of this study.

This paper aims to improve the precision landing method for autonomous persistent drone-charging application without human intervention. This application means that when a vehicle is low in battery in ocean surveillance, then another vehicle can replace this vehicle to charge sequentially. In contrast to previous studies, this study proposes a low-cost landing method using a multi-ranger sensor that can measure the relative position between the drone and objects to improve horizontal errors. The advantage of this method is that it can operate in both bright and dark environments. It can also reduce the noise as opposed to techniques based on vision sensors. The contributions of this study can be summarized as follows:

• Modifies the open-source software of Crazyflie drones, and a Kalman filter is applied to estimate the velocity from the relative position provided by using a multi-ranger sensor.
• A sequential charging strategy is proposed for autonomous persistent drone-charging of three quadcopters.
• Different to vision-based control techniques in previous studies in that a single drone can land precisely; this work can allow drones to land accurately with persistent feature.

2. Methodology

2.1. UAV Platform

In this study, a Crazyflie 2.1 (as shown in Figure 1), developed by Bitcraze [31], was used for experimentation. The Crazyflie 2.1 is a nano-quadcopter that weighs 27 g and measures 92 × 92 × 92 mm³. It communicates with the ground station through the CrazyRadio PA [32], which is a 2.4 GHz radio USB dongle. The microcontroller for the main application of Crazyflie 2.1 is the STM32F405 with the following specifications: Cortex-M4 core, 168 MHz, 192 kB SRAM, and 1 Mb flash. The inertial measurement unit (IMU) consists of a 3-axis gyroscope, a 3-axis accelerometer, and a high-precision pressure sensor. Bitcraze provides several sensors through a so-called deck compatible with Crazyflie 2.1. In this study, a distance sensor, UWB indoor positioning system (IPS), and wireless charging were utilized. The sensors are comprehensively described in Section 3.1.

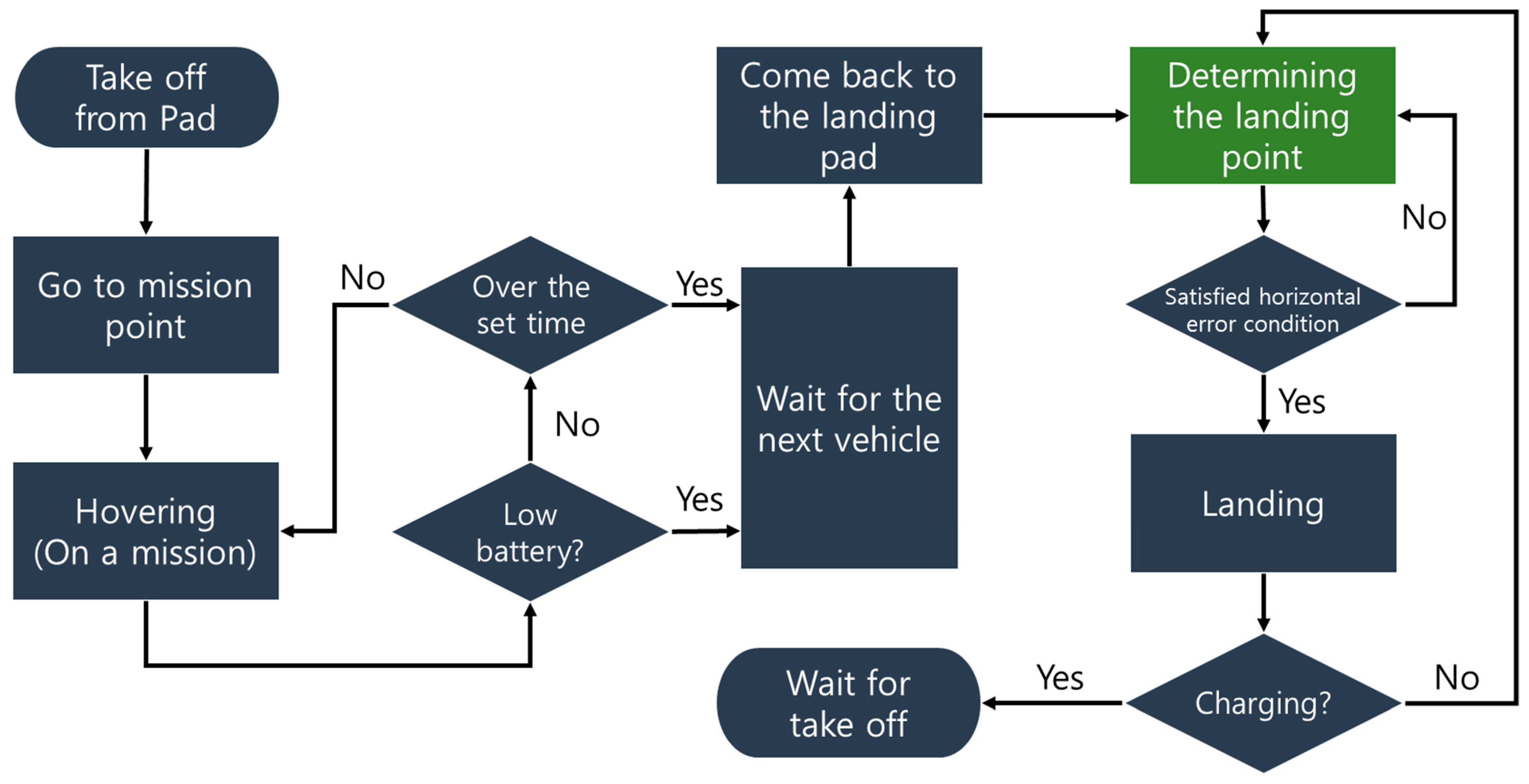
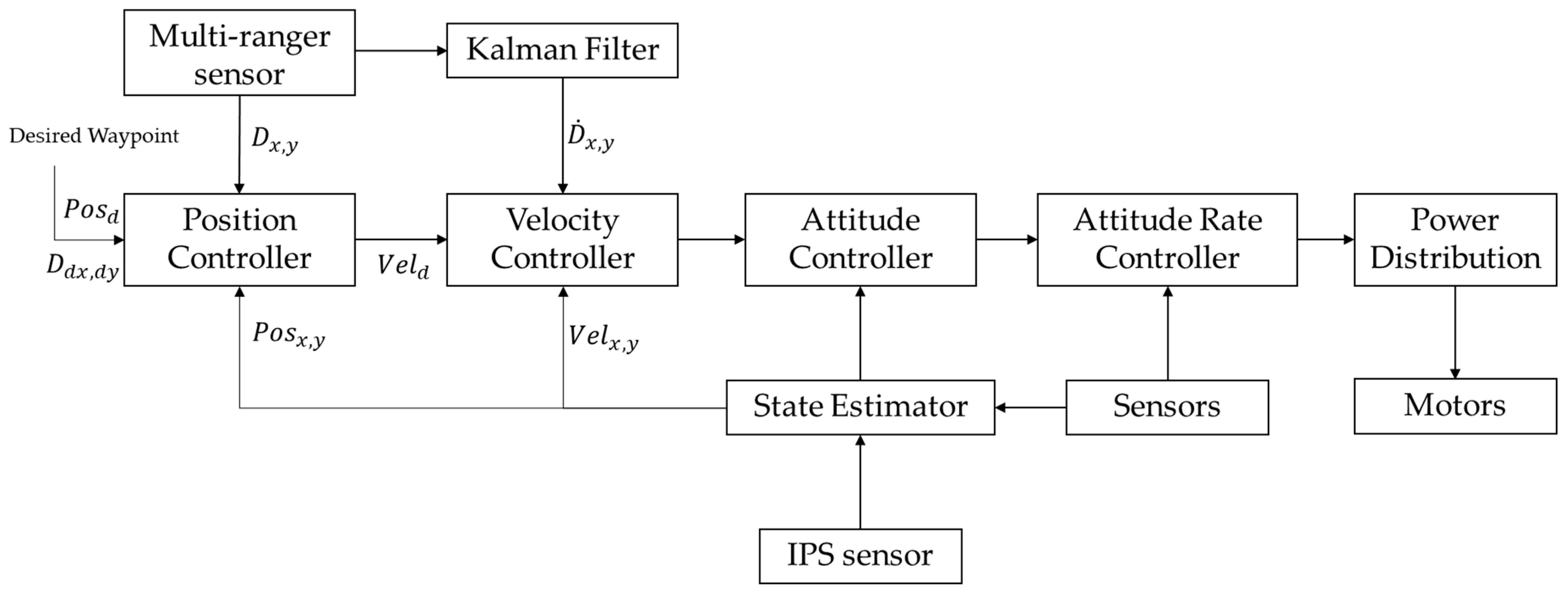
2.2. Charging State Machine Strategy and Control Scheme

The experiments were conducted using three Crazyflies to verify the persistent and continuous charging system. In these experiments, it was assumed that a Crazyflie needs to hover at a specific point to perform a mission. The ground station must receive the status of the vehicles through permanent communication. The battery capacity of the Crazyflie exceeds the allowed capacity. First, the Crazyflie took off from the landing pad (state 3) and reached the mission/target point; it then hovered for a preset time of 20 s (state 7). Note that the battery capacity of the Crazyflie should be larger than the allowed capacity during the hovering condition. When the Crazyflie satisfied either the hovering time or battery capacity, it was controlled to move a short distance in position mode and wait for the next coming vehicle. When the second Crazyflie satisfied the battery condition, it could take off and reached the target point where the first Crazyflie hovered. While the second Crazyflie moved to the hovering point, the first Crazyflie was controlled to return (state 8), adjust the home position (state 9), and land (state 10) at its home position/landing pad. The retry mission was required if there was a fault during the landing phase; thus, this mission was used to adjust the landing position. The scenario was the same for the third Crazyflie. By repeating the above sequential process, the mission could be continuously performed without human intervention. The whole charging state machine strategy is shown in Figure 2.

The defined parameters are shown in Figure 3, while the control structure is presented in Figure 4. The loco positioning system $(Po{s}_d,Po{s}_{x,y}, Ve{l}_{x,y})$ was used in this study because the tests were conducted in an indoor environment. The position controller used this loco positioning system as an absolute coordinate system. In a normal case, the loco positioning system is used to control the position. However, in the landing phase, a relative positioning system $(D_{dx,dy}, D_{x,y}, {\dot{D}}_{x,y})$ was applied to reduce the horizontal error. The relative information was obtained by using the wall that was set up. This is described in Section 3.2.

It should be noted that the relative position $D_{x,y}$ is measured from a multi-ranger sensor which is discussed in the next section. However, the multi-ranger sensor does not provide the relative velocity ${\dot{D}}_{x,y}$ for the drone system. Therefore, the value of ${\dot{D}}_{x,y}$ is estimated from the position of the multi-ranger sensor through Kalman filter algorithm. In actuality, the speed of the indoor positioning system $Ve{l}_{x,y}$ is estimated in a similar way. Because the $Po{s}_{x,y}$ of indoor positioning is insufficient for landing task, the proposed system is used for the pair of data $D_{x,y}$ and ${\dot{D}}_{x,y}$ (not pair of data $D_{x,y}$ and $Ve{l}_{x,y}$) to synchronize sensor signal and to improve the accuracy.

3. Experimental Setup

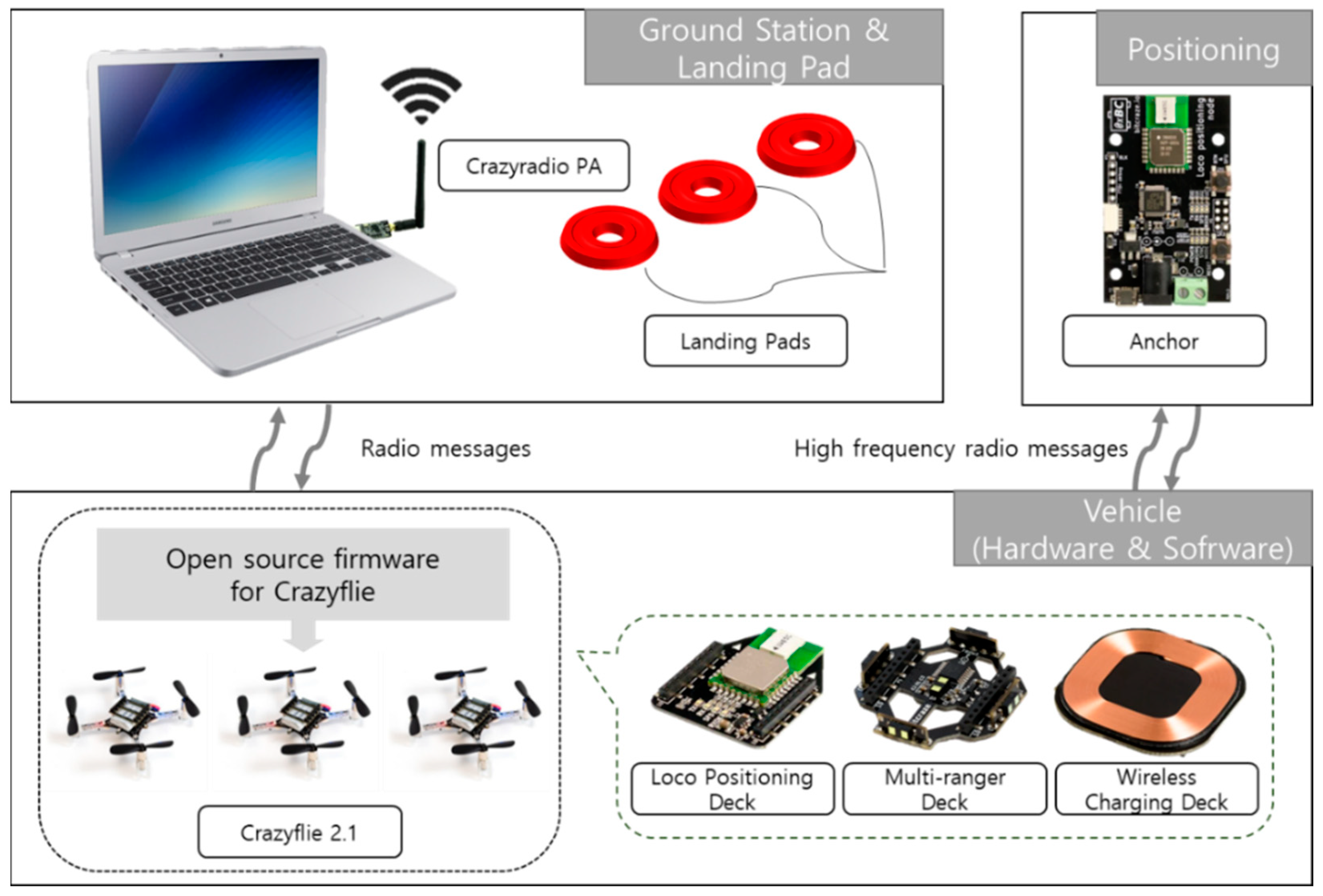
3.1. UAV Platform Description

3.1.1. Sensors

As mentioned in Section 2.1, Bitcraze provides several sensors that are compatible with Crazyflie. The sensors used in this study are as follows:

• Loco positioning system (indoor positioning system).
• Multi-ranger deck (5-way distance sensor).
• Wireless charging deck.

The loco positioning system operates in indoor environments. Several anchors were placed in a specific space. The loco positioning deck is attached to the Crazyflie to calculate the position of Crazyflie by exchanging high-frequency radio messages with the anchors. The user can select a position estimation method among the following three: TWR (two-way ranging), TDoA2 (time differential of arrival 2), and TDoA3 (time differential of arrival 3). TDoA2 was used in this study. When using the multi-ranger deck, a laser-ranging sensor can detect surrounding objects in five directions, namely, front, back, left, right, and up directions, with a maximum distance of 4 m. The wireless charging deck implements the Qi wireless charging standard (WPC v1.2 Qi) [33], which can support charging up to 1 A at 5 V.

3.1.2. System Configuration

Figure 5 shows the overall system configuration. The loco positioning deck, multi-range deck, and wireless charging deck were attached to the Crazyflie. The Crazyflie 2.1 firmware [34] is an open-source firmware for drones provided by Bitcraze. A ground control station (GCS) was set up with a Crazyradio PA to interface the state of the drone. The battery status, logging data, and transmission of commands to each drone were performed by the GCS, while most of the calculations were performed using an onboard flight controller. The landing pad can provide high-speed wireless charging for drones with a consumption of 9 W.

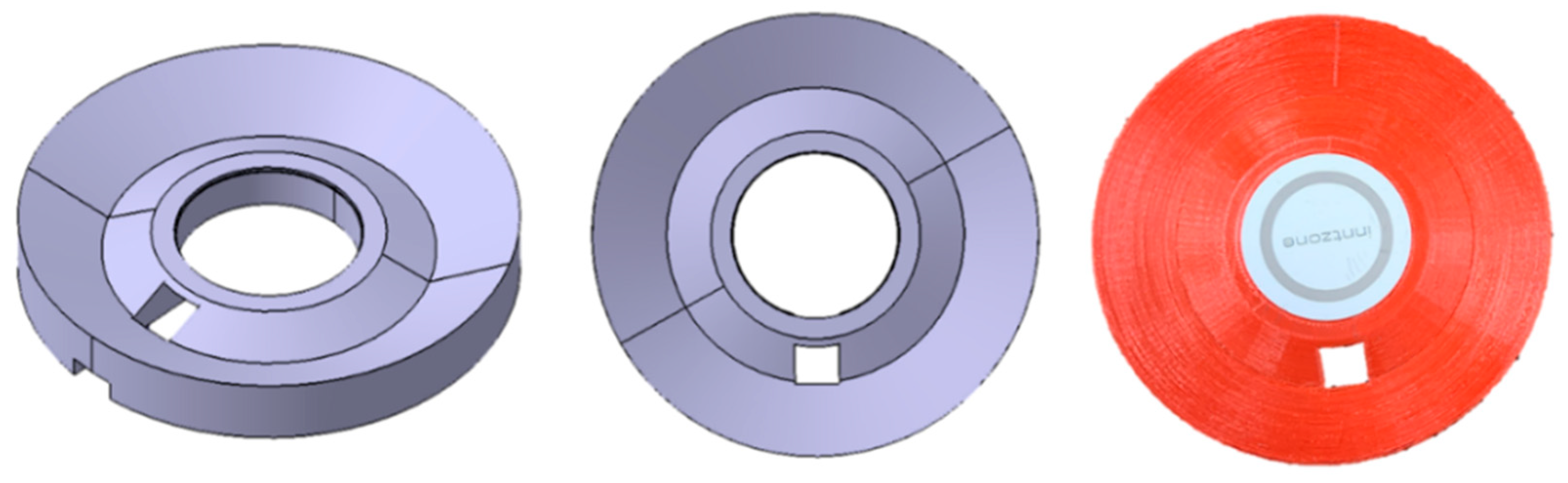
3.2. Wireless Charging Setup

Figure 6 shows the wireless charging setup. Three wireless charging stations were installed according to the number of Crazyflies. This is because each drone can return to home position for charging in case of low battery. Normally, when we use the original local position system from the Crazyflie manufacturer, the average accuracy is 10 cm.

In order to overcome this issue, a multi-ranger sensor was used to use to improve the accuracy of the system. It was placed diagonally so that a multi-ranger sensor could measure the relative distance to the wall, which was used to increase the precision in the landing phase.

The landing pads with a wireless charger were designed according to the charging pad [35] manufactured by Bitcraze. The landing pad was designed with an incline angle so that the landing gear of the drone contacts the wireless charger accurately. It should be noted that if we apply this method for large drones under outdoor environment, then the cost for design of the charging system is expensive. Therefore, in this paper, the landing pad is designed in a small size. Figure 7 shows the CAD part design and the resulting drawing with a three-dimensional printer. The Crazyflie uses a 1-cell LiPo (lithium polymer) battery with a capacity of 240 mAh. When a voltage of 3.5 V is set as the threshold, the charging time is approximately one hour. The maximum operation time is 4 min.

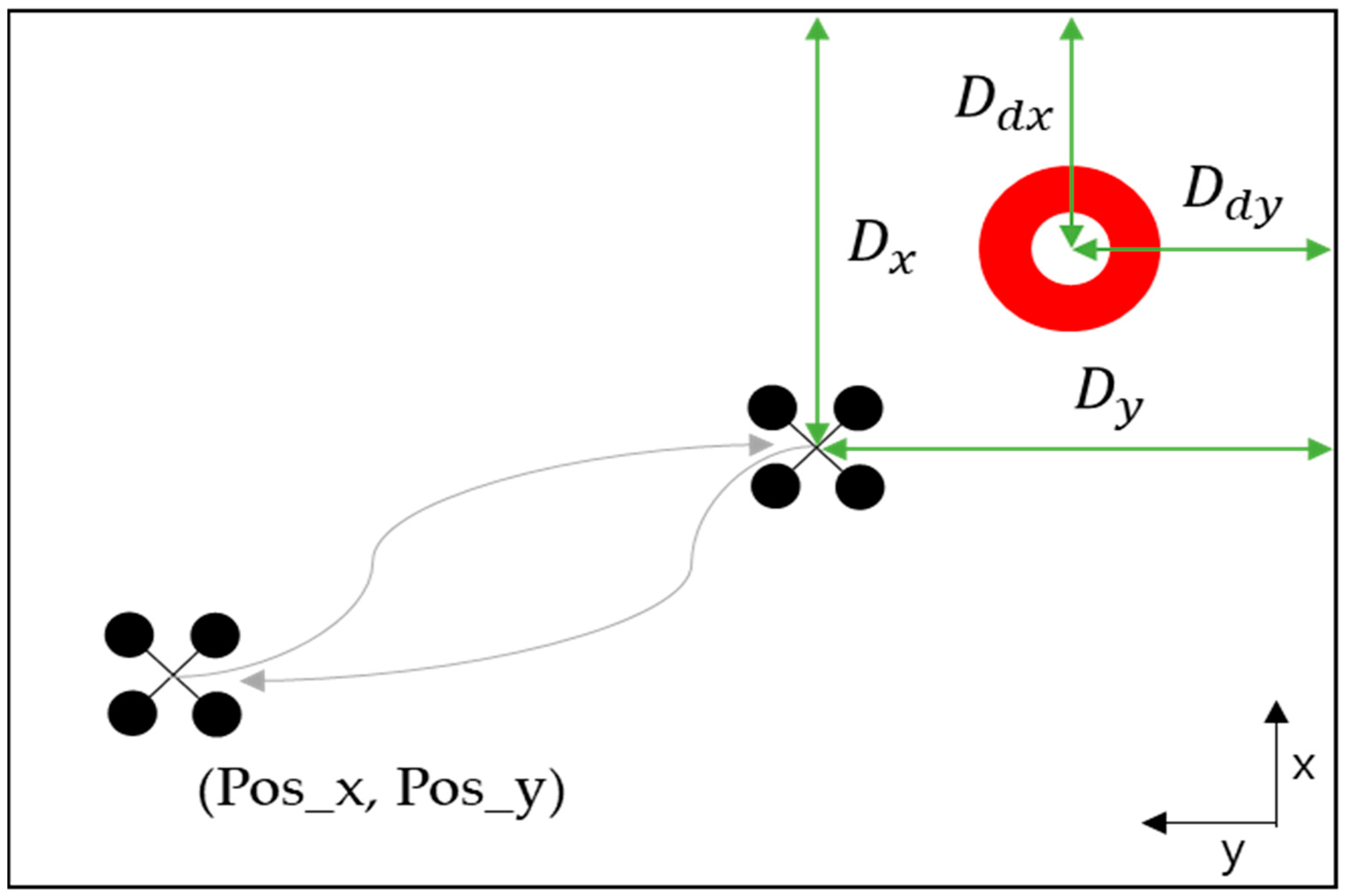
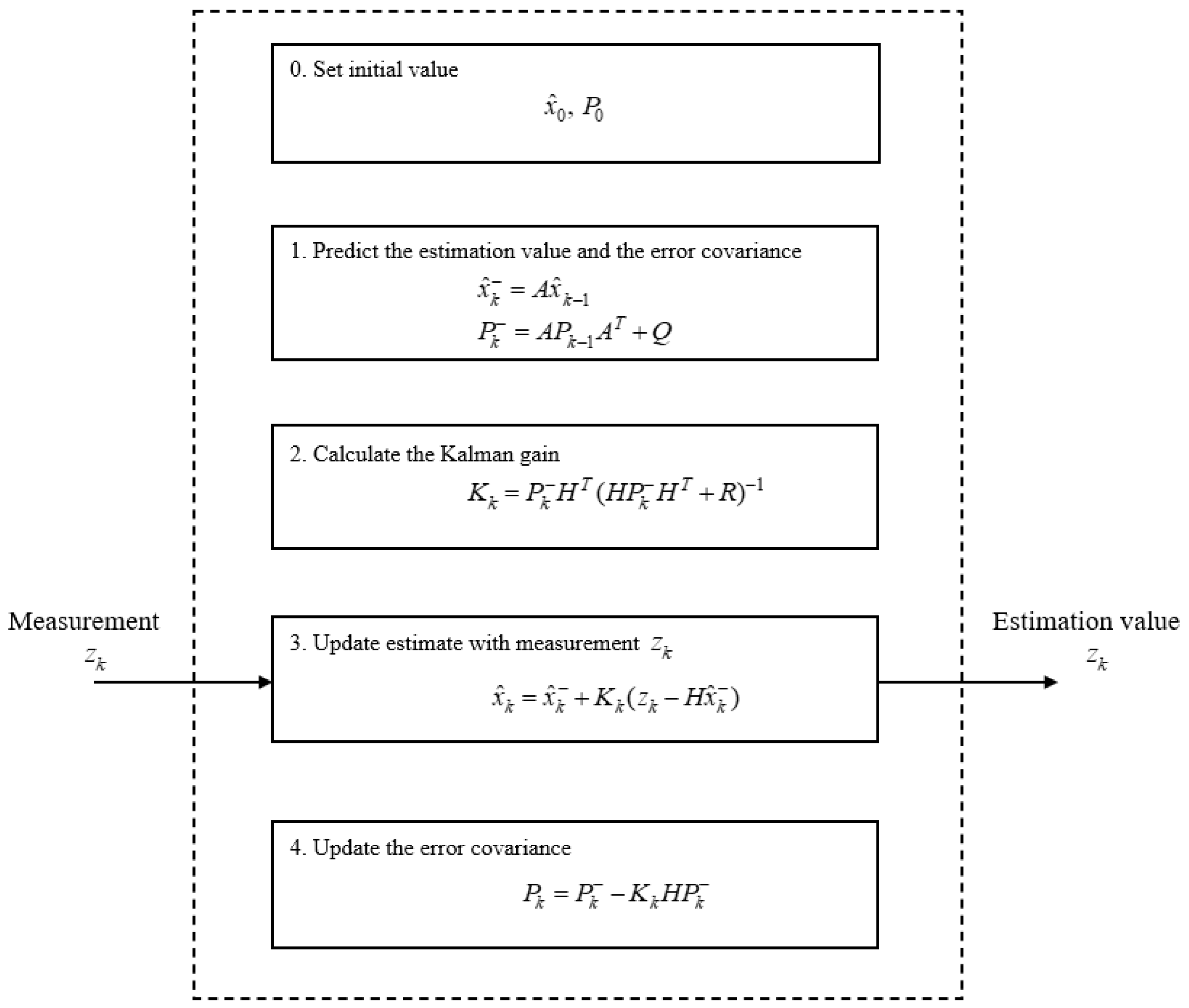
3.3. Kalman Filter for Landing Phase

As mentioned in Section 2, the position controller of the landing phase made use of the relative position provided by the multi-range sensor instead of the absolute position. The relative velocity was estimated using the Kalman filter algorithm [36]. Equation (1) represents the state variable, and the system model can be expressed as Equation (2):

$$x={\left[\begin{array}{cc}p& v\end{array}\right]}^T$$

(1)

$$x_{k+1}=A{x}_k+w_k$$

(2)

$$z_k=H{x}_k+v_k$$

(3)

where $p$ is the position, $v$ is the velocity, $z_k$ is the measurement, $w_k$ is the system noise, $v_k$ is the measurement noise, and $x_k$ is the state variable. $A, H, Q, R$ denote the system model matrices and they are defined as:

$$A=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right], H=\left[\begin{array}{cc}1& 0\end{array}\right], Q=\left[\begin{array}{cc}1& 0\\ 0& 3\end{array}\right], R=10$$

where $A$ is the system state matrix, $H$ is the observation matrix, $Q$ is the covariance matrix of the system noise, and $R$ is the covariance matrix of the measurement noise. The Kalman filter algorithm is presented in Figure 8. The first step is used for prediction; it calculates the predicted state $({\widehat{x}}_k^{-})$ and predictive error covariance $(P_k^{-})$ from the system matrices $(A, Q)$. The Kalman gain $(K_k)$ is computed from the predictive error covariance $(P_k^{-})$ and related system matrices ($H$ and $R$). In step 3, an estimate $({\widehat{x}}_k)$ is computed from the measurement input $(z_k)$, Kalman gain, and predicted state. The error covariance is updated in step 4 using the Kalman gain from step 2 and the predictive error covariance from step 1.

It should be noted that increasing value of the matrix $Q$ will increase Kalman gain [34]. This made the estimate closer to the measured value. If the value of matrix $Q$ is decreased, the estimate is less affected by the measurement and moves closer to the previous estimate. This makes the noise in the measurement less influential on the result, and, in turn, the estimate becomes smoother. However, the matrix R affects the results in the opposite way.

4. Results

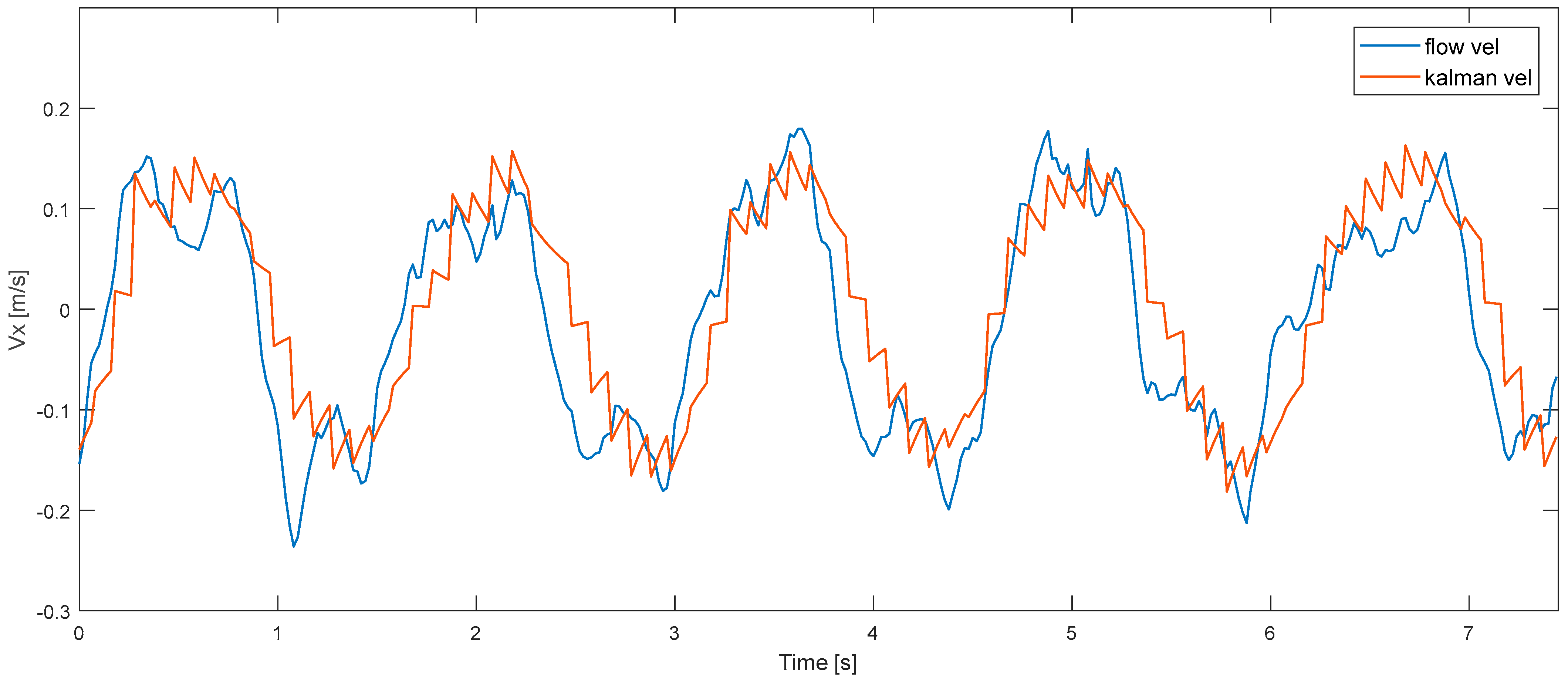
4.1. Velocity Estimation from Position

As shown in Section 2.2, to use the PID controller in Crazyflie, a feedback velocity should be obtained from the sensor. However, the multi-ranger sensor does not provide the feedback velocity to the quadcopter system. To overcome this issue, the Kalman filter algorithm is applied to estimate the velocity from the position. To validate the proposed method, an optical-flow sensor was used as a reference sensor. In actuality, there is no available sensor to measure the speed attached on the Crazyflie platform. Therefore, the optical-flow sensor which can connect to the Crazyflie platform was chosen for simple purpose. Figure 9 compares the velocity of the optical-flow sensor with the estimation velocity of the Kalman filter algorithm. In actuality, the sinusoidal signal was tested to verify the time-varying response of estimation. Note that the estimation velocity of the Kalman filter algorithm shows a similar trend to that of the optical flow sensor. The user can tune the matrices $Q$ and $R$ to achieve a better performance.

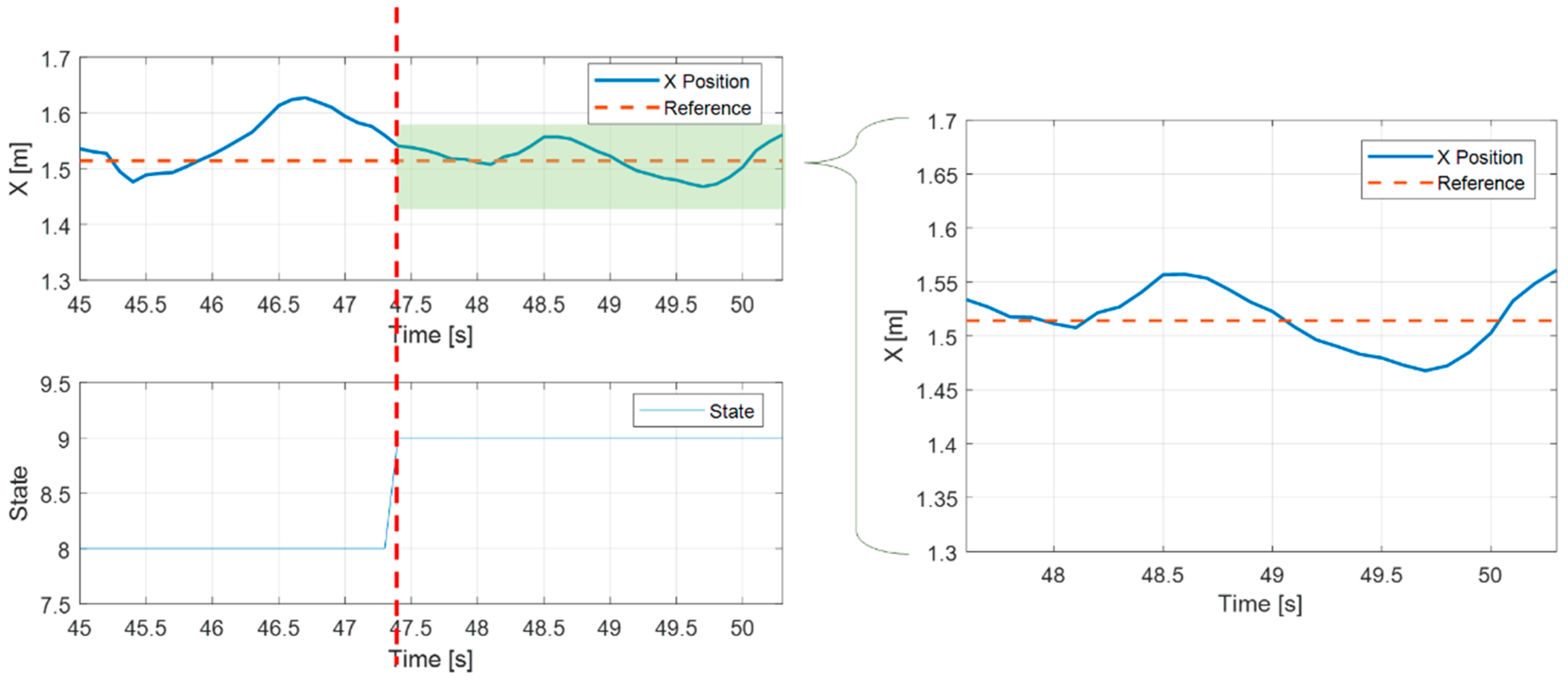
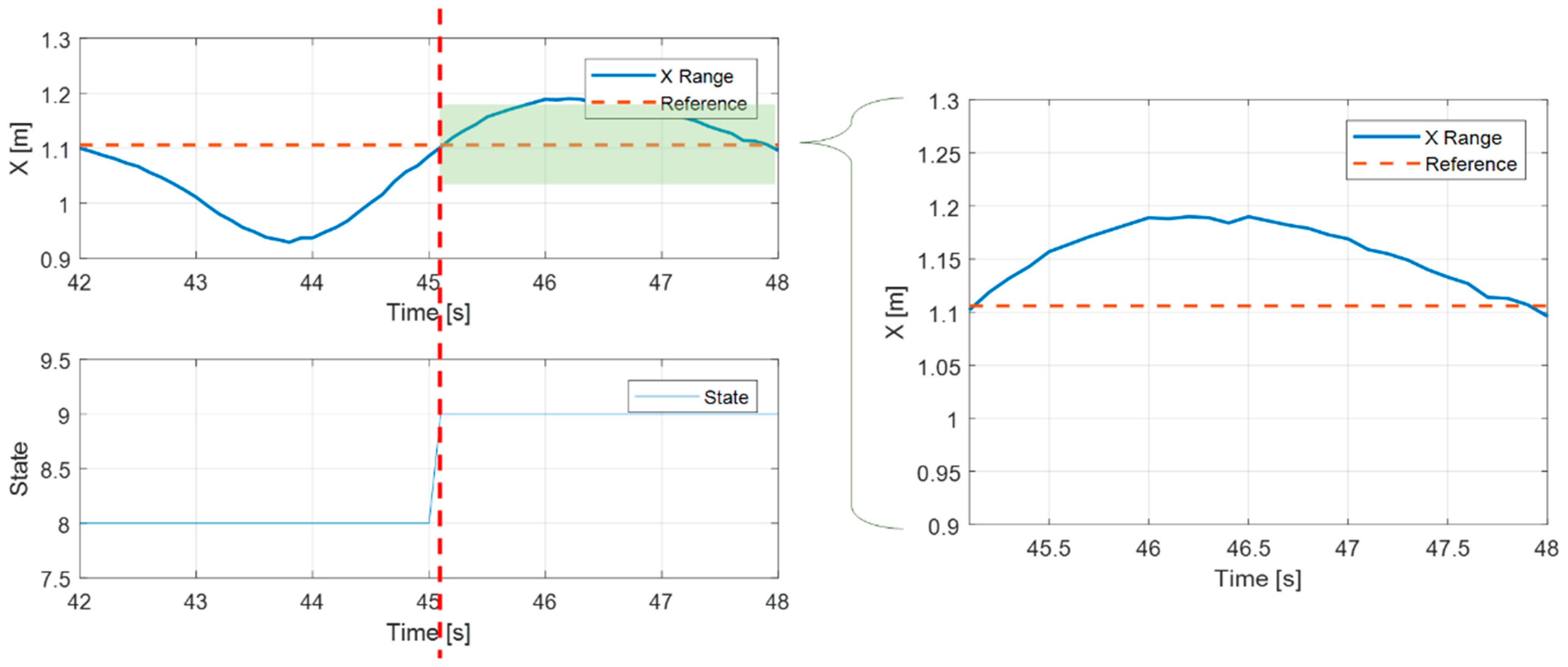
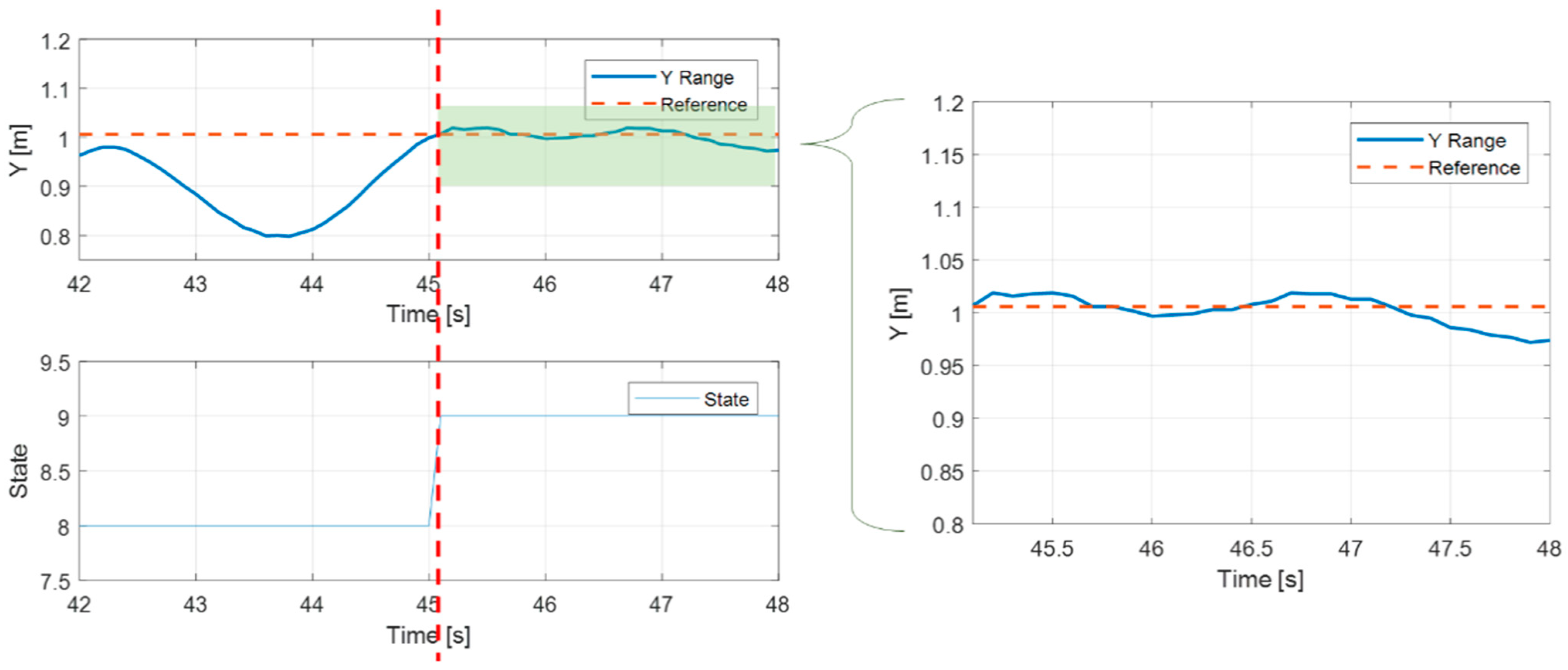
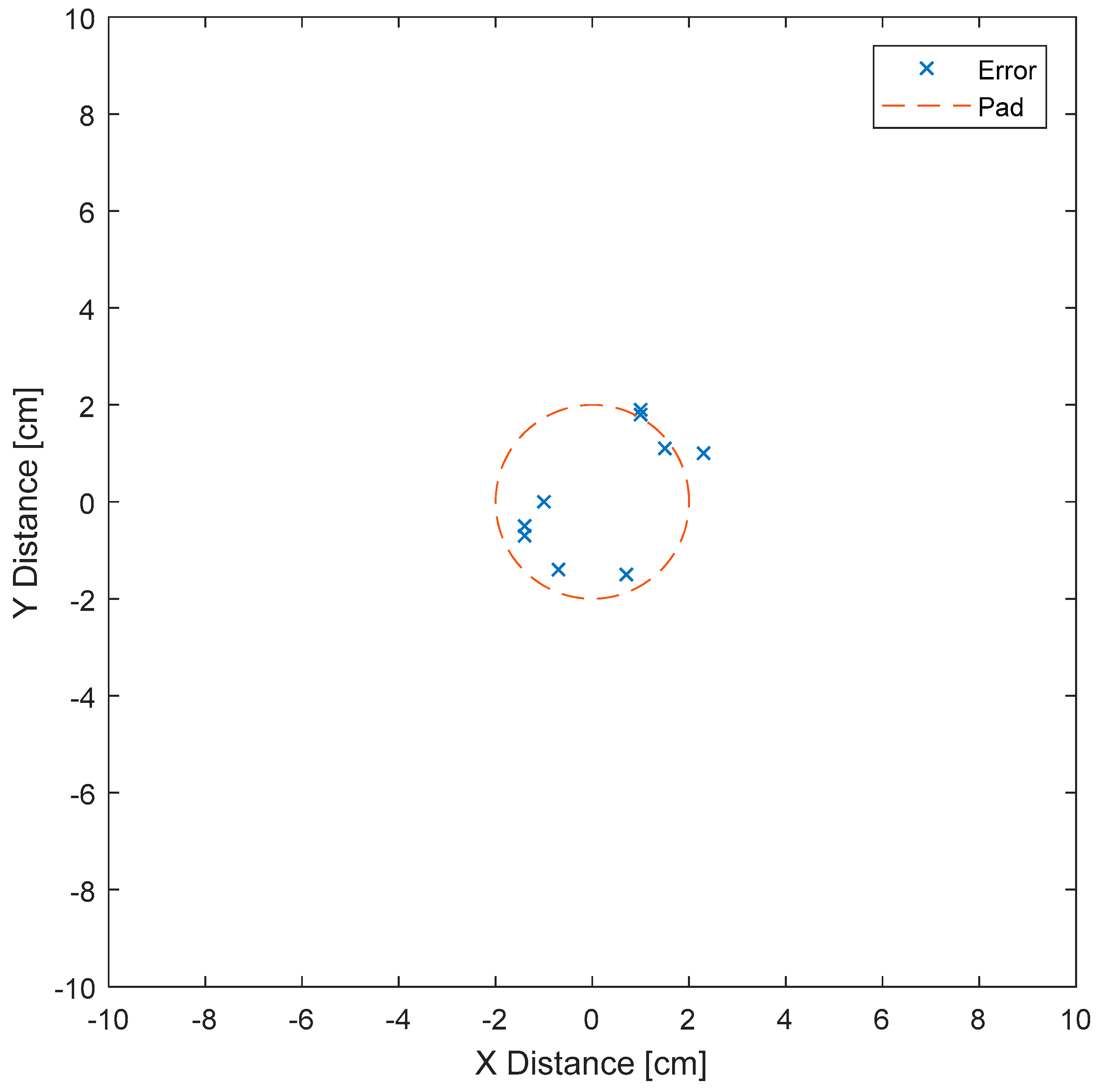
4.2. Trajectory Tracking and Landing Accuracy Performance

In this section, it is assumed that the Crazyflie drones operate under no windy conditions. Because Crazyflie drones are lightweight, they are difficult to land accurately under windy conditions. The further research will consider this limitation with bigger drones. Moreover, before flight test, the rangefinder sensor of each drone can be set up in a way such that it can measure the distance from the wall in x and y directions.

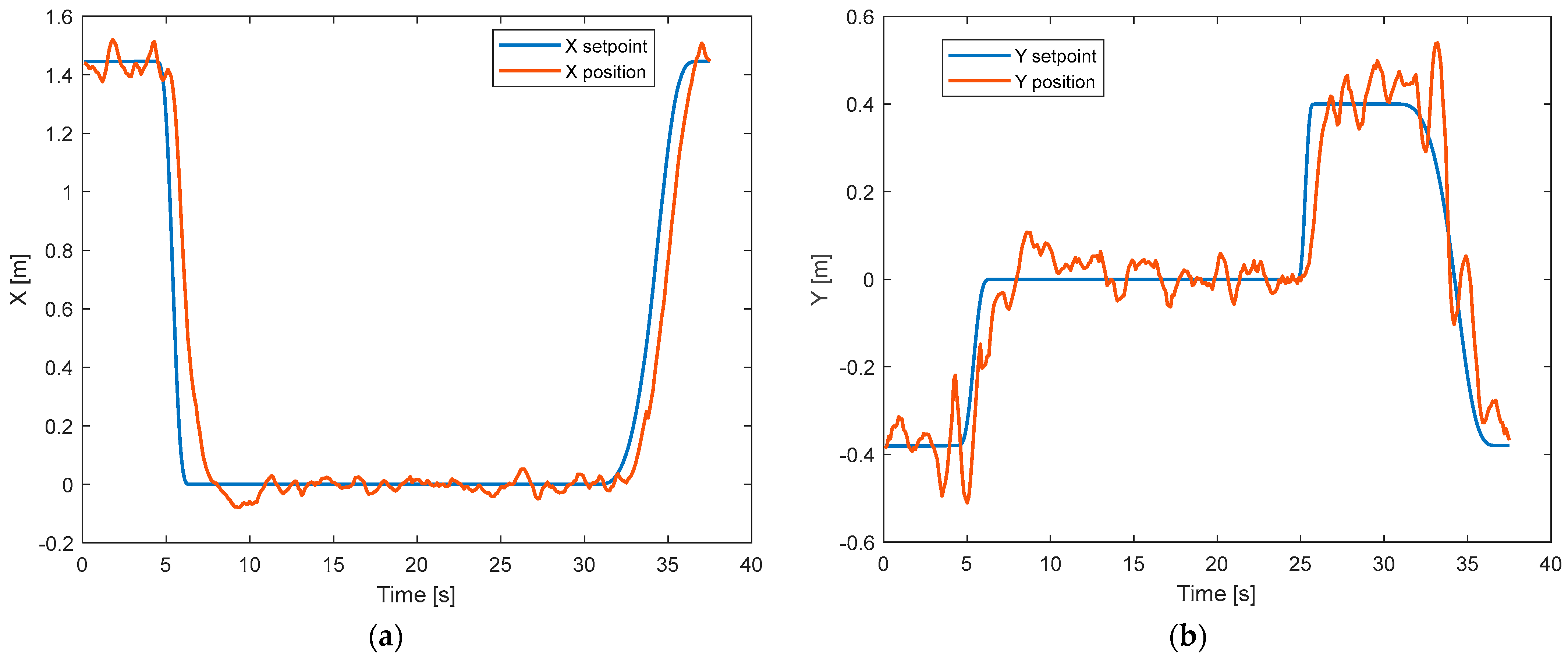
4.2.1. Trajectory Tracking Performance

The trajectory tracking performance of the position controller in $x$ and $y$ directions using the IPS is presented in Figure 10. Figure 10 shows the overall flight performance until just before landing, and shows the setpoint and measured position values. Note that the feedback positions can track the desired positions well. The integral absolute error ($IAE$) in Equation (4) was used as a performance index that can quantitatively evaluate the control system.

$$IAE={\displaystyle \underset{t_1}{\overset{t_2}{\int }}e(t)dt}$$

(4)

The $IAE$ refers to the integral area of the difference between the set value and the response. The $IAE$ of each axis is shown in

Table 1. The $IAE$ of full flight ($x$ axis, $y$ axis).

	IAE Value
$x$ axis	2.7930
$y$ axis	2.2099

.

4.2.2. Landing Accuracy Performance

To show the operation of the proposed algorithm, the performance of the position controller using IPS and the performance of the position controller using a multi-ranger sensor (proposed system) are compared in both $x$ and $y$ directions. In Figure 11, Figure 12, Figure 13 and Figure 14, state 8 means “come back to the landing pad” and state 9 means “determining the landing point”, as mentioned in Figure 2. Figure 11 and Figure 12 show the landing performance using IPS from $t=47s$ to $t=50.2s$. When the state was switched from 8 to 9, the landing process took place. Note that the accuracy in $x$ and $y$ directions is approximately 10 cm, which was not enough for a successful landing during the flight tests.

Figure 13 and Figure 14 show the landing performance using a multi-ranger sensor from $t=45s$ to $t=48s$. When the state was switched from 8 to 9, the landing process took place. Note that the accuracy in $x$ and $y$ directions is approximately 2 cm, which was enough for a successful landing during the flight tests.

The experiment was conducted and repeated three times. This means that the flight test of each drone was repeated three times. Therefore, experimental results for a total of nine landings were obtained.

Table 2. The results regarding flight experiments (IAE).

Error	1	2	3	4	5	6	7	8	9	Average
$IA{E}_x$	0.1603	0.0704	0.1130	0.0972	0.1713	0.2658	0.0454	0.8405	0.1489	0.2125
$IA{E}_y$	0.0492	0.1472	0.1796	0.0564	0.1473	0.5881	0.0833	0.4940	0.3020	0.2275

shows the landing results of the flight test. The landing results were derived using the $IAE$. The $IAE$ of each direction is defined as

$$IA{E}_{x,y}={\displaystyle \underset{t_{9s}}{\overset{t_{9e}}{\int }}e(t)dt}$$

(5)

where $IA{E}_x, IA{E}_y$ are the $IAE$ values in $x$—direction and $y$—direction. $IAE$ value was calculated from the start of state 9 to the end of state 9.

In order to show the experimental results more visually, they were summarized as landing errors. The error of each direction is defined as

$$e_x=\left|x_v-x_c\right|$$

(6)

$$e_y=\left|y_v-y_c\right|$$

(7)

$$e_{xy}=\sqrt{{\left(x_v-x_c\right)}^2+{\left(y_v-y_c\right)}^2}$$

(8)

where $e_x, e_y, e_{xy}$ are the errors in $x$—direction, $y$—direction, and in both $x$ and $y$ directions.

It should be noted that the average error from $x$ or $y$ directions is less than 2 cm. This is better than that of the existing open-source software (10 cm). Figure 15 shows the landing zone of each test. Note that the accuracy is high, and the drone achieved a successful landing during the flight tests.

Note that the accuracies of precision-landing-based fuzzy algorithm in [36] and PD control in [37] are 19.43 cm and 20 cm, respectively, but the proposed method in this article is better, with the accuracy of 2 cm.

It should be mentioned that the hardware for implementation in this article is lightweight and different to the methods in [36,37]. It is more fair if we can compare with the same open-source structure, but this is time-consuming and is a limitation of this paper. Future work will be implemented on a bigger drone and the same open-source code under outdoor conditions for comparison, which will make the drone more reliable.

Remark 1.

Different to current studies, the proposed algorithm does not use the vision system. This is low-cost and can help the drone to perform in both bright and dark environments. Moreover, the proposed precision landing technique is the first used for autonomous persistent drone-charging systems.

Remark 2.

The proposed system using multi-ranger sensor is applied to indoor persistent drone-charging application. The application may fail to achieve if the original hardware is used. Therefore, the proposed system aims to improve the hardware issue using low-cost solutions and aims to introduce new software and application for nano drone systems.

Remark 3.

The proposed control can be replaced with a robust controller, such as sliding mode control [38], for disturbance rejection. This is a limitation of this paper because the aim of this work is to propose a system which can improve upon the current open-source code from Crazyflie firmware. The future work will focus more on this issue.

Remark 4.

In this manuscript, the PID controller is used instead of a nonlinear controller because this is the first modification from open-source firmware. The PID controller was designed by trial-and-error method. In future work, the nonlinear controller will be applied to handle the disturbance and uncertainties.

The complete work can be found in the following link: https://www.youtube.com/watch?v=qoLPiGrLJcc&feature=youtu.be (accessed on 1 August 2022).

5. Conclusions

In this study, a precision landing method based on a Kalman filter was investigated for an autonomous persistent drone system. A multi-ranger sensor was used during the landing stage instead of an IPS. The estimation velocity was computed from the relative position of the multi-ranger sensor. A charging state machine strategy is proposed for battery charging in sequence. The proposed method was validated through a flight test on the Crazyflie quadcopter platform. The results show that the estimation velocity can track the optical-flow sensor, which was considered as the reference sensor for comparison. The accuracy was improved significantly for landing performance when compared with existing open-source firmware. Future work should address the health management of batteries for drone systems to increase the reliability of the proposed system. Moreover, the future work will also tackle the outdoor performance under disturbances with bigger drones.