Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation
Abstract
:1. Introduction
- There are no systematic design and analysis theorems that can be used to adapt an existing exponentially stable flight controller to a universal AVA system.
- The configuration space of an AVA is non-Euclidean. Moreover, the traditional attitude control based on local coordinates is not globally effective. This may reduce the maneuverability of the AVA.
- In previous research, wireless communications have commonly been used for traditional UAV swarms. However, the delay in wireless communications makes it harder to realize cooperative control of the multiple sub-aircraft in an AVA.
- Unlike the most common aerial transportation systems that rely on cables, our proposed AVA is connected via spherical joints. These joints reduce the complexity of the entire dynamics. Thus, some existing controllers for quadrotors can be conveniently adapted to our system, which enhances the expandability of the system.
- The design criteria for a controller for this kind of AVA are carefully analyzed. An existing flight controller can be adapted for an AVA following the criteria. A geometric controller is designed for the AVA. The controller is singularity-free and does not have the unwinding problem induced by quaternions. Therefore, it is suitable for a fully actuated AVA system.
- Unlike existing systems, we develop the hardware and the software of the system based on the CAN bus. Compared to existing work that relies on wireless communications, the CAN bus has low-latency communications, does not rely on external devices, and supports an expansion of the number and placement of the multiple sub-aircraft in an AVA.
- Real-world experiments with three sub-aircraft were conducted. These illustrated the expandability of the system and the feasibility of the proposed methodology.
2. Dynamics Modeling and Controller Design Criteria
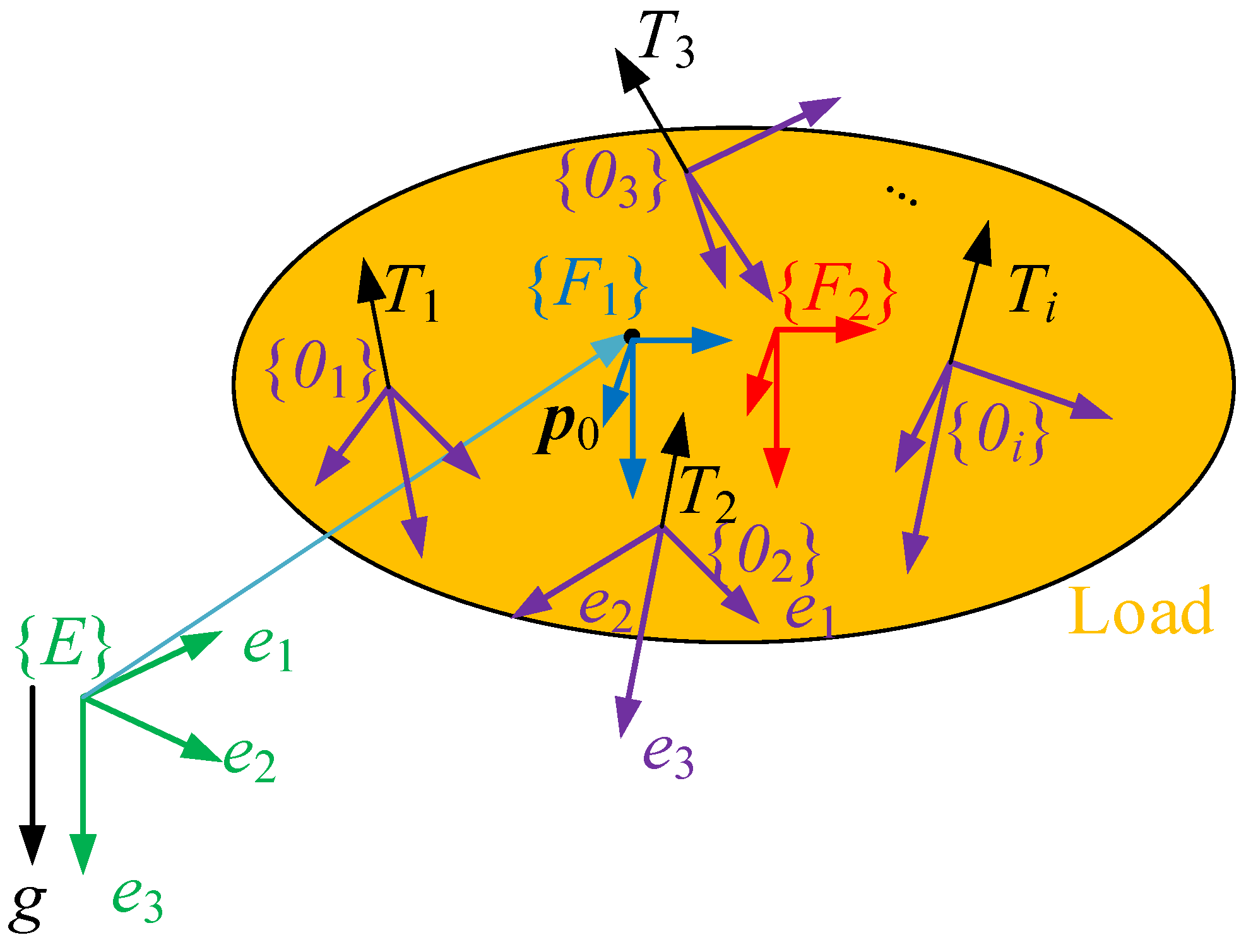
2.1. Modeling of an AVA
2.2. Adapting an Exponentially Stable Flight Controller
3. Example Design of a Geometric Controller
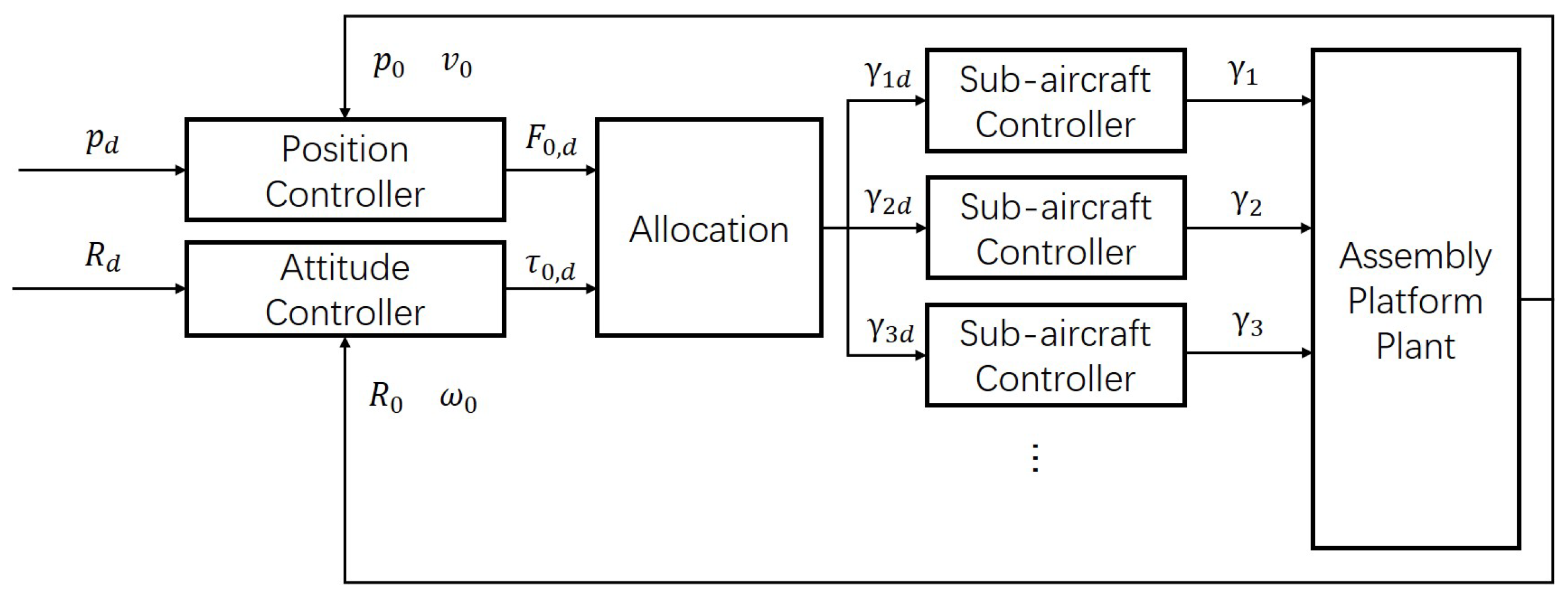
3.1. Overall Controller Architecture
3.2. Payload Controller Design
3.2.1. Outer Loop of Payload Attitude Control
3.2.2. Inner Loop of Payload Attitude Control
3.2.3. Position Control of the Payload Platform
3.2.4. Allocating the Wrench
3.3. Stability Analysis
- 1.
- There exists a positive constant such that for all , the closed-loop tracking error is exponentially stable at the origin .
- 2.
- Moreover, suppose that the initial attitude error satisfies . Then, if the control gains are selected appropriately, the closed-loop attitude tracking error is exponentially stable at and , where .
- 1.
- There exists a positive constant such that for all , the closed-loop tracking error converges to the region containing the origin in finite time.
- 2.
- Moreover, suppose that the initial attitude error satisfies . If the control gains are selected appropriately, then the closed-loop attitude tracking error converges to the region containing the origin in finite time.
- 3.
- If the control parameters are selected appropriately such that is a Hurwitz matrix, then the closed-loop tracking error converges to the region containing the origin in finite time.
4. Real-World System Implementation
4.1. Configuration of the Prototype
4.2. Real-Time Simulation of the Software
4.3. Development and Implementation of a Prototype
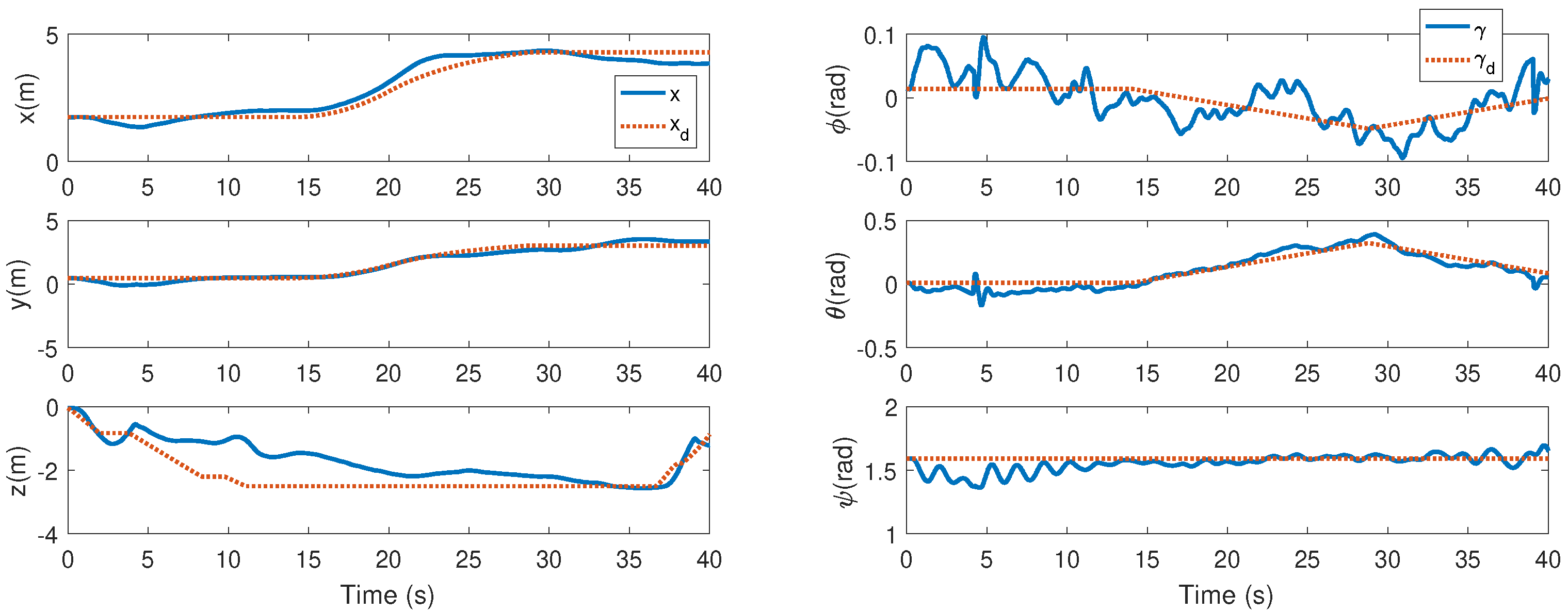
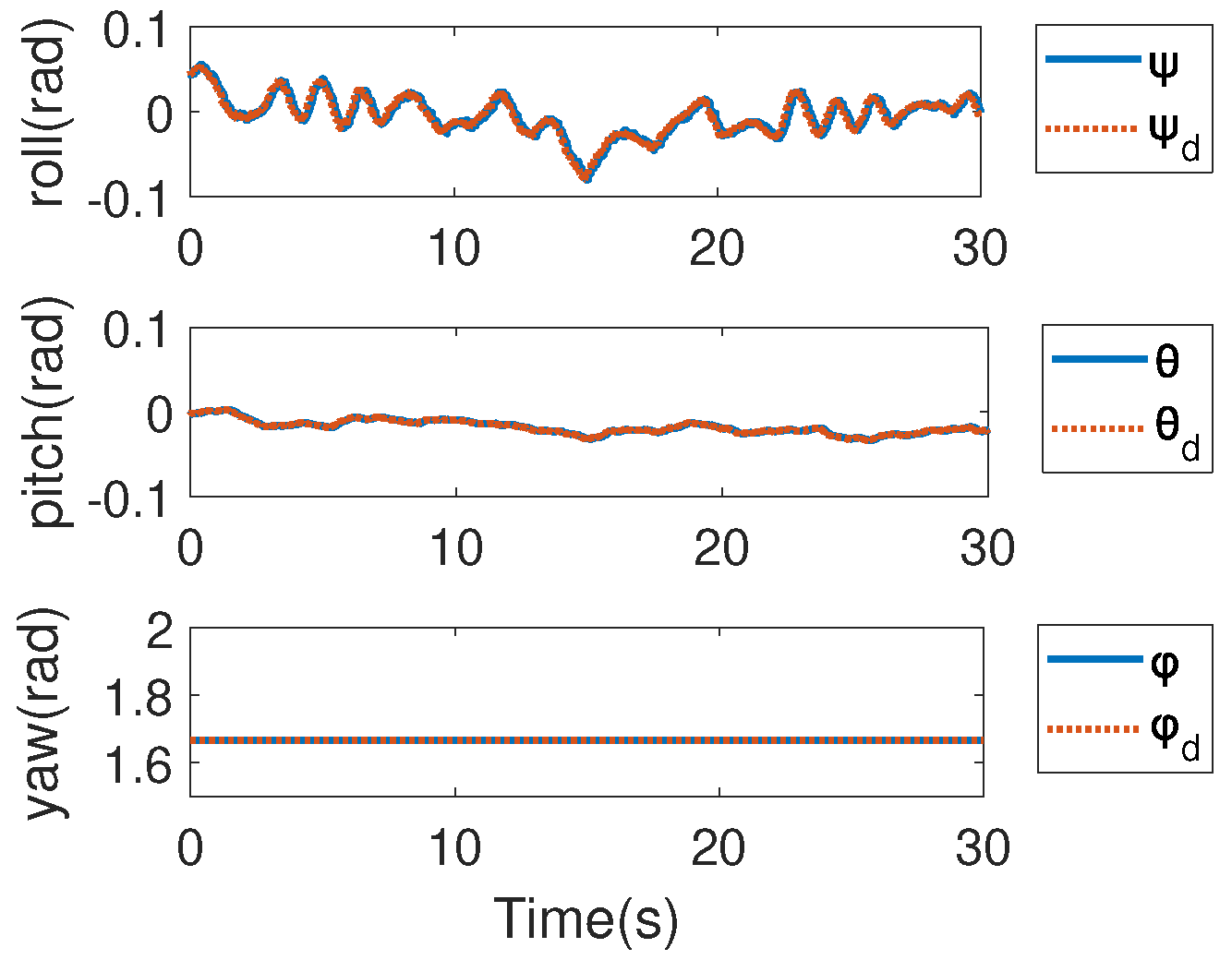
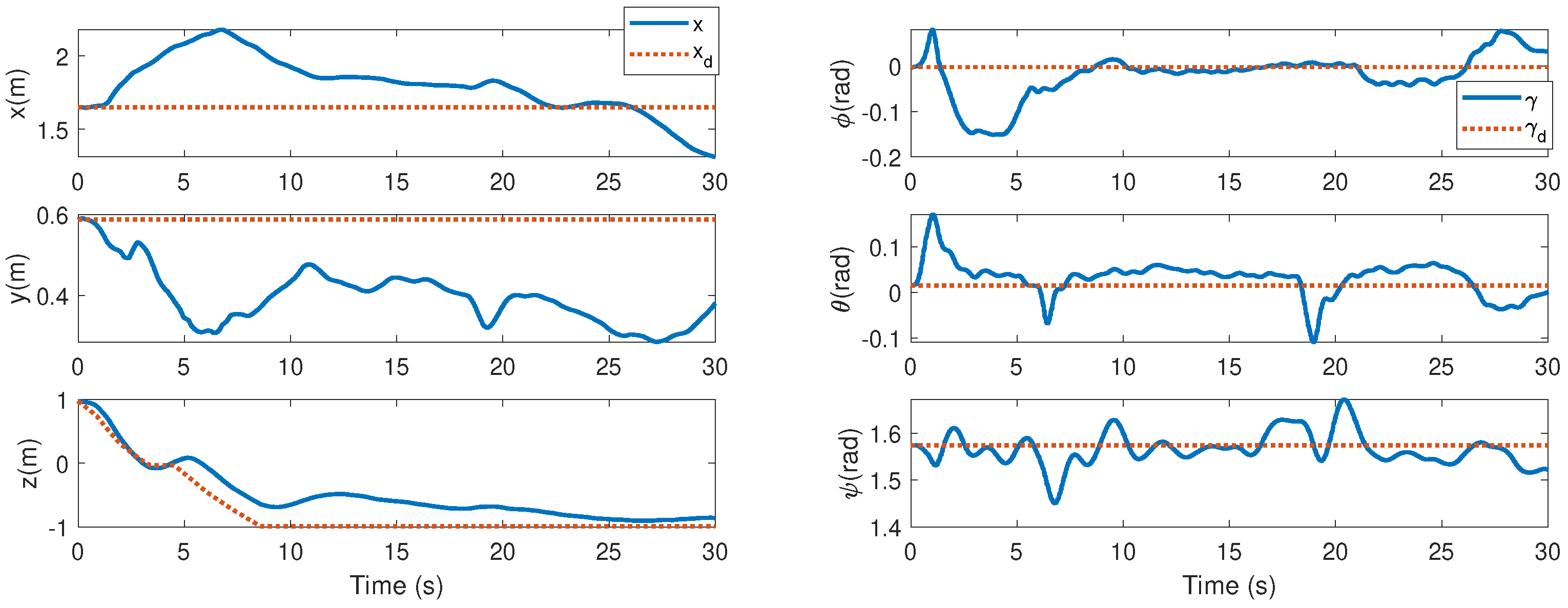
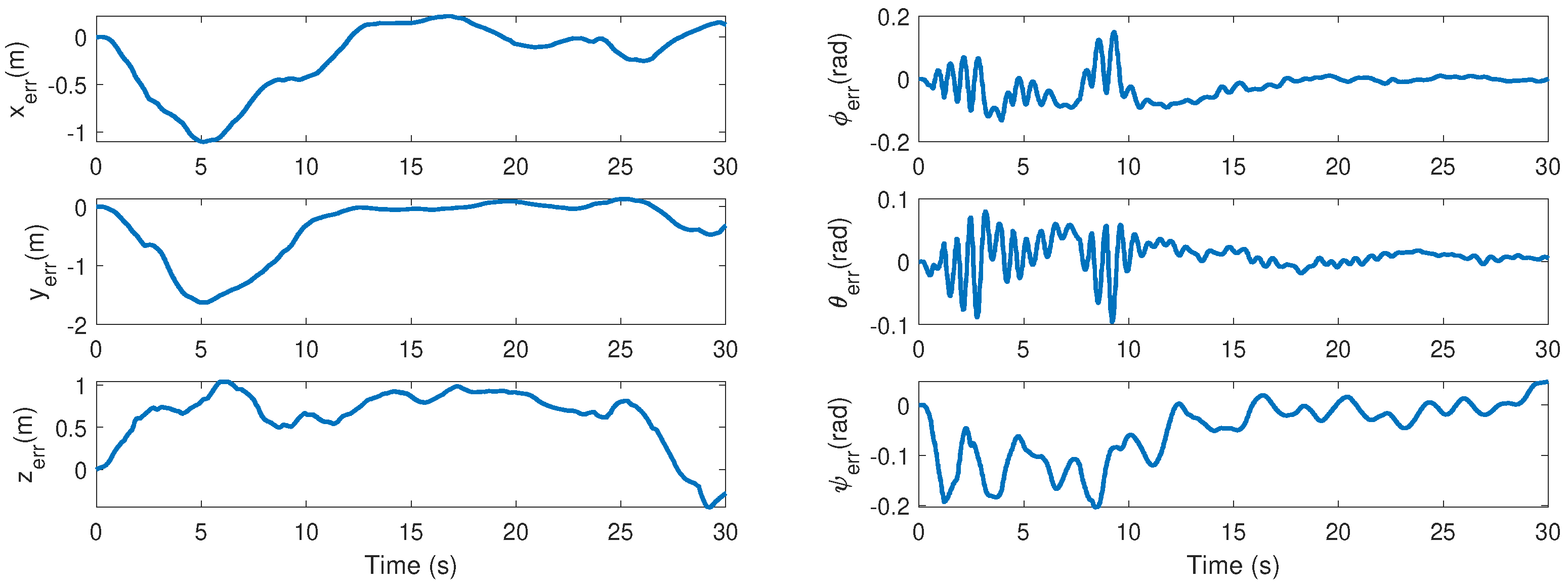
4.4. Real-World Experimental Results
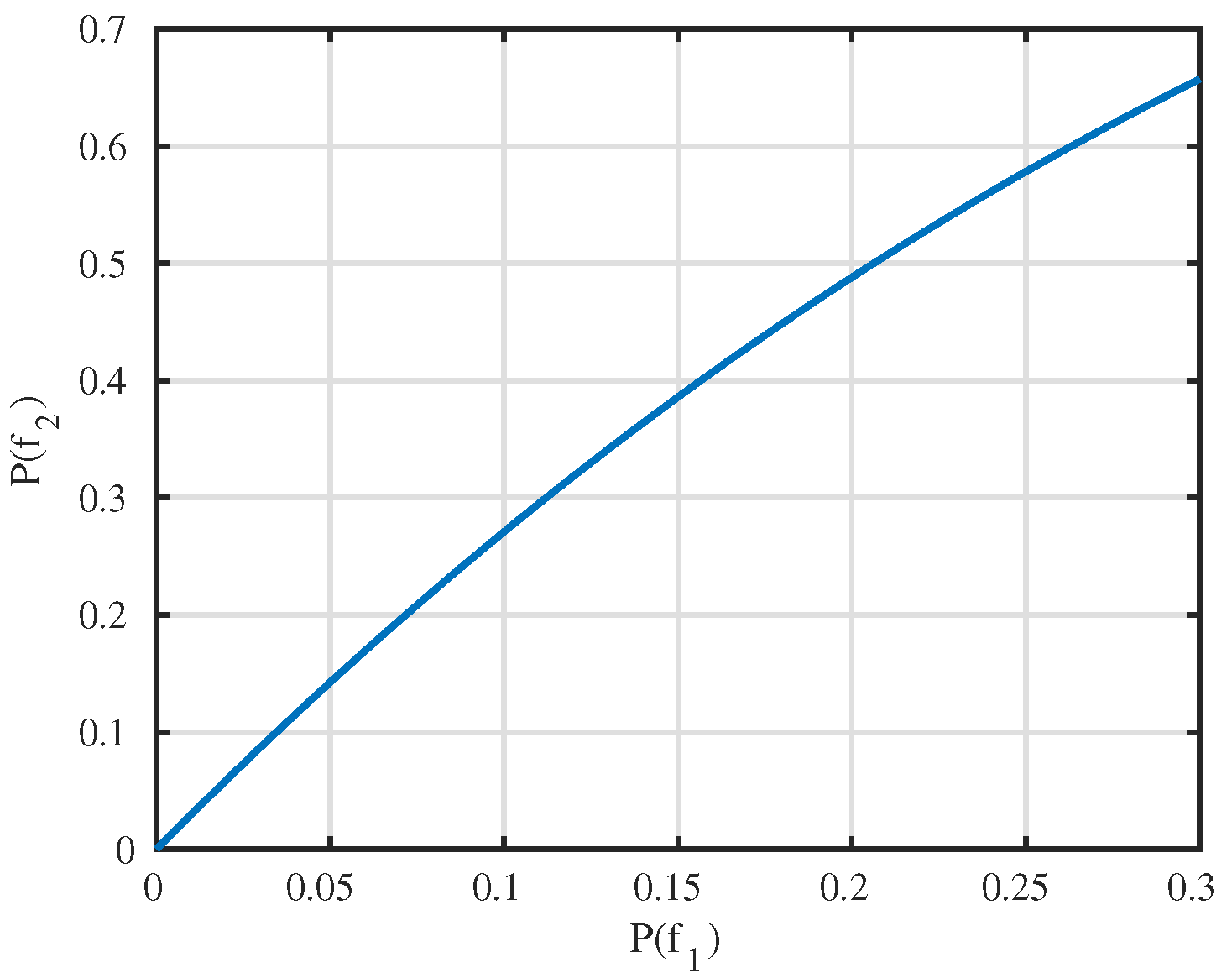
4.5. Comparison with MPC-Based Control Scheme
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kim, S.J.; Lee, D.Y.; Jung, G.P.; Cho, K.J. An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 2018, 3, eaar2915. [Google Scholar] [CrossRef]
- Estrada, M.A.; Mintchev, S.; Christensen, D.L.; Cutkosky, M.R.; Floreano, D. Forceful manipulation with micro air vehicles. Sci. Robot. 2018, 3, eaau6903. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Guo, P.; Xu, K.; Yu, Y. A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems. Chin. J. Aeronaut. 2019, 32, 200–214. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Ollero, A. Aerial manipulation: A literature review. IEEE Robot. Autom. Lett. 2018, 3, 1957–1964. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Han, J. Survey on aerial manipulator: System, modeling, and control. Robotica 2020, 38, 1288–1317. [Google Scholar] [CrossRef]
- Yu, Y.; Ding, X. A Global Tracking Controller for Underactuated Aerial Vehicles: Design, Analysis, and Experimental Tests on Quadrotor. IEEE/ASME Trans. Mechatronics 2016, 21, 2499–2511. [Google Scholar] [CrossRef]
- Jimenez-Cano, A.E.; Sanchez-Cuevas, P.J.; Grau, P.; Ollero, A.; Heredia, G. Contact-based bridge inspection multirotors: Design, modeling, and control considering the ceiling effect. IEEE Robot. Autom. Lett. 2019, 4, 3561–3568. [Google Scholar] [CrossRef]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Dexterous aerial robots—Mobile manipulation using unmanned aerial systems. IEEE Trans. Robot. 2017, 33, 1453–1466. [Google Scholar] [CrossRef]
- Zhang, G.; He, Y.; Dai, B.; Gu, F.; Yang, L.; Han, J.; Liu, G.; Qi, J. Grasp a moving target from the air: System & control of an aerial manipulator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1681–1687. [Google Scholar]
- Lippiello, V.; Fontanelli, G.A.; Ruggiero, F. Image-based visual-impedance control of a dual-arm aerial manipulator. IEEE Robot. Autom. Lett. 2018, 3, 1856–1863. [Google Scholar] [CrossRef]
- Yu, Y.; Li, P.; Gong, P. Finite-time geometric control for underactuated aerial manipulators with unknown disturbances. Int. J. Robust Nonlinear Control. 2020, 30, 5040–5061. [Google Scholar] [CrossRef]
- Ollero, A.; Tognon, M.; Suarez, A.; Lee, D.; Franchi, A. Past, Present, and Future of Aerial Robotic Manipulators. IEEE Trans. Robot. 2022, 38, 626–645. [Google Scholar] [CrossRef]
- Yu, Y.; Lippiello, V. 6D Pose Task Trajectory Tracking for a Class of 3D Aerial Manipulator From Differential Flatness. IEEE Access 2019, 7, 52257–52265. [Google Scholar] [CrossRef]
- Nguyen, H.; Park, S.; Park, J.; Lee, D. A Novel Robotic Platform for Aerial Manipulation Using Quadrotors as Rotating Thrust Generators. IEEE Trans. Robot. 2018, 34, 353–369. [Google Scholar] [CrossRef]
- Petitti, A.; Sanalitro, D.; Tognon, M.; Milella, A.; Cortés, J.; Franchi, A. Inertial Estimation and Energy-Efficient Control of a Cable-suspended Load with a Team of UAVs. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 158–165. [Google Scholar] [CrossRef]
- Yang, H.; Park, S.; Lee, J.; Ahn, J.; Son, D.; Lee, D. LASDRA: Large-Size Aerial Skeleton System with Distributed Rotor Actuation. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7017–7023. [Google Scholar] [CrossRef]
- Hamandi, M.; Usai, F.; Sable, Q.; Staub, N.; Tognon, M.; Franchi, A. Design of multirotor aerial vehicles: A taxonomy based on input allocation. Int. J. Robot. Res. 2021, 40, 1015–1044. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, K.; Guo, R.; Lippiello, V.; Yi, X. A framework to design interaction control of aerial slung load systems: Transfer from existing flight control of under-actuated aerial vehicles. Int. J. Syst. Sci. 2021, 52, 2845–2857. [Google Scholar] [CrossRef]
- Lee, T. Geometric Control of Quadrotor UAVs Transporting a Cable-Suspended Rigid Body. IEEE Trans. Control. Syst. Technol. 2018, 26, 255–264. [Google Scholar] [CrossRef]
- Wei, L.; Chen, M.; Li, T. Disturbance-observer-based formation-containment control for UAVs via distributed adaptive event -triggered mechanisms. J. Frankl. Inst. 2021, 358, 5305–5333. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Hou, J.; Zhao, Q. Event-Triggered-Based Discrete-Time Neural Control for a Quadrotor UAV Using Disturbance Observer. IEEE/ASME Trans. Mechatronics 2021, 26, 689–699. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J.; Guo, D.; Xie, A.H.; Song, D.L. Backstepping Sliding-Mode and Cascade Active Disturbance Rejection Control for a Quadrotor UAV. IEEE/ASME Trans. Mechatronics 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Yu, Y.; Ding, X.; Zhu, J.J. Attitude tracking control of a quadrotor UAV in the exponential coordinates. J. Frankl.-Inst.-Eng. Appl. Math. 2013, 350, 2044–2068. [Google Scholar] [CrossRef]
- Yu, Y.; Ding, X. Trajectory linearization control on SO(3) with application to aerial manipulation. J. Frankl. Inst. 2018, 355, 7072–7097. [Google Scholar] [CrossRef]









| Aircraft | Mass | Payload Capacity | Computing Unit |
|---|---|---|---|
| Sub-aircraft | 1.58 kg | 1.50 kg | PX4 FMUv5 |
| AVA | 6.24 kg | 3.02 kg | Nvidia nano computer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Wang, K.; Yu, Y. Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation. Drones 2022, 6, 272. https://doi.org/10.3390/drones6100272
Shi C, Wang K, Yu Y. Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation. Drones. 2022; 6(10):272. https://doi.org/10.3390/drones6100272
Chicago/Turabian StyleShi, Chuanbeibei, Kaidi Wang, and Yushu Yu. 2022. "Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation" Drones 6, no. 10: 272. https://doi.org/10.3390/drones6100272
APA StyleShi, C., Wang, K., & Yu, Y. (2022). Expandable Fully Actuated Aerial Vehicle Assembly: Geometric Control Adapted from an Existing Flight Controller and Real-World Prototype Implementation. Drones, 6(10), 272. https://doi.org/10.3390/drones6100272










