A Unified Airspace Risk Management Framework for UAS Operations †
Abstract
1. Introduction
- it should be conservative (since it is always preferable to overestimate risk for a Safety of Life application);
- it should explicitly budget contributions from different CNS elements to the overall risk;
- it should be capable of seamlessly and efficiently handling free routes and arbitrary trajectories.
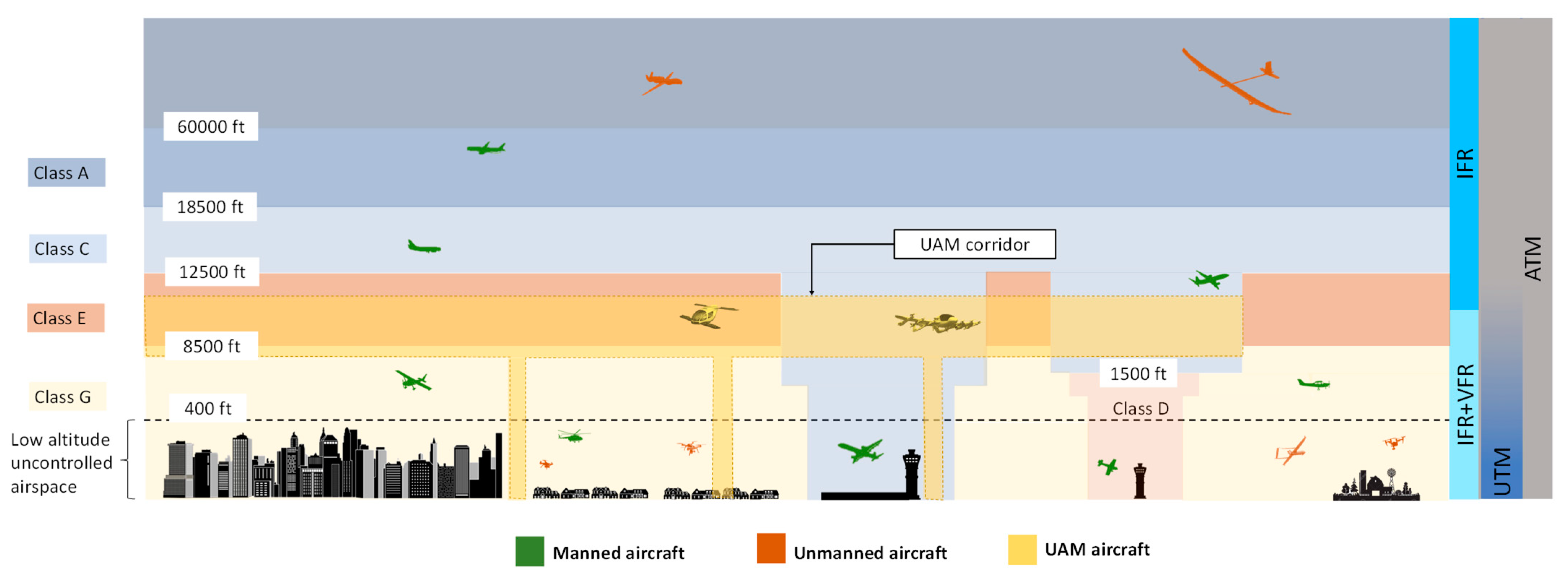
1.1. Scope and Structure of the Article
1.2. Prior Work in Collision Risk Modelling
2. Models and Methods
2.1. Fundamental Definitions
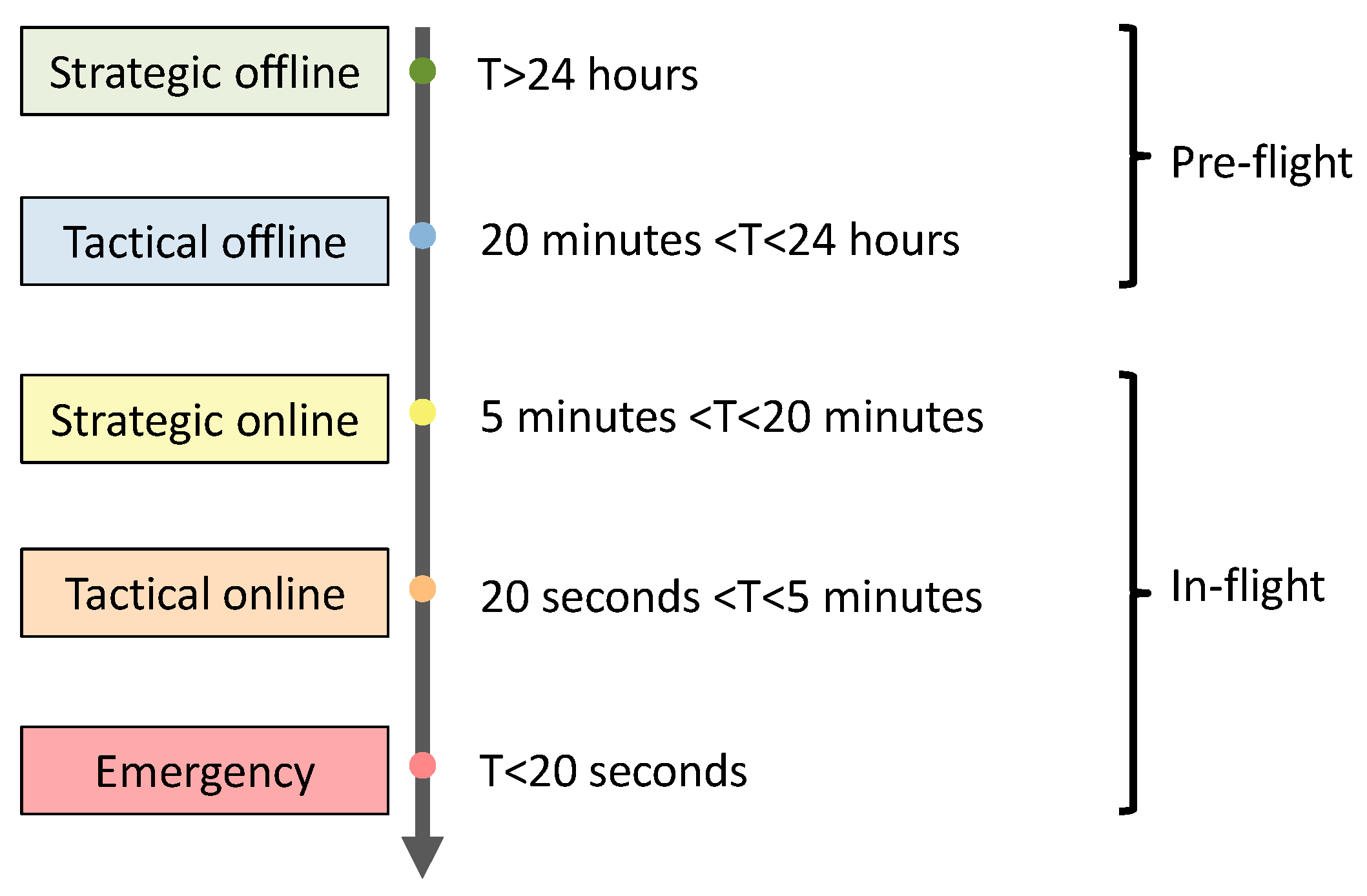
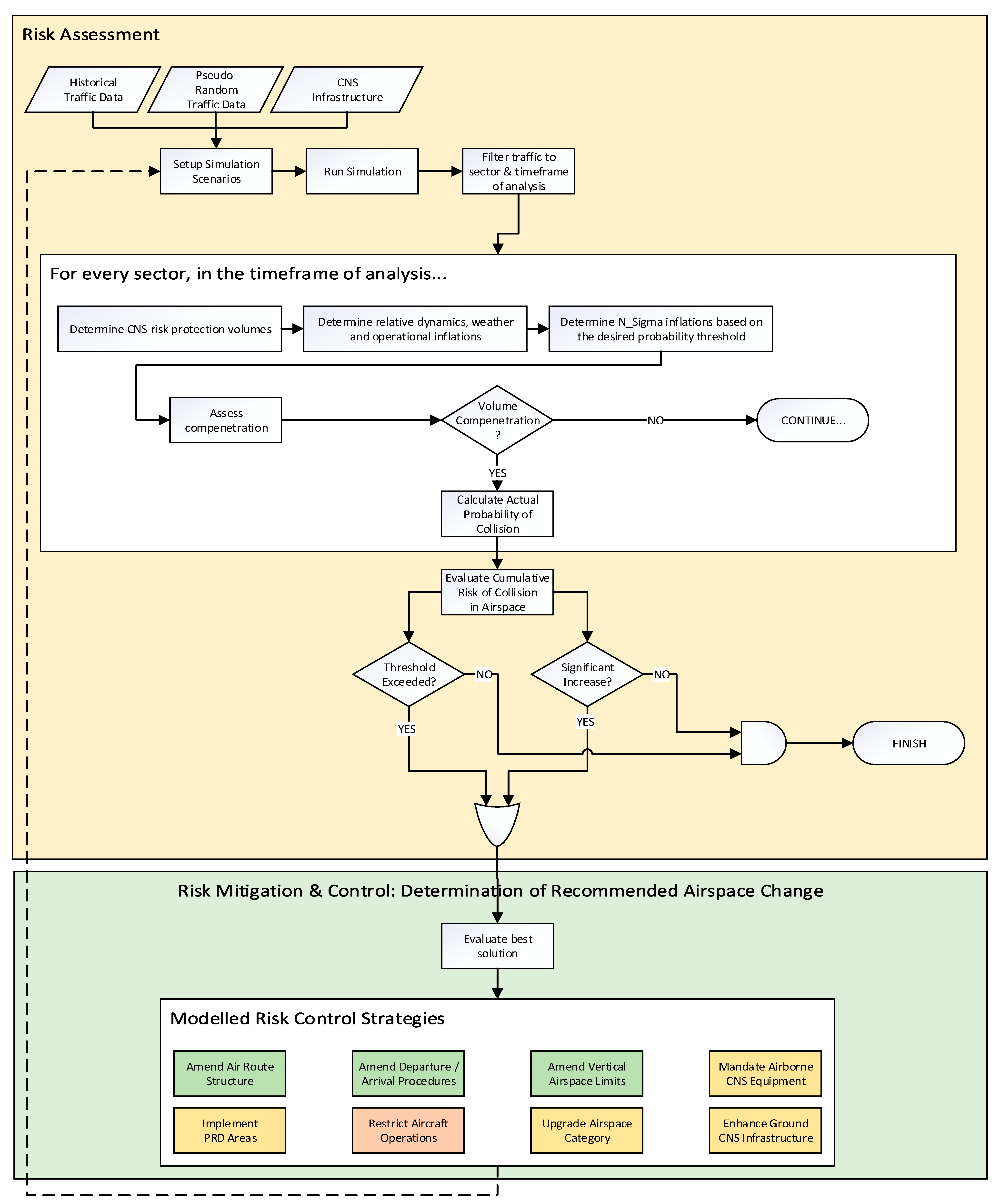
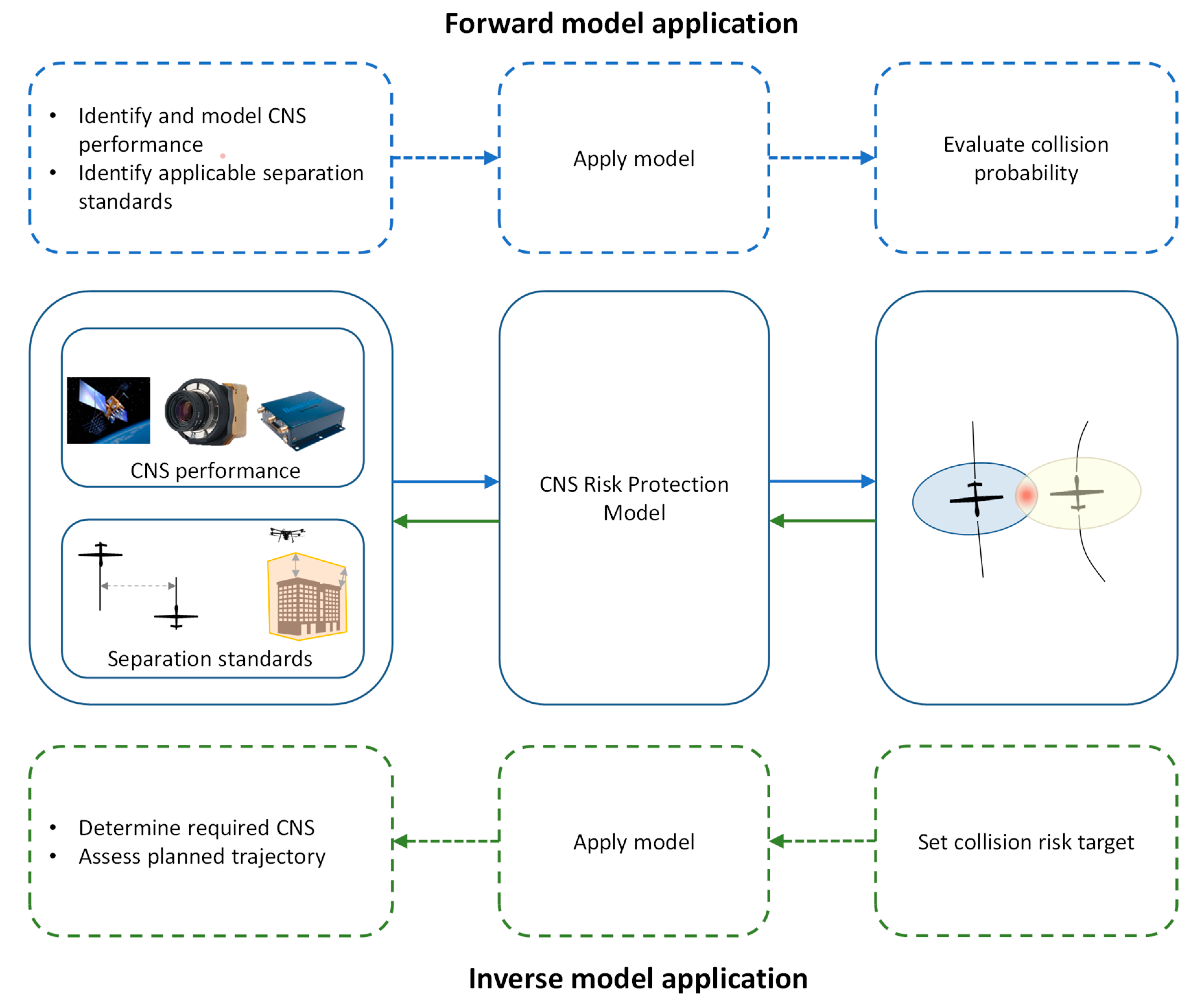
2.2. Unified Airspace Risk Management Framework
2.3. Collision Risk Mitigation and Control Measures
2.4. CNS Performance-Based Collision Risk Modelling
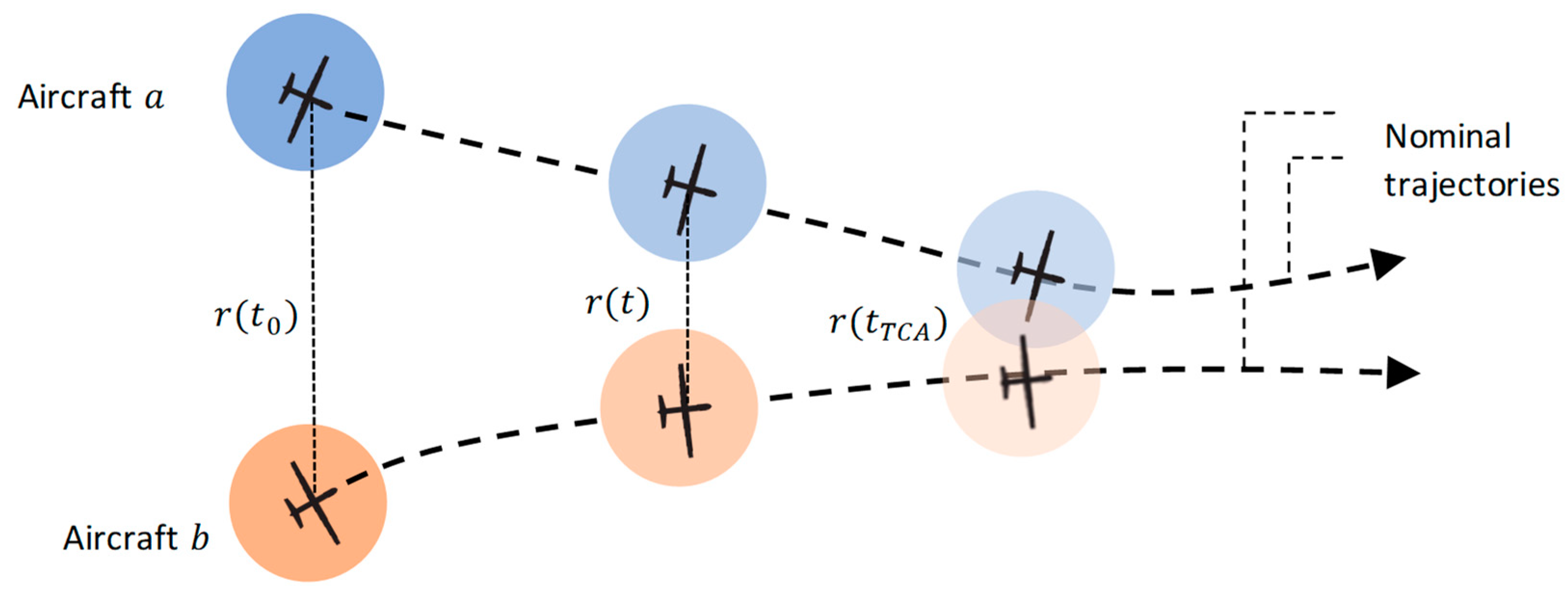
2.5. Model Formulation
- position of the host aircraft;
- position of the intruder aircraft.
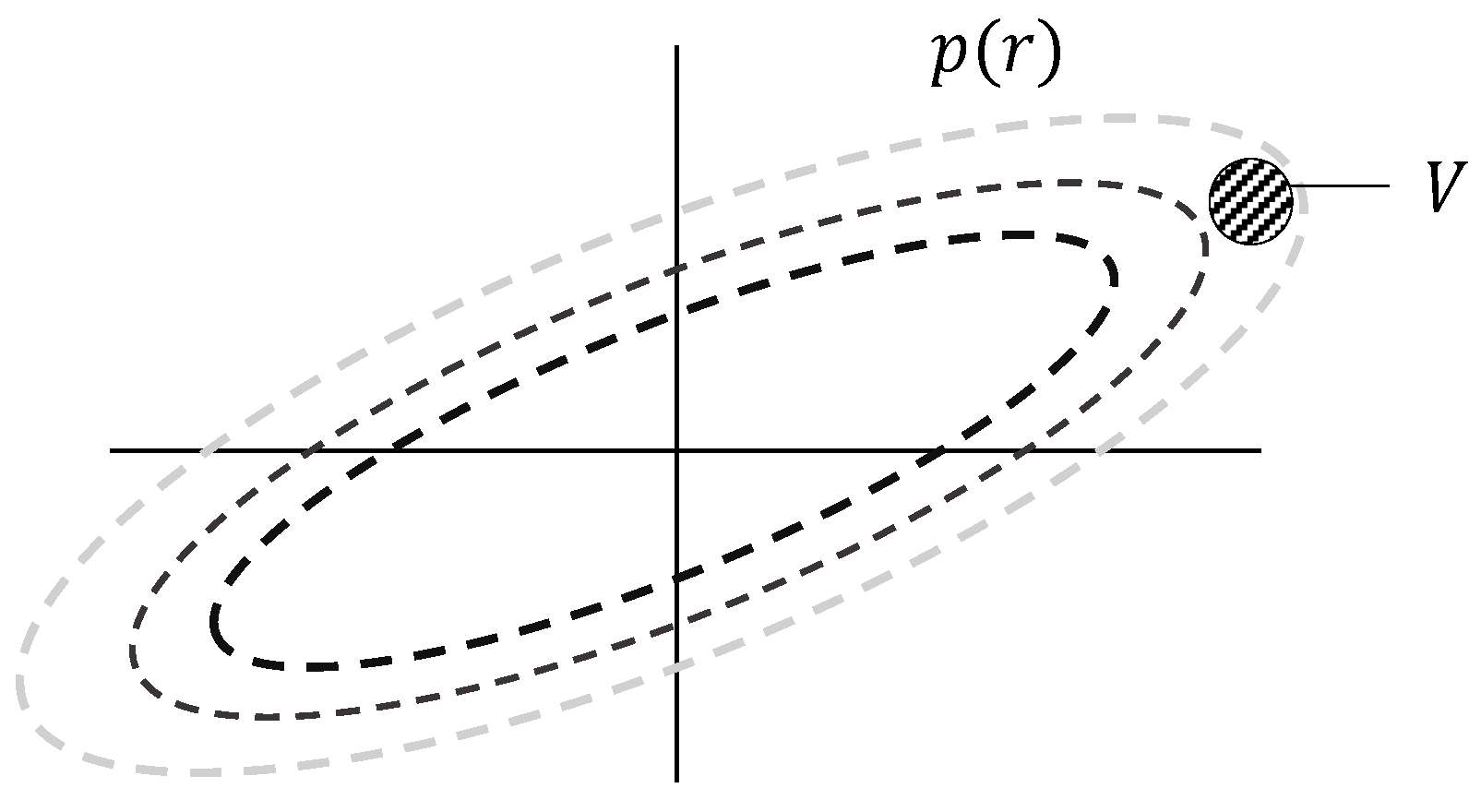
2.6. Risk Evaluation
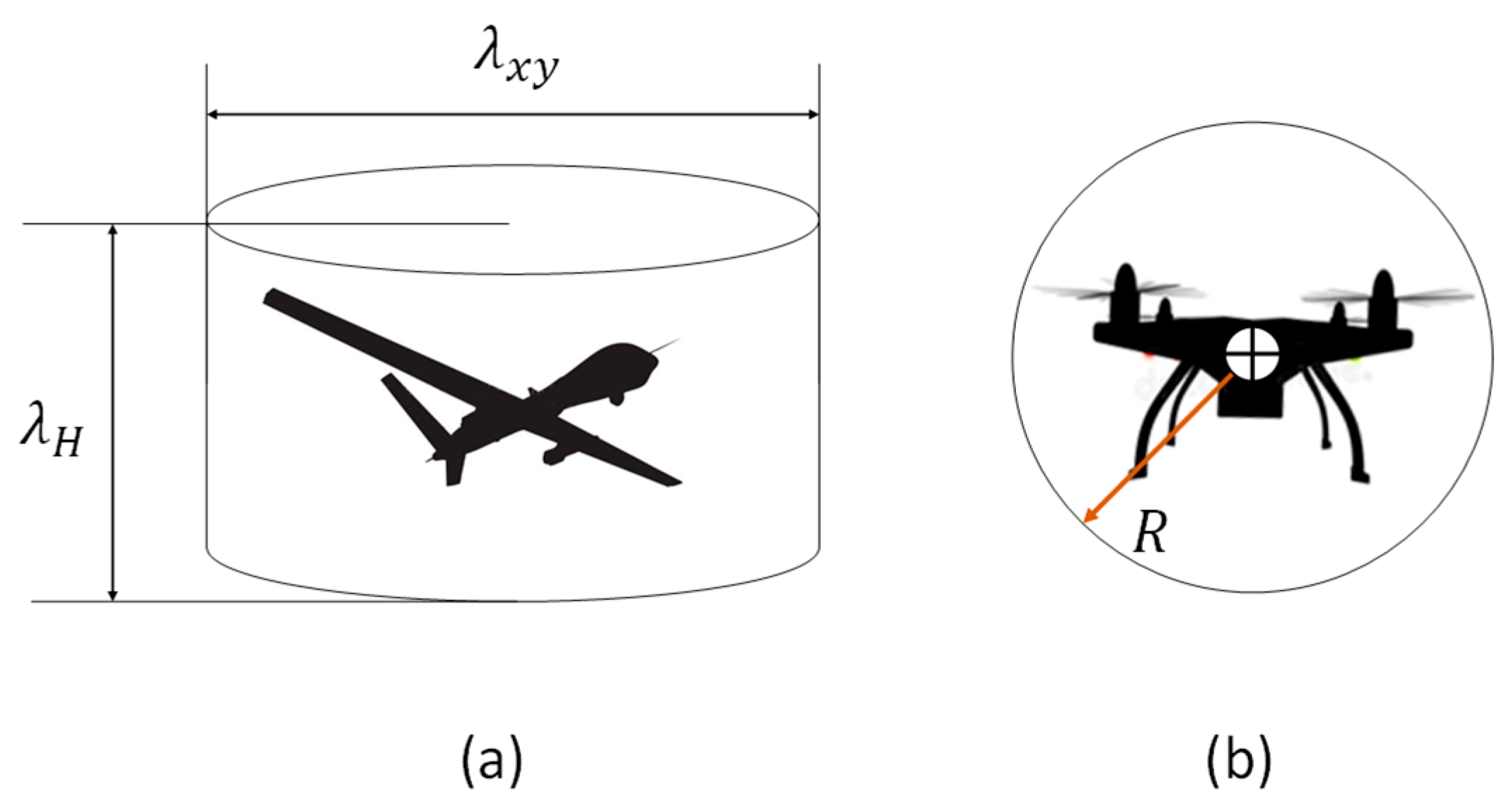
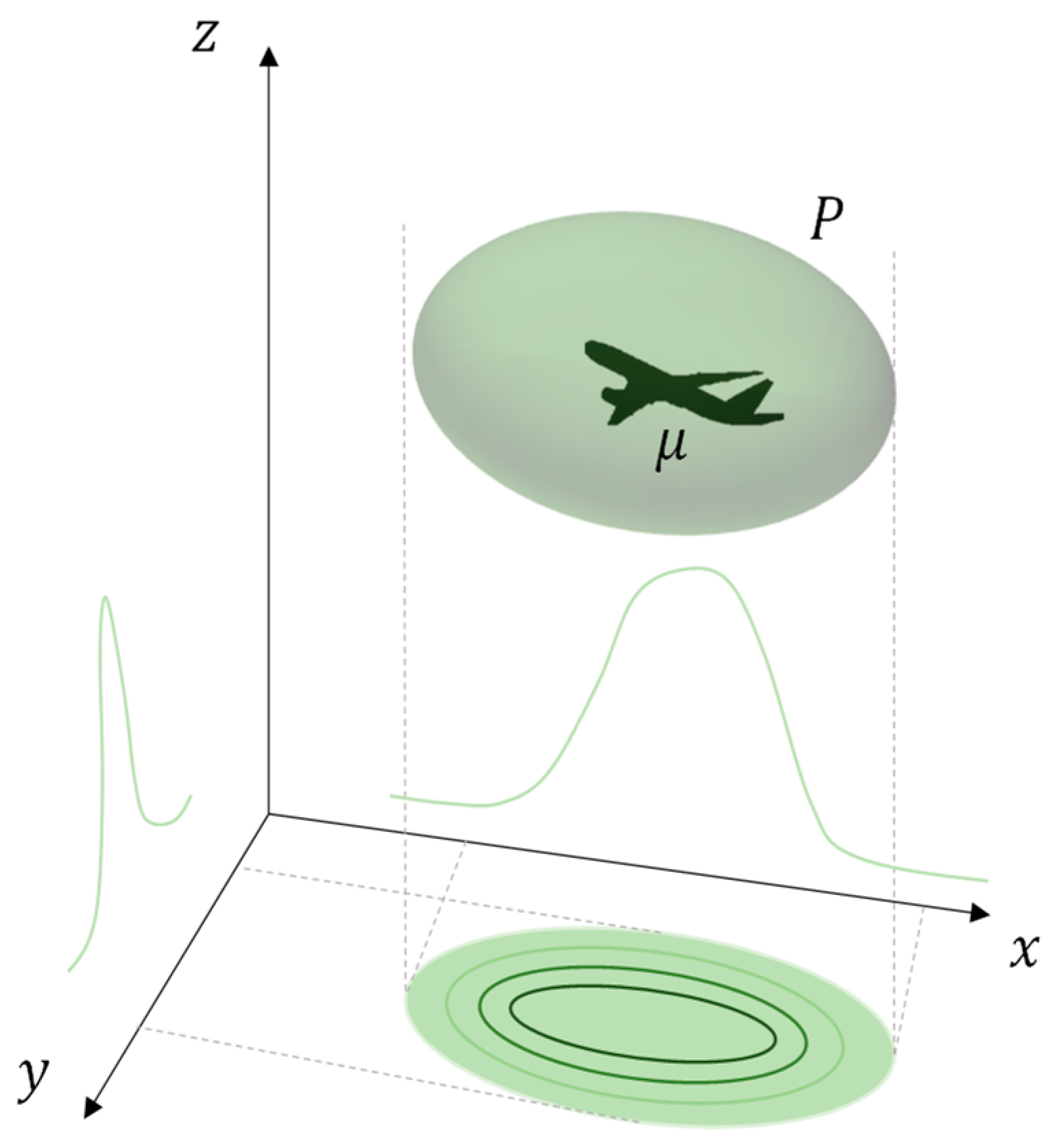
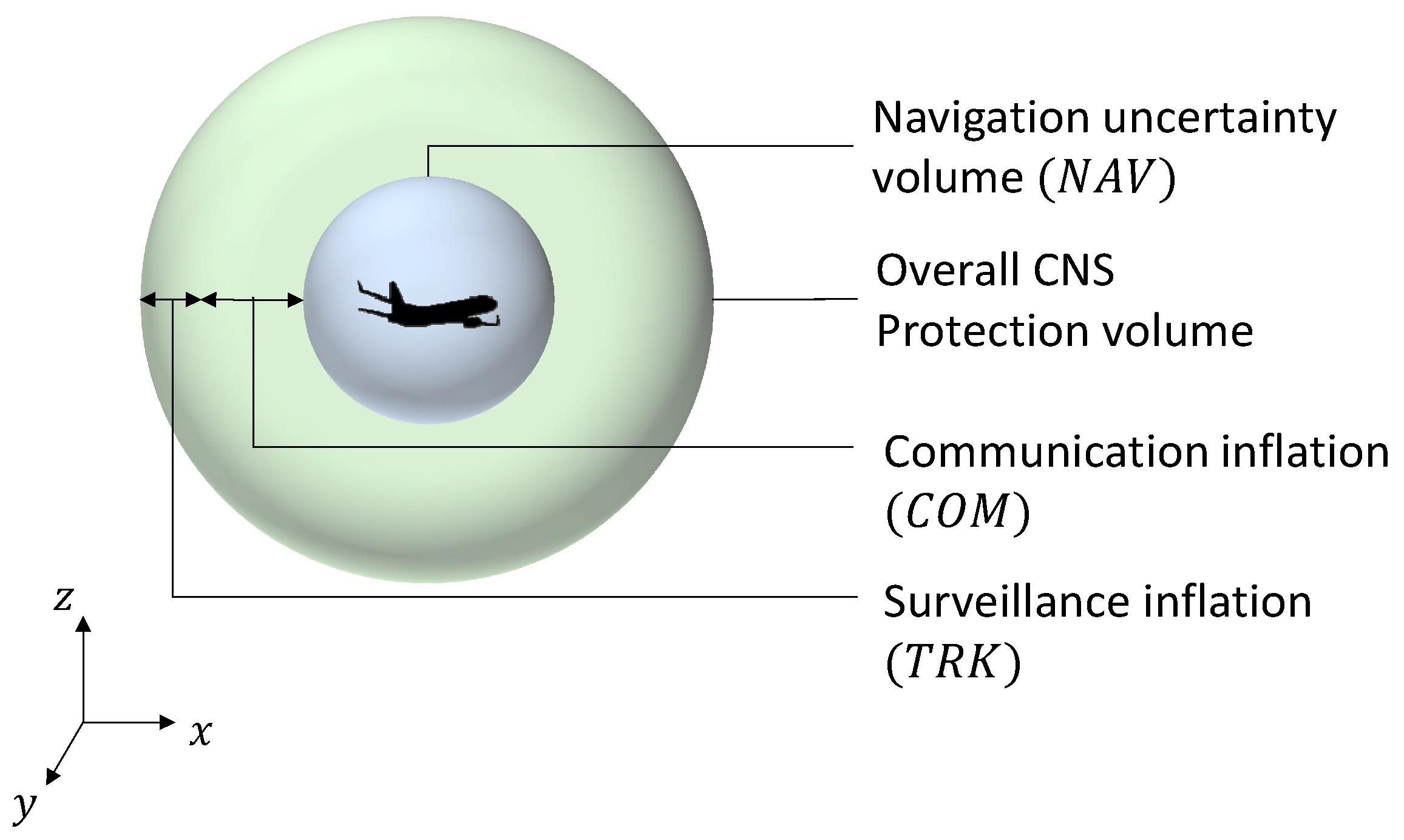
2.7. CNS Risk Volume
- Failure of navigation systems: loss of accuracy beyond a specified limit without timely detection. This constitutes hazardously misleading information preventing timely recovery action from pilots/controllers;
- Failure of surveillance systems: loss in accuracy of aircraft localisation and non-timely relay of surveillance information to downstream sub-systems for recovery actions;
- Failure of Communication: loss/degradation of a link to the point where necessary recovery actions cannot be implemented in a timely manner.
- Relative dynamics: an inflation is introduced, which is commensurate with the known or assumed closure rate of the aircraft;
- Wake turbulence: a buffer region is added, which guarantees sufficient separation from the hazardous region in the wake of the preceding aircraft.
2.7.1. Risk Volume Decomposition
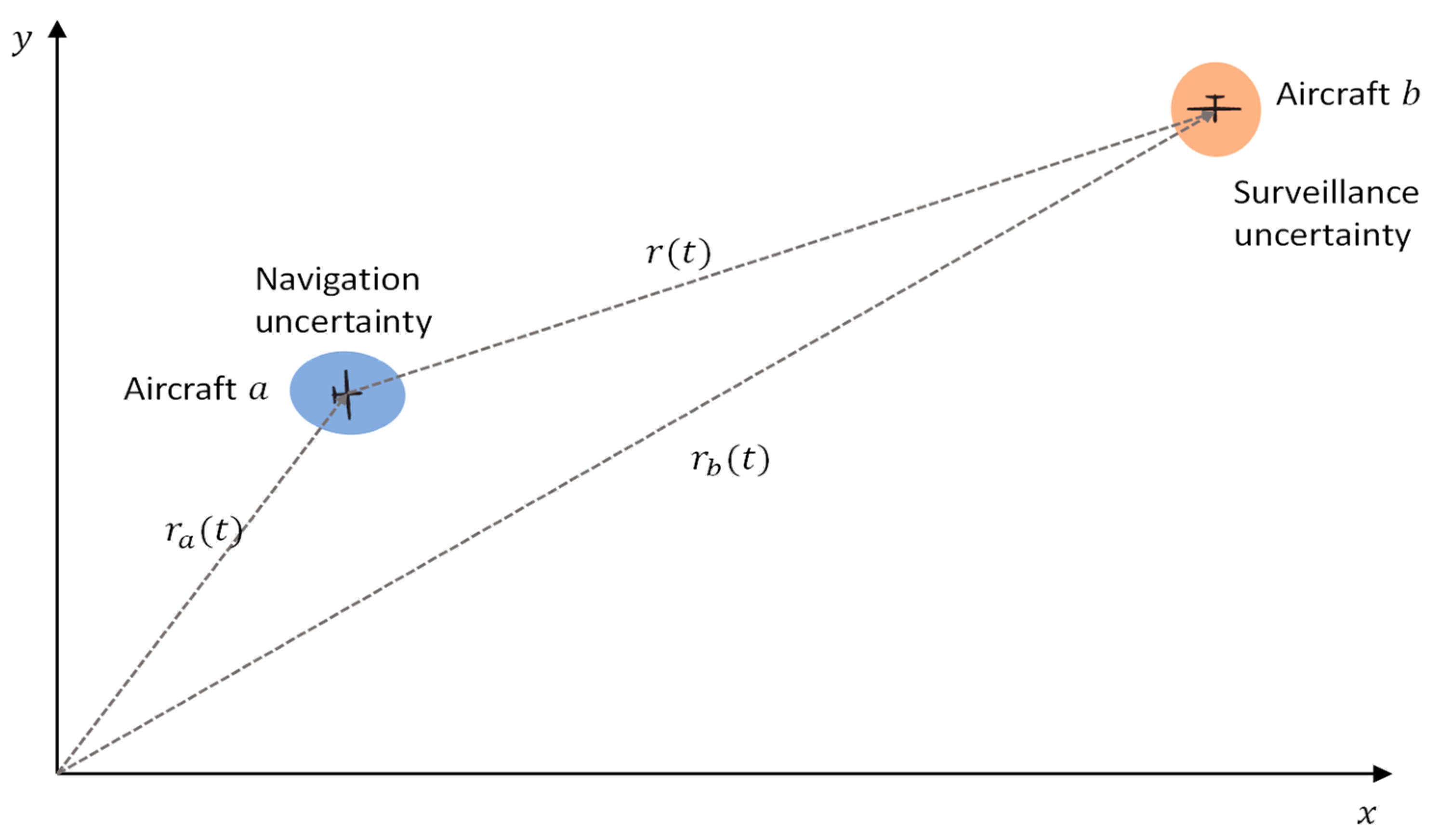
- Navigation: The navigation component of the volume is conveniently represented by a Gaussian ellipsoid. For most avionics systems, navigation sensor outputs are typically fused in a state estimator such as a Kalman filter, which outputs an optimal estimate of aircraft position as well as position uncertainty in the form of a state covariance matrix. Alternately, a more standardised and conservative representation of position uncertainty, the protection level, can be utilised. A protection level is essentially an upper bound on the position error for a given navigation system, which also takes into account the employed fault detection and isolation algorithm. The methodology of inflating the protection level to bound errors to a target probability is also well defined.
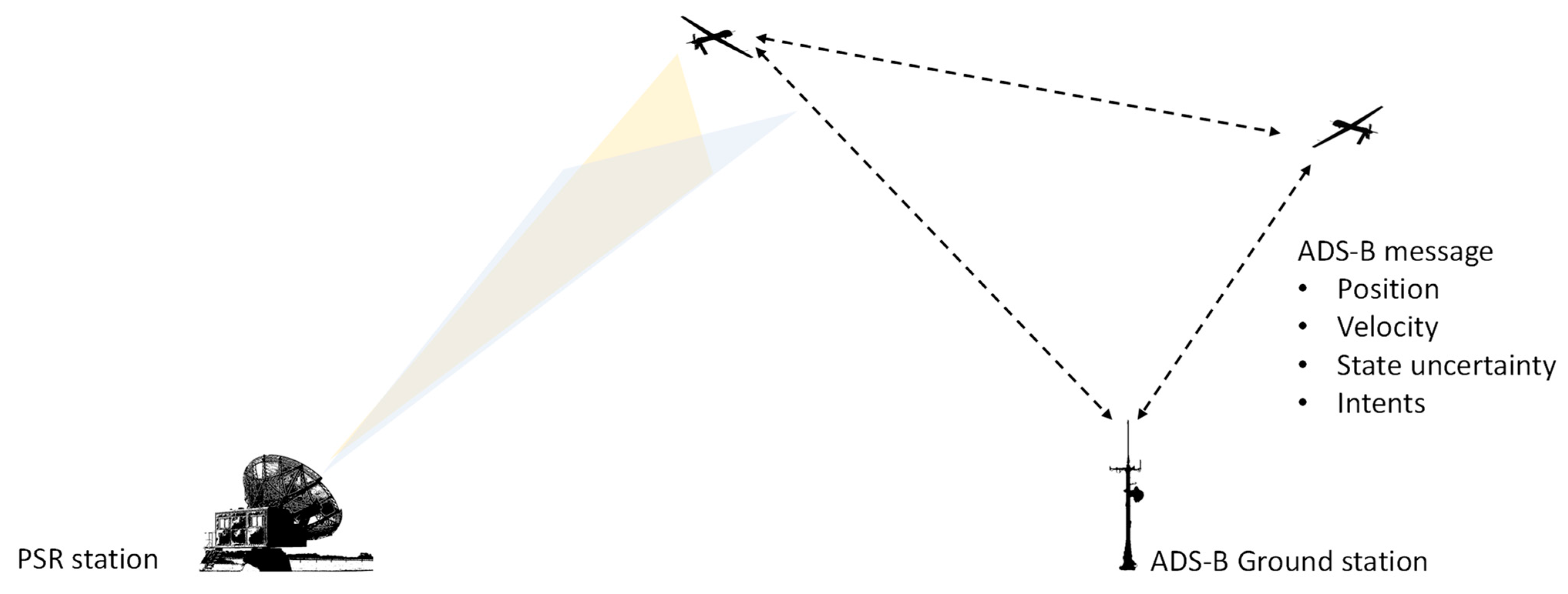
- Surveillance: The error in localising the intruder aircraft arises from two sources. The first of these is the error arising from the sensor used to measure the states of the intruder. The second arises from the time difference between observing the intruder and utilising the observation to assess the likelihood of a threat. Depending on the type of employed system, there can be a significant component of latency in the surveillance system. If the intruder aircraft are observed through a cooperative surveillance system such as ADS-B, then the error in localising the aircraft error will essentially be dependent on the error of the onboard GNSS system [43,44]. If a non-cooperative system such as radar is used to observe the intruder, then the localisation error will depend on the deployed radar characteristics and the intruder parameters. Before the estimated position of the intruder is used to assess the likelihood of a collision, it is compensated for latency in the system. Since latency cannot be directly observed in real-time, latency compensation is based on a priori modelled or measured system characteristics. Therefore, a residual error component will remain.
- Communication: If the assessment of collision risk is performed on the ground, either through an autonomous system or through visual observation by the remote PIC, then the execution of an avoidance manoeuvre is performed through the communication link between the GCS and the unmanned platform. The communication component of the risk volume is determined to provide a sufficient buffer that protects against a loss of separation due to a failure of the communication system.
2.7.2. Navigation and Surveillance Modelling
Primary Surveillance Radar Errors
- A Signal to Noise (S/N) dependent random measurement error
- Random measurement error with fixed standard deviation due to noise sources in the radar receiver’s final stages. These errors are usually small and correspond to the S/N dependent errors that are produced when S/N is high
- A bias error that occurs due to radar calibration and measurement
- Errors due to conditions of radar propagation and the uncertainties in correcting these errors
- Interference errors that occur due to various reasons such as radar clutter
- is the random error with a fixed standard deviation produced when S/N is high.
- is the range bias error as a result of calibration and measurement.
GNSS Errors
- Receiver Dependent Errors such as Clock Error, Noise and Resolution;
- Ephemeris Prediction Errors;
- Satellite Dependent Errors that include Clock Offset and Group Delays;
- Propagation Errors such as Ionospheric Delay, Tropospheric Delay and Multipath;
- User Dynamics Error.
ADS-B Errors
2.7.3. Volume Coordinate Transformation
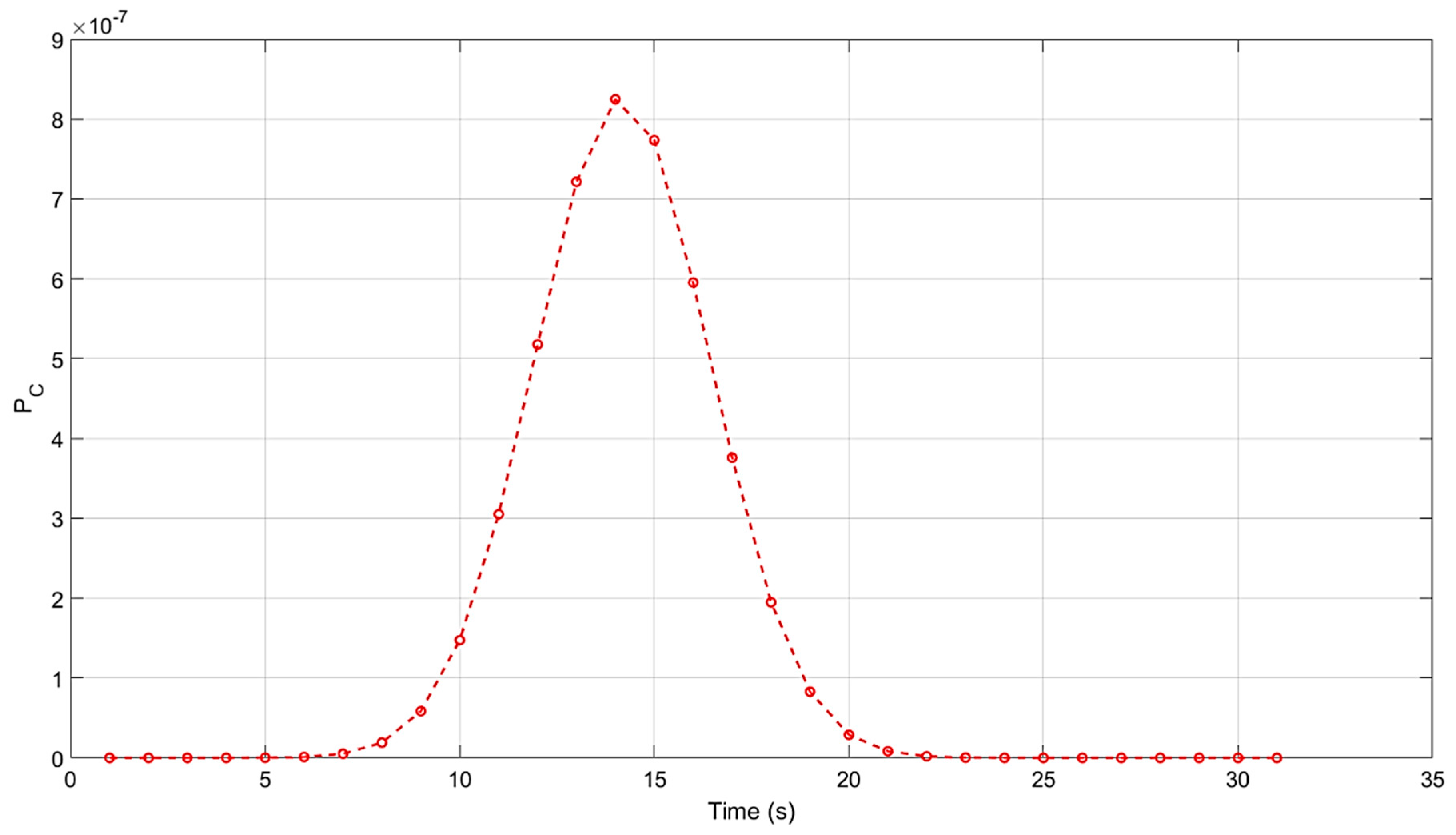
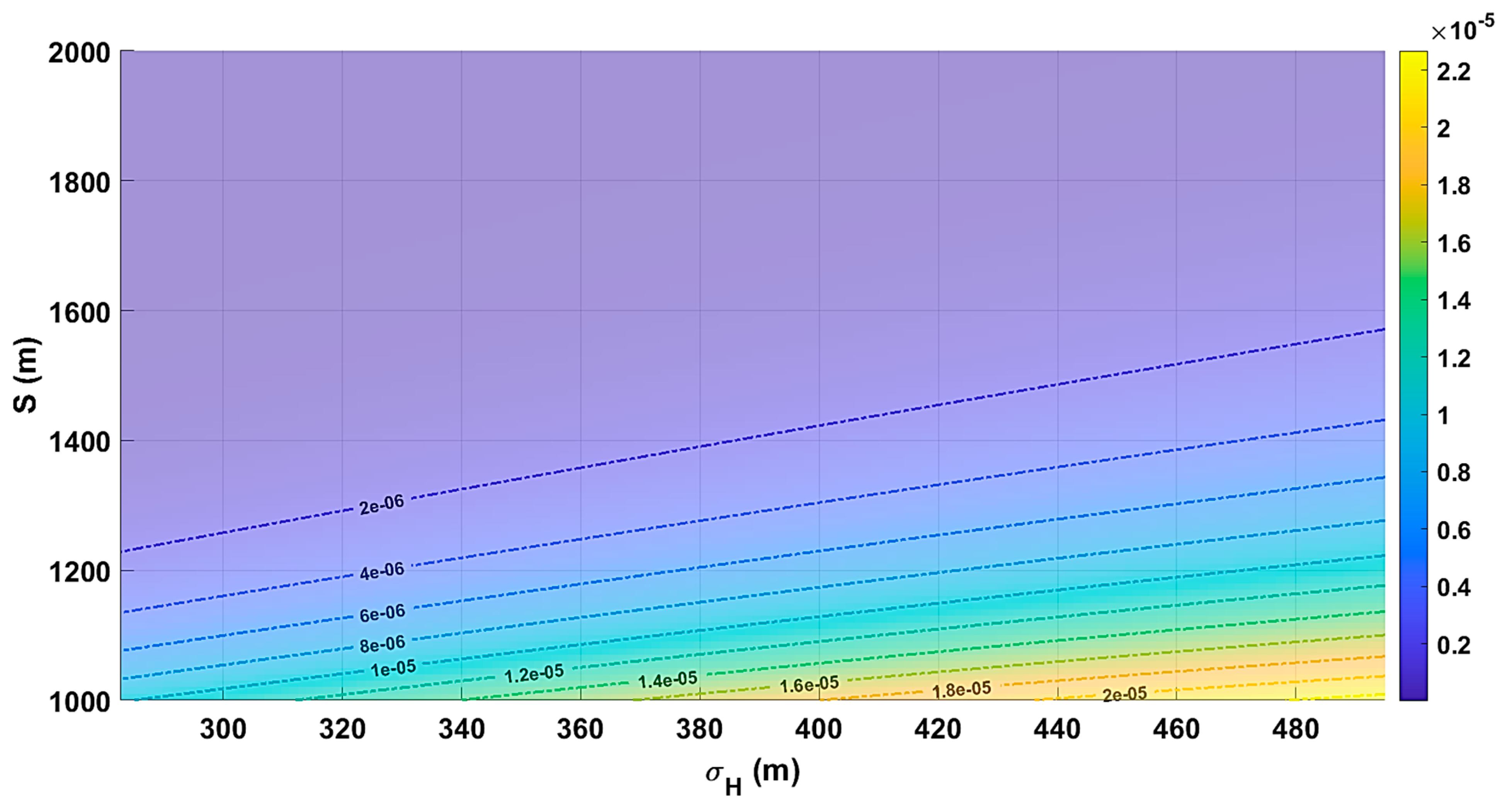
3. Application Case Studies
3.1. Terminal Control Area
3.2. Enroute
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAA. Unmanned Aircraft System (UAS) Traffic Management (UTM) Concept of Operations v2.0; Federal Aviation Administration: Washington, DC, USA, 2020.
- Kopardekar, P.H. Unmanned Aerial System (UAS) Traffic Management (UTM): Enabling Low-Altitude Airspace and UAS Operations; NASA Ames: Mountain View, CA, USA, 2014.
- Prevot, T.; Rios, J.; Kopardekar, P.; Robinson, J.E., Jr.; Johnson, M.; Jung, J. UAS traffic management (UTM) concept of operations to safely enable low altitude flight operations. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; p. 3292. [Google Scholar]
- Urban Air Mobility Concept of Operations v1.0; US Department of Transportation: Washington, DC, USA, 2020.
- Mendonca, N.; Metcalfe, M.; Wiggins, S.; Griffin, C.; DeCarme, D. AAM Ecosystem Working Groups (AEWG): Urban Air Mobility (UAM) Concept of Operations (ConOps) Airspace Breakout [PowerPoint presentation]. In Proceedings of the AAM AirSpace Working Group Kickoff, National Aeronautical and Space Administration (NASA) AAM Mission and Deloitte, Virtual Conference, 16 July 2020. [Google Scholar]
- Lacher, A. Thoughts on AAM Routes. In Proceedings of the NASA AAM Airspace Working Group, Virtual Conference, 1 September 2020. [Google Scholar]
- Gardi, A.; Sabatini, R.; Ramasamy, S. Multi-objective optimisation of aircraft flight trajectories in the ATM and avionics context. Prog. Aerosp. Sci. 2016, 83, 1–36. [Google Scholar] [CrossRef]
- Gardi, A.; Sabatini, R.; Kistan, T.; Lim, Y.; Ramasamy, S. 4 Dimensional Trajectory Functionalities for Air Traffic Management Systems. In Proceedings of the IEEE 15th Integrated Communication, Navigation and Surveillance Conference, ICNS 2015, Herndon, VA, USA, 21–23 April 2015; pp. N31–N311. [Google Scholar] [CrossRef]
- Gardi, A.; Sabatini, R.; Kistan, T. Multiobjective 4D Trajectory Optimization for Integrated Avionics and Air Traffic Management Systems. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 170–181. [Google Scholar] [CrossRef]
- Kistan, T.; Gardi, A.; Sabatini, R.; Ramasamy, S.; Batuwangala, E. An evolutionary outlook of air traffic flow management techniques. Prog. Aerosp. Sci. 2017, 88, 15–42. [Google Scholar] [CrossRef]
- Nagaoka, S.; Brown, M. A Review of Safety Indices for Trajectory-Based Operations in Air Traffic Management. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2014, 12, a43–a49. [Google Scholar] [CrossRef][Green Version]
- Breunig, J.; Forman, J.; Sayed, S.; Audenaerd, L.; Branch, A.; Hadjimichael, M. Modeling Risk-Based Approach for Small Unmanned Aircraft Systems; MITRE Corporation: Bedford, MA, USA, 2018. [Google Scholar]
- Policy for Unmanned Aerial Vehicle (UAV) Certification; European Aviation Safety Authority (EASA) NPA: Cologne, Germany, 2005.
- Ancel, E.; Capristan, F.M.; Foster, J.V.; Condotta, R.C. Real-time risk assessment framework for unmanned aircraft system (UAS) traffic management (UTM). In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; p. 3273. [Google Scholar]
- Gardi, A.G.; de Ridder, K.; Sabatini, R.; Ramasamy, S. 4-Dimensional Trajectory negotiation and validation system for the next generation air traffic management. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4893. [Google Scholar]
- Pilots Role in Collision Avoidance; US Dept. of Transportation: Washington, DC, USA; Federal Aviation Administration: Washington, DC, USA, 2016.
- Reich, P.G. Analysis of long-range air traffic systems: Separation Standards—I. J. Navig. 1966, 19, 88–98. [Google Scholar] [CrossRef]
- Reich, P.G. Analysis of long-range air traffic systems: Separation Standards—II. J. Navig. 1966, 19, 169–186. [Google Scholar] [CrossRef]
- Reich, P.G. Analysis of long-range air traffic systems: Separation Standards—III. J. Navig. 1966, 19, 331–347. [Google Scholar] [CrossRef]
- Hsu, D.A. The Evaluation of Aircraft Collision Probabilities at Intersecting Air Routes. J. Navig. 1981, 34, 78–102. [Google Scholar] [CrossRef]
- Aldis, G.K.; Barry, S.I. Fast Evaluation of the Anderson-Hsu Collision Risk for a Crossing Track Scenario. In Proceedings of the ICAO SASP-WGH-27 Meeting, Oklahoma City, OK, USA, 17–19 November 2015. [Google Scholar]
- Geisinger, K.E. Airspace Conflict Equations. Transp. Sci. 1985, 19, 139–153. [Google Scholar] [CrossRef]
- Paielli, R.A.; Erzberger, H. Conflict probability estimation for free flight. J. Guid. Control. Dyn. 1997, 20, 588–596. [Google Scholar] [CrossRef]
- Pérez-Castán, J.A.; Comendador, F.G.; Rodríguez-Sanz, A.; Valdés, R.M.A. Conflict-risk assessment model for continuous climb operations. Aerosp. Sci. Technol. 2019, 84, 812–820. [Google Scholar] [CrossRef]
- Hernández-Romero, E.; Valenzuela, A.; Rivas, D. A probabilistic approach to measure aircraft conflict severity considering wind forecast uncertainty. Aerosp. Sci. Technol. 2019, 86, 401–414. [Google Scholar] [CrossRef]
- Stroeve, S.H.; Blom, H.A.P.; Bakker, G.J. Systemic accident risk assessment in air traffic by Monte Carlo simulation. Saf. Sci. 2009, 47, 238–249. [Google Scholar] [CrossRef]
- Lum, C.; Waggoner, B. A risk based paradigm and model for unmanned aerial systems in the national airspace. In Proceedings of the Infotech@Aerospace 2011, St. Louis, MO, USA, 29–31 March 2011; p. 1424. [Google Scholar]
- la Cour-Harbo, A.; Schiøler, H. Probability of Low-Altitude Midair Collision Between General Aviation and Unmanned Aircraft. Risk Analysis 2019, 39, 2499–2513. [Google Scholar] [CrossRef]
- McFadyen, A.; Martin, T. Understanding Vertical Collision Risk and Navigation Performance for Unmanned Aircraft. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–10. [Google Scholar]
- McFadyen, A.; Martin, T.; Perez, T. Low-level collision risk modelling for unmanned aircraft integration and management. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–10. [Google Scholar]
- Wang, C.J.; Tan, S.K.; Low, K.H. Three-dimensional (3D) Monte-Carlo modeling for UAS collision risk management in restricted airport airspace. Aerosp. Sci. Technol. 2020, 105, 105964. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Y. Sense and avoid technologies with applications to unmanned aircraft systems: Review and prospects. Prog. Aerosp. Sci. 2015, 74, 152–166. [Google Scholar] [CrossRef]
- Sabatini, R.; Richardson, M.A.; Gardi, A.G.M.; Ramasamy, S. Airborne laser sensors and integrated systems. Prog. Aerosp. Sci. 2015, 79, 15–63. [Google Scholar] [CrossRef]
- Ramasamy, S.; Sabatini, R.; Gardi, A.; Liu, J. LIDAR obstacle warning and avoidance system for unmanned aerial vehicle sense-and-avoid. Aerosp. Sci. Technol. 2016, 55, 344–358. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, Y.; Ding, M.; Zhuang, L.; Tao, J. Monocular vision based obstacle avoidance trajectory planning for Unmanned Aerial Vehicle. Aerosp. Sci. Technol. 2020, 106, 106199. [Google Scholar] [CrossRef]
- Ramasamy, S.; Sabatini, R.; Gardi, A. A Unified Analytical Framework for Aircraft Separation Assurance and UAS Sense-and-Avoid. J. Intell. Robot. Syst. 2017, 91, 735–754. [Google Scholar] [CrossRef]
- Ramasamy, S.; Sabatini, R. A Unified Approach to Cooperative and Non-Cooperative Sense-and-Avoid. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems, ICUAS 2015, Denver, CO, USA, 9–12 June 2015; pp. 765–773. [Google Scholar] [CrossRef]
- RTCA. Minimum Operational Performance Standards (MOPS) for Detect and Avoid (DAA) Systems (DO-365A); RTCA: Washington, DC, USA, 2020. [Google Scholar]
- Jamoom, M.B.; Joerger, M.; Khanafseh, S.; Pervan, B. Unmanned aircraft system sense and avoid integrity and continuity risk for non-cooperatve intruders. In Proceedings of the AIAA Infotech@Aerospace, Kissimmee, FL, USA, 5–9 January 2015; p. 0484. [Google Scholar]
- Pérez-Castán, J.A.; Rodríguez-Sanz, A. Risk-Based Framework for the Integration of RPAS in Non-Segregated Airspace. In Risk Assessment in Air Traffic Management; IntechOpen: London, UK, 2020. [Google Scholar]
- Netjasov, F.; Janic, M. A review of research on risk and safety modelling in civil aviation. J. Air Transp. Manag. 2008, 14, 213–220. [Google Scholar] [CrossRef]
- Lin, X.; Fulton, N.; Westcott, M. Target level of safety measures in air transportation—review, validation and recommendations. In Proceedings of the IASTED International Conference, Cambridge, MA, USA, 2–4 November 2009; p. 222. [Google Scholar]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. GNSS Performance Modelling and Augmentation for Urban Air Mobility. Sensors 2019, 19, 4209. [Google Scholar] [CrossRef] [PubMed]
- Bijjahalli, S.; Gardi, A.; Sabatini, R. GNSS Performance Modelling for Positioning and Navigation in Urban Environments. In Proceedings of the 5th IEEE International Workshop on Metrology for Aerospace, MetroAeroSpace 2018, Rome, Italy, 20–22 June 2018. [Google Scholar] [CrossRef]
- Curry, G.R. Radar System Performance Modeling; Artech House: London, UK, 2005; Volume 1. [Google Scholar]
- Li, H.-J.; Kiang, Y.-W. Radar and inverse scattering. In The Electrical Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2005; pp. 680–682. [Google Scholar]
- Sabatini, R.; Moore, T.; Ramasamy, S. Global navigation satellite systems performance analysis and augmentation strategies in aviation. Prog. Aerosp. Sci. 2017, 95, 45–98. [Google Scholar] [CrossRef]
- RTCA. Minimum Aviation System Performance Standards for Automatic Dependent Surveillance Broadcast (ADS-BRTCA); RTCA: Washington, DC, USA, 2002. [Google Scholar]
- Sabatini, R.; Moore, T.; Hill, C. Avionics-Based GNSS Augmentation for Unmanned Aerial Systems Sense-and-Avoid. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Ramasamy, S.; Sabatini, R. Communication, navigation and surveillance performance criteria for safety-critical avionics and ATM systems. In Proceedings of the AIAC 16: Multinatioinal Aerospace Programs-Benefits and Challenges, Melbourne, Australia, 23–24 February 2015; pp. 1–12. [Google Scholar]
- Hilton, S.; Cairola, F.; Gardi, A.; Sabatini, R.; Pongsakornsathien, N.; Ezer, N. Uncertainty Quantification for Space Situational Awareness and Traffic Management. Sensors 2019, 19, 4361. [Google Scholar] [CrossRef] [PubMed]
- Bahr, M.; McKay, M.; Niemiec, R.; Gandhi, F. Handling qualities of fixed-pitch, variable-speed multicopters for urban air mobility. Aeronaut. J. 2021, 126, 952–972. [Google Scholar] [CrossRef]
- Wang, M.; Diepolder, J.; Zhang, S.; Söpper, M.; Holzapfel, F. Trajectory optimization-based maneuverability assessment of eVTOL aircraft. Aerosp. Sci. Technol. 2021, 117, 106903. [Google Scholar] [CrossRef]
- Pavel, M.D. Understanding the control characteristics of electric vertical take-off and landing (eVTOL) aircraft for urban air mobility. Aerosp. Sci. Technol. 2022, 125. [Google Scholar] [CrossRef]
- Klyde, D.H.; Pitoniak, S.P.; Schulze, P.C.; Manriquez, J.A.; Gray, J.R. Developing Methods of Compliance for eVTOL Vehicles; Phase 1 Final Report; US Federal Aviation Administration: Washington, DC, USA, 2021.








| Operational Factors | Specifications |
|---|---|
| Aircraft | Fixed wing UAVs Wingspan: 15 m |
| Surveillance |
Monostatic scanning PSR = 10 m = 13 = 26 |
| Trajectories | Level flight (altitude: 110 m AGL) Constant speed (25 m/s) and heading Intersecting routes |
| Operational Factors | Specifications |
|---|---|
| Aircraft | Fixed wing UAVs Wingspan: 15 m |
| Surveillance | ADS-B |
| Navigation | GNSS receiver: GPS RNP 0.1; Accuracy: 185.2 m RNP 0.04; Accuracy: 75 m |
| Trajectories | Level flight (altitude: 110 m/s AGL) Constant speed (25 m/s, 40 m/s) and heading Parallel routes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bijjahalli, S.; Gardi, A.; Pongsakornsathien, N.; Sabatini, R.; Kistan, T. A Unified Airspace Risk Management Framework for UAS Operations. Drones 2022, 6, 184. https://doi.org/10.3390/drones6070184
Bijjahalli S, Gardi A, Pongsakornsathien N, Sabatini R, Kistan T. A Unified Airspace Risk Management Framework for UAS Operations. Drones. 2022; 6(7):184. https://doi.org/10.3390/drones6070184
Chicago/Turabian StyleBijjahalli, Suraj, Alessandro Gardi, Nichakorn Pongsakornsathien, Roberto Sabatini, and Trevor Kistan. 2022. "A Unified Airspace Risk Management Framework for UAS Operations" Drones 6, no. 7: 184. https://doi.org/10.3390/drones6070184
APA StyleBijjahalli, S., Gardi, A., Pongsakornsathien, N., Sabatini, R., & Kistan, T. (2022). A Unified Airspace Risk Management Framework for UAS Operations. Drones, 6(7), 184. https://doi.org/10.3390/drones6070184








