An Error Prediction Model for Construction Bulk Measurements Using a Customized Low-Cost UAS-LIDAR System

Abstract

Small unmanned aerial systems (UAS) have been increasingly popular in surveying and mapping tasks. While photogrammetry has been the primary UAS sensing technology in other industries, construction activities can also benefit from accurate surveying measurements from airborne LIDAR. This paper discusses a custom-designed low-cost UAS-based LIDAR system that can effectively measure construction excavation and bulk piles. The system is designed with open interfaces that can be easily upgraded and expanded. An error model was developed to predict the horizontal and vertical errors of single point geo-registration for a generic UAS-LIDAR. This model was validated for the proposed UAS-LIDAR system using calibration targets and real-world measurements from different scenarios. The results indicated random errors from LIDAR at approximately 0.1 m and systematic errors at or below centimeter level. Additional pre-processing of the raw point cloud can further reduce the random errors in LIDAR measurements of bulk piles.

1. Introduction

A successful construction project depends on many quantitative and qualitative surveying measurements, including both the fine dimensions for building structures and the bulk measurements for civil infrastructures. Traditional construction surveying equipment includes total stations and GNSS devices [1] and their accuracy of measurements varies depending on the equipment calibration, jobsite environment, and the specific surveying application. For example, the accuracy standard of earthwork measurements is more tolerant than that of the locations of pile foundations. The accuracy requirements typically range from a minimum of 1:2500 up to 1:20,000, as set forth by construction professional organizations, such as the American Society for Photogrammetry and Remote Sensing, the American Society of Civil Engineers, the American Congress on Surveying and Mapping, and the American Land Title Association [2].

With the rapid advancement of technology, the construction industry has embraced many new surveying and mapping techniques for better work efficiency and more consistent levels of accuracy. These new surveying technologies include terrestrial, aerial, and satellite imaging, which acquire planimetric, topographic, hydrographic, or feature attribute data for photogrammetry, as well as terrestrial and aerial light detection and ranging (LIDAR) that directly captures 3D point clouds of objects and surfaces. One of the most promising approaches for the implementation of these new surveying technologies is using a small unmanned aerial system (UAS). Due to the significant improvements in their flight time, payload capability, and affordability in the last decade, the small UAS has been increasingly applied in broader surveying areas, such as agriculture, civil infrastructure, and disaster management [3]. While photogrammetry has been the primary UAS sensing technology in these areas, the construction industry, on the other side, can also benefit from accurate surveying measurements from a UAS-based LIDAR. The level of accuracy and error prediction of UAS-based LIDAR measurements, however, have been less studied for construction uses. Consequently, there is a knowledge gap regarding UAS-based LIDAR technology and its application in construction projects.

This paper presents the design of a custom UAS-based LIDAR system that is capable of effectively measuring construction excavation and bulk piles. The system mainly consists of a commercial small UAS equipped with a video camera, an industrial image camera, a LIDAR sensor, a GNSS receiver, an inertial measurement unit, and three embedded computers. The onboard GNSS receiver is paired to an onsite GNSS base station for post-processed navigation measurements. The effectiveness of the overall system was validated with point clouds collected from three different measurement scenarios using surveyed results as the truth reference.

Using this system as an example, a robust and generic error prediction model is developed to estimate the position accuracy of individual point in the LIDAR point cloud. With this model, systematic and random error components have been estimated, respectively. The model shows that the random error is the dominant component for a low-flying UAS-based LIDAR, and the error level is tolerable for construction applications, such as excavation and bulk pile measurements. The random error in the vertical direction could be further reduced in post processing. The UAS-LIDAR systems and the error model could have significant potential for the civil engineering and construction industries.

2. Background

The accurate and efficient surveying of the construction site and construction materials is critical to the safety, quality, and overall success of the construction process. Several different approaches exist to perform construction surveying and measuring activities, including traditional manual tools, such as tape measures, straight edges, levels, and transits for lengths, angles, areas, and volume quantities [4,5]; and modern automated equipment, such as total stations, GNSS, and cameras for spatial positions, coordinates, and 3D digital models [6,7,8]; as well as a combination of different types of measuring equipment [9]. Nevertheless, all the conventional techniques or their combinations have certain disadvantages, which have limited their overall applications. For example, the robotic total station is one of the commonly used pieces of surveying equipment due to its efficiency in capturing the information of multiple locations within a short amount of time [10,11]. However, a robotic total station is usually cost-prohibitive and is heavy and bulky to transport, making it inconvenient to use for large areas. GNSS receivers have also been used frequently for construction surveying activities due to their high accuracy in measurements and rapid relocation in large areas [12]. However, GNSS applications are often limited by the conditions of their operational environment, especially in urban areas with obstructed view of the sky, electromagnetic shielding, multipath reflection, etc., which can significantly reduce the accuracy of measurements [13,14].

Furthermore, conventional building and construction surveying activities in most cases require the equipment operators to physically enter the structure or site to be able to perform such activities. With considerations of safety, efficiency, approachability, and practicality, it is imperative to implement new technologies with less or no human labor at the site [15,16,17]. In response to this demand, different types of innovative devices have been developed during the last decade for construction surveying, such as robotic platforms [18,19]. Due to their own limitations, however, most of these systems have not yet been used widely in construction projects.

UAS-based surveying equipment is another type of innovative device that can address some of the drawbacks and limitations faced by traditional surveying technologies. With the recent technological advancement in materials, batteries, sensors, navigation, and flight control, the performance of small UASs has improved dramatically. In the meantime, their cost has decreased considerably. As a result, small UASs have been increasingly used for forest inventory, package delivery, and agriculture growth monitoring [20,21,22,23]. At the same time, the improvements of payload capability and flight time of small UAS have enabled their uses in many types of civil and construction applications, such as the post-disaster assessment of infrastructure [24,25,26], construction site planning [27,28,29,30], construction process monitoring [31], and infrastructure inspections [32,33]. Small UASs deployed for construction applications use either a fixed-wing airframe or a rotary-wing airframe. Fixed-wing airframes provide much longer flight time whereas rotary-wing airframes do not require a special taking off/landing pad and are thus more versatile [34,35].

Vision-based sensors are most commonly equipped on UAS for general purposes, including high-definition image cameras and video cameras [36,37,38,39]. To conduct civil and construction surveying applications, a LIDAR system or other active ranging/imaging devices are proven to provide better performance [20]. Operations at night or in low visibility scenarios require infrared or thermal sensors to detect structural conditions [40]. Other types of sensors, such as ultrasound or compact continuous-wave radar, can also be deployed with a small UAS for specific purposes [41,42]. Sophisticated tasks and operations often require a small UAS to carry multiple types of sensors simultaneously to perform comprehensive measurements. Due to the limited UAS payload and the challenges in integrating different sensing systems, however, it is still challenging to find a capable small UAS with integrated multiple sensor modalities for civil engineering and construction surveying applications.

It is well proven that a ground-based LIDAR system, such as a terrestrial laser scanner (TLS), can provide a dense and accurate point cloud for construction measurements. The same however does not apply to UAS-based LIDAR, because the position and orientation of the UAS constantly change during a flight. As a result, the point clouds captured by LIDAR cannot be geo-referenced as that of a stationary TLS. Instead, raw point cloud measurements from the airborne LIDAR must be integrated and synchronized with the UAS navigation measurements during pre-processing, which is typically a challenge and roadblock. The accuracy of geo-registration in airborne LIDAR point cloud has been studied for large, manned aircraft systems. It has been recognized that the errors in the navigation system, LIDAR installation, laser beam, and ranging can all contribute to the geo-registration error [43]. The general error model can also apply to UAS-based systems [44]. A UAS typically flies at a lower altitude and has a lower-grade navigation system than manned aircraft. The LIDAR equipped on a UAS can have lower power and shorter range as well. Therefore, the error in a UAS-LIDAR point cloud may manifest itself in a way that is slightly different from ALS. In practice, the observed error magnitude and pattern is related to the target application as well. For example, errors have been assessed for forestry [45], meadow steppe [46], mountainous areas [47], flood plains [48], and different vegetation levels [49]. The focus of this work is on the vertical error on bulk measurements, such as piles or excavation.

3. System Design

3.1. Hardware Components

The presented UAS-LIDAR system uses a commercial rotary-wing small UAS, DJI Matrice 600 Pro, equipped with an auxiliary sensing system, including the following components:

• A GoPro Hero 5 video camera;
• An IDS uEye industrial RGB image camera;
• A SICK LD-MRS LIDAR sensor;
• A NovAtel SPAN GNSS receiver with an integrated inertial measurement unit (IMU);
• Three Raspberry Pi III-embedded computers;
• A rigid lightweight cage to mount all the components above.

In addition, the GNSS receiver can use both the US constellation GPS and the Russian constellation Global Navigation Satellite System (GLONASS). This receiver is paired with an onsite GNSS base station (NovAtel OEM 6 receiver) for post-processed navigation measurements. A close-up look of the major components of the sensing system is shown in Figure 1.

The cage attached to the bottom of the airframe is made of a rigid resin board supported by carbon fiber and 3D printed components. The system components are mounted on both sides of the board to conserve space and at the same time improve the rigidity of lever arms between the sensors. The total weight of the sensing system is approximately 3.6 kg and the maximum flight time of the UAS with this configuration is approximately 17 min.

Two lightweight cameras are mounted onboard, a GoPro video camera and an IDS industrial RGB image camera. The video camera captures continuous video frames of the flight that can be used for 2D imaging and 3D mapping via Structure from Motion (SfM), which operates independently from the other sensors. By contrast, the image camera is tightly integrated with navigation and LIDAR sensors. The image camera collects images with a global shutter triggered by the navigation system, which is also synchronized to the LIDAR. Consequently, the image camera is effectively synchronized to the LIDAR and provides 2D imagery of the point cloud observed by it. The imagery was only used to identify targets from the LIDAR point cloud and was therefore not incorporated into the point cloud in the results reported in this work.

The LIDAR is a SICK LD-MRS unit capable of scanning four layers simultaneously with a field of view of approximately 110° facing downwards at the ground. The aperture size is no greater than ±0.4° in one direction and ±0.04° in the other, corresponding to 0.23° and 0.023° in standard deviations, respectively. The LIDAR scans at 0.125° of angular resolution with a frequency of 12.5 Hz, and it takes approximately 10 ms to complete one sweep of the field of view, collecting around 3000 ground points. It is assumed that all points from a single scan will be collected simultaneously, which is timestamped by the navigation system through a synchronization mechanism, although the precise scanning time of each point could be retrieved if needed. Therefore, the potential discrepancy in timing is up to ±5 ms for each point and is considered part of the error sources. SICK provides an estimation of nominal ranging accuracy for the LD-MRS unit, which includes a noise level of a single point at ${\sigma }_{\epsilon R}$ ≈ 0.1 m (quantization step 0.04 m) and a systematic bias ≈ 0.3 m (estimated ahead of time and removed from the data). It is noted from field testing that the specified noise level is rather conservative compared with results from actual observations, which ranges between 0.04 m and 0.1 m. This unit cost approximately USD 10,000 in 2018, which is significantly lower than the price of other UAS-LIDAR systems on the market (estimated average cost USD 23,000 [50]). However, more low-cost UAS-LIDARs are expected to become available commercially.

The NovAtel SPAN GNSS-inertial integrated receiver is used as the primary navigation system for data collection over the native flight control system of Matrice 600 Pro, due to the superior performance in limiting potential systematic error [51]. The GNSS receiver is paired with a GNSS base station to record raw data for accurate post-processed kinematic (PPK) solutions without relying on a live real-time kinematic (RTK) solution. The GNSS measurements are also tightly coupled with the integrated IMU, which enables precise position, velocity, and orientation measurements at a high update rate. Nevertheless, any residual uncertainty in the position and orientation from the GNSS-IMU will propagate to raw data of all the attached sensors, which becomes part of the systematic error. Figure 1 shows four GNSS antennas mounted on top of the airframe, of which three are used by the UAS for the redundancy and safety of flight control, and the fourth is part of the GNSS-IMU system.

The LIDAR and the GNSS receiver are both powered by a 3-cell lithium-polymer battery, which supplies approximately 12VDC. Both sensors can accept a wide range of voltage level and their performance is not dependent on the voltage [52,53]. As illustrated in Figure 2, the battery voltage is also converted into 5VDC through a DC–DC voltage converter, to support the onboard embedded computers for data recording. The sensor power system is completely separated from the airframe batteries, such that they do not interfere with each other.

3.2. System Synchronization

The time synchronization function is the core mechanism of sensor integration in the UAS-LIDAR system, also shown in Figure 2. Naturally, GNSS is synchronous to GPS time, which also enables additional timing services via input and output triggers to the receiver. The GNSS receiver in the UAS-LIDAR system triggers the shutter of the image camera and receives a timing trigger from the LIDAR. Raw data with corresponding timing information recorded by the image camera, LIDAR, and GNSS-IMU are streamed into three onboard Raspberry Pi-embedded computers, which also control and initialize all the sensors. Due to the time-sensitivity of data collection, each computer records the raw data from only one sensor and stores it on a separate SD card for post-processing, avoiding onboard processing to allow sufficient throughput capability.

The configuration of the sensing system can be easily adjusted for other applications. As illustrated in Figure 2, the various sensors use a parallel configuration: the GNSS-IMU sensors establish the accurate position, orientation, and timing, which is essential to the system, whereas other sensors can be either replaced or expanded as long as they can be synchronized via a triggering mechanism.

3.3. Post-Processed Navigation Measurements

The NovAtel Inertial Explorer software was used to process the raw data recorded by the GNSS and IMU sensors. GNSS carrier phase-based differential solution needs to be computed with respect to a nearby reference GNSS station, which could be either an onsite setup or from a local reference station, such as a Continuously Operating Reference Station (CORS). In this study, an onsite GNSS base station was set up and the positioning accuracy was defined based on the uncertainty of absolute positioning, which refers to the position geo-registered in a global frame. The positioning error from post-processing typically does not exceed centimeter level. The orientation accuracy was computed separately and differently. While the roll and pitch angles from the IMU are typically accurate and stable, the accuracy of true heading (geographic north instead of magnetic north), however, depends on the flight trajectory of the UAS. Since the IMU used in this work cannot directly sense the true heading, it must be inferred from an accurate position measurement while the UAS is moving. Therefore, the UAS must perform specific maneuvers at the beginning of each data collection flight to gain an accurate heading.

3.4. Pre-Processed Point Clouds

The point clouds collected by the LIDAR are referenced in the LIDAR body frame (L frame), which is constructed with Forward, Right, Down (FRD) directions. Since the LIDAR is constantly moving and rotating in the air, the point clouds cannot be directly geo-referenced in a global frame (G frame). The conversion between the two frames relies on the accurate position, orientation, and true heading of the LIDAR, as well as the accuracy in relative timing between each LIDAR scan point and the GNSS receiver.

When a LIDAR point in the L frame is synchronized to GNSS time, it can be geo-referenced into a G frame based on the reference GNSS station. For example, if the reference station is located with World Geodetic System (such as WGS-84) coordinates, the G frame will use local North, East, Down (NED) coordinates based on the WGS-84 coordinates. The potential positioning error in the reference station is ignored in this study.

The following algorithm of frame conversion was implemented in a custom code in MATLAB.

• Record the 3D position of a static ground point x in L frame, ${{\mathit{P}}_x}^L\left(t\right)$, at time t. The position error $\epsilon {{\mathit{P}}_x}^L\left(t\right)$ is caused by LIDAR ranging error and beam angular error (aperture size);
• Convert ${{\mathit{P}}_x}^L\left(t\right)$ into the G frame:

$${{\mathit{P}}_x}^G=C_L^G\left(t\prime \right){{\mathit{P}}_x}^L\left(t\right)+{{\mathit{P}}_L}^G\left(t\prime \right)$$

(1)

where ${{\mathit{P}}_x}^G$ is the static position of this point in the G frame (no longer a function of time), $C_L^G$ reflects the rotation from L frame to G frame, and ${{\mathit{P}}_L}^G$ stands for the LIDAR position.

$t\prime$ is the time of measurement of this LIDAR point perceived by the system, which could be slightly different from the actual time of measurement t. This time difference exists because the position and rotation of the LIDAR are computed based on measurements from the GNSS and IMU sensors at $t\prime$ instead of $t$. The LIDAR timing error is thus specified as $\epsilon t=t^{\prime }-t$ and could be up to 5 ms in a single scan point in the presented UAS-LIDAR system, as noted before.

$C_L^G$ is not directly measurable and is computed via the real-time IMU orientation and relative orientation of LIDAR from the IMU, also known as boresighting [54]:

$$C_L^G\left(t\prime \right)=C_V^G\left(t\prime \right)C_L^V$$

(2)

where $C_L^V$ is the fixed rotation from L frame to the vehicle frame (V) and $C_V^G\left(t\prime \right)$ reflects the rotation from the vehicle frame (IMU in this system) to G frame.

${{\mathit{P}}_L}^G$ is not directly measurable either. The GNSS antenna location on the UAS ${{\mathit{P}}_{ant}}^G$ is measured at time $t\prime$, and the lever arm between the antenna and the LIDAR is measured in the vehicle frame as ${{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V$. Thus,

$${{\mathit{P}}_L}^G\left(t\prime \right)=C_V^G\left(t\prime \right)\left[ {{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V\right]+{{\mathit{P}}_{ant}}^G\left(t\prime \right)$$

(3)

3.

Finally, the geo-referenced location of point x is found using

$${{\mathit{P}}_x}^G=C_V^G\left(t\prime \right)C_L^V{{\mathit{P}}_x}^L\left(t\right)+C_V^G\left(t\prime \right)\left[ {{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V\right]+{{\mathit{P}}_{ant}}^G\left(t\prime \right)$$

(4)

4. Error Prediction Model

The error prediction model introduced in this work follows the same principles of ALS [43,44], which includes errors in position, orientation, lever arm, and boresighting. It can be expanded to include synchronization errors as well. More importantly, this model can be used to understand and differentiate the random and relative errors from the systematic and absolute errors.

4.1. Measurement Error Prediction

Errors in $t\prime$, $C_V^G\left(t\prime \right)$, $C_L^V$, ${{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V$ and ${{\mathit{P}}_{ant}}^G\left(t\prime \right)$ can contribute to the overall system error. It is further assumed in this study that with a rigorous calibration procedure in place, errors, such as the ones found in boresighting, are at least one order of magnitude smaller than those from IMU orientation. For simplicity of analysis, boresighting errors were not modeled in this study. Similarly, it is assumed that the lever arm error is also negligible. Therefore, the contributions of UAS orientation, positioning, timing, and LIDAR are considered in the error prediction model.

First, smaller angular errors in UAS roll ($\epsilon \phi$), pitch ($\epsilon \theta$), and heading ($\epsilon \psi$) angles are considered. In addition, a rotating or vibrating airframe will experience additional angular errors due to uncertainties in time, such that

$${\Delta }^{\mathit{T}}=\left[\epsilon \phi \epsilon \theta \epsilon \psi \right]+\left[\frac{d\phi }{dt} \frac{d\theta }{dt} \frac{d\psi }{dt}\right]\epsilon t$$

(5)

$$\epsilon C_V^G\left(t\prime \right)={\Delta }_{\times }{C}_V^G\left(t\right)$$

(6)

where ${\Delta }_{\times }$ is a skew-symmetric matrix. Ideally, $\epsilon \psi$ is at a sub-degree level for the sensor used in the system, whereas $\epsilon \phi$ and $\epsilon \theta$ are substantially smaller.

Next, the UAS position error, including the impact from the timing uncertainties, is represented with $\epsilon t\frac{d{{\mathit{P}}_{ant}}^G\left(t\right)}{dt}+\epsilon {{\mathit{P}}_{ant}}^G\left(t\right)$, where $\frac{d{{\mathit{P}}_{ant}}^G\left(t\right)}{dt}$ is the velocity of the antenna in the G frame.

Finally, $\epsilon {{\mathit{P}}_x}^L$ is considered in the L frame in forward, right, and down directions. Since the LIDAR is pointing to the ground, the LIDAR forward direction is the vehicle down direction. The position error without timing error is

$$\epsilon {{\mathit{P}}_x}^L\left(t\right)={\left[0 {\delta }_r {\delta }_d\right]}_{\times }{{\mathit{P}}_x}^L\left(t\right)+\epsilon R\frac{{{\mathit{P}}_x}^L\left(t\right)}{\left|{{\mathit{P}}_x}^L\left(t\right)\right|}$$

(7)

where $\epsilon R\frac{{{\mathit{P}}_x}^L\left(t\right)}{\left|{{\mathit{P}}_x}^L\left(t\right)\right|}$ represents the LIDAR ranging error projected onto the direction of point x. ${\delta }_r$ and ${\delta }_d$ indicate right and downward angular errors with respect to LIDAR.

The error in x is thus modeled with

$$\epsilon {{\mathit{P}}_x}^G=\left[\epsilon C_V^G\left(t\prime \right)\right]C_L^V{{\mathit{P}}_x}^L\left(t\right)+\left[\epsilon C_V^G\left(t\prime \right)\right]\left[ {{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V\right]+C_V^G\left(t\right)C_L^V·\left[\epsilon {{\mathit{P}}_x}^L\left(t\right)\right]+\epsilon {{\mathit{P}}_{ant}}^G\left(t\right)+\epsilon t\frac{d{{\mathit{P}}_{ant}}^G\left(t\right)}{dt}$$

(8)

Equation (8) can be used to predict the 3D error magnitude in a global frame for individual scan points. Noticeably, the LIDAR errors (${\delta }_r$,${\delta }_d$ and $\epsilon R$) are not considered systematic errors. Instead, $\epsilon {{\mathit{P}}_x}^L$ from Equation (7) is modeled as a random process, which is uncorrelated either among multiple points within the same scan or among repeated scans of the same point from a moving LIDAR. The other components from Equation (8) may be correlated among the points within the same scan but are likely uncorrelated among repeated scans. Therefore, the total errors in $\epsilon {{\mathit{P}}_x}^G$ are expected to include a major component of random errors and a minor component of systematic errors. Since the random error component is caused by the LIDAR, it is considered a relative error, whereas the systematic error component was largely related to errors in the G frame, which is an absolute error.

In a set of points X that are approximately collocated in the G frame horizontally, the vertical dimension can be estimated based on all the points, ${{\mathit{P}}_{\mathit{X}}}^G$. In this study, the points were computed with a mean or median value. Therefore, a dense raw point cloud could be preprocessed, decimated, and turned into a more accurate elevation model. The expected accuracy can be significantly improved with the number of points. For example, the down-sampled point ${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G$ could be an average of all the points, as shown in Equation (9).

$${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G=\mathrm{mean}\left\{{{\mathit{P}}_{x,v}}^G,\forall x\in \mathit{X}\right\}$$

(9)

The standard deviation of vertical errors in ${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G$ is reduced by the square root of the number of points in X. With a sufficiently large number of points in X, the random and relative errors in ${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G$ will approach zero, and therefore the systematic and absolute errors will dominate.

Alternatively, ${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G$ can be calculated based on the median value of all the points in X. Median values are less likely to be affected by outliers in the set. An implicit assumption is made that all the points in the set share similar heights in a small horizontal neighborhood (centimeter to decimeter level), which is a valid assumption for most smooth surfaces. The median value shown in Equation (10) is expected to be a robust estimation. To better find all the points, some optimization methods will be applied in future work [55].

$${{\mathit{P}}_{\mathit{X},\mathit{v}}}^G=\mathrm{median}\left\{{{\mathit{P}}_{x,v}}^G,\forall x\in \mathit{X}\right\}$$

(10)

While the error model can predict horizontal and vertical errors separately, it is independent of the target surface. The texture, smoothness, and slope of a surface can contribute to the errors in the point cloud. For instance, a horizontal error can be perceived as a vertical error in a sloped surface. Vegetation on the surface could also result in additional uncertainty and, as a result, the optimal choice of the down-sampling method, i.e., mean vs. median values, may be dependent on the target surface. In general, the UAS-LIDAR system can measure a smooth and flat surface that is not covered by any vegetation with lower errors.

Furthermore, this error model is generic and would be applicable to any UAS-LIDAR system that has LIDAR synchronized to an onboard navigation system. However, in order to implement Equation (8), it does require intermediate data, such as the error models of navigation and synchronization, which may not be available from a commercial system.

4.2. An Ilustrative Example of Error Prediction Model

The presented error model helps with the quantification of the contribution of individual error sources in a single point in a LIDAR point cloud. As an illustrative example, consider a typical slow and smooth flight (speed = 5 m/s, no vibration or vertical velocity considered), where the UAS holds a constant altitude of 15 m above ground. The UAS flight control is often based on a standalone GNSS receiver, which can only achieve meter-level accuracy. For example, the 3D position error of GPS alone is 4.5 m (95% value) [56]. However, the UAS is not required to fly at a precise altitude. Instead, the precise position of the UAS and the LIDAR will be computed in the PPK solution. Since the UAS flights discussed in this work all had open sky conditions, typically there are at least 15 GNSS satellites from GPS and GLONASS combined. The number of satellites has always been sufficient for a successful PPK or RTK solution. The precise LIDAR position, instead of the approximate flight altitude, will be used to compute a point cloud as shown in Equation (1).

Based on the typical performance provided by the manufacturer in [52], it is assumed that $\left[\epsilon \phi \epsilon \theta \epsilon \psi \right]=\left[0.01, 0.01, 0.1\right]°$ (1 standard deviation) and $\epsilon {{\mathit{P}}_{ant}}^G=\left[0.01, 0.01, 0.02\right]\mathrm{m}$ for positioning errors (1 standard deviation). The lever arm between the LIDAR and the antenna $\left|{{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V\right|=0.17 \mathrm{m}$. The LIDAR is pointing downward, thus $C_L^V=\left[\begin{array}{ccc}0& 0& -1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]$. It is further assumed that the UAS is leveled and facing north, thus $C_V^G\left(t\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$. The error magnitude on a ground point x right underneath the LIDAR (${{\mathit{P}}_x}^L\left(t\right)={[15 \mathrm{m},0,0]}^T$) is analyzed and illustrated below:

Let $\epsilon {{\mathit{P}}_{x,\Delta }}^G$ represent the error component contributed by the orientation uncertainty. In a leveled flight with little vibration, it is assumed that there is unsensed orientation change within $\epsilon t$, so that $\left[\frac{d\phi }{dt} \frac{d\theta }{dt} \frac{d\psi }{dt}\right]\epsilon t=0$. Although this assumption may be too optimistic for the UAS in some practical fight conditions, it would be acceptable for the presented sensing system since the vibration of the sensing system could be damped or separated from the vibration of the UAS airframe. In this case, the orientation error has a simplified model ${\Delta }^T=\left[\epsilon \phi \epsilon \theta \epsilon \psi \right]$.

Since the distance between x and the LIDAR is much greater than the lever arm, i.e., $\left|{{\mathit{P}}_x}^L\left(t\right)\right|\gg \left|{{\mathit{P}}_L}^V-{{\mathit{P}}_{ant}}^V\right|$, the main contribution from the orientation error will be based on the term $\left[\epsilon C_V^G\left(t\prime \right)\right]C_L^V{{\mathit{P}}_x}^L\left(t\right)$. Recall that $\epsilon C_V^G\left(t\prime \right)={\Delta }_{\times }{C}_V^G\left(t\right)$; therefore,

$$\epsilon {{\mathit{P}}_{x,\Delta }}^G={\Delta }_{\times }{C}_V^G\left(t\right)C_L^V{{\mathit{P}}_x}^L\left(t\right)={[0.0026,-0.0026, 0]}^T\mathrm{m}.$$

(11)

where $\epsilon {{\mathit{P}}_{x,\Delta }}^G$ is a component of the overall error, $\epsilon {{\mathit{P}}_x}^G$, which is caused by the orientation uncertainty $\Delta$. The errors are provided in North, East, and vertical directions, respectively.

Similarly, the error component caused by UAS positioning can be estimated by

$$\epsilon {{\mathit{P}}_{x,P}}^G=\epsilon {{\mathit{P}}_{ant}}^G={[0.010, 0.010, 0.020]}^T\mathrm{m}.$$

(12)

In this simplified model, the contribution of timing error is purely horizontal and is only proportional to UAS velocity. The magnitude is limited by

$$\left|\epsilon {{\mathit{P}}_{x,t}}^G\right|=\left|\frac{d{{\mathit{P}}_{ant}}^G\left(t\right)}{dt}·\epsilon t\right|\le 0.025 \mathrm{m}.$$

(13)

A greater contribution comes from LIDAR error $\epsilon {{\mathit{P}}_x}^L\left(t\right)$. As aforementioned, ${\delta }_r=0.023°$, ${\delta }_d=0.23°$, and $\epsilon R=0.1 \mathrm{m}$ (a conservative error level) are assumed for this LIDAR.

$$\epsilon {{\mathit{P}}_x}^L\left(t\right)={\left[0 {\delta }_r {\delta }_d\right]}_{\times }{{\mathit{P}}_x}^L\left(t\right)+\epsilon R\frac{{{\mathit{P}}_x}^L\left(t\right)}{\left|{{\mathit{P}}_x}^L\left(t\right)\right|}={[0.10, 0.06,-0.006]}^T\mathrm{m}$$

(14)

which contributes to the overall error via

$$\epsilon {{\mathit{P}}_x}^G=C_V^G\left(t\right)C_L^V·\left[\epsilon {{\mathit{P}}_x}^L\left(t\right)\right]={[0.006,0.06, 0.10]}^T\mathrm{m}.$$

(15)

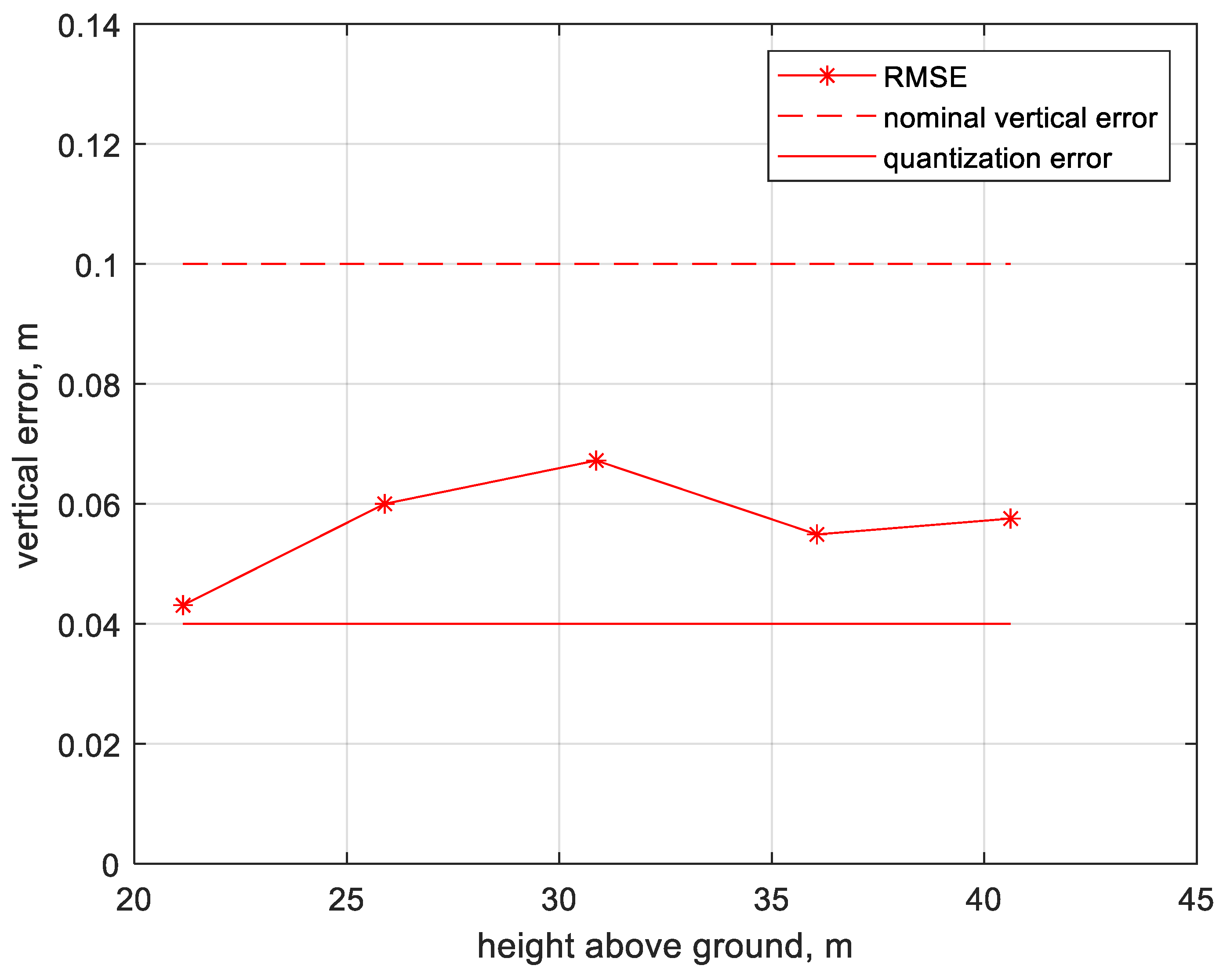
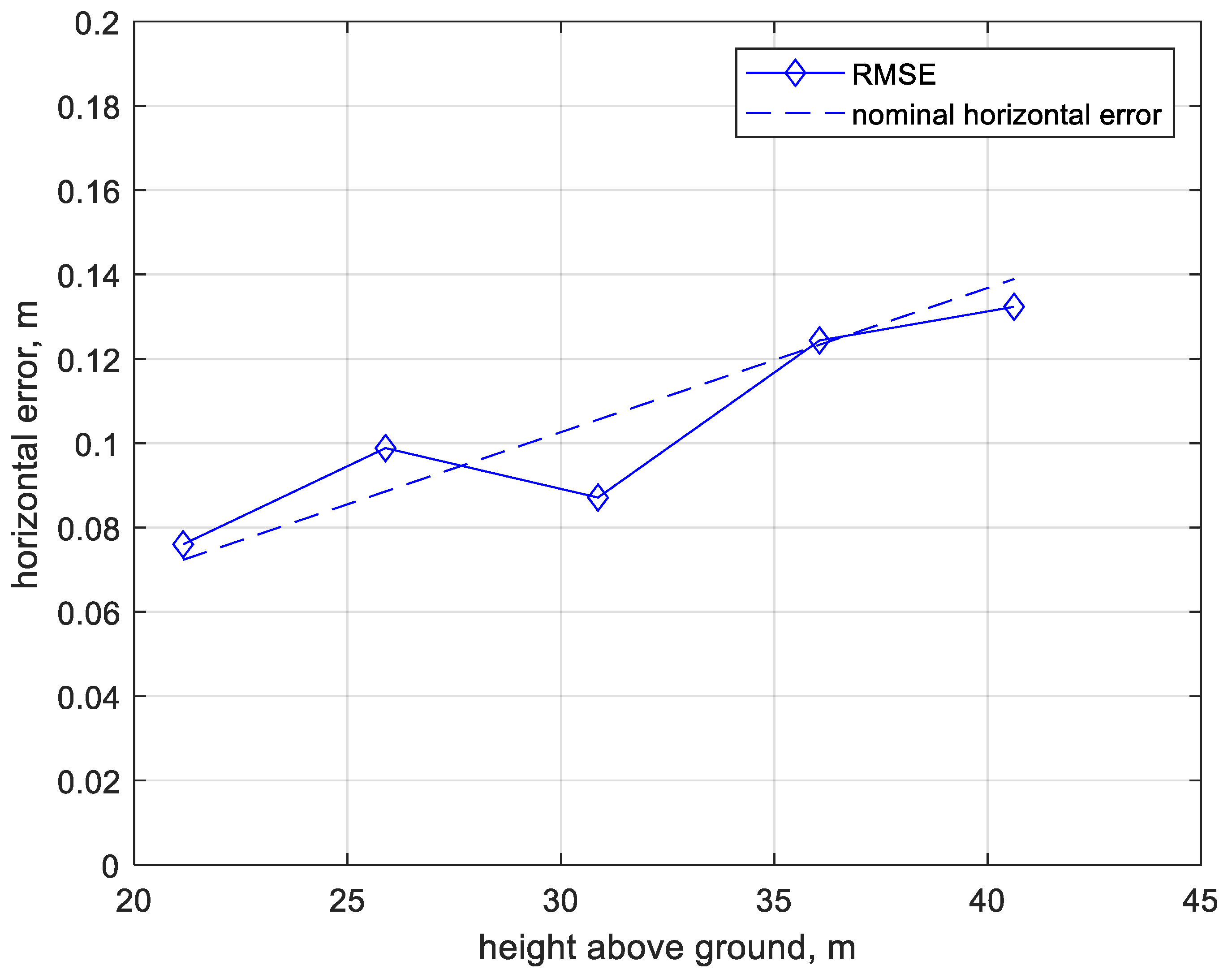
It is evident from comparing Equations (11)–(15) that the LIDAR is the dominant error source ($\epsilon {{\mathit{P}}_x}^L)$ for point x. Since the majority of $\epsilon {{\mathit{P}}_x}^G$ is considered a random process that is independent among points, as mentioned earlier, the integration and synchronization with the navigation measurements does not introduce substantial systematic errors in the LIDAR point. As a result, the error magnitude is on the order of 0.1 m for both horizontal and vertical directions in a typical low-altitude flight.

5. Error Model Validation

5.1. Validation of Random Errors

The vertical and horizontal performance of raw point measurements ${{\mathit{P}}_x}^G$ can be validated with customized calibration targets. The error prediction model was first validated for random errors with a flat surface cardboard box. The dimensions of this target can be found in

Table 1. Box Target Dimensions.

Width	Depth	Height	Volume
1.24 m	0.94 m	0.95 m	1.11 m3

. The box target was placed on flat paved ground with a reference GNSS antenna next to it to record raw data for post-processing. The UAS scanned the target at different heights from 20 m to 40 m above the target (~21 m to ~41 m above ground) with 5 m intervals. Figure 3 illustrates the raw point cloud collected at 20 m above target with both the target and the reference antenna. The exact height of the UAS above ground during this flight was measured with the PPK solution, which can be found in Figure 4.

To improve the heading accuracy, the UAS performed initialization maneuvers immediately after taking off. After the flight, raw data were retrieved from the SD cards from both the UAS and the reference receivers. The data were post-processed, and the accuracy has been summarized in

Table 2. Post-Processed Error Level for Flat Surfaces, Averaged over the Entire Flight.

Error Level	Positioning			Orientation
	North	East	Down	Roll	Pitch	Heading
1 $\sigma$	0.006 m	0.007 m	0.008 m	0.006$°$	0.007$°$	0.02$°$

.

The vertical and horizontal errors in ${{\mathit{P}}_x}^G$ were assessed with the consistency of raw point cloud data collected from the top surface and one side surface of the box target, which contains mainly random and relative errors. As aforementioned, the vertical root mean square error (RMSE) of the raw point cloud is expected to be between 0.04 m and 0.1 m regardless of the height above the target, which was verified with results presented in Figure 5. On the other hand, Equation (8) indicates that the horizontal error would grow proportionally with the distance to target as it is mainly contributed by angular uncertainties. As demonstrated in Figure 6, the observed RMSE in the horizontal direction closely follows the estimated nominal error level.

The box target used to validate the single point error model described in Equation (8) has known flat surfaces that are either vertical or horizontal. The error magnitude presented in Figure 5 and Figure 6 are representative of the vertical and horizontal error components of individual scan points, which are dominated by random errors contributed to by the LIDAR. Figure 4, however, does not include the potential contribution of horizontal errors. On a box-shaped target, the horizontal errors of points on the edge of a surface could result in greater vertical errors, which will be discussed next.

5.2. Validation of Systematic Errors

Next, the magnitude of random and systematic errors was validated respectively, using a point cloud dataset with slope surfaces and survey points. Two tent-shape target objects were placed on flat paved ground, each with two smooth planar surfaces covered by white canvas, as shown in Figure 7. Both targets are identical and their dimensions have been provided in

Table 3. Tent Target Dimensions.

Left Side	Right Side	Width	Depth	Height	Volume
0.70 m	0.64 m	0.90 m	0.90 m	0.50 m	0.20 m3

. The UAS hovered at approximately 15 m to 17 m above the ground and scanned the targets multiple times. The navigation data were post-processed, and the accuracy is summarized in

Table 4. Post-Processed Error Level for Slope Surfaces, Averaged over the Entire Flight.

Error Level	Positioning			Orientation
	North	East	Down	Roll	Pitch	Heading
1 $\sigma$	0.007 m	0.006 m	0.001 m	0.007$°$	0.008$°$	0.07$°$

.

The raw LIDAR point cloud georeferenced in a G frame (NED) is shown in Figure 8, and Figure 9 provides a zoomed-in view with the two corners of both tent targets marked, which were surveyed separately by post-processed GNSS with an accuracy of 0.005 m, 0.005 m, 0.01 m in NED. The raw point cloud included laser returns from the open ends of both targets, which appear lower than the surface. Therefore, the side view of the point cloud will include more noisy points between the target surfaces and the ground. This artifact is excluded from the error analysis in this section. If both targets were piles of bulk materials, there would be no open ends, and the point cloud would not include these points.

In this dataset, raw point cloud (${{\mathit{P}}_{x,v}}^G)$ reports 0.04 m relative vertical error (1 $\sigma$) on a flat ground surface, which is consistent with the results reported in Figure 5. However, the vertical error observed on the tent targets was expected to be greater. Since the slope on both sides of the targets is approximately 45$°$, a portion of the horizontal errors was mapped onto the vertical direction at a 1:1 ratio. In other words, the observed vertical error from a raw LIDAR point cloud would be a combination of the actual horizontal and vertical error components. As a result, the absolute vertical error of raw point cloud on slope surfaces is approximately 0.1 m (1 $\sigma$), which is also consistent with the error prediction model in Equation (8).

Although the UAS-LIDAR system can collect relatively dense point clouds, it is not guaranteed that all surfaces of the target will be captured directly in the raw point cloud during a flight. As a result, it should not be assumed that the entire target will be included in the raw point cloud. Instead, the system is able to extract the geometry of targets from the raw point cloud in addition to measurements. The systematic error component of the point cloud can be estimated by using known geometric information of the target, such as shape and dimensions, and the target location from GNSS surveys. The geometric features of the target, such as planar surfaces, can then be extracted from a partial point cloud, and it is more convenient and robust to identify and extract planar features than point features on small-scale objects.

The average height of an object can be estimated from two planar features that are extracted from all points measured by the UAS-LIDAR system, and the absolute positioning error on a point reflects the magnitude of systematic and absolute error. The measurements from one of the two tent targets are validated here as a demonstration. Figure 10 illustrates 8280 points from Target 2 that are projected onto a 2D plane perpendicular to the ridgeline of the target. These points form the cross-section shape of the tent target as a triangle, and its left side and right side, colored in red and blue, respectively, represent all the points from both planar surfaces. An orthogonal linear fit is applied to each side to recover the shape of the triangle. The top of the triangle is then compared against its GNSS survey reference projected onto the same plane. As shown in

Table 5. Height of Tent Target 2 Measured by LIDAR and GNSS Survey.

Target 2	LIDAR	GNSS Survey	Difference	$\mathbf{GNSS} \mathbf{Accuracy} (1 \mathit{\sigma })$
Height	2.504 m	2.512 m	0.008 m	0.01 m

, the LIDAR measurement of the height of Target 2 is 2.504 m whereas the GNSS measurement is 2.512 m (averaged between two corners), resulting in a vertical difference of 0.008 m. Since this difference is smaller than the GNSS survey accuracy of 0.01 m, it may not accurately represent the actual vertical error. Nonetheless, the absolute systematic error is indeed much smaller than the overall vertical error of 0.1 m, as predicted in Equation (8).

LIDAR measurements of bulk piles will face the same challenges as the tent targets, and it would be impractical to directly extract the height, surface, and volume from a noisy raw point cloud. Instead, an averaged, down-sampled point cloud will be more reliable, assuming that the errors on single points are mostly independent of each other, which has been validated in this dataset. The vertical errors can be effectively reduced by pre-processing based on mean or median values introduced in Equations (9) and (10). As a demonstration, the pre-processed point cloud of the tent targets shown in Figure 11 appears much less noisy than the raw data point cloud in Figure 8.

5.3. Test Site Bulk Measurements

Finally, the presented system was validated with bulk materials at a test site located by Town Creek in Greenville, North Carolina. The UAS-LIDAR system scanned a stretch of the creek (approximately 100 m long) multiple times at a speed of approximately 5 m/s or lower, where a bulk pile of rock stairs was built on a dry riverbed as part of the creek drainage system. An image of the test site from the synchronous camera is shown in Figure 12.

In this test, the collected raw point cloud was pre-processed and decimated into a lower resolution. The site was divided into small cells of 0.05 m by 0.05 m, and a single point ${{\mathit{P}}_X}^G$ was reported for every cell following Equation (9). The magnitude of random error in point cloud would be reduced by the down-sampling process, whereas the systematic error is expected to remain the same. The processed point cloud of the site with rock stairs is presented in Figure 13. The navigation performance of this flight is shown in

Table 6. Post-Processed Error Level for Test Site, Averaged over the Entire Flight.

Error Level	Positioning			Orientation
	North	East	Down	Roll	Pitch	Heading
1 $\sigma$	0.007 m	0.006 m	0.01 m	0.007$°$	0.008$°$	0.07$°$

.

A terrestrial laser scan (TLS) of the test site was performed separately [57], where a Leica ScanStation P40 with a 3 mm (1 $\sigma$) accuracy at 50 m was used. In this validation of the test site, the TLS point cloud was used as a true reference for the comparison with a vertical profile of down-sampled UAS-LIDAR point cloud collected on the rock stairs at the test site. As shown in

Table 7. Measurements Difference of Rock Stairs between TLS and UAS-LIDAR.

TLS-UAS Difference	Mean	$1 \mathit{\sigma }$	Max
Rock Stairs	0.055 m	0.064 m	0.24 m

, the difference between the measurements from the two sensors was 0.055 m in $1 \sigma$ with a 0.064 m mean, and the maximum observed difference was 0.24 m. The vertical profiles measured by the TLS and UAS-LIDAR are illustrated in Figure 14, where deviation between the two profiles can be seen at a few locations. It is likely due to the changes in horizontal locations that can contribute to vertical errors in UAS-LIDAR measurements, as previously discussed. At this test site, the rock stairs have irregular rock shapes with steep slopes on the edge, resulting in a substantial level of mean and maximum error. Nevertheless, the overall error is still consistent with the predictions suggested by the presented error model. Designated calibration targets placed in a controlled environment can be used to compare the performance of bulk measurement with both technologies in the future.

6. Conclusions

Technology advancement in the last decade has given the construction industry many new approaches for traditional daily jobs, among which using a small UAS for surveying and mapping tasks has been increasingly adopted due to its unparalleled efficiency. A custom-designed high-accuracy UAS-LIDAR system is discussed in this work. It is equipped with a combination of camera and LIDAR sensors that are synced to an onboard GNSS-IMU navigation system to enable precise time-stamping and geo-referencing. The presented UAS-LIDAR system also provides the flexibility of upgrading existing sensors or including additional sensors for other civil and construction applications, thanks to its parallel sensor configuration with a core navigation and timing system.

A robust error model was developed for a generic UAS-LIDAR system to predict the horizontal and vertical errors of single point geo-registration. The contributions of errors from different components, such as navigation, timing, and LIDAR are all considered.

This model was validated for the proposed UAS-LIDAR system with calibration targets and real-world data from three different measurement scenarios: a box target with smooth flat surfaces for random error validation, targets of known sloped surfaces for systematic error validation, and a test site rock stair pile for bulk measurement validation. The test results indicated that the random errors from raw LIDAR point cloud reach approximately 0.1 m in the horizontal and vertical directions, respectively, during typical low-altitude flight conditions.

Some of the error sources, such as angular error from navigation or boresighting, are considered systematic. Other error sources, such as LIDAR ranging error, are modeled as random errors. This error model can be used to estimate the magnitude for each error type individually. Different strategies can be developed to reduce the overall error level based on that. For example, systematic errors could leave a bias in the point cloud, which affects the absolute accuracy. It can be limited by a carefully designed calibration process. It has been shown in these flights that the systematic errors are at or below centimeter-level, suggesting that the presented UAS-LIDAR had introduced negligible systematic errors. Random errors affect the relative precision. Random errors can be reduced via the pre-processing of the raw point cloud.

The comprehensive validation of the system has proven the capability and effectiveness of a downward-looking UAS-LIDAR system in construction applications, such as excavation and bulk pile measurements, and therefore has significant potential for civil engineering and construction projects. The prediction model currently focuses on the errors originated from the UAS and the LIDAR and can be further expanded to include characteristics of the target surfaces, such as material, texture, smoothness, and slope in future work.