Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method
Abstract
:1. Introduction
- (1)
- We present a novel problem formulation for distance-based formation control of fixed-wing UAVs. For fixed-wing UAVs with minimum forward velocity, we modify the problem description of the general unicycle model, i.e., the formation is required to keep moving at a uniform velocity simultaneously.
- (2)
- We design a low-gain formation controller, which can keep the input of the system from saturation. The proposed controller is a general gradient controller with a low gain coefficient, which is designed based on the distance-based potential function. Furthermore, we give the complete stability analysis to prove that the desired distance-based formation can be achieved while the input constraints of each UAV are satisfied.
- (3)
- We simulate our proposed controller, including numerical simulation and semi-physical simulation, and verify that the proposed method can effectively solve the distance-based formation control problem under the input constraints of fixed-wing UAVs.
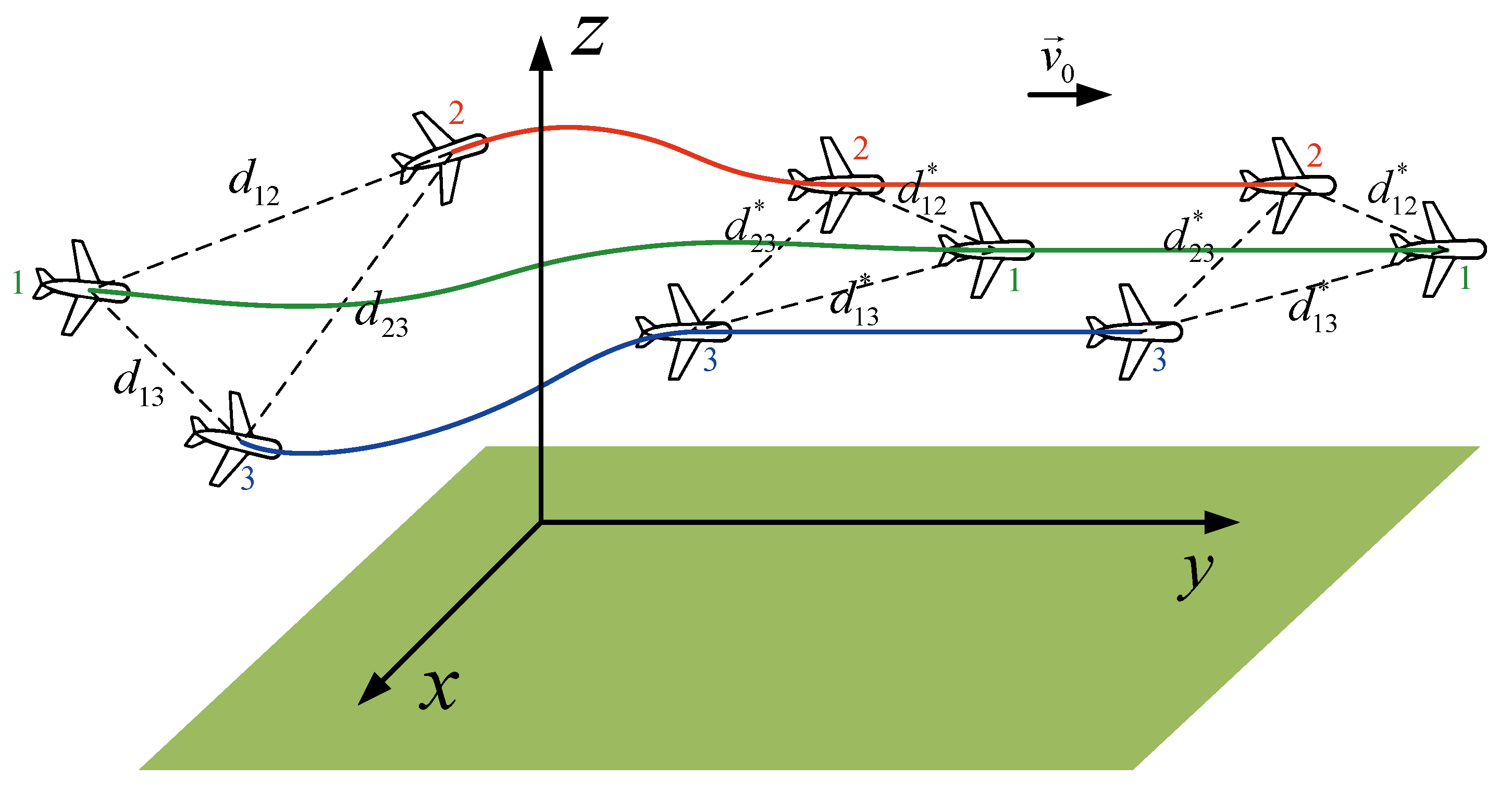
2. Problem Formulation
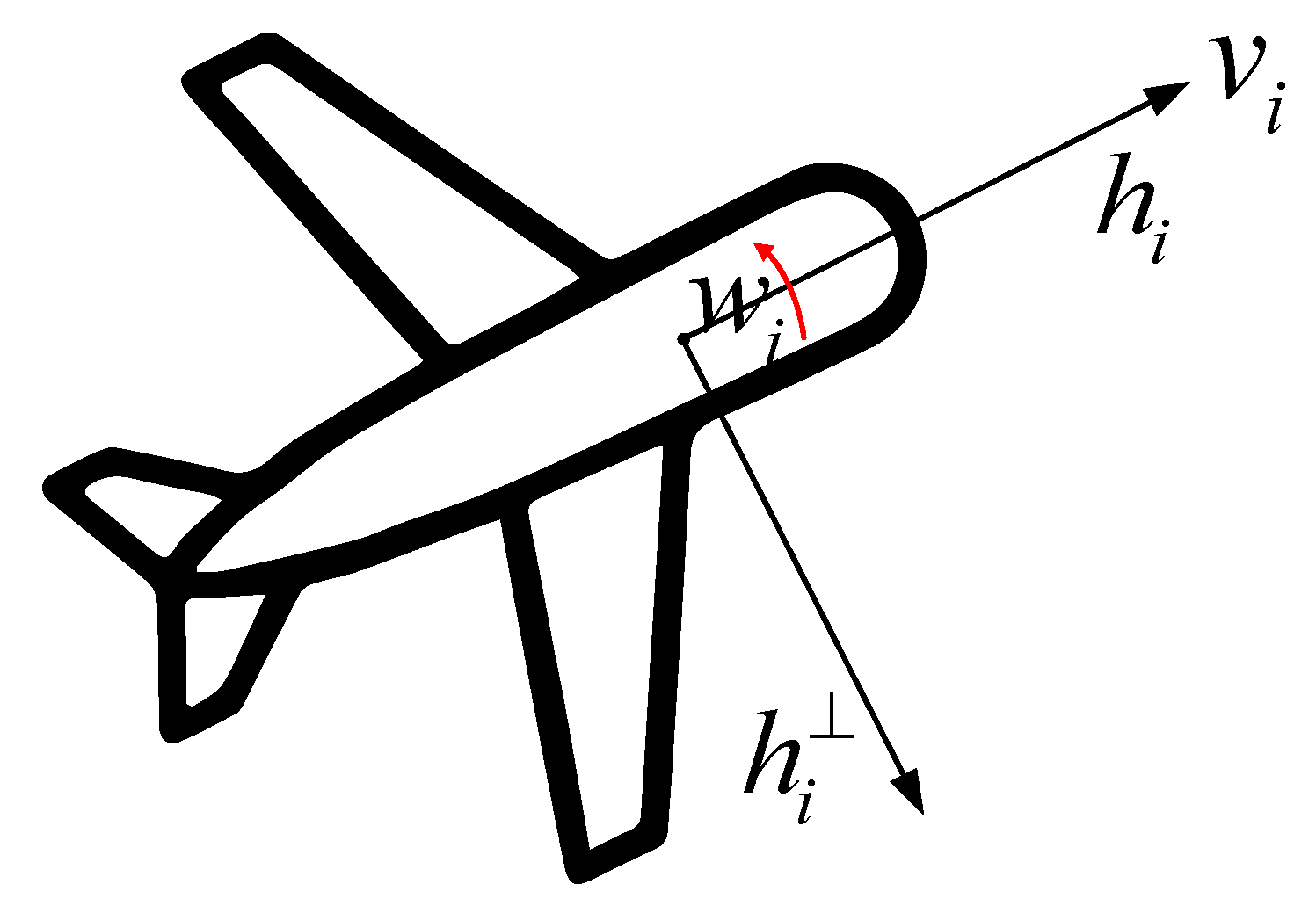
2.1. UAV Modeling
2.2. Desired Formation
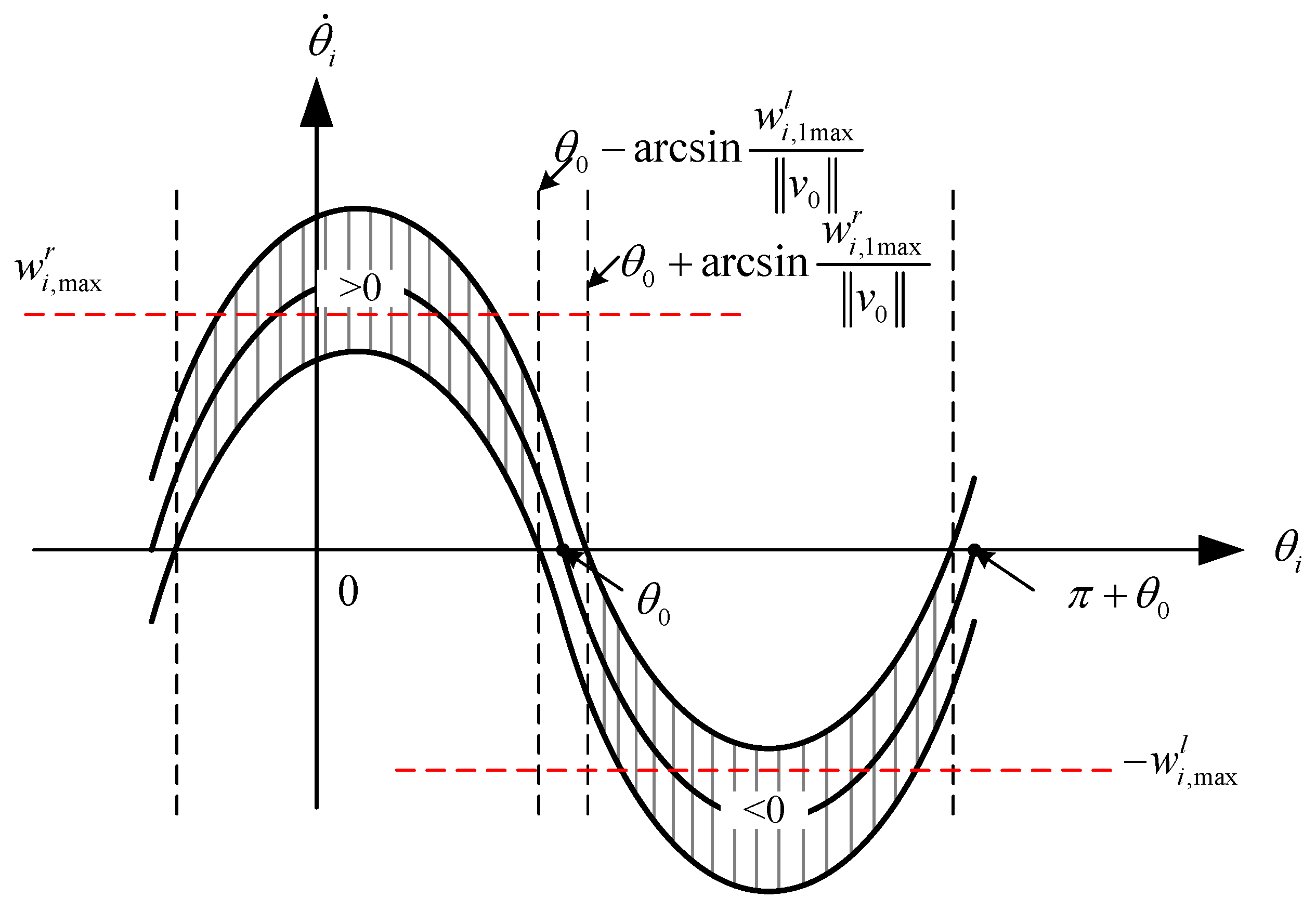
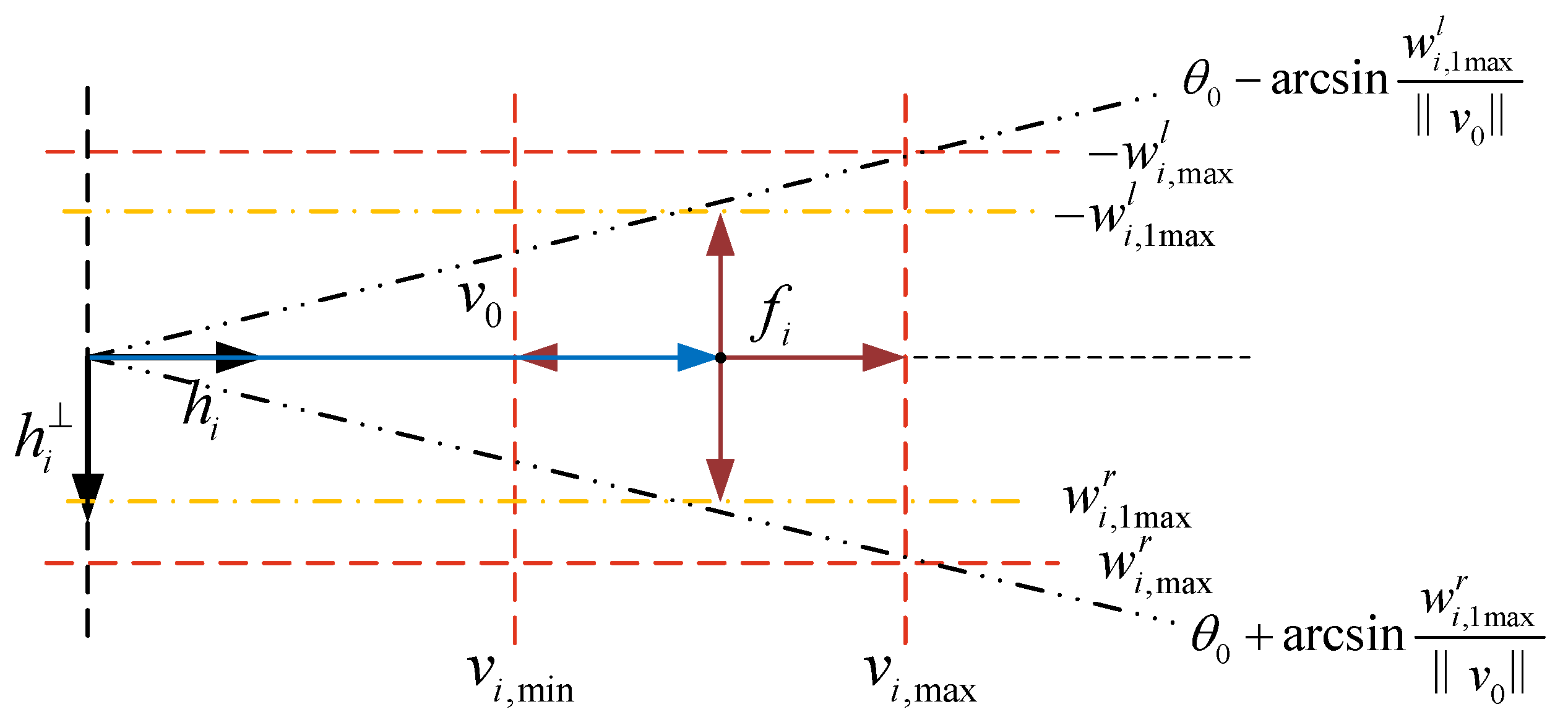
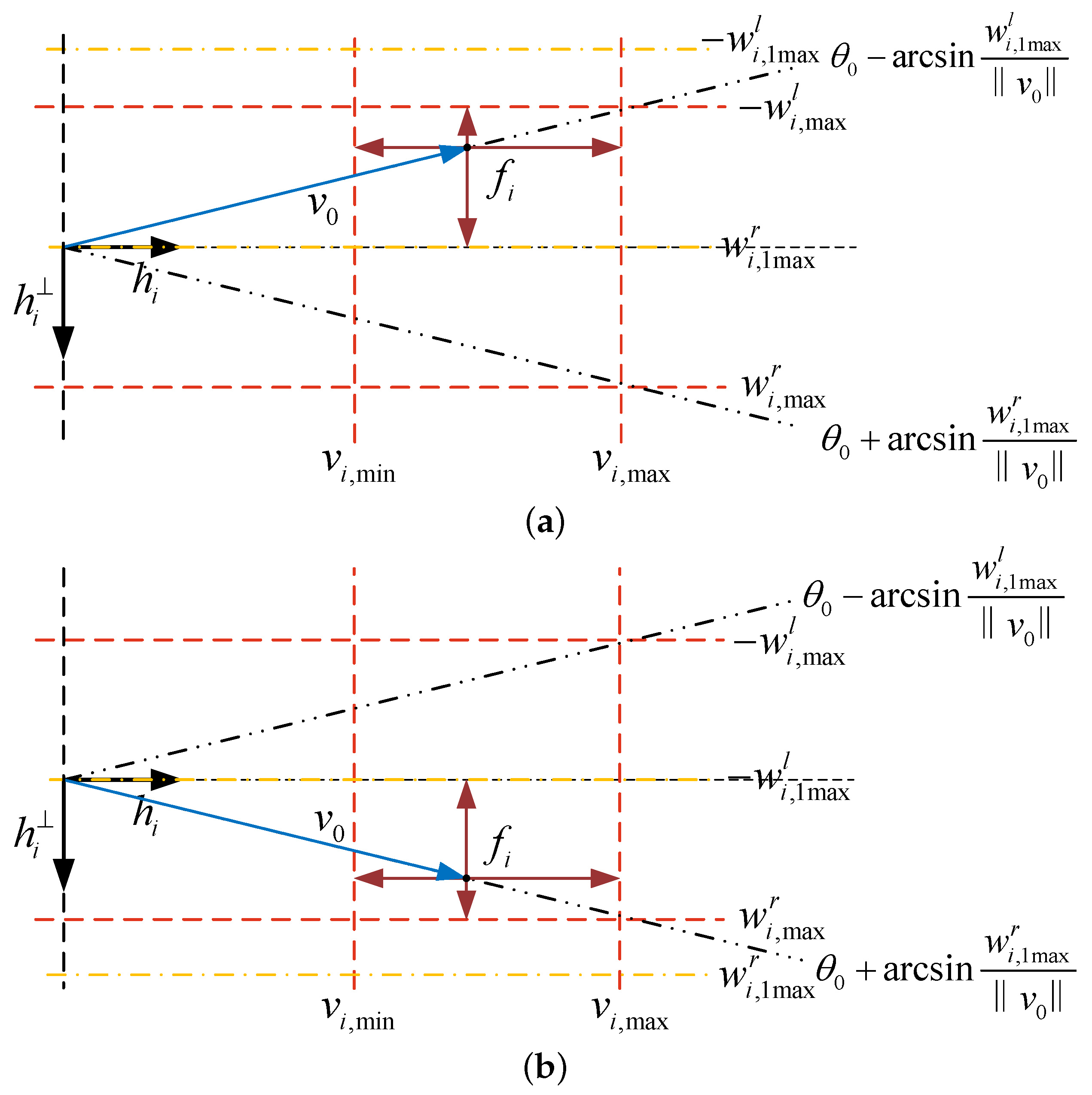
2.3. Problem Statement
3. Controller Design
3.1. Distance-Based Potential Function
- always holds, where if and only if for all ;
- For the function , if , it holds that , where denotes differentiation of the function G;
- Denoteand there exists such that in .
3.2. Low-Gain-Based Controller
3.3. Stability Analysis
- ;
- but .
4. Simulations
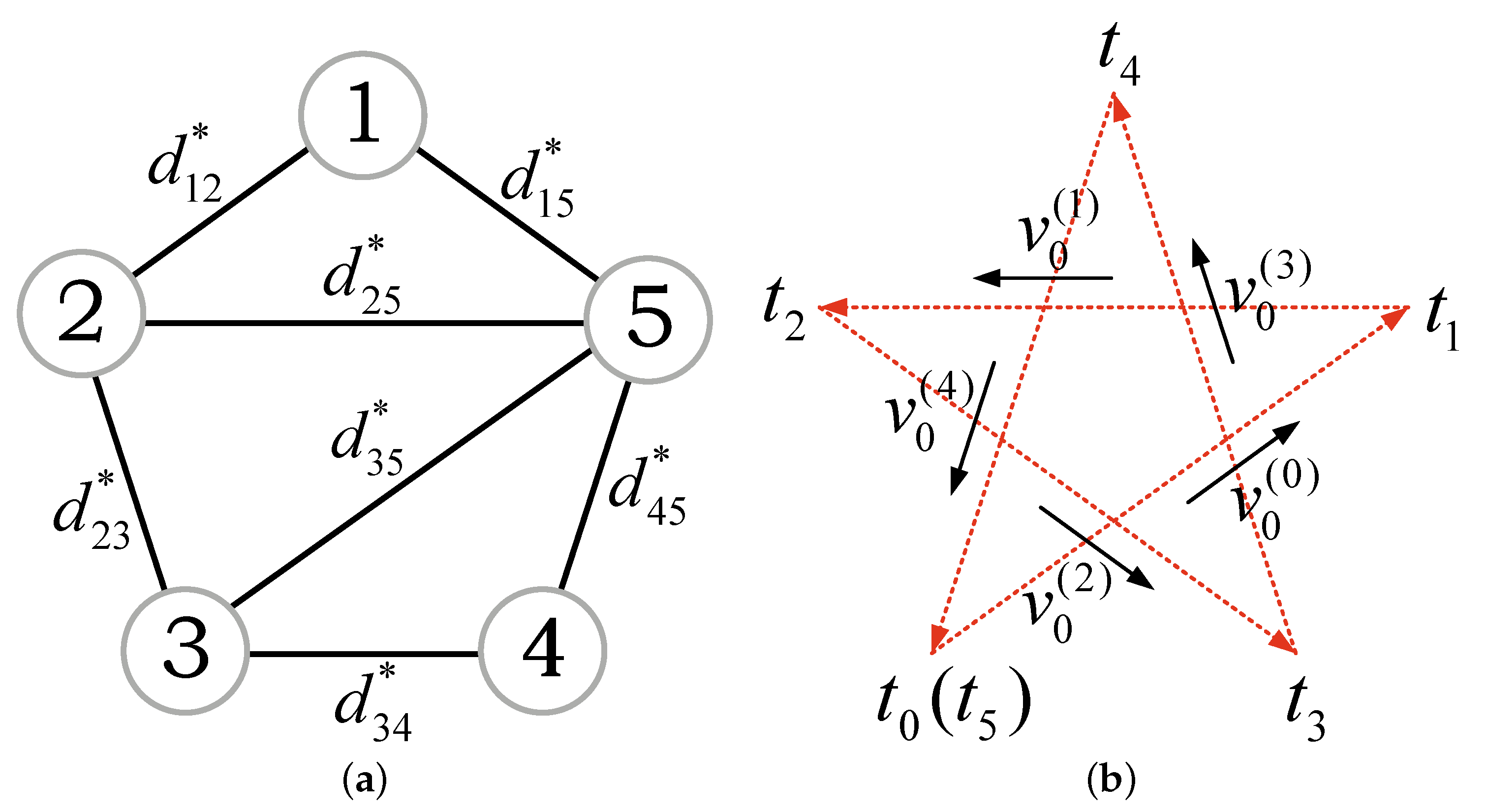
4.1. Simulation Setup
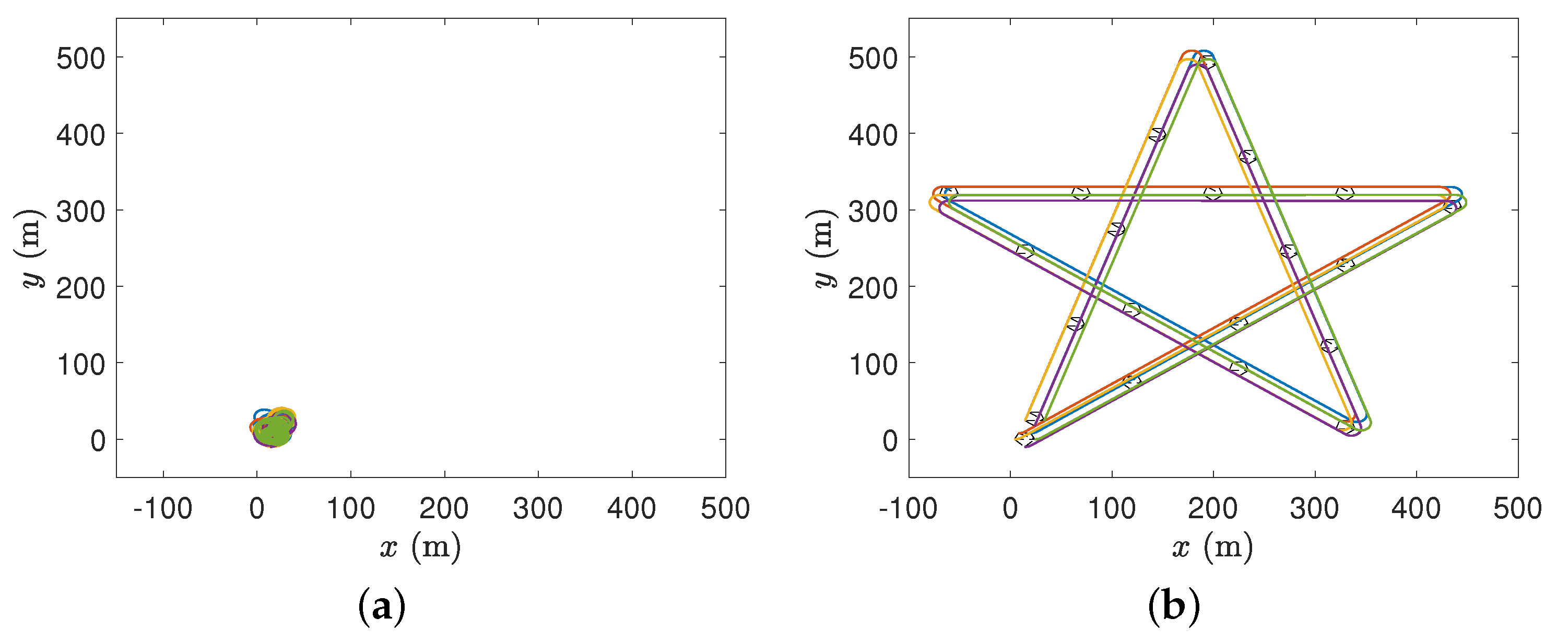
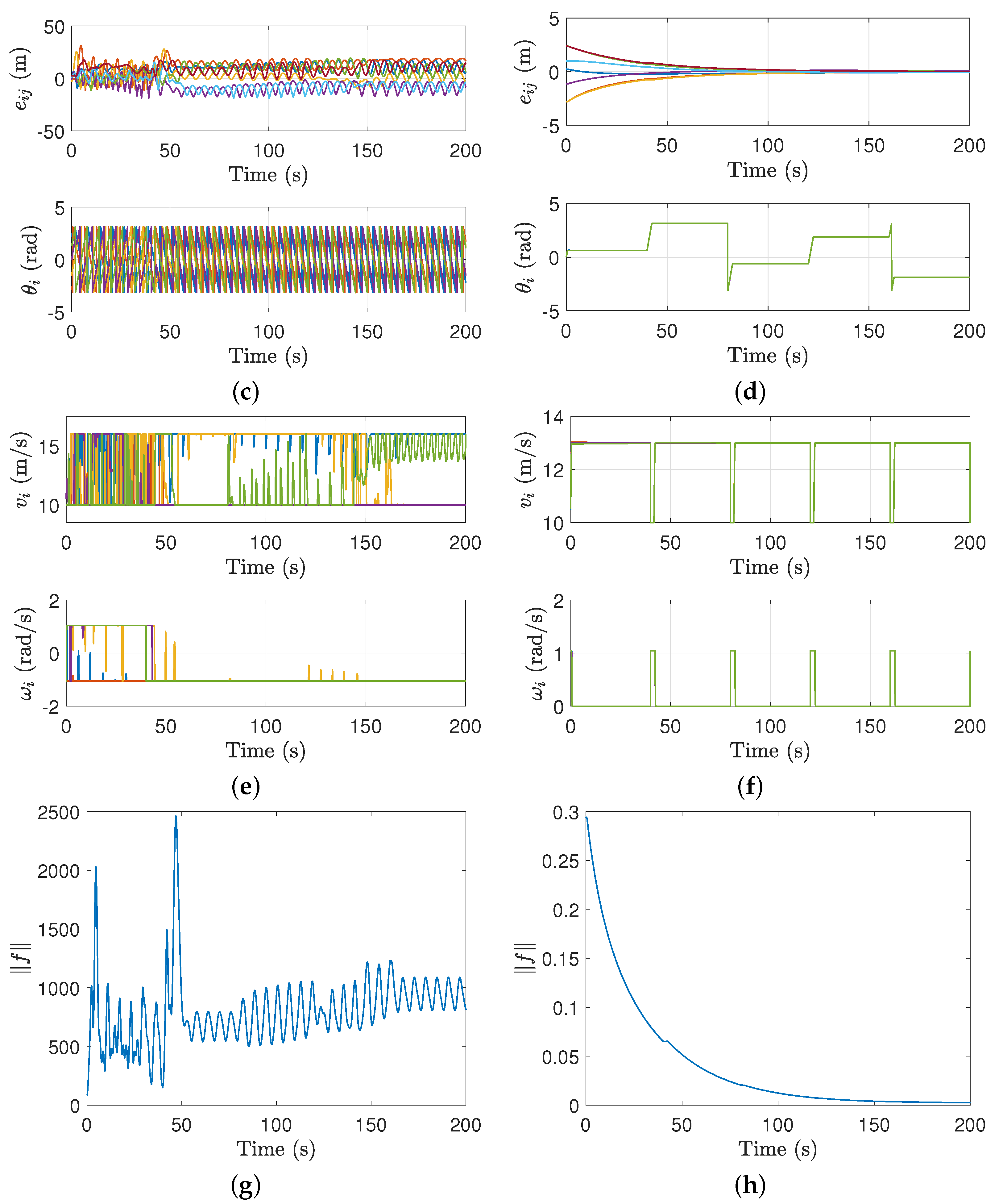
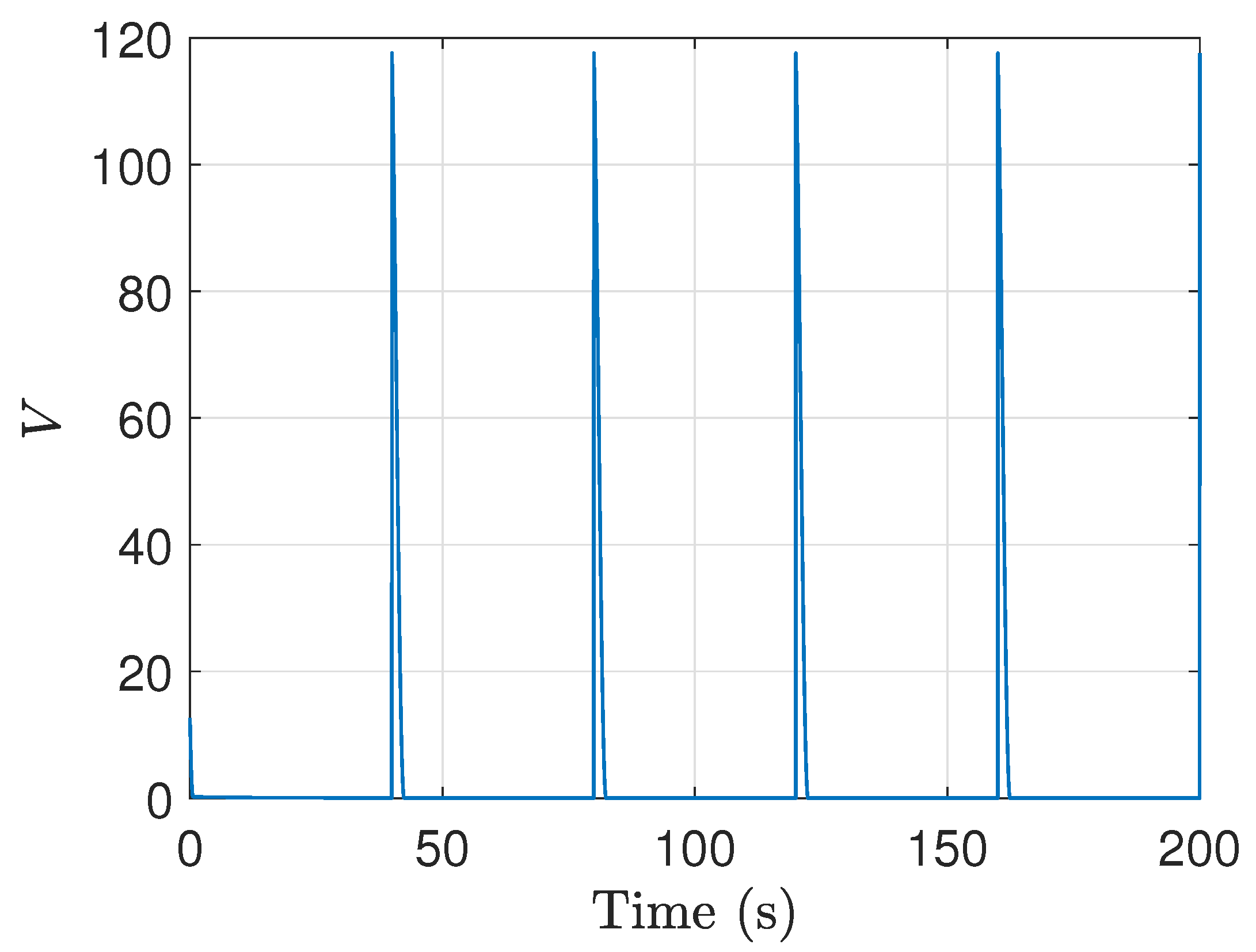
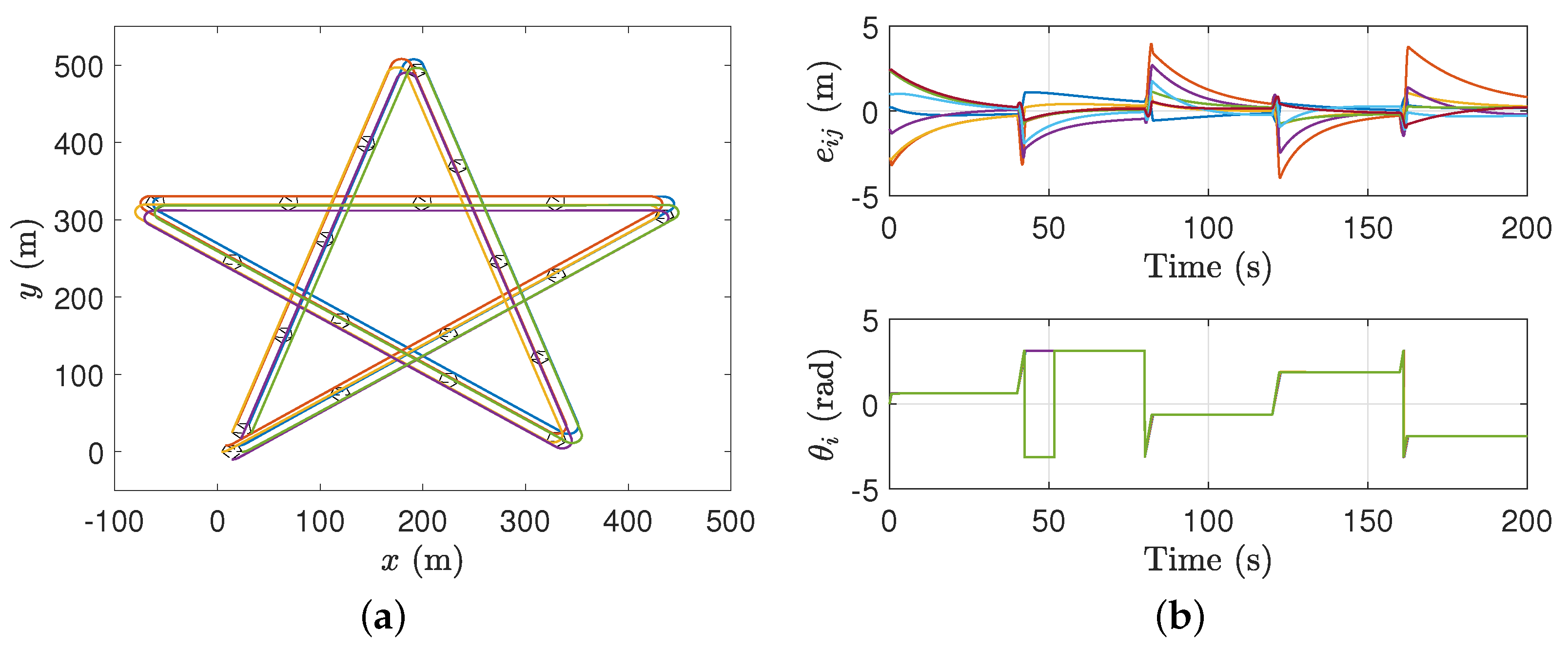
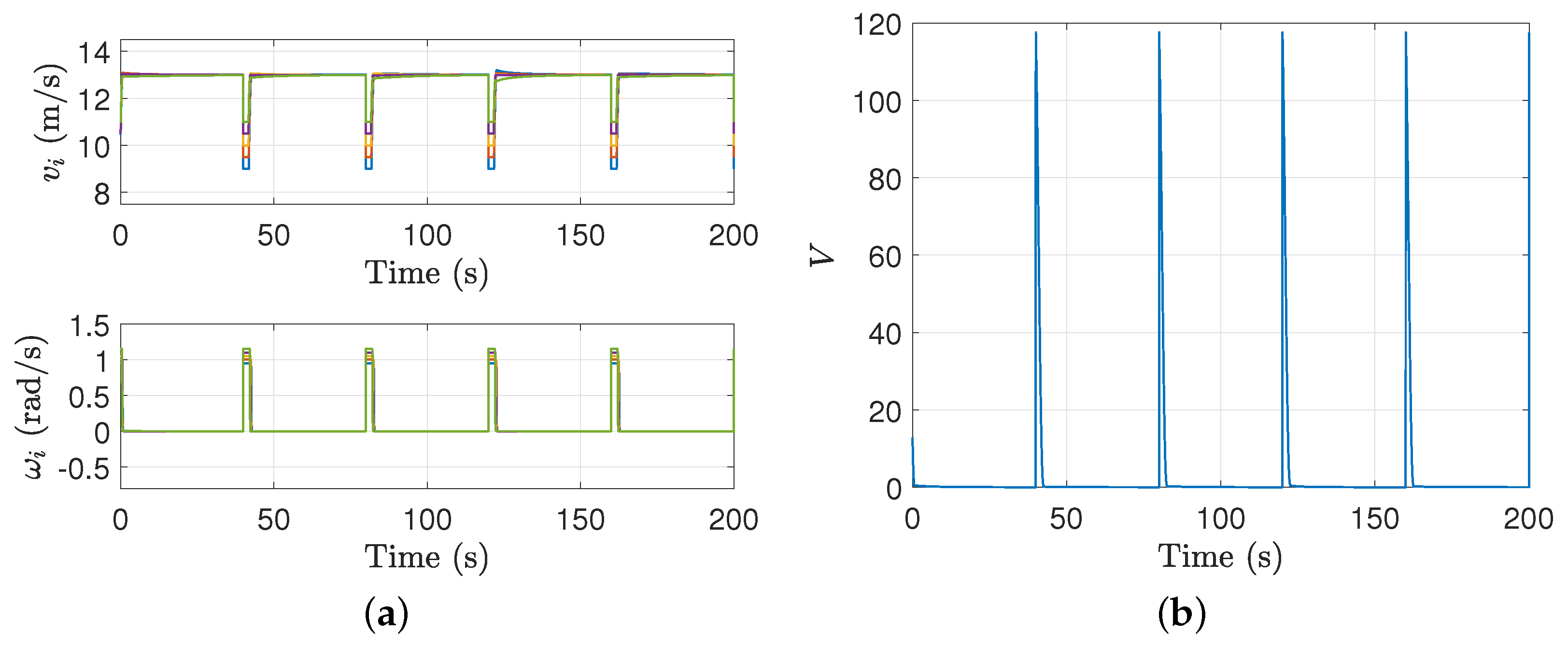
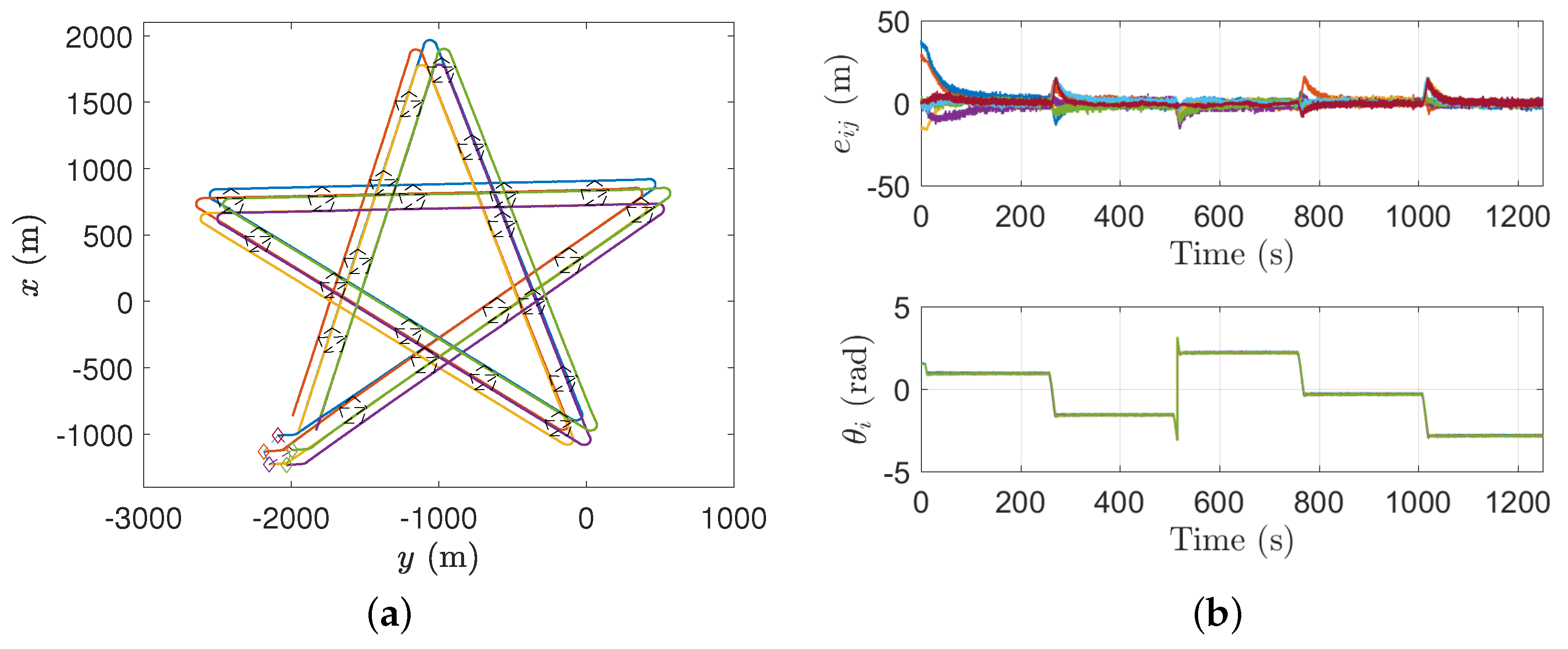
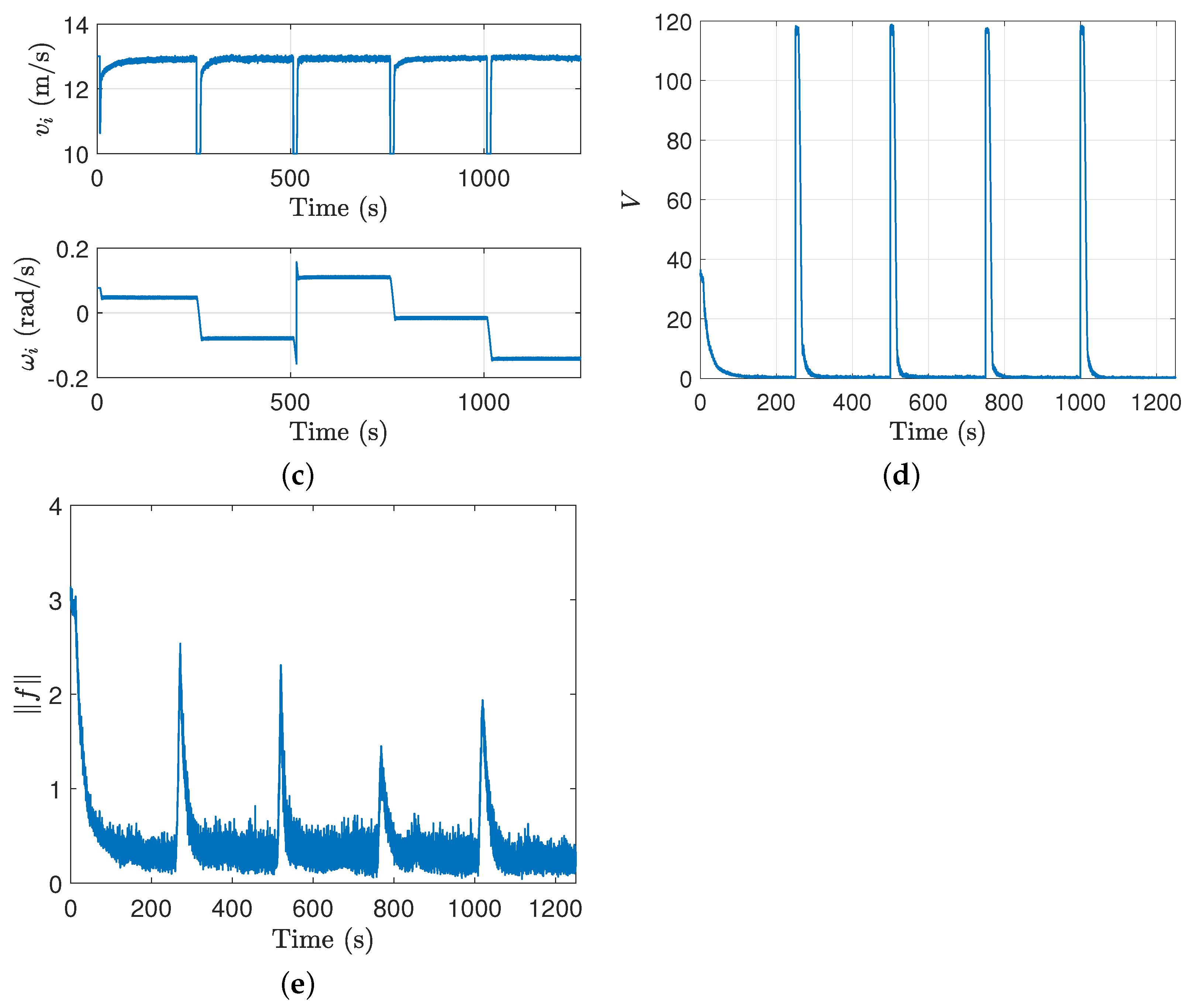
4.2. Numerical Simulation
4.3. Semi-Physical Simulation
4.3.1. Semi-Physical Simulation System
4.3.2. Semi-Physical Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A survey on aerial swarm robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wu, F.; Shen, L.; Chen, J.; Ramchurn, S.D. Decentralized patrolling under constraints in dynamic environments. IEEE Trans. Cybern. 2015, 46, 3364–3376. [Google Scholar] [CrossRef] [PubMed]
- Fathian, K.; Safaoui, S.; Summers, T.H.; Gans, N.R. Robust distributed planar formation control for higher order holonomic and nonholonomic agents. IEEE Trans. Robot. 2020, 37, 185–205. [Google Scholar] [CrossRef]
- Scherer, J.; Yahyanejad, S.; Hayat, S.; Yanmaz, E.; Andre, T.; Khan, A.; Vukadinovic, V.; Bettstetter, C.; Hellwagner, H.; Rinner, B. An autonomous multi-UAV system for search and rescue. In Proceedings of the First Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use, Florence, Italy, 18 May 2015; pp. 33–38. [Google Scholar]
- Liu, Z.; Wang, X.; Shen, L.; Zhao, S.; Cong, Y.; Li, J.; Yin, D.; Jia, S.; Xiang, X. Mission-oriented miniature fixed-wing UAV swarms: A multilayered and distributed architecture. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1588–1602. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Nuno, E.; Loria, A.; Hernández, T.; Maghenem, M.; Panteley, E. Distributed consensus-formation of force-controlled nonholonomic robots with time-varying delays. Automatica 2020, 120, 109114. [Google Scholar] [CrossRef]
- Maghenem, M.; Bautista, A.; Nuño, E.; Loría, A.; Panteley, E. Consensus of multi-agent systems with nonholonomic restrictions via Lyapunov’s direct method. IEEE Control Syst. Lett. 2018, 3, 344–349. [Google Scholar] [CrossRef] [Green Version]
- Babazadeh, R.; Selmic, R. Anoptimal displacement-based leader-follower formation control for multi-agent systems with energy consumption constraints. In Proceedings of the 26th Mediterranean Conference on Control and Automation, Zadar, Croatia, 19–22 June 2018; pp. 179–184. [Google Scholar]
- de Marina, H.G. Maneuvering and robustness issues in undirected displacement-consensus-based formation control. IEEE Trans. Autom. Control 2020, 66, 3370–3377. [Google Scholar] [CrossRef]
- Mehdifar, F.; Bechlioulis, C.P.; Hashemzadeh, F.; Baradarannia, M. Prescribed performance distance-based formation control of multi-agent systems. Automatica 2020, 119, 109086. [Google Scholar] [CrossRef]
- Krick, L.; Broucke, M.E.; Francis, B.A. Stabilisation of infinitesimally rigid formations of multi-robot networks. Int. J. Control 2009, 82, 423–439. [Google Scholar] [CrossRef]
- Oh, K.K.; Ahn, H.S. Formation control of mobile agents based on inter-agent distance dynamics. Automatica 2011, 47, 2306–2312. [Google Scholar] [CrossRef]
- Oh, K.K.; Ahn, H.S. Distance-based undirected formations of single-integrator and double-integrator modeled agents in n-dimensional space. Int. J. Robust. Nonlinear Control 2014, 24, 1809–1820. [Google Scholar] [CrossRef]
- Sun, Z.; Mou, S.; Anderson, B.D.; Cao, M. Exponential stability for formation control systems with generalized controllers: A unified approach. Syst. Control Lett. 2016, 93, 50–57. [Google Scholar] [CrossRef]
- Van Vu, D.; Trinh, M.H.; Nguyen, P.D.; Ahn, H.S. Distance-based formation control with bounded disturbances. IEEE Control Syst. Lett. 2020, 5, 451–456. [Google Scholar] [CrossRef]
- Mou, S.; Belabbas, M.A.; Morse, A.S.; Sun, Z.; Anderson, B.D. Undirected rigid formations are problematic. IEEE Trans. Autom. Control 2015, 61, 2821–2836. [Google Scholar] [CrossRef]
- Bae, Y.B.; Lim, Y.H.; Ahn, H.S. Distributed robust adaptive gradient controller in distance-based formation control with exogenous disturbance. IEEE Trans. Autom. Control 2020, 66, 2868–2874. [Google Scholar] [CrossRef]
- Babazadeh, R.; Selmic, R. Optimal distance-based formation producing control of multi-agent systems with energy constraints and collision avoidance. In Proceedings of the 59th IEEE Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 3847–3853. [Google Scholar]
- Wang, Y.; Cheng, L.; Hou, Z.G.; Yu, J.; Tan, M. Optimal formation of multirobot systems based on a recurrent neural network. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 322–333. [Google Scholar] [CrossRef]
- Sun, Z.; Mou, S.; Deghat, M.; Anderson, B.D.; Morse, A.S. Finite time distance-based rigid formation stabilization and flocking. IFAC Proc. Vol. 2014, 47, 9183–9189. [Google Scholar] [CrossRef] [Green Version]
- Deghat, M.; Anderson, B.D.; Lin, Z. Combined flocking and distance-based shape control of multi-agent formations. IEEE Trans. Autom. Control 2015, 61, 1824–1837. [Google Scholar] [CrossRef] [Green Version]
- Khaledyan, M.; Liu, T.; Fernandez-Kim, V.; de Queiroz, M. Flocking and target interception control for formations of nonholonomic kinematic agents. IEEE Trans. Control Syst. Technol. 2019, 28, 1603–1610. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Sun, D.; Yang, J.; Chen, H. Leader-follower formation control of multiple non-holonomic mobile robots incorporating a receding-horizon scheme. Int. J. Robot. Res. 2010, 29, 727–747. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A. Decentralized cooperative control of multiple nonholonomic dynamic systems with uncertainty. Automatica 2009, 45, 706–710. [Google Scholar] [CrossRef]
- Gazi, V.; Fidan, B.; Ordonez, R.; İlter Köksal, M. A target tracking approach for nonholonomic agents based on artificial potentials and sliding mode control. J. Dyn. Syst. Meas. Control 2012, 134, 061004. [Google Scholar] [CrossRef]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader–follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Yu, X.; Liu, L. Distributed formation control of nonholonomic vehicles subject to velocity constraints. IEEE Trans. Ind. Electron. 2015, 63, 1289–1298. [Google Scholar] [CrossRef]
- Meng, Z.; Zhao, Z.; Lin, Z. On global leader-following consensus of identical linear dynamic systems subject to actuator saturation. Syst. Control Lett. 2013, 62, 132–142. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Y.; Li, Z. Distributed sliding mode control for leader-follower formation flight of fixed-wing unmanned aerial vehicles subject to velocity constraints. Int. J. Robust. Nonlinear Control 2021, 31, 2110–2125. [Google Scholar] [CrossRef]
- Zhao, S.; Dimarogonas, D.V.; Sun, Z.; Bauso, D. A general approach to coordination control of mobile agents with motion constraints. IEEE Trans. Autom. Control 2017, 63, 1509–1516. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Yi, H. Backstepping control design for UAV formation with input saturation constraint and model uncertainty. In Proceedings of the 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 6056–6060. [Google Scholar]
- Wei, J.; Li, H.; Guo, M.; Li, J.; Huang, H. Backstepping control based on constrained command filter for hypersonic flight vehicles with AOA and actuator constraints. Int. J. Aerosp. Eng. 2021, 2021, 8620873. [Google Scholar] [CrossRef]
- Zhao, M.; Peng, Y.; Wang, Y.; Zhang, D.; Luo, J.; Pu, H. Concise leader-follower formation control of underactuated unmanned surface vehicle with output error constraints. Meas. Control 2022, 44, 1081–1094. [Google Scholar] [CrossRef]
- Su, H.; Chen, M.Z.; Lam, J.; Lin, Z. Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1881–1889. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.L. Robust low gain output feedback sliding mode control design against actuator saturation. IMA J. Math. Control Inf. 2019, 36, 1237–1253. [Google Scholar]
- Xu, J.; Lin, Z. Low gain feedback for fractional-order linear systems and semi-global stabilization in the presence of actuator saturation. Nonlinear Dyn. 2022, 107, 3485–3504. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, Z.; Fu, X. Fully distributed dynamic event-triggered semiglobal consensus of multi-agent uncertain systems with input saturation via low-gain feedback. Int. J. Control Autom. Syst. 2021, 19, 1451–1460. [Google Scholar] [CrossRef]
- Li, H.; Chen, H.; Yang, S.; Wang, X. Standard formation generation and keeping of unmanned aerial vehicles through a potential functional approach. In Proceedings of the 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 4771–4776. [Google Scholar]
- Li, H.; Chen, H.; Wang, X. Affine formation tracking control of unmanned aerial vehicles. Front. Inf. Technol. Electron. Eng. 2022, 1–11. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C.; Lan, Z. Flocking and collision avoidance for a dynamic squad of fixed-wing UAVs using deep reinforcement learning. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September 2021; pp. 4738–4744. [Google Scholar]
- Chen, H.; Wang, X.; Shen, L.; Yu, Y. Coordinated path following control of fixed-wing unmanned aerial vehicles in wind. ISA Trans. 2022, 122, 260–270. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Yu, Y.; Wang, X. Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method. Drones 2022, 6, 159. https://doi.org/10.3390/drones6070159
Yan J, Yu Y, Wang X. Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method. Drones. 2022; 6(7):159. https://doi.org/10.3390/drones6070159
Chicago/Turabian StyleYan, Jiarun, Yangguang Yu, and Xiangke Wang. 2022. "Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method" Drones 6, no. 7: 159. https://doi.org/10.3390/drones6070159
APA StyleYan, J., Yu, Y., & Wang, X. (2022). Distance-Based Formation Control for Fixed-Wing UAVs with Input Constraints: A Low Gain Method. Drones, 6(7), 159. https://doi.org/10.3390/drones6070159






