Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers
Abstract
:1. Introduction
- The ODDDM algorithm solves the offense–defense confrontation problem with the moving high-priority target (HPT) like an aircraft carrier, which needs to be addressed further in the literature. A real-time combat model is established to update the states of all the UAVs and HPTs for both sides. The dynamic nature of the swarm is well maintained in case of UAV(s) loss. The work is an extension of the previously published work with some realistic amendments [13]. For instance, in previous work, continuous data communication among neighbors was required unless the target was finalized. The communication systems for high update rates are relatively expensive from a practical viewpoint. However, the UAVs in the swarm are cost-efficient, rendering the possibility of continuous communication hard to realize. The proposed ODDDM algorithm requires one-time data communication among neighbors for target finalization of the selected UAV in one time step.
- The target allocation decision-making in the proposed ODDDM algorithm leads to the offense/defense behavior of a particular UAV in the swarm. This determines the target selection and firing of the weapon at the target in range. To this end, the proposed ODDDM algorithm uses a distributed estimation-based allocation approach to obtain data on enemy UAVs in the neighborhood and allocate a target for the particular UAV to maximize profit. In contrast, in our earlier work [13], the cumulative allocation algorithm was employed. The proposed algorithm is more applicable in practical combat situations, as the enemy UAVs are unknown, unlike in the earlier work. The proposed algorithm is efficient as it considers only the enemy UAVs in the detection range, rather than all the enemy UAVs.
- The UAV-motion decision making generates UAV guidance commands. The guidance command has two main components, i.e., one is generated from the target position and second is generated from the neighbors to deal with the swarm principles of cohesion, separation and alignment. Only the real-time location of the neighboring UAVs is required for this part of the algorithm.
2. UAVs Swarm vs. Swarm Confrontation Problem Description
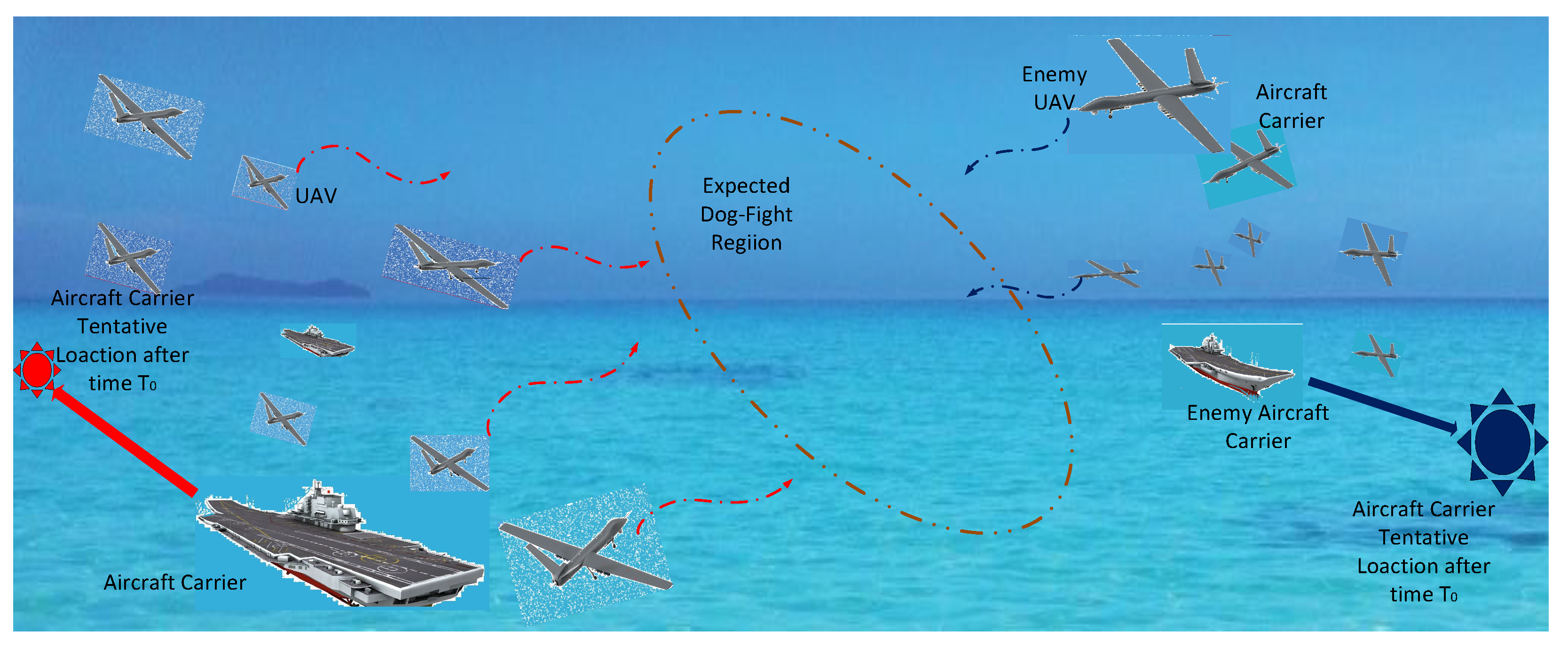
2.1. UAV Swarm-Based Combat Scenario
2.2. Combat Dynamics
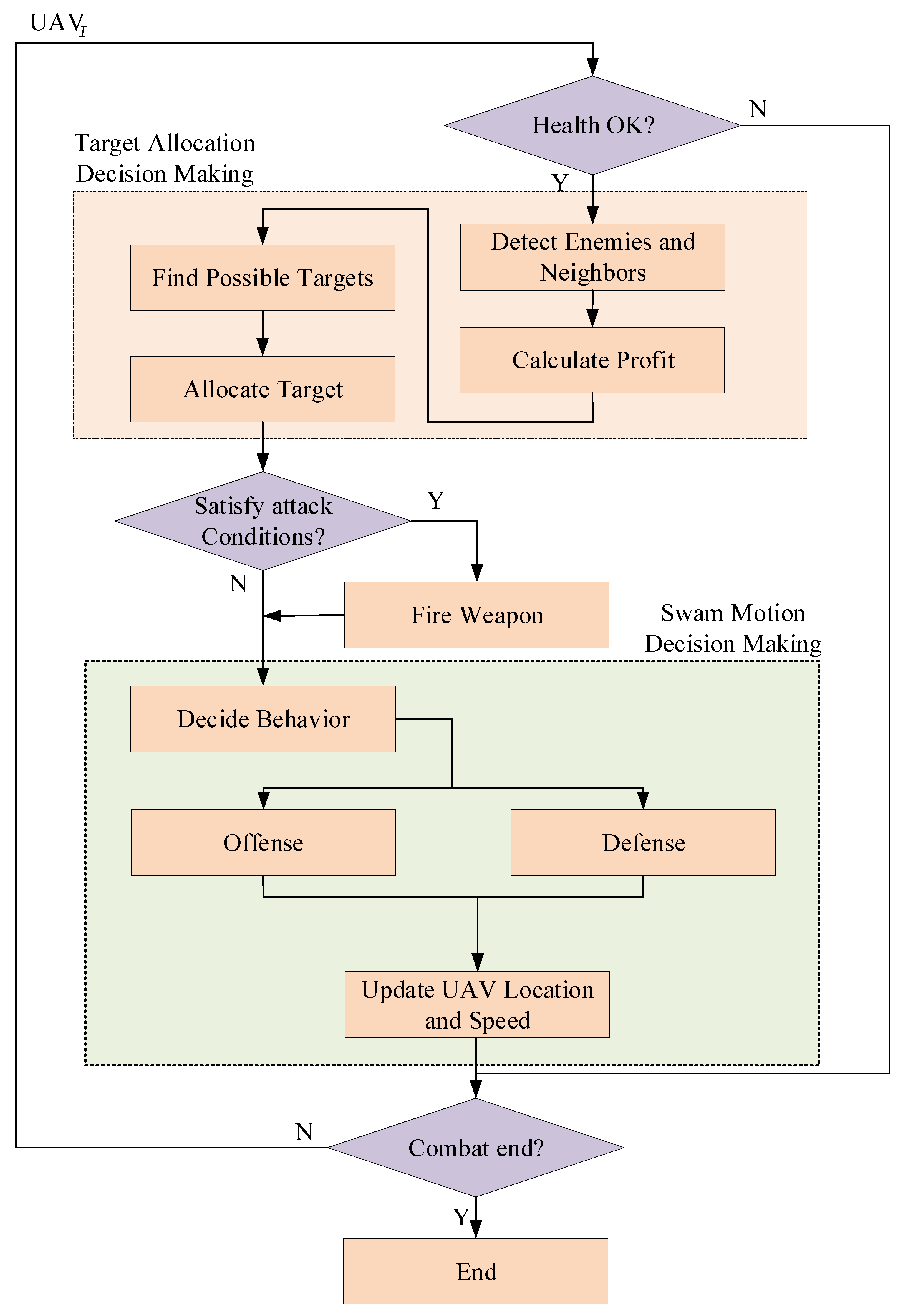
3. Structure of ODDDM Algorithm
3.1. Target Allocation Decision Making
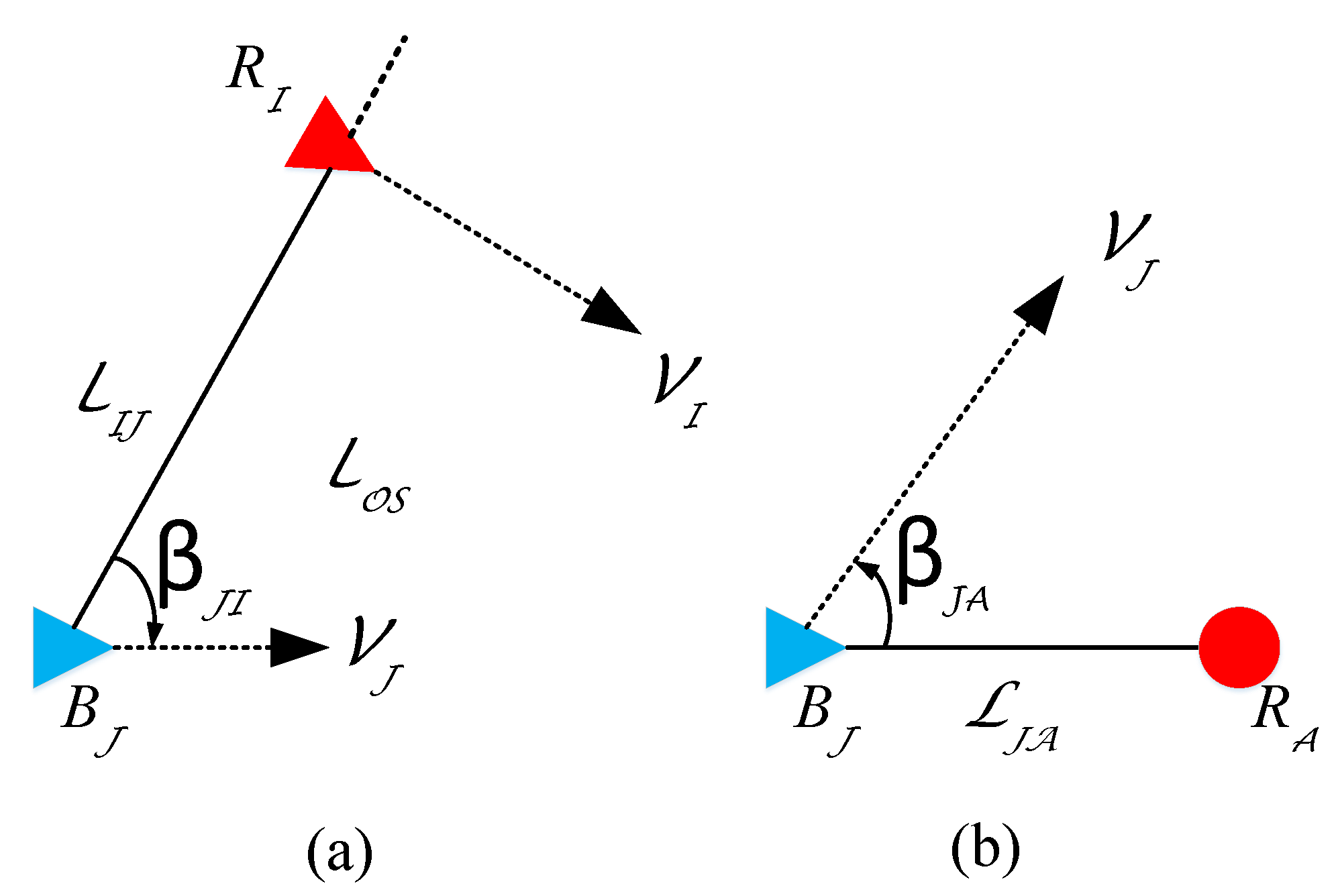
3.1.1. Profit Calculation
3.1.2. Neighbor Detection
3.1.3. Consensus-Based Estimated Target Allocation
| Algorithm 1 Consensus-Based Auction Algorithm for a UAV. |
|
3.2. Swarm Motion Decision Making
3.2.1. Control Input Components Based on Behavioral Rules
3.2.2. Mission-Based Components of the Control Input
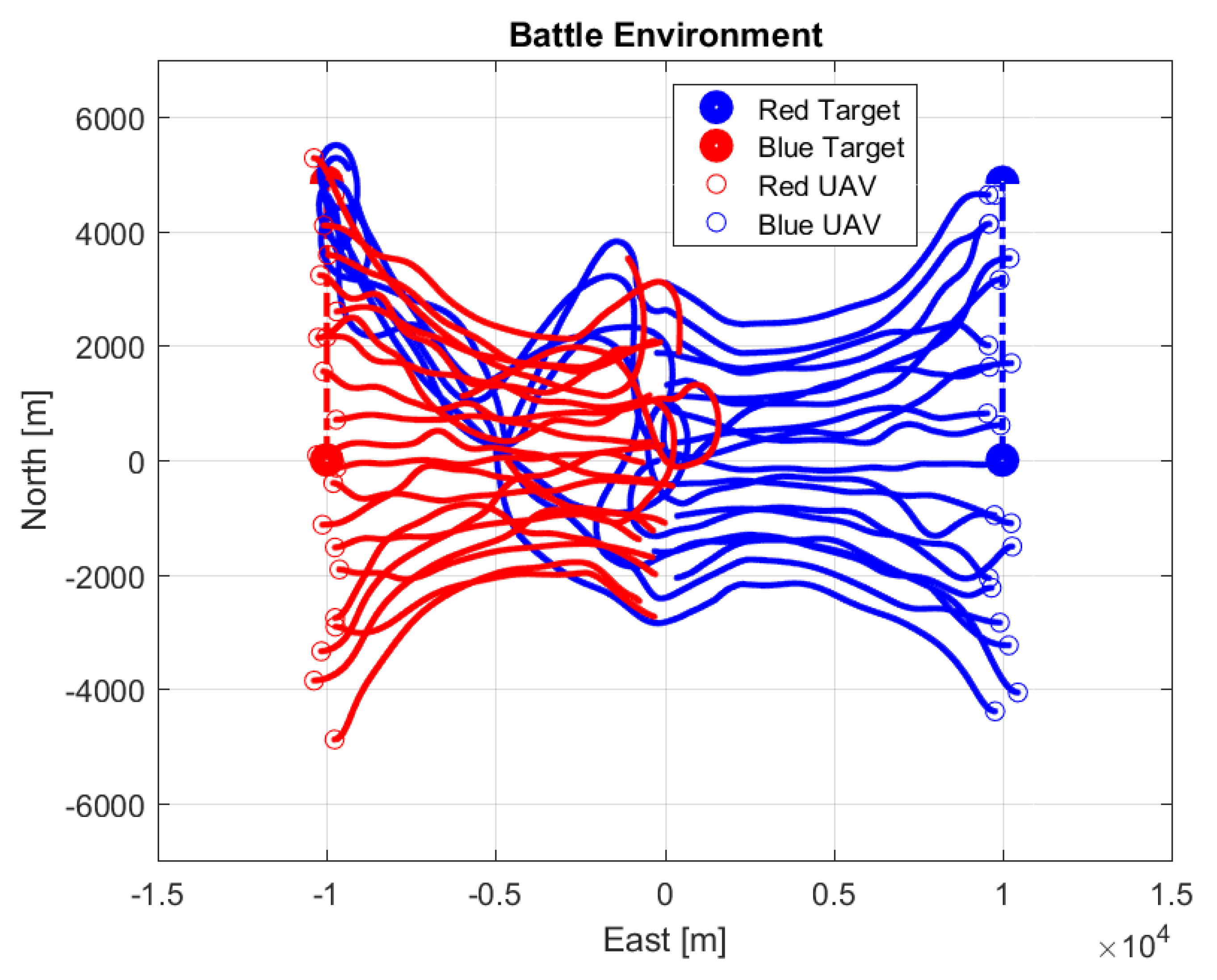
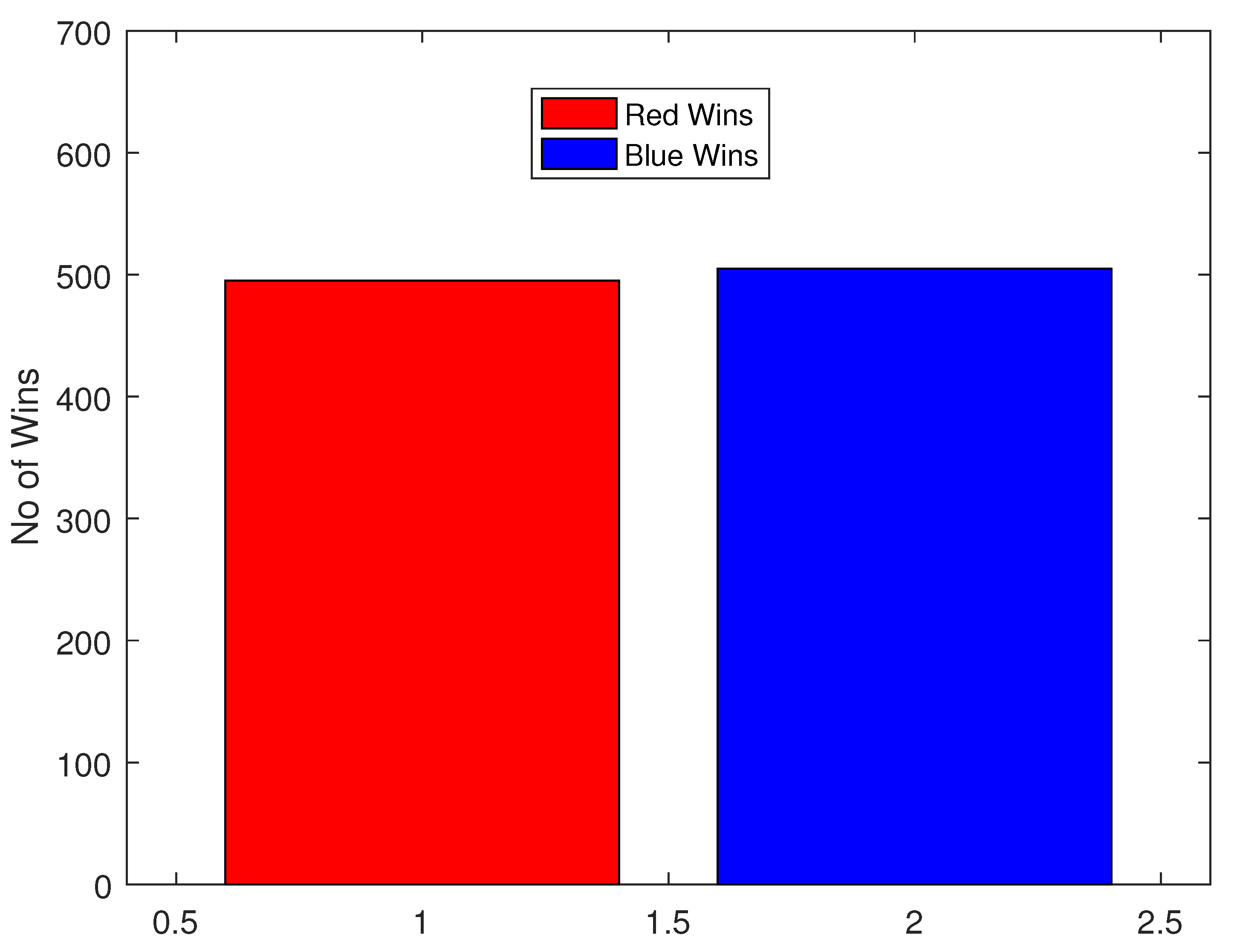
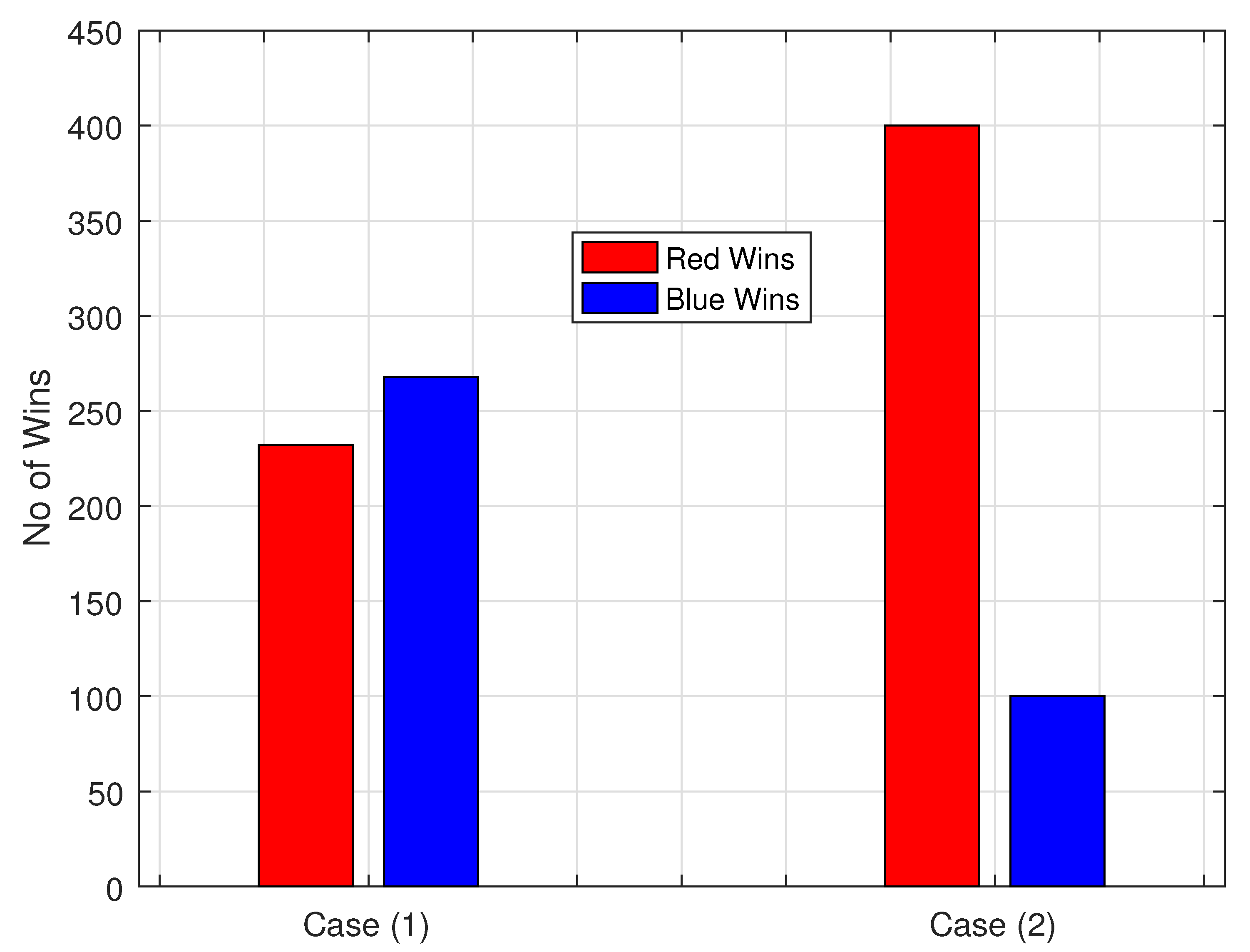
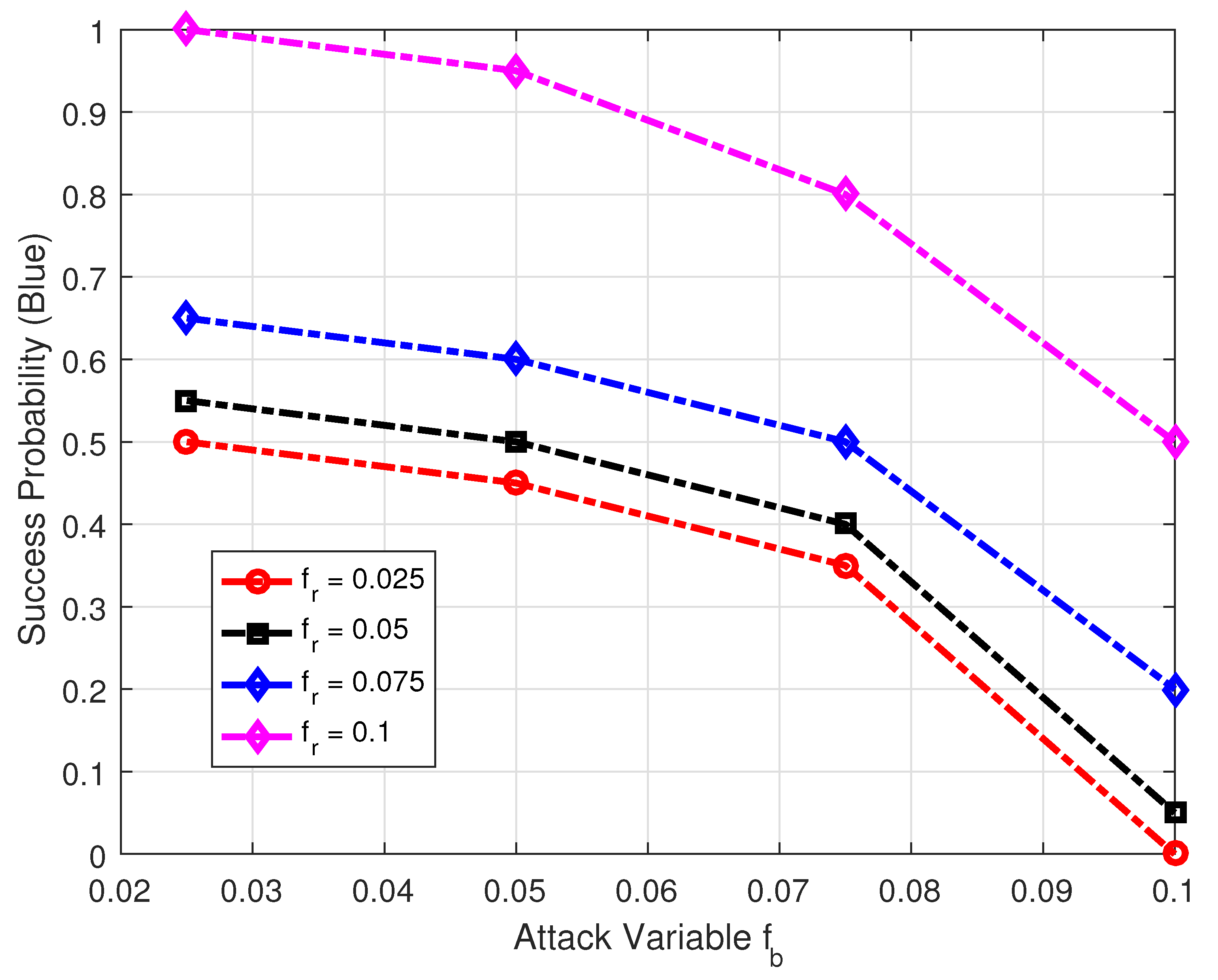
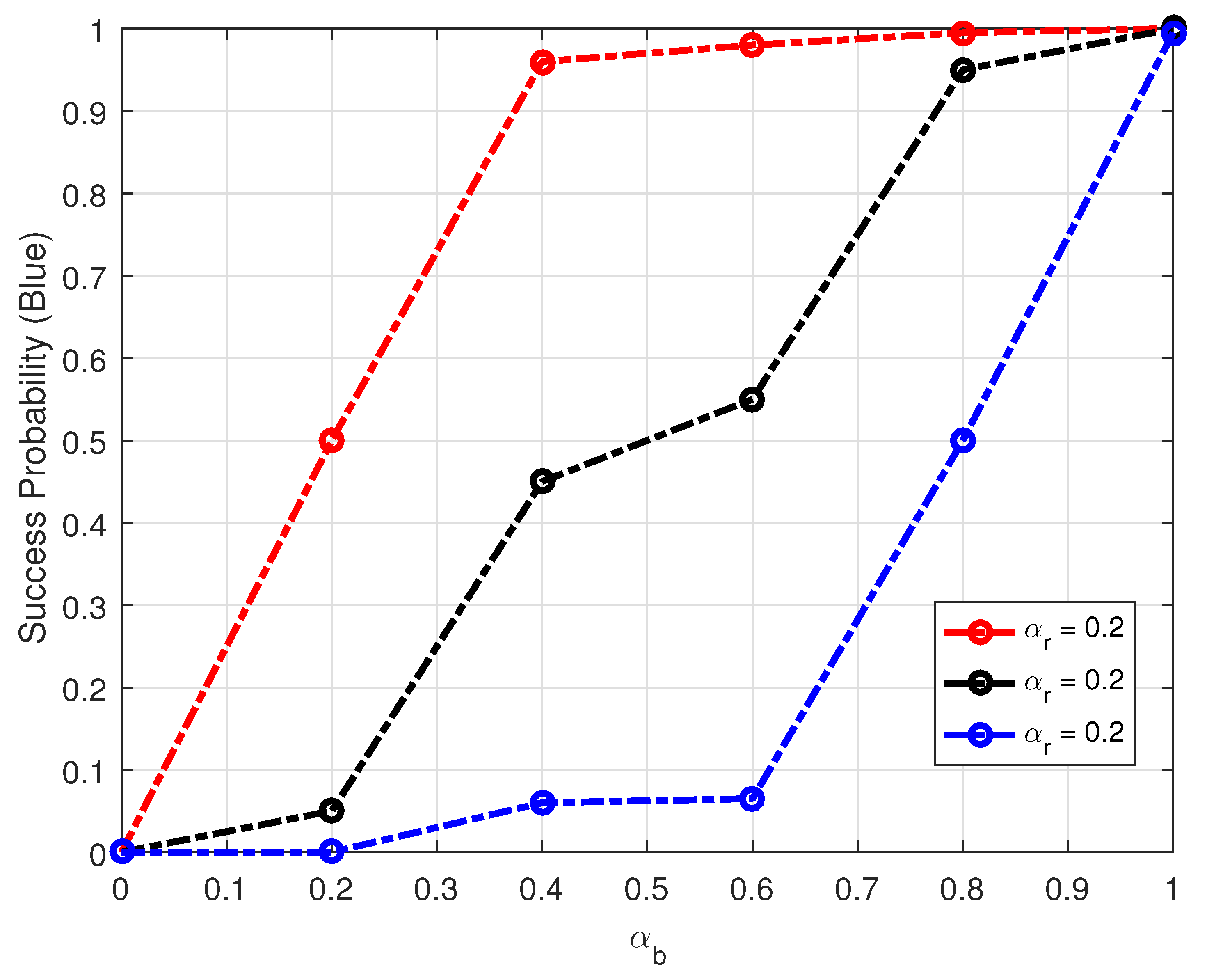
4. Simulation and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, J.; Wu, H.; Zhan, R.; Menassel, R.; Zhou, X. Self-organized search-attack mission planning for UAV swarm based on wolf pack hunting behavior. J. Syst. Eng. Electron. 2021, 32, 1463–1476. [Google Scholar]
- Goodrich, M.A.; Cooper, J.L.; Adams, J.A.; Humphrey, C.; Zeeman, R.; Buss, B.G. Using a Mini-UAV to Support Wilderness Search and Rescue: Practices for Human-Robot Teaming. In Proceedings of the 2007 IEEE International Workshop on Safety, Security and Rescue Robotics, Rome, Italy, 27–29 September 2007; pp. 1–6. [Google Scholar]
- Waharte, S.; Trigoni, N. Supporting Search and Rescue Operations with UAVs. In Proceedings of the 2010 International Conference on Emerging Security Technologies, Canterbury, UK, 6–7 September 2010; pp. 142–147. [Google Scholar]
- Riehl, J.R.; Collins, G.E.; Hespanha, J.P. Cooperative Search by UAV Teams: A Model Predictive Approach using Dynamic Graphs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2637–2656. [Google Scholar] [CrossRef]
- Cui, J.Q.; Phang, S.K.; Ang, K.Z.Y.; Wang, F.; Dong, X.; Ke, Y.; Lai, S.; Li, K.; Li, X.; Lin, F.; et al. Drones for cooperative search and rescue in post-disaster situation. In Proceedings of the 2015 IEEE 7th International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Siem Reap, Cambodia, 15–17 July 2015; pp. 167–174. [Google Scholar]
- Viguria, A.; Maza, I.; Ollero, A. Distributed Service-Based Cooperation in Aerial/Ground Robot Teams Applied to Fire Detection and Extinguishing Missions. Adv. Robot. 2010, 24, 1–23. [Google Scholar] [CrossRef]
- Sadeghi, M.; Abaspour, A.; Sadati, S.H. A Novel Integrated Guidance and Control System Design in Formation Flight. J. Aerosp. Technol. Manag. 2015, 7, 432–442. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Shen, L.; Zhao, S.; Cong, Y.; Li, J.; Yin, D.; Jia, S.; Xiang, X. Mission-Oriented Miniature Fixed-Wing UAV Swarms: A Multilayered and Distributed Architecture. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1588–1602. [Google Scholar] [CrossRef]
- Zhen, Z.Y.; Jiang, J.; Sun, S.S.; Wang, B.L. Cooperative Control and Decision of UAV Swarm Operations; National Defense Industry Press: Beijing, China, 2022. [Google Scholar]
- Otto, R.P. Small Unmanned Aircraft Systems (SUAS) Flight Plan: 2016–2036. Bridging the Gap Between Tactical and Strategic. By Airforce Deputy Chief of Staff, Washington DC, United States. 2016. Available online: https://apps.dtic.mil/sti/pdfs/AD1013675.pdf (accessed on 10 August 2022).
- Aweiss, A.; Homola, J.; Rios, J.; Jung, J.; Johnson, M.; Mercer, J.; Modi, H.; Torres, E.; Ishihara, A. Flight Demonstration of Unmanned Aircraft System (UAS) Traffic Management (UTM) at Technical Capability Level 3. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–7. [Google Scholar]
- Lappas, V.; Zoumponos, G.; Kostopoulos, V.; Shin, H.; Tsourdos, A.; Tantarini, M.; Shmoko, D.; Munoz, J.; Amoratis, N.; Maragkakis, A.; et al. EuroDRONE, A European UTM Testbed for U-Space. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1766–1774. [Google Scholar]
- Xing, D.J.; Zhen, Z.Y.; Gong, H.J. Offense–defense confrontation decision making for dynamic UAV swarm versus UAV swarm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5689–5702. [Google Scholar] [CrossRef]
- García, E.; Casbeer, D.W.; Pachter, M. Active target defence differential game: Fast defender case. IET Control. Theory Appl. 2017, 11, 2985–2993. [Google Scholar] [CrossRef]
- Alfeo, A.L.; Cimino, M.G.C.A.; Francesco, N.D.; Lazzeri, A.; Lega, M.; Vaglini, G. Swarm coordination of mini-UAVs for target search using imperfect sensors. Intell. Decis. Technol. 2018, 12, 149–162. [Google Scholar] [CrossRef]
- Cevik, P.; Kocaman, I.; Akgul, A.S.; Akca, B. The Small and Silent Force Multiplier: A Swarm UAV—Electronic Attack. J. Intell. Robot. Syst. 2013, 70, 595–608. [Google Scholar] [CrossRef]
- Muñoz, M.V.F. Agent-based simulation and analysis of a defensive UAV swarm against an enemy UAV swarm. In Proceedings of the Naval Postgraduate School, Monterey, CA, USA, 1 June 2011. [Google Scholar]
- Day, M.A. Multi-Agent Task Negotiation Among UAVs to Defend Against Swarm Attacks. In Proceedings of the Naval Postgraduate School, Monterey, CA, USA, 21 March 2012. [Google Scholar]
- Zhang, X.; Luo, P.; Hu, X. Defense Success Rate Evaluation for UAV Swarm Defense System. In Proceedings of the ISMSI ’18, Phuket, Thailand, 24–25 March 2018. [Google Scholar]
- Gaertner, U. UAV swarm tactics: An agent-based simulation and Markov process analysis. In Proceedings of the Naval Postgraduate School, Monterey, CA, USA, 31 March 2013. [Google Scholar]
- Fan, D.D.; Theodorou, E.A.; Reeder, J. Evolving cost functions for model predictive control of multi-agent UAV combat swarms. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017. [Google Scholar]
- Choi, H.L.; Brunet, L.; How, J.P. Consensus-Based Decentralized Auctions for Robust Task Allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- Johnson, L.B.; Ponda, S.S.; Choi, H.L.; How, J.P. Asynchronous Decentralized Task Allocation for Dynamic Environments. In Proceedings of the Infotech@Aerospace 2011, AIAA 2011-1441, St. Louis, MI, USA, 29–31 March 2011. [Google Scholar] [CrossRef]
- Mercker, T.; Casbeer, D.W.; Millet, P.; Akella, M.R. An extension of consensus-based auction algorithms for decentralized, time-constrained task assignment. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6324–6329. [Google Scholar]
- Zhang, K.; Collins, E.G.; Shi, D. Centralized and distributed task allocation in multi-robot teams via a stochastic clustering auction. Acm Trans. Auton. Adapt. Syst. 2012, 7, 1–22. [Google Scholar] [CrossRef]
- Shin, H.S.; Segui-Gasco, P. UAV Swarms: Decision-Making Paradigms. In Encyclopedia of Aerospace Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’87, Anaheim, CA, USA, 27–31 July 1987; Association for Computing Machinery: New York, NY, USA, 1987; pp. 25–34. [Google Scholar]
- Mission reliability modeling of UAV swarm and its structure optimization based on importance measure. Reliab. Eng. Syst. Saf. 2021, 215, 107879. [CrossRef]
- An improved Vicsek model of swarm based on remote neighbors strategy. Phys. Stat. Mech. Its Appl. 2022, 587, 126553. [CrossRef]
- Chapman, A.; Mesbahi, M. UAV Swarms: Models and Effective Interfaces. In Handbook of Unmanned Aerial Vehicles; Valavanis, K.P., Vachtsevanos, G.J., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 1987–2019. [Google Scholar]
- Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M. A Leader-Follower Formation Control of Multi-UAVs via an Adaptive Hybrid Controller. Complexity 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H. Multi-unmanned aerial vehicle swarm formation control using hybrid strategy. Trans. Inst. Meas. Control. 2021, 43, 2689–2701. [Google Scholar] [CrossRef]
- Yinka-Banjo, C.O.; Owolabi, W.A.; Akala, A.O. Birds Control in Farmland Using Swarm of UAVs: A Behavioural Model Approach. In Intelligent Computing; Arai, K., Kapoor, S., Bhatia, R., Eds.; Springer: Cham, Switzerland, 2019; pp. 333–345. [Google Scholar]
- Wu, J.; Luo, C.; Luo, Y.; Li, K. Distributed UAV Swarm Formation and Collision Avoidance Strategies Over Fixed and Switching Topologies. IEEE Trans. Cybern. 2021, 1–11. [Google Scholar] [CrossRef] [PubMed]
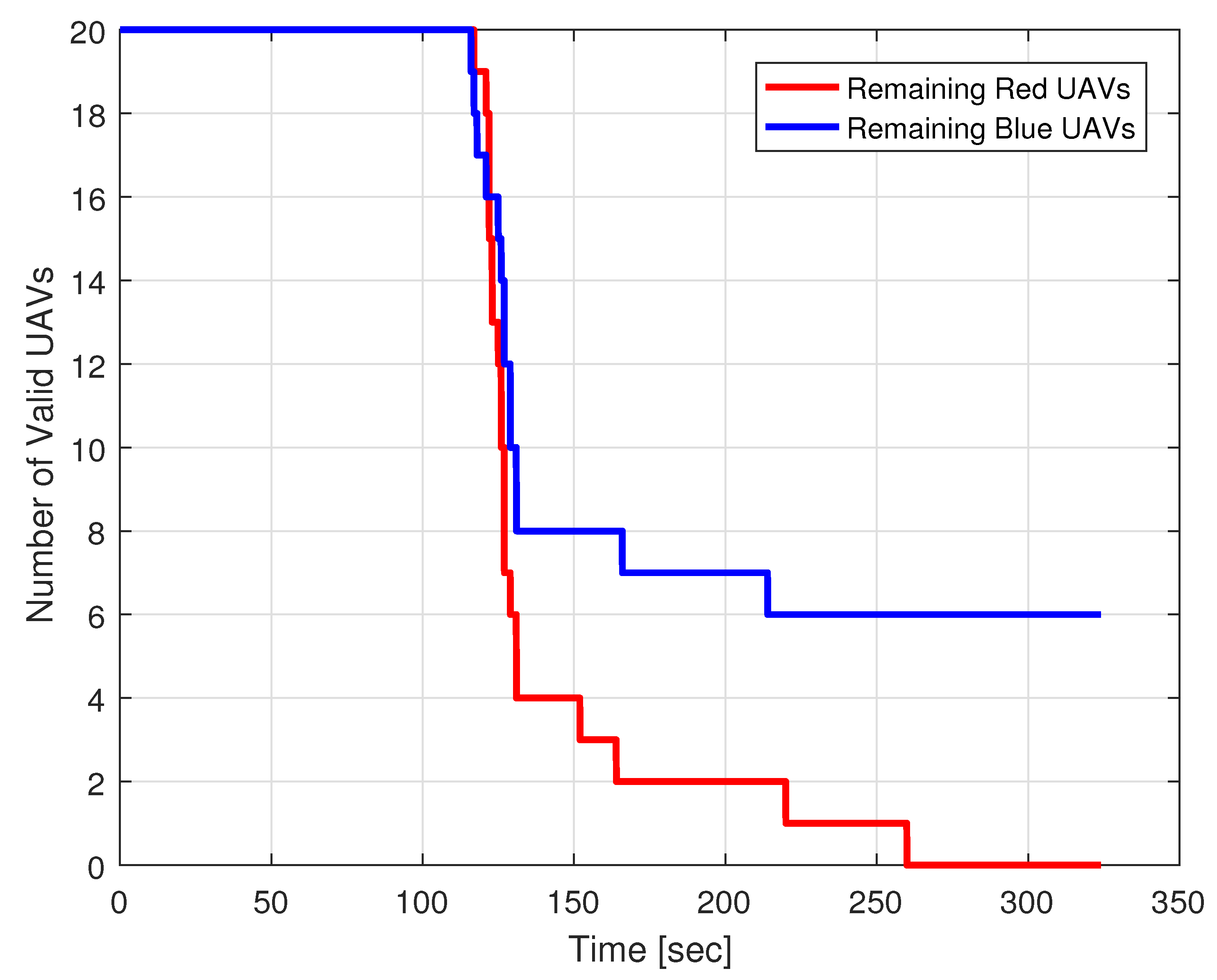
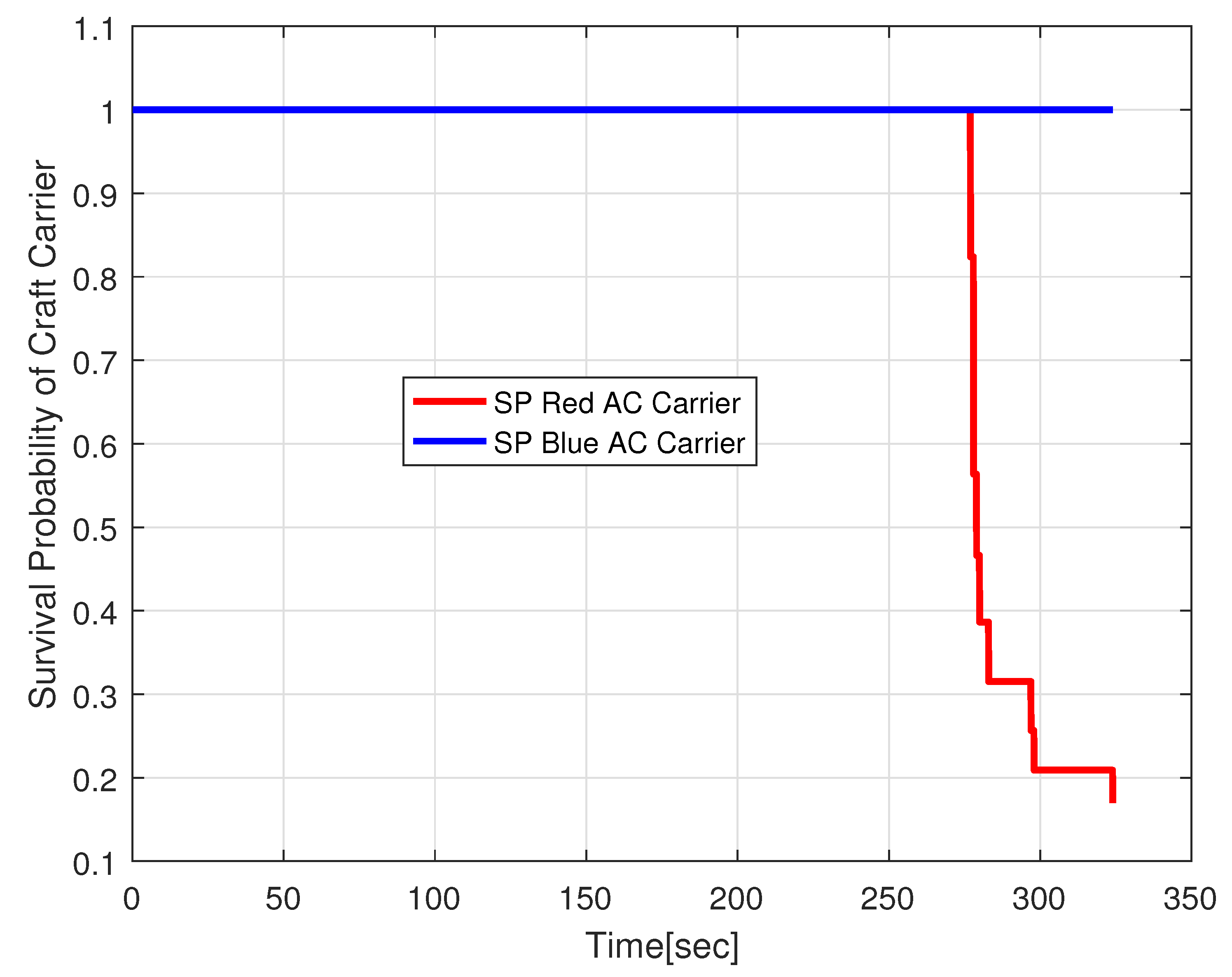
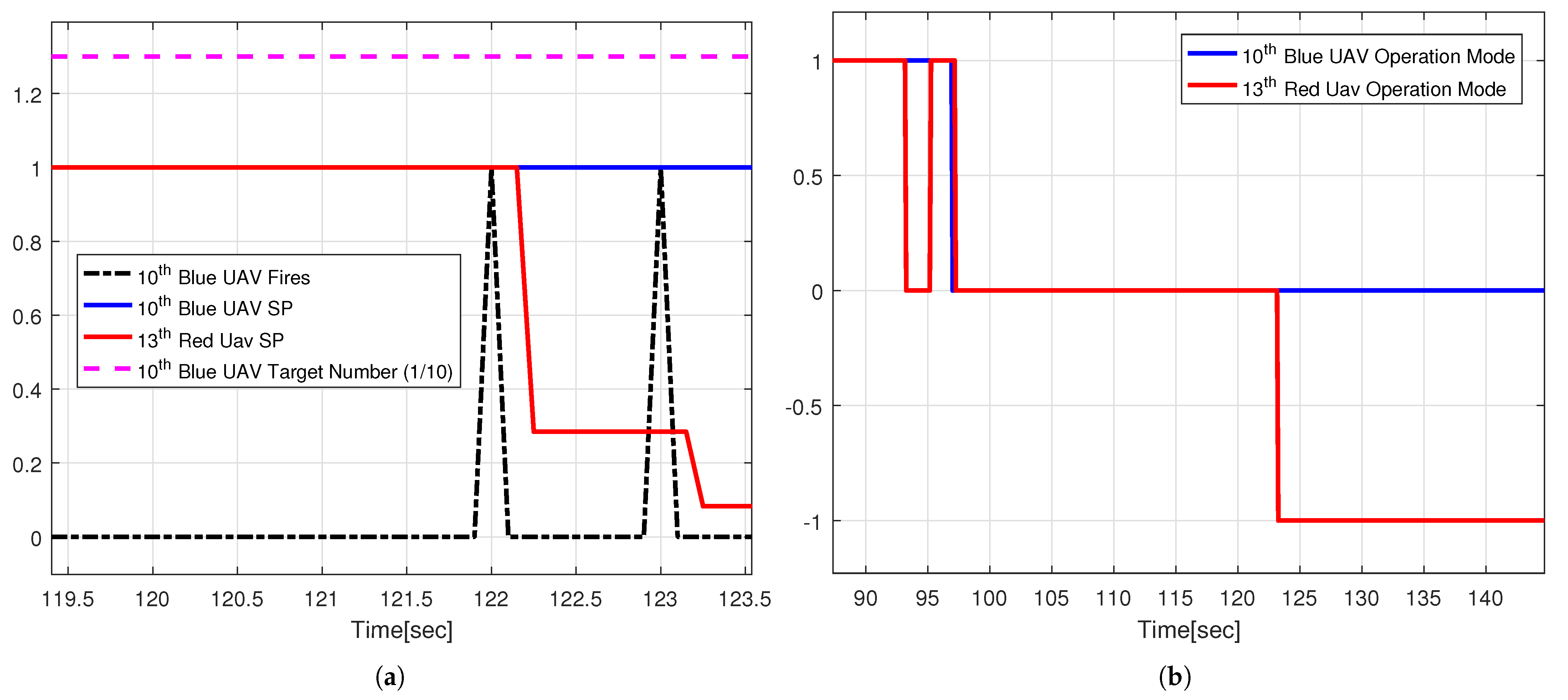
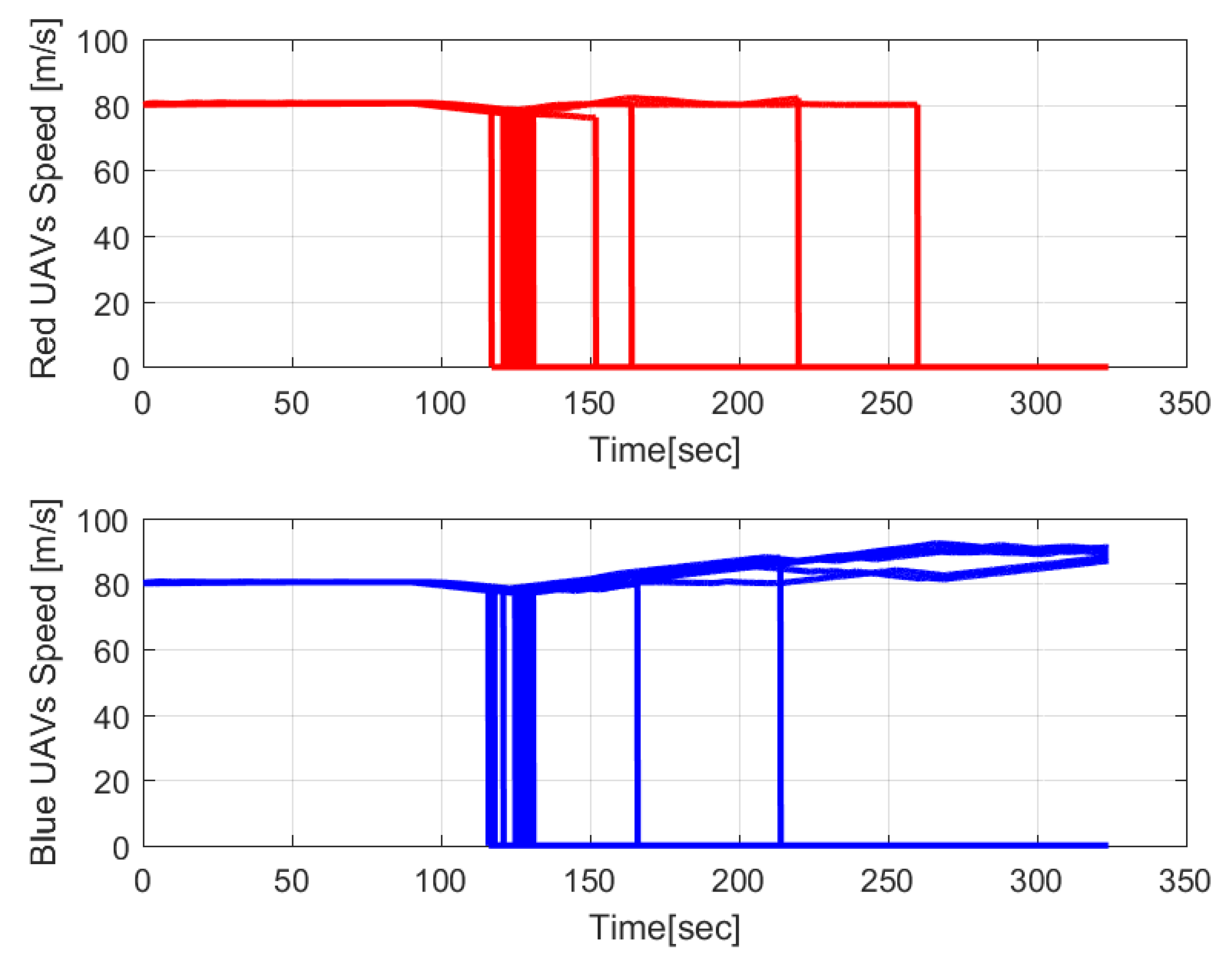
| Parameter Type | Parameter Name | Value |
|---|---|---|
| UAV Parameters | Minimum Speed | 60 m/s |
| Maximum Speed | 100 m/s | |
| Lateral Acceleration limit | 5 m/s | |
| Maximum Turn Angular Velocity | rad/s | |
| Detection Radius | 5000 m | |
| Attack Radius | 1000 m | |
| Attraction/Repulsion | ||
| Control Gains | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, S.; Zhen, Z.; Javaid, U.; Wen, L. Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers. Drones 2022, 6, 271. https://doi.org/10.3390/drones6100271
Shahid S, Zhen Z, Javaid U, Wen L. Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers. Drones. 2022; 6(10):271. https://doi.org/10.3390/drones6100271
Chicago/Turabian StyleShahid, Sami, Ziyang Zhen, Umair Javaid, and Liangdong Wen. 2022. "Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers" Drones 6, no. 10: 271. https://doi.org/10.3390/drones6100271
APA StyleShahid, S., Zhen, Z., Javaid, U., & Wen, L. (2022). Offense-Defense Distributed Decision Making for Swarm vs. Swarm Confrontation While Attacking the Aircraft Carriers. Drones, 6(10), 271. https://doi.org/10.3390/drones6100271







