Optimum Sizing of Photovoltaic-Battery Power Supply for Drone-Based Cellular Networks
Abstract
:1. Introduction
- Proposing an optimization framework to minimize the total investment and operational costs of a PV-battery-powered off-grid UAV-based cellular telecommunication network in a rural area;
- Extracting the power consumption profile for recharging stations in the UAV-based cellular telecommunication network based on the results of energy-efficient UAVs’ mission planning in [3];
- Developing a detailed model for PV power generation estimation that compromises PV panels’ installation (azimuth and tilt) angles, ambient temperature, and PV module characteristics;
- Considering the battery’s technical constraints in the problem formulation and the battery’s economic specifications in the system’s operational cost.
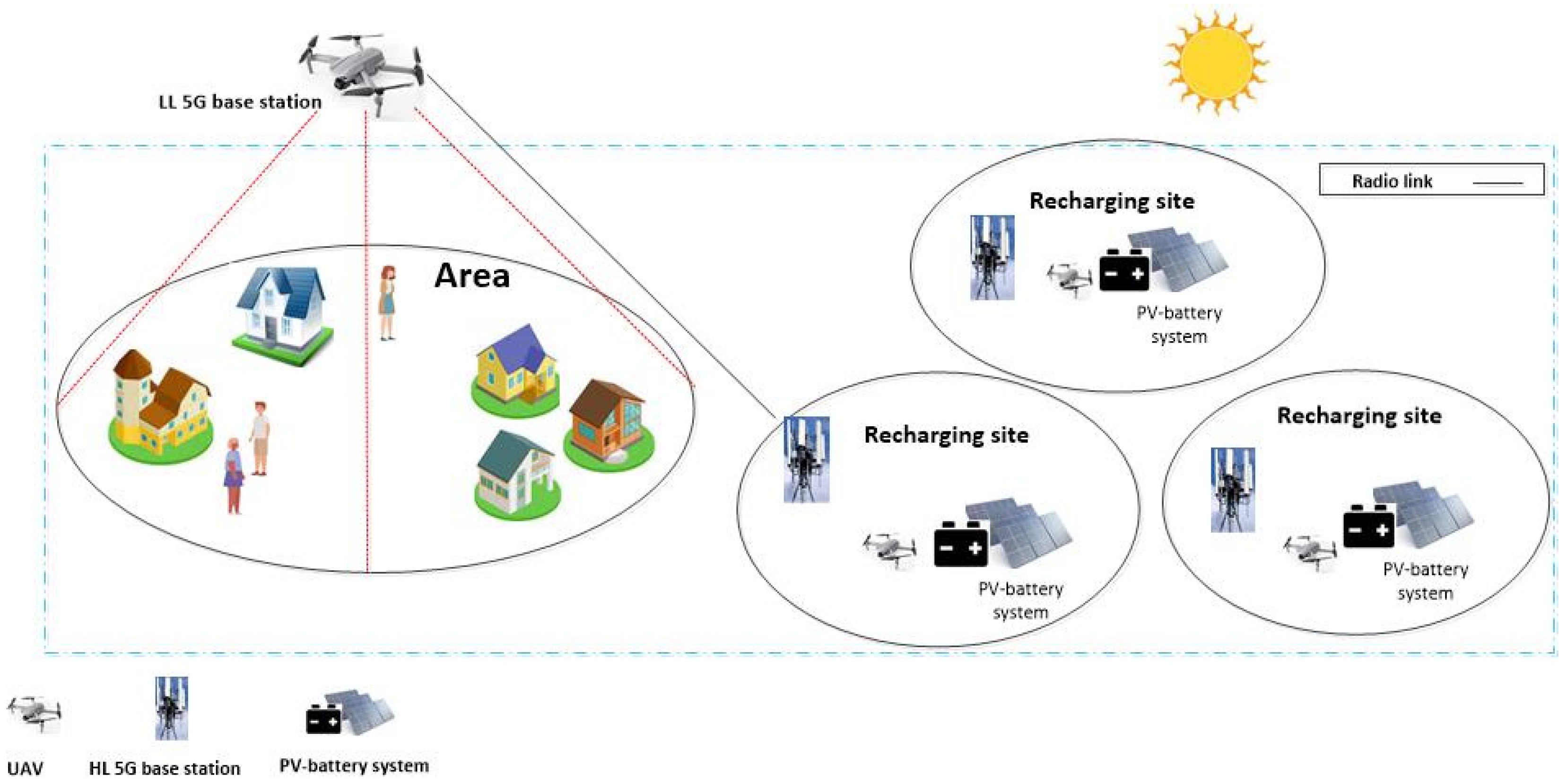
2. UAV-Aided Cellular Network
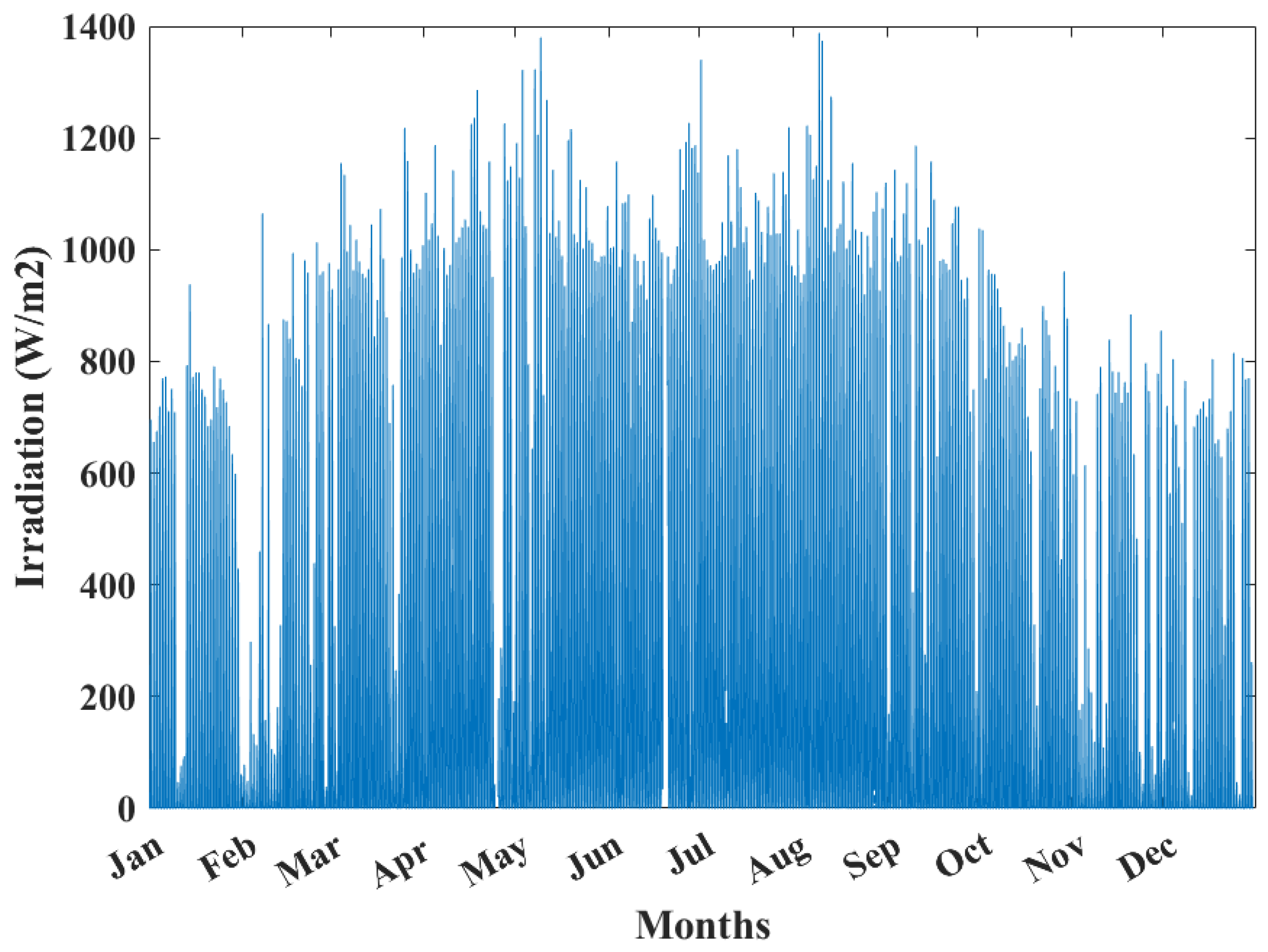
2.1. PV-Battery System Modelling
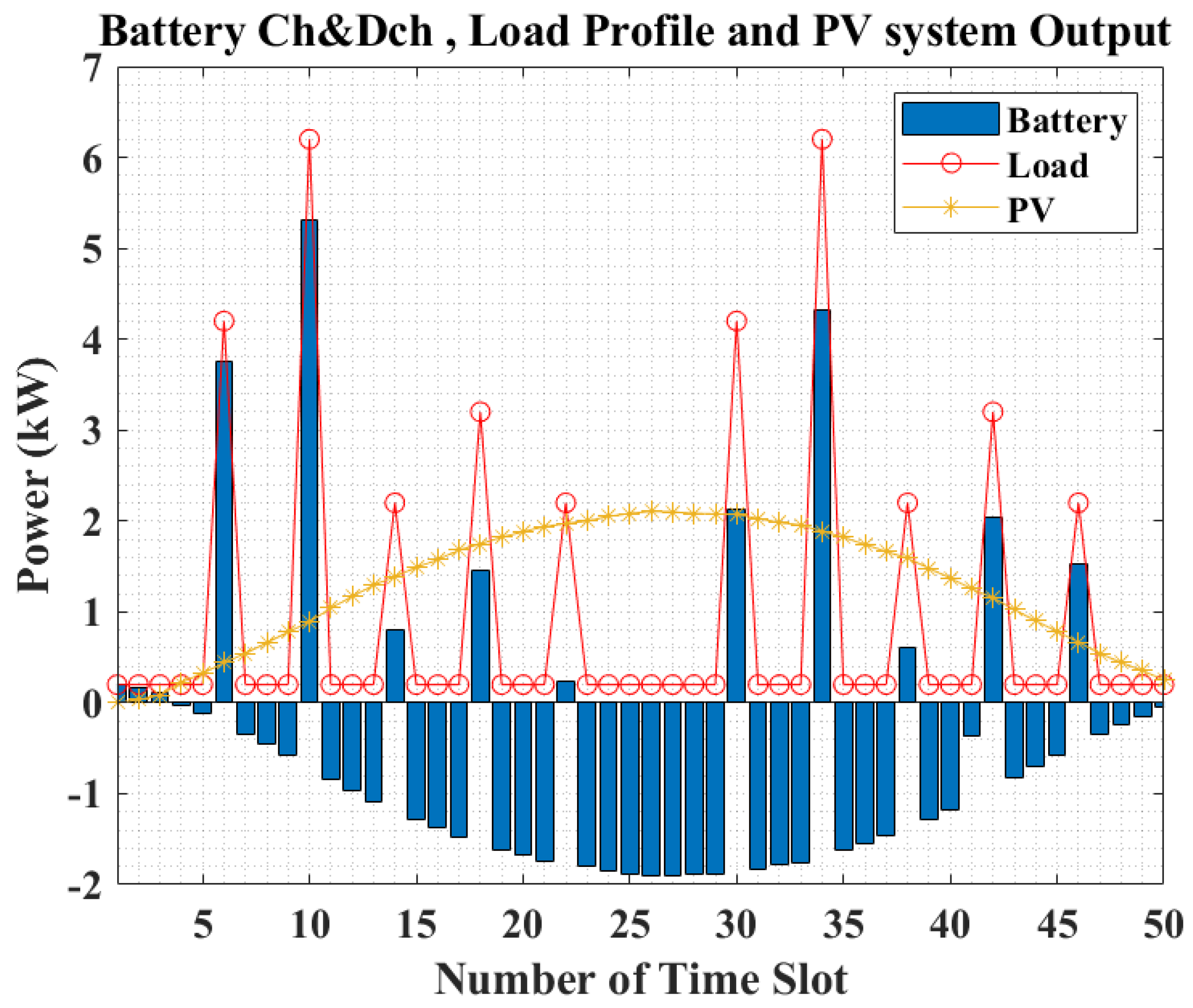
2.2. Energy Consumption Model
3. Problem Formulation
3.1. Objective Function
3.2. Technical Constraint
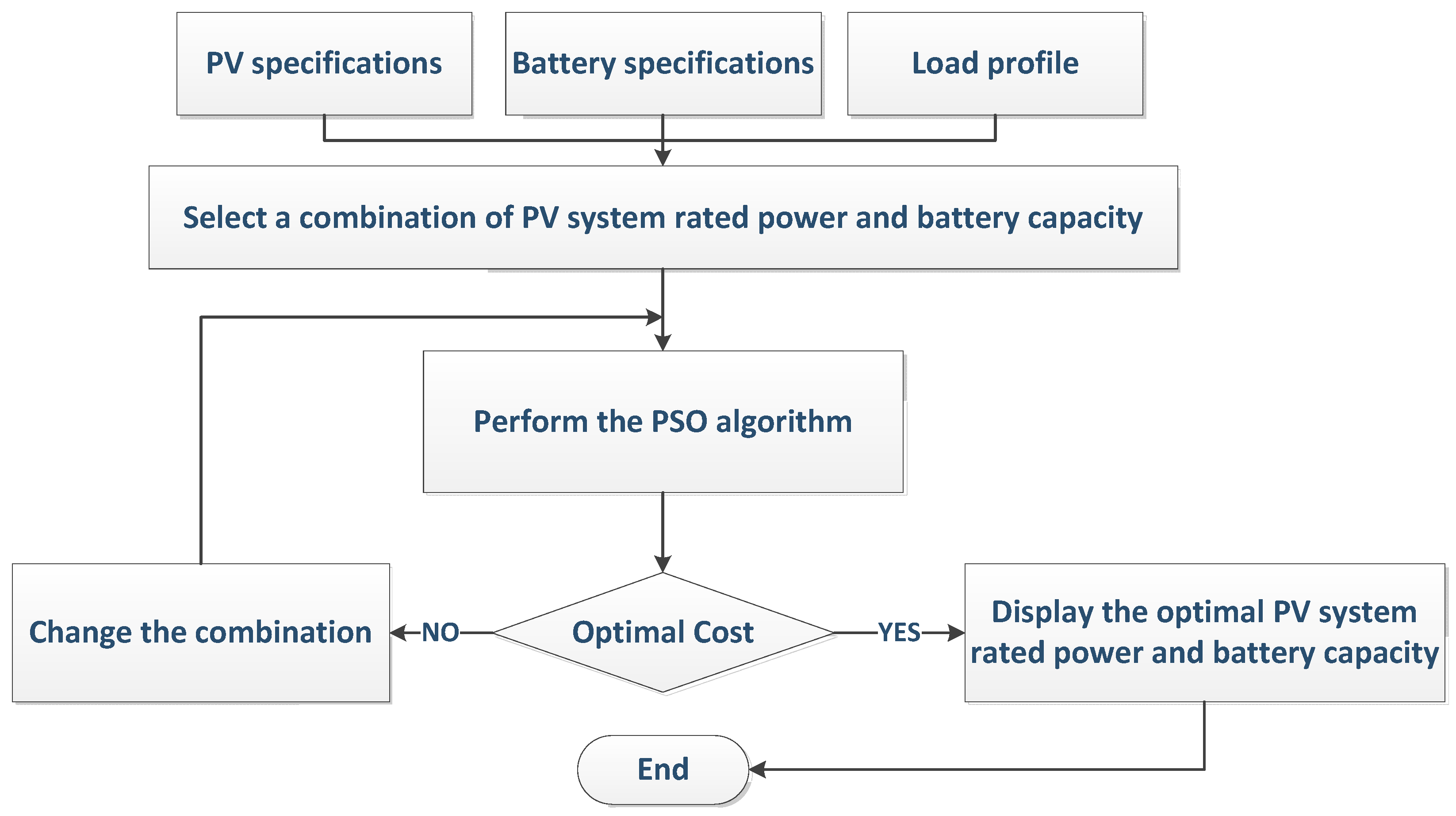
4. Optimization Algorithm
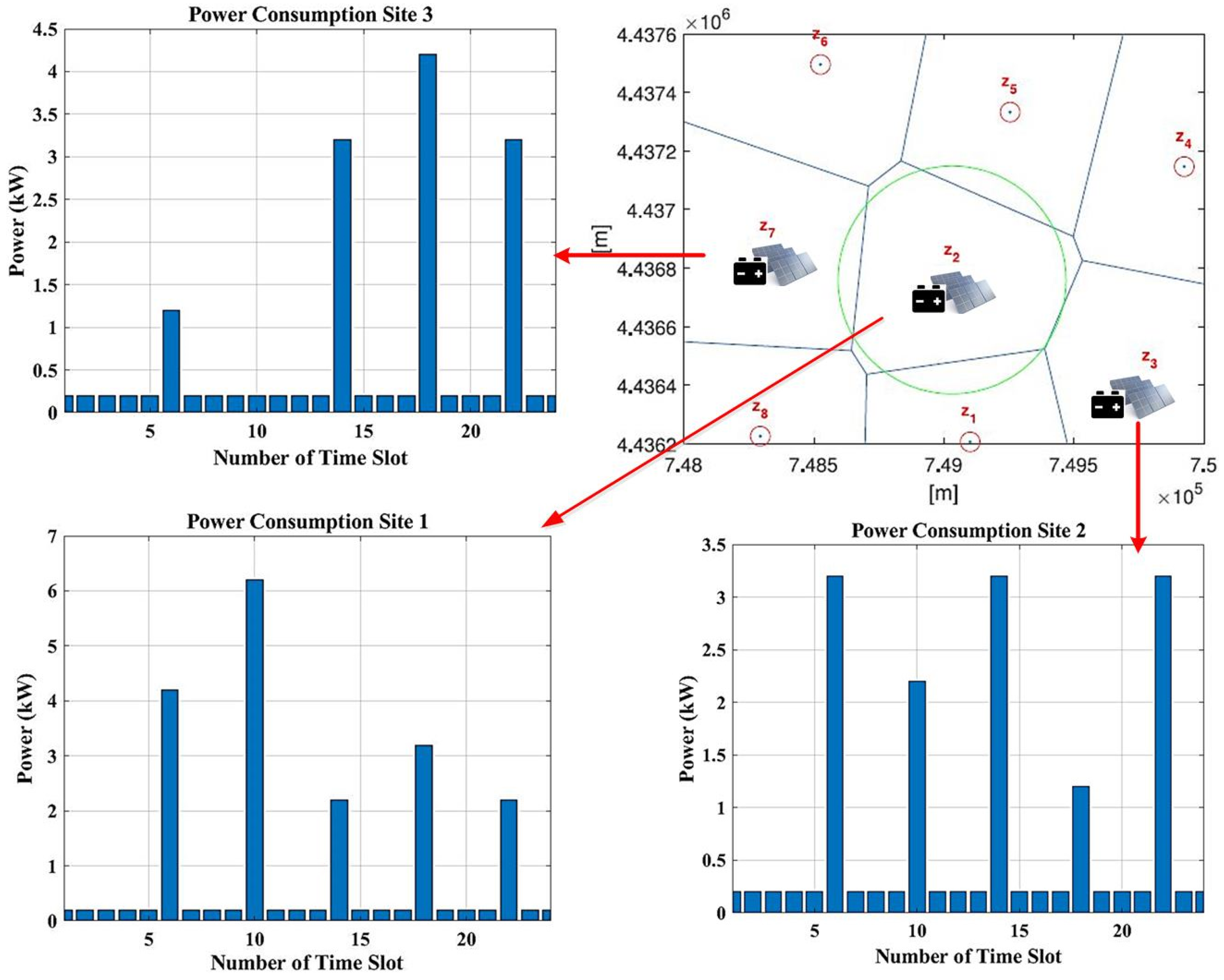
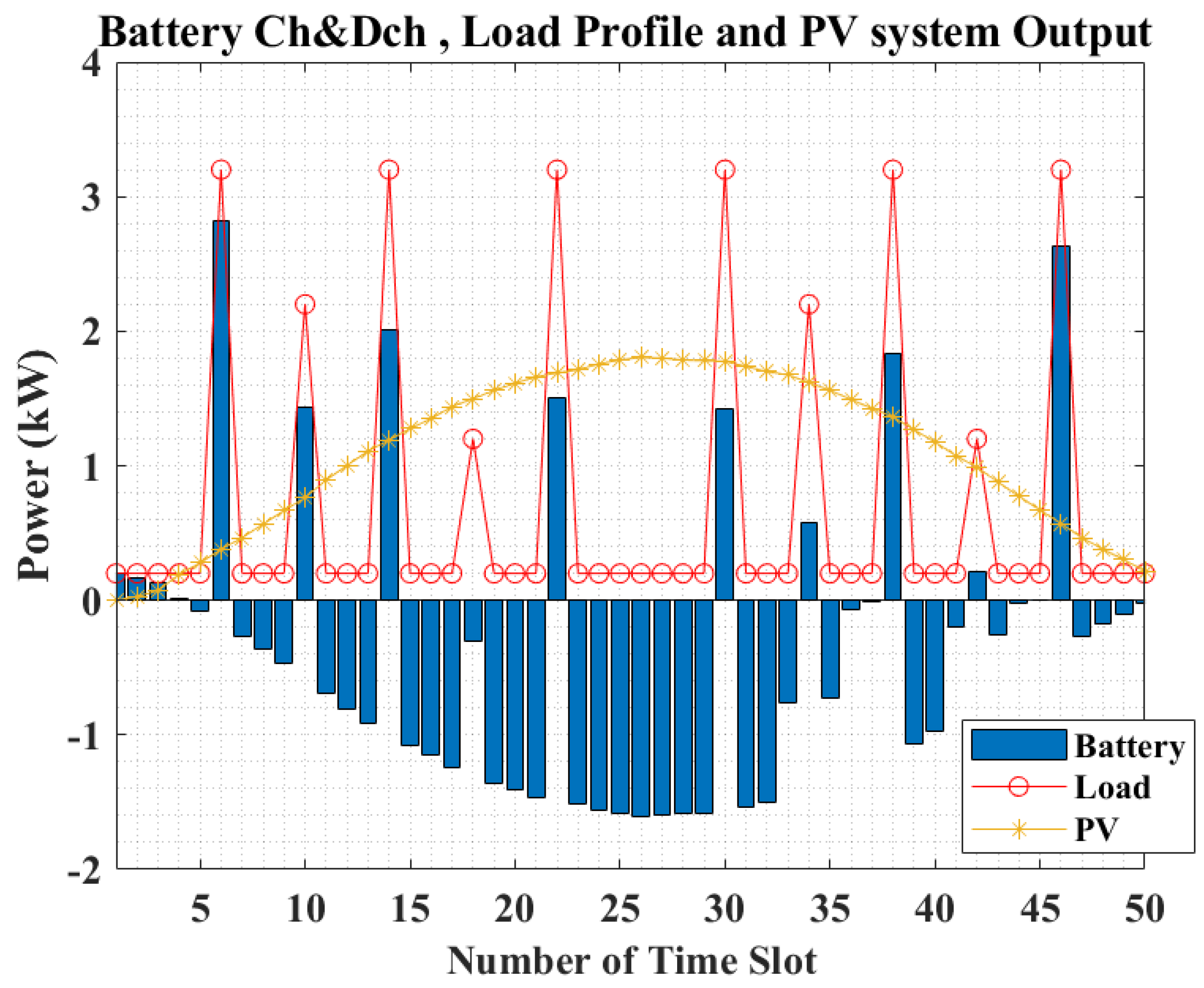
5. Simulation Results
6. Discussion and Future Research
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bahia, K.; Suardi, S. The State of Mobile Internet Connectivity 2019; Tech. Rep.; GSMA Connected Society: London, UK, 2019. [Google Scholar]
- Chiaraviglio, L.; Amorosi, L.; Blefari-Melazzi, N.; Dell’Olmo, P.; Mastro, A.L.; Natalino, C.; Monti, P. Minimum Cost Design of Cellular Networks in Rural Areas with UAVs, Optical Rings, Solar Panels, and Batteries. IEEE Trans. Green Commun. Netw. 2019, 3, 901–918. [Google Scholar] [CrossRef] [Green Version]
- Galán-Jiménez, J.; Moguel, E.; García-Alonso, J.; Berrocal, J. Energy-efficient and solar powered mission planning of UAV swarms to reduce the coverage gap in rural areas: The 3D case. Ad Hoc Netw. 2021, 118, 102517. [Google Scholar] [CrossRef]
- Valiulahi, I.; Javidsharifi, M.; Virgili, M.; Masouros, C. D3. 1–Energy Models and Optimisation Framework: Phase 1. Available online: http://painless-itn.com/wp-content/uploads/2020/10/D3.1_final.pdf (accessed on 12 November 2021).
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef] [Green Version]
- Israr, A.; Yang, Q.; Li, W.; Zomaya, A.Y. Renewable energy powered sustainable 5G network infrastructure: Opportunities, challenges and perspectives. J. Netw. Comput. Appl. 2020, 175, 102910. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Pourroshanfekr, H.; Kerekes, T.; Sera, D.; Spataru, S.; Guerrero, J.M. Optimum Sizing of Photovoltaic and Energy Storage Systems for Powering Green Base Stations in Cellular Networks. Energies 2021, 14, 1895. [Google Scholar] [CrossRef]
- Rokrok, E.; Javidsharifi, M.; Pourroshanfekr, H.; Javidsharifi, B. Adaptive Nonlinear Control Scheme for Three-Phase Grid-Connected PV Central Inverters. In Proceedings of the 29th International Power System Conference (PSC), Terhan, Iran, 27 October 2014; pp. 1–7. [Google Scholar]
- Meo, M.; Zhang, Y.; Gerboni, R.; Marsan, M.A. Dimensioning the power supply of a LTE macro BS connected to a PV panel and the power grid. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 178–184. [Google Scholar]
- Marsan, M.G.A.; Bucalo, G.; Di Caro, A.; Meo, M.; Zhang, Y. Towards Zero Grid Electricity Networking: Powering BSs with Renewable Energy Sources. In Proceedings of the 2013 IEEE International Conference on Communications Workshops (ICC), Budapest, Hungary, 9–13 June 2013; pp. 596–601. [Google Scholar]
- Ahmed, F.; Naeem, M.; Ejaz, W.; Iqbal, M.; Anpalagan, A.; Kim, H.S. Renewable energy assisted traffic aware cellular base station energy cooperation. Energies 2018, 11, 99. [Google Scholar] [CrossRef] [Green Version]
- Alsharif, M.H.; Kim, J.; Kim, J.H. Green and sustainable cellular base stations: An overview and future research directions. Energies 2017, 10, 587. [Google Scholar] [CrossRef]
- Kusakana, K.; Vermaak, H.J. Hybrid renewable power systems for mobile telephony base stations in developing countries. Renew. Energy 2013, 51, 419–425. [Google Scholar] [CrossRef]
- Aris, A.M.; Shabani, B. Sustainable power supply solutions for off-grid base stations. Energies 2015, 8, 10904–10941. [Google Scholar] [CrossRef] [Green Version]
- Khare, V.; Nema, S.; Baredar, P. Status of solar wind renewable energy in India. Renew. Sustain. Energy Rev. 2013, 27, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Krishnamurthy, V.; Kwasinski, A.; Sharma, R. Development of a Markov-chain-based energy storage model for power supply availability assessment of photovoltaic generation plants. IEEE Trans. Sustain. Energy 2012, 4, 491–500. [Google Scholar] [CrossRef]
- Leonardi, G.; Meo, M.; Marsan, M.A. Markovian Models of Solar Power Supply for a LTE Macro BS. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–7. [Google Scholar]
- Chamola, V.; Sikdar, B. Outage Estimation for Solar Powered Cellular Base Stations. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 172–177. [Google Scholar]
- Ibrahim, I.A.; Sabah, S.; Abbas, R.; Hossain, M.J.; Fahed, H. A novel sizing method of a standalone photovoltaic system for powering a mobile network base station using a multi-objective wind driven optimization algorithm. Energy Convers. Manag. 2021, 238, 114179. [Google Scholar] [CrossRef]
- Virgili, M.; Forysth, A.J.; James, P. A Multi-Objective Genetic Algorithm Methodology for the Design of Standalone Energy Systems. In Proceedings of the 2021 IEEE Design Methodologies Conference (DMC), Bath, UK, 14–15 July 2021; pp. 1–6. [Google Scholar]
- Thakur, R.; Mishra, S.; Murthy, C.S.R. An energy and cost aware framework for cell selection and energy cooperation in rural and remote femtocell networks. IEEE Trans. Green Commun. Netw. 2017, 1, 423–433. [Google Scholar] [CrossRef]
- Du, P.; Ran, L.; Zhai, D.; Ren, R.; Zeng, Q. Admm-based distributed online algorithm for energy management in hybrid energy powered cellular networks. IEEE Access 2019, 7, 83343–83353. [Google Scholar] [CrossRef]
- Fletscher, L.; Suarez, L.; Grace, D.; Peroni, C.; Maestre, J. Energy-aware resource management in heterogeneous cellular networks with hybrid energy sources. IEEE Trans. Netw. Serv. Manag. 2019, 16, 279–293. [Google Scholar] [CrossRef]
- Leithon, J.; Lim, T.J.; Sun, S. Cost-aware renewable energy management with application in cellular networks. IEEE Trans. Green Commun. Netw. 2018, 2, 316–326. [Google Scholar] [CrossRef]
- Mendil, M.; De Domenico, A.; Heiries, V.; Caire, R.; Hadjsaid, N. Battery-aware optimization of green small cells: Sizing and energy management. IEEE Trans. Green Commun. Netw. 2018, 2, 635–651. [Google Scholar] [CrossRef]
- Han, T.; Ansari, N. Provisioning green energy for base stations in heterogeneous networks. IEEE Trans. Veh. Technol. 2016, 65, 5439–5448. [Google Scholar] [CrossRef] [Green Version]
- Chamola, V.; Sikdar, B. Power outage estimation and resource dimensioning for solar powered cellular base stations. IEEE Trans. Commun. 2016, 64, 5278–5289. [Google Scholar] [CrossRef]
- Ghiassi-Farrokhfal, Y.; Keshav, S.; Rosenberg, C.; Ciucu, F. Solar power shaping: An analytical approach. IEEE Trans. Sustain. Energy 2015, 6, 162–170. [Google Scholar] [CrossRef]
- Renga, D.; Meo, M. Dimensioning renewable energy systems to power mobile networks. IEEE Trans. Green Commun. Netw. 2019, 3, 366–380. [Google Scholar] [CrossRef]
- Jing, X.; Sun, J.; Masouros, C. Energy Aware Trajectory Optimization for Aerial Base Stations. IEEE Trans. Commun. 2021, 69, 3352–3366. [Google Scholar] [CrossRef]
- Babu, N.; Papadias, C.B.; Popovski, P. Energy-Efficient 3D Deployment of Aerial Access Points in a UAV Communication System. IEEE Commun. Lett. 2020, 24, 2883–2887. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Amorosi, L.; Blefari-Melazzi, N.; Dell’Olmo, P.; Natalino, C.; Monti, P. Optimal design of 5G networks in rural zones with UAVs, optical rings, solar panels and batteries. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; pp. 1–4. [Google Scholar]
- Amorosi, L.; Chiaraviglio, L.; D’Andreagiovanni, F.; Blefari-Melazzi, N. Energy-efficient mission planning of UAVs for 5G coverage in rural zones. In Proceedings of the 2018 IEEE International Conference on Environmental Engineering (EE), Milan, Italy, 12–14 March 2018; pp. 1–9. [Google Scholar]
- Amorosi, L.; Chiaraviglio, L.; Galan-Jimenez, J. Optimal energy management of UAV-based cellular networks powered by solar panels and batteries: Formulation and solutions. IEEE Access 2019, 7, 53698–53717. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; D’andreagiovanni, F.; Choo, R.; Cuomo, F.; Colonnese, S. Joint optimization of area throughput and grid-connected microgeneration in uav-based mobile networks. IEEE Access 2019, 7, 69545–69558. [Google Scholar] [CrossRef]
- Available online: http://www.solartech.polimi.it/activities/forecasting/dataset/ (accessed on 23 August 2021).
- Javidsharifi, M.; Niknam, T.; Aghaei, J.; Mokryani, G.; Papadopoulos, P. Multi-objective day-ahead scheduling of microgrids using modified grey wolf optimizer algorithm. J. Intell. Fuzzy Syst. 2019, 36, 2857–2870. [Google Scholar] [CrossRef] [Green Version]
- Javidsharifi, M.; Niknam, T.; Aghaei, J.; Mokryani, G. Multi-objective short-term scheduling of a renewable-based microgrid in the presence of tidal resources and storage devices. Appl. Energy 2018, 216, 367–381. [Google Scholar] [CrossRef] [Green Version]
- Narimani, M.R.; Vahed, A.A.; Azizipanah-Abarghooee, R.; Javidsharifi, M. Enhanced gravitational search algorithm for multi-objective distribution feeder reconfiguration considering reliability, loss and operational cost. IET Gener. Transm. Distrib. 2014, 8, 55–69. [Google Scholar] [CrossRef]
- Javidsharifi, M.; Niknam, T.; Aghaei, J.; Shafie-khah, M.; Catalão, J.P. Probabilistic Model for Microgrids Optimal Energy Management Considering AC Network Constraints. IEEE Syst. J. 2019, 14, 2703–2712. [Google Scholar] [CrossRef] [Green Version]
- Mahboubi-Moghaddam, E.; Narimani, M.R.; Khooban, M.H.; Azizivahed, A.; Sharifi, M. Multi-objective distribution feeder reconfiguration to improve transient stability, and minimize power loss and operation cost using an enhanced evolutionary algorithm at the presence of distributed generations. Int. J. Electr. Power Energy Syst. 2016, 76, 35–43. [Google Scholar] [CrossRef]
- Pourroshanfekr, H.; Javidsharifi, M.; Javidsharifi, B. Solving Non-convex Economic Dispatch with Valve Point Loading Effect using Imperialist Competitive Algorithm. Int. J. Manag. Perspect. 2015, 4, 41–45. [Google Scholar]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Ahmadi, S.; Arabani, H.P.; Haghighi, D.A.; Guerrero, J.M.; Ashgevari, Y.; Akbarimajd, A. Optimal use of vehicle-to-grid technology to modify the load profile of the distribution system. J. Energy Storage 2020, 31, 101627. [Google Scholar] [CrossRef]
- Al-Kazemi, B.; Habib, S. Complexity analysis of problem-dimension using PSO. In Proceedings of the WSEAS International Conference on Evolutionary Computing, Cavat, Croatia, 12–14 June 2006; pp. 45–52. [Google Scholar]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Nasrollahzadeh, S.; Maadani, M.; Pourmina, M.A. Optimal motion sensor placement in smart homes and intelligent environments using a hybrid WOA-PSO algorithm. J. Reliab. Intell. Environ. 2021. [Google Scholar] [CrossRef]
- Yiyang, L.; Xi, J.; Hongfei, B.; Zhining, W.; Liangliang, S. A General Robot Inverse Kinematics Solution Method Based on Improved PSO Algorithm. IEEE Access 2021, 9, 32341–32350. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hazim, H.; Ahmadipour, M. Sizing and implementing off-grid stand-alone photovoltaic/battery systems based on multi-objective optimization and techno-economic (MADE) analysis. Energy 2020, 207, 118163. [Google Scholar] [CrossRef]

| Variable | Symbol | Unit | Variable Range |
|---|---|---|---|
| Peak PV power | kWp | (0–10) | |
| Azimuth angle | degree | (−90–90) | |
| Tilt angle | degree | (0–90) | |
| Battery capacity | kWh | (0–35) | |
| Battery state of charge | SOC | % | (10–90) |
| Recharging Site | Installed PV (kWp) | Battery Capacity (kWh) | Total Cost (USD) | |
|---|---|---|---|---|
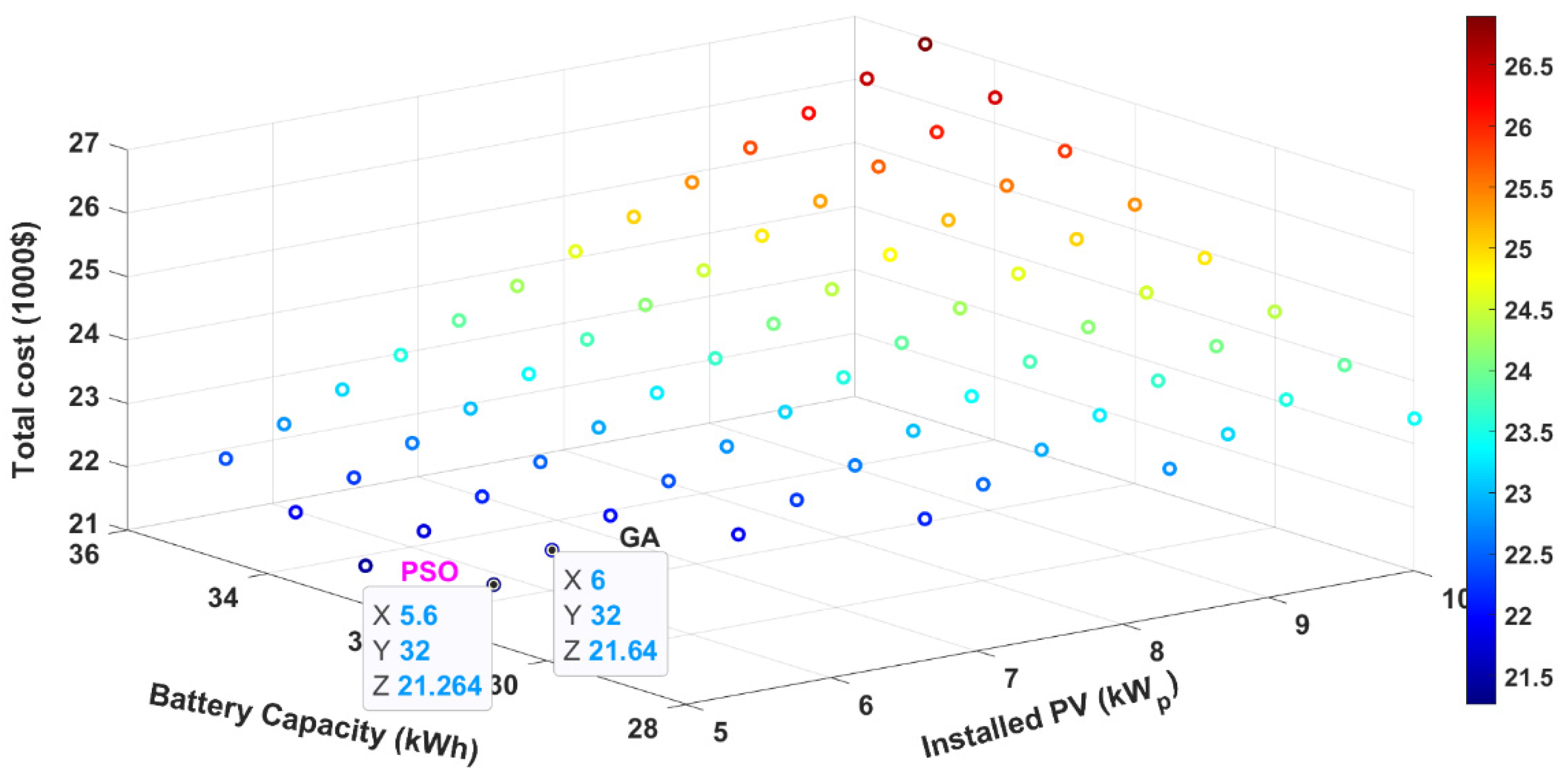
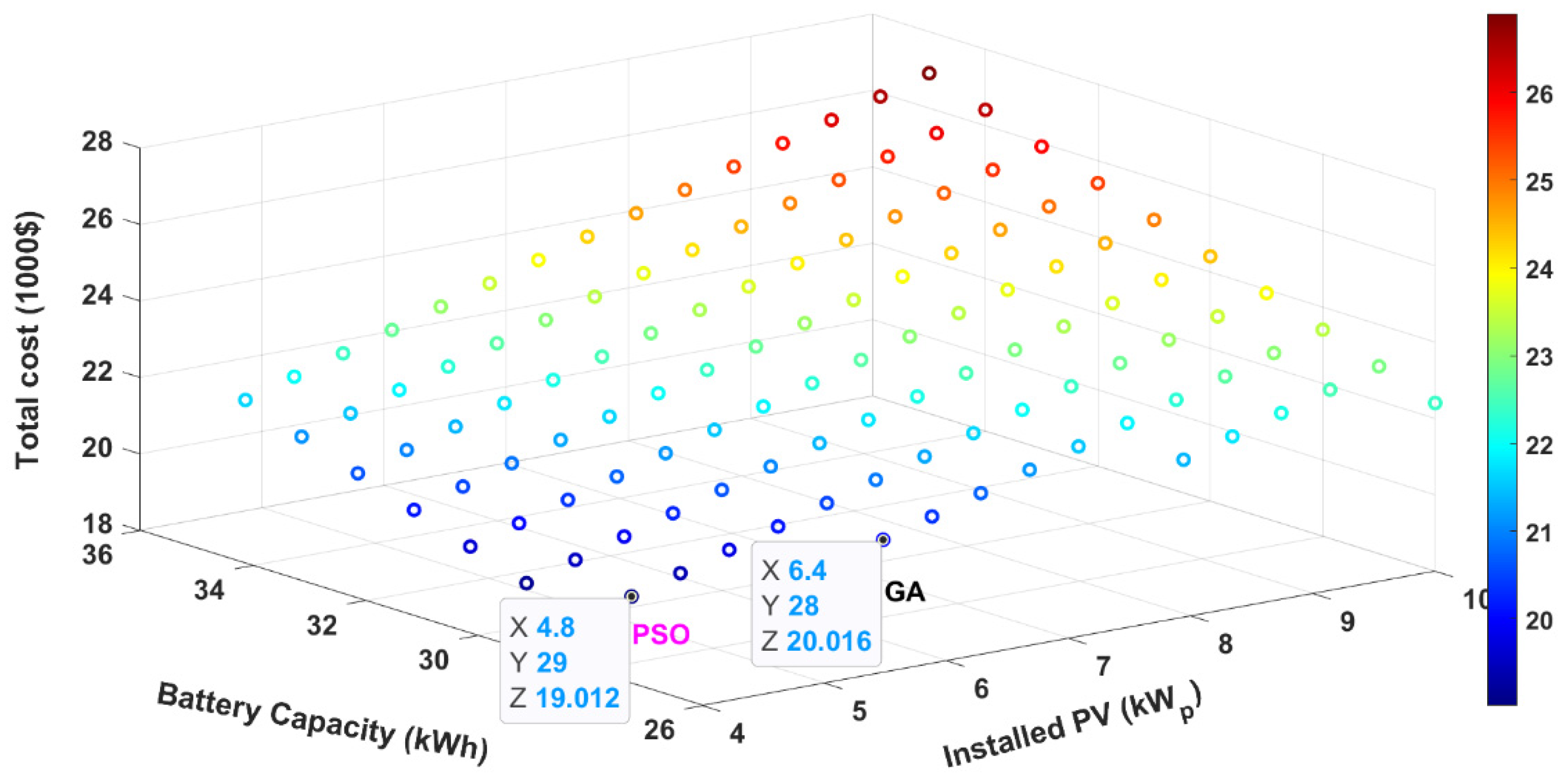
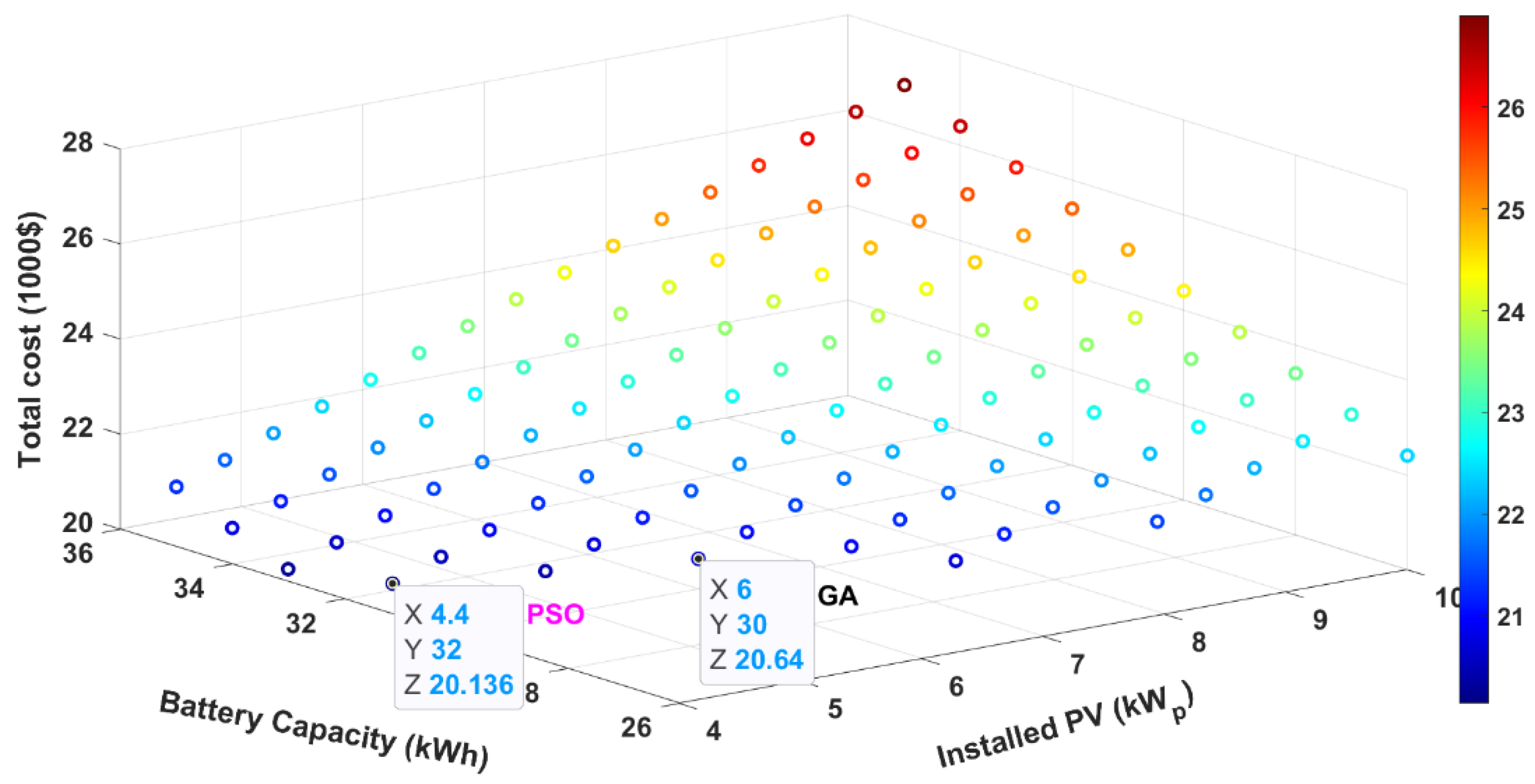
| PSO | Site 1 | 5.6 | 32 | 21,264 |
| Site 2 | 4.8 | 29 | 19,012 | |
| Site 3 | 4.4 | 32 | 20,136 | |
| GA | Site 1 | 6 | 32 | 21,640 |
| Site 2 | 6.4 | 28 | 20,016 | |
| Site 3 | 6 | 30 | 20,640 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javidsharifi, M.; Pourroshanfekr Arabani, H.; Kerekes, T.; Sera, D.; Spataru, S.V.; Guerrero, J.M. Optimum Sizing of Photovoltaic-Battery Power Supply for Drone-Based Cellular Networks. Drones 2021, 5, 138. https://doi.org/10.3390/drones5040138
Javidsharifi M, Pourroshanfekr Arabani H, Kerekes T, Sera D, Spataru SV, Guerrero JM. Optimum Sizing of Photovoltaic-Battery Power Supply for Drone-Based Cellular Networks. Drones. 2021; 5(4):138. https://doi.org/10.3390/drones5040138
Chicago/Turabian StyleJavidsharifi, Mahshid, Hamoun Pourroshanfekr Arabani, Tamas Kerekes, Dezso Sera, Sergiu Viorel Spataru, and Josep M. Guerrero. 2021. "Optimum Sizing of Photovoltaic-Battery Power Supply for Drone-Based Cellular Networks" Drones 5, no. 4: 138. https://doi.org/10.3390/drones5040138
APA StyleJavidsharifi, M., Pourroshanfekr Arabani, H., Kerekes, T., Sera, D., Spataru, S. V., & Guerrero, J. M. (2021). Optimum Sizing of Photovoltaic-Battery Power Supply for Drone-Based Cellular Networks. Drones, 5(4), 138. https://doi.org/10.3390/drones5040138











