UAV Patrolling for Wildfire Monitoring by a Dynamic Voronoi Tessellation on Satellite Data
Abstract
:1. Introduction
2. Related Works and Main Contributions
- the design of an integrated system for drone surveillance/patrolling against wildfires, employing a dynamical system that is built starting from satellite-sensed data;
- the formulation of an adaptive Voronoi tessellation-based solution for the identification of the optimal waypoints for the drone patrolling, determined on a fire propagation risk index;
- the validation of the proposed scheme on a case study in Italy on a simulated environment; and
- the presentation of the open-sourced simulator used for the validation of the proposed system [26].
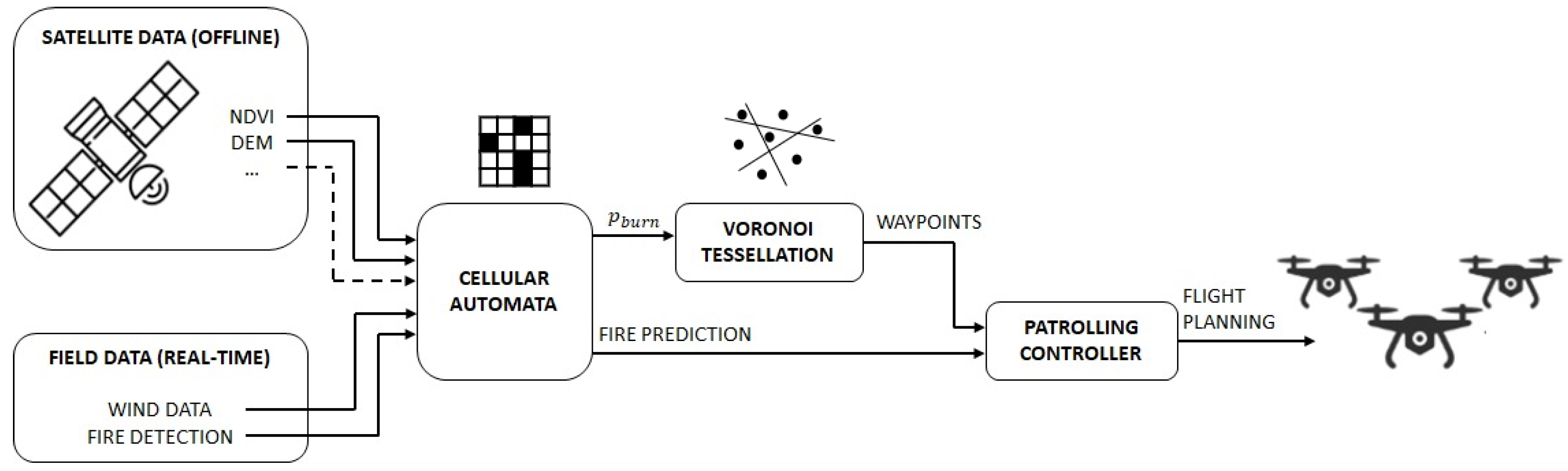
3. System Architecture
4. Fire Propagation Modeling
4.1. Satellite Data
4.2. Fire Dynamics
4.2.1. Cell State
- 1: not burnable cell,
- 2: burnable cell,
- 3: burning cell, and
- 4: burned cell.
- an index that captures how likely the area is to catch fire due to the type of vegetation present in the cell, denoted by ;
- an index that captures the impact of the vegetation density on the burn likelihood, denoted by ; and
- the (average) cell altitude from the DEM, which we obtained from reference [37].
4.2.2. Cell Neighborhood
4.2.3. Local Transition Function
5. Voronoi Tessellation Based Dynamic Drone Patrolling
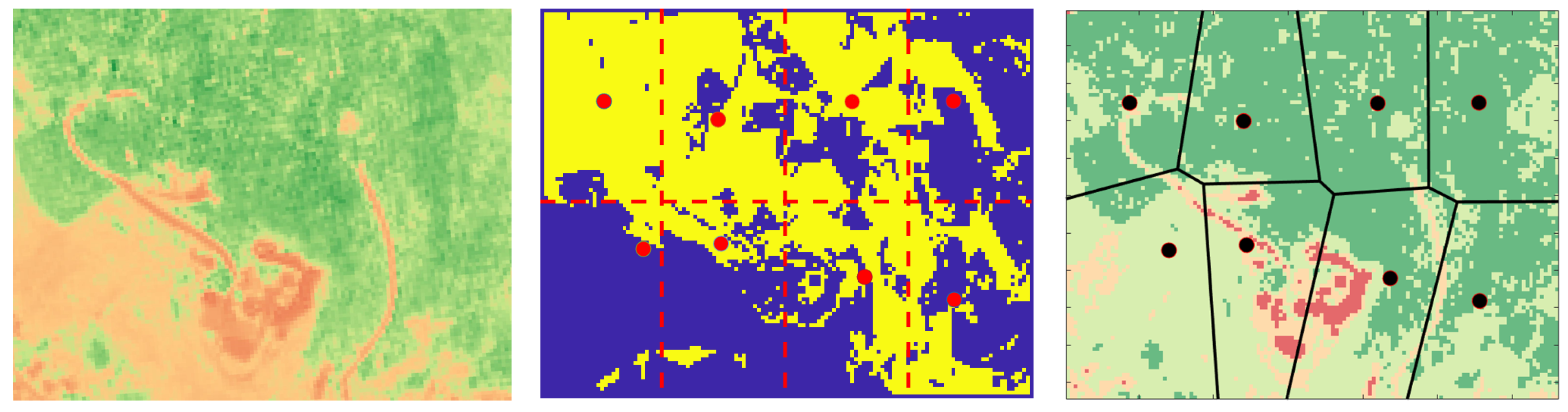
5.1. Background on Voronoi Tessellation
- compute the distance with respect to all centroids , ;
- assign each point s to the centroid from which it has the shortest distance, ; and
- the points which are equidistant from two or more centroids are the edge points of the regions; for practical purposes, these points can be assigned arbitrarily to any of such centroids.
5.2. Voronoi Tessellation for Forest Fires Monitoring
- the maximum distance between two centroids must be limited (e.g., by the range of observation of the drones), so that no area remain uncovered during the waypoint-based patrolling, independently from the path taken by the drone fleet when moving from one waypoint to the following one; and
- the centroids shall be positioned so that they offer a good coverage of the most critical areas (e.g., their position shall be closer to areas associated with an higher fire risk probability) in order to assure faster early fire detection and better monitoring of the vegetation.
| Algorithm 1 Voronoi tessellation of the monitored area to identify drone patrolling waypoints. |
| 1: Divide the monitored area into M macro-cells 2: for all macro-cells m do 3: for all cell i ∈ m do 4: Evaluate based on the given threshold 5: end for 6: Compute the center of mass cm of the macro-cell m with respect to and add it to the centroid set C 7: Associate to the macro-cell m its average burn probability 8: end for 9: Determine the Voronoi tessellation of the given area determined by the centroids in C and the selected distance metric (e.g., weighted Euclidean distance) |
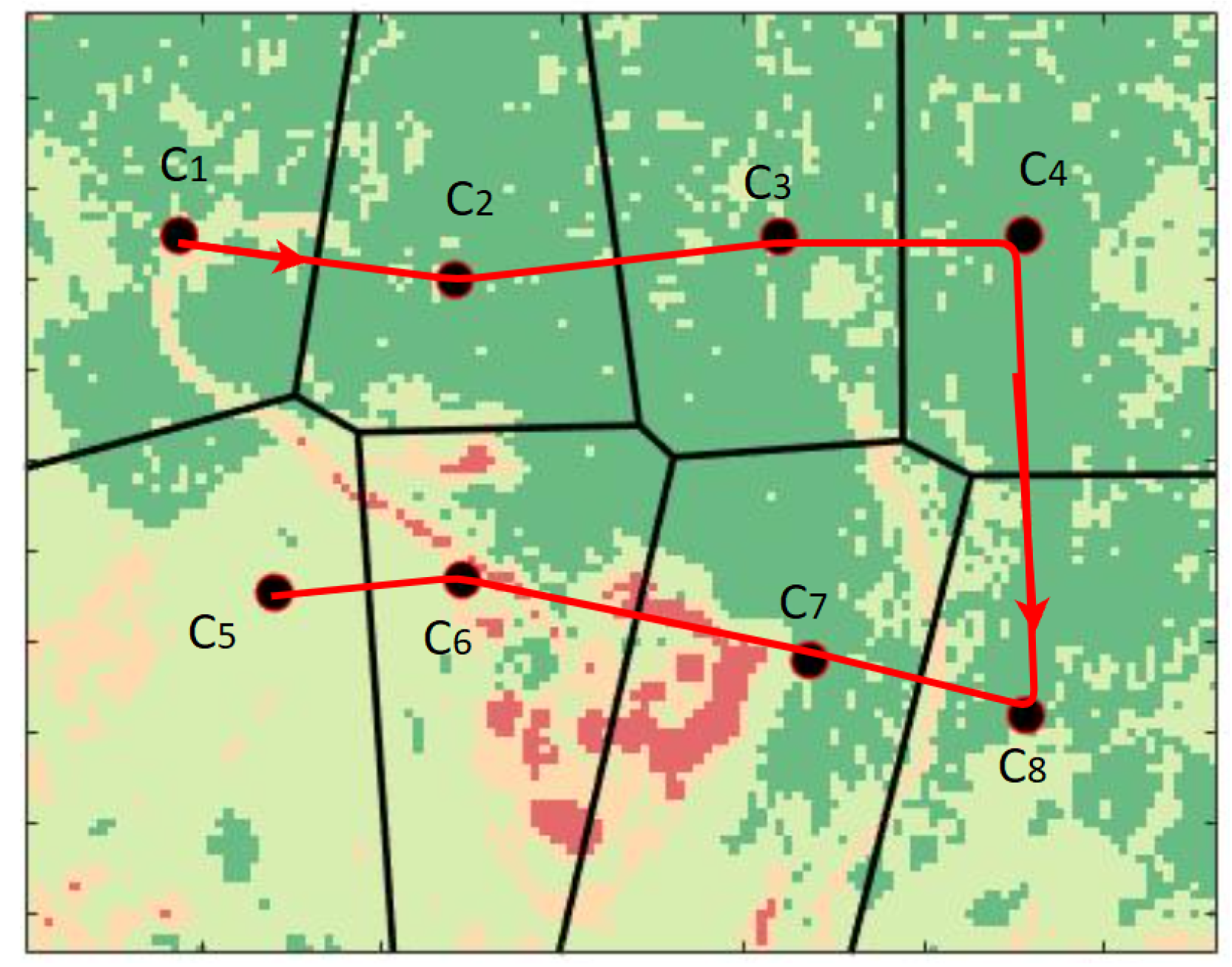
5.3. Dynamic Drone Patrolling
- periodically update the values of all the various cells, in order to adapt the Voronoi tessellation depending on factors, such as the wind or new NDVI measurements (coming either from satellite or UAV sources);
- collect data from the drones and the ground sensors to monitor instant-by-instant the fire events inside the Voronoi regions and provide the overall system with adequate situational awareness; and
- to guide the UAV fleet towards strategical monitoring points (i.e., the Voronoi centroids), depending on the ongoing situation.
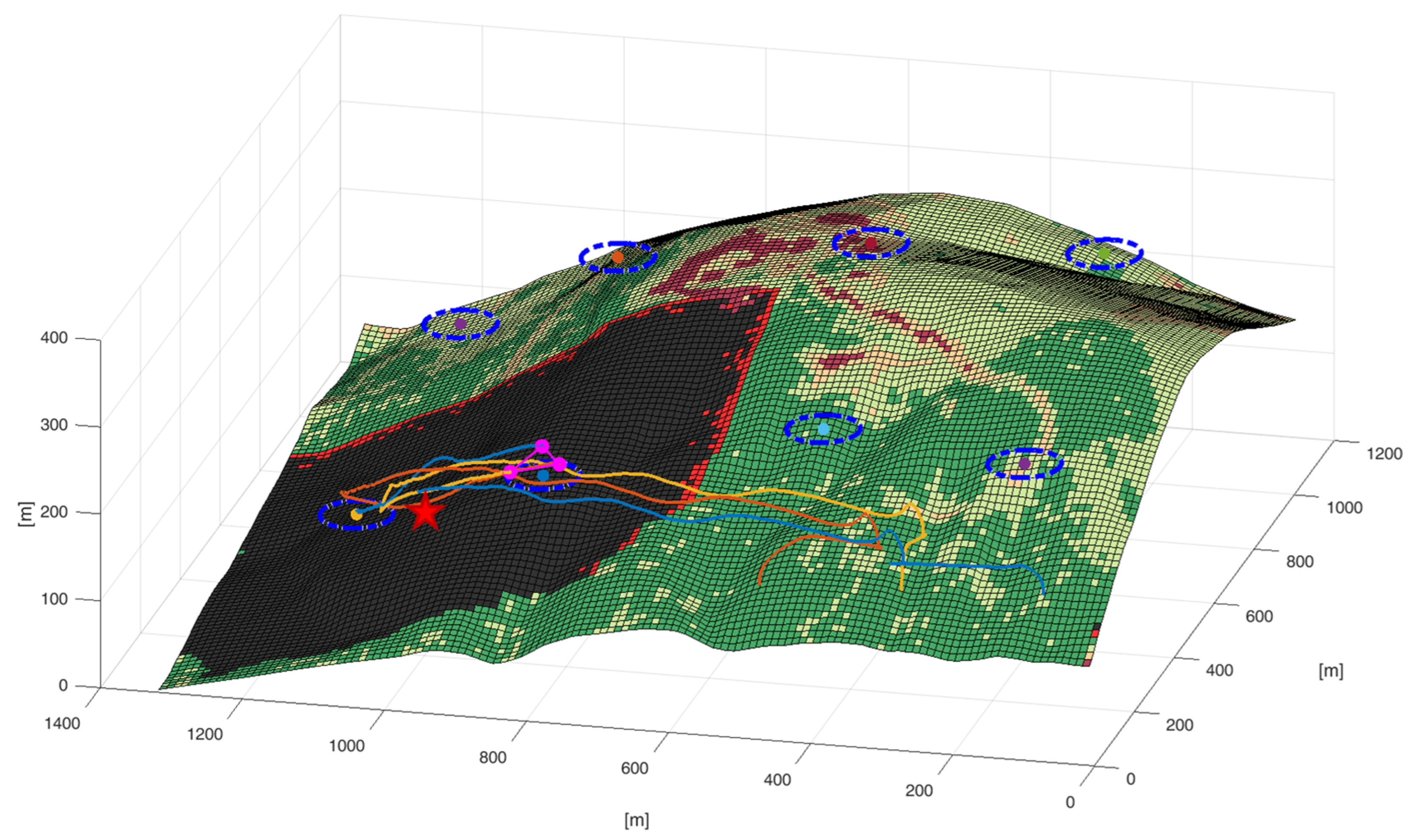
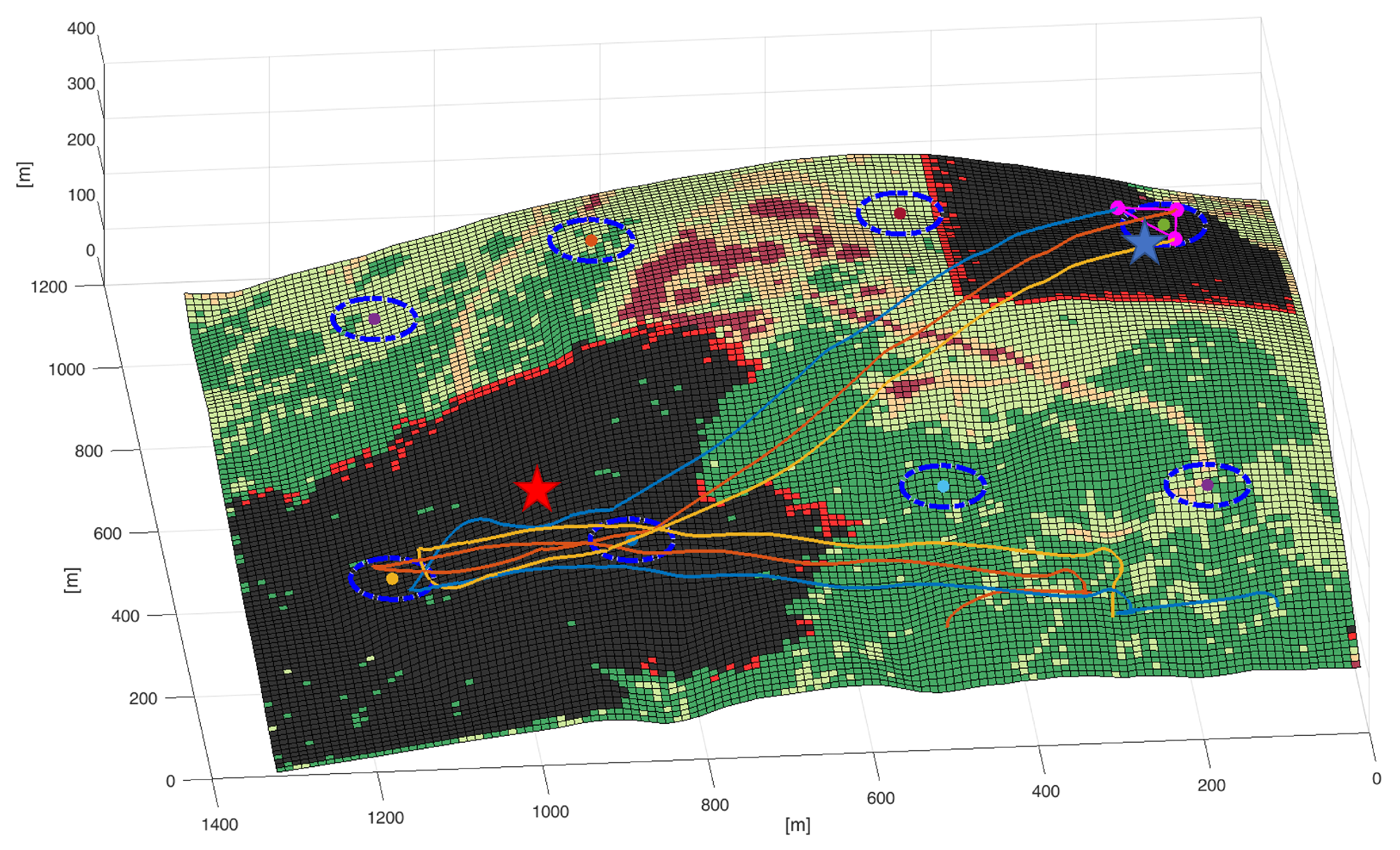
6. Case Study and Simulations
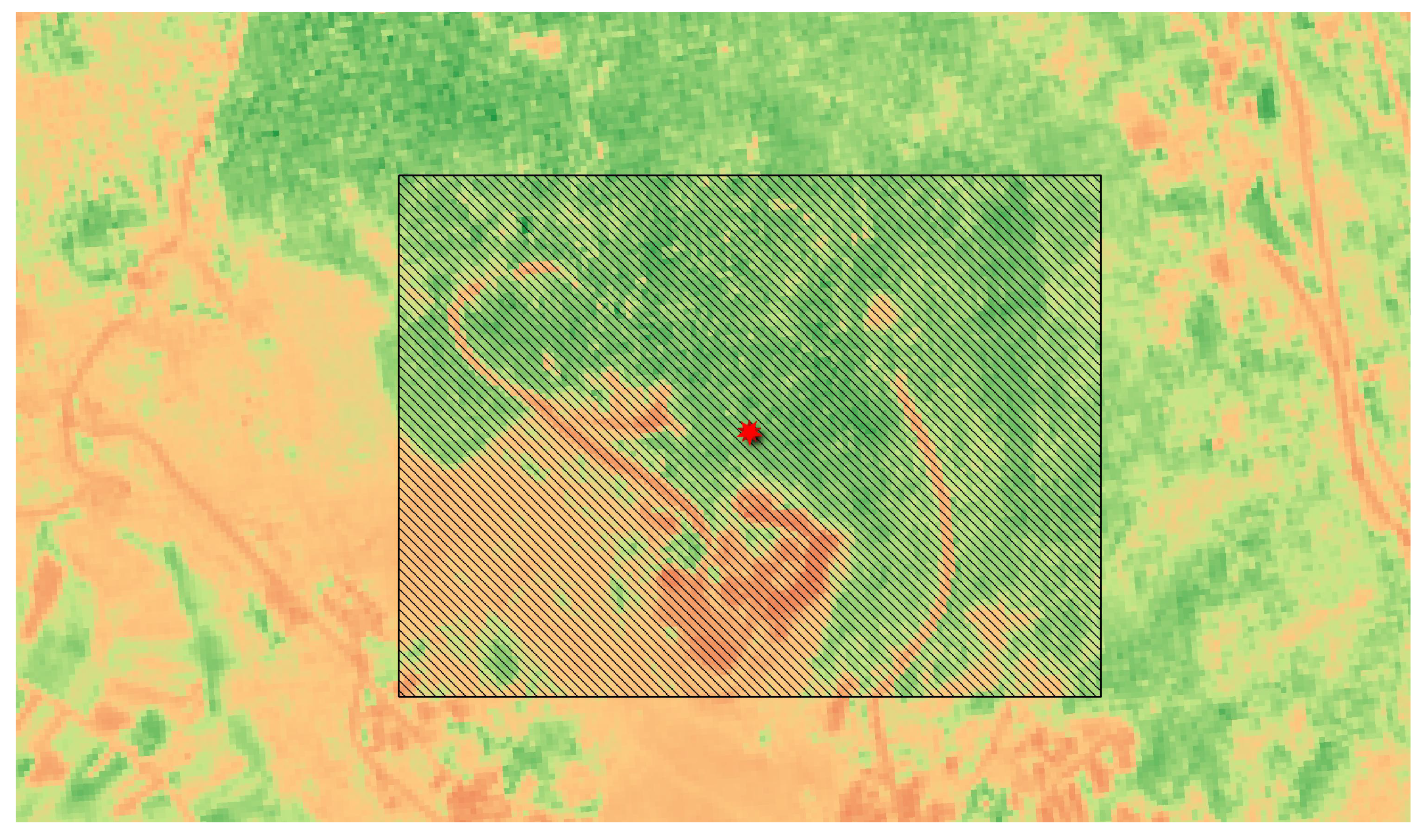
6.1. Case Study in Italy, City of L’aquila
6.2. Simulation Setup
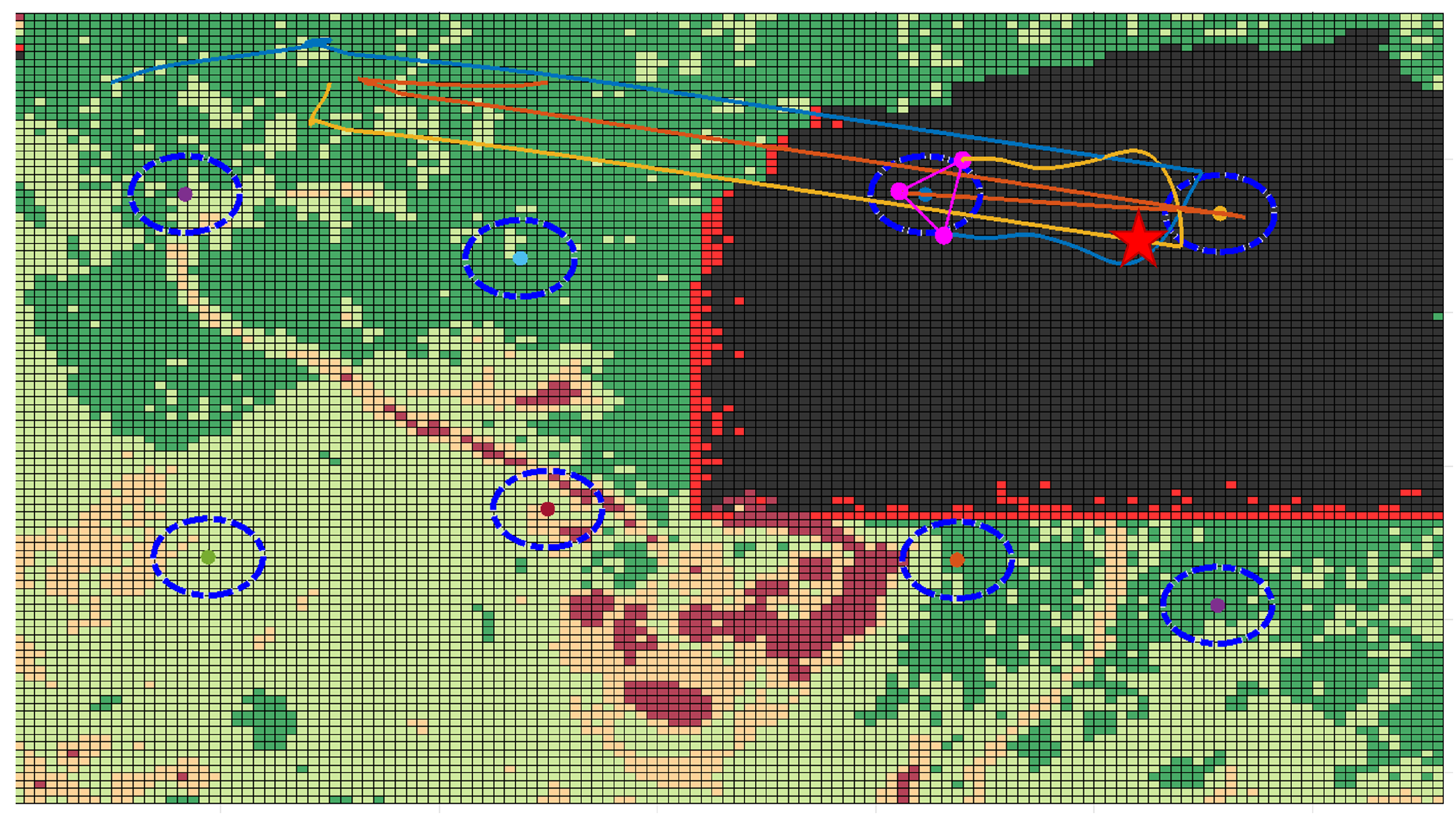
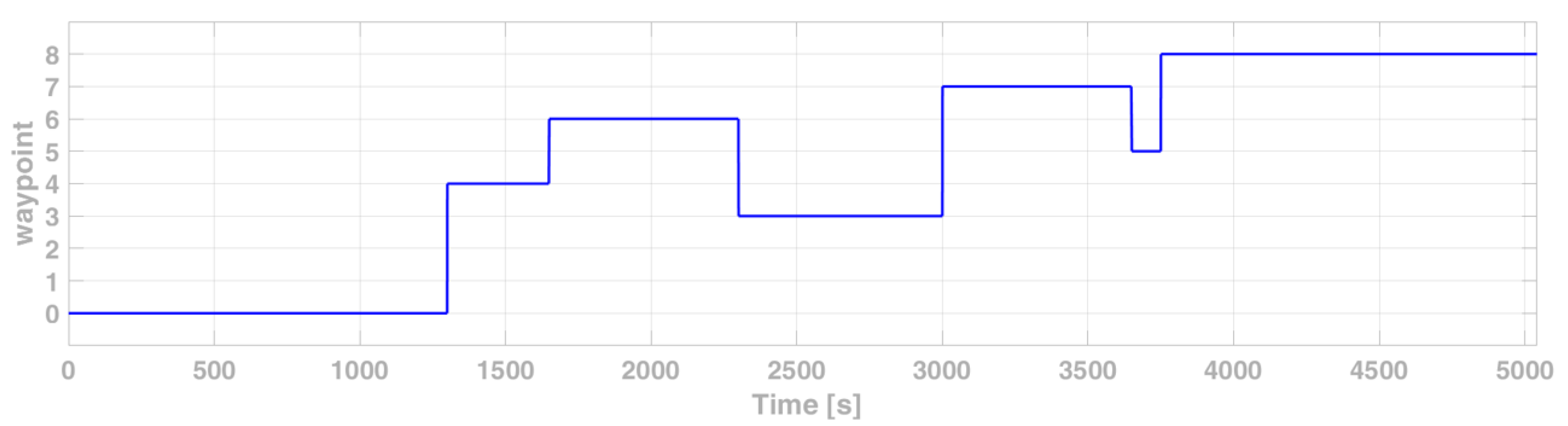
6.3. First Simulation: Normal Conditions-Drone Patrolling for Area Monitoring
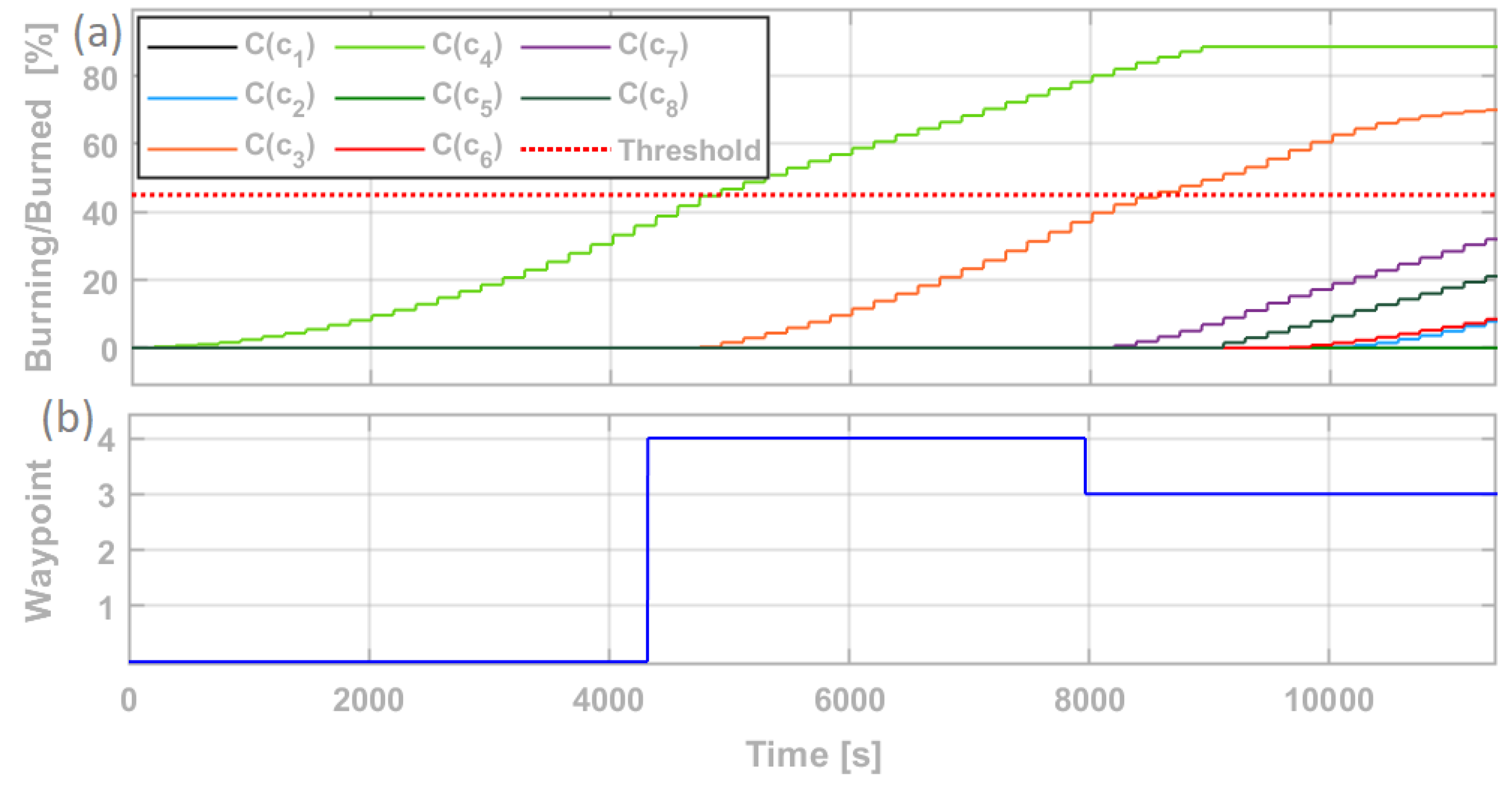
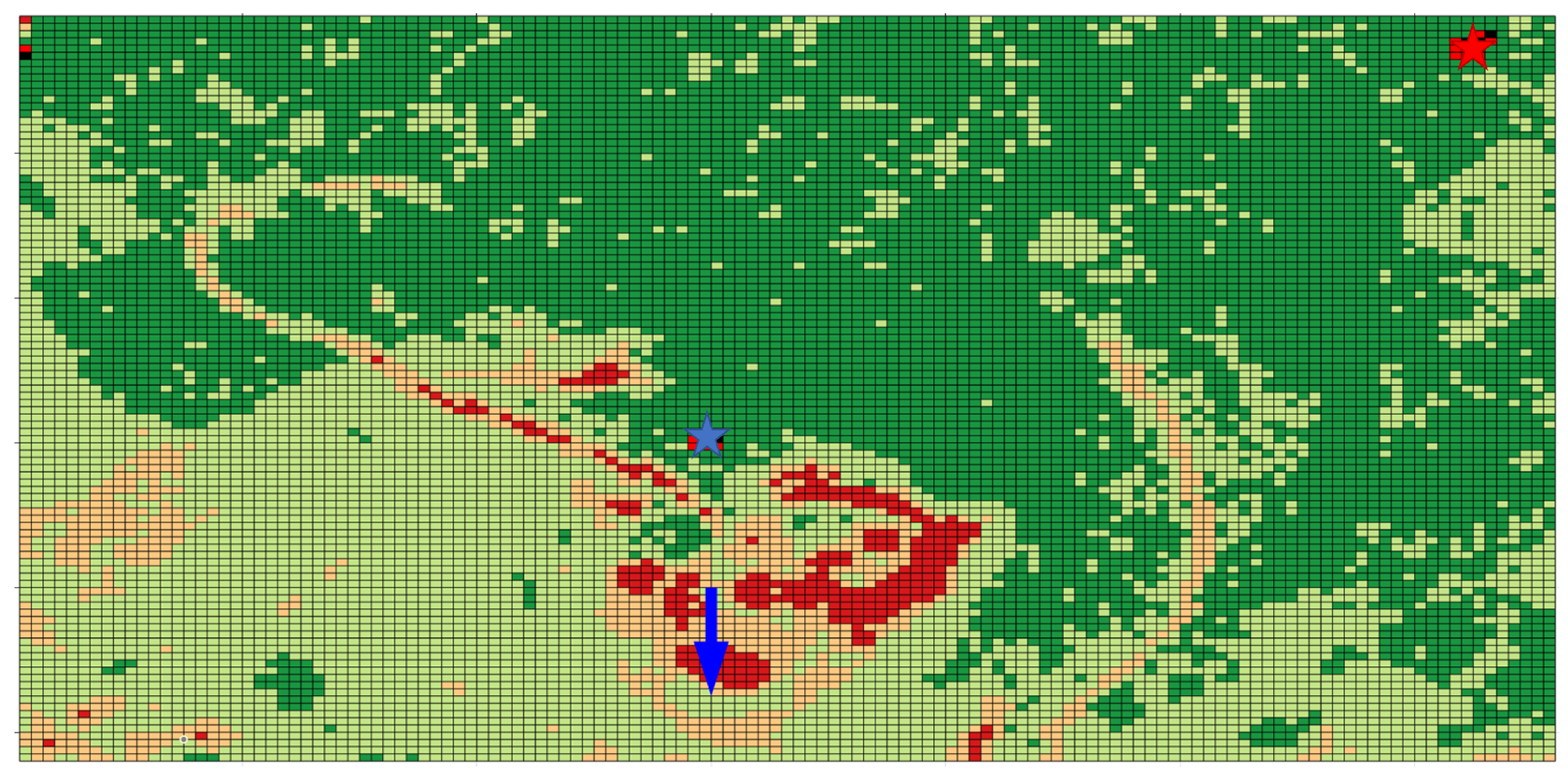
6.4. Second Simulation: Single Ignition Point
6.5. Third Simulation: Multiple Ignition Points
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bond, W.; Keeley, J. Fire as a global ‘herbivore’: The ecology and evolution of flammable ecosystems. Trends Ecol. Evol. 2005, 20, 387–394. [Google Scholar] [CrossRef]
- de Rigo, D.; Libertà, G.; Houston Durrant, T.; Artés Vivancos, T.; San-Miguel-Ayanz, J. Forest Fire Danger Extremes in Europe under Climate Change: Variability and Uncertainty; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar] [CrossRef]
- Celermajer, D.; Lyster, R.; Wardle, G.M.; Walmsley, R.; Couzens, E. The Australian bushfire disaster: How to avoid repeating this catastrophe for biodiversity. WIREs Clim. Chang. 2021, 12, e704. [Google Scholar] [CrossRef]
- Ward, M.; Tulloch, A.I.T.; Radford, J.Q.; Williams, B.A.; Reside, A.E.; Macdonald, S.L.; Mayfield, H.J.; Maron, M.; Possingham, H.P.; Vine, S.J.; et al. Impact of 2019–2020 mega-fires on Australian fauna habitat. Nat. Ecol. Evol. 2020, 4, 1321–1326. [Google Scholar] [CrossRef]
- Khaykin, S.; Legras, B.; Bucci, S.; Sellitto, P.; Isaksen, L.; Tencé, F.; Bekki, S.; Bourassa, A.; Rieger, L.; Zawada, D.; et al. The 2019/20 Australian wildfires generated a persistent smoke-charged vortex rising up to 35 km altitude. Commun. Earth Environ. 2020, 1, 22. [Google Scholar] [CrossRef]
- Biddle, N.; Bryant, C.; Gray, M.; Marasinghe, D. Measuring the Economic Impact of Early Bushfire Detection; Centre for Social Research and Methods (ANU): Canberra, Australia, 2020. [Google Scholar]
- Restas, A. Drone Applications for Supporting Disaster Management. World J. Eng. Technol. 2015, 3, 316–321. [Google Scholar] [CrossRef] [Green Version]
- Moulianitis, V.C.; Thanellas, G.; Xanthopoulos, N.; Aspragathos, N.A. Evaluation of UAV Based Schemes for Forest Fire Monitoring. In Advances in Service and Industrial Robotics; Springer International Publishing: New York, NY, USA, 2018; pp. 143–150. [Google Scholar] [CrossRef]
- Skorput, P.; Mandzuka, S.; Vojvodic, H. The use of Unmanned Aerial Vehicles for forest fire monitoring. In Proceedings of the 2016 International Symposium ELMAR, Zadar, Croatia, 12–14 September 2016. [Google Scholar] [CrossRef]
- Khabarov, N.; Moltchanova, E.; Obersteiner, M. Valuing Weather Observation Systems for Forest Fire Management. IEEE Syst. J. 2008, 2, 349–357. [Google Scholar] [CrossRef]
- Casbeer, D.W.; Kingston, D.B.; Beard, R.W.; McLain, T.W. Cooperative forest fire surveillance using a team of small unmanned air vehicles. Int. J. Syst. Sci. 2006, 37, 351–360. [Google Scholar] [CrossRef]
- Onderka, M.; Melicherčik, I. Fire-prone areas delineated from a combination of the Nesterov Fire-risk Rating Index with multispectral satellite data. Appl. Geomat. 2009, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Giitsidis, T.; Karakasis, E.; Gasteratos, A.; Sirakoulis, G.C. Human and Fire Detection from High Altitude UAV Images. In Proceedings of the 2015 23rd Euromicro International Conference on Parallel, Distributed, and Network-Based Processing, Turku, Finland, 4–6 March 2015. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A.; Dritsas, L. Coordination of Helicopter UAVs for Aerial Forest-Fire Surveillance. In Applications of Intelligent Control to Engineering Systems; Springer: Dordrecht, The Netherlands, 2009; pp. 169–193. [Google Scholar] [CrossRef]
- Ollero, A.; de Dios, J.M.; Merino, L. Unmanned aerial vehicles as tools for forest-fire fighting. For. Ecol. Manag. 2006, 234, S263. [Google Scholar] [CrossRef]
- Hristov, G.; Raychev, J.; Kinaneva, D.; Zahariev, P. Emerging Methods for Early Detection of Forest Fires Using Unmanned Aerial Vehicles and Lorawan Sensor Networks. In Proceedings of the 2018 28th EAEEIE Annual Conference (EAEEIE), Hafnarfjordur, Iceland, 26–28 September 2018. [Google Scholar] [CrossRef]
- Kinaneva, D.; Hristov, G.; Raychev, J.; Zahariev, P. Early Forest Fire Detection Using Drones and Artificial Intelligence. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019. [Google Scholar] [CrossRef]
- Afghah, F.; Razi, A.; Chakareski, J.; Ashdown, J.D. Wildfire Monitoring in Remote Areas Using Autonomous Unmanned Aerial Vehicles. CoRR 2019, abs/1905.00492. Available online: http://xxx.lanl.gov/abs/1905.00492 (accessed on 1 October 2021).
- Kaur, H.; Sood, S.K. Energy-Efficient IoT-Fog-Cloud Architectural Paradigm for Real-Time Wildfire Prediction and Forecasting. IEEE Syst. J. 2020, 14, 2003–2011. [Google Scholar] [CrossRef]
- Mao, S.; He, S.; Wu, J. Joint UAV Position Optimization and Resource Scheduling in Space-Air-Ground Integrated Networks With Mixed Cloud-Edge Computing. IEEE Syst. J. 2020, 1–11. [Google Scholar] [CrossRef]
- Simoes, D.; Rodrigues, A.; Reis, A.B.; Sargento, S. Forest Fire Monitoring Through a Network of Aerial Drones and Sensors. In Proceedings of the 2020 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Austin, TX, USA, 23–27 March 2020. [Google Scholar] [CrossRef]
- Papadopoulos, G.D.; Pavlidou, F.N. A Comparative Review on Wildfire Simulators. IEEE Syst. J. 2011, 5, 233–243. [Google Scholar] [CrossRef]
- Muzy, A.; Innocenti, E.; Aiello, A.; Santucci, J.F.; Marcelli, T.; Santoni, P.A. Discrete-event modelling of fire spreading. Int. J. Syst. Sci. 2008, 39, 193–206. [Google Scholar] [CrossRef]
- Séro-Guillaume, O.; Ramezani, S.; Margerit, J.; Calogine, D. On large scale forest fires propagation models. Int. J. Therm. Sci. 2008, 47, 680–694. [Google Scholar] [CrossRef]
- Preisler, H.K.; Ager, A.A. Forest-Fire Models. In Encyclopedia of Environmetrics; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Consortium for the Research in Automation and Telecommunication (CRAT). Fire Simulator for the ARIES Project. Available online: https://github.com/FedericoFi/ARIES-FireSimulator (accessed on 1 October 2021).
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Lima, M.C.F.; Krus, A.; Valero, C.; Barrientos, A.; del Cerro, J.; Roldán-Gómez, J.J. Monitoring Plant Status and Fertilization Strategy through Multispectral Images. Sensors 2020, 20, 435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- del Cerro, J.; Ulloa, C.C.; Barrientos, A.; de León Rivas, J. Unmanned Aerial Vehicles in Agriculture: A Survey. Agronomy 2021, 11, 203. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.; Mund, J.P.; Greve, K. UAV-Based Photogrammetric Tree Height Measurement for Intensive Forest Monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef] [Green Version]
- Torresan, C.; Berton, A.; Carotenuto, F.; Gennaro, S.F.D.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2016, 38, 2427–2447. [Google Scholar] [CrossRef]
- Roldán, J.; Joossen, G.; Sanz, D.; del Cerro, J.; Barrientos, A. Mini-UAV Based Sensory System for Measuring Environmental Variables in Greenhouses. Sensors 2015, 15, 3334–3350. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- European Space Agency. Radiometric Resolution. Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-2-msi/resolutions/radiometric (accessed on 1 October 2021).
- USGS. What Are the Acquisition Schedules for the Landsat Satellites? Available online: https://www.usgs.gov/faq/mapping-remote-sensing-and-geospatial-data (accessed on 1 October 2021).
- European Space Agency. Copernicus Open Access Hub. 2021. Available online: https://scihub.copernicus.eu (accessed on 1 October 2021).
- QGIS Development Team. QGIS Geographic Information System; QGIS Association: Berne, Switzerland, 2021. [Google Scholar]
- Tarquini, S.; Isola, I.; Favalli, M.; Battistini, A. TINITALY, a Digital Elevation Model of Italy with a 10 Meters Cell Size; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Bologna, Italy, 2007. [Google Scholar] [CrossRef]
- Alexandridis, A.; Vakalis, D.; Siettos, C.; Bafas, G. A cellular automata model for forest fire spread prediction: The case of the wildfire that swept through Spetses Island in 1990. Appl. Math. Comput. 2008, 204, 191–201. [Google Scholar] [CrossRef]
- Mutthulakshmi, K.; Wee, M.R.E.; Wong, Y.C.K.; Lai, J.W.; Koh, J.M.; Acharya, U.R.; Cheong, K.H. Simulating forest fire spread and fire-fighting using cellular automata. Chin. J. Phys. 2020, 65, 642–650. [Google Scholar] [CrossRef]
- Karafyllidis, I.; Thanailakis, A. A model for predicting forest fire spreading using cellular automata. Ecol. Model. 1997, 99, 87–97. [Google Scholar] [CrossRef]
- Gharakhanlou, N.M.; Hooshangi, N. Dynamic simulation of fire propagation in forests and rangelands using a GIS-based cellular automata model. Int. J. Wildland Fire 2021, 30, 652. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra land surface temperature/emissivity 8-day L3 global 1km SIN grid V006. NASA EOSDIS Land Processes DAAC; LP DAAC: Sioux Falls, SD, USA, 2015; Volume 10. [Google Scholar]
- Jaiswal, R.K.; Mukherjee, S.; Raju, K.D.; Saxena, R. Forest fire risk zone mapping from satellite imagery and GIS. Int. J. Appl. Earth Obs. Geoinf. 2002, 4, 1–10. [Google Scholar] [CrossRef]
- Zhou, Q.; Robson, M. Automated rangeland vegetation cover and density estimation using ground digital images and a spectral-contextual classifier. Int. J. Remote Sens. 2001, 22, 3457–3470. [Google Scholar] [CrossRef]
- Weise, D.R.; Biging, G.S. Effects of wind velocity and slope on flame properties. Can. J. For. Res. 1996, 26, 1849–1858. [Google Scholar] [CrossRef]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi tessellations: Applications and algorithms. SIAM Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef] [Green Version]
- Toksoz, M.A.; Oguz, S.; Gazi, V. Decentralized Formation Control of a Swarm of Quadrotor Helicopters. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019. [Google Scholar] [CrossRef]
- Santopaolo, A.; Saif, S.S.; Pietrabissa, A.; Giuseppi, A. Forest Fire Risk Prediction from Satellite Data with Convolutional Neural Networks. In Proceedings of the 2021 29th Mediterranean Conference on Control and Automation (MED), Puglia, Italy, 22–25 June 2021; pp. 360–367. [Google Scholar] [CrossRef]
- ARIES Project Website. Available online: https://business.esa.int/projects/aries (accessed on 1 October 2021).







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giuseppi, A.; Germanà, R.; Fiorini, F.; Delli Priscoli, F.; Pietrabissa, A. UAV Patrolling for Wildfire Monitoring by a Dynamic Voronoi Tessellation on Satellite Data. Drones 2021, 5, 130. https://doi.org/10.3390/drones5040130
Giuseppi A, Germanà R, Fiorini F, Delli Priscoli F, Pietrabissa A. UAV Patrolling for Wildfire Monitoring by a Dynamic Voronoi Tessellation on Satellite Data. Drones. 2021; 5(4):130. https://doi.org/10.3390/drones5040130
Chicago/Turabian StyleGiuseppi, Alessandro, Roberto Germanà, Federico Fiorini, Francesco Delli Priscoli, and Antonio Pietrabissa. 2021. "UAV Patrolling for Wildfire Monitoring by a Dynamic Voronoi Tessellation on Satellite Data" Drones 5, no. 4: 130. https://doi.org/10.3390/drones5040130
APA StyleGiuseppi, A., Germanà, R., Fiorini, F., Delli Priscoli, F., & Pietrabissa, A. (2021). UAV Patrolling for Wildfire Monitoring by a Dynamic Voronoi Tessellation on Satellite Data. Drones, 5(4), 130. https://doi.org/10.3390/drones5040130






