Abstract
Owing to the combination of technological progress in Unmanned Aerial Vehicles (UAVs) and recent advances in photogrammetry processing with the development of the Structure-from-Motion (SfM) approach, UAV photogrammetry enables the rapid acquisition of high resolution topographic data at low cost. This method is particularly widely used for geomorphological surveys of linear coastal landforms. However, linear surveys are generally pointed out as problematic cases because of geometric distortions creating a “bowl effect” in the computed Digital Elevation Model (DEM). Secondly, the survey of linear coastal landforms is associated with peculiar constraints for Ground Control Points (GCPs) measurements and for the spatial distribution of the tie points. This article aims to assess the extent of the bowl effects affecting the DEM generated above a linear beach with a restricted distribution of GCPs, using different acquisition scenarios and different processing procedures, both with PhotoScan® software tool and MicMac® software tool. It appears that, with a poor distribution of the GCPs, a flight scenario that favors viewing angles diversity can limit DEM’s bowl effect. Moreover, the quality of the resulting DEM also depends on the good match between the flight plan strategy and the software tool via the choice of a relevant camera distortion model.
1. Introduction
Computing Digital Elevation Models (DEM) at centimetric resolution and accuracy is of great interest for all geomorphological sciences [1]. For high dynamic geomorphological processes (coastal or riverine environment for example), it is fundamental to collect accurate topographic data allowing the comparison of DEMs computed with images of successive campaigns in order to calculate a sediments budget, assess risks of erosion or flooding or initialize numerical models [2].
As small Unmanned Aerial Vehicles (UAVs) allow the rapid acquisition of high resolution (<5 cm) topographic data at low cost, they are now widely used for geomorphological surveys [2,3,4,5]. The use of UAVs for civil or research purposes notably increases with the development of Structure-from-Motion (SfM) algorithms [6]. In comparison with classic digital photogrammetry, the SfM workflow allows more automation and is therefore more straightforward for users [7,8,9]. The status of SfM photogrammetry among other topographic survey techniques is fully described in reference [10]. A literature review addressing performance assessment of methods and software solutions for georeferenced point clouds or DEMs production is proposed in reference [11]. As reported in reference [7], SfM photogrammetry methods offer the opportunity to extract high resolution and accurate spatial data at very low-cost using consumer grade digital cameras that can be embedded on small UAVs. Nevertheless, several articles highlight the fact that the reconstructed results may be affected by systematic broad-scale errors restricting their use [1,12,13,14]. These reconstruction artefacts may be sometimes difficult to detect if no validation dataset is available or if the user is not aware that such artefacts may appear. It is therefore helpful to propose some practical guidance to limit such geometric distortions.
Possible error sources of SfM photogrammetry are thoroughly reviewed in reference [1], distinguishing local errors due to surface quality or lighting conditions and more systematic errors due to referencing and image network geometry. In particular, image acquisition along a linear axis is a critical configuration [9,15,16]. As reported in references [13,15], inappropriate modelling of lens distortion results in systematic deformations. Weak network geometries, common in linear surveys, result in errors when recovering distortion parameters [13]. But changing the distortion model can reduce the sensitivity to distortion parameters [15], limiting “doming” deformation or the “bowl effect”. They suggest two strategies to correct this drift: to densify GCPs distribution (which is not always possible depending on field configurations or implies additional field work), or to improve the estimation of exterior orientation of each image.
Use of an adequate spatial distribution of Ground Control Points (GCPs) can limit these effects [17]. One common method for GCPs consists in putting targets whose position is measured by DGPS. Reference [18] develops a Monte-Carlo approach to find the best configuration to optimize bundle adjustment among the GCPs network. However, such approaches require deploying a large number of GCPs all over the study area, which is very time-consuming, both on the field during the survey and during the processing [1,9].
In practice, corridor mapping is a today a matter of concern for transportation [19,20], inspection of pipelines or power lines [21,22], and coastlines or river corridors monitoring [15,23]. Various strategies are proposed to improve accuracy with a minimal GCP network [24] or without GCP, for instance: (i) equipping the UAV with precise position and attitude sensors and a pre-calibrated camera [25], or (ii) using Kinematic GPS Precise Point Positioning (PPP) [26] under certain conditions (long flights, favourable satellite constellation), or (iii) using point-and-scale measurements of kinematic ground control points [20]. Nevertheless, these solutions without GCP involve computing lever arm offsets and boresight corrections, and ensuring synchronisation between the different sensors. Furthermore, as mentioned in reference [24], this demand on precision and thus on high quality of inertial navigation system and/or GNSS sensors can be incompatible with the limited UAV payload capability and radically increase the price of the system. In coastal environments, linear landforms are also usual (Figure 1), but their survey can present some peculiarities, such as being time-limited because of tides or tourist attendance. Moreover, it can be impossible to install and measure GCPs in some parts of the study area because of the spatial extent, inaccessibility (topography, rising tide, vegetation, private properties) or because of GNSS satellite masking (cliffs, vegetation cover, buildings, etc.). These constraints can also limit the spatial distribution of tie points detected during image matching.

Figure 1.
Examples of linear coastal landforms on French coasts: (a) Sillon de Talbert thin trail of pebbles, (b) Mimbeau bank in Cap Ferret, (c) Suscinio beach, (d) Ermitage back-reef beach (GoogleEarth© images).
This article aims to provide practical suggestions to limit “bowl effect” on the resulting DEM in linear context with sub-optimal distribution of GCPs. The field experiment conceived for this study does not seek to be realistic or to optimize the DEM quality. The purpose is to assess in which extent the acquisition conditions can impact the topographic modelling performed with SfM photogrammetric software. Different flight plans are tested to identify the most relevant flight scenario for each camera model to limit geometric distortions in the reconstructed surface. As DEM outputs may be significantly different depending on the selected software package [27], the quality of the reconstruction is examined using two software solutions based on SfM algorithms: Agisoft PhotoScan® Pro v1.2.3 and the open-source IGN® MicMac®, using different camera distortion models.
2. Photogrammetric Processing Chain
2.1. Principle and Outline of the Photogrammetric Workflow
Nowadays, the photogrammetry workflows often combine principles of conventional photogrammetry and two computer vision approaches: “Structure from Motion” (SfM) and “Multi-View Stereo” (MVS). Unlike traditional photogrammetry, SfM photogrammetry allows for determining the internal camera geometry without prior calibration. Camera external parameters can also be determined without the need for a pre-defined set of GCPs [7].
A detailed explanation of the SfM photogrammetry workflow is given in reference [10]. The main steps are depicted in Figure 2. Homologous points are identified in overlapping photos and matched. Generally, this step is based on the use of a Scale Invariant Feature Transform (SIFT) registration algorithm [28]. This algorithm identifies the keypoints, creates an invariant descriptor and matches them even under a variety of perturbing conditions such as scale changes, rotation, changes in illumination, and changes in viewpoints or image noise. Taking into account the tie points and the GCPs, (i) the external parameters of the camera, (ii) the intrinsic camera calibration, also called the “camera model” (defined by the principal point, the principal distance and the distortion parameters introduced by the lens) and (iii) the 3D positions of tie points in the study area are estimated. The estimation is optimized by minimization of a cost function. A dense point cloud is then computed using algorithms inspired from Computer Vision tools [29], which filter out noisy data and allow for generating very high-resolution datasets [7,9].
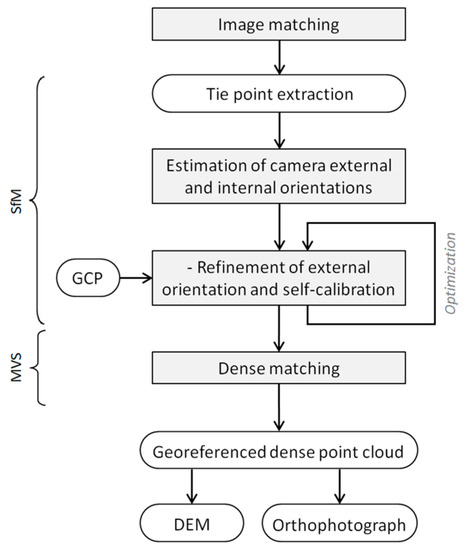
Figure 2.
Main steps of the SfM-MVS photogrammetry workflow.
The GCPs are used for georeferencing and for the optimization of camera orientation (Figure 2), providing additional information of the geometry of the scene, to be used to refine the bundle adjustment. Therefore, the spatial distribution of GCPs can be critical for the quality of the results [3,9,10].
In this study, each dataset was processed using two software tools in parallel: Agisoft PhotoScan® Pro v1.2.3 (a widely used integrated processing chain commercialized by AgiSoft®) and MicMac® (an open-source photogrammetric toolset developed by IGN® (the French National Institute of Geographic and Forestry Information). Both PhotoScan® and MicMac® workflows allow control measurements to be included in the bundle adjustment refinement of the estimated camera parameters. For a more coherent comparison, the camera model parameters are not fixed for both forms of software.
2.2. PhotoScan Overview
PhotoScan® Professional (version 1.2.3) is a commercial product developed by AgiSoft®. The procedure for deriving orthophotographs and the DEM follows the workflow presented in Figure 2. Some parameters can be adjusted at each of these steps:
- Image orientation by bundle adjustment. Homologous keypoints are detected and matched on overlapping photographs so as to compute the external camera parameters for each picture. The “High” accuracy parameter is selected (the software works with original size photos) to obtain a more accurate estimation of camera exterior orientation. The number of tie points for every image can be limited to optimize performance. The default value of this parameter (4000) is kept. Tie point accuracy depends on the scale at which they were detected. Camera calibration parameters are refined, including GCPs (ground and image) positions and modelling the distortion of the lens with Brown’s distortion model [30].
- Creation of the dense point cloud by dense image matching using the estimated camera external and internal parameters. The quality of the reconstruction is set to “High” to obtain a more detailed and accurate geometry.
- DEM computation by rasterizing the dense point cloud data on a regular grid.
- Orthophotograph generation based on DEM data.
The intermediate results can be checked and saved at each step. At the end of the process, the DEM and the orthophotograph are exported in GeoTiff format, without any additional post-processing (optimization, filtering, etc.). The software is user-friendly, but the adjustment of parameters is only limited to pre-defined values. Nevertheless, with the versions upgrading, more parameters are adjustable and more detailed quality reports are available.
2.3. MicMac Overview
MicMac (acronym for “Multi-Images Correspondances, Méthodes Automatiques de Corrélation”) is an open-source photogrammetric software suite developed by IGN® for computing 3D models from sets of images [31,32] Micmac® chain is open and most of the parameters can be finely tuned. In this study, we use the version v.6213 for Windows.
The standard “pipeline” for transforming a set of aerial images in a 3D model and generating an orthophotograph with MicMac consists of four steps:
- Tie point computation: the Pastis tool uses the SIFT++ algorithm [33] for the tie points pairs generation. Here, we used Tapioca, the simplified tool interface, since the features available using Tapioca are sufficient for the purpose of this study. For this step, it is possible to limit processing time by reducing the images size by a factor 2 to 3. By default, the images have been therefore shrunk to a scaling of 0.3.
- External orientation and intrinsic calibration: the Apero tool generates external and internal orientations of the camera. A large panel of distortion models can be used. As mentioned later, two of them are tested in this study. Using GCPs, the images are transformed from relative orientations into an absolute orientation within the local coordinate system using a 3D spatial similarity (“GCP Bascule” tool). Finally the Campari command is used to refine camera orientation by compensation of heterogeneous measures.
- Matching: from the resulting oriented images, MicMac computes 3D models according to a multi-resolution approach, the result obtained at a given resolution being used to predict the next step solution.
- Orthophotograph generation: the tool used to generate orthophotographs is Tawny, the interface of the Porto tool. The individual rectified images that have been previously generated are merged in a global orthophotograph. Optionally, some radiometric equalization can be applied.
With MicMac, at each step, the user can choose any numerical value, whereas PhotoScan only offers preset values (“low”, “medium” and “high”), which is more limiting. As for PhotoScan, the intermediate results can be checked and saved at each step. At the end of the process, a DEM and an orthophotograph are exported in GeoTiff format.
For both software packages, the processing time depends on the RAM capacity of the computer, as memory requirements increase with the size and number of images and with the desired resolution.
2.4. Camera Calibration Models
Camera calibration estimates the parameters of a given camera, including considerations for lens distortion, that are required to model how scenes are represented within images. Camera self-calibration is an essential component of photogrammetric measurements. As outlined in reference [34], self-calibration involves recovering the properties of the camera and the imaged scene without any calibration object but using constraints on the camera parameters or on the imaged scene. A perspective geometrical model allows computing exterior orientation and calibration by means of SfM. Non-linear co-linearity equations provide the basic mathematical model, which may be extended by additional parameters.
Both PhotoScan and MicMac propose models for frame cameras, spherical or fisheye cameras. In PhotoScan, all models assume a central projection camera. Non-linear distortions are modeled using Brown’s distortion model [30]. The following parameters can be accepted as input arguments of this model:
- f: focal length
- cx, cy: principal point offset
- K1, K2, K3, K4: radial distortion coefficients
- P1, P2, P3, P4: tangential distortion coefficients
- B1, B2: affinity and non-orthogonality (skew) coefficients
In MicMac, various distortion models can be used, the distortion model being a composition of several elementary distortions. Typical examples of basic distortions are given in MicMac’s user manual [32]. For instance, the main contribution to distortion can be represented by a physical model with few parameters (e.g., a radial model). A polynomial model, with additional parameters, can be combined with the initial model to account for the remaining contributions to distortion. A typical distortion model used in Apero module is a Fraser’s radial model [35] with decentric and affine parameters and 12 degrees of freedom (1 for focal length, 2 for principal point, 2 for distortion center, 3 for coefficients of radial distortion, 2 for decentric parameters and 2 for affine parameters). [15] presents the last evolutions of MicMac’s bundle adjustment and some additional camera distortion models, in particular “F15P7”, specifically designed to address issues arising with UAV linear photogrammetry. In our study, the “F15P7” refined radial distortion model is used according to the description in reference [15]. It consists of a radial camera model to which is added a complex non radial degree 7 polynomial correction.
3. Conditions of the Field Survey
3.1. Study Area
The test surveys of this study were carried out during a beach survey in Reunion Island. As part of the French National Observation Service (SNO), several beach sites in France, including overseas, are regularly monitored, which includes some beaches of the west coast of Reunion Island.
The study area consists of a 250 m long (in longshore direction) section of a 25 m wide beach (Figure 3). There is only a limited time window with suitable conditions to perform the survey: shortly after sunrise, before people come to the beach. While the tidal range is limited in Reunion Island (40 cm or less), tide can also be a constraint on the available time to carry out the survey in other parts of the world.
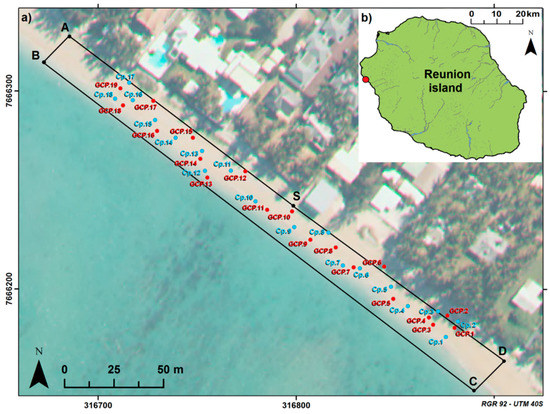
Figure 3.
(a) Overview of the study area showing the spatial distribution of targets. Red targets are Ground Control Points (GCP) used in the SfM photogrammetry process. Blue targets are check points (Cp) used for quantifying the accuracy of the results. The flight plan is depicted by the black line, S being the starting and stopping point. (Background is an extract from the BD Ortho®—orthorectified images database of the IGN©, 2008, coord. RGR92-UTM 40S). (b) Location of the study area on the West coast of Reunion Island.
3.2. Ground Control Points and Check Points
GCPs are an essential input not only for data georeferencing, but also to refine the camera parameters, the accuracy of which is critical to limit bowl effects. In some cases, clearly identifiable features of the survey area can be used as “natural GCP”, provided they are stable over time and present a strong contrast with the rest of the environment for unambiguous identification [1]. As coastal contexts are exceptionally dynamic environments, it is rare to encounter natural GCPs and complicated to set up permanent ones.
For the present test survey, 37 circular targets of 20 cm in diameter were distributed along the beach. Among these, 19 red targets (Figure 4) were used as Ground Control Points (tagged as GCP in Figure 3) and used in the SfM processing chain. The others, 18 blue targets (Figure 4), served as Check points (tagged as Cp. in Figure 3). These check points were used to assess the quality of the DEM reconstruction. The position of each target was measured using post-processed Differential GPS (DGPS). The base station GPS receiver was installed in an open-sky environment and collected raw satellite data during 4 hours. During the survey, the base station transmits correction data to the rover, situated in a radius of 200 m. Measurements are post-processed using data from permanent GPS network, allowing to achieve an accuracy of 1 cm horizontally and 2 cm vertically.

Figure 4.
(a) Example of red target used as Ground Control Point. (b) Example of blue target used as check point to assess the quality of the reconstructed DEM. (c) DRELIO 10, Unmanned Aerial Vehicle (UAV) designed from a hexacopter platform 80 cm in diameter.
3.3. UAV Data Collection
Data were all collected on May 12th, 2016. The survey was performed using DRELIO 10, an UAV based on a multi-rotor platform DS6, assembled by DroneSys (Figure 4). This electric hexacopter UAV has a diameter of 0.8 m and is equipped with a collapsible frame allowing the UAV to be folded back for easy transportation. DRELIO 10 weighs less than 4 kg and can handle a payload of 1.6 kg, for a flight autonomy of about 20 min. The camera is mounted on a tilting gyro-stabilized platform. It is equipped with a reflex camera Nikon D700 with a focal length of 35 mm, taking one 6.7 Mpix photo in intervalometer mode every 2 seconds. The images have no geolocation information encoded in their EXIF. The flight control is run by the DJI® software iOSD. DRELIO 10 is lifted and landed manually and it performs autonomous flights controlled from the ground station software. The mean speed of autonomous flight is programed at 4 m/s.
A set of three flights (Table 1) has been performed over the studied beach:

Table 1.
Comparisons of the parameters for the different flight plans (PS: PhotoScan; MM-F15P7: MicMac with F15P7 distortion model; MM-Fra.: MicMac with Fraser distortion model).
- Flight 1 was performed following a typical flight plan (from S to A, B, C, D and S on Figure 3) with nadir pointing camera and parallel flight lines at a steady altitude of 50 m.
- Flight 2 was performed following the same parallel flight lines at 50 m of altitude with an oblique pointing camera tilted at 40° forward. The inclination has been set to 40° because this angle would be compatible with a survey of the cliff front [36] or of parts of the upper beach situated under the canopy of coastal trees. The two flight lines were carried out in opposite direction. Large viewing angles induce scale variations within each image (from 1.64 cm/pixel to 2.95 cm/pixel). Increasing the tilting angle makes the manual GCPs tagging more difficult.
- Flight 3 was performed following the two parallel flight lines with a nadir-pointing camera but at different altitudes. The altitude was about 40 m from S to A, then 60 m from B to C and finally 40 m from D to S (Figure 3). The disadvantage is that the footprint and the spatial resolution of the photos vary from one flight line to another and therefore the ground coverage is more difficult to plan.
4. Approach for Data Processing
The approach of this study is based on the fact that changing the flight scenario modifies the image network geometry, which can impact the quality of reconstruction by changing the spatial distribution of tie points detected during image matching. We compare thereafter the results obtained for different flight plans (i.e., Flight 1, Flight 2 and Flight 3) to assess to what extent the flight scenario can limit or emphasize the geometrical distortion effects, particularly in case of restricted GCPs distribution. The restricted GCPs distribution does not seek to be realistic or to minimise the topographic modelling error, the purpose is to assess the extent of the predictable “bowl” effect after more than hundred meters without GCP and how the flight scenario can influence this effect. In the same way, using images with geolocation information encoded in their EXIF would limit the geometric distortions, but our aim is rather to enhance the impact of the flight scenario on the “bowl effect”.
For each flight (Table 1), the mean flight altitude is kept around 50 m. As the flight plan and the footprint of images vary from one flight to another, the overlap between images is also shown. For Flight 2 and Flight 3, the viewing angle and the scale significantly change from one flight line to another. That implies less resemblance between images and therefore keypoints identification is likely to be more difficult prior to image matching.
Figure 5 shows an example of tie points detection in PhotoScan® for images acquired from different flight lines for Flight 2 (Figure 5a) and Flight 3 (Figure 5b). The beach surface is sufficiently textured (coral debris, footprints, depressions or bumps in the sand) to have detectable features for image matching. Nevertheless, considering the environmental constraints inherent to the study area, only a small proportion of the photos is taken into account in the image matching (Figure 5). This restricted spatial distribution of the tie points can affect the quality of the SfM reconstruction. The images being processed by different operators with PhotoScan® and MicMac®, to avoid variations in the delineation of masks, it has been decided to not use mask. Indeed, as very few valid tie points are situated in water (Figure 5), the noise they would introduce in bundle adjustment is considered negligible.

Figure 5.
Example of tie points identification in photos from different flight lines for Flight 2 (a) and Flight 3 (b). (a) In this example, among 719 tie points detected, 525 matchings have been detected as valid (blue lines) and 194 as invalid (red lines). (b) In this example, among 1457 tie points detected, 1161 matchings have been detected as valid and 296 as invalid.
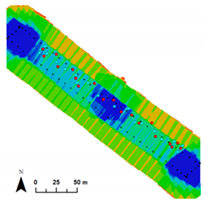
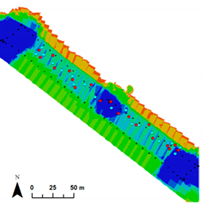
Comparing the total number of valid tie points from one flight to another (Table 1), it can be noticed that for PhotoScan® the number of tie points is ≈12–13% higher for Flight 2 than for Flights 1 and 3. On the contrary, for MicMac®, the number of tie points is 36% higher for Flight 3 than for Flight 1 and 2. These results have to be tempered (i) by the maps of tie point density (Figure 6) showing a higher spatial coverage for Flight 2, and (ii) by the average density of tie points (computed in a radius of 1 m—Table 1) showing a higher density for Flight 3, both with PhotoScan® and MicMac®. The fact that the numbers of tie points detected by PhotoScan® and MicMac® are not of the same order of magnitude is due to the parametrization of image alignment: with a number of tie points limited to 4000 for every image in PhotoScan® and image size reduced by 3 in image matching in MicMac®. That can imply differences in matching robustness or PhotoScan® may have a smaller reprojection error tolerance.
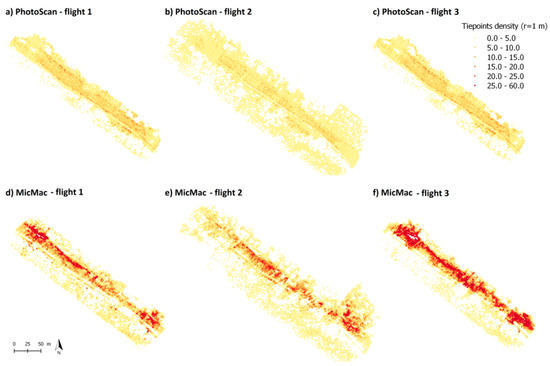
Figure 6.
Tie point density calculated in a radius of 1 m for the different scenarios.
Over a first phase of processing, the 19 GCPs (Figure 3a—red targets) were all used as control points within the bundle adjustment to reconstruct a DEM and an orthophotograph (Figure 7). For each flight, the datasets are processed using both PhotoScan® workflow and MicMac® workflow with “F15P7” optical camera model.

Figure 7.
Reconstructed orthophotograph (a) and DEM (b) generated with PhotoScan from the dataset acquired during Flight 1 and processed using the 19 GCPs.
In a second phase, the number of used GCPs was reduced to only the 5 GCPs (selected among the 19 GCPs) in the South-Eastern part, so-called “control region” (Figure 8) to simulate a very poor GCPs distribution. To assess which flight plan strategy provides the best DEM quality for an ineffective GCPs distribution, each dataset was processed for the “5 GCPs” configuration, using both the default PhotoScan® workflow and, concurrently, MicMac® “F15P7” workflows and MicMac® workflow with a standard Fraser’s distortion model.

Figure 8.
Overview of the targets spatial distribution with a reduced number of GCPs. 5 GCPs in the South-Eastern part of the study area are kept for the configuration “5 GCPs”. These GCPs define a “control region”. The cross-shore profile (MN) defines the starting point of longshore measurements in the study area.
5. Impact of Flight Scenarios on Bowl Effect
For each configuration, the results of the different processings are assessed using the 18 check points (Figure 3a—blue targets, not used in the photogrammetric workflow), comparing their position on the reconstructed DEM and orthophotograph to their position measured by DGPS.
Considering the rapidly changing nature of a beach, the uncertainty on RTK DGPS measurements and on GCP pointing, we assumed that a Root Mean Square Error (RMSE) lower than 5 cm is sufficient for the resulting DEM. Using 19 GCPs widely distributed over the study area, the total error varies from 1.7 cm (for Flight 2 processed with PhotoScan) to 4.0 cm (for Flight 1 processed with MicMac) (Table 2). Thus, whatever the flight plan and whatever the software tool, all the computed DEM meet the criterion of RMSE lower than 5cm. For these three flights with 19 GCPs, the errors appear a bit smaller (less than 1.6 cm of difference) with PhotoScan® than with MicMac®, which is possibly due to differences in filtering algorithm or in the minimization algorithm during the step of bundle adjustment. With the “5 GCPs” configuration, the errors are considerably larger (up to 161.8 cm for Flight 3 with PhotoScan and up to 146.8 cm for Flight 1 with MicMac-Fraser), the vertical error being significantly higher than the horizontal error (Table 2). Figure 9 shows the spatial repartition of the error, depicting the error on each check point as a function of the distance to the (MN) profile (Figure 8). As expected, the error increases with distance away from the control region. The extremity of the area (on Cp. 18) is located over 160 m away from the control region.

Table 2.
Comparisons of the performances obtained for the different flight plans (PS: PhotoScan; MM-F15P7: MicMac with F15P7 distortion model; MM-Fra.: MicMac with Fraser distortion model).
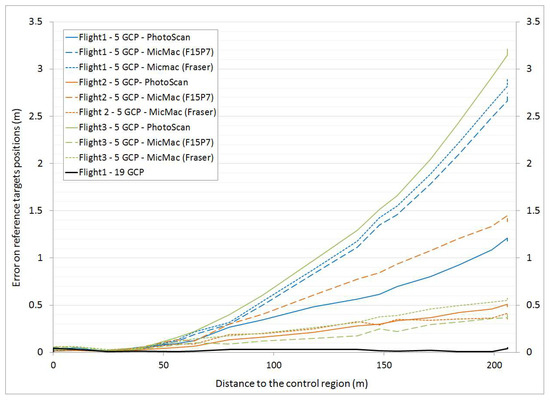
Figure 9.
Comparison of the error (estimated using the check points) obtained with different processing chains for each flight. The error on each check points is represented as a function of the distance to the (MN) profile at the extremity of the control region.
For the “classical” flight plan (Flight 1), with a limited number and limited distribution of GCPs, PhotoScan® gives better results than Micmac®, with respective mean Z-errors of 55.6 cm for PhotoScan®, 1.39 m for MicMac® “F15P7” and 1.47 m for MicMac® “Fraser” (Table 2). It appears that for PhotoScan® the best results are obtained for Flight 2, with an oblique pointing camera. In this case, the mean Z-error is of 19.2 cm and the maximum Z-error is about 50 cm on Cp. 18. Using MicMac® workflow with “F15P7” optical camera model, the best results are obtained for Flight 3 (2 parallel lines at different altitudes), with a mean Z-error of 17.7 cm and a maximum error, on Cp. 18, of 40 cm. For Flight 2 (with oblique imagery), with MicMac® workflow, the quality of the results is largely improved using Fraser’s distortion model rather than “F15P7” since the vertical RMS error is of 26 cm for Fraser against 80 cm for “F15P7”.
It has to be noticed that the RMS reprojection error, quantifying image residuals, is nearly equivalent for both GCPs configurations and from one flight to another, varying from 0.69 to 0.93 pixels with 19 GCPs and varying from 0.67 to 0.92 pixels with 5 GCPs (Table 2). The quality of the results in 5 GCPs configuration is not correlated with this RMS reprojection error. In the same way, the quality of the results in 5 GCPs (Table 2) configuration is not clearly proportional either to the number of tie points or the tie point density (Table 1). Even if tie points detection varies from one software tool to another and for one flight scenario to another, the great disparity in quality among the results is also linked to the suitability of the combination between flight scenario and optical camera model used during SfM processing.
6. Discussion
For indirect georeferencing, the most reliable strategy to guarantee the DEM quality consists in installing targets all along the study area. However, when it is not possible to achieve an optimal GCPs distribution, some strategies enable us to limit distortion effects.
This study highlights the fact that, in case of poor GCPs distribution, a good match between the flight plan strategy and the choice of camera distortion model is critical to limit bowl effects. Some of the observed differences between PhotoScan and MicMac reconstructions may be due to the step of tie point automatic detection, which is based on C++ SIFT algorithm [32] in Micmac [31] while PhotoScan claims to achieve higher image matching quality using custom algorithms that are similar to SIFT [3]. As mentioned in Section 2.4, the degrees of freedom in bundle adjustment depend on the camera model (for example, 8 degrees of freedom for the Brown’s model used with PhotoScan® and 12 degrees of freedom for the Fraser’s model used with MicMac®). As already mentioned, variation can also be due to differences in the filtering algorithm or in the minimization algorithm during the step of bundle adjustment. For MicMac®, this step is well described in reference [15], but for PhotoScan®, it is a “black-box”. That stresses the need for detailed information about the algorithms and parameters used in SfM processing software.
The fact that MicMac “F15P7” gives very poor results for oblique pointing camera (Flight 2) is consistent with reference [15], which mentions that in certain conditions, oblique imagery can reduce the quality of the results obtained using the “F15P7” distortion model. They hypothesize that the determination of many additional parameters can lead to over-parametrization of the least-square estimation and they advise in such cases to use a physical camera model. Our results are in agreement with this hypothesis since, for the same dataset, MicMac—Fraser provides the best results, with a RMS error of 25.9 cm.
More generally, oblique pointing camera or change in flight altitude contribute to diversifying viewing angles throughout the whole survey. A point is therefore seen on several images with very variable viewing angles, which can make the tie points detection more difficult but seems to increase the quality of the reconstruction, limiting the uncertainty in camera parameters assessment.
To improve the quality of the resulting DEM, one could also consider:
- combining Flight 2 and Flight 3 scenarios, i.e., different altitude of flight with an oblique pointing camera, with perhaps even better results;
- combining Flight 2 or Flight 3 scenario with other optical camera models or processing strategies.
Optimizing the optical camera model and/or the processing strategy could also improve the quality of the resulting DEM. As an example, [18] have identified that with PhotoScan®, a camera model parametrization using focal length (f), principal point offset (cx, cy), radial distortions (K1, K2, K3) and tangential distortions (P1, P2) (default configuration in PhotoScan®) is more efficient than adding skew coefficients to this parameters set. About the choice of camera distortion model, as mentioned in reference [34], using additional parameters introduces new unknowns into the bundle-adjustment procedure and an improper use of these parameters can adversely affect the determinability of all system parameters in the procedure of self-calibration.
Moreover, it is known that the precision of tie points can contribute to reduce geometric distortion. Therefore, in a case of very restrictive tie point distribution, another option for distortion limitation would consist of changing the default parameters in image matching (i.e., number of tie points limited to 4000 for every image in PhotoScan® and image size reduced by 3 in images matching in MicMac®). A test have been conducted processing Flight 1 dataset with unlimited number of tie points in PhotoScan® and full size images in Micmac®. As expected, both PhotoScan® and MicMac® show a higher density of tie points (Table 3 and Figure 10). The number of tie points and the density are still higher with MicMac®. With this new configuration, the RMS reprojection error is reduced (more than divided by two with MicMac®—Table 3).

Table 3.
Impact of changing the default parameters in images alignment (for Flight 1) on the tie points sparse point cloud.
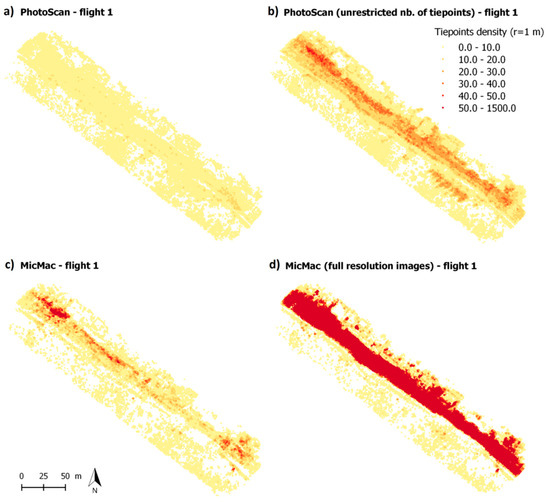
Figure 10.
Comparison of tie point density for different parametrization in image alignment: (a) PhotoScan—Flight 1, (b) PhotoScan (unrestricted nb. of tie points)—Flight 1, (c) MicMac—Flight 1 and (d) MicMac (full resolution images)—Flight 1.
Nevertheless, as depicted in Figure 11, bowl effects remain in the DEM reconstruction despite the higher tie point density. The results are very similar with PhotoScan®, the vertical error with an unlimited number of tie points being 58 cm, against 63 cm with default parameters. With MicMac®, the processing time is largely increased when using full size images, but the vertical error is decreased to 97 cm, against 138 cm with a “reduced image size” configuration. This suggests that number and density of tie points are not a key parameter compared to the tie points “quality” (accuracy, relevant distribution) in relation to the camera distortion model.
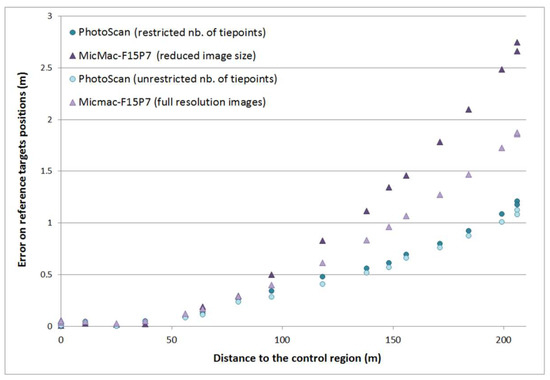
Figure 11.
Impact of the number of tie points in image alignment on the quality of the results in 5 GCPs configuration for Flight 1. The “default” parametrizations (i.e., number of tie points limited to 4000 for every image in PhotoScan® and image size reduced by 3 in images alignment in MicMac®) are compared to PhotoScan® processing with unrestricted number of tie points and MicMac® processing with full resolution images.
Distortion problems can be encountered in UAV monitoring of non-linear areas [13,27]. We have not yet tested the applicability of Flight 2 and Flight 3 scenarios for surveys of non-linear landforms, but it is very likely that choosing a scenario that offers a great variety of viewing angles for each homologous point would improve the quality of the reconstruction. In practice, several processing strategies can be tested. The problem is that, in case of lack of GCPs, the validation points are also lacking. It is therefore complex to quantify the bowl effect and to what extent the tested strategy corrects it.
7. Conclusions
Constraints inherent to the survey of coastal linear landforms (mainly restricted spatial distribution of tie points and restricted distribution of GCPs) cause detrimental effects in topography reconstruction using SfM photogrammetry.
This study shows that adopting a flight scenario that favors viewing angles diversity can limit DEM’s bowl effect, but this flight strategy has to be well matched with the choice of camera distortion model. For this study, in the 5 GCPs configuration, with PhotoScan® (Brown’s distortion model), the best results are obtained for Flight 2 (2 parallel lines, with a 40° oblique-pointing camera). In this case, the mean Z-error is of 19.2 cm and the maximal error is about 50 cm (respectively compared to 55.6 cm and 118.0 cm for Flight 1). With MicMac® (using “F15P7” distortion model), the best results are obtained for Flight 3 (2 parallel lines at different altitudes, 40 m and 60 m in this study) and a nadir-pointing camera. In this case, the mean Z-error is of 17.7 cm and the maximal error of 40 cm (respectively compared to 138.7 cm and 274.6 cm for Flight 1. Results of similar quality are obtained for Micmac® - “Fraser” but for Flight 2.
More generally, this study highlights the need to acquire sufficient understanding of the algorithms and models used in the SfM processing tools, particularly regarding the camera distortion model used in the bundle adjustment step. On the whole, survey strategies offering a variety of viewing angles of each homologous point are preferred, particularly in the case of sub-optimal GCPs distribution. This result can most likely be extended to non-linear surveys.
Author Contributions
Conceptualization, M.J.; Formal analysis, M.J., S.P., P.A. and N.L.D.; Funding acquisition, C.D.; Methodology, M.J. and P.G.; Project administration, C.D.; Writing—original draft, M.J. and S.P.; Writing—review & editing, P.A. and N.L.D.
Acknowledgments
This work is part of the Service National d’Observation DYNALIT, via the research infrastructure ILICO. It was supported by the French “Agence Nationale de la Recherche” (ANR) through the “Laboratoire d’Excellence” LabexMER (ANR-10-LABX-19-01) program, a grant from the French government through the “Investissements d’Avenir”. The authors also acknowledge financial support provided by the TOSCA project HYPERCORAL from the CNES (the French space agency).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-Based Surface Reconstruction in Geomorphometry Merits—Limits and Developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using Unmanned Aerial Vehicles (UAV) for High-Resolution Reconstruction of Topography: The Structure from Motion Approach on Coastal Environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-Motion Photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- Delacourt, C.; Allemand, P.; Jaud, M.; Grandjean, P.; Deschamps, A.; Ammann, J.; Cuq, V.; Suanez, S. DRELIO: An Unmanned Helicopter for Imaging Coastal Areas. J. Coast. Res. 2009, 56, 1489–1493. [Google Scholar]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic Structure from Motion: A New Development in Photogrammetric Measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Micheletti, N.; Chandler, J.H.; Lane, S.N. Structure from motion (SFM) photogrammetry. In Geomorphological Techniques; online ed.; Cook, S.J., Clarke, L.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2015. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. Structure-from-Motion Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera: Accuracy and Geoscience Application. J. Geophys. Res. Earth Surf. 2012, 117, F3. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from Motion Photogrammetry in Physical Geography. Progr. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Jaud, M.; Grasso, F.; Le Dantec, N.; Verney, R.; Delacourt, C.; Ammann, J.; Deloffre, J.; Grandjean, P. Potential of UAVs for Monitoring Mudflat Morphodynamics (Application to the Seine Estuary, France). ISPRS Int. J. Geoinf. 2016, 5, 50. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating Systematic Error in Topographic Models Derived from UAV and Ground-Based Image Networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Rosnell, T.; Honkavaara, E. Point Cloud Generation from Aerial Image Data Acquired by a Quadrocopter Type Micro Unmanned Aerial Vehicle and a Digital Still Camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
- Tournadre, V.; Pierrot-Deseilligny, M.; Faure, P.H. UAV Linear Photogrammetry. Int. Arch. Photogramm. Remote Sens. 2015, XL-3/W3, 327–333. [Google Scholar] [CrossRef]
- Wu, C. Critical Configurations for Radial Distortion Self-Calibration. In Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G. Ground-Control Networks for Image Based Surface Reconstruction: An Investigation of Optimum Survey Designs Using UAV Derived Imagery and Structure-from-Motion Photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Congress, S.S.C.; Puppala, A.J.; Lundberg, C.L. Total system error analysis of UAV-CRP technology for monitoring transportation infrastructure assets. Eng. Geol. 2018, 247, 104–116. [Google Scholar] [CrossRef]
- Molina, P.; Blázquez, M.; Cucci, D.; Colomina, I. First Results of a Tandem Terrestrial-Unmanned Aerial mapKITE System with Kinematic Ground Control Points for Corridor Mapping. Remote Sens. 2017, 9, 60. [Google Scholar] [CrossRef]
- Skarlatos, D.; Vamvakousis, V. Long Corridor survey for high voltage power lines design using UAV. ISPRS Int. Arch. Photogramm. Remote Sens. 2017, XLII-2/W8, 249–255. [Google Scholar] [CrossRef]
- Matikainen, L.; Lehtomäki, M.; Ahokas, E.; Hyyppä, J.; Karjalainen, M.; Jaakkola, A.; Kukko, A.; Heinonen, T. Remote sensing methods for power line corridor surveys. ISPRS J. Photogramm. Remote Sens. 2016, 119, 10–31. [Google Scholar] [CrossRef]
- Dietrich, J.T. Riverscape mapping with helicopter-based Structure-from-Motion photogrammetry. Geomorphology 2016, 252, 144–157. [Google Scholar] [CrossRef]
- Zhou, Y.; Rupnik, E.; Faure, P.-H.; Pierrot-Deseilligny, M. GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping. Sensors 2018, 18, 2783. [Google Scholar] [CrossRef] [PubMed]
- Rehak, M.; Skaloud, J. Fixed-wing micro aerial vehicle for accurate corridor mapping. ISPRS Int. Arch. Photogramm. Remote Sens. 2015, II-1/W1, 23–31. [Google Scholar] [CrossRef]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS precise point positioning for UAV photogrammetry. Available online: https://onlinelibrary.wiley.com/doi/full/10.1111/phor.12259 (accessed on 22 December 2018).
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the Accuracy of High Resolution Digital Surface Models Computed by PhotoScan® and MicMac® in Sub-Optimal Survey Conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–23 June 2006. [Google Scholar] [CrossRef]
- AgiSoft PhotoScan User Manual, Professional Edition v.1.2. Agisoft LLC. 2016. Available online: http://www.agisoft.com/pdf/photoscan-pro_1_2_en.pdf (accessed on 14 June 2016).
- Pierrot-Deseilligny, M.; Clery, I. APERO, an Open Source Bundle Adjustment Software for Automatic Calibration and Orientation of Set of Images. ISPRS Int. Arch. Photogramm. Remote Sens. 2011, XXXVIII-5/W16, 269–276. [Google Scholar] [CrossRef]
- Pierrot-Deseilligny, M. MicMac, Apero, Pastis and Other Beverages in a Nutshell! 2015. Available online: http://logiciels.ign.fr/IMG/pdf/docmicmac-2.pdf (accessed on 27 July 2016).
- Vedaldi, A. An Open Implementation of the SIFT Detector and Descriptor; UCLA CSD Technical Report 070012; University of California: Los Angeles, CA, USA, 2007. [Google Scholar]
- Remondino, F.; Fraser, C. Digital Camera Calibration Methods: Considerations and Comparisons. ISPRS Int. Arch. Photogramm. Remote Sens. 2006, XXXVI, 266–272. [Google Scholar]
- Fraser, C.S. Digital camera self-calibration. ISPRS J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Letortu, P.; Jaud, M.; Grandjean, P.; Ammann, J.; Costa, S.; Maquaire, O.; Davidson, R.; Le Dantec, N.; Delacourt, C. Examining high-resolution survey methods for monitoring cliff erosion at an operational scale. GISci. Remote Sens. 2018, 55, 457–476. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).