A Generalized Simulation Framework for Tethered Remotely Operated Vehicles in Realistic Underwater Environments
Abstract
:1. Introduction
1.1. Background
1.2. Importance of Underwater Simulation
1.3. Related Work
1.4. Our Contribution
1.5. Paper Organization
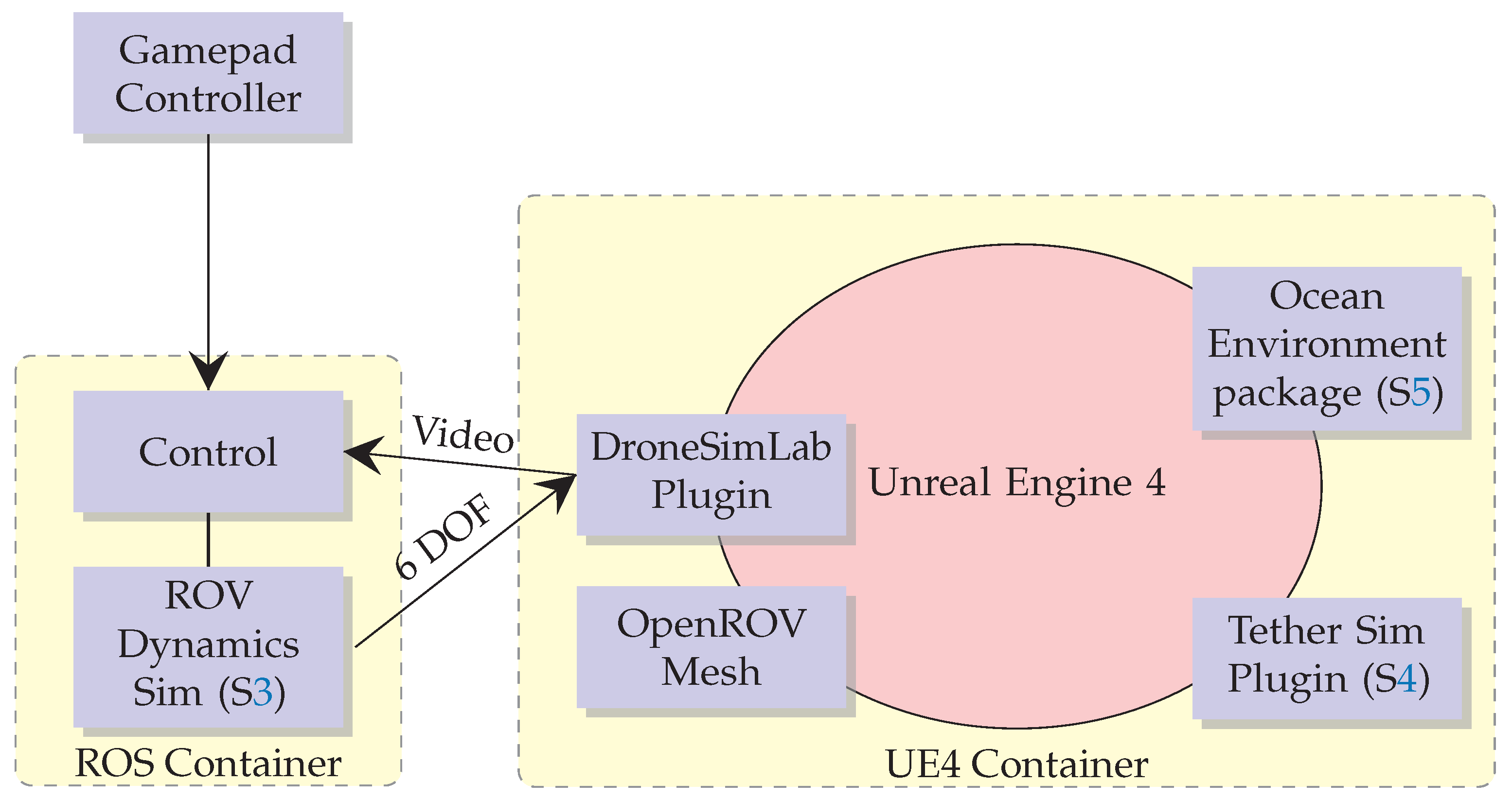
2. Simulation Framework Overview
3. Simulating ROV Dynamics
3.1. Method Overview
3.1.1. Kinematics
3.1.2. Inertia
3.1.3. Dynamics
3.1.4. Kane’s Method
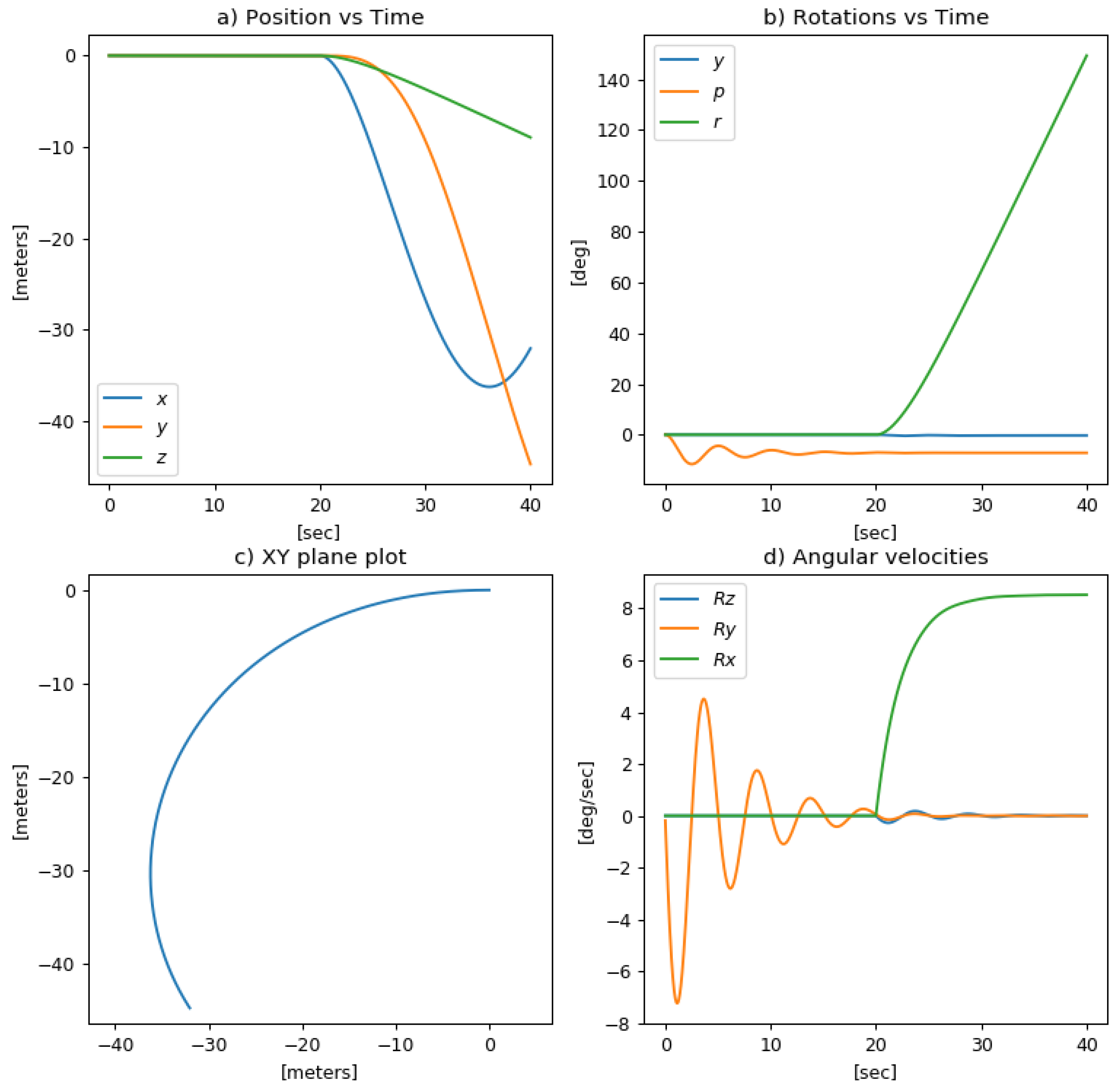
3.1.5. Dynamic Simulation Results
3.2. Conclusions
4. Tether Simulation
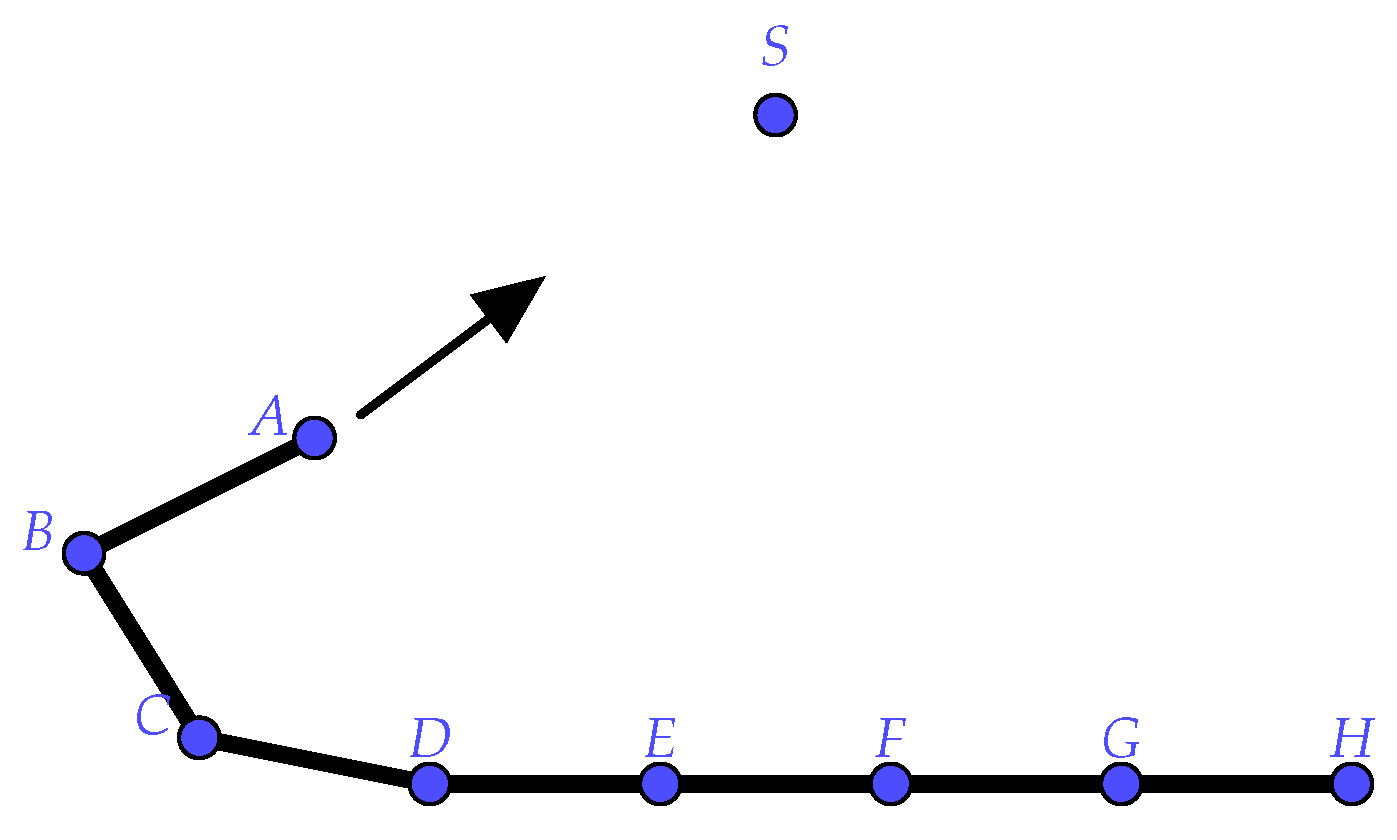
4.1. Algorithm Overview
| SolveDistanceConstraint(PosA,PosB,TargetDistance): Delta = PosB-PosA ErrorFactor=(|Delta| - TargetDistance)/ |Delta| PosA += ErrorFactor/2 ∗ Delta PosB -= ErrorFactor/2 ∗ Delta SolveConstraints(): for iter=0 to SolverIterations for ParticleIndex=0 to NumOfParticles-1 SolveDistanceConstraint( Particles[i],Particle[i+1],TargetDistance) for ParticleIndex=0 to NumOfParticles-2 SolveDistanceConstraint( Particles[i],Particle[i+2],2∗TargetDistance) |
4.2. Variable Length Cables
4.3. Methods and Tools
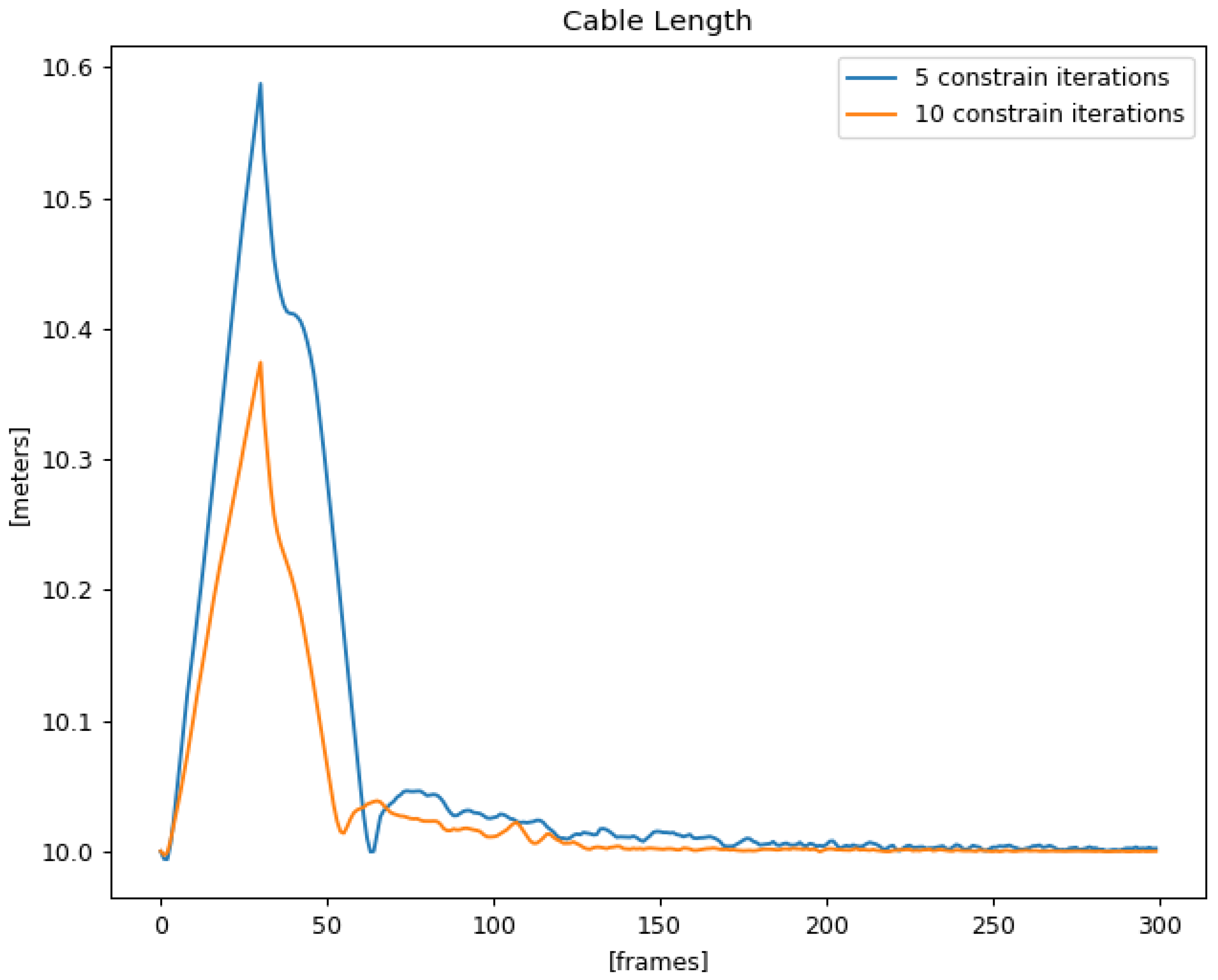
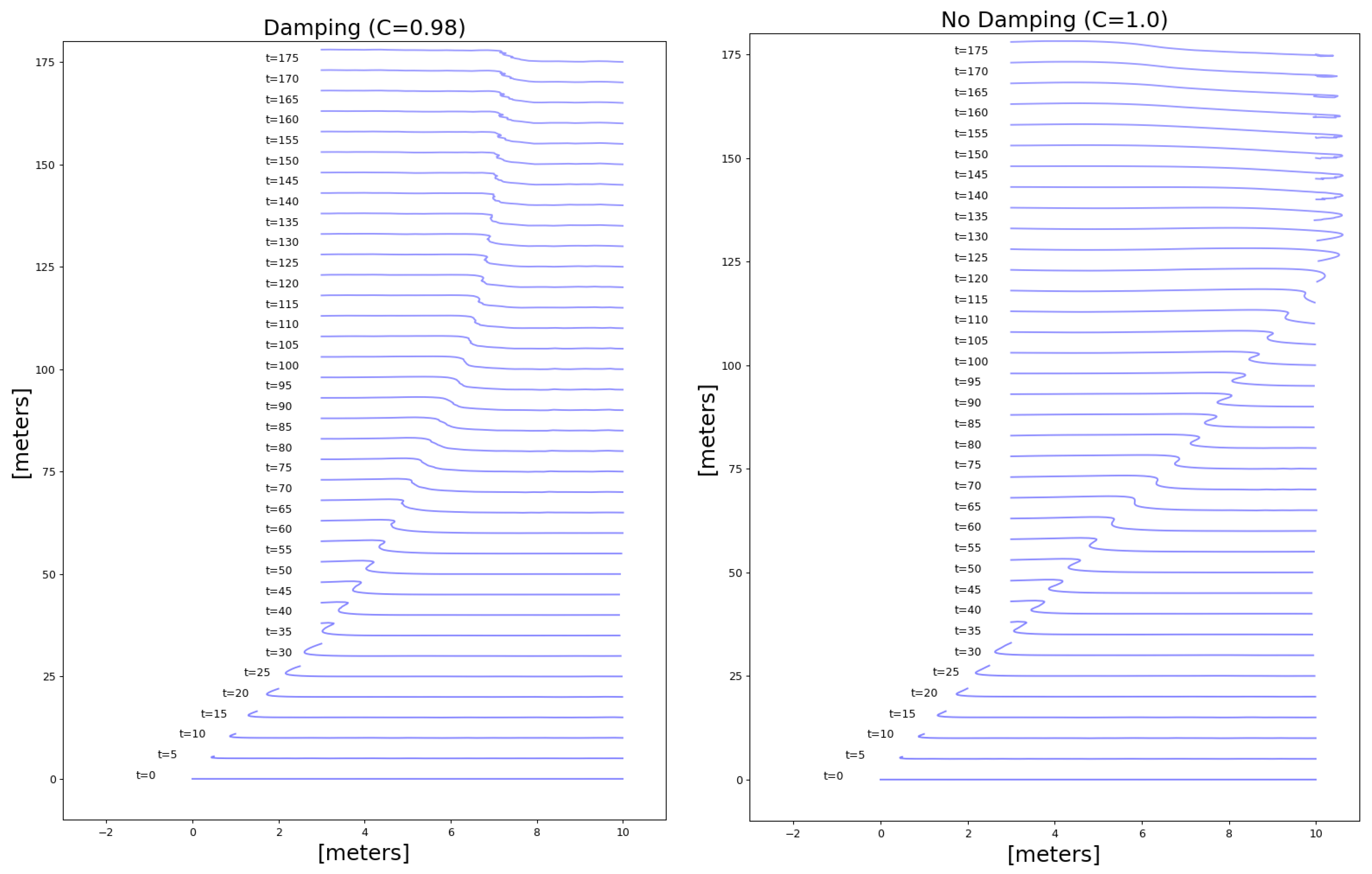
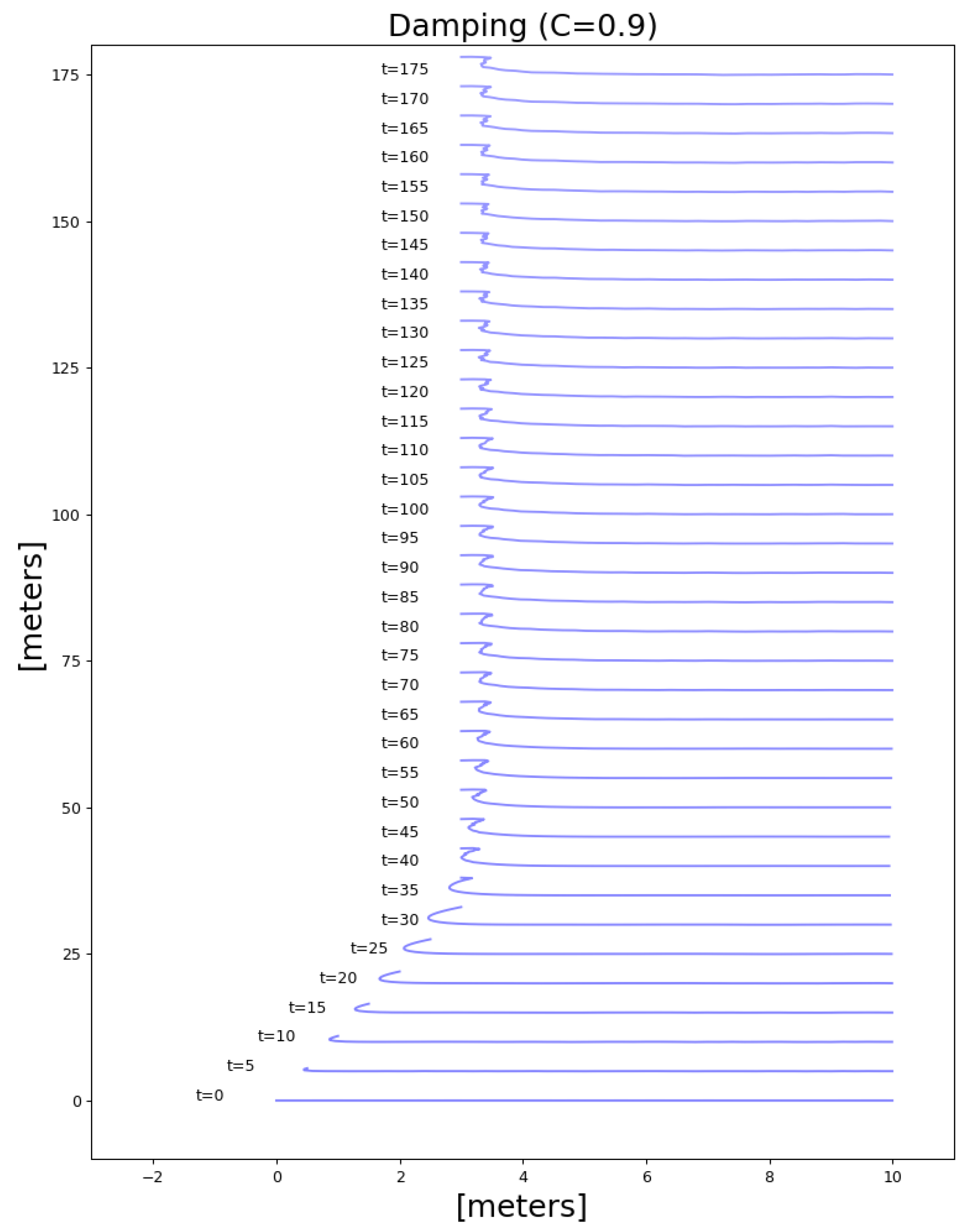
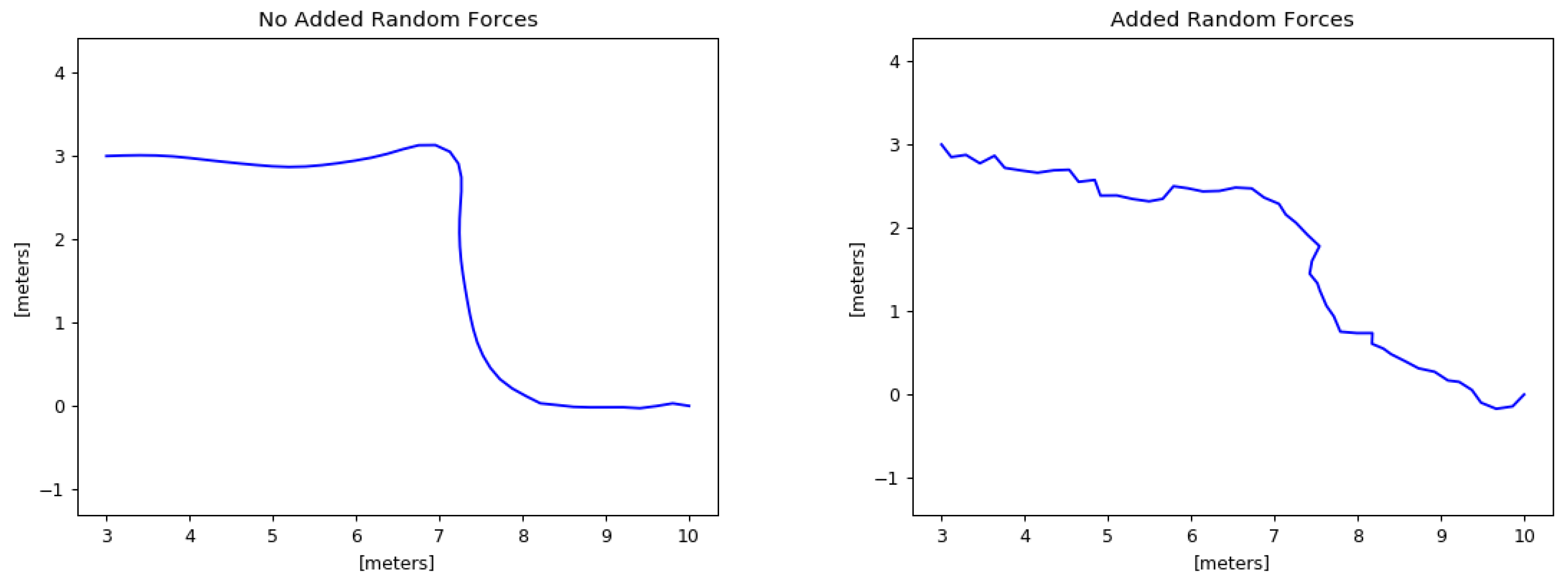
4.4. Experimental Results
4.5. Conclusions
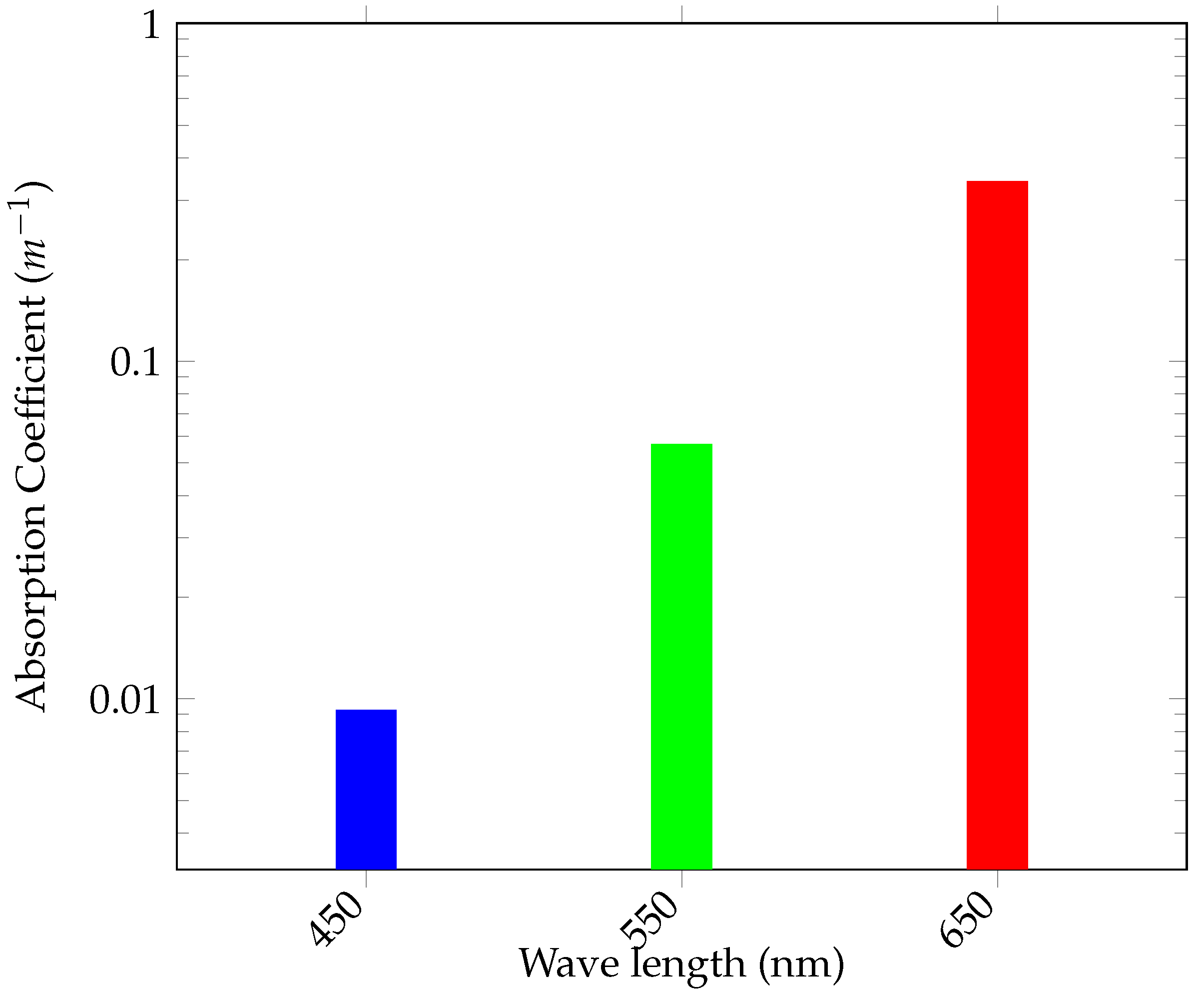
5. The Underwater Ocean Environment
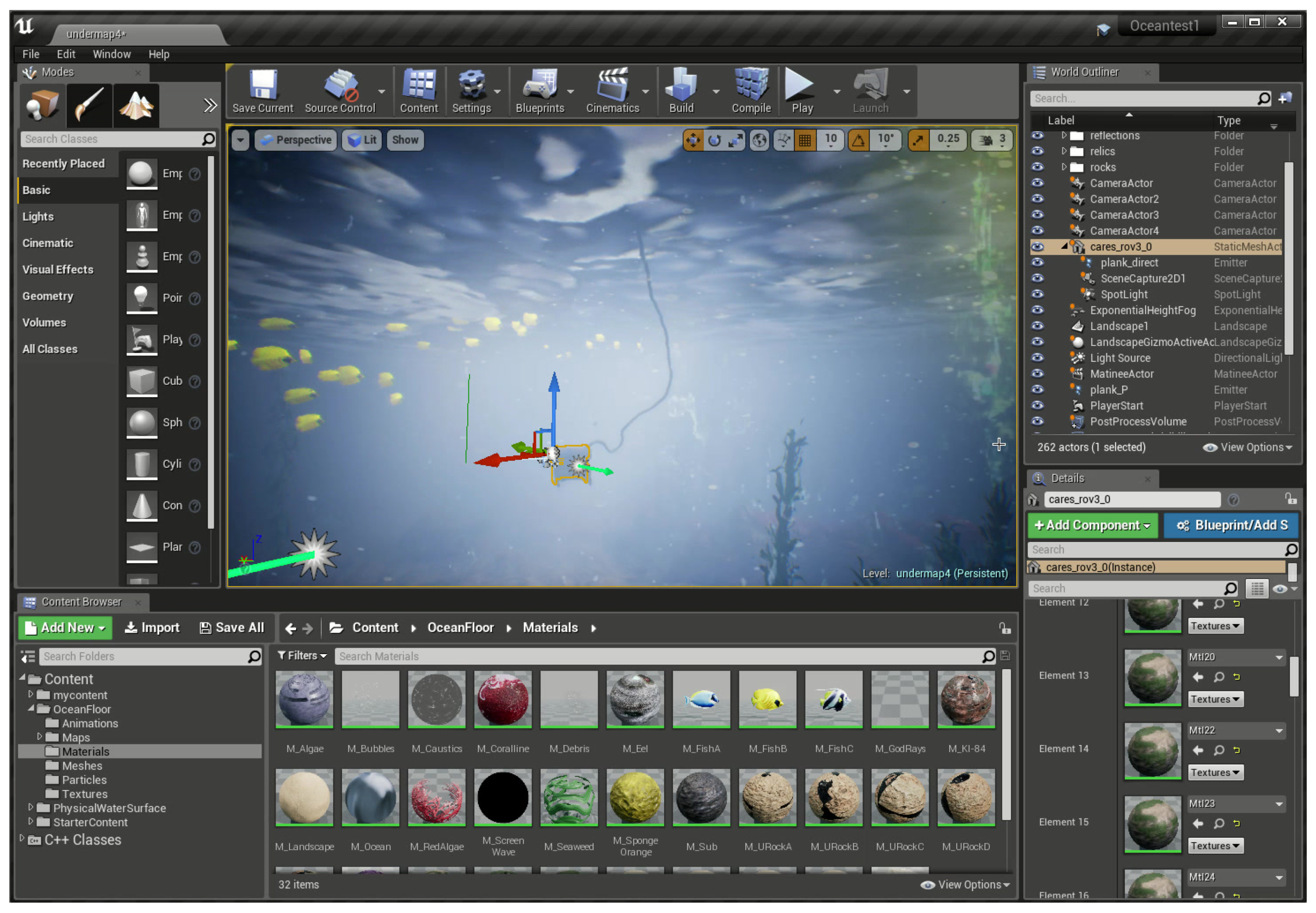
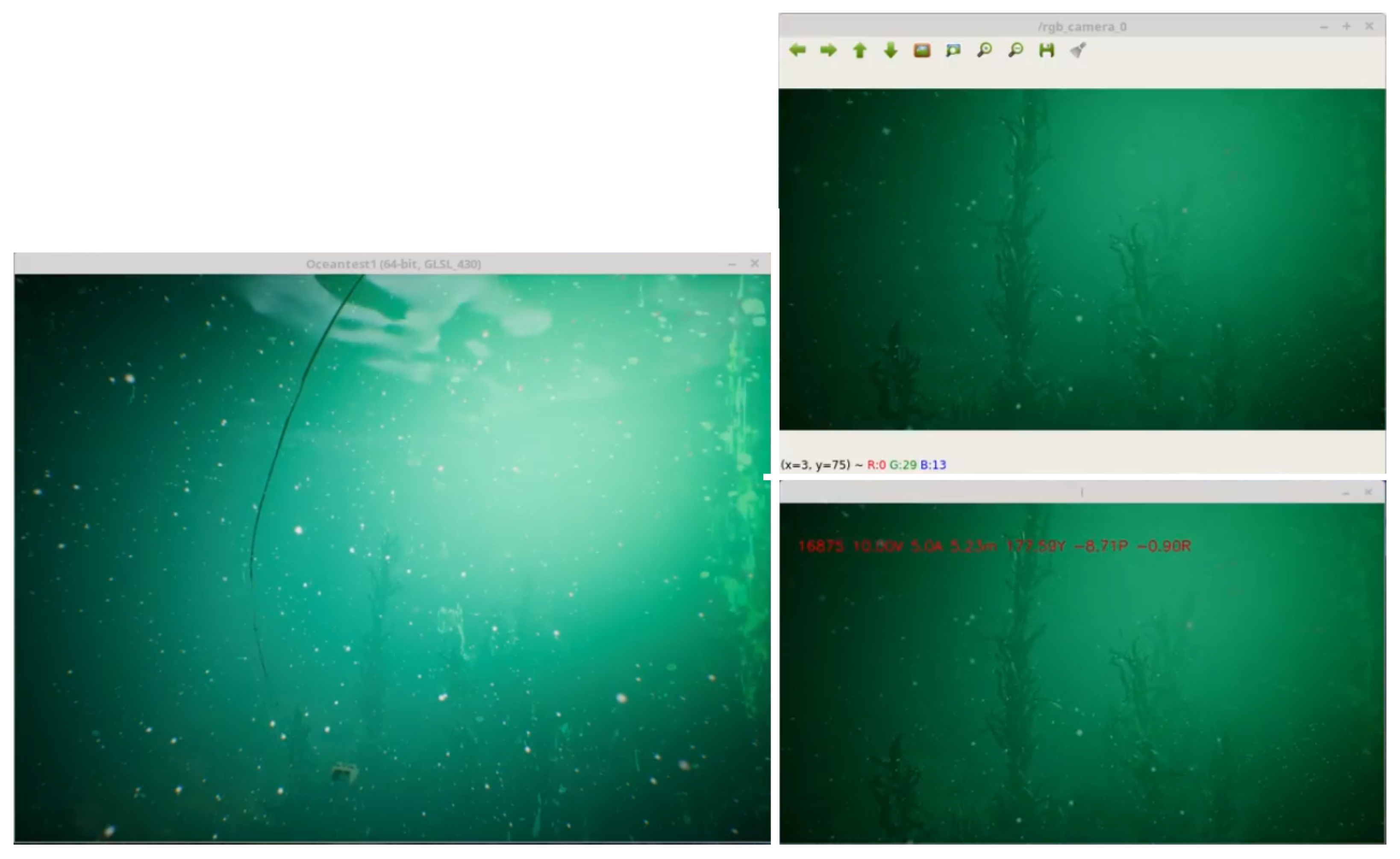
5.1. Generating Marine Environment in a Game Engine
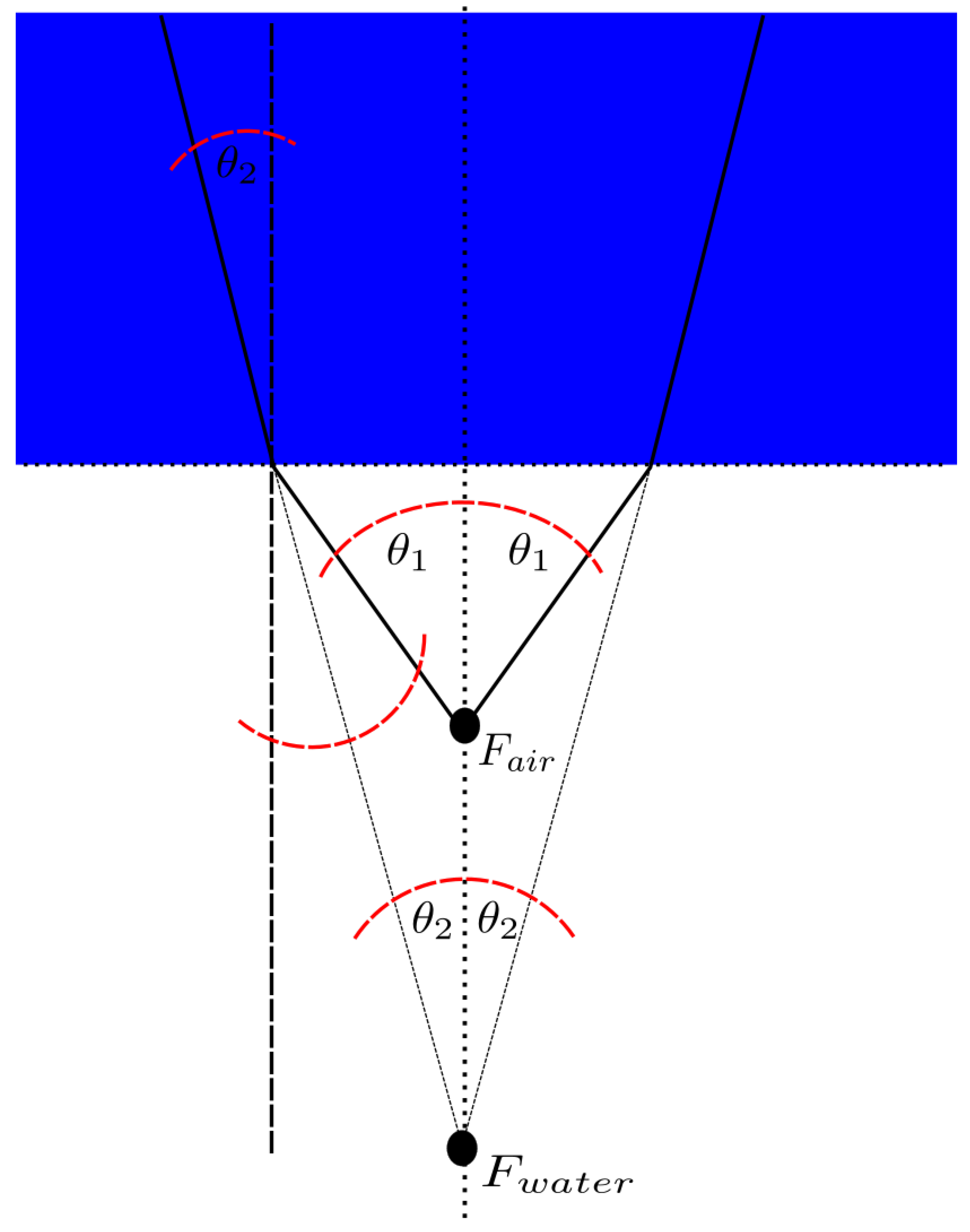
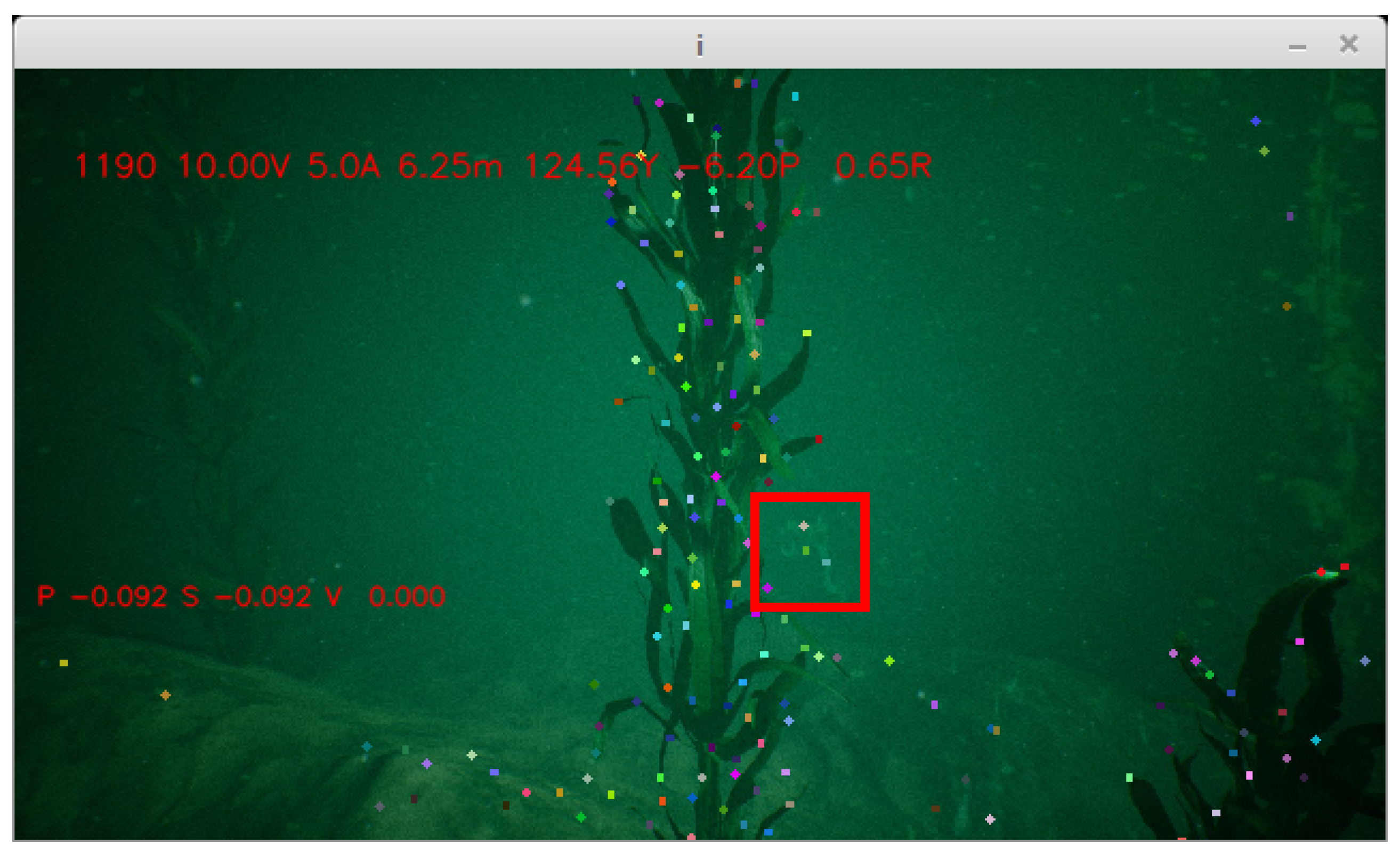
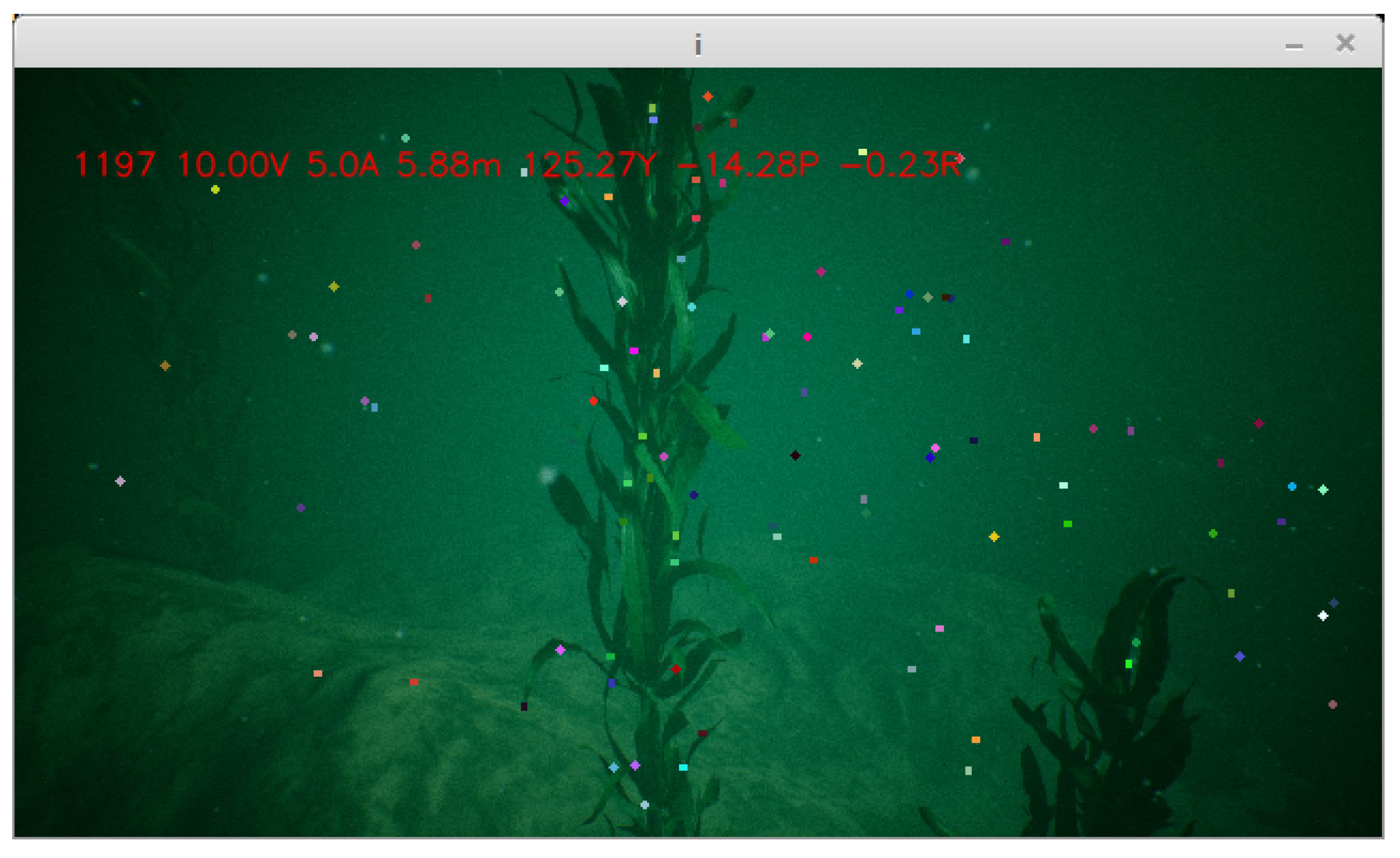
5.2. Simulating The Camera
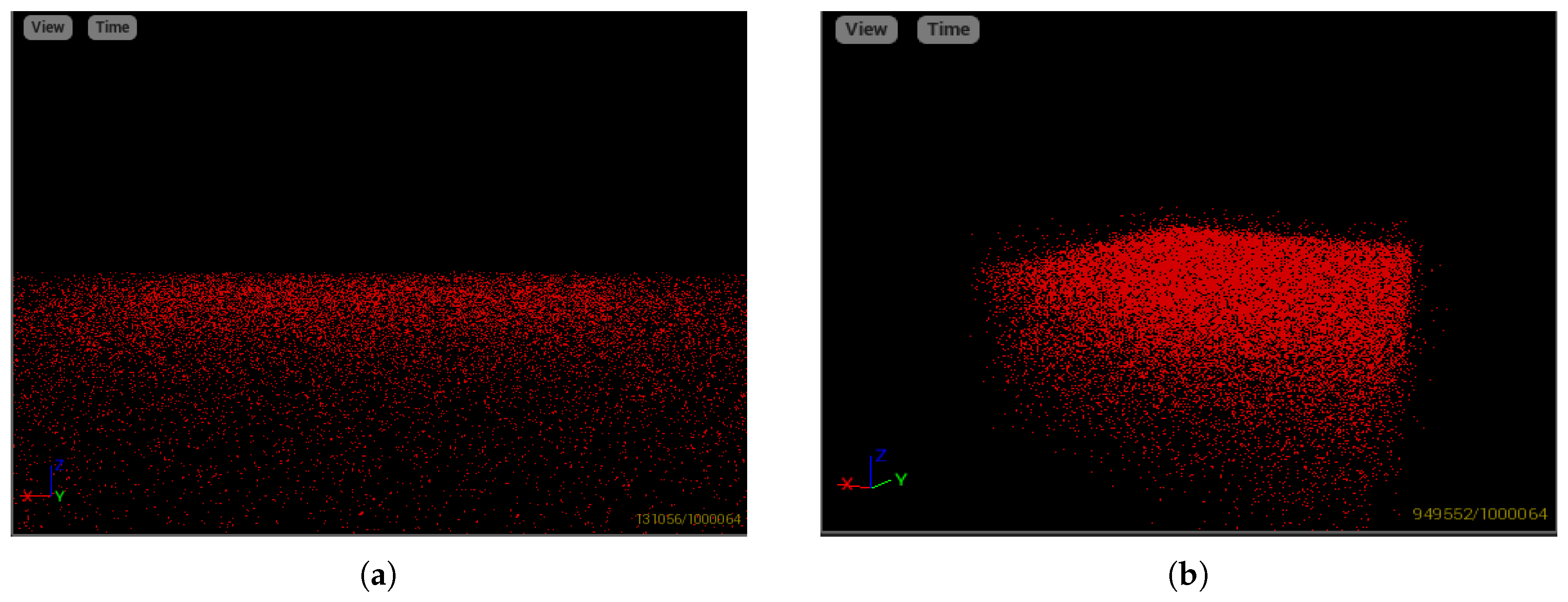
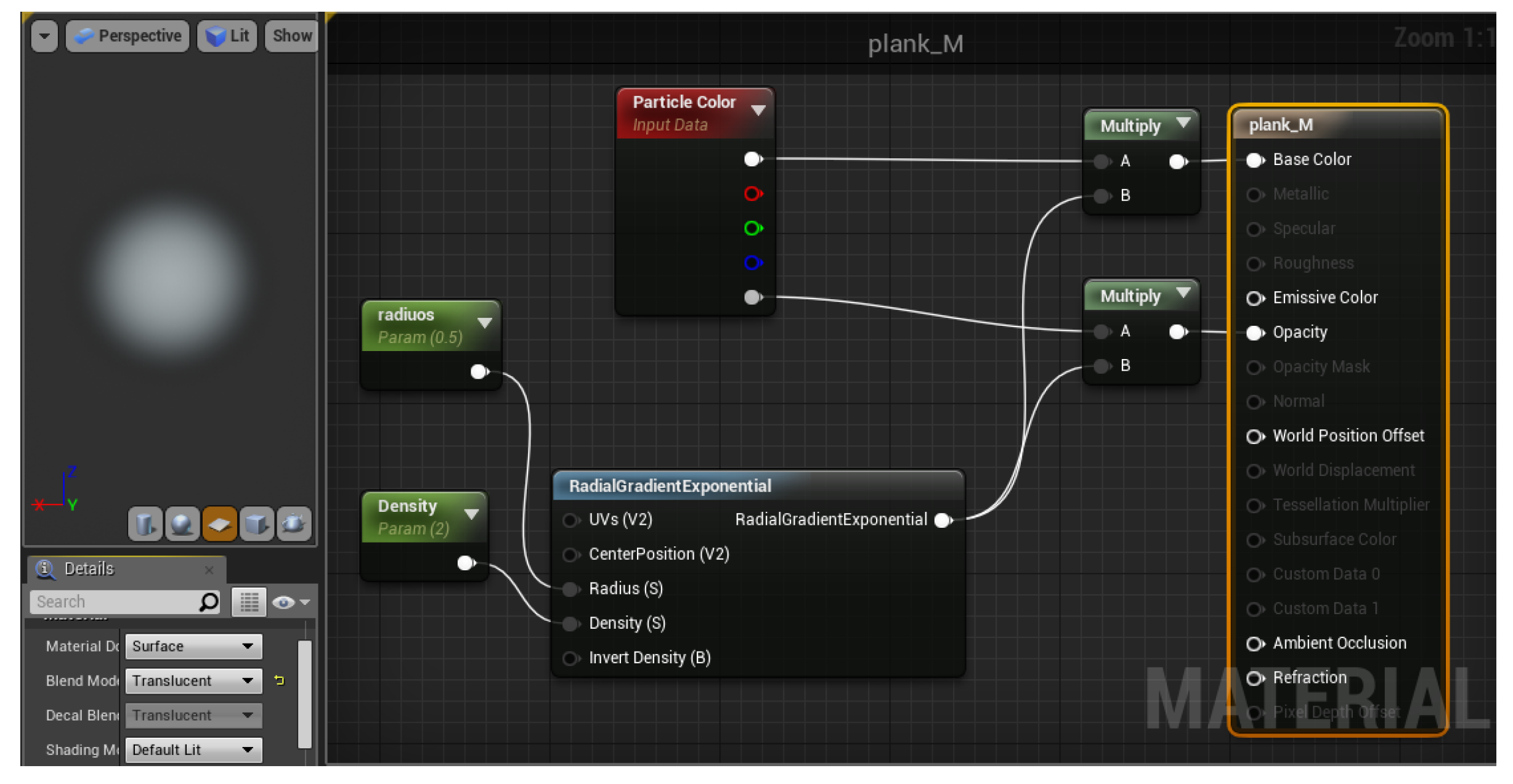
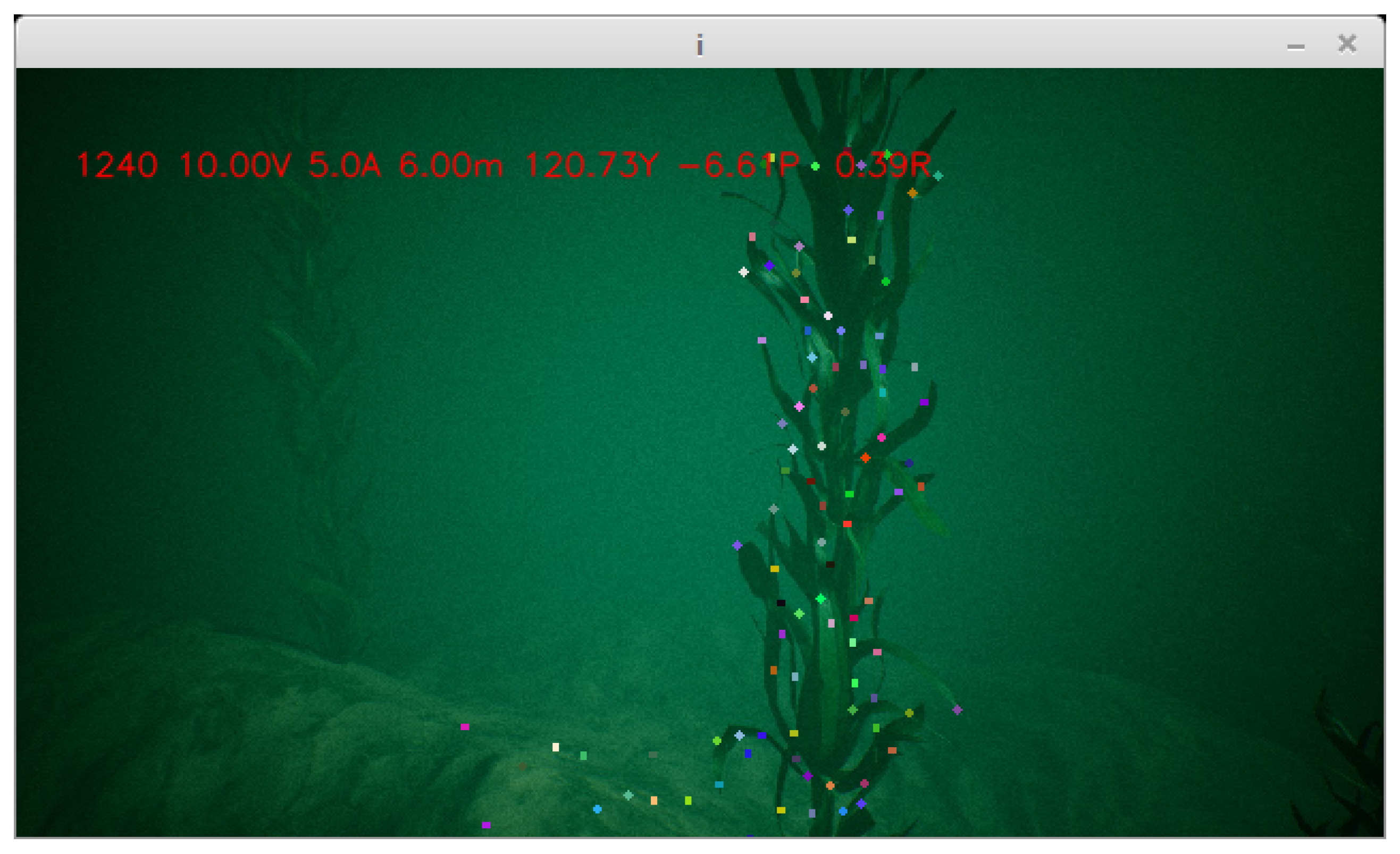
5.3. Simulating Plankton
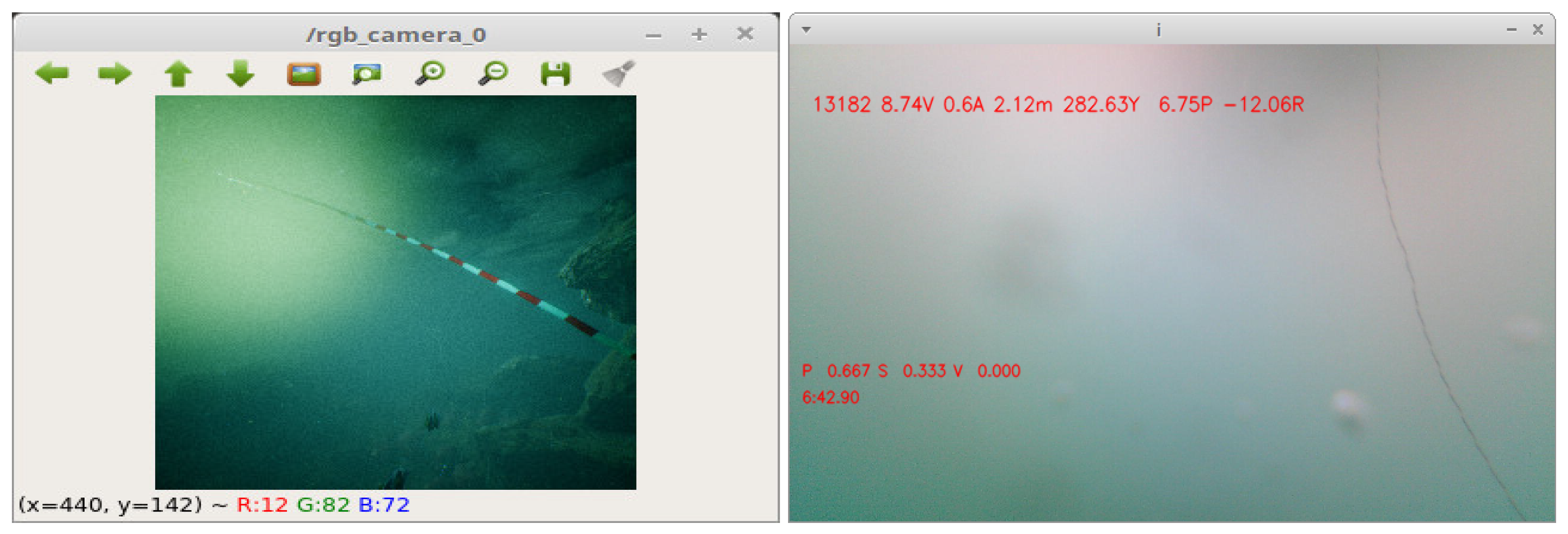
5.4. Test Case Results
6. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
Appendix A. ROV Dynamics Implementation
| import matplotlib.pyplot as plt from sympy import ∗ import sympy.physics.mechanics as me from sympy import sin, cos, symbols, solve from pydy.codegen.ode_function_generators import generate_ode_function from scipy.integrate import odeint from IPython.display import SVG me.init_vprinting(use_latex=’mathjax’) |
| N = me.ReferenceFrame(’N’) # Inertial Reference Frame O = me.Point(’O’) # Define a world coordisympynate origin O.set_vel(N, 0) # Setting world velocity to 0 #generelized coordinates #q0..3 = xyz positions q4..6 = yaw,pitch,roll rotations q = list(me.dynamicsymbols(’q0:6’)) #generlized speeds u = list(me.dynamicsymbols(’u0:6’)) kin_diff=Matrix(q).diff()-Matrix(u) |
| Wx = symbols(’W_x’) Wh = symbols(’W_h’) T1 = symbols(’T_1’) T2 = symbols(’T_2’) Bh = symbols(’B_h’) Bw = symbols(’B_w’) m_b = symbols(’m_b’) # Mass of the body v_b = symbols(’v_b’) # Volume of the body mu = symbols(’\mu’) #drag mu_r = symbols(’\mu_r’) #rotational drag g = symbols(’g’) I = list(symbols(’Ixx, Iyy, Izz’)) #Moments of inertia of body |
| Rz=N.orientnew(’R_z’, ’Axis’, (q[3+2], N.z)) Rz.set_ang_vel(N,u[3+2]∗N.z) Ry=Rz.orientnew(’R_y’, ’Axis’, (q[3+1], Rz.y)) Ry.set_ang_vel(Rz,u[3+1]∗Rz.y) R=Ry.orientnew(’R’, ’Axis’, (q[3+0], Ry.x)) R.set_ang_vel(Ry,u[3+0]∗Ry.x) |
| # Center of mass of body COM = O.locatenew(’COM’, q[0]∗N.x + q[1]∗N.y + q[2]∗N.z) # Set the velocity of COM COM.set_vel(N, u[0]∗N.x + u[1]∗N.y + u[2]∗N.z) # center of bouyency COB = COM.locatenew(’COB’, R.x∗Bw+R.z∗Bh) COB.v2pt_theory(COM, N, R); |
| Ib = me.inertia(R, ∗I , ixy=0, iyz=0, izx=0) Body = me.RigidBody(’Body’, COM, R, m_b, (Ib, COM)) |
| v=N.x∗u[0]+N.y∗u[1]+N.z∗u[2] Fd=-v∗mu T_z=(R,-u[3+2]∗N.z∗mu_r) T_x=(R,-u[3+0]∗Rz.x∗mu_r) T_y=(R,-u[3+1]∗Rx.y∗mu_r) #rotaional dumping Torqe |
| Fg = -N.z ∗ m_b ∗ g # gravity Fb = N.z ∗ v_b ∗ 1e3 ∗g # buoyancy F1, F2, F3 = symbols(’f_1, f_2, f_3’) # thrusters |
| #multiplying by inverse mass matrix: u_dot=kane.mass_matrix.inv()∗kane.forcing #replacing the constants with actual numerical values: subs=[(Wx,0.1), (Wh,0.15), (T1,0.1), (T2,0.05), (Bh,0.08), (Bw,0.01), (m_b,1.0), (v_b,0.001), (mu,0.3), (mu_r,0.2), (g,9.8), (I[0],0.5), (I[1],0.5), (I[2],0.5) ] u_dot_simp=u_dot.subs(subs) u_dot_simp=trigsimp(u_dot_simp) #generating a lambda function to compute the values of the u_dot vector from sympy import lambdify def get_next_state_lambda(subs): u_dot_simp_q_u_f=u_dot_simp.subs(subs) return lambdify((q,u,F1,F2,F3),u_dot_simp_q_u_f) #integrating function which takes the current state and returns the next state def get_next_state(curr_q,curr_u,control,curr_t,dt,lamb): forces=control(curr_t) u_dot_f=lamb(curr_q,curr_u,∗forces).flatten() next_q=curr_q+curr_u∗dt next_u=curr_u+u_dot_f∗dt return next_q,next_u |
References
- Fahlstrom, P.; Gleason, T. Introduction to UAV Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- AirSim, Simulator for Drones. 2016. Available online: https://github.com/microsoft/airsim/ (accessed on 21 December 2018).
- NVIDIA DRIVE CONSTELLATION. 2018. Available online: https://www.nvidia.com/en-us/self-driving-cars/drive-constellation/ (accessed on 21 December 2018).
- Underwater Simulation. Available online: https://github.com/uji-ros-pkg/underwater_simulation (accessed on 21 December 2018).
- Kermorgant, O. A dynamic simulator for underwater vehicle-manipulators. In Proceedings of the International Conference on Simulation, Modeling, and Programming for Autonomous Robots, Bergamo, Italy, 20–23 October 2014; pp. 25–36. [Google Scholar]
- Multi-ROV Training Simulator. Available online: http://marinesimulation.com/rovsim-gen3/ (accessed on 21 December 2018).
- Myint, M.; Yonemori, K.; Lwin, K.N.; Yanou, A.; Minami, M. Dual-eyes vision-based docking system for autonomous underwater vehicle: An approach and experiments. J. Intell. Robot. Syst. 2018, 92, 159–186. [Google Scholar] [CrossRef]
- Myint, M.; Yonemori, K.; Yanou, A.; Ishiyama, S.; Minami, M. Robustness of visual-servo against air bubble disturbance of underwater vehicle system using three-dimensional marker and dual-eye cameras. In Proceedings of the IEEE OCEANS’15 MTS/IEEE, Washington, DC, USA, 19–22 October 2015; pp. 1–8. [Google Scholar]
- Ganoni, O.; Mukundan, R.; Green, R. Visually Realistic Graphical Simulation of Underwater Cable. In Proceedings of the 26th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Plzen, Czech, 28 May–1 June 2018. [Google Scholar]
- Ganoni, O.; Mukundan, R. A Framework for Visually Realistic Multi-robot Simulation in Natural Environment. arXiv, 2017; arXiv:1708.01938. [Google Scholar]
- Mechanics, S.C. Kane Method Implementation. Available online: http://docs.sympy.org/latest/modules/physics/mechanics/kane.html (accessed on 21 December 2018).
- SymPy. Available online: http://docs.sympy.org (accessed on 21 December 2018).
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985; Chapter 7; pp. 30–31. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; pp. 233–245. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985; Chapter 6; pp. 158–159. [Google Scholar]
- SymPy Mechanics. Available online: http://docs.sympy.org/latest/modules/physics/mechanics/index.html (accessed on 21 December 2018).
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985; Chapter 7; pp. 204–205. [Google Scholar]
- Bender, J.; Müller, M.; Otaduy, M.A.; Teschner, M.; Macklin, M. A survey on position-based simulation methods in computer graphics. Comput. Graph. Forum 2014, 33, 228–251. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. (TOG) 2013, 32, 104. [Google Scholar] [CrossRef]
- Jakobsen, T. Advanced character physics. In Proceedings of the Game Developers Conference, San Jose, CA, USA, 22 March 2001; Volume 3. [Google Scholar]
- Marshall, R.; Jensen, R.; Wood, G. A general Newtonian simulation of an n-segment open chain model. J. Biomech. 1985, 18, 359–367. [Google Scholar] [CrossRef]
- Cable Component in Unreal Engine 4. Available online: https://docs.unrealengine.com/latest/INT/Engine/Components/Rendering/CableComponent/ (accessed on 21 December 2018).
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98. [Google Scholar] [CrossRef]
- OpenRov. Available online: https://www.openrov.com/ (accessed on 21 December 2018).
- Cable Simulation Video. 2018. Available online: https://youtu.be/_QoMUSlQCsg (accessed on 21 December 2018).
- Underwater Cable Reel Simulation Video. 2018. Available online: https://youtu.be/DO-x2RaZHso (accessed on 21 December 2018).
- Cable Sim Project. 2018. Available online: https://github.com/UnderwaterROV/UWCableComponent (accessed on 21 December 2018).
- Jupyter. Available online: http://jupyter.org/ (accessed on 21 December 2018).
- Cable Sim Notebook. 2018. Available online: https://github.com/UnderwaterROV/underwaterrov/blob/master/notebooks/rope.ipynb (accessed on 21 December 2018).
- Lalli, C.; Parsons, T.R. Biological Oceanography: An Introduction; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Capuzzo, E.; Stephens, D.; Silva, T.; Barry, J.; Forster, R.M. Decrease in water clarity of the southern and central North Sea during the 20th century. Glob. Chang. Biol. 2015, 21, 2206–2214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haltrin, V.I. Chlorophyll-based model of seawater optical properties. Appl. Opt. 1999, 38, 6826–6832. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, J.S.; Moore, K.D.; McLean, J.; Strand, M.P. Underwater optical imaging: Status and prospects. Oceanography 2001, 14, 66–76. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Buiteveld, H.; Hakvoort, J.; Donze, M. Optical properties of pure water. In Proceedings of the Ocean Optics XII, Bergen, Norway, 13–15 June 1994; Volume 2258, pp. 174–184. [Google Scholar]
- Thibos, L.; Bradley, A.; Still, D.; Zhang, X.; Howarth, P. Theory and measurement of ocular chromatic aberration. Vis. Res. 1990, 30, 33–49. [Google Scholar] [CrossRef]
- Unreal Engine 4 Chromatic Aberration. Available online: https://docs.unrealengine.com/latest/INT/Engine/Rendering/PostProcessEffects/SceneFringe/ (accessed on 21 December 2018).
- Ocean Floor Environment. Available online: https://www.unrealengine.com/marketplace/ocean-floor-environment (accessed on 21 December 2018).
- Unreal Engine 4 SimpleGrassWind. Available online: https://docs.unrealengine.com/en-us/Engine/Rendering/Materials/Functions/Reference/WorldPositionOffset (accessed on 21 December 2018).
- Exponential Height Fog User Guide. Available online: https://docs.unrealengine.com/latest/INT/Engine/Actors/FogEffects/HeightFog/index.html (accessed on 21 December 2018).
- NatGeoPauly-Freshwater Fish Feeding on Plankton “Peacock Bass”. 2014. Available online: https://www.youtube.com/watch?v=JAd2jZuNkd8 (accessed on 21 December 2018).
- Unreal Engine 4 Particle Systems. Available online: https://docs.unrealengine.com/latest/INT/Engine/Rendering/ParticleSystems/ (accessed on 21 December 2018).
- Schroeder, W.J.; Lorensen, B.; Martin, K. The Visualization Toolkit: An Object-Oriented Approach to 3D Graphics; Kitware: Clifton Park, NY, USA, 2004. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Bouguet, J.Y. Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm. Intel Corp. 2001, 5, 4. [Google Scholar]
- Underwater Simulation. 2018. Available online: https://youtu.be/MP2xG_Tms3E (accessed on 21 December 2018).
- ROV Dynamics Notebook. 2018. Available online: https://github.com/UnderwaterROV/underwaterrov/blob/master/notebooks/openrov_sim.ipynb (accessed on 21 December 2018).












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganoni, O.; Mukundan, R.; Green, R. A Generalized Simulation Framework for Tethered Remotely Operated Vehicles in Realistic Underwater Environments. Drones 2019, 3, 1. https://doi.org/10.3390/drones3010001
Ganoni O, Mukundan R, Green R. A Generalized Simulation Framework for Tethered Remotely Operated Vehicles in Realistic Underwater Environments. Drones. 2019; 3(1):1. https://doi.org/10.3390/drones3010001
Chicago/Turabian StyleGanoni, Ori, Ramakrishnan Mukundan, and Richard Green. 2019. "A Generalized Simulation Framework for Tethered Remotely Operated Vehicles in Realistic Underwater Environments" Drones 3, no. 1: 1. https://doi.org/10.3390/drones3010001
APA StyleGanoni, O., Mukundan, R., & Green, R. (2019). A Generalized Simulation Framework for Tethered Remotely Operated Vehicles in Realistic Underwater Environments. Drones, 3(1), 1. https://doi.org/10.3390/drones3010001






