Multirotor Drone Aerodynamic Interaction Investigation
Abstract
:1. Introduction
2. Material and Methods
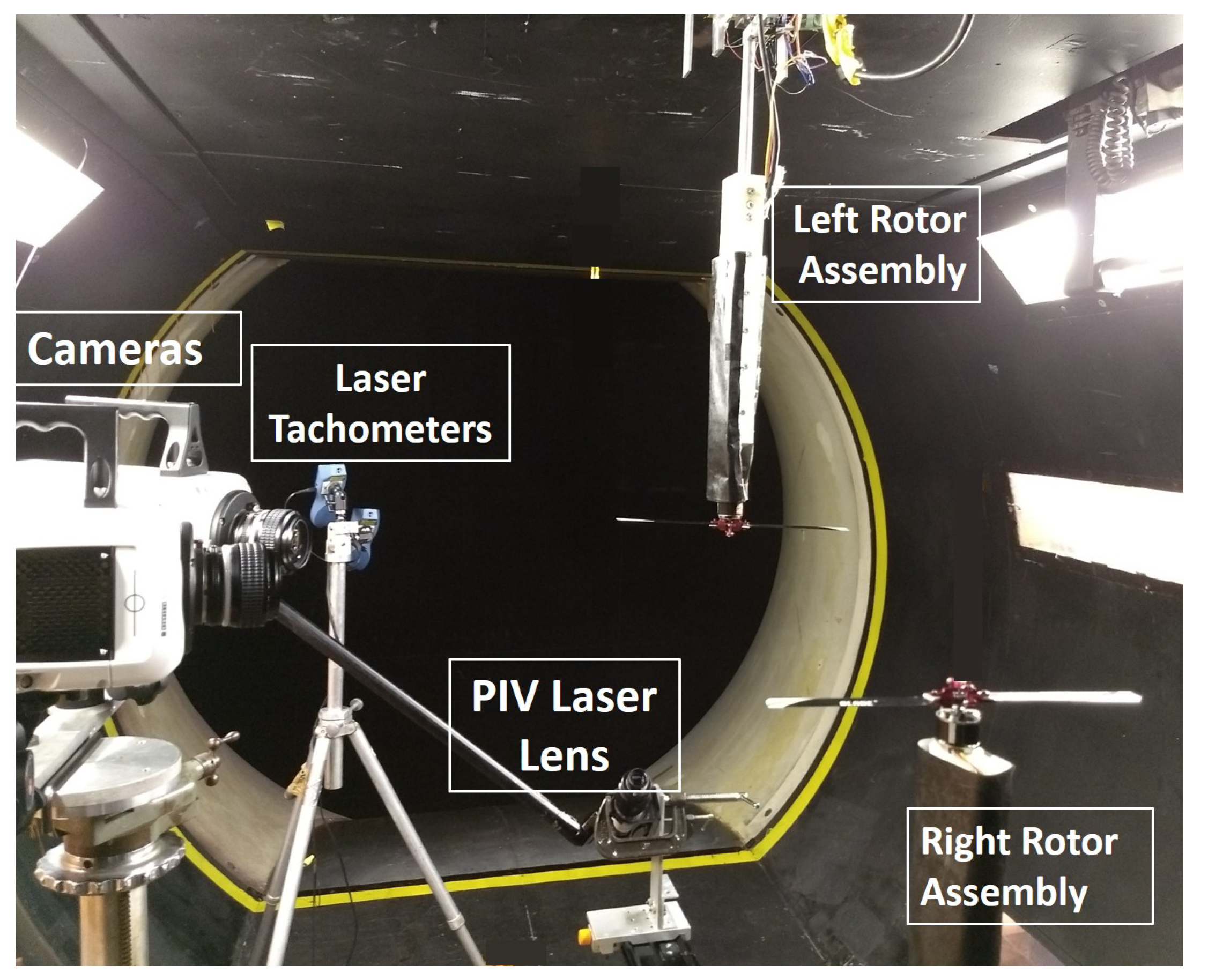
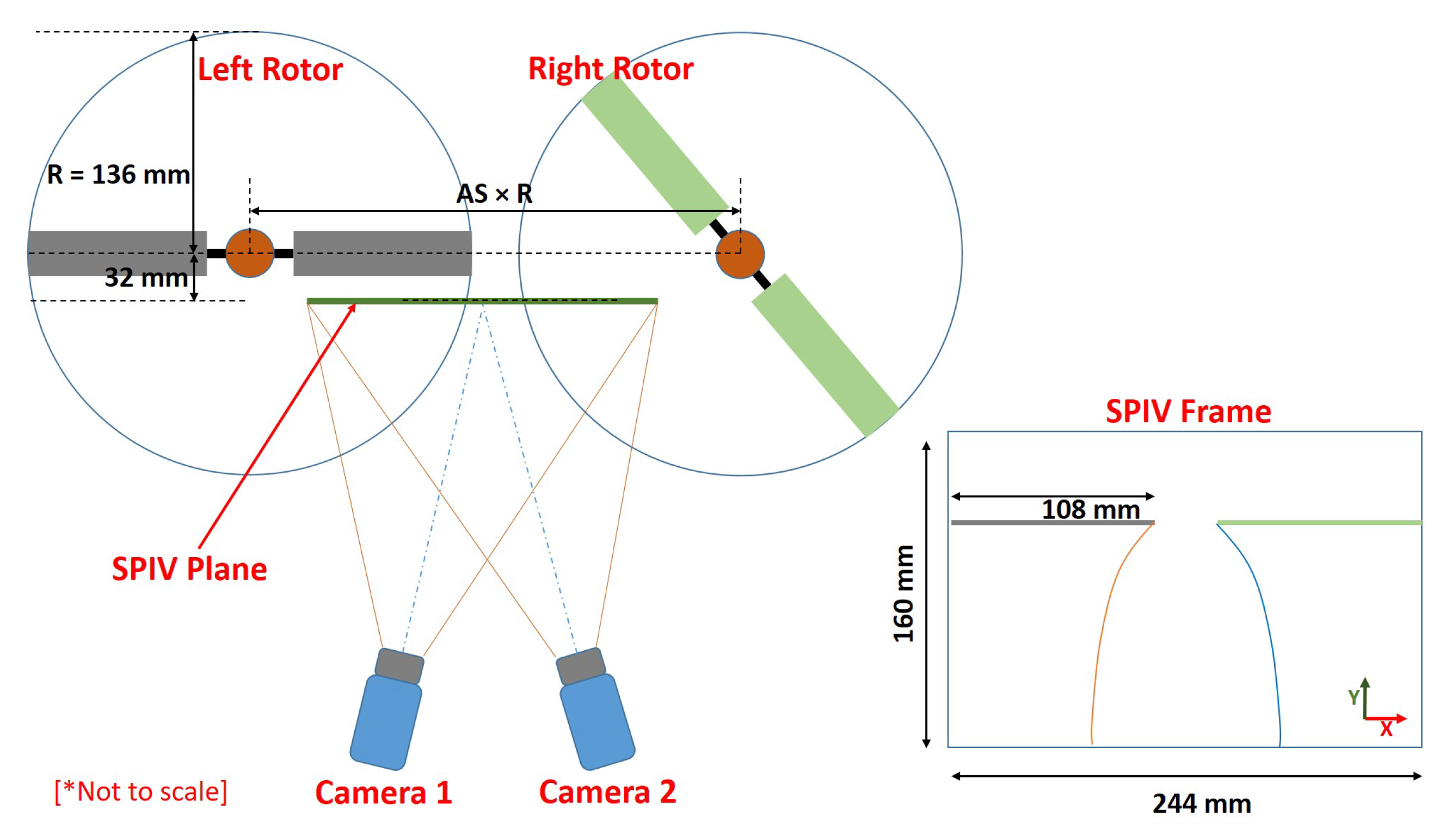
2.1. Facility and Experimental Setup
2.2. Trim and Test Conditions
2.3. Uncertainty Estimates
3. Results
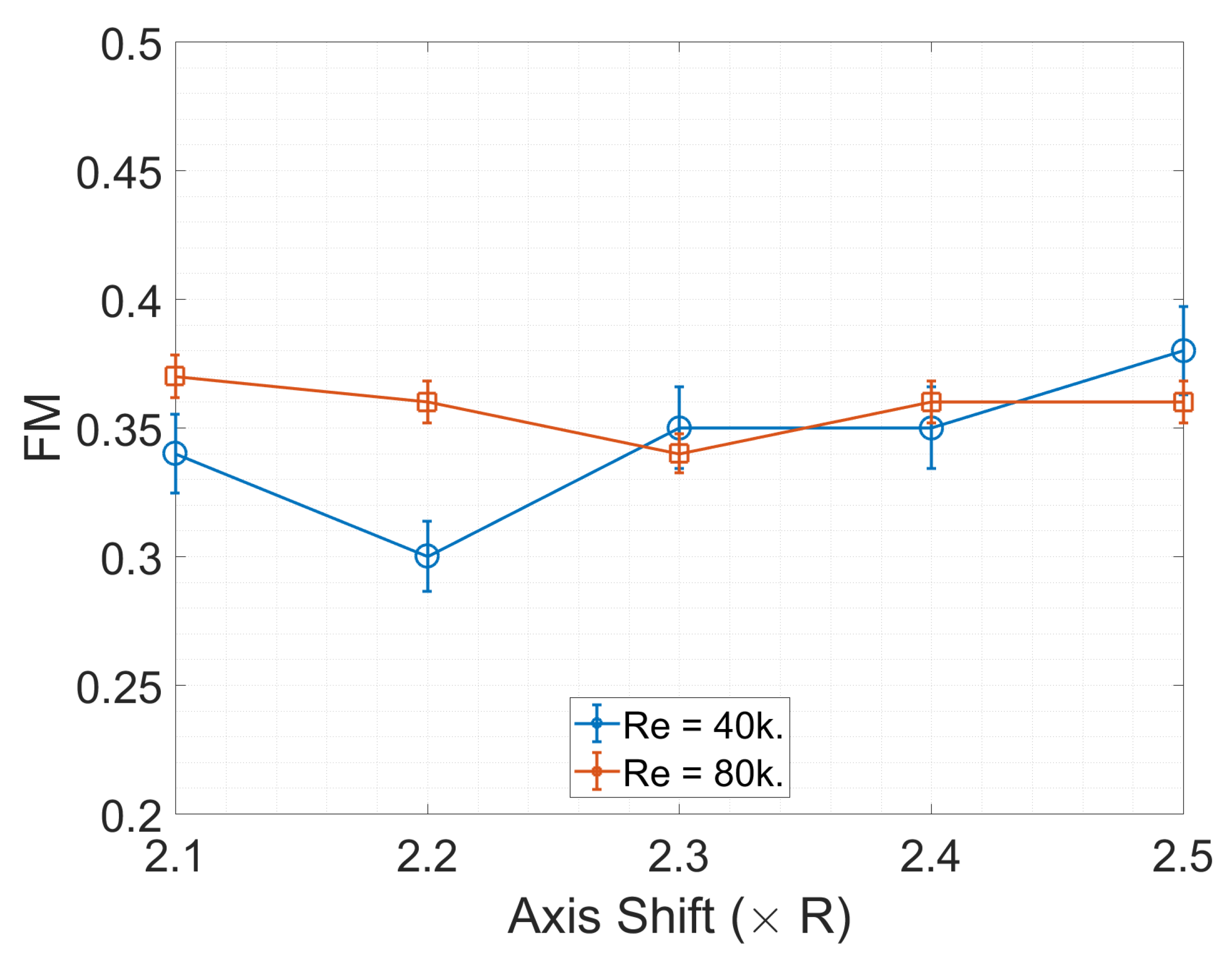
3.1. Performance Measurements
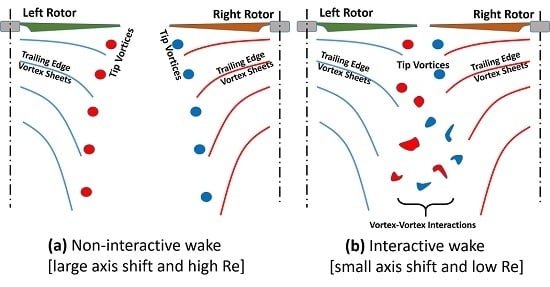
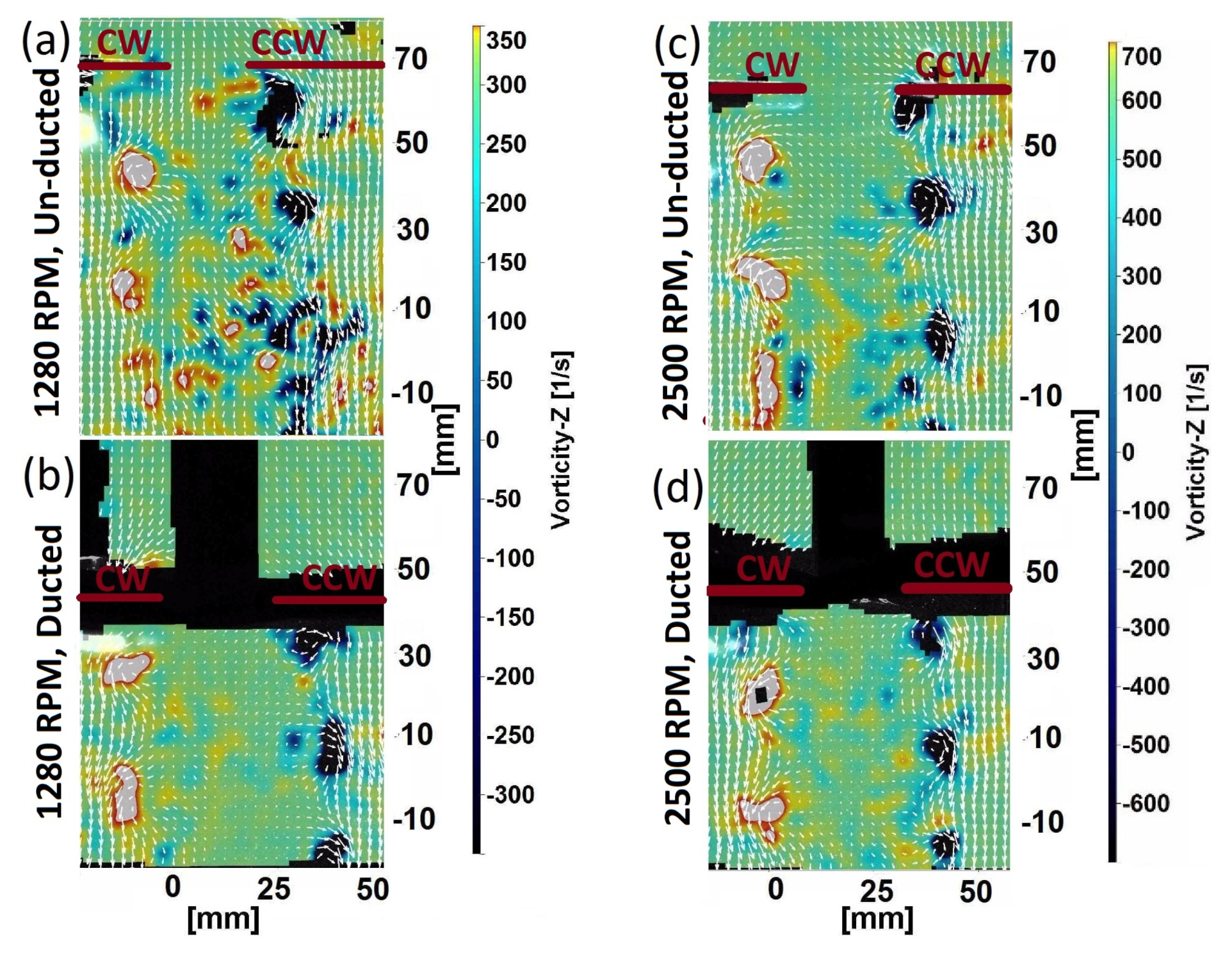
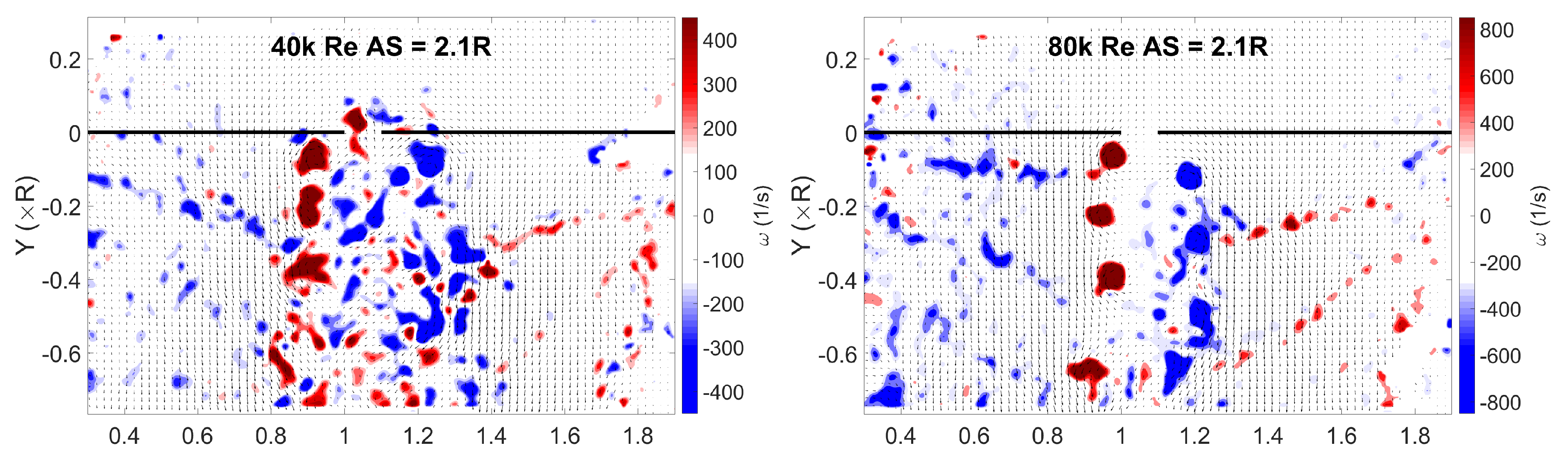
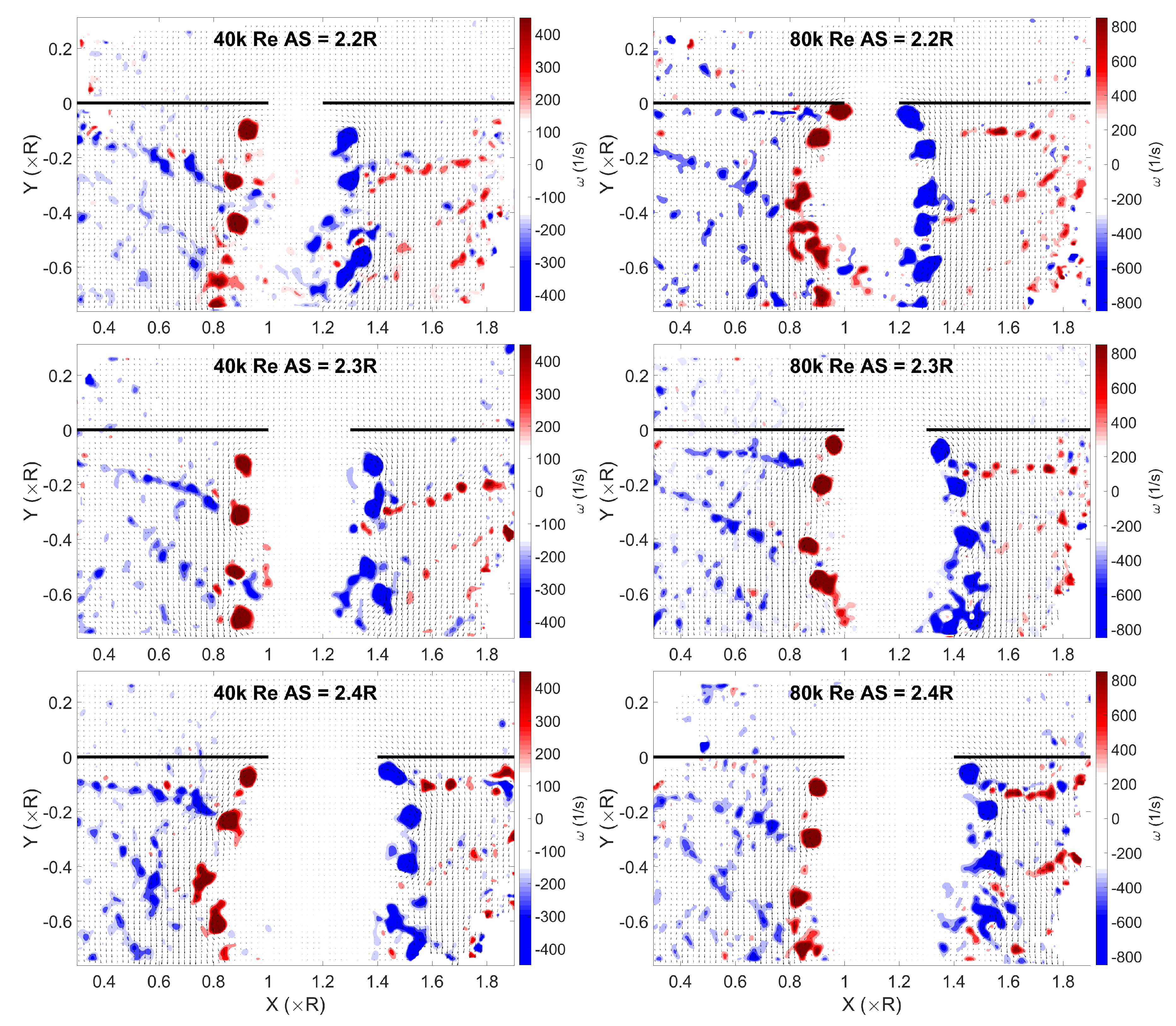
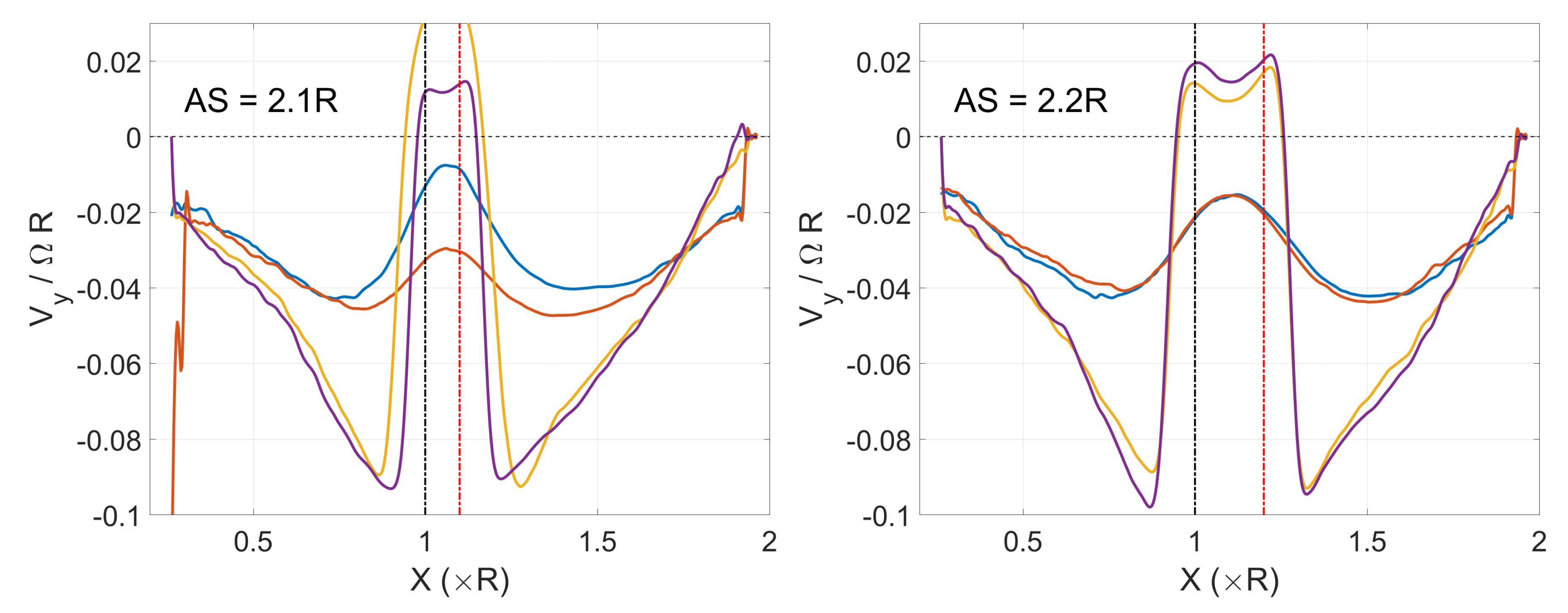
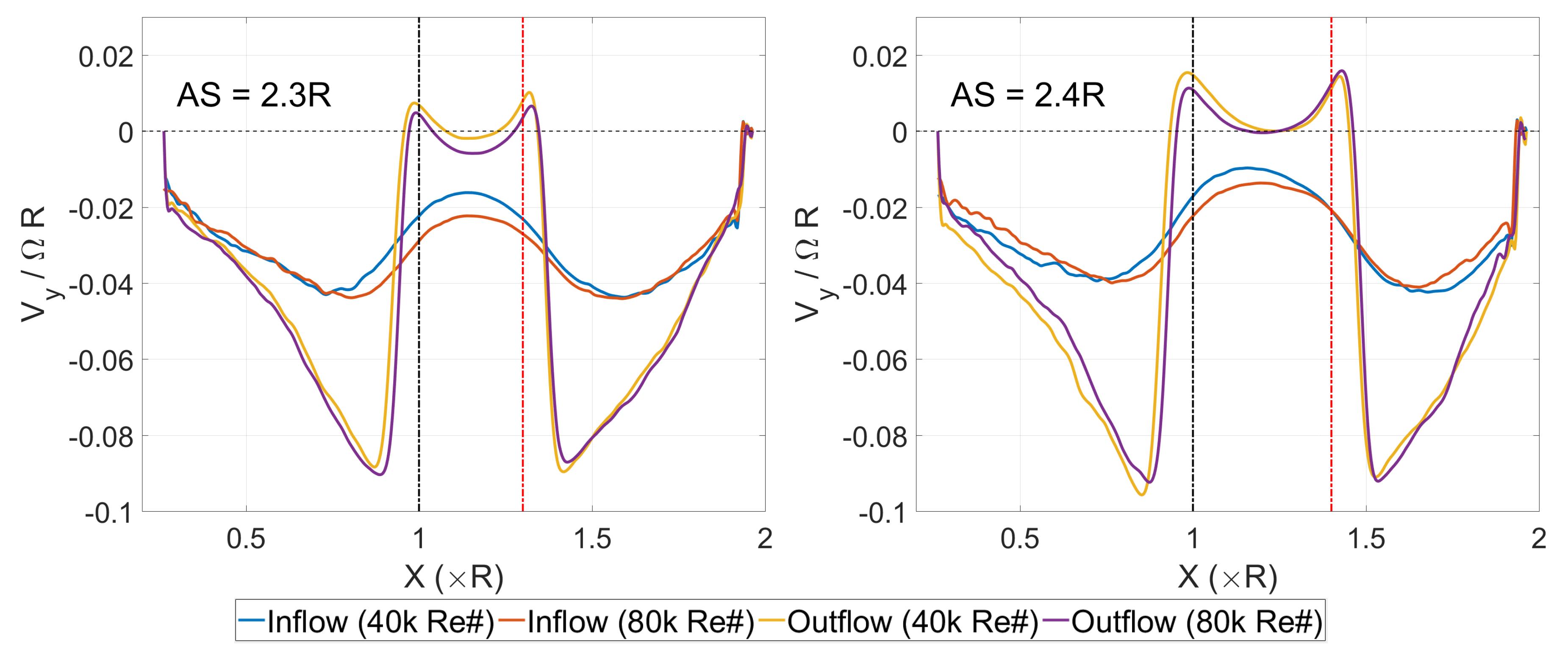
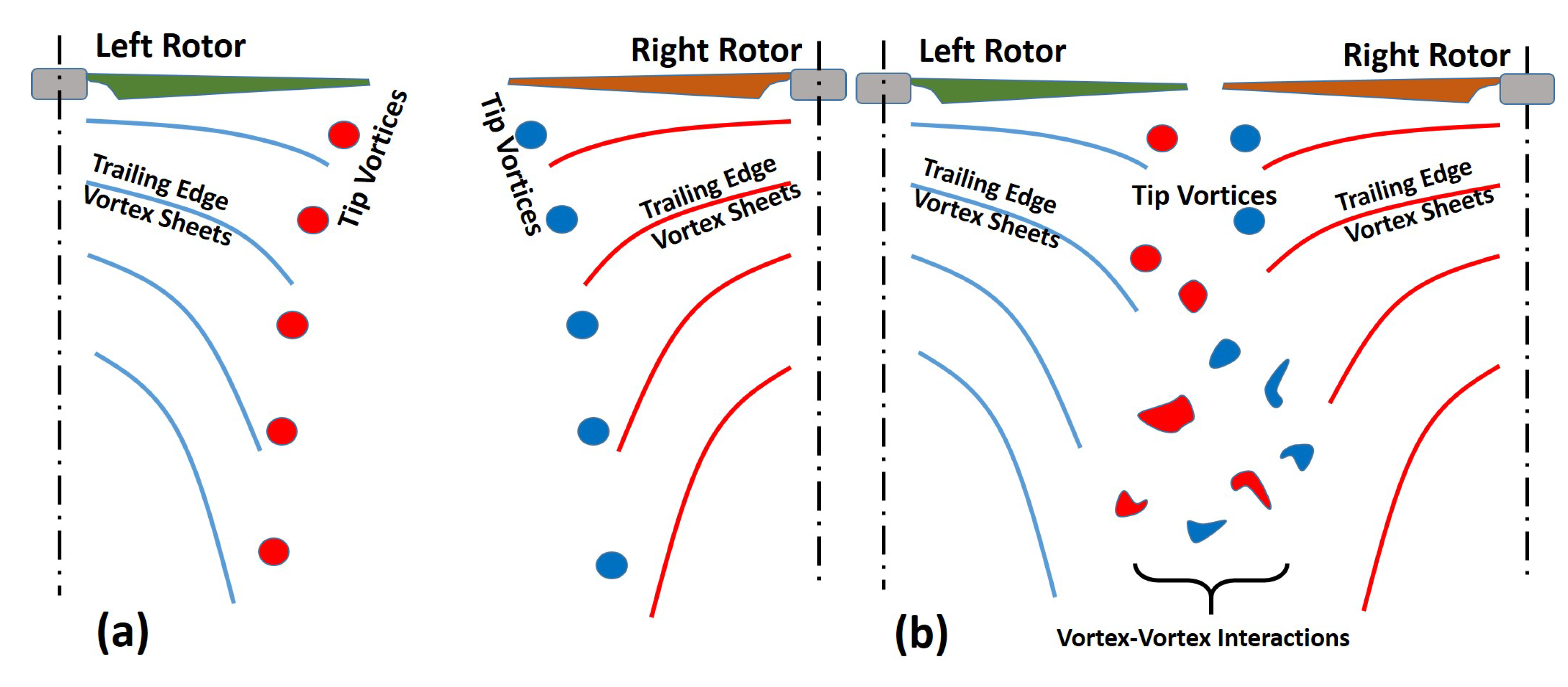
3.2. Instantaneous Flow Fields
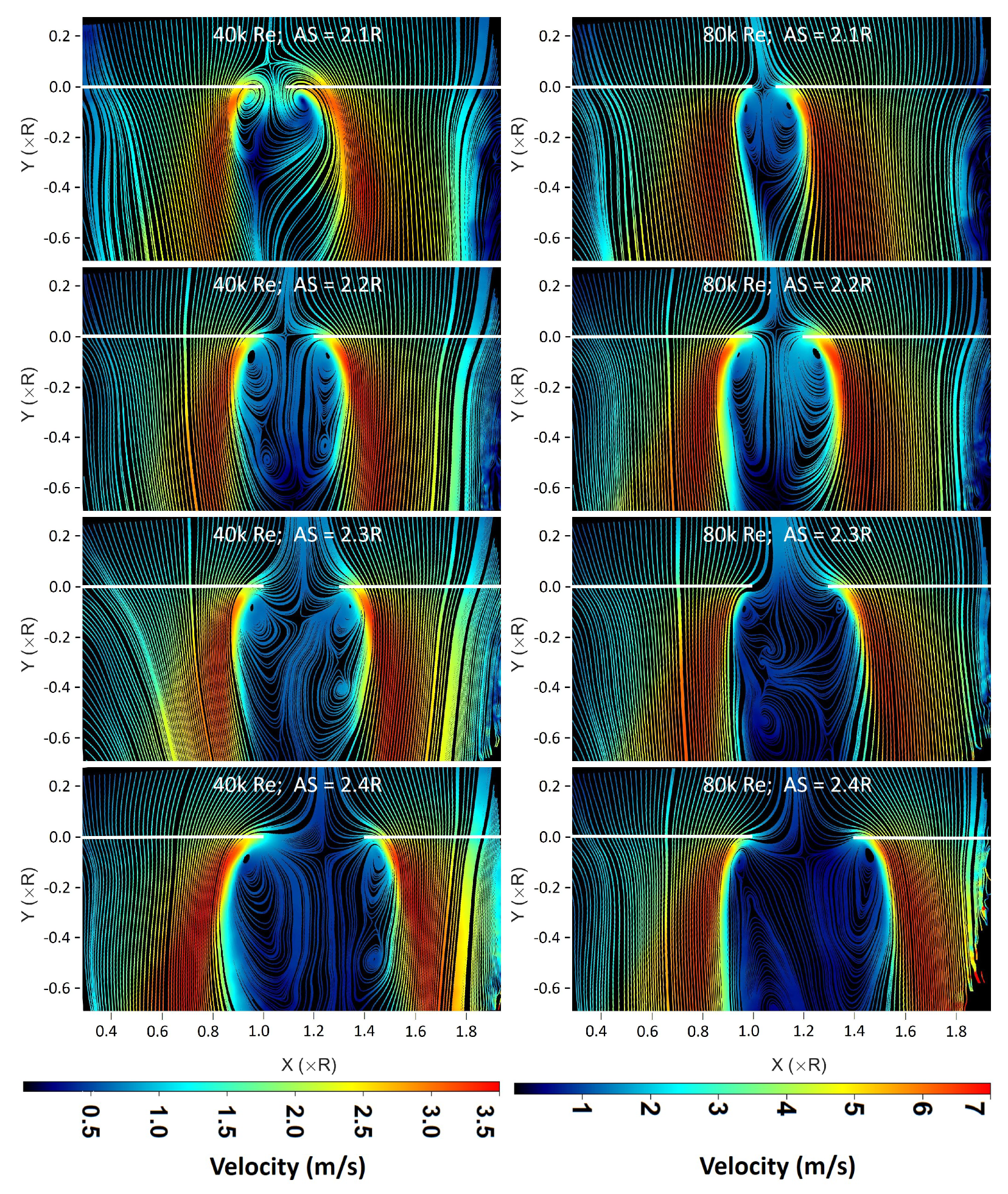
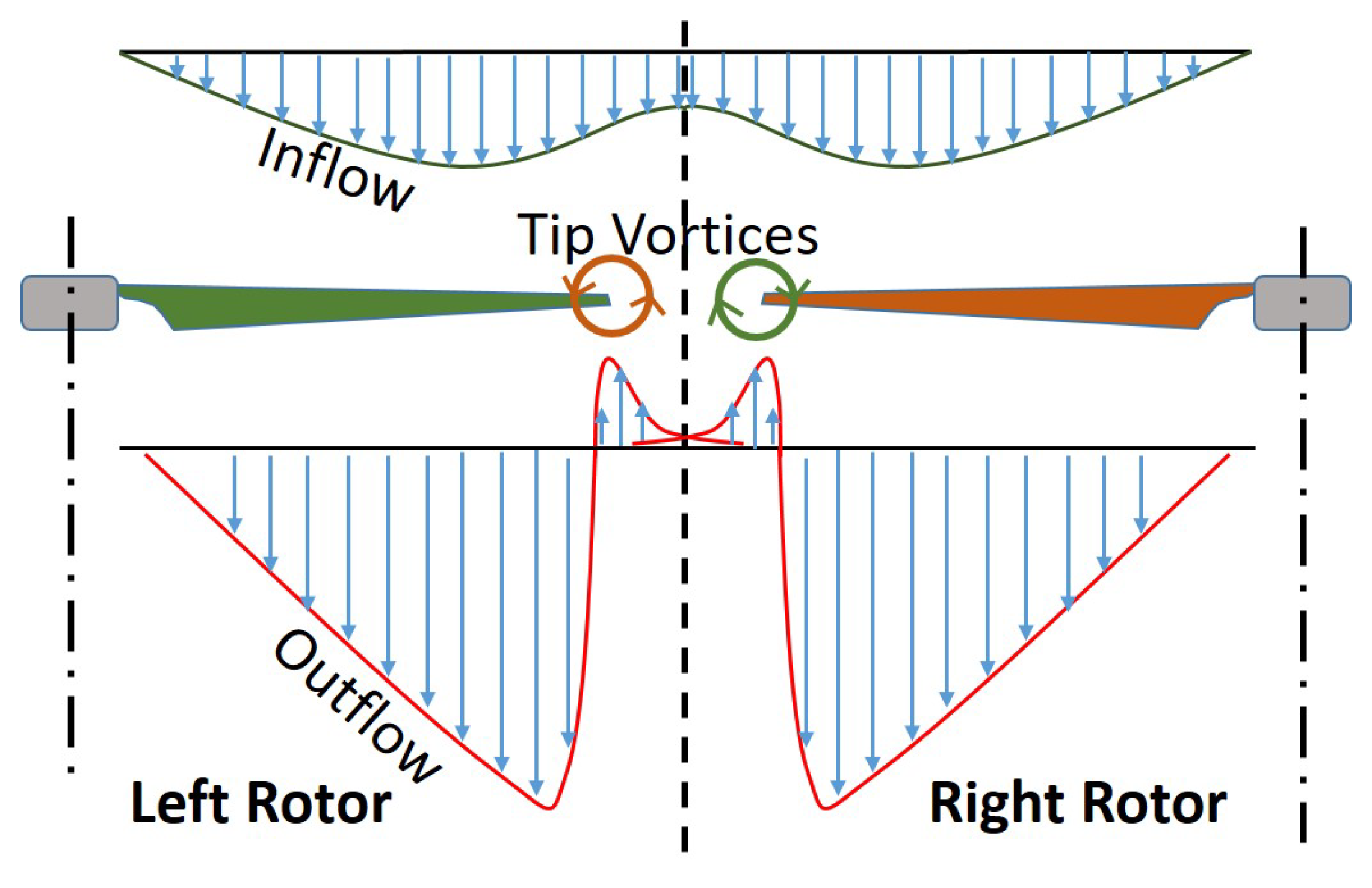
3.3. Mean Flow Fields
4. Discussion
5. Conclusions
- Very close proximity of adjacent rotors adversely affects rotor performance
- Blade–vortex interaction hypothesized to be a reason behind the noticed effect on performance.
- High inter-rotor wake interaction observed for close proximity rotors at low Reynolds numbers.
- Similarities observed in instantaneous and mean flow fields for the range of tested conditions, useful in extending the understanding to a wider range of vehicle configurations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AS | Axis shift. |
| c | Blade chord. |
| R | Rotor radius. |
| r | Spanwise radial location. |
| Rotor angular velocity. | |
| Density of air. | |
| Dynamic viscosity of air. |
References
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M. Unmanned aerial systems for civil applications: A review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460. [Google Scholar] [CrossRef] [PubMed]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerospace Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Bohorquez, F.; Pines, D. Hover Performance of Rotor Blades at Low Reynolds Numbers for Rotary Wing Micro Air Vehicles. An Experimental and CFD Study; AIAA Paper: Reston, VA, USA, 2003; Volume 3930, p. 2003. [Google Scholar]
- Bohorquez, F. Rotor Hover Performance and System Design of an Efficient Coaxial Rotary Wing Micro Air Vehicle. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2007. [Google Scholar]
- Hein, B.R.; Chopra, I. Hover performance of a Micro Air Vehicle: Rotors at low Reynolds number. J. Am. Helicopter Soc. 2007, 52, 254–262. [Google Scholar] [CrossRef]
- Kunz, P.J.; Strawn, R.C. Analysis and design of rotors at ultra-low Reynolds numbers. In Proceedings of the 40th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Rubio, O.; Gutiérrez, F.; Zuñiga, J.C.; Funes-Gallanzi, M. Low-Re μUAV Rotor Design. In Fluid Dynamics in Physics, Engineering and Environmental Applications; Springer: Berlin, Germany, 2013; pp. 489–500. [Google Scholar]
- Lakshminarayan, V.K.; Bush, B.L.; Duraisamy, K.; Baeder, J.D. Computational investigation of micro hovering rotor aerodynamics. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006; pp. 5–8. [Google Scholar]
- Lakshminarayan, V.K.; Baeder, J.D. Computational investigation of micro hovering rotor aerodynamics. J. Am. Helicopter Soc. 2010, 55, 22001. [Google Scholar] [CrossRef]
- Schroeder, E.J.; Baeder, J.D. Using computational fluid dynamics for micro-Air vehicle airfoil validation and prediction. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 7–8 June 2005. [Google Scholar]
- Schroeder, E.J. Low Reynolds Number Flow Validation Using Computational Fluid Dynamics with Application to Micro Air Vehicles; University of Maryland: College Park, MD, USA, 2005. [Google Scholar]
- Radhakrishnan, A.; Schmitz, F. An experimental investigation of a quad tilt rotor in low speed forward flight. In Proceedings of the 4th Decennial Specialists’ Conference on Aeromechanics, American Helicopter Society, San Francisco, CA, USA, 21–23 January 2004. [Google Scholar]
- Ramasamy, M. Measurements comparing hover performance of single, coaxial, tandem, and tilt-rotor configurations. In Proceedings of the 69th AHS Annual Forum, Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Griffiths, D. A study of dual-rotor interference and ground effect using a free-vortex wake model. In Proceedings of the AHS International 58th Annual Forum, Montreal, QC, Canada, 11–13 June 2002; Volume 1, pp. 592–612. [Google Scholar]
- Gupta, V.; Baeder, J.D. Quad Tilt Rotor Aerodynamics in Helicopter Mode. In Annual Forum Proceedings; American Helicopter Society, Inc.: Fairfax, VA, USA, 2005; Volume 61, p. 416. [Google Scholar]
- Lee, J.; Yee, K.; Oh, S. Aerodynamic characteristic analysis of multi-rotors using a modified free-wake method. Trans. Jpn. Soc. Aeronaut. Space Sci. 2009, 52, 168–179. [Google Scholar] [CrossRef]
- Rajagopalan, R.G.; Baskaran, V.; Hollingsworth, A.; Lestari, A.; Garrick, D.; Solis, E.; Hagerty, B. RotCFD-A Tool for Aerodynamic Interference of Rotors: Validation and Capabilities. In Proceedings of the Future Vertical Lift Aircraft Design Conference, San Francisco, CA, USA, 18–20 January 2012. [Google Scholar]
- Yoon, S.; Lee, H.C.; Pulliam, T.H. Computational Analysis of Multi-Rotor Flows. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0812. [Google Scholar]
- Huang, H.; Hoffmann, G.M.; Waslander, S.L.; Tomlin, C.J. Aerodynamics and control of autonomous quadrotor helicopters in aggressive maneuvering. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’09), Kobe, Japan, 12–17 May 2009; pp. 3277–3282. [Google Scholar]
- Carroll, T.; George, I.R.E.; Bramesfeld, G. Design Optimization of Small Rotors in Quad-Rotor Configuration. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1788. [Google Scholar]
- Shukla, D.; Hiremath, N.; Komerath, N. Aerodynamic Interactions Study on Low-Re Coaxial and Quad-Rotor Configurations. In Proceedings of the ASME International Mechanical Engineering Conference & Exposition IMECE2017, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Shukla, D.; Hiremath, N.; Komerath, N.M. Low Reynolds Number Aerodynamics Study on Coaxial and Quad-Rotor. In Proceedings of the 2018 Applied Aerodynamics, AIAA Aviation and Aeronautics Forum and Exposition, Atlanta, GA, USA, 25–29 June 2018; p. 4118. [Google Scholar]
- Sciacchitano, A.; Neal, D.R.; Smith, B.L.; Warner, S.O.; Vlachos, P.P.; Wieneke, B.; Scarano, F. Collaborative framework for PIV uncertainty quantification: Comparative assessment of methods. Meas. Sci. Technol. 2015, 26, 074004. [Google Scholar] [CrossRef]
- Ramasamy, M.; Leishman, J.G.; Lee, T.E. Flowfield of a rotating-wing micro air vehicle. J. Aircr. 2007, 44, 1236–1244. [Google Scholar] [CrossRef]
| Rotor | |
| # of rotors | 2 |
| # of blades per rotor | 2 |
| Radius (R) | 0.136 m |
| Root cutout radius | 0.021 m |
| Airfoil | NACA 0010 |
| Blade planform | Constant chord, Untwisted |
| Chord length (c) | 0.019 m |
| Blade pitch angle () | Variable |
| Test Conditions | |
| Rotor tip Re # | 40,000, 80,000 |
| AS | 2.1, 2.2, 2.3, 2.4, |
| 2.5 (performance only) | |
| 0.004 (average per rotor) | |
| Case | FM | Case | FM |
|---|---|---|---|
| Un-ducted, 1280 RPM | 0.29 | Ducted, 1280 RPM | 0.43 |
| Un-ducted, 2500 RPM | 0.46 | Ducted, 2500 RPM | 0.50 |
| Un-ducted, 3500 RPM | 0.45 | Ducted, 3500 RPM | 0.47 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Radius (R) | 66 mm | Blade planform | Untwisted, Tapered |
| Camber | 14% | Chord length (c) | 19.5 mm @ r/R = 0.2 |
| 15.3 mm @ r/R = 1 | |||
| Blade thickness | 7% | Blade pitch angle () | |
| Adjacent rotor axis shift (AS) | 160 mm | Duct radius | 73 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shukla, D.; Komerath, N. Multirotor Drone Aerodynamic Interaction Investigation. Drones 2018, 2, 43. https://doi.org/10.3390/drones2040043
Shukla D, Komerath N. Multirotor Drone Aerodynamic Interaction Investigation. Drones. 2018; 2(4):43. https://doi.org/10.3390/drones2040043
Chicago/Turabian StyleShukla, Dhwanil, and Narayanan Komerath. 2018. "Multirotor Drone Aerodynamic Interaction Investigation" Drones 2, no. 4: 43. https://doi.org/10.3390/drones2040043
APA StyleShukla, D., & Komerath, N. (2018). Multirotor Drone Aerodynamic Interaction Investigation. Drones, 2(4), 43. https://doi.org/10.3390/drones2040043