Non-Parametric Shape Optimization of a Football Boot Bottom Plate ^†

Abstract

This paper describes the non-parametric shape optimization process for a football boot bottom plate. The non-parametric shape optimization process changes the nodes’ location of a model and outputs an optimum shape, which satisfies an optimization objective. The methodology presented in this study was able to change the shape of the football boot bottom plate, especially the dimensions of key features, to achieve four different target bending stiffnesses. Tosca Structure sensitivity-based shape optimization was used to perform the optimization process and output optimum bottom plates. Future research is needed to investigate the accuracy of the process in comparison with that of the previously developed parametric optimization process.

1. Introduction

Football footwear, known as the football boot, is an essential piece of equipment required by players to enhance their performance [1]. Since each football player has their own playstyle, level of ability, anthropometry, movement style, body weight and position, it is anticipated that there is scope to optimize the functional properties of a boot to suit an individual player.

The bending stiffness of the bottom plate is one of the important functional properties of the shoe [2]. Several studies have investigated the relationship between the bending stiffness of the boot and performance [3,4]. For example, increasing the bending stiffness of sports shoes has been reported to improve sprint performance [3]. However, relatively little work has been reported concerned with the design of the bottom plate to achieve a target bending stiffness. Schröder [5] introduced a parametric optimization loop for a football boot bottom plate where a number of parameters could be adjusted, and the process utilized a parameterised CAD (Computer-Aided Design) model. However, there were some restrictions found from the optimization loop such as a potential loss of design freedom and an increase in time investment when setting up parameters in the CAD model. These limitations historically have been discussed when using the parametric optimization process [6]. Therefore, the focus of this work is on the development of a non-parametric optimization system for a football boot bottom plate in order to overcome the limitations found in the parametric optimization process.

This present study aimed to apply a non-parametric shape optimization process to a football boot bottom plate based on Finite Element Analysis (FEA). A finite element model of the bottom plate was set up using the commercial FEA tool, Abaqus [7] (Dassault Systèmes, Vélizy-Villacoublay, France). The non-parametric optimization process was performed by Tosca Structure sensitivity-based shape optimization [8] (Dassault Systèmes, Vélizy-Villacoublay, France).

2. Non-Parametric Optimization

The optimization techniques used in the engineering industry can be classified into two categories; parametric optimization and non-parametric optimization [9]. Parametric optimization seeks to obtain a target objective function by searching the design space made up of design variables [10]. A geometric model is defined by parametric variables, and these variables are used as design variables in the optimization process. In the case of non-parametric optimization, it achieves a required optimum shape by either directly moving a node or multiple nodes’ locations (shape optimization) or removing mass without controlling the nodes’ locations (topology optimization).

The main disadvantage of the parametric optimization process is that a fully parameterized CAD model is required. This can also lead the design freedom being too restricted, which means only limited parameters can be adjusted during the optimization process [11]. This issue can be avoided in the non-parametric optimization process, since the parameterised CAD model is not necessary [6]. Therefore, it could provide greater design freedom than the parametric optimization process [11].

Tosca Structure is a non-parametric optimization commercial software package developed by Dassault Systèmes. Since it also has seamless integration with commercial FEA solvers (ABAQUS, ANSYS, ANSA), it has solved many industrial optimization problems [11]. In this present study, Tosca Structure sensitivity-based shape optimization was used to perform the non-parametric shape optimization process for the bottom plate.

3. Methods

The workflow of this research paper is highlighted with red colour in Figure 1. The non-parametric optimization of the bottom plate midfoot part could be carried out by the following procedures:

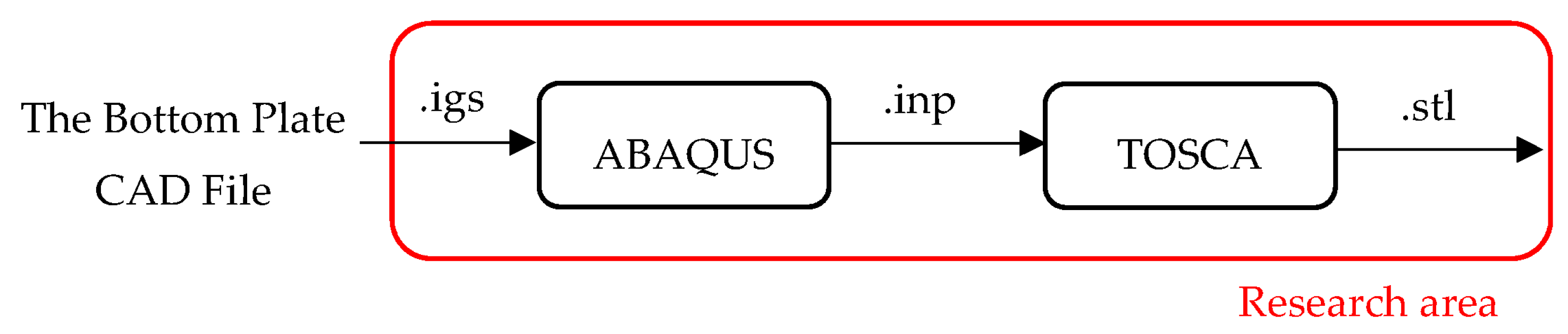
• The full model of the bottom plate CAD file was created (Figure 2a).
• The IGES file (.igs) of the bottom plate midfoot part (Figure 2b) was imported into the Abaqus Part section.
• The mechanical 3-point bending test boundary condition was applied in Abaqus.
• After Abaqus completed the analysis, an input file (.inp) was generated.
• The generated input file (.inp) was imported into Tosca Structure and preprocessed for shape optimization.
• Four different bending stiffnesses were targeted.
• The optimum shape of the bottom plate was saved to a .stl file.

3.1. FEA Pre-Processing

In this present study, bending stiffness was determined by 3-point bending in a simple and repeatable way. Figure 3a shows the mechanical test set up. In the mechanical testing, two supporting rigs carry the weight out each end and one rig in the middle applies a displacement to the center of the plate. The reaction force generated between the rig in the middle and the plate is measured. This testing condition was applied as the boundary condition in Abaqus. A displacement of 5 mm, referenced from Schröder [5], was applied in Abaqus. Figure 3b shows the deformed shape of the bottom plate in Abaqus. In this present study, the rigs were not modeled. Therefore, the effect of the rigs was ignored, for instance, the contact friction between the rigs and the plate.

3.2. Calculation of Bending Stiffness

The bending stiffness of the bottom plate was defined by the bending moment divided by the deflection angle, as shown in Equation (1). The bending moment was calculated by the reaction force multiplied by the distance, which is (d) in Figure 4. In the case of the deflection angle ($\theta$), it was the angle at which the plate was bent, as shown in Figure 4.

$$\mathrm{Bending}\mathrm{stiffness}[\mathrm{N}·\mathrm{m}/\text{°}]=\frac{\mathrm{Reaction}\mathrm{force} \left[\mathrm{N}\right]\text{×}\mathrm{Distance}\left(\mathrm{d}\right)\left[\mathrm{m}\right]}{\mathrm{Deflection}\mathrm{angle}\left(\theta \right) \left[\text{°}\right]}$$

(1)

3.3. Non-Parametric Shape Optimization Pre-Processing

In this study, the optimization task was defined as follows:

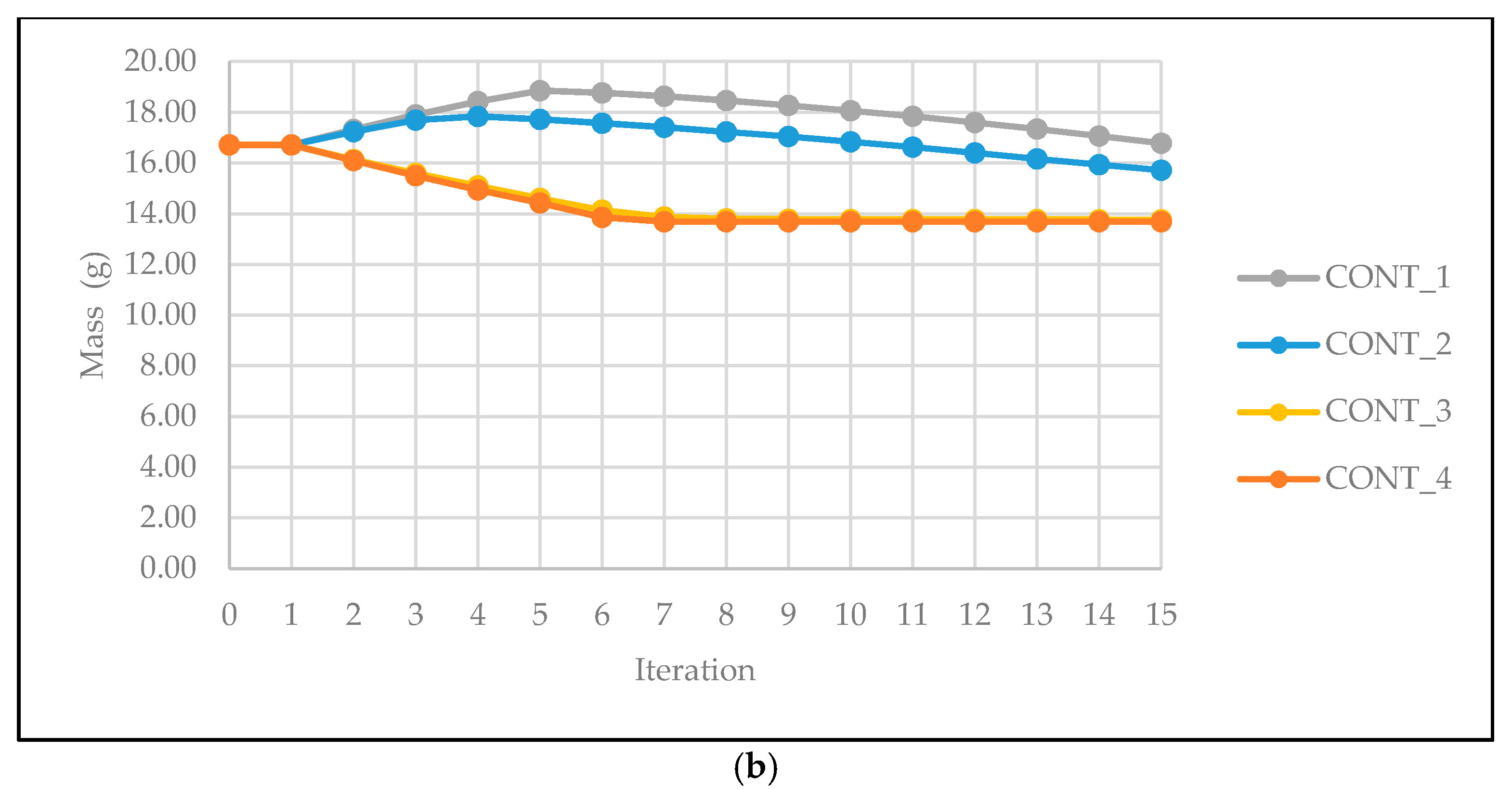
• The optimization objective was set to minimize the mass of the bottom plate.
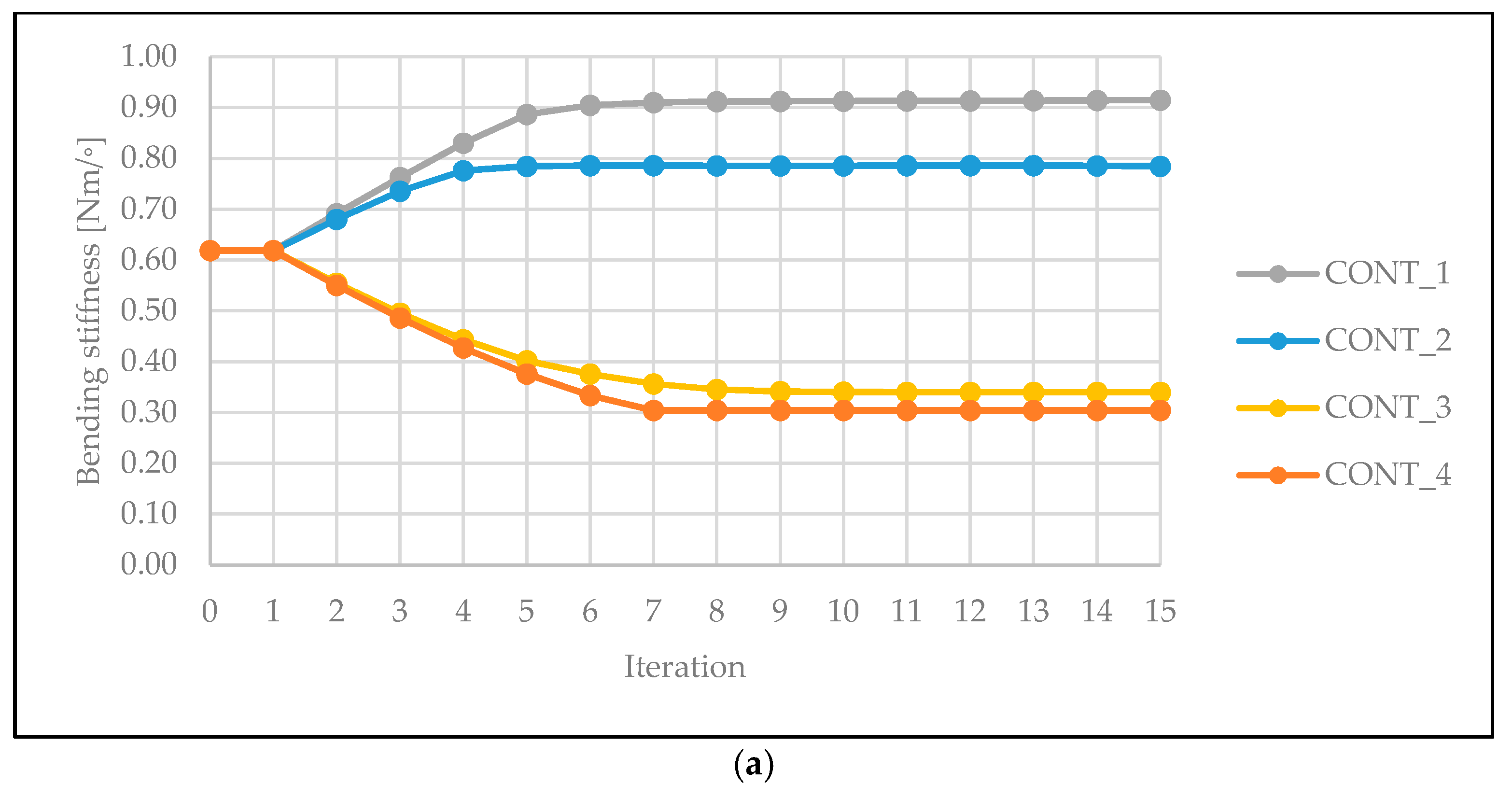
• Four different inequality constraints (CONT_#) were set as follows:

  CONT_1

  : 145% ≤ the target bending stiffness ≤ 155% of the initial bending stiffness

  CONT_2

  : 125% ≤ the target bending stiffness ≤ 135% of the initial bending stiffness

  CONT_3

  : 55% ≤ the target bending stiffness ≤ 65% of the initial bending stiffness

  CONT_4

  : 45% ≤ the target bending stiffness ≤ 55% of the initial bending stiffness

In order to optimize the shape of the ribs on the bottom plate, the nodes on the ribs were selected as shown in Figure 5. The movement direction of the nodes during the optimization process was restricted to be only y- and z-axis. The maximum positive and negative displacement values were 3 mm and 1 mm, respectively. The other nodes excluding the selected nodes were set to be frozen during the optimization process.

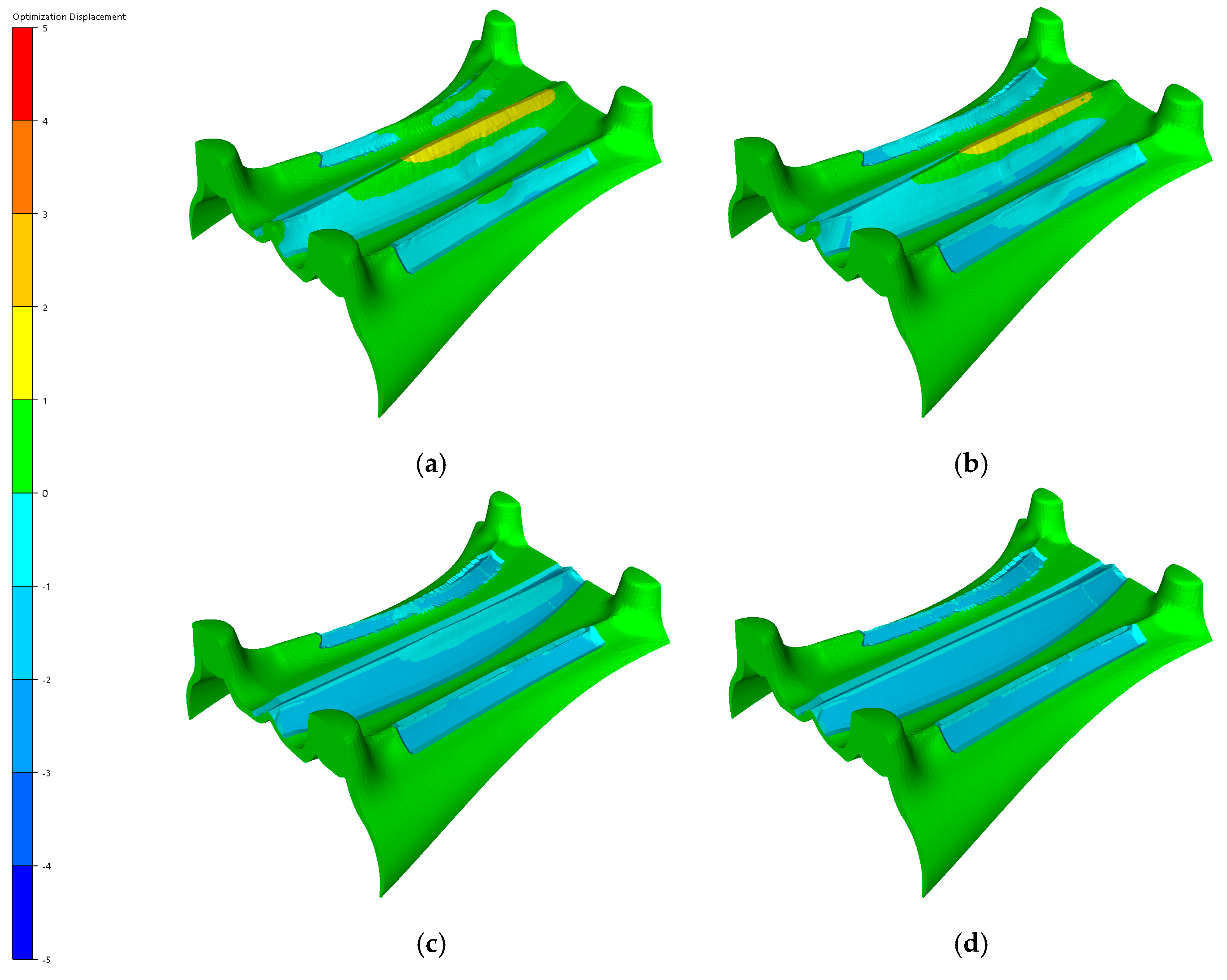
4. Results and Discussion

Figure 6 presents the changes in the bending stiffness and the mass of the bottom plate during the optimization process. For all cases, the bending stiffness was shown to have converged within the range of the target bending stiffness. In the case of mass, when the target bending stiffness was lower than the initial bending stiffness, it tended to converge to one specific value. However, when the target bending stiffness was higher than the initial bending stiffness, it increased the mass until the fifth iteration and tended to keep decreasing through the iteration. This implied the possibility that if the requested number of iterations is more than 15, these two cases can output the optimum bottom plate shape with a more decreased mass.

Figure 7 shows the optimized bottom plate midfoot part after the 15^th iteration. The side ribs tended to shrink regardless of the target bending stiffness. In the case of the middle rib, however, it grew as the target bending stiffness increased and shrank as the target bending stiffness decreased. A growing or shrinking of the ribs means the increasing or decreasing of the height and the thickness of the ribs. Additionally, during the optimization process, the change in size during the optimization process between the side ribs and the middle rib was not even, with the latter being increased by more. This is presumably because the initial size of the middle rib is bigger than the side ribs. As the bending stiffness is related to the dimensions of the structure, therefore, the changes in the size of the middle rib have more effect on the changes in the bending stiffness than the changes in the size of the side ribs. However, this needs to be demonstrated in a future study.

The limitation of Tosca Structure sensitivity-based shape optimization is that only static and linear perturbation analyses in Abaqus are supported. Thus, the deformation of the plate was evaluated by static analysis in this present study. Further study is required to validate these optimum bottom plates obtained from Tosca Structure with the mechanical 3-point bending test. Additionally, the accuracy of the current optimization tool can be compared with that of the previous parametric optimization tool.

5. Conclusions

In this study, the non-parametric shape optimization process for the football boot bottom plate was carried out. This methodology is different from the previously developed parametric optimization process for the bottom plate since it adjusts the node’s location on the bottom plate. Additionally, the parameterized CAD model was not required. The applied non-parametric optimization process enabled the adjustment of key features of the bottom plate. Especially, the changes in the middle rib were bigger than the ones on both ends. For future research, the validation of the results obtained from Tosca Structure with the 3-point bending test should be investigated to assess the accuracy of the process in comparison to that of the previous parametric optimization process.