Abstract
Here we seek to control mechanical power output in outdoor cycling by adjusting commanded cadence of a cyclist. To understand cyclist’s dynamic behavior, we had one participant match their cadence to a range of commanded cadences. We then developed a mathematical model that predicts the actual mechanical power as a function of commanded cadence. The average absolute error between the predicted power of our model and the actual power was 15.9 ± 11.7%. We used this model to simulate our closed-loop controller and optimize for proportional and integral controller gains. With these gains in outdoor cycling experiments, the average absolute error between the target and the actual power was 3.2 ± 1.2% and the average variability in power was 2.9 ± 1.3%. The average responsiveness, defined as the required time for the actual power to reach 95% of the target power following changes in target power, was 7.4 ± 2.0 s.
1. Introduction
Wearable sensors quantify our everyday lives by counting our steps, calories, heartbeats, and more [1]. This provides us with valuable feedback about our lifestyle and can encourage us to increase our exercise intensity and improve our health [2]. While such encouragement is useful, it is still up to the person to determine how to achieve this improvement. Instead, control algorithms that can use such wearable sensor feedback to regulate user’s behavior could be more effective to support people in reaching their athletic and physiological goals.
Endurance sports is an area where we can implement such control algorithms and help athletes to better pace themselves. Currently, endurance athletes are intrinsically poor at pacing. For example, self-paced runners have pacing errors of 4–8% [3,4]. On a 10 km race, this would add up to a substantial error of 2–4 min given a target time of 50 min. Therefore, our lab recently developed a system to improve pacing in running. A closed-loop feedback control system measured the user’s current running speed and compared it to a target speed. Based on the difference, the controller adjusted the commanded step frequency for the runner in real-time. This system reduced the pacing error to under 1% [4].
In this paper, we develop a similar system to control an athlete’s mechanical power output in cycling. We accomplished this using a closed-loop feedback control system that adjusts the cadence of the cyclist in real-time. Mechanical power is a non-tangible quantity for a user. Matching the actual power with the desired power without our proposed feedback system leaves the cyclist with the responsibility of deciding about the proper cadence changes by themselves, which leaves potential for human errors. Therefore, a cadence-controlled system could help athletes to more accurately and more comfortably control their power in cycling. In a simple system, at a fixed gear ratio, an increase in cadence is directly proportional to an increase in power. However, in practice, other parameters such as acceleration and drag, make this relationship more complex. To get accurate control authority over the cyclist, our first step was to understand the dynamics of the system. To do so, we first built a microcontroller-operated system that provides the cyclists with changes in cadence and measures the power output. Using these data, we developed and parameterized a mathematical model that best fit the simulated power to the actual power. We then used computer simulations of cycling of this model to optimize for the proportional and integral controller gains. Finally, we implemented the optimized feedback controller into the microcontroller to test its performance in actually controlling the power output in outdoor cycling.
2. Materials and Methods
2.1. Identifying Cyclist Dynamics
To understand the cyclist’s behavior, we first identified the dynamic relationship between the commanded cadence as an input and the power output. A participant completed two trials of 20 min cycling in upright position on an outdoor bike during which a metronome prompted pseudo-random step changes in cadence. We considered the participant as a dynamic system that can be experimentally identified by providing controlled inputs (commanded cadence) to the system and measuring its dynamic response (actual power). The step changes were ±5% and ±10% of their preferred cadence for a duration of 60 s each. A microcontroller (Teensy 3.1, Pjrccom Llc, Sherwood, OR, USA) controlled the metronome frequency of the subject’s earphones. It also recorded the torque and angular velocity from a power meter (Dura-Ace, SRM GmbH, Jülich, Germany) and calculated the applied power twice per crank revolution. We modeled the system as forces acting on a point-mass m. We assumed the sum of the forces to be the horizontal forward force of cyclist and bike and some counteracting air resistance force . By using Newton’s second law, with being the rate of change of the cyclist’s speed, we formulated the following equation to describe the cyclist’s motion:
By assuming the force applied from the cyclist on the pedal to be representative of and multiplying the forces with the respective velocities at their points of application, we then derived an equation that describes the mechanical power generated at the pedals as a sum of the inertial and the drag power. The drag component represents the power that the cyclist must apply to overcome drag, whereas the inertial component represents the power the cyclist has to apply when accelerating.
We then expressed and as a function of the radius of the wheel r, the length of the crank arm l, the gear ratio GR, the speed v, the acceleration , and the drag number c:
We calculated speed as a function of cadence, f, measured in revolutions per minute:
We took the derivative of v with respect to time t to get and by substituting for v and in Equation (3), we determined the power as a function of cadence:
The only unknown in this equation was the drag number c. We used a Levenberg-Marquardt optimization algorithm, implemented in MATLAB’s nlinfit function (The MathWorks Inc., Natick, MA, USA), to estimate the drag number that best fits the predicted power to the actual power. To evaluate the accuracy of the model, we determined the average absolute pacing error between the predicted and the actual power of the whole trial. We then defined the time delay between the commanded and the actual cadence, to get an equation that describes as a function of commanded cadence :
In search for the time delay that best matched the actual cadence to the commanded cadence, we normalized all step changes to −1 before and 0 after the step change, and searched for the transfer function of the step changes with the commanded cadence being the input and the actual cadence being the output. The transfer function fits the modeled output to the measured output given the same input data [5].
2.2. Design of Feedback Controller
We used the mathematical model in a simulation of a closed-loop feedback controller. Equation (6) replaced the cyclist’s dynamic relationship between the commanded cadence of the metronome and the actual power. We used a control algorithm in Simulink (The MathWorks, Inc.) to minimize the error between the target and the actual power, by adjusting the commanded cadence for the model of the cyclist. We used a discrete solver with a fixed-step size of 1, for which each time step represents one crank revolution. To determine the commanded cadence, we used a PI (Proportional Integral) controller. We chose the PI controller as it is both simple and tractable, and as a consequence, it has by far the largest track record of successful implementations [5]. The PI controller measured the error between the target and the actual power and calculated the change in commanded cadence as a weighed sum of a signal proportional to the error (), and a signal proportional to the integral of this error ().
We then used the feedback controller simulation to optimize for the proportional and integral gains. The target power was step changes of +10% of the subject’s preferred power with each step change lasting for around 60 s, and the feedback controller tried to minimize the error between the target power and the actual power. To find the best combination of gains, we employed a brute-force search. We created a grid of values between 0 and 0.05 with a resolution of 0.002 to generate 26 values per gain. We chose this range based on prior tests. We ran the feedback simulation with all 676 combinations and quantified the performance using accuracy and responsiveness. For accuracy, we calculated the average absolute pacing error between the target power and the actual power during the last 30 s of each step, and the pacing variability, calculated as the coefficient of variation, during the same time period (Figure 1b). We quantified responsiveness as the response time, defined as the required time for the actual power to reach 95% of the target power following changes in target power, which was calculated by fitting a single exponential to each response and multiplying the resulting time constant by three (Figure 1a).
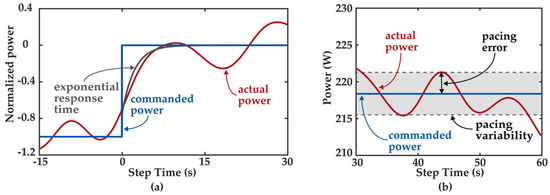
Figure 1.
We calculated responsiveness as three times the time constant of the single exponential (a). The average absolute pacing error was the difference between the target power and the actual power, and the variability was the coefficient of variation within the last 30 s of each step (b).
2.3. Testing of Feedback Controller
We tested the performance of the feedback controller using the optimized gains in outdoor cycling. To do so, a participant completed two trials of 16 min of cycling in upright position, during which they were guided through a range of target powers. The target power consisted of step changes of ±7.5% and ±15% of their preferred power. The microcontroller measured the error between the target and the actual power twice per crank revolution, calculated the change in cadence to minimize this error based on the proportional and integral gains, and adjusted the commanded cadence in real-time via a metronome (Figure 2). To evaluate the performance of the control system, we again quantified accuracy and responsiveness as described in Section 2.2.

Figure 2.
A closed-loop feedback system measures the error between the target and the actual power. Based on the error, a PI controller adjusts the commanded cadence. The plant (cyclist or model of cyclist) receives this change in commanded cadence and adapts the actual cadence. A change in cadence induces a change in actual power, which closes the feedback-loop.
3. Results
3.1. Identifying Cyclist Dynamics
The estimated drag number well fit our modeled data to the measured data. The fitted value for c was 0.36 ± 0.004. Pilot data are shown in Figure 3. The average absolute difference between the predicted power and the actual power was 15.9 ± 11.7% or about 37 W. The time delay was 1.8 data points or approximately one revolution of the crank.
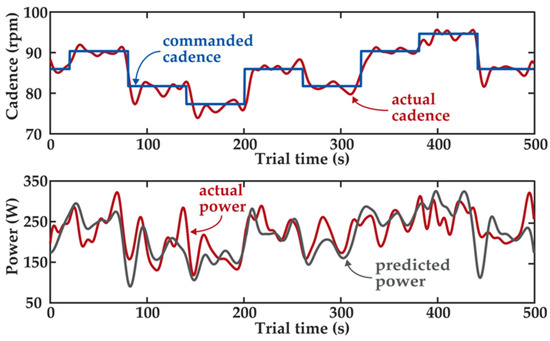
Figure 3.
In the open-loop experiment, the subject had to follow step changes in commanded cadence (top). We measured the actual mechanical power of the trial and predicted the power with a mathematical model (bottom).
3.2. Design of Feedback Controller
In simulations, the optimized controller gains enabled rapid and accurate controller performance. The brute force search suggested values of 0.012 and 0.02 for the proportional and the integral gain, respectively. The average absolute pacing error between the target and the actual power during the last 30 s of the target power was <0.01% and the variability in actual power during this time period, calculated as the coefficient of variation, was 0.1%. The response time was 23.1 s.
3.3. Experiment 3: Real-Time Controller
Optimized controller gains in outdoor experiments obtained accurate and responsive feedback control. Figure 4 shows pilot data of the outdoor controller. The average absolute pacing error between the target power and the actual power during the last 30 s of the target power was 3.2 ± 1.2% or about 7.6 W. The variability in power, calculated as the coefficient of variation during the same time period, was 2.9 ± 1.3% or about 6.8 W. The response time was 7.4 ± 2.0 s.

Figure 4.
In the closed-loop experiment, the participant was asked to match the actual power to step changes in target power (bottom). To succeed, the subject had to change the actual cadence based on the constantly adjusted commanded cadence calculated from the feedback controller, and communicated via a metronome in the subject’s earphones (top).
4. Discussion and Conclusions
This paper presents our approach to develop a novel system to control mechanical power in cycling. To understand the cyclist’s dynamic behavior, we first developed a mathematical model that can predict the mechanical power output following changes in cadence. With this model, we performed simulations to optimize the design of a closed-loop feedback control system that controlled power by changing the cadence. We optimized for the proportional and integral controller gains of the controller and then used these gains to test the performance of the actual feedback controller in outdoor cycling where a subject was guided through a range of target powers and the feedback controller adjusted the cyclist’s power accordingly with a metronome.
Our mathematical model estimated a realistic c value, but we will further leverage the model for higher accuracy. Our c can be defined by the drag area and the air density ρ:
For an air density of 1.23–1.25 kg/ and a drag area of 0.27–0.36 for an upright position [6,7,8] c would be between 0.17 and 0.23. With a value of 0.36 our c was slightly larger. We expected a larger value, because our drag number subsumes all unmodeled losses, such as rolling resistance or wind direction. For higher accuracy between the predicted and the actual power, we will further refine our model. This might include adding measurements of the rolling resistance, the wind strength and direction, or other parameters.
Accuracy was better in the simulations, but responsiveness was better in outdoor experiments. We expected better performance in accuracy in simulations than in outdoor experiments for several reasons. First, our mathematical model does not perfectly represent the cyclist. We did not include any measurement noise, subject noise, or disturbances to our model, which contributes to a larger pacing error and variability in cycling. Since we did not include a derivative gain to our control system, which is a gain that is very sensitive to measurement noise, it was not crucial for us to include noise to our simulation. Second, we optimized for the best gains for the model and not for the cyclist. We then transferred these gains to the cyclist, which might have a different gain optimum. Response time of the outdoor experiment was about a third of the responsiveness of the simulation. This discrepancy can again be explained by an imperfect simulation, but we will have to more closely investigate the model.
It is unclear whether our feedback control system led to an increase in performance. Literature is limited on data in cycling pacing accuracy. For pacing variability in 4 km time trials, Mauger et al. found a coefficient of variation of around 3.5% when giving no feedback compared to 2.2% when giving visual feedback [9]. A coefficient of variation of 2.9% in our study indicates a performance improvement compared to cycling without feedback, but a performance deterioration compared to cycling with visual feedback. It is difficult to draw comparisons between these two studies because of differences in their experimental designs. Thus, we will conduct our own experiment, comparing cycling that is self-paced, with cycling with a monitor that displays the power, and with cycling with our feedback system.
Our approach has several limitations. First, our model is just an approximation of the cyclist’s dynamic behavior. This leads to discrepancies between the feedback control simulations and the outdoor experiments with the feedback controller. To minimize these discrepancies, we will have to more closely investigate our mathematical model, to understand its limitations and improve its performance. Second, the results shown in this paper are from a pilot study with one participant, which adds uncertainty to the results presented. Third, we used one gear ratio for the whole study, determined by the subject before the first experiment. The mathematical model accounts for the gear ratio but we have not yet investigated if changing gear ratio will change the accuracy of our model and if it affects the performance of the closed-loop feedback controller.
Our next steps will be to improve this control system to provide cyclists with high performance feedback. Towards this goal, we will fine tune our mathematical model using data from more cyclists and using a larger number of gear ratios. This system will provide cyclists with stroke by stroke control over their power. Athletes or their coaches will be able to set and complete different training protocols, such as interval training, with high accuracy, and hence, improve their performance.
Acknowledgments
This study was funded by an NSERC Discovery Grant to JMD.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mukhopadhyay, S.C. Wearable sensors for human activity monitoring: A review. IEEE Sens. J. 2015, 15, 1321–1330. [Google Scholar] [CrossRef]
- Munson, S.A.; Consolvo, S. Exploring goal-setting, rewards, self-monitoring, and sharing to motivate physical activity. In Proceedings of the 6th International Conference on Pervasive Computing Technologies for Healthcare, San Diego, CA, USA, 21–24 May 2012; IEEE: Piscataway, NJ, USA; pp. 25–32. [Google Scholar]
- Green, J.M.; Sapp, A.L.; Pritchett, R.C.; Bishop, P.A. Pacing accuracy in collegiate and recreational runners. Eur. J. Appl. Physiol. 2010, 108, 567–572. [Google Scholar] [CrossRef] [PubMed]
- Snaterse, M. Automatic Pacing: On the Use of External Timing Cues to Regulate Speed during Human Walking and Running. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, Spring. 2014. [Google Scholar]
- Åström, K.; Murray, R. Feedback Systems: An Introduction for Scientists and Engineers, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2009; pp. 235–319. [Google Scholar]
- Blocken, B.; van Druenen, T.; Toparlar, Y.; Andrianne, T. CFD analysis of an exceptional cyclist sprint position. Sports Eng. 2019, 22, 1–11. [Google Scholar] [CrossRef]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. J. Biomech. 2010, 43, 1262–1268. [Google Scholar] [CrossRef] [PubMed]
- Jeukendrup, A.E.; Martin, J. Improving cycling performance: How should we spend our time and money. Sports Med. 2001, 31, 559–569. [Google Scholar] [CrossRef] [PubMed]
- Mauger, A.R.; Jones, A.M.; Williams, C.A. The effect of non-contingent and accurate performance feedback on pacing and time trial performance in 4-km track cycling. Br. J. Sports Med. 2011, 45, 225–229. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).