1. Introduction
It is known that when a sports ball flies through the air while spinning, a lateral force, known as the Magnus force, is generated by the spin, and it deflects the ball’s flight trajectory [
1,
2]. In soccer, it is possible to laterally deflect the flight trajectory of the ball by giving it spin with a vertical spin axis, which leads to a side-force; this technique is often used in curve kicks [
3]. The flight trajectory and deflection properties of the ball are heavily dependent on its aerodynamic factors.
One previous study on the aerodynamic factors affecting soccer balls was based on wind-tunnel experiments, and it determined the coefficients of drag, side-force, and lifting force of many balls of different designs [
4]. Further, there have been studies that examined the relationship between the spin parameters and the side-forces acting on spinning balls using different types of jigs (supporting stings) [
5,
6,
7,
8]. Moreover, researchers have analysed aerodynamic factors with free-flight experiments that eliminate the influence of the jigs that are required for wind-tunnel experiments [
9,
10]. Recent free-flight experiments have focused on steady aerodynamic factors, and only a few have sought to examine the unsteady side-forces and side-force coefficients over long distances, as would occur in an actual soccer match [
11].
In the present study, the flight trajectory and angular speed of a spinning ball traveling over a long distance (>20 m)—as a result of a curve kick—were measured using an optical three-dimensional motion-capture system to analyse the relationship between the horizontal flight trajectory of the ball and the unsteady side-force (Magnus force) acting on it. The results indicated that an unsteady side-force, generated by the spin, decreased during the entire flight. The decrease in the unsteady side-force was caused by the reduction in the speed of the ball, whereas the impact of the decrease in the angular speed of the ball appeared to be relatively small.
2. Materials and Methods
A soccer ball was placed directly in front of a soccer goal, at a distance of 23 m, and a research participant performed a curve kick with rotation aimed at the goal. The participants in this study were two male collegiate soccer players, both right-foot dominant. Each participant executed seven curve kicks under conditions similar to those that would be experienced in an actual game, and all participants attempted to kick the ball with a spin axis that was strictly vertical. A VICON optical motion capture system (100 Hz: Oxford Metrics Ltd., Oxfordshire, UK) with 24 cameras was used to capture the free-flight ball trajectory and angular speed (see
Figure 1). A hemispherical reflection marker was placed on the top, front, right, and left intersection points of the ball surface and the three axes from the centre of the gravity of the ball. The axis of the rotation of the ball was detected by the hemispherical reflection markers on the ball. The marker placed on the top of the soccer ball indicates the direction of the vertical spin-axes [
12]. The trajectory and angular speed of the curve ball were detected from the three-dimensional positions of reflection markers using the NEXUS analysis software (Oxford Metrics Ltd.) [
12]. To reduce the amount of noise captured, we used the simple moving average of nine points for the marker position data.
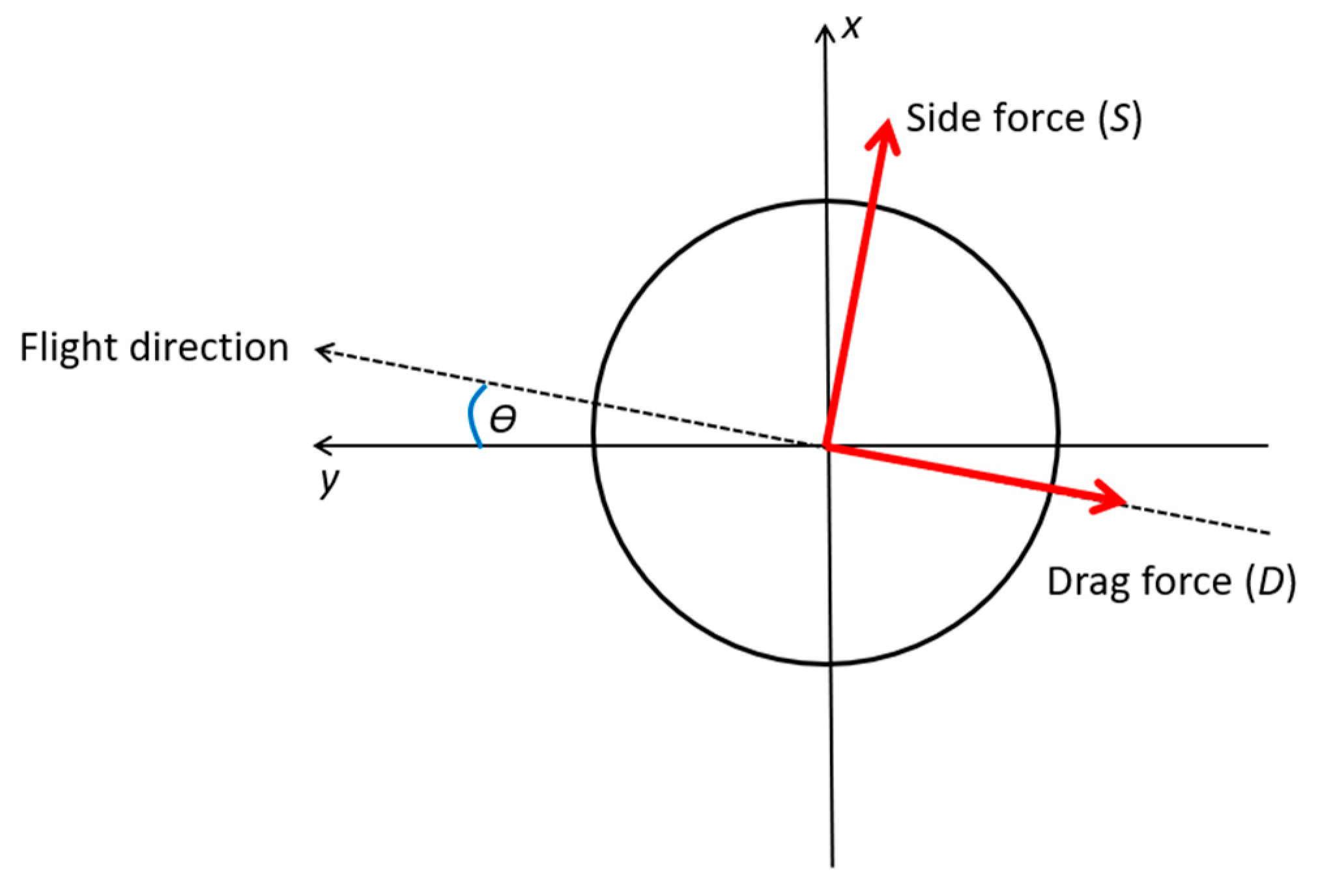
The force acting sideways is calculated by Newton’s second law of motion. According to
Figure 2, when the soccer ball is moving at an angle of
with respect to the
y-axis, both the side-force and the drag force can be split into
x and
y components. The equation of motion in the
x direction is given by
and that in the
y-direction is given by
. With values of
and
, which can be found by taking numerical derivatives of the position function obtained from the VICON system of the soccer ball, the side-force may be determined to be
. The method described here assumes that all kicks have strictly vertical spin axes, which implies there is no lift force component of the total force of the air on a soccer ball. This two-dimensional simplification allows for generate fast estimates of the side-force and its corresponding aerodynamic coefficient.
The side-force, or Magnus force, is related to the side-force coefficient,
Cs, as follows:
where
is the density of air,
U is the ball speed in m/s, and
A = 0.038 m
2 is the cross-sectional area of the ball. The ratio of the equatorial speed to the ball’s centre-of-mass speed is the spin parameter,
Sp, defined as
where
is the angular speed and
R = 0.11 m is the radius of the soccer ball.
The time-averaged spin parameter, Ave_Sp, and the time-averaged side-force coefficient, Ave_Cs, were calculated from the unsteady spin parameter, Sp, and unsteady side-force coefficient, Cs, respectively, obtained in each trial conducted as part of this experiment. Curvature was calculated from a virtual circumscribed circle at points of interest on the ball’s trajectory.
3. Results
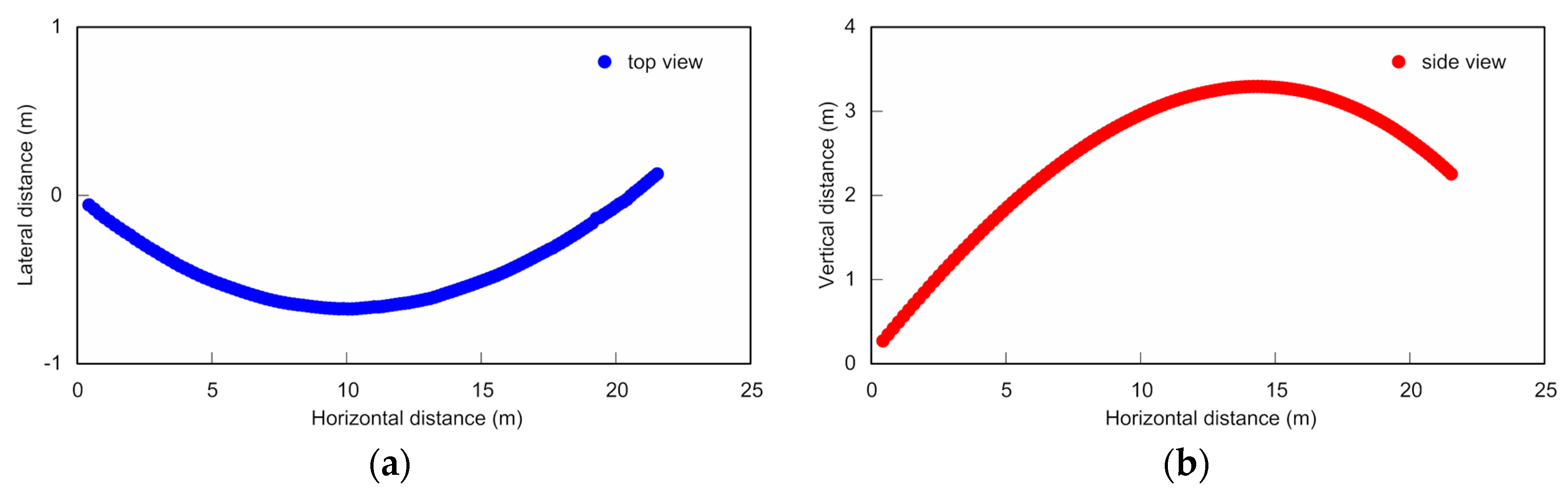
In an example of a curve-kick trial—trial 1—the ball had an initial speed of approximately 19 m/s and angular speed of around 5.8 rev/s. Its flight trajectory deflected by over 0.7 m in the horizontal plane in 1 s (see
Figure 3a). The curvature of the ball trajectory is 1.1 m
−1 at 0.2 s, 31.1 m
−1 at 0.5 s, and 0.9 m
−1 at 0.8 s. In the vertical plane of the flight trajectory, the ball exhibited a vertical deflection (a drop) caused by gravity and the vertical component of the drag force (see
Figure 3b).
Figure 3a,b are representative of the ball trajectories in most other trials.
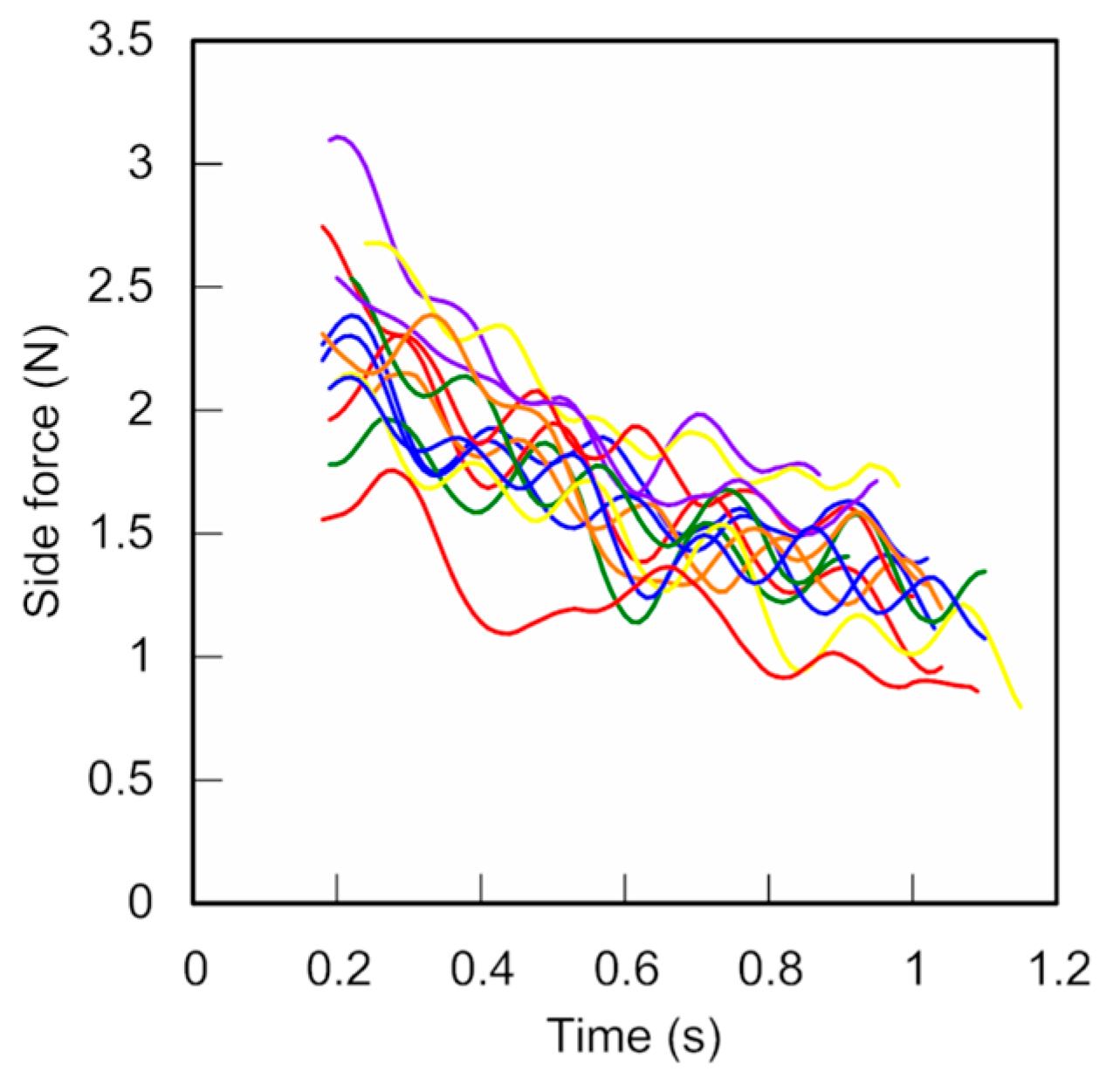
Approximately 1 s after the beginning of the flight in trial l, the Magnus force acting sideways on the ball,
S, had decreased by approximately 50%, from approximately 2 N to 1 N (see
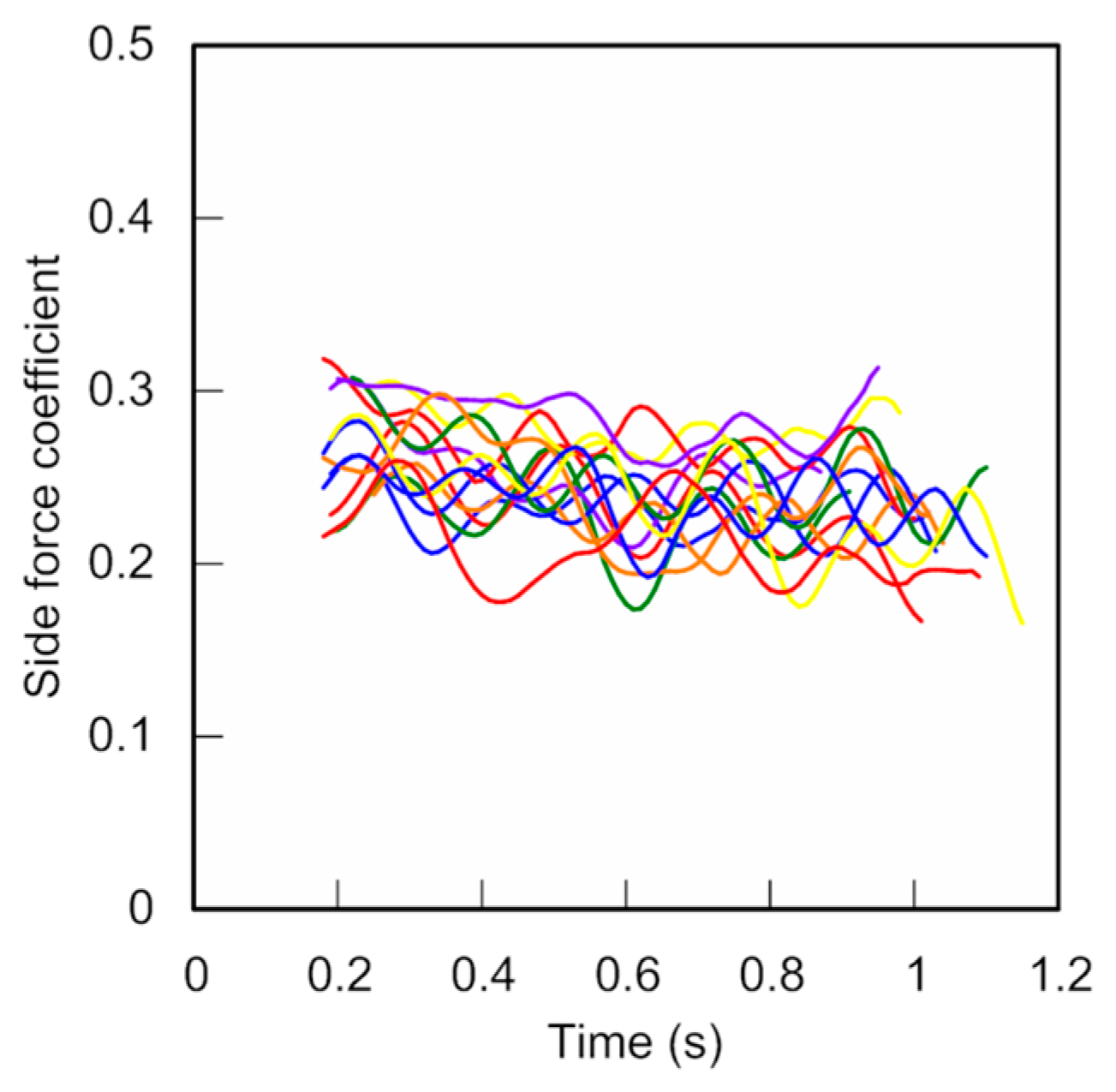
Figure 4). The side-force coefficient,
Cs, had decreased by approximately 10%, from 0.27 to 0.24 (see
Figure 4). The side-force tended to decrease in all other trials (see
Figure 5). The side-force coefficient also decreased in all other trials, albeit at a lower rate than the side-force (see
Figure 6).
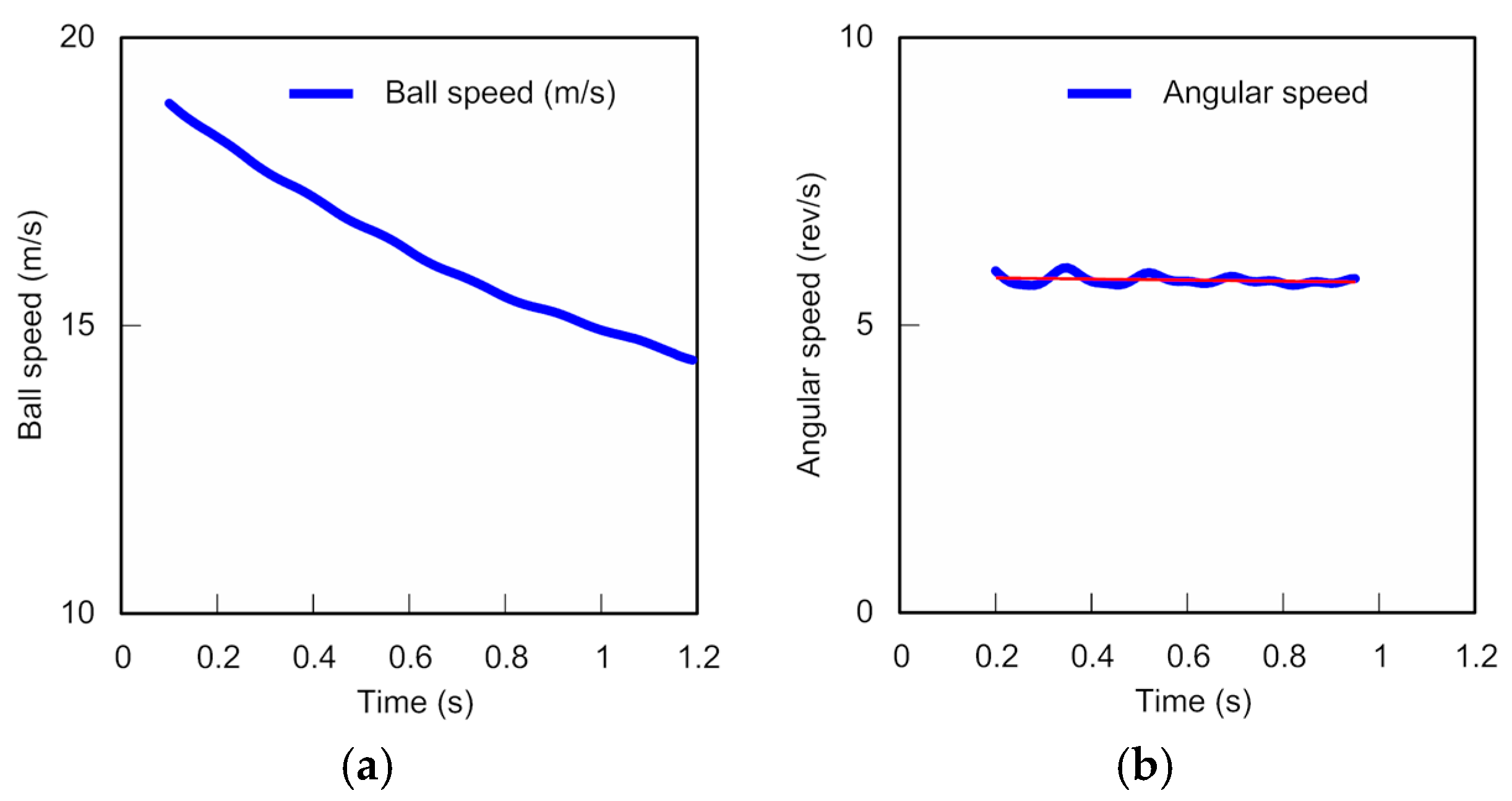
In trial 1, the speed of the ball decreased from an initial speed of around 18.8 m/s to around 14.7 m/s, a drop of approximately 22% in 1 s (see
Figure 7a). The angular speed of the ball decreased from around 5.8 rev/s to around 5.7 rev/s, or only about 2% in 0.8 s, which is a lower rate of decrease than that of the ball speed (see
Figure 7b). The angular speed decreased at roughly the same rate in the other trials as well, despite the different initial velocities and angular speeds of the ball.
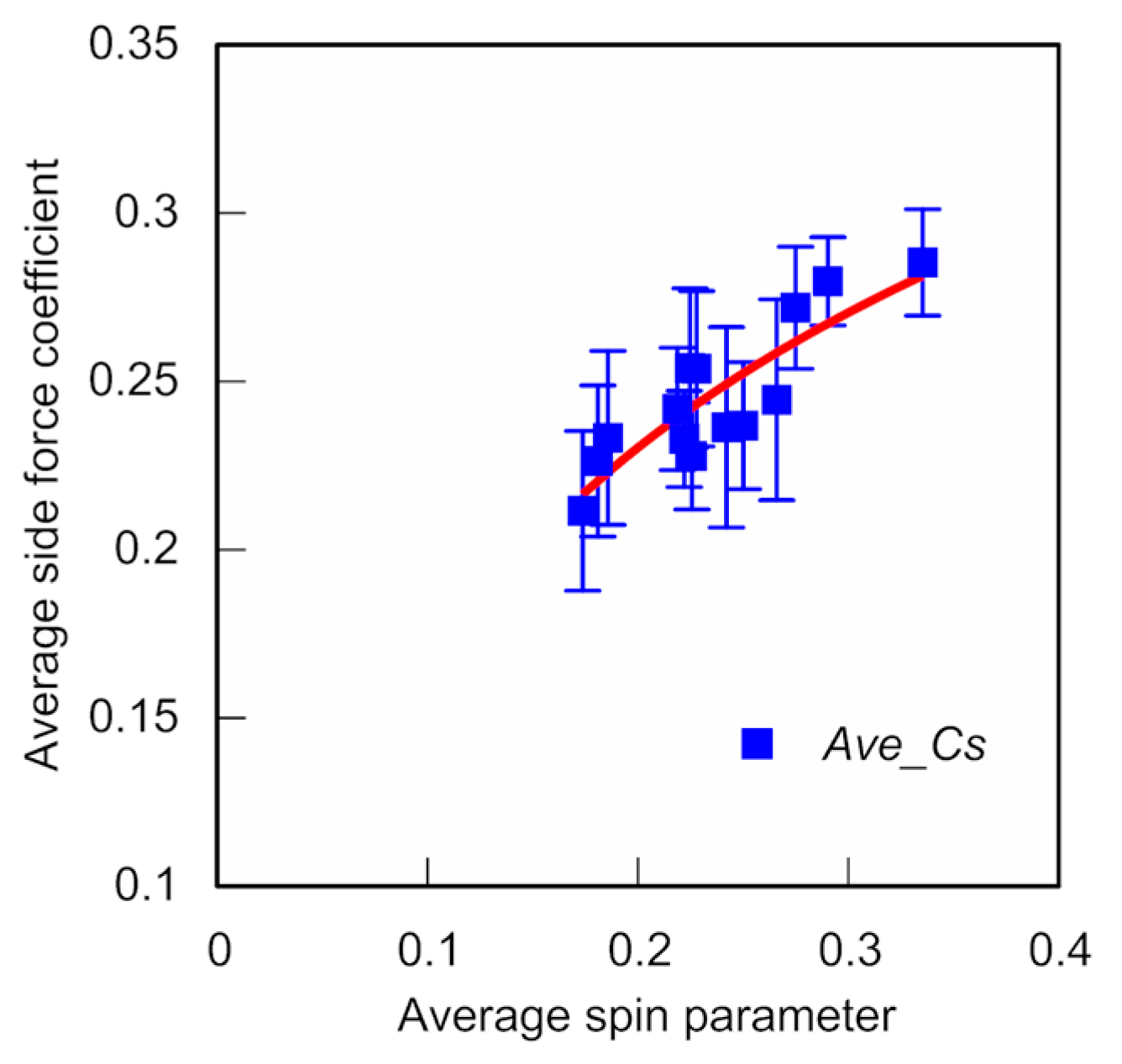
In all trials, the time-averaged spin parameter and the time-averaged side-force coefficient demonstrated the same relationship as that observed in the wind-tunnel experiments [
4,
5,
6], in which the side-force coefficient increases along with the spin parameter (see
Figure 8).
4. Discussion
In this experiment, the time-averaged side-force coefficients are 0.21, 0.24, and 0.29 for time-averaged spin parameters of 0.18, 0.22, and 0.34, respectively (see
Figure 8). The time-averaged side-force coefficients are 0.20, 0.23, and 0.24 for time-averaged spin parameters of 0.14, 0.18, and 0.23, respectively, in the wind-tunnel test [
5]. The values of the side-force coefficient in this experiment were similar to those obtained in the wind-tunnel experiments conducted as part of previous studies [
5,
6,
7,
8], as was the relationship between the average side-force coefficient and the average spin parameters [
5,
6,
7,
8]. From these comparisons, it is possible to claim that the ball trajectory and side-force (or Magnus force) obtained in this experiment were reasonable, despite the use here of an assumption that the side-force remains in the plane parallel to the ground throughout the balls’ flights. The oscillation of the side-force can be observed in this study. It may be caused by the error of the geometrical centre position from the actual centre of rotation of the ball, and the error that occurs when detecting the spin axes.
Dupeux et al. (2011) indicate that aerodynamics imposes a spiral trajectory of the spinning balls in the case of angular speeds of ~14 rev/s [
13]. In the case of angular speeds of ~6.0 rev/s, however, spiral trajectories could not be observed, though trajectories with decreasing lateral deflection could be observed. The side-force acting on the balls decreased monotonically during the entire flight. Ball speed dropped monotonically because of air resistance, and that fact with Equation (1) shows that the side-force should decrease monotonically, too. Due to air viscosity, the balls’ angular speeds decreased slightly during flight, which also caused a decrease in the side-force. When a ball’s angular speed decreases, the side-force coefficient also decreases, which in turn causes the side-force to decrease (see Equation (2)). It was found that the ball speed decreased at a much higher rate than the angular speed. The side-force is thus more strongly affected by the ball’s speed than by the ball’s angular speed through the side-force coefficient (see Equation (1)).
When curving the ball in an actual soccer game, the player should consider the fact that the deflection (or bending) of the ball peaks in the middle of its flight trajectory and then subsequently decreases. The player should choose to attempt a trajectory that goes around the goalkeeper’s range of defence and free-kick wall. In a curved kick, the ball has a flight trajectory with no radical changes in its path, and it is up to the goalkeeper to read and react to the curve trajectory as quickly as possible.
This study focused on the flight trajectories and side-forces acting in the horizontal plane of a spinning ball. The kicked balls were influenced not only by the spin but also by gravity, which made the balls drop in the vertical direction, thereby creating three-dimensional movement. The direction of the ball’s spin axis, which may change during flight, makes the trajectory even more complex. The next phase of this study will therefore involve measuring and analysing the ball flight trajectory and ball’s spin with a high accuracy in three dimensions.
5. Conclusions
In this experiment, the trajectory and angular speed of a ball in free flight following a curve kick were measured with an optical three-dimensional motion capture system to analyse the relationship between the flight trajectory and the unsteady side-force (or Magnus force) in the horizontal plane. The results suggested that the unsteady side-force in a curve kick decreases during the entire flight. The decrease in the unsteady side-force after a curve kick is believed to be caused by a decrease in the ball speed, whereas the impact of the decrease in the ball’s angular speed appears to be relatively small. When actually curving a ball, the player should be aware that the deflection (or bend) is larger in the middle part of the ball’s trajectory than at the end of it and; with this in mind, try for a trajectory that goes around the goalkeeper’s defence range and the free-kick wall.