An Innovative Circular Ring Method for Measuring Young’s Modulus of Thin Flexible Multi-Layered Materials ^†

Abstract

An innovative mechanical testing method (Compressive Circular Ring Method) is provided for measuring Young’s modulus of each layer in a flexible multi-layered material. The method is based on a nonlinear large deformation theory. By just measuring the vertical displacement or the horizontal displacement of the ring, Young’s modulus of each layer can be easily obtained for various thin multi-layered materials. Measurements were carried out on an electrodeposited two-layered wire. The results confirm that the new method is suitable for flexible multi-layered thin wires. In the meantime, the new method can be applied widely to measure Young’s modulus of thin layers formed by PVD, CVD, Coating, Paint, Cladding, Lamination, and others.

1. Introduction

Young’s modulus of multi-layered materials is very important to predict large deformation in both analytical and technological interests. A new testing method (Circular Ring Method) is based on a nonlinear theory. This paper deals with the compressive technique. Exact analytical solutions are obtained in terms of elliptic integrals. In order to assess the applicability of the proposed method, several experiments were carried out using a two-layered material (Cu: an electrodeposited material + SWPA: a spring steel material). As a result, the new method was found to be suitable for flexible multi-layered materials. Besides the Circular Ring Method studied here, the Axial Compression Method [1], the Own-weight Cantilever Method [2,3] for a flexible multi-layered material have already been developed and reported, based on the nonlinear large deformation theory.

2. Fundamental Theory

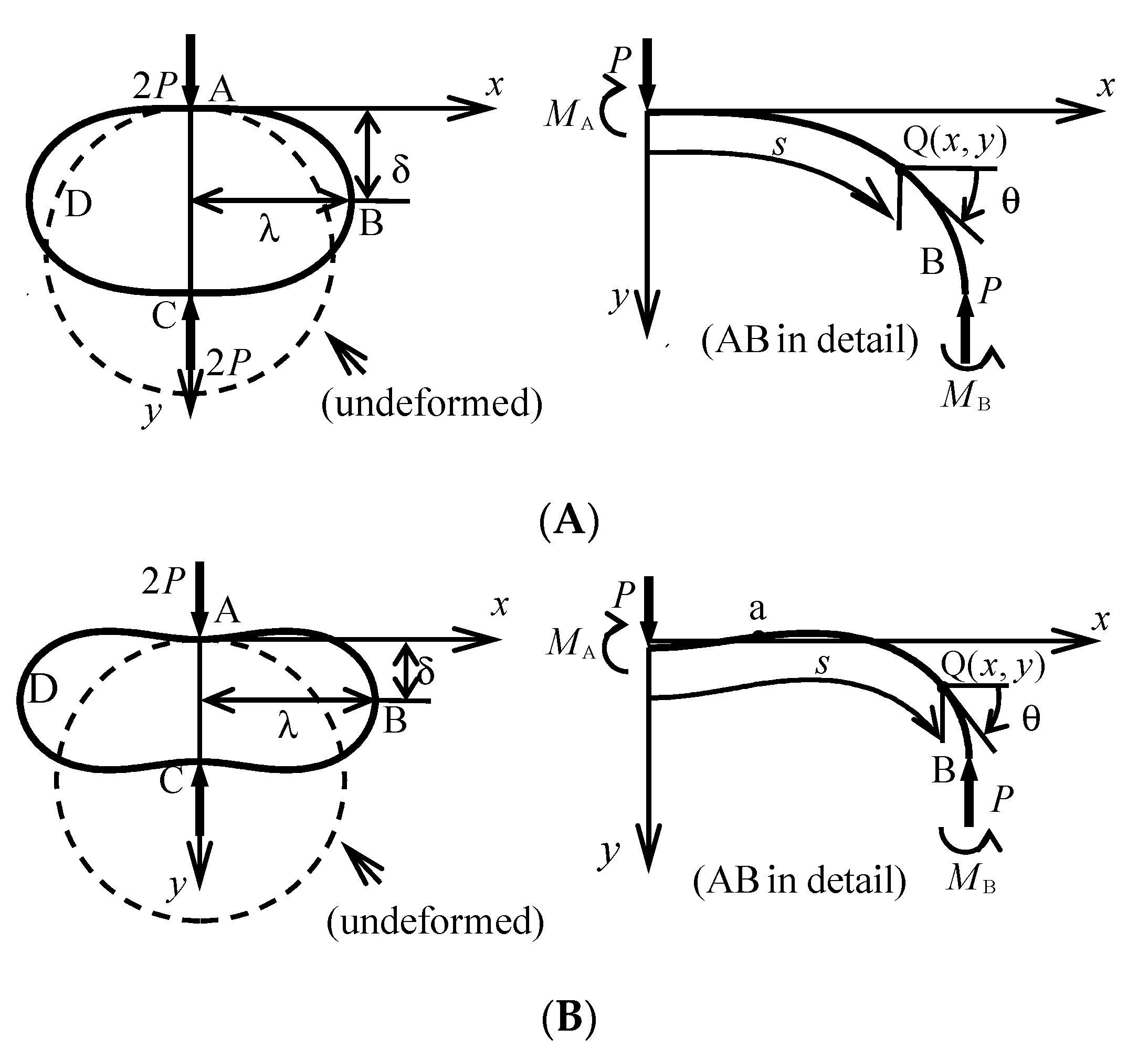
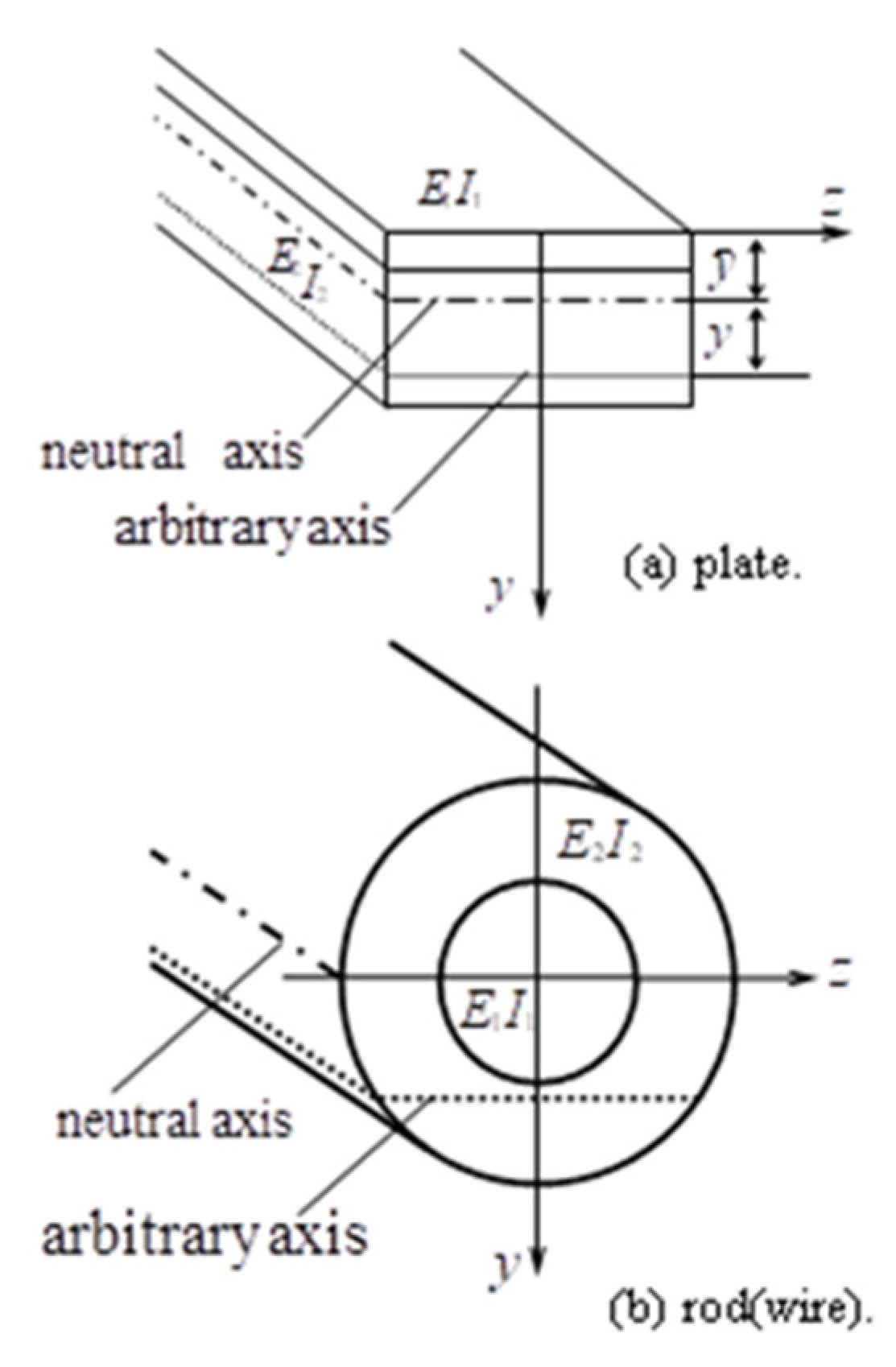
A typical load-deformation shape is given in Figure 1 for a circular ring (the initial radius: R₀, the whole length of the circular ring: 4L = 2πR₀) subjected to opposite compressive forces at two points. As an example, Figure 2 shows the cross-section of a two-layered material.

The analysis is carried out for only the 1/4 part (Region AB, arc length L). The horizontal displacement is denoted by x, the vertical displacement by y, and θ is the deflection angle. Furthermore, the arc length is denoted by s, the radius of curvature by R and the bending moment by M. The relationship among R, M, s, x, y and θ are given by:

$$\begin{array}{l}1/R=-d\theta /ds=M/{\displaystyle \sum _{i=1}^n(E_i{H}_i)+1/R_0}\\ dy=ds\cdot \sin \theta ,dx=ds\cdot \cos \theta \end{array}\}$$

(1)

where E_i I_i = the flexural rigidity of each layer.

The bending moment applied at an arbitrary position Q(x, y) is expressed as

$$M=-P\cdot x+M_{\mathrm{A}}$$

(2)

Introducing the following non-dimensional variables,

$$\xi =x/L,\hspace{1em}\eta =y/L,\hspace{1em}\zeta =s/L,\hspace{1em}\rho =R/L,\hspace{1em}\gamma =P{L}_2/{\displaystyle \sum _{i=1}^n(E_i{I}_i}),\hspace{1em}\alpha =M_{\mathrm{A}}L/{\displaystyle \sum _{i=1}^n(E_i{I}_i})$$

(3)

Considering the boundary condition, ${(d\theta /d\zeta )|}_{\theta ={\theta }_{\mathrm{A}}=0}=-\alpha -1/{\rho }_0$ at the point A, the basic equation is derived from Equations (1)–(3) in the form of:

$$d\theta /d\zeta =\pm \sqrt{2\gamma sin\theta +{(\alpha +1/{\rho }_0)}^2}$$

(4)

This nonlinear differential Equation (4) is the basic equation that determines large deformation behaviors of a compressive ring.

$$\begin{array}{ll}k=\sqrt{\left\{2\gamma +{\left(\alpha +1/{\rho }_0\right)}^2/(4\gamma )\right\}}& \\ 1-\sin \theta =2k^2{\sin }^2\varphi & (0\le \varphi \le \pi /2)\end{array}\}$$

(5)

2.1. In the Case with No Inflection Point [See Figure 1A]

2.1.1. Coverage $0\le k\le 1$ of the Variable k in Equation (5)

Considering the boundary conditions ${\zeta }_{\max }(=s_{\max }/L)=1$, ${\eta }_{\max }=\delta /L$ and ${\xi }_{\max }=\lambda /L$, the maximum non-dimensional arc length ζ_AB, the maximum non-dimensional vertical displacement η_AB and the maximum non-dimensional horizontal displacement ξ_AB are obtained as follows.

$${\zeta }_{\mathrm{AB}}=1=F\left(k,{\varphi }_{\mathrm{A}}\right)/\sqrt{\gamma }$$

(6)

$${\eta }_{\mathrm{AB}}=\delta /L=\left\{2E\left(k,{\varphi }_{\mathrm{A}}\right)-F\left(k,{\varphi }_{\mathrm{A}}\right)\right\}/\sqrt{\gamma }$$

(7)

$${\xi }_{\mathrm{AB}}=\lambda /L=2k\cdot (1-cos{\varphi }_{\mathrm{A}})/\sqrt{\gamma }$$

(8)

Similarly, the non-dimensional load γ is

$$\gamma =P{L}^2/(EI)={\{F(k,{\varphi }_{\mathrm{A}})\}}^2$$

(9)

where ${\varphi }_{\mathrm{A}}={\mathrm{Sin}}^{-1}[\sqrt{\{1/(2k^2)\}}]$.

2.1.2. Coverage $k\ge 1$ of the Variable k in Equation (5)

By transforming the variables $k\sin \varphi =\sin Z$ the maximum non-dimensional arc length ζ_AB, the maximum non-dimensional vertical displacement η_AB and the maximum non-dimensional horizontal displacement ξ_AB are obtained as follows.

$${\zeta }_{\mathrm{AB}}=1=F(1/k,\pi /4)/(k\sqrt{\gamma })$$

(10)

$${\eta }_{\mathrm{AB}}=\delta /L=2k\cdot E(1/k,\pi /4)-(2k-1/k)\cdot F(1/k,\pi /4)/(\sqrt{\gamma })$$

(11)

$${\xi }_{\mathrm{AB}}=\lambda /L=2k\cdot (1-\cos {\varphi }_{\mathrm{A}})/\sqrt{\gamma }$$

(12)

where ${\varphi }_{\mathrm{A}}{\mathrm{Sin}}^{-1}[\sqrt{\{1/(2k^2)\}}]$ .

Similarly, the non-dimensional load γ is

$$\gamma =P{L}^2/(EI)={\{F(1/k,\pi /4)/k\}}^2$$

(13)

2.2. In the Case with Inflection Point [See Figure 1B]

In this case, a measuring theory can be derived under the coverage of the variable k, $0\le k\le 1$. Details of the analytical theory will be omitted here.

Equations (6)–(13) are fundamental formulas to obtain Young’s modulus of each layer, based on the nonlinear large deformation theory. The functions F(k,ϕ), E(k,ϕ) appeared in Equations (6)–(13) are Legendre-Jacobi’s elliptic integrals of the first and second kinds, respectively.

The following formula based on Equation (3) is useful in calculating each Young’s modulus E_i.

$${\displaystyle \sum _{i=1}^n(E_i}{I}_i)=P{L}^2/\gamma$$

(14)

where I_i is the second moment of area.

When calculating Young’s modulus E_i using Equation (14), it is not necessary to determine the neutral axis for multi-layered rods/wires because the cross section is symmetrical at any time with respect to the neutral axis. The second moment of area I_i of each cross section for multi-layered rods/wires (diameter d_i) with respect to the neutral axis is shown as

$$I_i=\pi (d_i{}^4-d_{i-1}{}^4)/64\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(d_0=0)$$

(15)

On the other hand, in case of multi-layered plates it is necessary to determine the neutral axis of materials. The second moment of area I_i of each cross section (thickness h_i, width b: common to all) with respect to the neutral axis is shown as

$$I_i=b{h}_i{}^3/12+b{h}_i{(\overline{y}-h_i/2-k=1{\displaystyle \sum _{k=1}^i{h}_{k-1})}}^2\hspace{1em}\hspace{1em}(h_0=0,i\le n)$$

(16)

The distance $\overline{y}$ to the neutral axis (see Figure 2a) is obtained as follows.

$$\overline{y}={\displaystyle \sum _{i=1}^n{E}_i(S_i}{)}_Z/{\displaystyle \sum _{i=1}^n(E_i{A}_i})$$

(17)

The first moment of area (S_i)_z of each cross section (A_i: the cross-sectional area) with respect to z axis is expressed as

$${(S_i)}_z=b{h}_i{}^2/2+b{h}_i\left({\displaystyle \sum _{k=1}^i{h}_{k-1}}\right)$$

(18)

One quantity γ (: the non-dimensional load) is required to calculate Young’s modulus E_i from Equation (14). The value of γ is obtained from a chart (: Nomograph) of γ-δ relation (δ the vertical displacement) [Method 1] or γ-λ relation (λ: the horizontal displacement) [Method 2].

3. Techniques of New Measuring Method (Compressive Circular Ring Method)

In this paper, two methods are introduced in order to measure Young’s modulus. The γ-δ and γ-λ relations are presented in Figure 3 and Figure 4, respectively. These charts are computed previously by using Equations (9)–(13). Here, the usage of the chart is recommend by the author. As a point to note, for example, a two-step procedure should be done in a measuring experiment, when Young’s modulus of each layer in a two-layered material is all unknown (Note that a multi-layered material with number of layers n requires a n-step procedure). In other words, it is possible to reduce a frequency of step in proportion to the number, if the number of layers with known Young’s modulus is proven.

3.1. Method 1: (Measurement of δ Only)

The usage of this method is shown below in a two-layered material. Each Young’s modulus E_i is obtained for a SWPA thin wire (: first layer) with 1/4 part length: L₁ = 125.0 [mm](4L₁(500 [mm]): whole length of the ring), diameter: d₁ = 0.38 [mm] and a Cu electrodeposited layer (: second layer) with length: L₂ (= L₁) = 125.0 [mm], thickness: (d₂ − d₁)/2 = 0.011 [mm] (d₂: 0.402 [mm]).

A chart (: Nomograph) is given in Figure 3, illustrating the relationship of γ and δ//L. Using this chart, each Young’s modulus E_i in a multi-layered material can be calculated from the relational expression given in Equation (14).

3.1.1. First Step Procedure (As a Two-Layered Specimen)

Under the condition of P = 39.24 [mN], δ = 64.7 [mm] (i.e., δ/L = 0.5176) is measured for a double layer and then the value of γ is taken from Figure 3 (γ = 2.470). Therefore, using Equation (14), the combined flexural rigidity (I₁ = 1.023 × 10⁻¹⁵[m⁴]: SWPA, I₂ = 2.584 × 10⁻¹⁶ [m⁴]: Cu) is derived as follows

$$E_1{I}_1+E_2{I}_2=P{L}_1{}^2/\gamma =0.03924\times {0.125}^2/2.470=2.480\times {10}^{-4}$$

(19)

3.1.2. Second Step Procedure (As a Single-Layered Specimen)

Similarly, δ is measured for a single layer after removing a second layer (Cu). In the condition of P = 34.34 [mN] for a SWPA single layer with length: L₁ = 125.5 [mm], diameter: d₁ = 0.38 [mm], δ = 64.4 [mm] (i.e., δ/L = 0.5148) is measured and γ is taken newly from Figure 3* (γ = 2.51) [*: Drawing is omitted here.]. Therefore, the flexural rigidity (I₁ = 1.023 × 10^{-15 [}m⁴]: SWPA) can be rewritten as follows from Equation (14) follows.

$$E_1{I}_1=P{L}_1{}^2/\gamma =0.03434\times {0.125}^2/2.51=2.135\times {10}^{-4}$$

(20)

Using the simultaneous Equations (19) and (20), Young’s modulus E₁, E₂ of each layer is calculated as E₁ = 209.3 [GPa] for a SWPA layer and E₂ = 129.9 [GPa] for a Cu layer.

3.2. Method 2: (Measurement of λ Only)

A similar chart (: Nomograph) is given in Figure 4, illustrating the relationship of γ and λ/L. Using this chart, each Young’s modulus E_i in a multi-layered material can be calculated from Equation (14). As an example, Young’s modulus E_i of each layer is obtained for a SWPA thin wire (: first layer) + a Cu thin layer (: second layer) mentioned above (see the tertiary Section 3.1).

3.2.1. First Step Procedure (As a Two-Layered Specimen)

Under the condition of P = 34.34 [mN], λ = 89.5 [mm] (i.e., λ/L = 0.7184) are measured for a double layer and then the value of γ is taken from Figure 4 (γ = 2.220). Therefore, from Equation (14) the combined flexural rigidity (I₁ = 1.023 × 10^{-15 [}m⁴]: SWPA, I₂ = 2.584 × 10^{-16 [}m⁴]: Cu) can be written as follows

$$E_1{I}_1+E_2{I}_2=P{L}_1{}^2/\gamma =0.03434\times {0.125}^2/2.220=2.414\times {10}^{-4}$$

(21)

3.2.2. Second Step Procedure (As a Single-Layered Specimen)

Similarly, λ is measured for a single layer after removing a second layer (Cu). In the condition of P = 29.43 [mN] for a SWPA single layer, λ = 89.5 [mm] (i.e., λ/L = 0.716) is measured and then γ is taken newly from Figure 4* (γ = 2.15) [*: Drawing is omitted here.]. Therefore, the flexural rigidity (I₁ = 1.023 × 10^{−15 [}m⁴]: SWPA) can be rewritten as follows from Equation (14).

$$E_1{I}_1=P{L}_1{}^2/\gamma =0.02943\times {0.125}^2/2.15=2.136\times {10}^{-4}$$

(22)

From the simultaneous Equations (21) and (22), Young’s modulus E₁, E₂ of each layer is calculated as E₁ = 209.5 [GPa] for a SWPA layer and E₂ = 104.57 [GPa] for a Cu layer.

4. Experimental Investigation

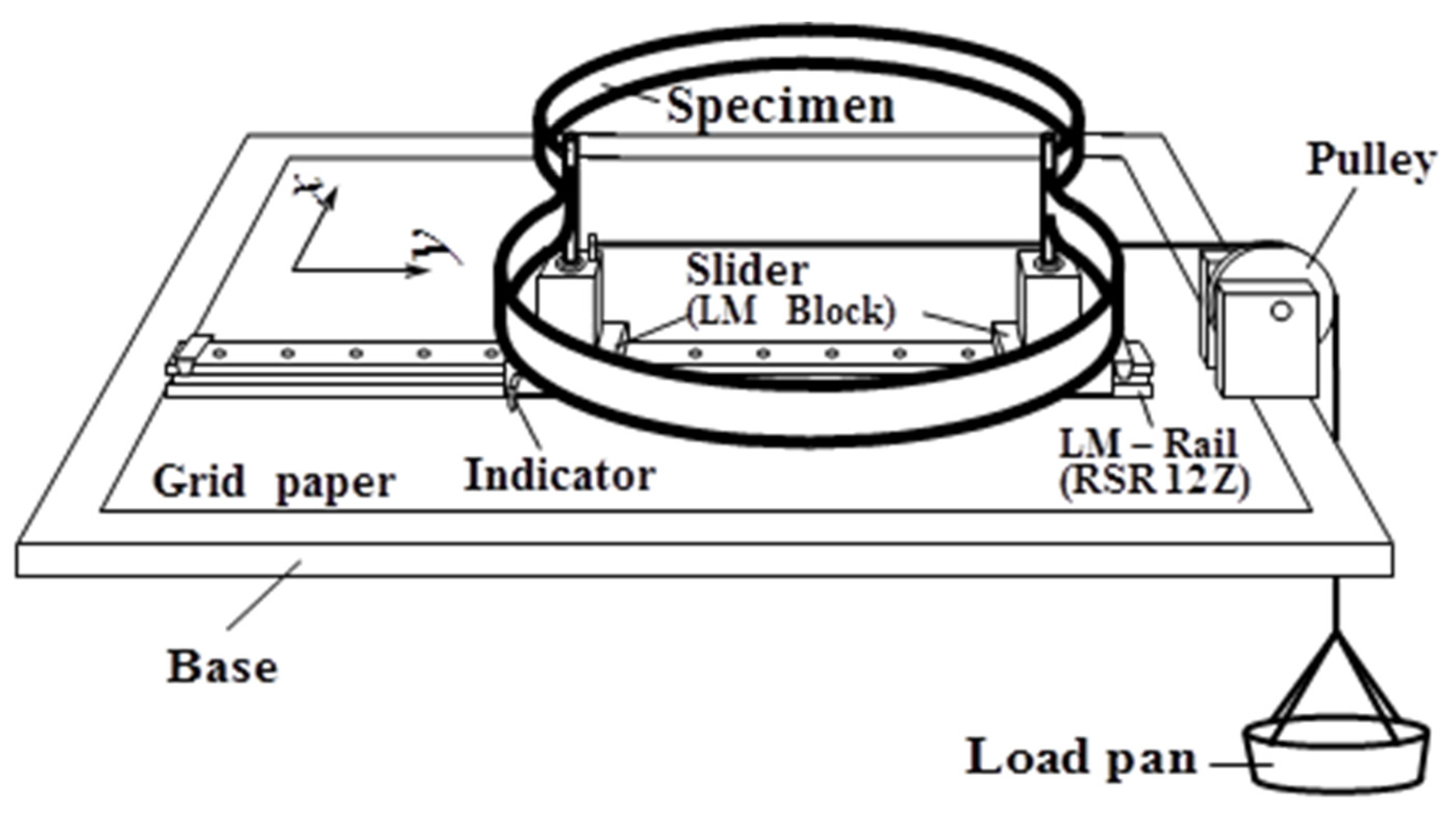
In order to assess the applicability of the Compressive Circular Ring Method, several large deformation experiments were carried out using a two-layered wire [Cu (Copper) layer: an electrodeposited material (0.011 mm thick, 500 mm long) + SWPA layer: a spring steel wire (0.38 mm diameter, 500 mm long)]. The experimental set-up is shown in Figure 5 (which shows a thin multi-layered plate, for example). Since Young’s modulus of each layer in the two-layered material is unknown, the measuring experiments were carried out by adopting the two-step procedure. In every step of the procedures, a vertical displacement δ and a horizontal displacement λ are measured for several compressive loads P by using a grid paper with 1mm spacing.

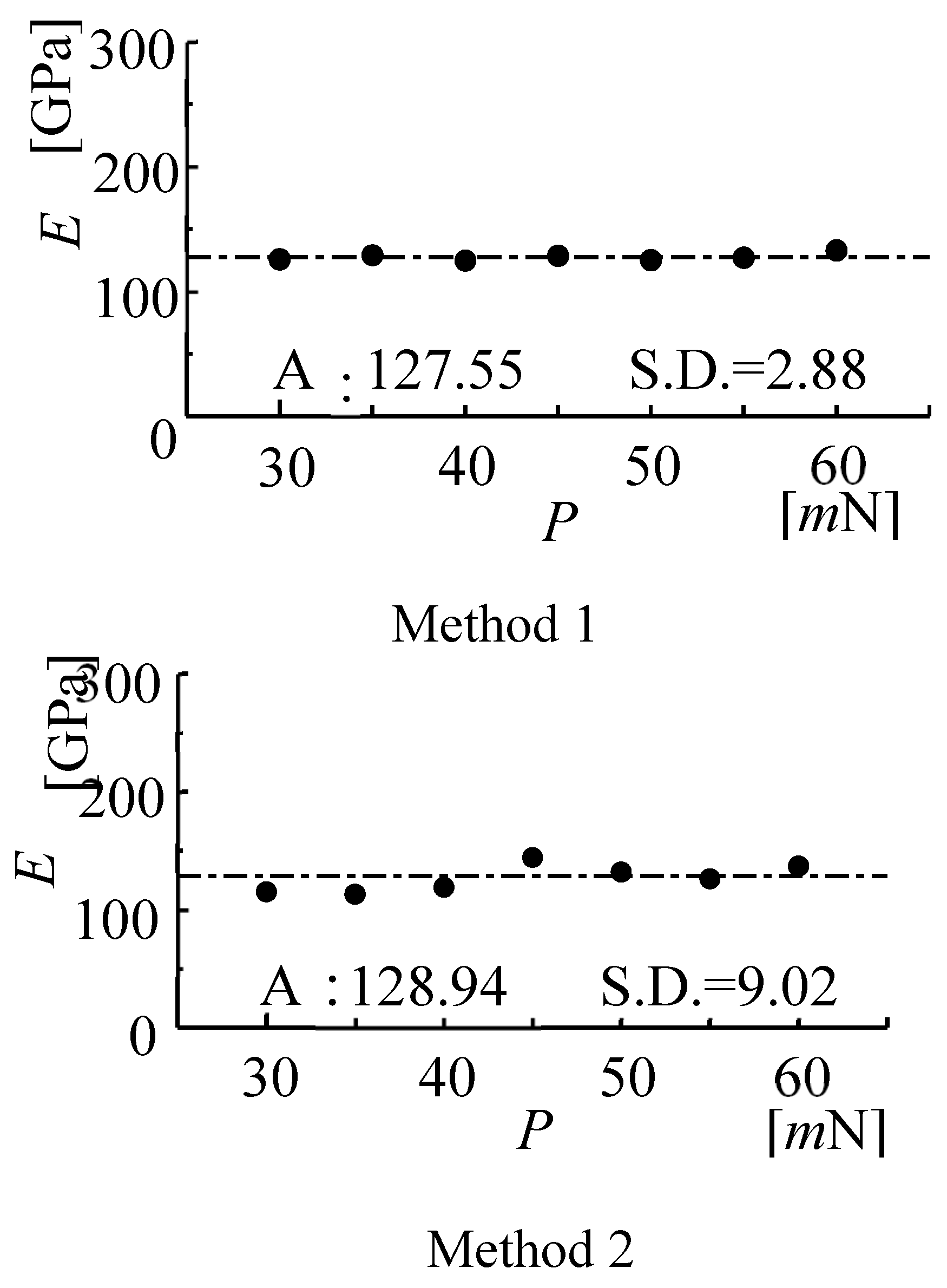
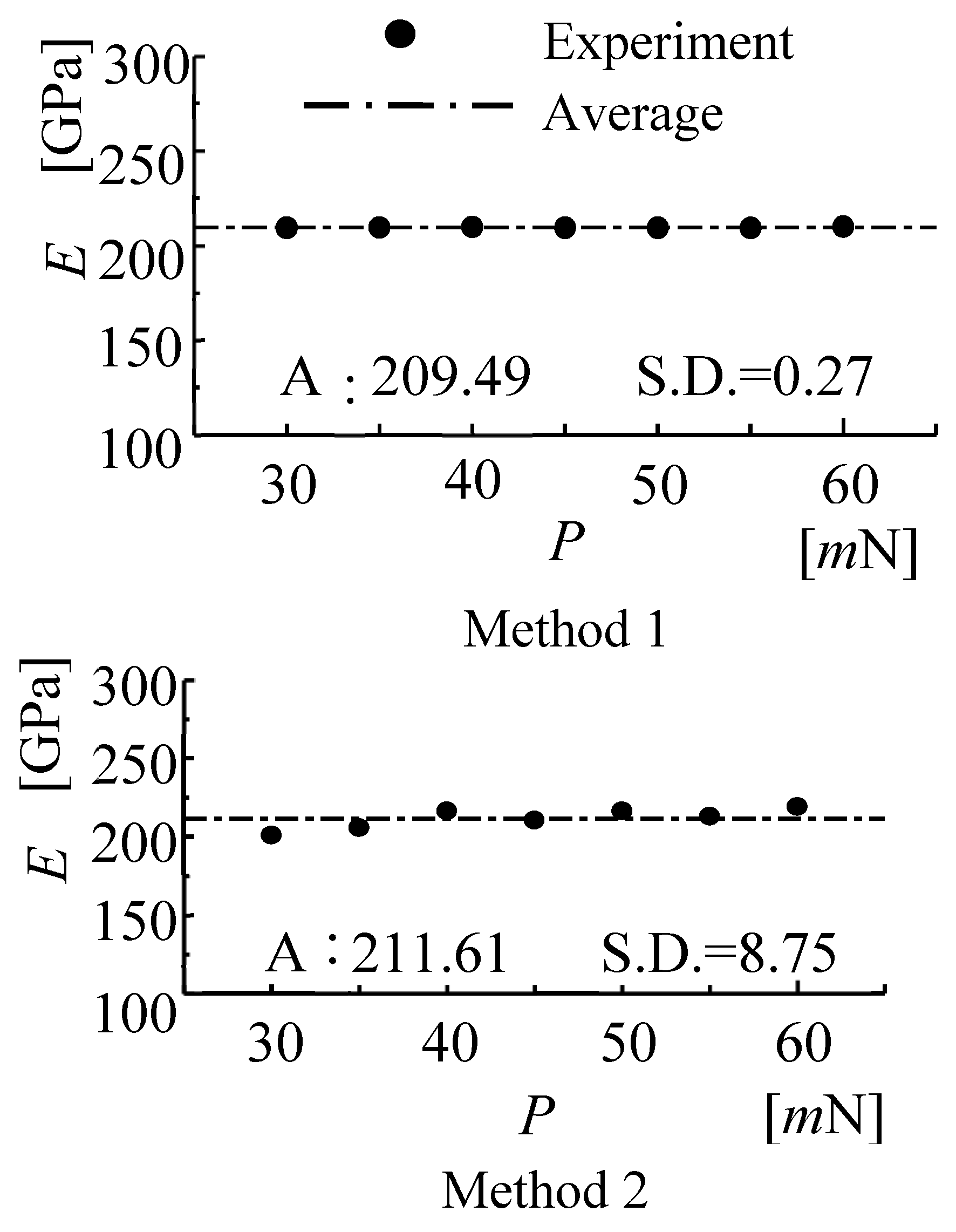
Young’s moduli of Cu and SWPA obtained by applying Method 1 and Method 2 are shown in Figure 6 and Figure 7, respectively. Here, the influence of a load (P) upon Young’s modulus (E) was examined.

The figures were described under a two-layered condition

In a Cu layer (see Figure 6), the measured values of Methods 1 and 2 remain nearly constant for a compressive load and the standard deviation (S.D.) is very small although every method has a little scattered values. As a whole, the mean Young’s moduli (shown as Av.: Average) determined by the two methods are reasonably in good agreement with each other. On the other hand, Trends similar to that of Figure 6 is observed for Young’s moduli of a SWPA layer (see Figure 7). The mean values obtained by the two methods agree well.

5. Conclusions

The “Compressive Circular Ring Method” is proposed as a new and simpler material testing method for measuring Young’s modulus of each layer in a flexible multi-layered material.

From the results of theoretical and experimental analyses, the new method is effective for measuring Young’s modulus of each layer in a flexible multi-layered material. Furthermore, the proposed new method is applicable widely to Young’s modulus measurement in a thin layer formed, for example, by PVD (Physical Vapor Deposition), CVD (Chemical Vapor Deposition), Coating (Graphite, Metal Oxide), Paint (Lacquer), etc.