Low Temperature and Resin Effects on the Mode I Interlaminar Fracture Toughness in Aeronautical Quality Polymer Composites ^†

Abstract

In the present research the fracture behavior in mode I under static loading of two aircraft quality composites materials has been analyzed at different test temperatures. The composites under study are made of the same unidirectional AS4 carbon fiber reinforcement and had different matrix of epoxy resin, one made of epoxy type 3501-6, and the other with epoxy type 8552 (modified to increase its toughness). Double cantilever beam (DCB) specimens were tested for different temperatures: 20 °C (room temperature), 0 °C, −30 °C and −60 °C, in order to simulate flight conditions. The results obtained from the static tests were analyzed using the Gompertz function.

1. Introduction

In the last years, the application of fiber reinforced composite materials in various branches of techniques (civil engineering, aeronautics, shipbuilding, etc.) has undergone a huge development, largely replaced traditional materials as is the case of many metals. The numerous features of composite materials have led to the widespread adoption and use through many different industries. It is because of these unique features of composites that people benefit: Lighweight (specially in comparison to materials like concrete, metal and wood), high strength (specially per unit of weight), corrosion and chemical resistance, elastic (properties), non-conductive.

The aircraft industry is probably one of the most beneficiaries of these materials, the use of them in commercial and military aircrafts has increased over the last 20 years. However, despite all their advantages, laminated reinforced composites have certain disadvantages as well, such as fiber breakage, fiber pull-out, fiber/matrix debonding, delamination, etc. Among these damage modes, delamination is one of the most important and least understood and is especially important because it can cause a disastrous loss of compressive strength. Small delamination cannot be detected by nondestructive inspections and in some cases, the structure can fail catastrophically without any external warning signs. This failure scenario makes delamination a major obstacle to wider utilization of advanced composite materials in structures and machinery. Therefore, it is a crucial to develop a better understanding of delamination.

There are three modes of loading that can be applied to the delamination. In current applications of composites the most commonly encountered conditions involves modes I, II and mixed mode. In the present study pure mode I, has been analyzed for unidirectional carbon/epoxy composites. This mode of loading has been considered for several researchers using Double Cantilever Beam (DCB) specimens [1,2,3,4].

The present research shows an experimental and numerical analysis of the delamination under mode I static loading for two aeronautical quality composite materials at different test temperatures (20, 0, −30 and −60 °C) in order to analyze the matrix and temperature influence (room temperature and flight conditions). To characterize the phenomenon of delamination crack growth curves had been obtained from the statics tests and an approximation with the Gompertz function [5] was created in order to obtain a trend for the initiation and crack growth fracture toughness (G_IC) as a function of the type of matrix and temperature analyzed.

2. Materials and Methods

Two types of materials were employed to carry out this research. One of the materials is composed of a 3501-6 epoxy resin prepeg reinforced with AS4 unidirectional carbon fibre and the other is composed of a 8552 epoxy resin prepeg, modified to increase its toughness and the same fibre reinforced. Laminates configuration is symmetric [0°]_16/S, employing a 20 µm thick Tygavac RF-260-R at the midplane, as insert to form an initiation site for the delamination.

Prior to the numerical analysis, experimental tests were performed according to the ASTM D5528-01 Standar [6]. The equipment employed for testing was formed by a servo-hydraulic MTS testing machine provided with a 1kN load cell controlled by a computer using the original software. A thermal chamber was coupled to the testing machine to carry out the low temperature tests (0, −30 and −60 °C). A video camera focused on the specimen and connected to a monitor was used to observe the advance of the crack. This solution was necessary because it was not possible in the test carried out inside the thermal chamber to observe the crack growth with a microscope as shown in the Standard.

Interlaminar fracture toughness under mode I loading (G_IC) was obtained from the quasi-static tests to reflect the behavior against delamination. Several analytical models can be used to reduce the data for DCB tests. The three data reduction methods recommended in ASTM D5528-01 are: Modified Beam Theory (MBT), Compliance Calibration (CC) and Modified Compliance Calibration (MCC). The main difference in these methods lies in the different models used for the compliance vs. crack length relation. Both MBT and MCC methods assume that compliance (C) is related to crack length (a) by a third polynomial but in different forms. In the present research MCC method has been employed to calculate the G_IC as recommend Kageyama and Hojo [7] for being one of the methods with less dispersion in the results obtained. G_IC values obtained from the mean values of all the specimens tested, were represented versus crack propagation (Δa) in order to approximate with the Gompertz function as is presented in the following.

3. Results

3.1. Gompertz Function

The analysis of growth data is important in many fields of study like biologists, chemists, engineering, medicine etc. For many types of growth data, the growth rate does not steadily decline, but rather increases to a maximum before steadily declining to zero. This is shown in the growth curve by an S-shaped, or sigmoidal, pattern. Assuming that the R-curve, (K_IC-Δa) where Δa the crack increment is known, (K_IC) the fracture toughness is obtained by the experimental results. At the present study is proposed to use the analytical expression of the R-curve (K_IC-Δa) using a Gompertz function as was employed in the research carried out by Catalanotti and Camanho to predict net-tension failure of mechanically fastened joints in composite laminates [8]. Using G_IC values from the experiments instead of K_IC values ($K_{IC}=\sqrt{E\times G_{IC}}$), the R-curve can be expressed as:

$$G_{IC}(\Delta a)\hspace{0.17em}=\hspace{0.17em}{G}_{IC}^{ss}·\hspace{0.17em}{e}^{log(G_{IC}^i/G_{IC}^{ss})?e^{b\Delta a}}$$

(1)

where $G_{IC}^i$and $G_{IC}^{ss}$ are respectively the initiation and propagation fracture toughness from experimental results, $e$ is the Euler’s number and $b$ is calculating fitting the experiments. To perform curve fitting Matlab Software [9] was employed.

Table 1. Gompertz parameters obtained from AS4/3501-6 material.

Ta (°C)	GICi (J/m2)	GICSS (J/m2)	δFPZ (mm)	b
20	129.91	154.06	20	−0.06179
0	88.54	123.02	23.33	−0.04796
−30	94.62	122.90	18.33	−0.08614
−60	81.33	99.56	21.67	−0.03606

and

Table 2. Gompertz parameters obtained from AS4/8552 material.

Ta (°C)	GICi (J/m2)	GICSS (J/m2)	δFPZ (mm)	b
20	293.44	308.6	25	−0.06378
0	308.57	232.39	23.33	-
−30	295.64	200.19	16.67	-
−60	286.97	234.93	11.67	−0.02989

show the parameters obtained from the experimental tests used to perform the Gompertz growth function.

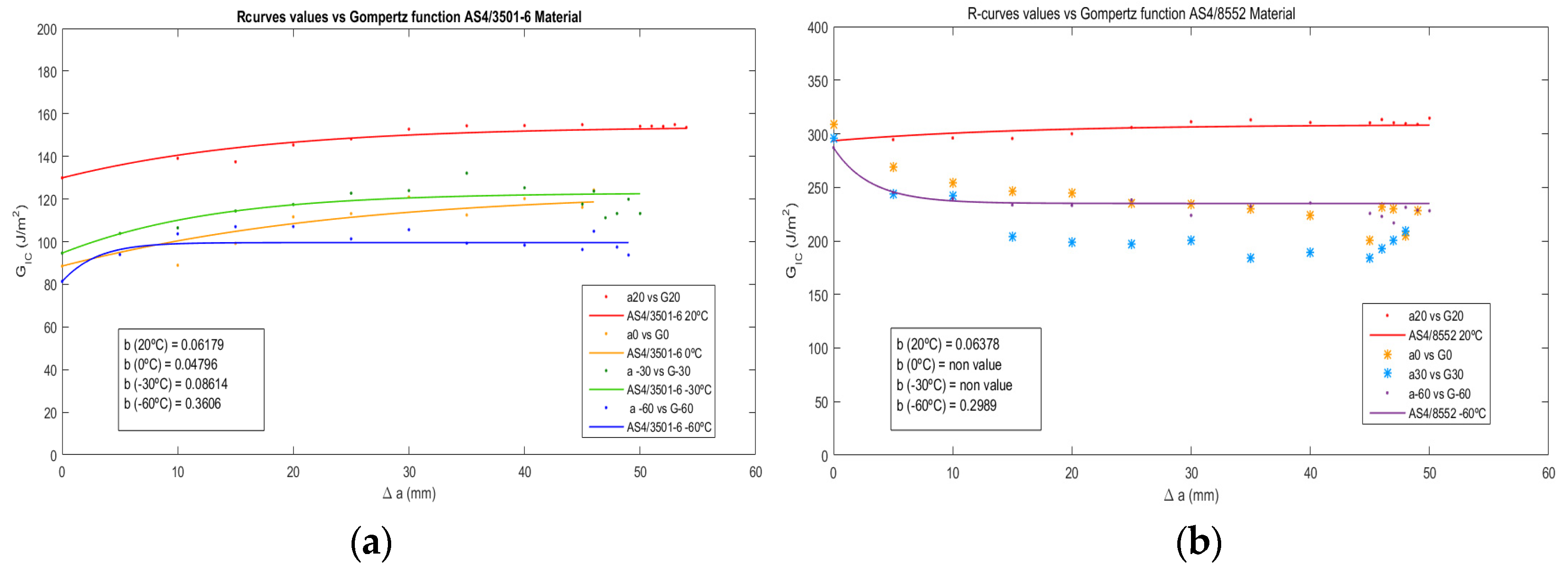
As it can be observed, for the AS4/8552 material is was not possible to obtain b parameter at 0 and −30 °C. This is due because when the R-curve is decreasing and when the $G_{IC}^i$ value is much higher tha $G_I^{ss}$ value the approximation of the Gomperzt function does not fit. These could be observed in the next paragraph where the approximation of the R-curves are presented. High values for the initiation of the crack are usually related with the manufacturing procedure (resin amounts generated in the initiator insert of the delamination zone) and/or higher toughness values of the resin compared with the composite.

Load-displacement curves and G_IC values of initiation were obtained too, in order to analyze the resistance of the materials to initiation to delamination. The results show a clearly influence of the temperature and the type of matrix.

3.2. Aproximation of R-Curves

Figure 1 shows the fitting function obtained for the both laminates at all the temperatures analysed. To obtain this fitting is necessary initiation toughness values lower than propagation values in general.

As it can be observed at the results, for the material with modified matrix (AS4-8552) a relatively flat and decreasing resistance curves were obtained for the low temperature tests performed, compared with the curves obtained for the AS4/3501-6 material. The flat resistance curves are typical of brittle matrix laminates as was found in some round robin tests [1]. For the other side, AS4/3501-6 material shows an increment of the values of toughness as the delamination progresses for all the temperatures of analysis, which represents a normal R-curve trend. This behavior can be due to the fiber bridging which produce an increment of the delamination resistance during the crack propagation. AS4/3501-6 material also provides a decrement of the delamination resistance with decreasing test temperatures, due to a more brittle behavior of the matrix.

In addition, the energy release rates obtained at those temperatures are lower than at room temperature for both materials, which indicated a worst mechanical behavior against delamination. In general, AS4/3501-6 material shows lower interlaminar fracture toughness values than the material with modified matrix for all the temperatures analysed, both during the initiation and during propagation of the crack.

The approximation of the R-curves (G_IC-Δa) using Gompertz growth function parameters shows the resistance to the initiation and growth of delamination. It can be observed that the material with non-modified matrix is more influenced by the temperature and shows lower resistance to delamination. For the material with 8552 epoxy prepeg decreasing R-curves were obtained for some of the testes performed. A fracture surface analysis of the specimens was carried out in order to analyze this behavior.

4. Conclusions

To perform Mode I testing at low temperatures some variations on the test procedure recommended by the Standard was required.

From the obtained interlaminar fracture toughness results, a decrease of the resistance to delamination was observed with the decrease of the test temperature for both materials. It seems that AS4/3501-6 material is more influenced by the temperature, with increased matrix fragility.

Comparing the epoxy matrix types, as is observed in the R-curves, the material with 8552 epoxy matrix shows a better behavior against delamination, obtaining higher G_IC values, at all the temperatures under study.

The Gompertz function allows for a realization of a good approximation of the R-curves obtained from the experimental results. When the curves obtained are high decreasing it is not possible to approximate the curves with a growth curve function, such as the Gompertz.