Analysis of Stochastic Time Response of Microfluidic Biosensors in the Case of Competitive Adsorption of Two Analytes †
Abstract
:1. Introduction
2. Theory
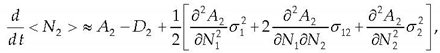 | (4) |
 | (5) |
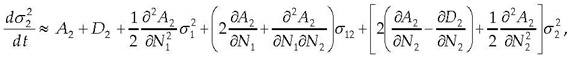 | (6) |
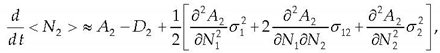 | (7) |
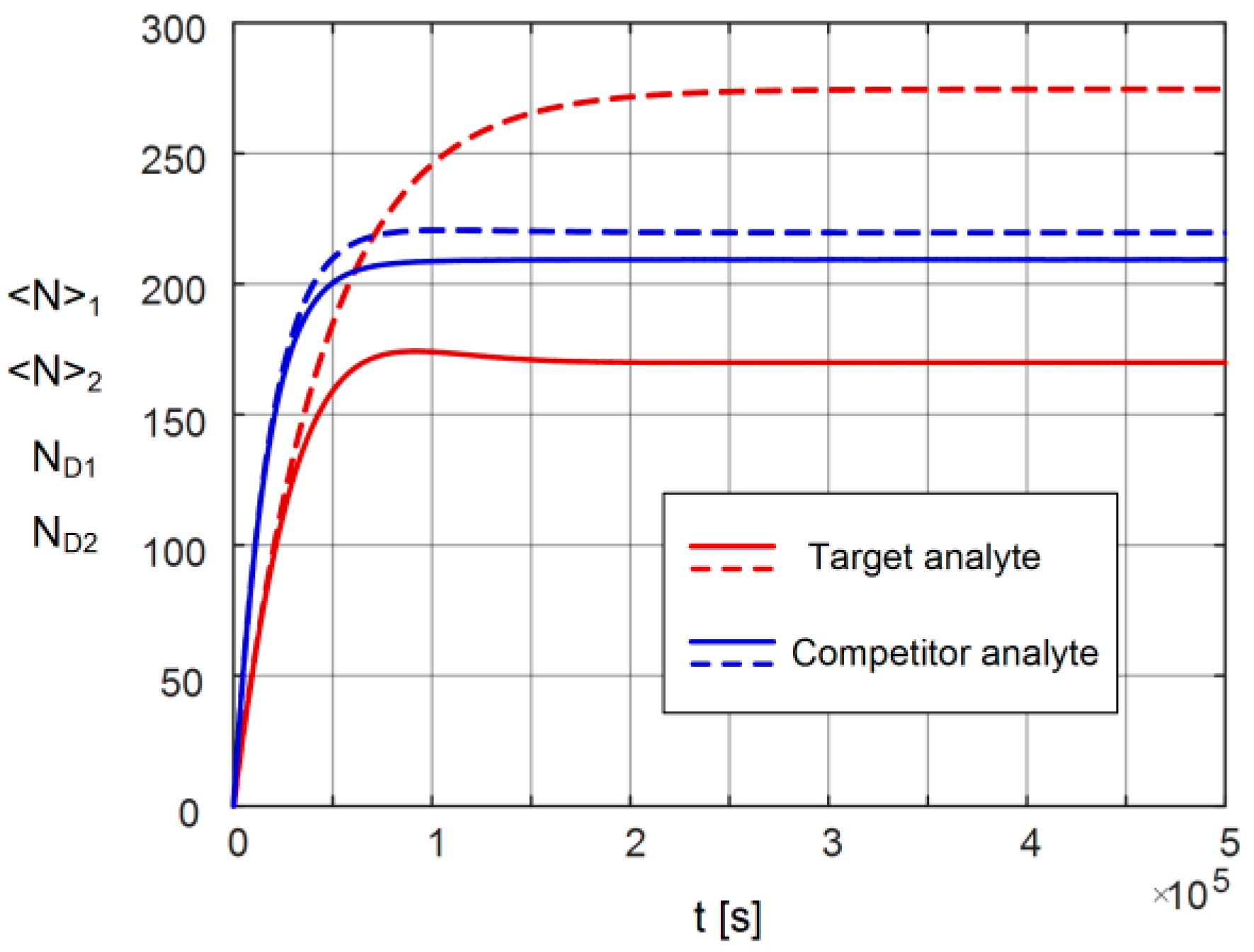
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jakšić, O.; Jakšić, Z.; Čupić, Ž; Randjelović, D; Kolar-Anić, L. Fluctuations in transient response of adsorption-based plasmonic sensors. Sens. Actuators B Chem. 2014, 190, 419–428. [Google Scholar] [CrossRef]
- Tulzer, G.; Heitzinger, C. Fluctuations due to association and dissociation processes at nanowire-biosensor surfaces and their optimal design. Nanotechnology 2015, 26, 025502. [Google Scholar] [CrossRef] [PubMed]
- Djurić, Z.; Jokić, I; Milovanović, G. Signal-to-noise ratio in adsorption-based microfluidic bio/chemical sensors. Procedia Eng. 2016, 168, 642–645. [Google Scholar] [CrossRef]
- Myszka, D.G.; He, X.; Dembo, M.; Morton, T.A.; Goldstein, B. Extending the Range of rate constants available from BIACORE: Interpreting mass transport-influenced binding data. Biophys. J. 1998, 75, 583–594. [Google Scholar] [CrossRef]
- Frantlović, M.; Jokić, I.; Djurić, Z.; Radulović, K. Analysis of the competitive adsorption and mass transfer influence on equilibrium mass fluctuations in affinity-based biosensors. Sens. Actuators B Chem. 2013, 189, 71–79. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jokić, I.; Djurić, Z.; Radulović, K.; Frantlović, M. Analysis of Stochastic Time Response of Microfluidic Biosensors in the Case of Competitive Adsorption of Two Analytes. Proceedings 2018, 2, 991. https://doi.org/10.3390/proceedings2130991
Jokić I, Djurić Z, Radulović K, Frantlović M. Analysis of Stochastic Time Response of Microfluidic Biosensors in the Case of Competitive Adsorption of Two Analytes. Proceedings. 2018; 2(13):991. https://doi.org/10.3390/proceedings2130991
Chicago/Turabian StyleJokić, Ivana, Zoran Djurić, Katarina Radulović, and Miloš Frantlović. 2018. "Analysis of Stochastic Time Response of Microfluidic Biosensors in the Case of Competitive Adsorption of Two Analytes" Proceedings 2, no. 13: 991. https://doi.org/10.3390/proceedings2130991
APA StyleJokić, I., Djurić, Z., Radulović, K., & Frantlović, M. (2018). Analysis of Stochastic Time Response of Microfluidic Biosensors in the Case of Competitive Adsorption of Two Analytes. Proceedings, 2(13), 991. https://doi.org/10.3390/proceedings2130991



