A Gradiometric Magnetic Sensor System for Stray-Field-Immune Rotary Position Sensing in Harsh Environment ^†

Abstract

Contactless magnetic position sensors are used in countless industrial and automotive applications. However, as a consequence of the electrification trend the sensors can be exposed to parasitic magnetic stray fields, and their desired robustness may be compromised. In this paper we publish for the first time how this challenge is addressed and constructively solved using a complete paradigm change leaving conventional magnetic field measurement behind and entering into the realm of magnetic field gradient measurement. Our novel sensor system consists of an integrated Hall sensor realized in 0.18 μm CMOS technology with magnetic concentrators and a four-pole permanent magnet. The intrinsic angular accuracy was assessed comparing the rotary position of the permanent magnet with the sensor output showing angle errors below 0.3°. Additional end-of-line calibration can be applied using built-in memory and processing capability to further increase the accuracy. Finally, we demonstrate the immunity against stray fields of 4000 A/m which led to errors below 0.1°, corresponding to 0.06% of the sensors fullscale angular range. In conclusion, this novel sensor system offers a compact and flexible solution for stray-field immune rotary position measurement in harsh environment.

1. Introduction

Magnetic sensors in general and magnetic position sensors in particular are increasingly popular means for manifold measurement tasks in industrial, automation, robotics, consumer, and automotive applications [1]. Their strength is the contactless, compact, and cost-effective position sensing nearly free from wearout and aging effects. In addition, magnetic vector position sensors feature thermal stability and are therefore suitable for harsh environment [2].

Modern vehicles however, with their electric drives, current flow between batteries, power inverters, and motors, as well as wireless charging induce parasitic magnetic fields [3]. This represents a tough challenge for conventional magnetic position sensors as the accuracy may be compromised by the parasitic fields [4] which not unlikely reach values up to 20 kA/m.

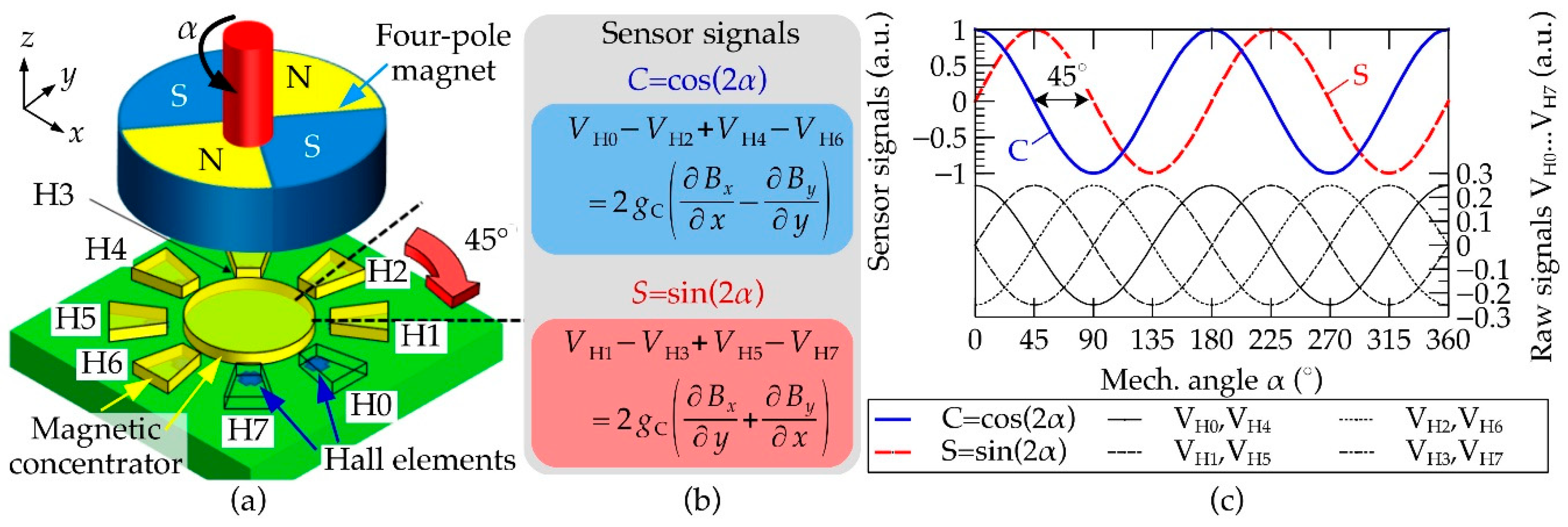
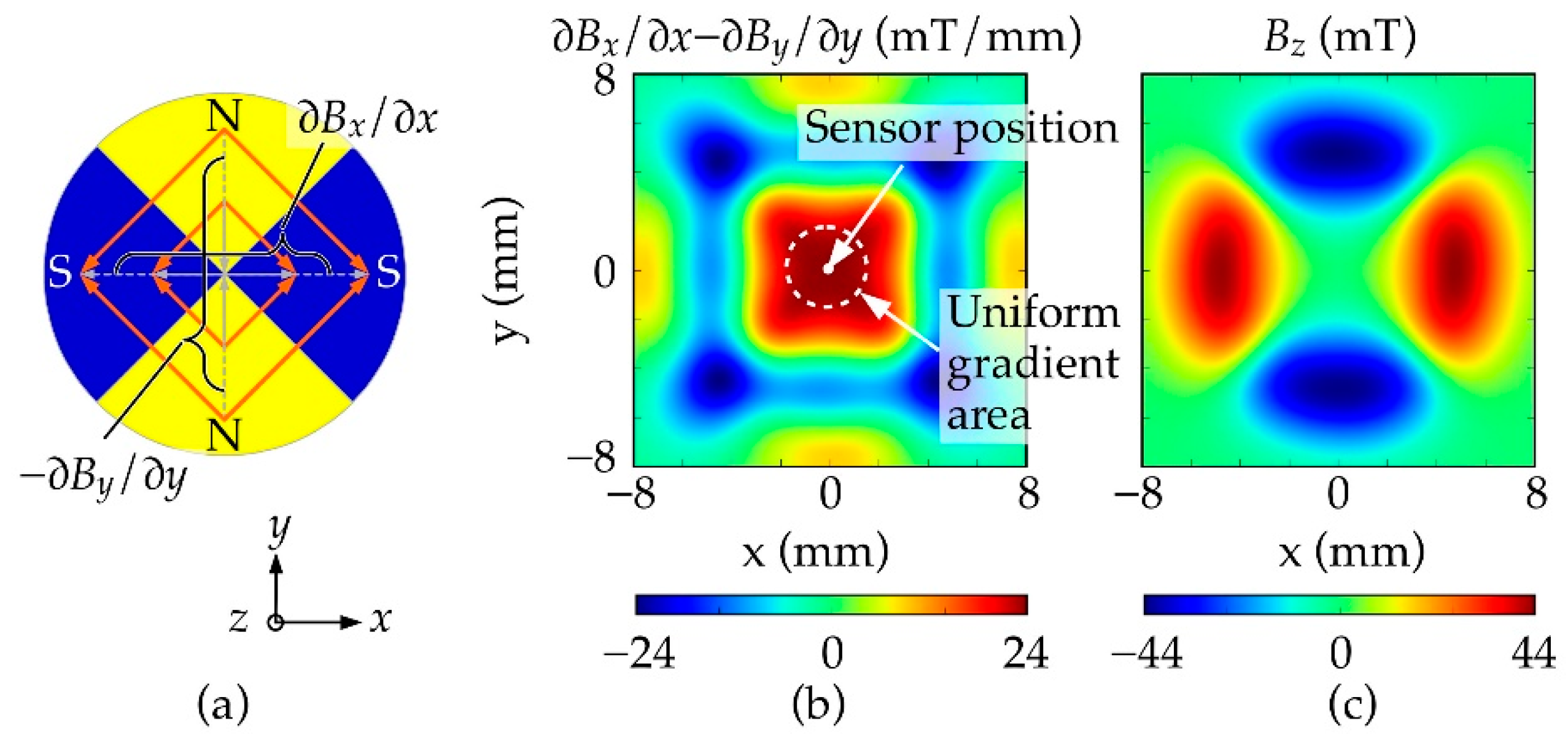
2. Concept

In contrast to conventional magnetic position sensors our novel sensor system exploits the inplane magnetic flux density gradients therefore being robust against uniform external magnetic fields. The system consists of a four-pole permanent magnet and an integrated CMOS Hall sensor with integrated magnetic concentrators [5], as shown in Figure 1a.

The four-pole permanent magnet can be based on various basic shapes, e.g., disk or ring shapes. Its alternating magnetization along the axial direction produces the desired in-plane flux density gradients ∂B_x/∂x, ∂B_y/∂y, ∂B_x/∂y, ∂B_y/∂x under the center of the magnet. At the same time the three components of the magnetic flux density vector B_x, B_y, B_z disappear.

Henceforth the useful flux density gradients are sensed by the CMOS Hall sensor microsystem consisting of eight circularly arranged Hall elements H0...H7 and magnetic concentrators. The combination of the raw signals V_H0...V_H7 with alternating signs, as shown in Figure 1b is a measure for the in-plane flux density gradients and simultaneously eliminates the impact from parasitic stray fields of arbitrary direction and intensity. As a result, we obtain the quadrature sensor signals C = V_H0 − V_H2 + V_H4 – V_H6 and S = V_H1 – V_H3 + V_H5 – V_H7 representing cos(2α) and sin(2α), respectively, having naturally a phase shift of 45°, as shown in Figure 1c.

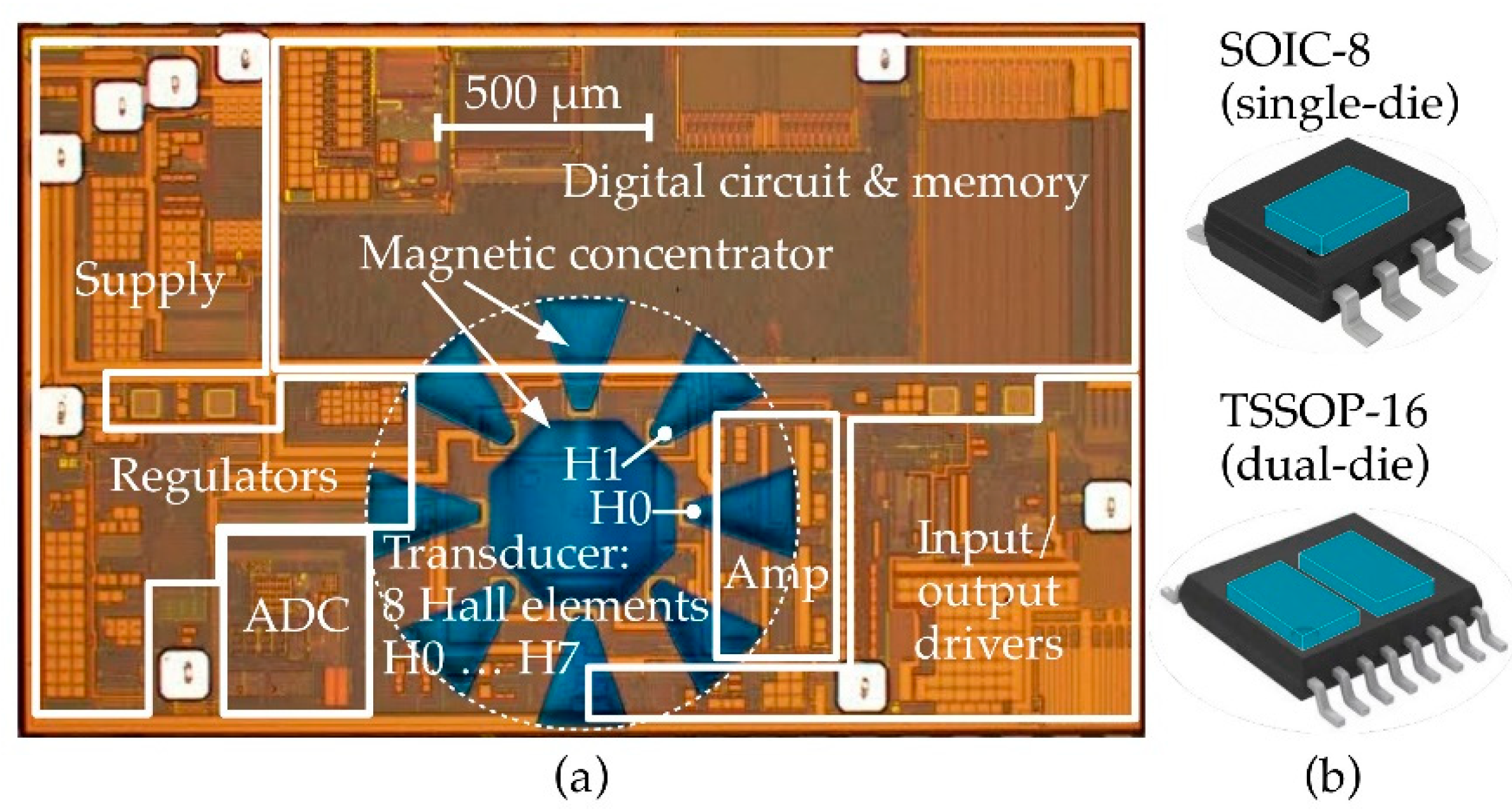
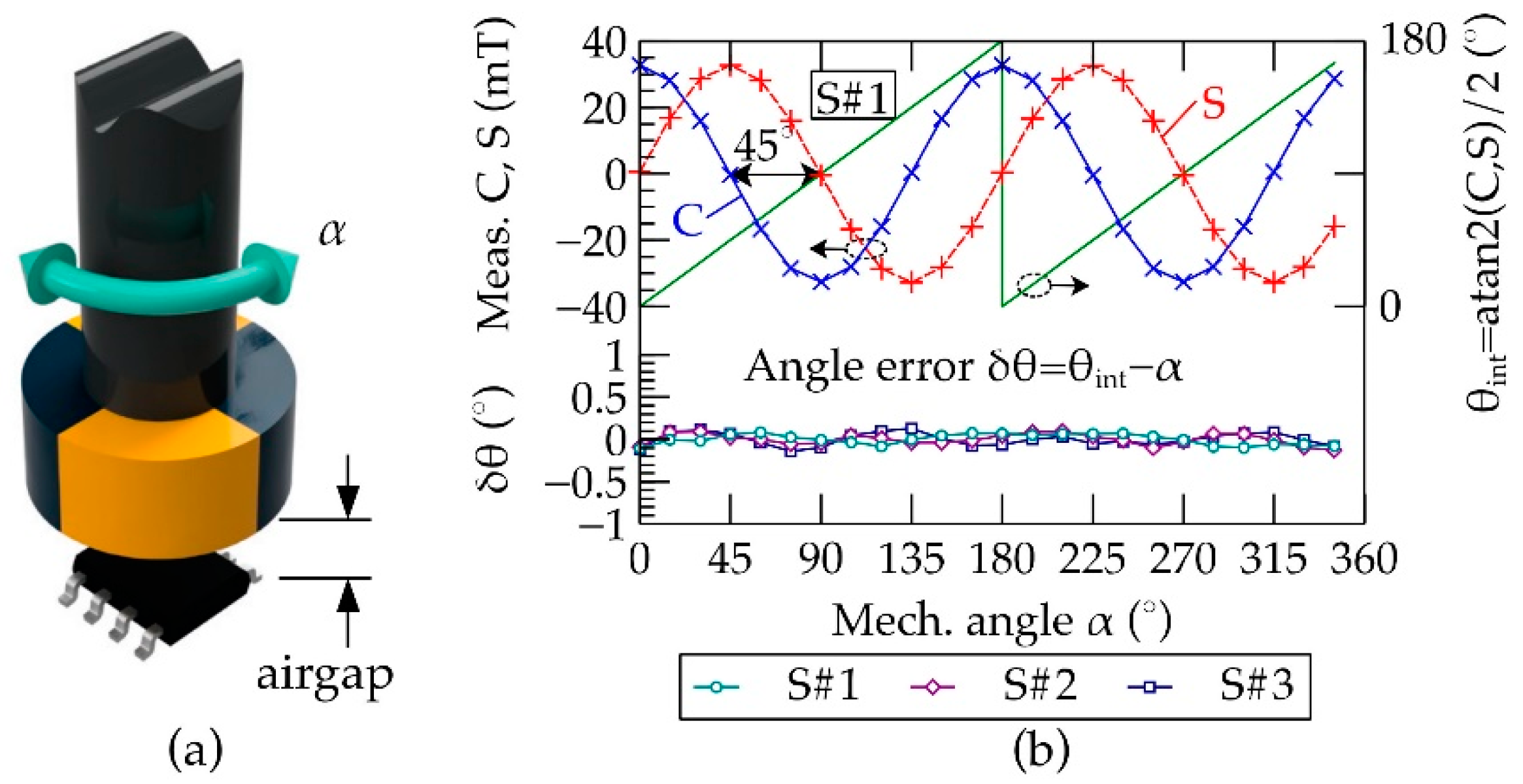
3. Materials and Methods

The Hall sensor microsystem was realized in a standard 0.18 μm CMOS technology with advanced circuitry for biasing, Hall read-out, and signal processing [6]. The eight Hall elements arranged on a virtual circle with a radius of 250 μm are complemented with 23-um-thin magnetic concentrators. An optical micrograph of the sensor microsystem is shown in Figure 2a.

A particular feature of the novel sensor system is the use of a four-pole permanent magnet and its resulting flux density gradients, as illustrated in Figure 3a. Despite the fact that a great variety of magnet shapes and sizes can be used, we show results obtained from a ring-shaped magnet with an outer diameter of 14 mm, inner diameter of 5 mm and a thickness of 3.5 mm. This injectionmolded magnet is made of anisotropic bonded ferrite material and magnetized axially, i.e., in directions parallel and anti-parallel to the rotation axis. The resulting in-plane flux density gradient G = ∂B_x/∂x − ∂B_y/∂y and the out-of-plane flux density B_z are shown in Figure 3b,c, respectively, for a vertical distance (airgap) of 1.5 mm.

4. Results

The sensor microsystem was exposed to the rotation of the four-pole magnet at various mechanical angles α between 0° and 360°, as schematically shown in Figure 4a. For a flux density gradient of G = 20 mT/mm signal amplitudes of about 33 mT were measured, being the product of Hall plate lateral distance and magnetic gain of the concentrator. Hence, a magnetic concentrator gain of g_C = 0.83 mm was reached. Comparing the sensor’s detected angle θ_int to the mechanical reference α showed deviations δθ lower than 0.3°. This represents the intrinsic accuracy of the position sensor system without any post-processing nor trimming whatsoever. The measured signals and angle errors are shown in Figure 4b.

Finally, the stray-field-immunity was assessed by measuring the sensor’s angular position θ_int for various directions of the parasitic stray field, as schematically illustrated in Figure 5a. Stray fields with magnitudes of 20,000 A/m and 4000 A/m were applied, which led to angle errors δθ below 0.5° and 0.1°, respectively, as shown in Figure 5b. Therefore, the error at 4000 A/m strayfield-exposure was found to be as low as 0.06% of the sensors fullscale range of 180°. Further details are unveiled in our companion article [7].

5. Discussion and Conclusion

We presented a novel absolute rotary position sensor system based on an integrated Hall magnetic gradiometer and a four-pole permanent magnet. In contrast to the existing and ubiquitously applied magnetic position sensors [1], our sensor measures the in-plane magnetic field gradients and is therefore inherently insensitive to parasitic magnetic stray fields. In-depth experimental characterization revealed intrinsic angle errors below 0.3° and stray-field (4000 A/m) related errors typically below 0.1°. Overall, the solution outperforms the state of the art [7].