Reduced Order Component & System Level Modelling for Fluid-Solid Interactions in Complex MEMS Devices ^†

Abstract

The time-efficient and accurate implementation of physics-based fluidic damping effects is still one of the biggest challenges in the simulation of complex MEMS devices. Two modelling approaches utilizing the CRAIG/BAMPTON component mode synthesis method are discussed and compared in context of a highly automated model generation procedure. The first approach uses a modal projection technique with pressure profiles obtained from REYNOLDS flow simulations using the thermal-fluidic analogy. The second approach is based on the representation of the fluidic domain in form of a generalized KIRCHHOFFian lumped flow resistance network model. Both methods are generally suited for the simulation of structures like gyroscopes or accelerometers, but show different behaviors in terms of scaling and complexity during the model generation step and in the final ROM. The methods are demonstrated on examples and are compared to optical measurements of an out-of-plane teeter-totter type accelerometer.

1. Introduction

The performance and cost efficiency of MEMS devices is already essentially determined during the design phase. Comprehensive data sampling is required to analyze different layout characteristics and their interactions in the involved physical domains, which necessitates time- and resource-efficient, yet accurate modelling approaches. Physics-based representations of the fluid domain come often along with extensive computational loads due to the high levels of detail caused by perforations and other design elements. Perforations are a typical technological requirement to ensure sufficient release etching in surface micro-machining. The fluid flow through the perforation channels has a significant influence on the fluidic damping behavior and is often utilized to optimize the dynamic characteristics of a structure. Equally, they can have a significant influence on the stiffness of seismic masses, which has an impact on high order eigenfrequencies and mode shapes.

The CRAIG/BAMPTON component mode synthesis approach [1] is a common strategy for ROM generation in complex systems to simulate intricate structures while avoiding time-consuming out-of-core runs. Subdividing the device into components as shown schematically in Figure 1a allows for a reduction of the complexity per generated ROM, but requires individual processing of each component. Identical components, mirrored or rotated instances as they often appear in MEMS in form of springs, seismic masses or support structures, can be reused and only need to be generated once. Internal degrees of freedom ui are represented as a superposition of fixed-interface vibration modes Φi and static constraint modes Φbi with the boundary DOF ub and the modal coordinates q:

u_i = Φ_bi u_b + Φ_i q

(1)

Figure 1b gives a schematic representation of the two types of shape functions. The components retain physical DOF at their boundaries, which can be used as interfaces to other components or for the application of loads and boundary conditions.

A modal projection approach to describe stimulation of modes through the fluid domain has been presented by MEHNER et al. [2]. During ROM generation it requires the calculation of pressure profiles associated with each mode and extracts modal damping and squeeze stiffness coefficients of the projected force responses for the other mode shapes. The pressure distribution in a gap between two moving plates is governed by the REYNOLDS equation for compressible gas films. Under the condition of small amplitudes the second-order non-linear differential equation can be linearized, assuming sectionally parallel plates and a perpendicular fluid flow. For an isothermal process the equation can be written as

$$\frac{p_a{d}^2}{12{\eta }_{eff}}{\nabla }^2\left(\frac{p}{p_a}\right)-\frac{\partial }{\partial t}\left(\frac{p}{p_a}\right)=\frac{\partial }{\partial t}\left(\frac{x}{d}\right)$$

(2)

where ηeff is the effective dynamic viscosity, d the local gap separation, pa the ambient pressure and x the variation of plate spacing. The 2-D heat flow equation

$$\lambda {\nabla }^2(T)-c\rho \frac{\partial T}{\partial t}=-Q$$

(3)

which is implemented in the thermal solids PLANE55 and PLANE77 in ANSYS Multiphysics, can be used as an analogy for this behavior [3]. Alternatively, the FLUID136 3-D squeeze film element can be applied, which additionally incorporates coupled-field interactions with the structural domain. Obtained coefficients are assembled to modal system matrices which can be utilized in digital signal flow processors such as MATLAB Simulink to simulate the dynamic behavior.

Another common approach to model the REYNOLDS flow domain is the representation of the gap region in form of a KIRCHHOFFian lumped flow resistance network model [4], allowing the simulation in electrical network simulators such as LTSpice or VHDL-AMS. SATTLER published an automated method to generate such models from a 2-D finite element region in ANSYS Multiphysics [5]. Perforations are represented as a compact model consisting of the transit domain underneath the perforation, the channel flow domain and an aperture flow resistance, which can be adopted to the thermal analogy approach by use of LINK33 or FLUID138 elements, respectively. Various compact models of different mechanics can be analogously represented in electrical notation and combined to full multi-domain system models [6].

Both methods represent different conceptional approaches for solving the same mathematical problem. In the context of an efficient simulation environment, strengths and weaknesses of each concept need to be determined to enable deliberate modelling decisions.

2. Approach

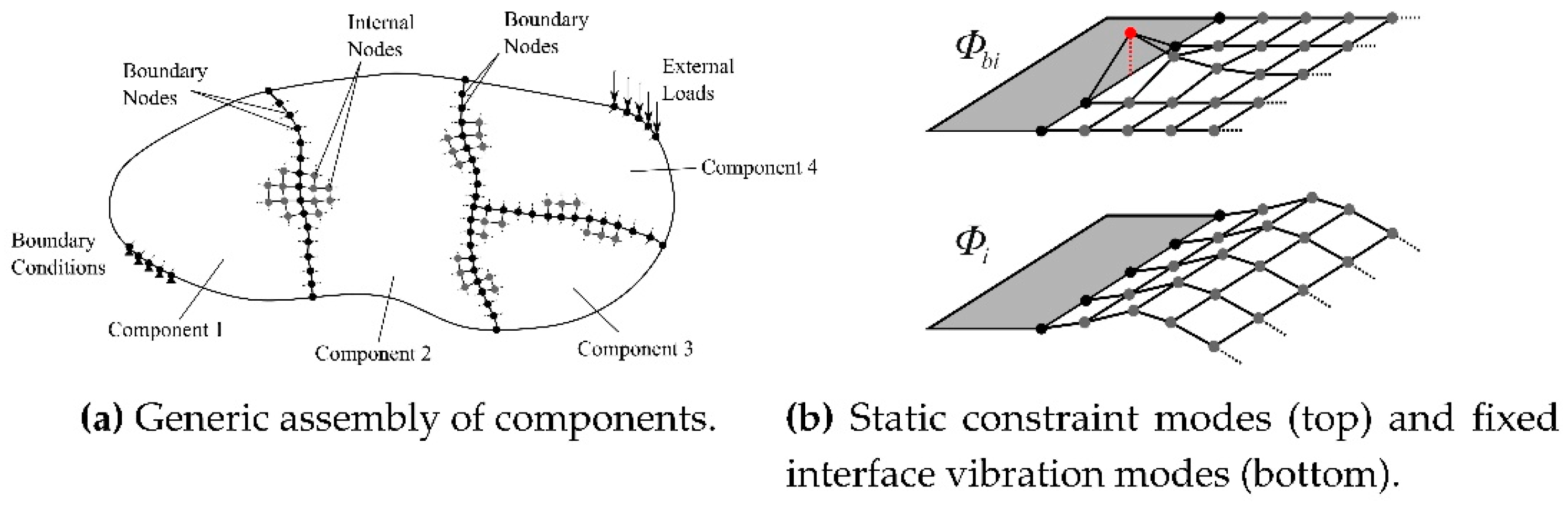
2.1. Modal Projection

A modal analysis of the assembly yields system eigenvectors Φsys which are expanded back to physical deflections on component level and serve as shape functions in the fluid simulations. Damping analyses are executed component-wise with focus on dominant plate regions, as design elements like springs are often neglectable if no substantial squeeze-film influence is present. As a result, projected frequency-dependent damping and stiffness coefficients are obtained as outlined in [2]. VEIJOLA published an approach to approximate the harmonic influence by introduction of equivalent spring-damper pairs. The damping contribution of all components can now either be accumulated on assembly level or projected to component level. It should be noted that coupling terms of modes can have a negative sign based in the direction of the eigenvector. Assembly of mirrored or rotated components without a reevaluation of the signs is just applicable for symmetrical mode shapes.

2.2. Lumped Flow Resistance Model

The chosen electrical network approach is shown in Figure 2a. The mechanical model is depicted on the left hand side. In the used analogy the voltage is equivalent to the velocity q˙ and the current represents the modal force $\tilde{f}$. A controlled voltage source serves as integrator to retrieve the modal deflections which are used in the fluid domain to determine physical deflections based on the shape function. The pressure responses of individual nodes control parallel variable current sources, which close the feedback loop. Figure 2b shows the theoretical resulting harmonic response of a test structure if only the first mode is driven and the second mode is stimulated by just the fluidic reaction force.

3. Results

Figure 3a,b show the simulated pressure distribution over the plate region of an out-of-plane accelerometer for the sense mode and the measured response to an applied voltage jump to one of the sense electrodes in comparison to simulation results for the same device. Both approaches show, beside slight deviations in timing, the same predicted behavior as identical model assumptions were made. The shown measured deflection curve was obtained from the vibrometer velocity readings by integration and has been adjusted for a systematic linear drift of the measurement setup. The predicted curves are in good accordance with the measured data upon voltage switch off. For applied voltage the behavior differs slightly, presumably due to the electrostatic softening effect, which is not considered in the models as the electrostatic force was only applied as a modal load without deflection dependence as the focus was on the fluid domain.

4. Discussion

The example of the MEMS accelerometer demonstrated that both approaches are able to provide accurate predictions of the mechanical damping behavior for a MEMS device. Differences can be observed in the computational effort relation between ROM generation and actual simulation. While modal projection has a large part of the computational effort in the ROM generation phase, the network model creation is computationally rather inexpensive. The results are a very compact and fast ROM for modal projection, compared to a relatively complex network model retaining a physical representation of the fluid domain. While it seems like a disadvantage, this property is also a strength of the network approach, as it allows the convenient implementation of deflection-dependent non-linearities, which would add an additional dimension to the parameter space in the modal projection. For the network approach, the computational load of the simulation scales strongly with the size and complexity of the fluid domain, even if it is much faster than known from full 3-D FEM models. The modal projection model, once created, is very efficient in simulations but is in nature linear and requires additional efforts to implement structural or fluidic non-linearities.