Abstract
Resonant micro- and nanoelectromechanical systems (MEMS/NEMS) are typically subject to interaction with a liquid or gaseous environment. Recently, it has been demonstrated that non-conventional eigenmodes exhibit remarkably high quality factors (Q factors) in liquids. However, the physical origin of this phenomenon remains elusive. Here we introduce a definition of non-conventional eigenmodes for cantilever structures and develop a boundary integral method for describing the interaction of an incompressible viscous fluid and a non-conventional eigenmode of a MEMS/NEMS resonator. With this framework we are able to study the influence of the mode shape on the fluid-structure interaction.
1. Introduction
Cantilever structures are a core component in micro- and nanoelectromechanical systems (MEMS/NEMS). MEMS/NEMS cantilevers are used in a plurality of fields ranging from atomic force microscopy to energy harvesting. One of the most challenging applications is the measurement of fluid properties where an oscillating cantilever is immersed in a fluid and fluid properties like density or viscosity are deduced from measured quantities like resonance frequency or quality factor (Q factor). The relation between the fluid properties and the measured quantities has been investigated in a large number of publications [1]. Despite this deep understanding of the measurements, cantilever-based fluid sensing suffers from some significant drawbacks. One of those is that the low Q factor prevents measurements in medium- to high-viscosity environments. Recently, it has been demonstrated that non-conventional cantilever eigenmodes exhibit surprisingly high Q factors in liquids [2]. This opens the door for usage of MEMS/NEMS resonators in parameter regimes which have been impenetrable so far. However, predicting the performance of non-conventional eigenmodes for sensing applications requires detailed understanding of the fluid-structure interaction between non-conventional eigenmodes and the surrounding fluid. Here, we introduce a definition for non-conventional cantilever eigenmodes and present a method for modelling the fluid-structure interaction.
2. Results
MEMS/NEMS cantilevers have been successfully modelled in the framework of Euler-Bernoulli theory (EBT). EBT correctly predicts eigenmodes with a mode shape which only varies along the length of a cantilever. Such a mode is depicted in Figure 1a where the long sides of the cantilever are aligned with the x-axis.
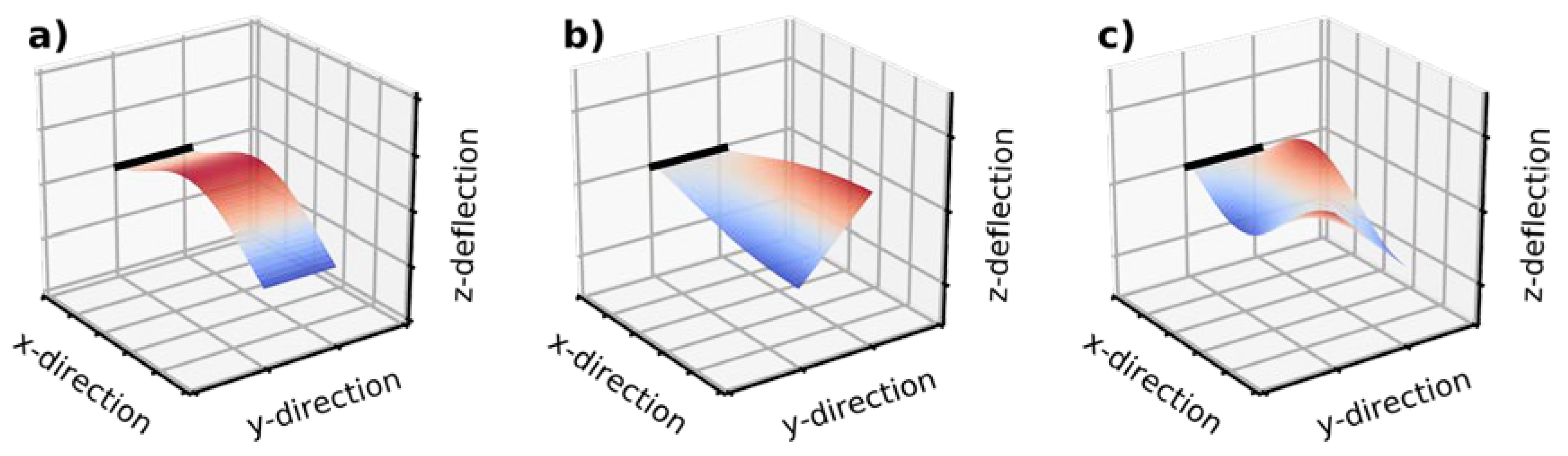
Figure 1.
Dynamic (a) 10-, (b) 01- and (c) 11-eigenmodes of a cantilever which is clamped at the side marked by the solid black line. The color coding corresponds to the normalized deflection in z-direction. The modes have been obtained numerically using the finite element package FEniCS [3]. We assume a rectangular cantilever geometry with a length of 2500 µm, a width of 518 µm and a thickness of 20 µm. The material is silicon with a Young’s modulus of 170 GPa and a Poisson’s ratio of 0.28.
However, since real MEMS/NEMS cantilevers always have a finite width mode shapes that vary along other spatial dimensions can exist. Indeed, numerical simulations predict eigenmodes like the mode in Figure 1b where the deflection depends both on the x- and on the y-coordinate. It is interesting to note that the shown mode shape is not a torsional mode since the deflection in z-direction greatly dominates over the deflection in x- and y-direction. Figure 1c shows an example of an even more complex mode with a non-trivial dependence of the deflection on both spatial coordinates.
We categorize these modes by the indices of the dominant component in the (spatial) 2D Fourier transform of the mode shapes. In this framework, EBT modes are x0-modes where x is a positive integer. The mode in Figure 1a is the 10-mode. The counterparts of the x0-modes are the 0x-modes which depend predominately on the y-coordinate like for the 01-mode in Figure 1b. Figure 1c shows an example of a xx-mode for which the deflection depends on both spatial coordinates.
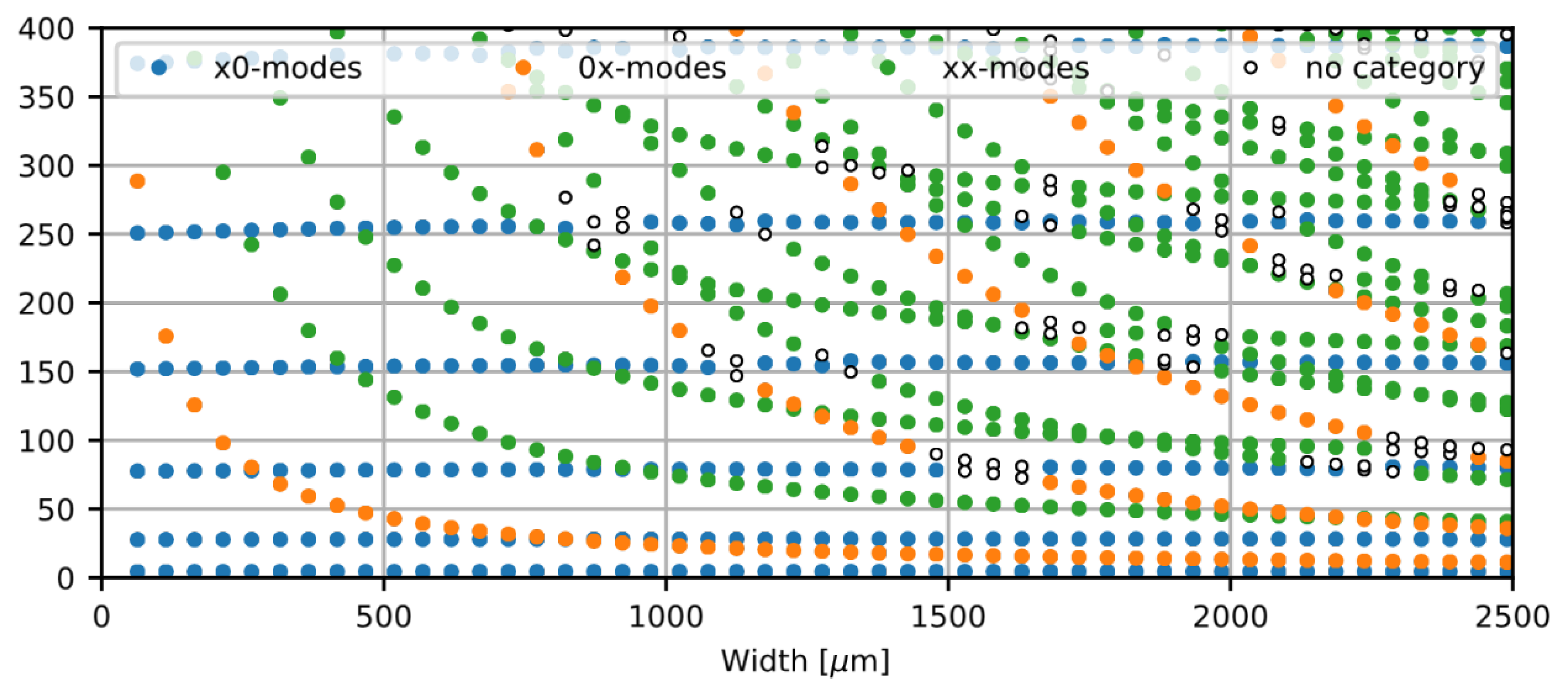
Figure 2 illustrates that non-conventional eigenmodes start to play a significant role as the planar aspect ratio (length/width) of the cantilevered structure decreases.
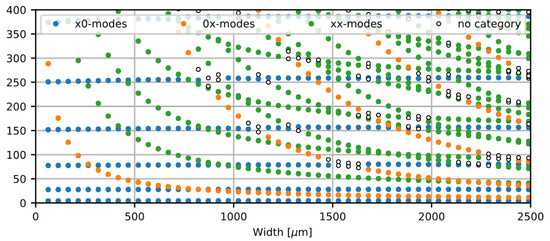
Figure 2.
The resonance frequencies of the eigenmodes of the cantilever described in Figure 1 as a function of cantilever width. The colors of the markers indicate the mode categorization. White markers are used for modes that do have two or more dominant Fourier component. These cases typically occur when two eigenfrequency approach each other [4].
While the resonance frequencies of the x0-modes are not affected by the cantilever aspect ratio, the resonance frequencies of the 0x- and xx-modes drastically decrease as the the cantilever width increases. This behaviour results in a high density of modes for lower aspect ratios.
To study the fluid-structure interaction of non-conventional modes we start from the Kirchhoff-Love plate equation
where D is the bending stiffness, the two dimensional del operator, is the deflection in z-direction depending on the spatial coordinates and and time , is the mass density of the cantilever, the thickness of the cantilever and the dot denotes differentiation with respect to time. We assume a cantilever of rectangular geometry where the sides with length are aligned parallel to the x-axis and the clamped side of the cantilever with width is located at . Please note that the hydrodynamic force depends on both the scalars , and and on the function . In contrast to the 1D EBT case, no analytic Green’s function to solve the elastic problem is known [5]. Nevertheless, with knowledge of the solution for is readily numerically determined. However, a numerical treatment of is computationally expensive since a very fine mesh over a large area is required. Therefore, we use an analytic approach which is based on writing the hydrodynamic problem as a boundary integral problem as described in [6]. With the additional assumptions of an infinitesimal thin cantilever and small z-deflections one can show that the pressure difference between the top and the bottom side of the cantilever is related to the Fourier transform of the deflection at frequency by
where is the dynamic viscosity of the fluid and the Green’s function satisfying with and the kinematic viscosity . Equation (2) can be solved numerically which gives the complex pressure which in turn yields the hydrodynamic force .
3. Discussion
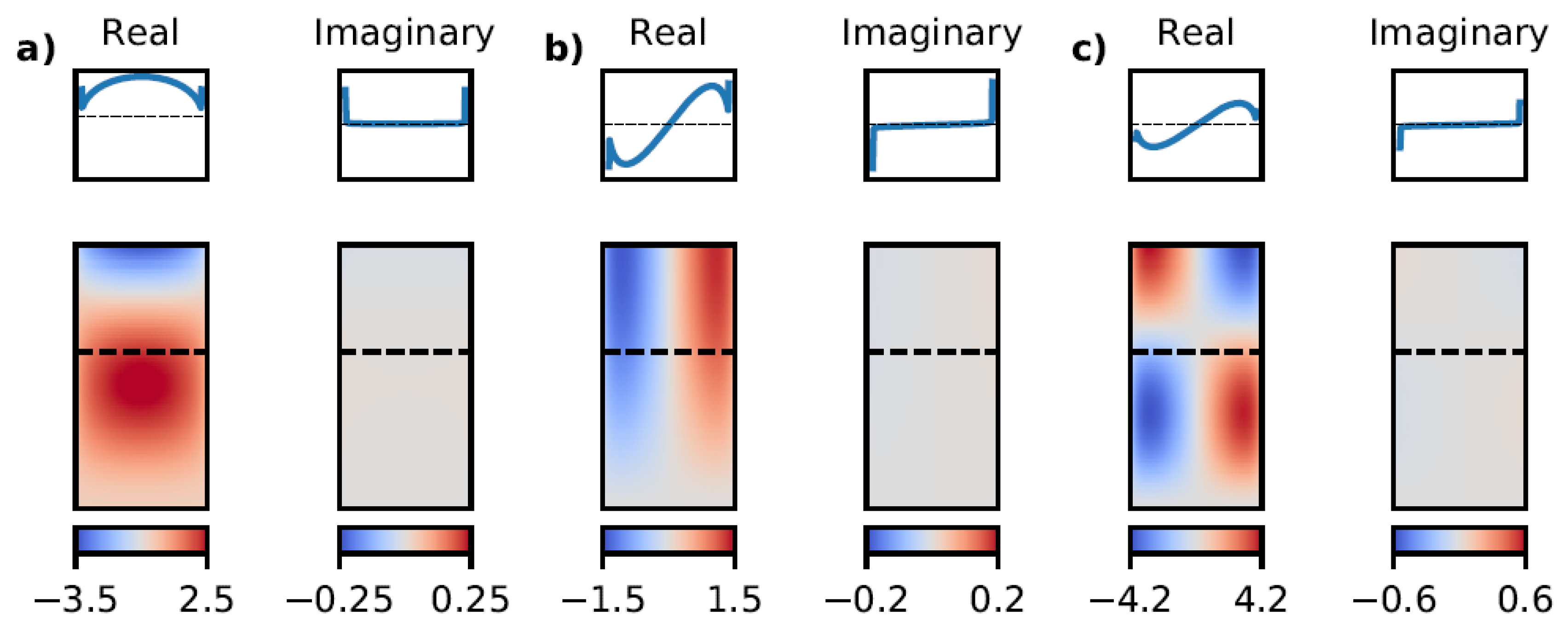
To illustrate the method we computed the position-dependent complex pressure for all modes in Figure 1. The results are shown in Figure 3.
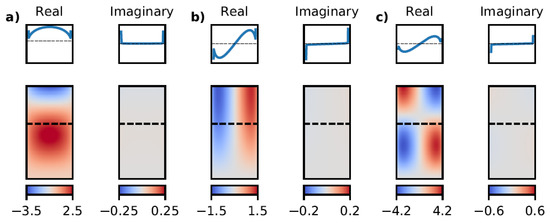
Figure 3.
Colormaps of the real and the imaginary part of the complex pressure in Pa for to the (a) 10-mode, (b) the 01-mode and (c) the 11-mode. The real part have been scaled by 1/β and the imaginary part by with . We assume a dynamic kinematic viscosity of which corresponds to water. The cantilever is clamped at the bottom of the colormaps and the dashed lines indicate the positions of the cross sections displayed above. The vertical cross section axis limits are the same as the limits for the corresponding colorbars.
For all modes the imaginary part of the pressure which is related to the added mass by the fluid is mostly unaffected by the mode shape and dominated by the singularities at the cantilever edges. In contrast, the real part related to the damping force in the fluid shows a strong mode-dependence in both in shape and in magnitude. Please note that the 01-mode exhibits smaller damping which is in line with experimental observations.
4. Conclusions
We introduced the notion of non-conventional eigenmodes and use Kirchhoff-Love plate theory to model the elastic behaviour of a cantilevered structure. The fluid interaction is described in terms of 2D Green’s functions. The presented framework can be used to calculate Q factors of various modes and lays the foundation for the treatment of the solid-structure interaction of non-conventional eigenmodes and 3D flows.
Author Contributions
D.P. performed the modelling and the calculations. All authors contributed to discussions. D.P. wrote the manuscript.
References
- Van Eysden, C.A.; Sader, J.E. Frequency Response of Cantilever Beams Immersed in Viscous Fluids. In Resonant MEMS: Fundamentals, Implementation and Application; Brand, O., Ed.; Wiley-VCH: Weinheim, Germany, 2015; pp. 29–53. ISBN 978-3-527-67633-0. [Google Scholar]
- Kucera, M.; Wistrela, E.; Pfusterschmied, G.; Ruiz-Díez, V.; Manzaneque, T.; Luis Sánchez-Rojas, J.; Schalko, J.; Bittner, A.; Schmid, U. Characterization of a roof tile-shaped out-of-plane vibrational mode in aluminum-nitride-actuated self-sensing micro-resonators for liquid monitoring purposes. Appl. Phys. Lett. 2014, 104, 233501. [Google Scholar] [CrossRef]
- Logg, A.; Mardal, K.A.; Wells, G. (Eds.) Automated Solution of Differential Equations by the Finite Element Method; Springer: Berlin, Germany, 2012; ISBN 978-3-642-23098-1. [Google Scholar]
- Perkins, N.C.; Mote, C.D., Jr. Perkins and Mote, Comments on curve veering in eigenvalue problems. J. Sound Vib. 1986, 103, 451–463. [Google Scholar] [CrossRef]
- Gazzola, F.; Grunau, H.C.; Sweers, G. Polyharmonic Boundary Value Problems; Springer: Berlin, Germany, 2010; ISBN 978-3-642-12244-6. [Google Scholar]
- Tuck, E.O. Calculation of unsteady flows due to small motions of cylinders in a viscous fluid. J. Eng. Math. 1969, 3, 29–44. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).