Stochastic Generation of Low Stream Flow Data of Iokastis Stream, Kavala City, NE Greece †
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
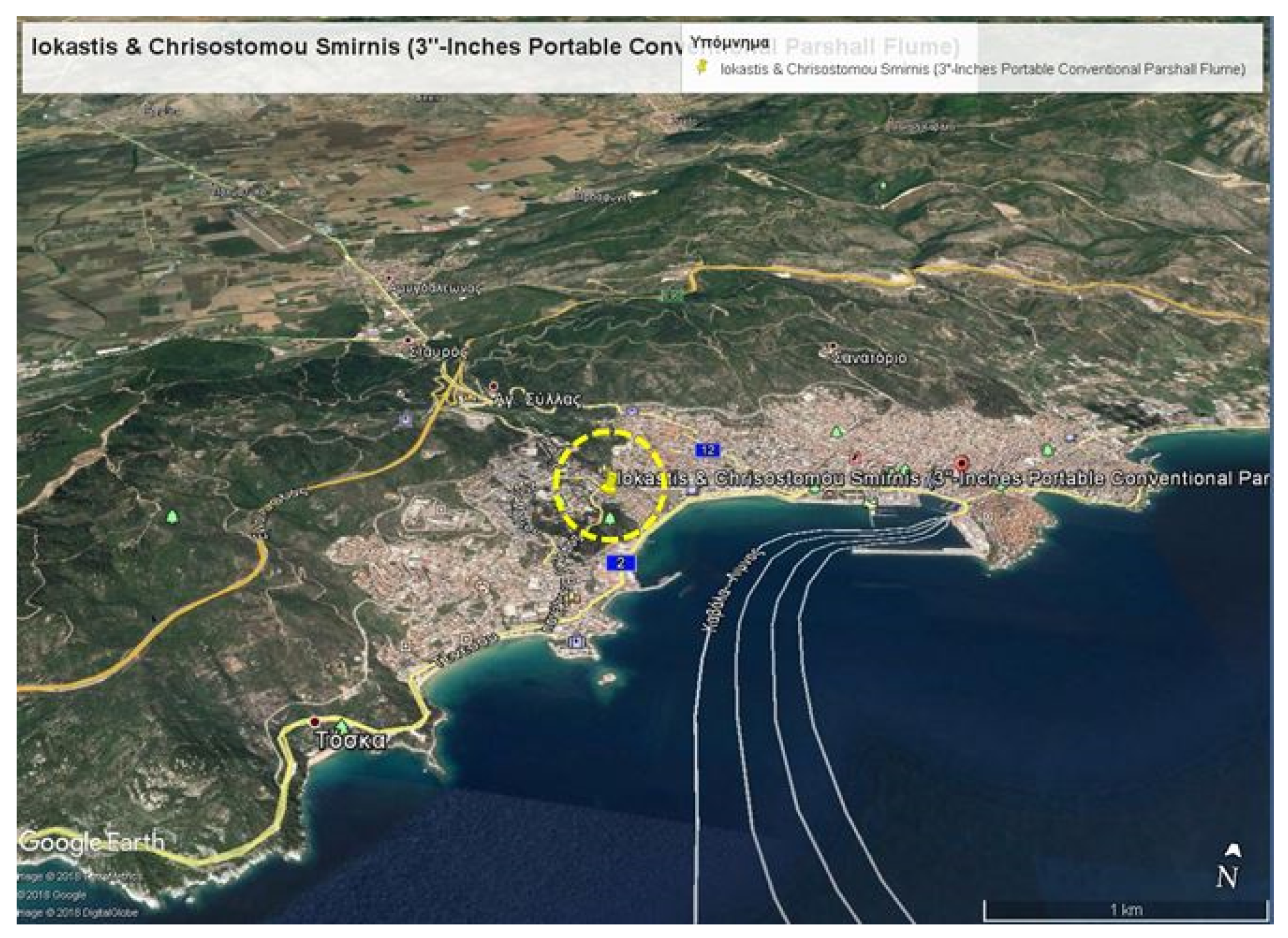
3.1. Study Area
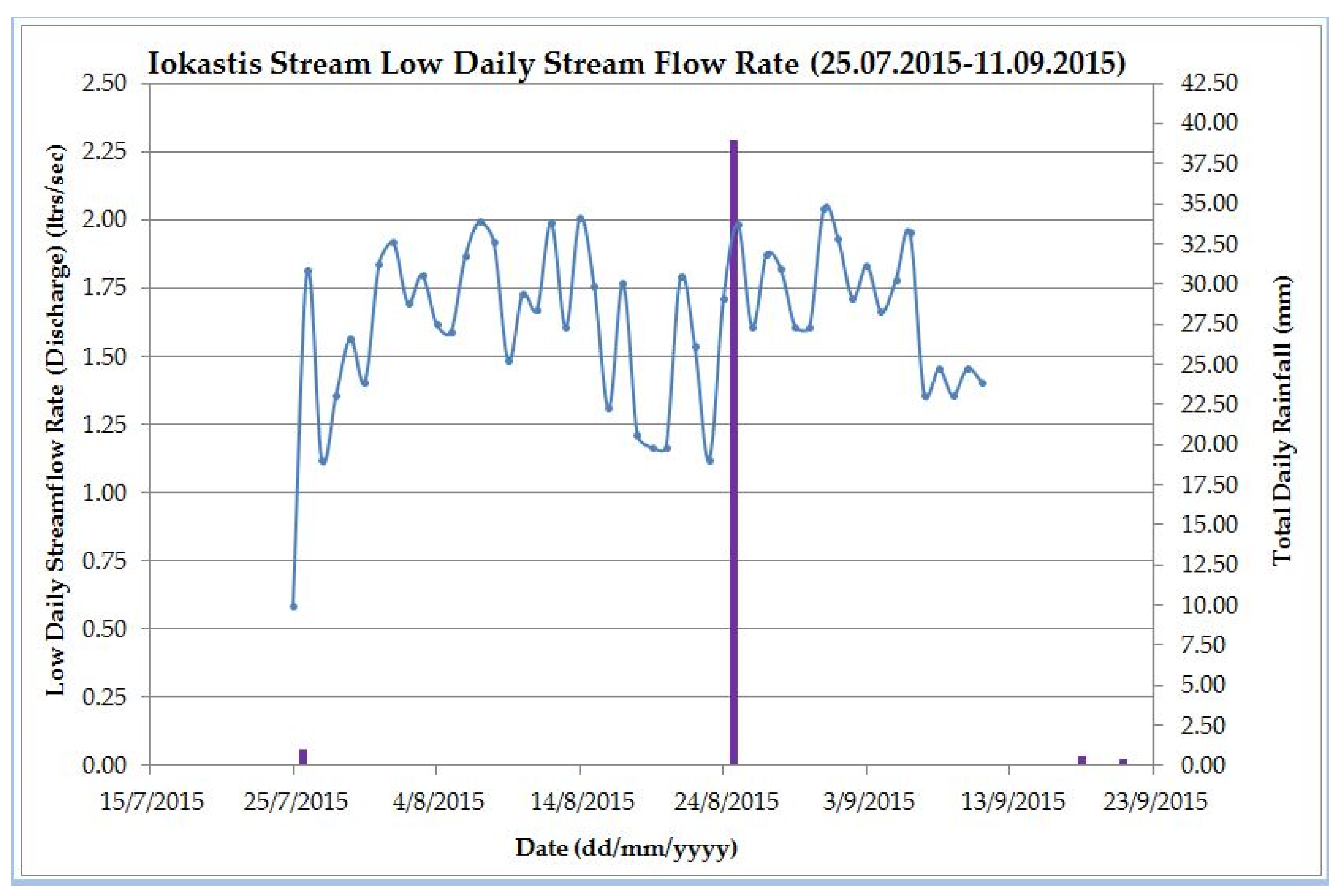
3.2. Sample Collection and Data Used in This Study
3.3. Sample Analysis and Checking the Goodness of Fit
3.4. Hydrodynamic Methods and Equipment for Sample Data Collection and Analysis
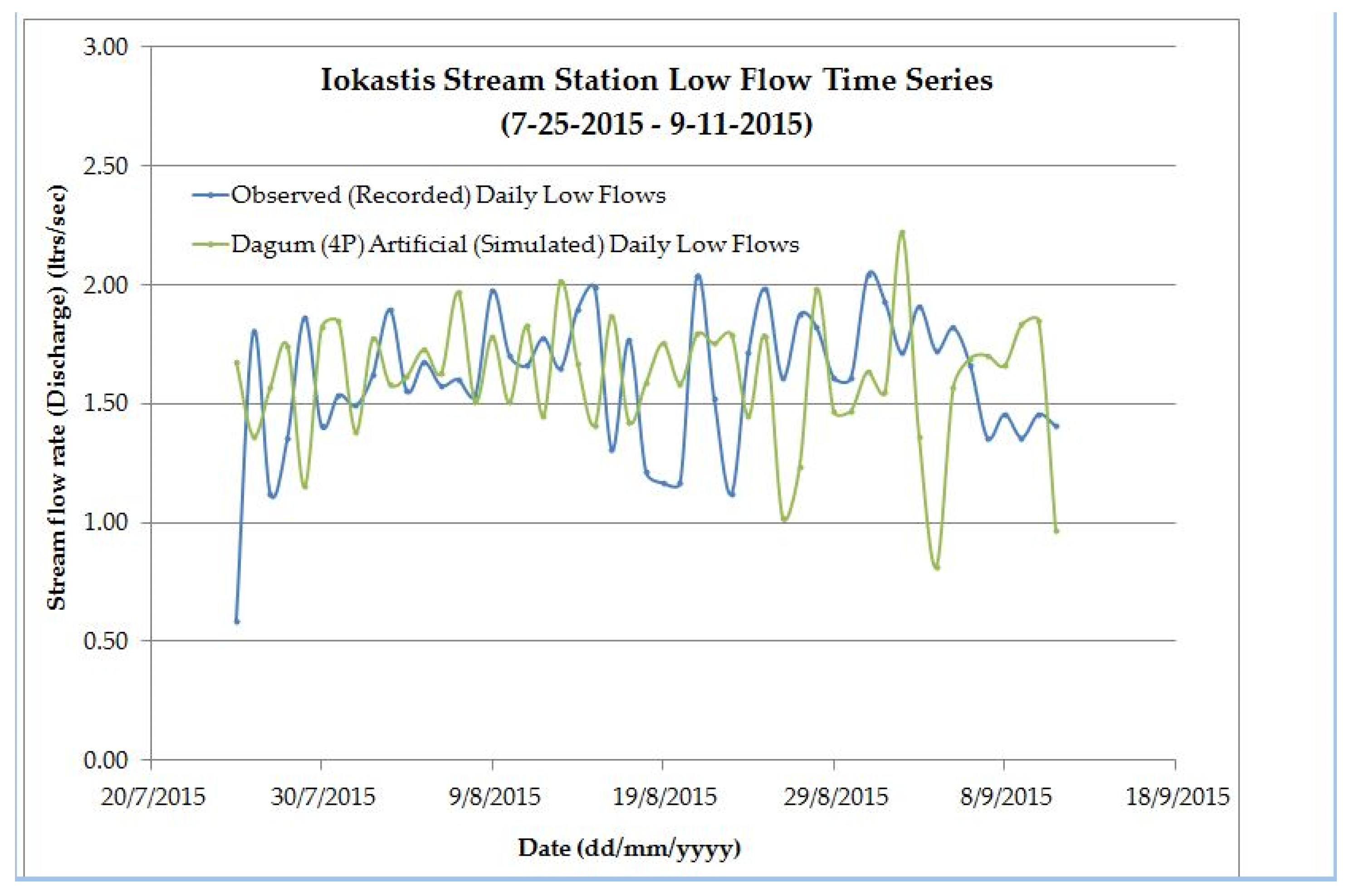
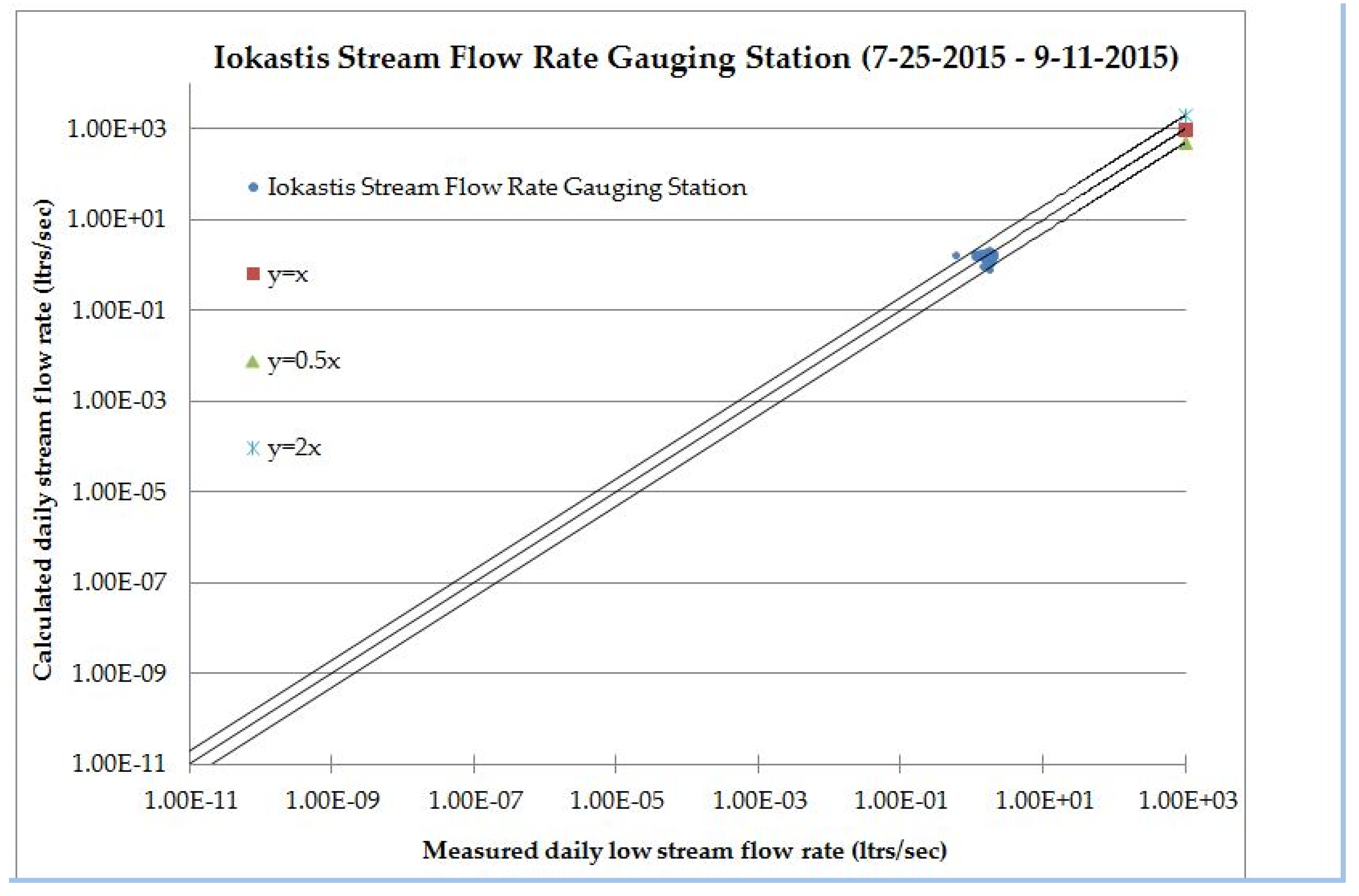
4. Comparison between Calculated and Site-Measured Low Stream Flow Rate (Discharge) Values
5. Results and Discussion
6. Conclusions and Further Research
Supplementary Materials
Conflicts of Interest
Appendix A
| No. | Date | Stream flow Rate (m3/s) Site-Measured | Stream flow rate (m3/s) Calculated (Dagum 4P) |
| 1 | 25-7-2015 | 0.5866 | 1.6780 |
| 2 | 26-7-2015 | 1.8030 | 1.3625 |
| 3 | 27-7-2015 | 1.1212 | 1.5697 |
| 4 | 28-7-2015 | 1.3574 | 1.7443 |
| 5 | 29-7-2015 | 1.8640 | 1.1514 |
| 6 | 30-7-2015 | 1.4066 | 1.8220 |
| 7 | 31-7-2015 | 1.5380 | 1.8466 |
| 8 | 1-8-2015 | 1.4930 | 1.3808 |
| 9 | 2-8-2015 | 1.6230 | 1.7739 |
| 10 | 3-8-2015 | 1.8970 | 1.5824 |
| 11 | 4-8-2015 | 1.5530 | 1.6168 |
| 12 | 5-8-2015 | 1.6750 | 1.7292 |
| 13 | 6-8-2015 | 1.5770 | 1.6290 |
| 14 | 7-8-2015 | 1.6030 | 1.9709 |
| 15 | 8-8-2015 | 1.5370 | 1.5107 |
| 16 | 9-8-2015 | 1.9760 | 1.7829 |
| 17 | 10-8-2015 | 1.7040 | 1.5061 |
| 18 | 11-8-2015 | 1.6600 | 1.8266 |
| 19 | 12-8-2015 | 1.7770 | 1.4494 |
| 20 | 13-8-2015 | 1.6500 | 2.0152 |
| 21 | 14-8-2015 | 1.8990 | 1.6676 |
| 22 | 15-8-2015 | 1.9870 | 1.4113 |
| 23 | 16-8-2015 | 1.3089 | 1.8694 |
| 24 | 17-8-2015 | 1.7675 | 1.4249 |
| 25 | 18-8-2015 | 1.2138 | 1.5888 |
| 26 | 19-8-2015 | 1.1671 | 1.7548 |
| 27 | 20-8-2015 | 1.1671 | 1.5853 |
| 28 | 21-8-2015 | 2.039 | 1.7942 |
| 29 | 22-8-2015 | 1.5200 | 1.7543 |
| 30 | 23-8-2015 | 1.1212 | 1.7927 |
| 31 | 24-8-2015 | 1.7142 | 1.4491 |
| 32 | 25-8-2015 | 1.9865 | 1.7850 |
| 33 | 26-8-2015 | 1.6093 | 1.0212 |
| 34 | 27-8-2015 | 1.8759 | 1.2364 |
| 35 | 28-8-2015 | 1.8214 | 1.9815 |
| 36 | 29-8-2015 | 1.6093 | 1.4679 |
| 37 | 30-8-2015 | 1.6093 | 1.4700 |
| 38 | 31-8-2015 | 2.0426 | 1.6379 |
| 39 | 1-9-2015 | 1.9309 | 1.5498 |
| 40 | 2-9-2015 | 1.7142 | 2.2219 |
| 41 | 3-9-2015 | 1.9110 | 1.3595 |
| 42 | 4-9-2015 | 1.7230 | 0.8125 |
| 43 | 5-9-2015 | 1.8200 | 1.5694 |
| 44 | 6-9-2015 | 1.6600 | 1.6919 |
| 45 | 7-9-2015 | 1.3574 | 1.7036 |
| 46 | 8-9-2015 | 1.4563 | 1.6623 |
| 47 | 9-9-2015 | 1.3574 | 1.8348 |
| 48 | 10-9-2015 | 1.4563 | 1.8508 |
| 49 | 11-9-2015 | 1.4066 | 0.9648 |
References
- Matalas, N. Probability Distribution of Low Flows (Statistical Studies in Hydrology), 1st ed.; United States Government Printing Office: Washington, DC, USA, 1963; pp. 1–27. [Google Scholar]
- Beard, L. Simulation of Daily Streamflow, 1st ed.; U.S. Army Corps of Engineers (Institute for Water Resources—Hydrologic Engineering Center): Davis, CA, USA, 1968; pp. 1–13. [Google Scholar]
- Singh, K.P.; Stall, J.B. The 7-Day 10-Year Low Flows of Illinois Streams, 1st ed.; State of Illinois-Ch.: Urbana, IL, USA, 1973; pp. 1–24. [Google Scholar]
- Vogel, R.M.; Kroll, C.N. Generalized Low-Flow Frequency Relationships for Ungaged Sites in Massachusetts. Water Resour. Bull. (Am. Water Resour. Assoc.) 1990, 26, 241–253. [Google Scholar] [CrossRef]
- Smakhtin, V.Y.; Toulouse, M. Relationships between low-flow characteristics of South African streams. Water SA 1998, 24, 107–112. Available online: https://www.researchgate.net/publication/264957822_Relationships_between_low-flow_characteristics_of_South_African_streams (accessed on 3 May 2018).
- Young, A.R.; Round, C.E.; Gustard, A. Spatial and temporal variations in the occurrence of low flow events in the UK. Hydrol. Earth Syst. Sci. 2000, 4, 35–45, hal-00304501, version 1. Available online: https://www.hydrol-earth-syst-sci.net/4/35/2000/hess-4-35-2000.pdf (accessed on 3 May 2018). [CrossRef]
- Smakhtin, V.U. Low flow hydrology: A review. J Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Zaidman, M.D.; Keller, V.; Young, A.R. Low Flow Frequency Analysis (Guidelines for Best Practice) (R & D Technical Report W6-064/TR1, Centre for Ecology and Hydrology), 1st ed.; Environment Agency, Rio House (Waterside Drive, Aztec West): Bristol (BS32 4UD), UK, 2002; pp. 1–33. [Google Scholar]
- Laaha, A.K.; Blöschl, G. Low flow estimates from short stream flow records—A comparison of methods. J. Hydrol. 2005, 306, 264–286. [Google Scholar] [CrossRef]
- Tallaksen, L.; Hewa, G. Manual on Low Flow Estimation and Prediction (WMO-No. 1029, Operational Hydrology Report No. 50), 1st ed.; Chairperson Publications Board—World Meteorological Organization (WMO): Geneva, Switzerland, 2008; pp. 1–138. [Google Scholar]
- Wittenberg, H. Groundwater abstraction for irrigation and its impacts on low flows in a watershed in Norhwest Germany. Resources 2015, 4, 566–576. [Google Scholar] [CrossRef]
- Yürekli, K.; Kurunç, A.; Gül, S. Frequency analysis of low flow series from Çekerek stream basin. J. Agric. Sci. 2005, 11, 72–77. [Google Scholar] [CrossRef]
- Papalaskaris, T.; Panagiotidis, T. Artificial low stream flow time series generation of Perigiali stream, Kavala city, NE Greece. In Proceedings of the 6th International Symposium on Environmental & Material Flow Management (6th E.M.F.M.), Bor, Serbia, 2–4 October 2016; Živković, Ž., Mihailović, I., Dordević, P., Eds.; University of Belgrade, Technical Faculty in Bor: Bor, Serbia, 2016; pp. 20–38. [Google Scholar]
- Papalaskaris, T.; Panagiotidis, T. Stochastic generation of low stream flow data of Perigiali Stream, Kavala city, NE Greece. In Proceedings of the 10th World Congress of European Water Resources Association (“E.W.R.A.”) on Water Resources and Environment “Panta Rhei” (10th “E.W.R.A.” “Panta Rhei”), Athens, Greece, 5–9 July 2017; Tsakiris, G., Tsihrintzis, V., Vangelis, H., Tigkas, D., Eds.; European Water Resources Association (E.W.R.A.): Athens, Greece, 2017; pp. 953–960. [Google Scholar]
- Papalaskaris, T.; Panagiotidis, T. Stochastic generation of low stream flow data of Perigiali Stream, Kavala city, NE Greece. Eur. Water 2017, 60, 299–306. [Google Scholar] [CrossRef]
- Papalaskaris, T.; Panagiotidis, T. Artificial low stream flow time series generation of Palaia Kavala Stream, Kavala City, NE Greece. In Proceedings of the 15th International Conference on Environmental Science & Technology (15th C.E.S.T.), Rhodes Island, Greece, 31 August–2 September 2017; Lekkas, D.F., Ed.; Global Network for Environmental Science & Technology (Global-NEST), University of the Aegean: Athens, Greece, 2017. cest2017_00842. [Google Scholar]
- Survey, G.; Rantz, S.E. Measurement of Discharge by Miscellaneous Methods (Chapter 8). In Measurement & Computation of Streamflow: (Volume 1.) (Measurement of Stage & Discharge), 1st ed.; United States Government Printing Office: Washington, DC, USA, 1982; Volume 1, pp. 260–272. [Google Scholar]
- Turnipseed, D.P.; Sauer, V.B. Portable Parshall-Flume Measurements. In Discharge Measurements at Gaging Stations (Chapter 8 of Book 3, Section A) (Techniques & Methods 3-A8), 1st ed.; (U.S. Department of the Interior) U.S. Geological Survey: Reston, VA, USA, 2010; pp. 83–84. [Google Scholar]
- Buchanan, T.J.; Somers, W.P. Discharge Measurements at Gaging Stations (Chapter A8) (Techniques of Water-Resources Investigations of the United States Geological Survey), 1st ed.; United States Government Printing Office: Washington, DC, USA, 1969; pp. 1–65. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97, SRef-ID: 1680-7359/adgeo/2005-5-89. Available online: https://www.adv-geosci.net/5/89/2005/adgeo-5-89-2005.pdf (accessed on 3 May 2018). [CrossRef]
- Papalaskaris, T.; Dimitriadou, P. Artificial Neural Network for Bed Load Transport Rate in Nestos River, Greece. Spec. Top. Rev. Porous Media Int. J. 2017, 8, 145–157. [Google Scholar] [CrossRef]
- Sentas, A.; Psilovikos, A.; Psilovikos, T.; Matzafleri, N. Comparison of the performance of stochastic modes in forecasting daily dissolved oxygen data in dam-Lake Thesaurus. Desalination Water Treat. 2016, 57, 11660–11674. [Google Scholar] [CrossRef]
| Probability Distribution | Anderson-Darling | Chi-Squared | Kolmogorov-Smirnov | Highest Final Goodness of Fit Score Obtained |
|---|---|---|---|---|
| Gumbel min (2P) | 0.22805 | 2.0846 | 0.07273 | 0 |
| Log-Normal (3P) | 0.85844 | 5.0268 | 0.14102 | 0 |
| Pearson type 5 (3P) | 1.0085 | 4.5353 | 0.15081 | 0 |
| Pearson type 6 (3P) | 1.4249 | 5.8527 | 0.1627 | 0 |
| Weibull (2P) | 1.4235 | 6.9916 | 0.11636 | 0 |
| Kumaraswamy (4P) | 0.23837 | 2.0756 | 0.07528 | 0 |
| Gen. Logistic (2P) | 0.21294 1 | 2.5684 | 0.06652 3 | 4 |
| Burr (4P) | 0.22641 3 | 2.5754 | 0.07015 | 1 |
| Burr (3P) | 0.32909 | 0.44185 1 | 0.09633 | 3 |
| Wakeby (5P) | 4.0874 | Ν/A | 0.06576 2 | 2 |
| Dagum (4P) | 0.22273 2 | 2.6245 | 0.05767 1 | 5 |
| Number of Paired Values | RMSE [kg/(m s)] | RE (%) | EC | r | r2 | Discrepancy Ratio |
|---|---|---|---|---|---|---|
| 49 | 0.4193 | −0.0563 | −1.1331 | −0.1420 | 0.0202 | 0.9592 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papalaskaris, T.; Panagiotidis, T. Stochastic Generation of Low Stream Flow Data of Iokastis Stream, Kavala City, NE Greece. Proceedings 2018, 2, 579. https://doi.org/10.3390/proceedings2110579
Papalaskaris T, Panagiotidis T. Stochastic Generation of Low Stream Flow Data of Iokastis Stream, Kavala City, NE Greece. Proceedings. 2018; 2(11):579. https://doi.org/10.3390/proceedings2110579
Chicago/Turabian StylePapalaskaris, Thomas, and Theologos Panagiotidis. 2018. "Stochastic Generation of Low Stream Flow Data of Iokastis Stream, Kavala City, NE Greece" Proceedings 2, no. 11: 579. https://doi.org/10.3390/proceedings2110579
APA StylePapalaskaris, T., & Panagiotidis, T. (2018). Stochastic Generation of Low Stream Flow Data of Iokastis Stream, Kavala City, NE Greece. Proceedings, 2(11), 579. https://doi.org/10.3390/proceedings2110579





