Laser-Machined Split-Ring Resonators Embedded in a Polymer Matrix for Glaucoma Monitoring †
Abstract
1. Introduction
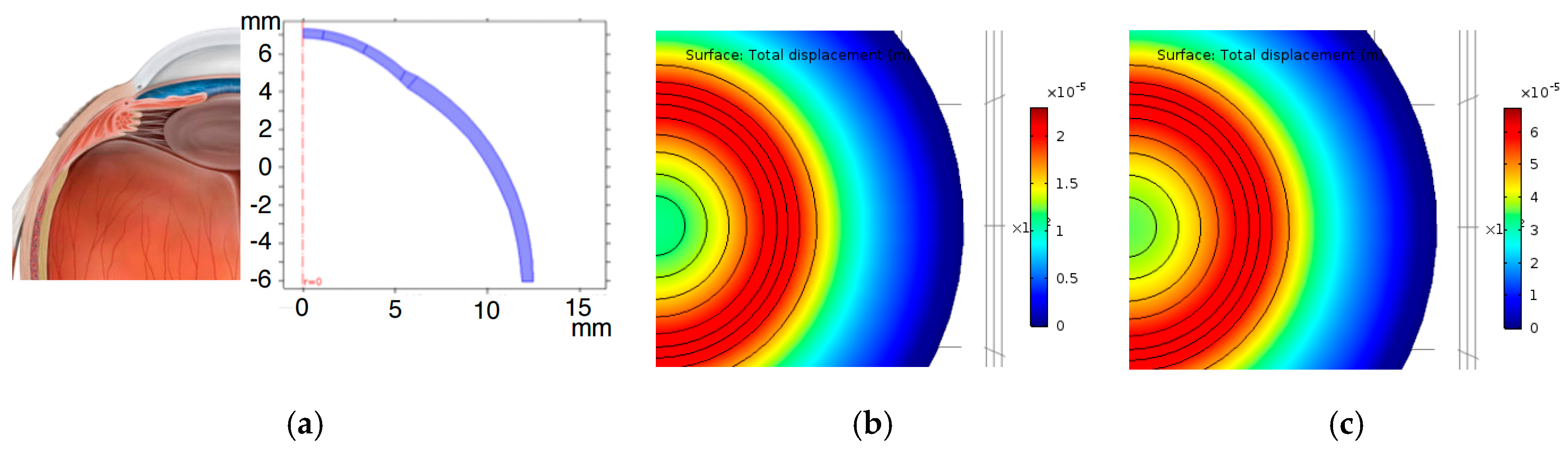
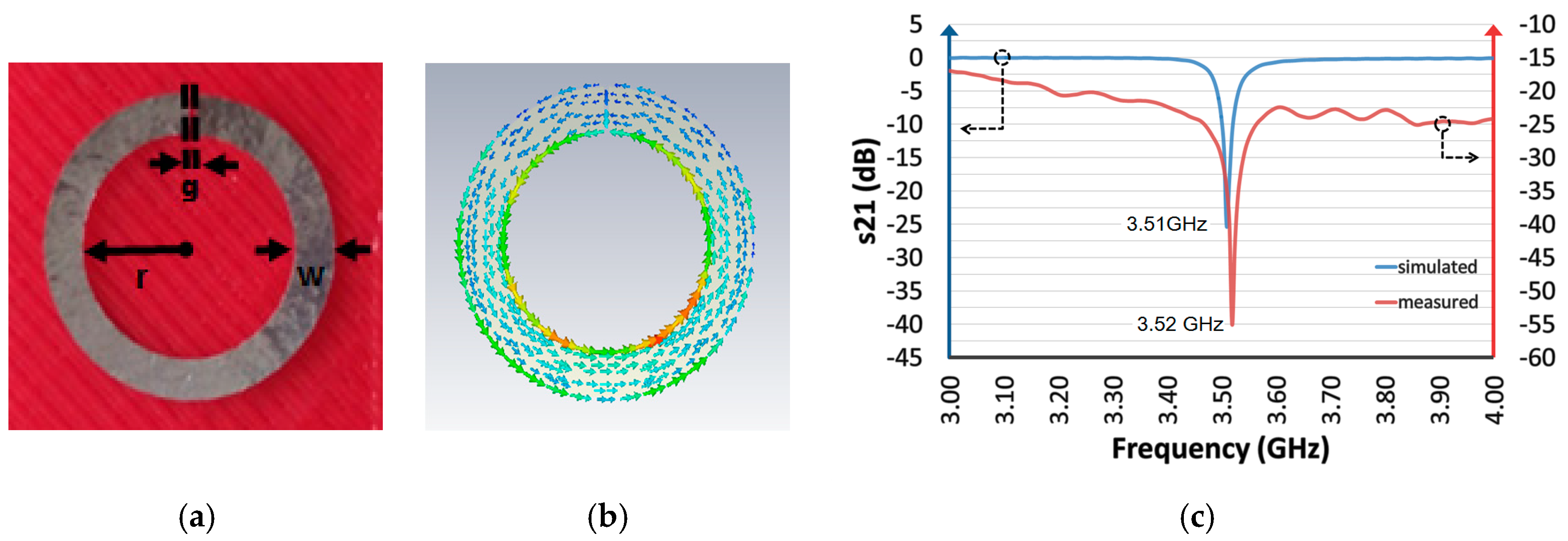
2. Design and Fabrication of the Sensors
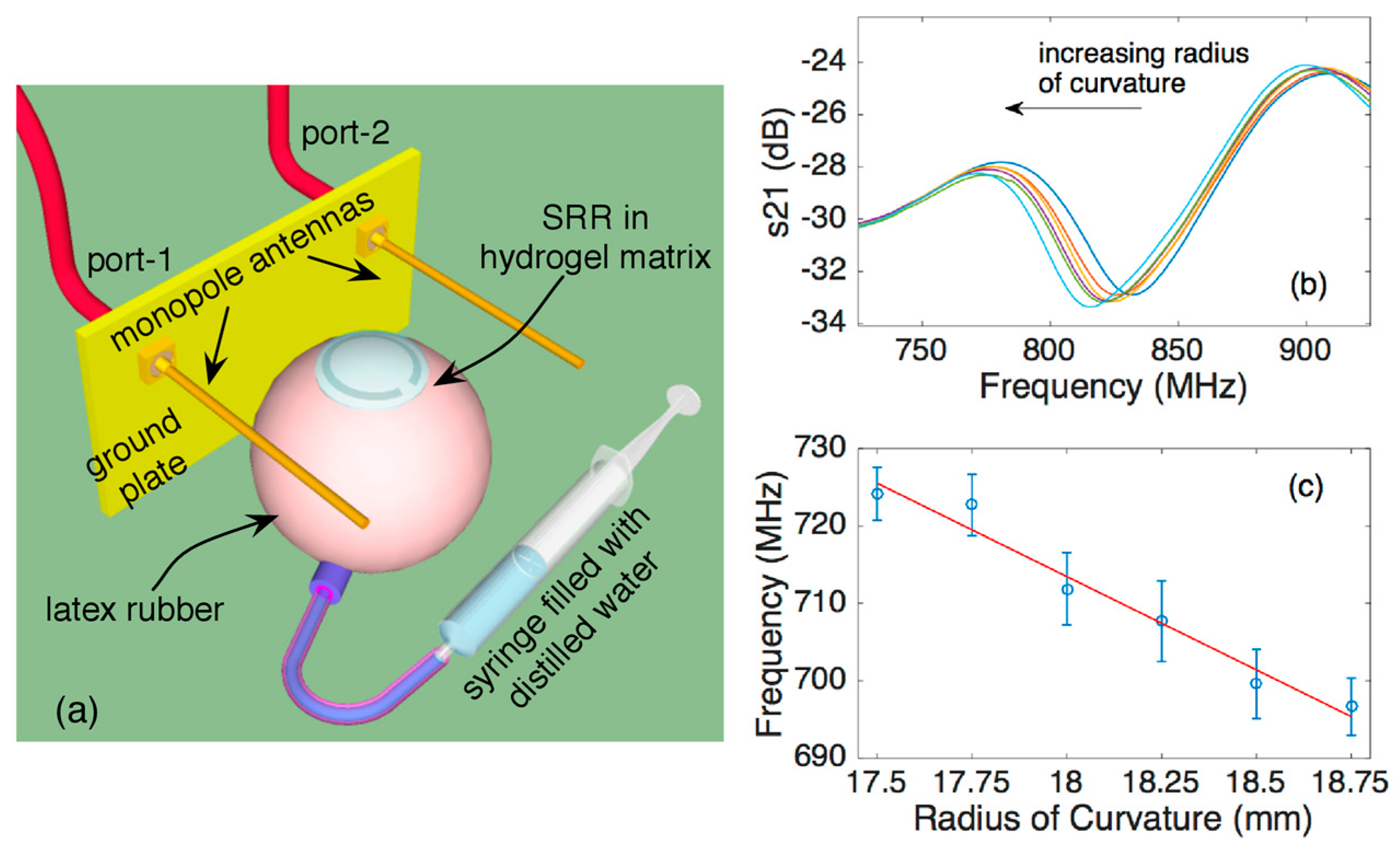
3. Experimental Setup and Results
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kingman, S. Glaucoma is second leading cause of blindness globally. Bull. World Health Organ. 2004, 82, 887–888. [Google Scholar] [CrossRef] [PubMed]
- Lam, A.K. The effect of an artificially elevated intraocular pressure on the central corneal curvature. Ophthalmic Physiol. Opt. 1997, 17, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Samuels, B.; Cantor, L.B.; Ziaie, B. A Minimally Invasive Implantable Wireless Pressure Sensor for Continuous IOP Monitoring. IEEE Trans. Bio-Med. Eng. 2013, 60, 250–256. [Google Scholar] [CrossRef]
- Leonardi, M.; Pitchon, E.M.; Bertsch, A.; Renaud, P.; Mermoud, A. Wireless contact lens sensor for intraocular pressure monitoring: Assessment on enucleated pig eyes. Acta Ophthalmol. 2009, 87, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of epsilon and mu. Sov. Phys. Uspekhi 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Ahmed, E.M. Hydrogel: Preparation, characterization, and applications: A review. J. Adv. Res. 2015, 6, 105–121. [Google Scholar] [CrossRef] [PubMed]
- Scott, A.R.; Michael, J.C.; Leo, G.C.; Ross, J.F. The Topography of the Central and Peripheral Cornea. Investig. Ophthalmol. Vis. Sci. 2006, 47, 1404–1415. [Google Scholar] [CrossRef]
- Rapuano, C.J. Nine-point corneal thickness measurements and keratometry readings in normal corneas using ultrasound pachymetry. Insight 1993, 18, 16–22. [Google Scholar] [PubMed]
- Hjortdal, J. Regional elastic performance of the human cornea. J. Biomech. 1996, 29, 931–942. [Google Scholar] [CrossRef]
- Vurgese, S.; Panda-Jonas, S.; Jonas, J.B. Scleral Thickness in Human Eyes. PLoS ONE 2012, 7, e29692. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, L.A.; Prado, M.; Chamon, W. Keratoconus prediction using a finite element model of the cornea with local biomechanical properties. Arq. Bras. Oftalmol. 2009, 72, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Z.; Liu, L.; Han, X.; Zhao, X.; Mu, G. Comparison of Riboflavin/Ultraviolet-A Cross-Linking in Porcine, Rabbit, and Human Sclera. BioMed. Res. Int. 2014, 2014, 194204. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Anterior Segment Sagittal Height and Soft Contact Lens Fitting: New Thoughts, New Understandings. Available online: http://www.softspecialedition.com/world_wide_vision_xii (accessed on 28 June 2017).
- Childs, A.; Li, H.; Lewittes, D.M.; Dong, B.; Liu, W.; Shu, X.; Sun, C.; Zhang, H.F. Fabricating customized hydrogel contact lens. Sci. Rep. 2016, 6, 34905. [Google Scholar] [CrossRef] [PubMed]

| Radius of Curvature (mm) | Thickness (mm) | Young’s Modulus (MPa) | |
|---|---|---|---|
| Central Cornea | 7.34 [7] | 0.494 [8] | 1.4 [9] |
| Paracentral Cornea | 7.69 [7] | 0.532 [8] | 1.64 [9] |
| Peripheral Cornea | 8.15 [7] | 0.607 [8] | 1.52 [9] |
| Limbus | ∞ [9] | 0.8 [10] | 3 [9] |
| Sclera | 12 [11] | 0.6 [10] | 7 [12] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calikoglu, A.; Dundar, G.; Yalcinkaya, A.D.; Torun, H. Laser-Machined Split-Ring Resonators Embedded in a Polymer Matrix for Glaucoma Monitoring. Proceedings 2017, 1, 531. https://doi.org/10.3390/proceedings1040531
Calikoglu A, Dundar G, Yalcinkaya AD, Torun H. Laser-Machined Split-Ring Resonators Embedded in a Polymer Matrix for Glaucoma Monitoring. Proceedings. 2017; 1(4):531. https://doi.org/10.3390/proceedings1040531
Chicago/Turabian StyleCalikoglu, Aybuke, Gunhan Dundar, Arda Deniz Yalcinkaya, and Hamdi Torun. 2017. "Laser-Machined Split-Ring Resonators Embedded in a Polymer Matrix for Glaucoma Monitoring" Proceedings 1, no. 4: 531. https://doi.org/10.3390/proceedings1040531
APA StyleCalikoglu, A., Dundar, G., Yalcinkaya, A. D., & Torun, H. (2017). Laser-Machined Split-Ring Resonators Embedded in a Polymer Matrix for Glaucoma Monitoring. Proceedings, 1(4), 531. https://doi.org/10.3390/proceedings1040531





