Fractal Characteristics and Controlling Factors of Pore-Throat Structure in Tight Sandstone Reservoirs: A Case Study of the 2nd Member of the Kongdian Formation in the Nanpi Slope, Cangdong Sag, Bohai Bay Basin
Abstract
1. Introduction
2. Geological Background
3. Samples and Methods
3.1. Sample Characteristics and Analytical Procedures
3.2. Fractal Theory
4. Characteristics of Pore Structure in Tight Sandstone Reservoirs
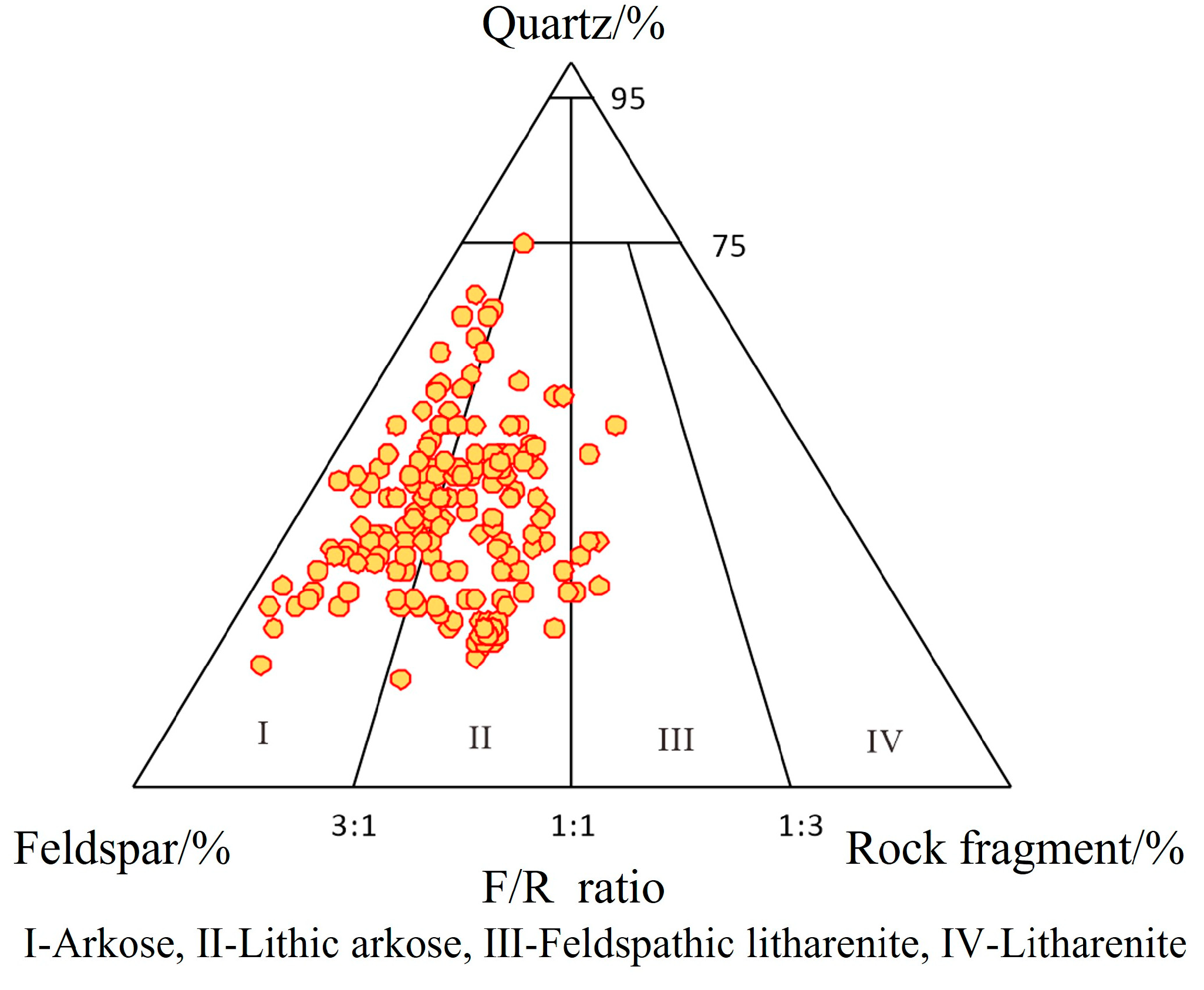
4.1. Types of Pores and Throats in Tight Sandstone Reservoirs
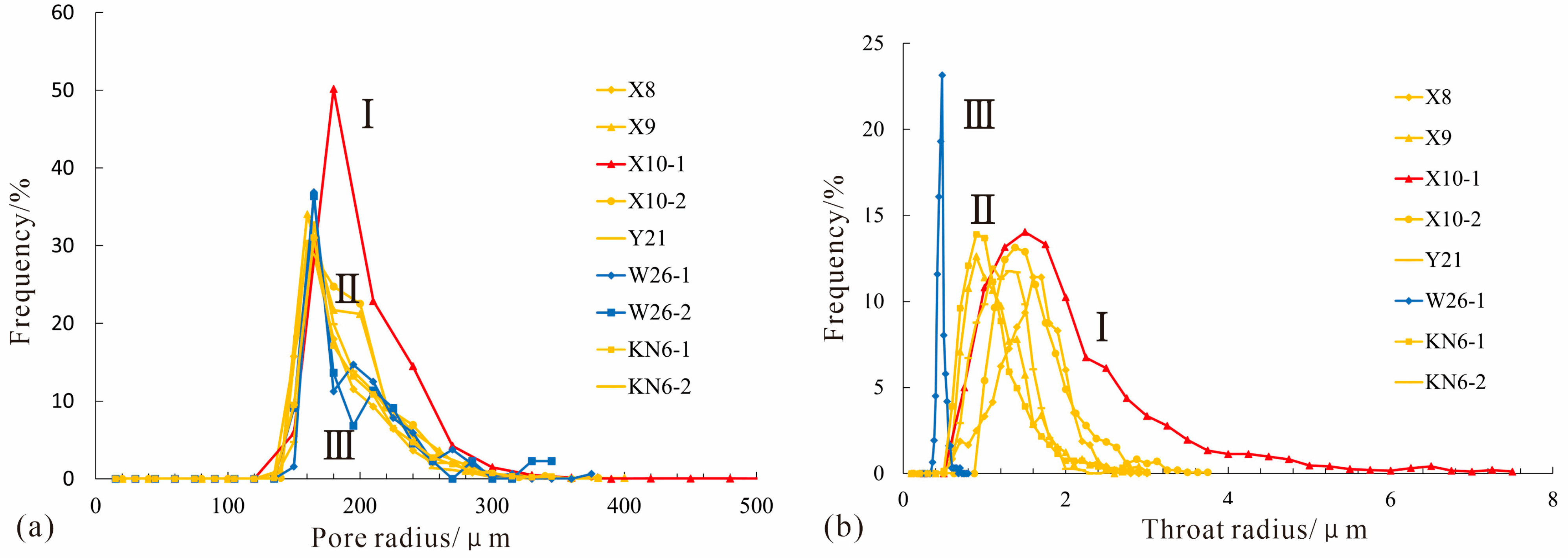
4.2. Pore-Throat Distribution Characteristics of Tight Sandstone Reservoirs
4.3. Fractal Characteristics of Pore-Throat in Tight Sandstone Reservoirs
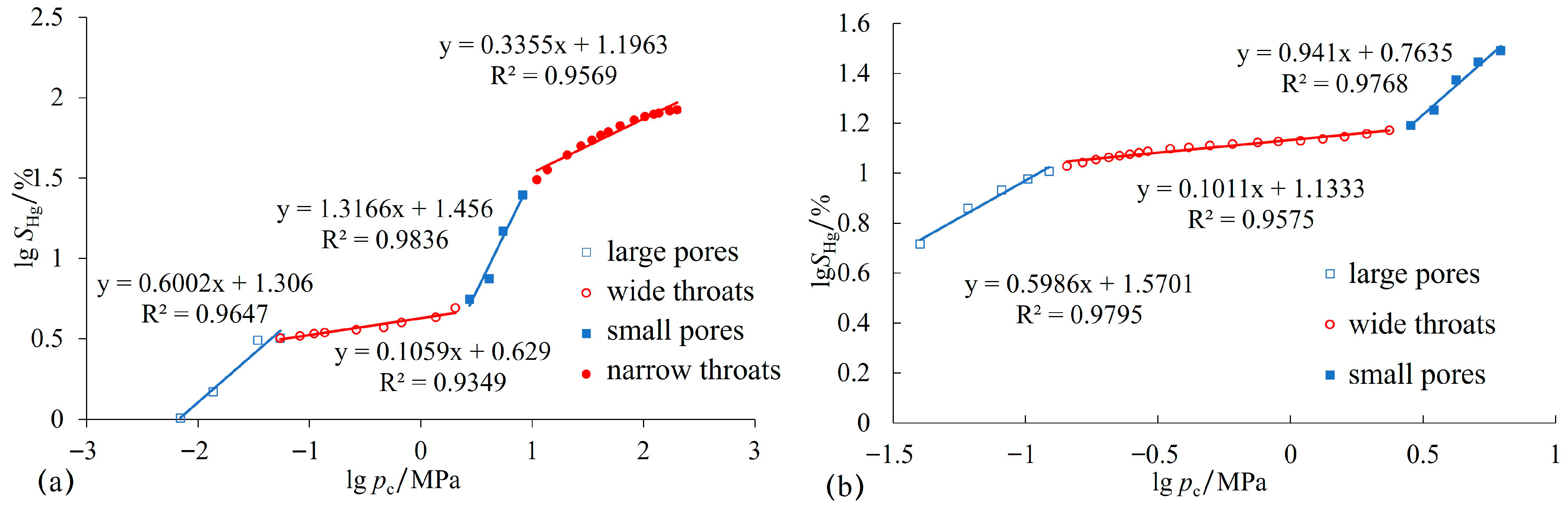
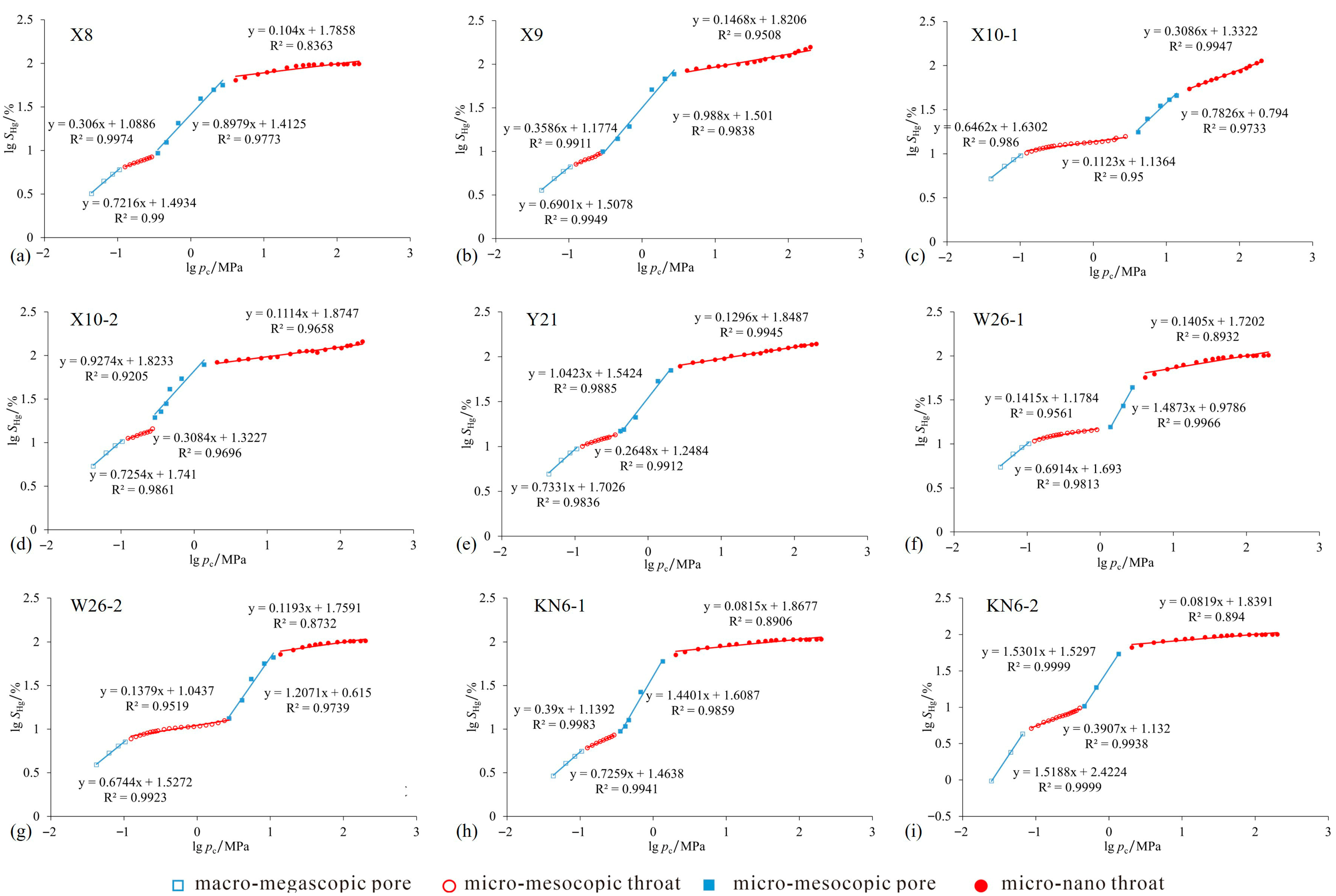
4.3.1. Fractal Dimensions Based on High-Pressure Mercury Intrusion and Constant-Rate Mercury Intrusion
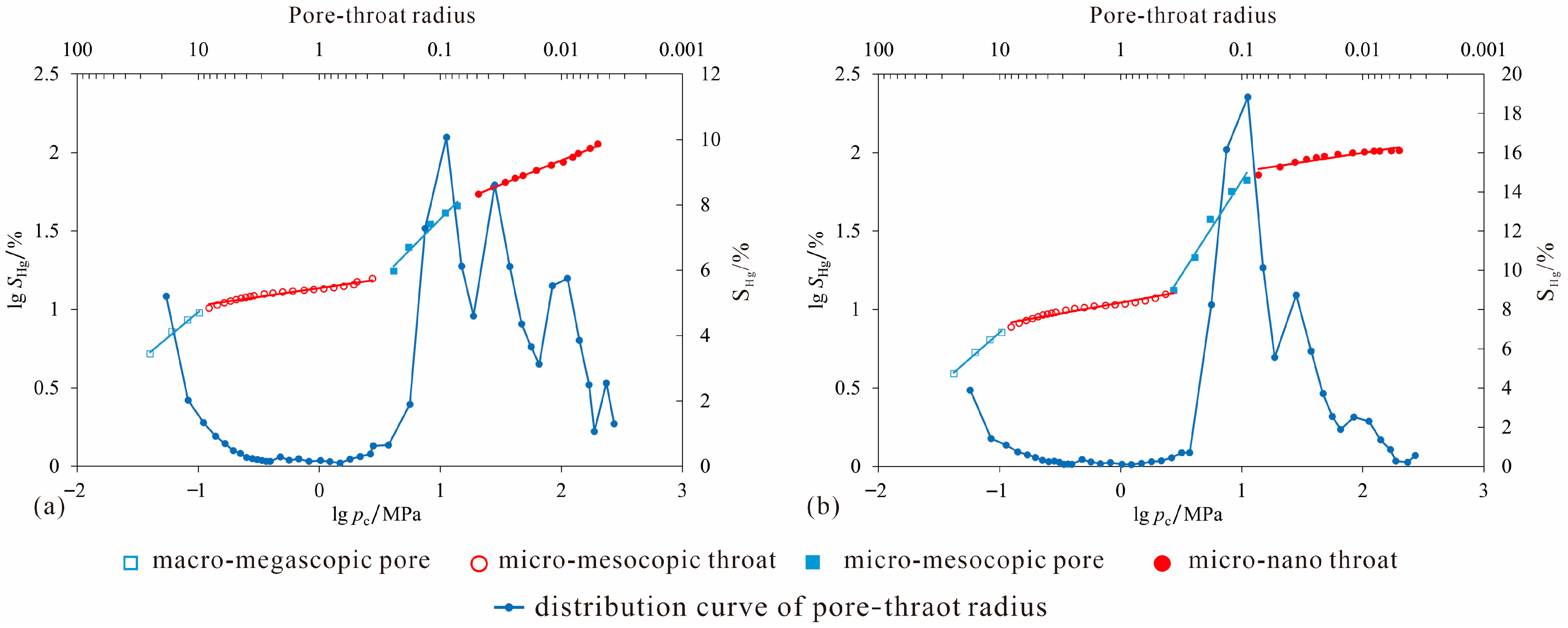
4.3.2. Combined Characterization of Full-Pore-Size Distribution Using High-Pressure Mercury Intrusion and Constant-Rate Mercury Intrusion
5. Factors Influencing Fractal Characteristics of Pore Structure, and Connection Between Fractal Results and Reservoir Performance
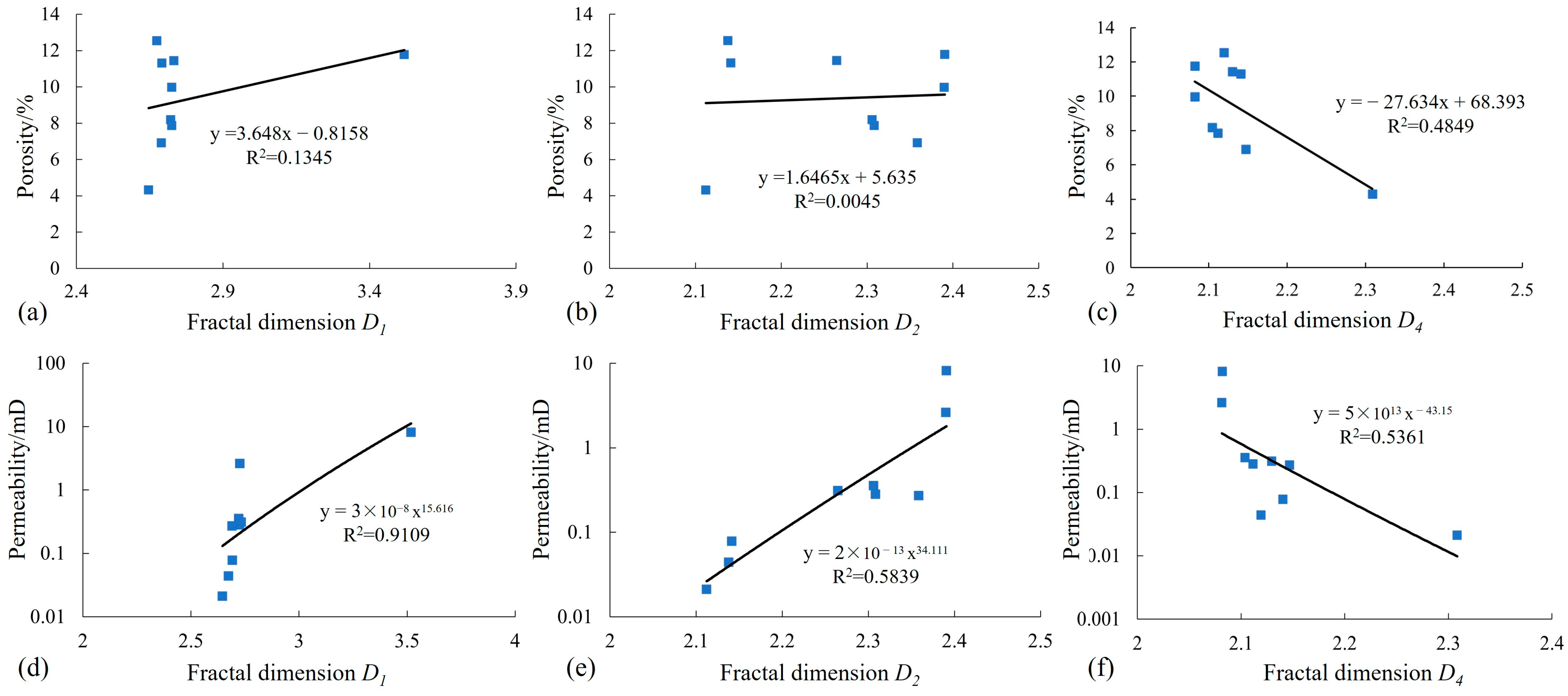
5.1. Factors Influencing Fractal Dimensions
5.2. Relationship Between Fractal Dimension and Physical Properties
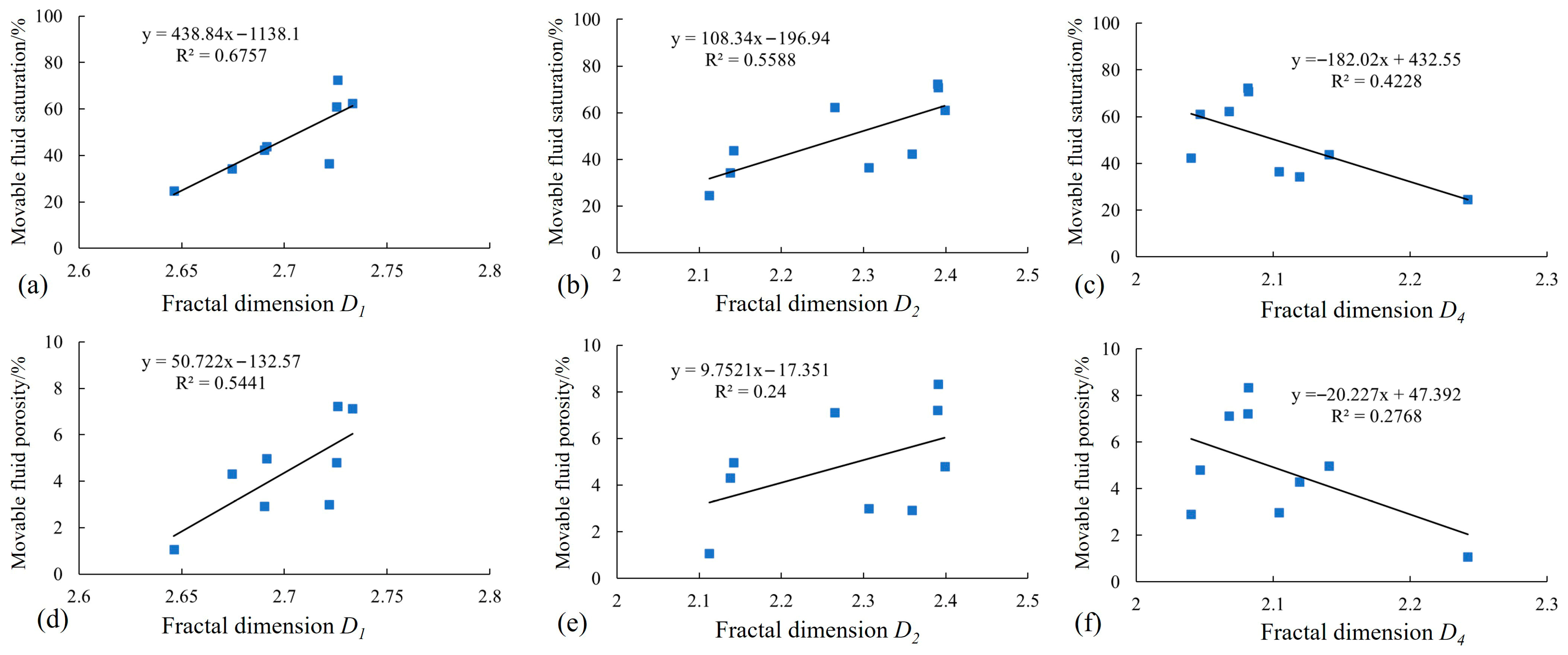
5.3. Fractal Dimension and Fluid Flow Characteristics
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HPMI | High-pressure mercury intrusion |
| MIP | Mercury intrusion porosimetry |
| NMR | Nuclear magnetic resonance |
| SEM | Scanning electron microscopy |
| CRMI | Constant-rate mercury injection |
| XRD | X-ray diffraction |
References
- Zou, C.N.; Zhang, G.Y.; Tao, S.Z.; Hu, S.Y.; Li, X.D.; Li, J.Z.; Dong, D.Z.; Zhu, R.K.; Yuan, X.J.; Hou, L.H.; et al. Geological features, major discoveries and unconventional petroleum geology in the global petroleum exploration. Pet. Explor. Dev. 2010, 37, 129–145. (In Chinese) [Google Scholar] [CrossRef]
- Zou, C.N.; Zhu, R.K.; Bai, B.; Yang, Z.; Hou, L.H.; Zha, M.; Fu, J.H.; Shao, Y.; Liu, K.Y.; Cao, H.; et al. Significance, geologic characteristics, resource potential and future challenges of tight oil and shale oil. Bull. Mineral. Petrol. Geochem. 2015, 34, 3–17. (In Chinese) [Google Scholar]
- Zou, C.N.; Yang, Z.; He, D.B.; Wei, Y.S.; Li, J.; Jia, A.L.; Chen, J.J.; Zhao, Q.; Li, Y.L.; Li, J.; et al. Theory, technology and prospects of conventional and unconventional natural gas. Pet. Explor. Dev. 2018, 45, 575–587. (In Chinese) [Google Scholar] [CrossRef]
- Jia, C.Z. Breakthrough and significance of unconventional oil and gas to classical petroleum geological theory. Pet. Explor. Dev. 2017, 44, 1–11. (In Chinese) [Google Scholar] [CrossRef]
- Hu, S.Y.; Zhu, R.K.; Wu, S.T.; Bai, B.; Yang, Z.; Cui, J.W. Profitable exploration and development of continental tight oil in China. Pet. Explor. Dev. 2018, 45, 737–748. (In Chinese) [Google Scholar] [CrossRef]
- Zou, C.N.; Zhu, R.K.; Liu, K.Y.; Su, L.; Bai, B.; Zhang, X.X.; Yuan, X.J.; Wang, J.H. Tight gas sandstone reservoirs in China: Characteristics and recognition criteria. J. Pet. Sci. Eng. 2012, 88–89, 82–91. (In Chinese) [Google Scholar] [CrossRef]
- Yao, J.L.; Deng, X.Q.; Zhao, Y.D.; Han, T.Y.; Chu, M.J.; Pang, J.L. Characteristics of tight oil in Triassic Yanchang Formation, Ordos Basin. Pet. Explor. Dev. 2013, 40, 150–158. (In Chinese) [Google Scholar] [CrossRef]
- Ming, D.Q.; Chang, X.C.; Shang, F.K.; Zhang, P.F.; Xu, Y.D.; Qu, Y.S.; Gao, W.Z.; Ge, T.C.; Zhao, H.K. Heterogeneity of pore structure in braided river delta tight sandstone reservoirs: Implications for tight oil enrichment in the Jurassic Badaowan Formation, central Junggar Basin. Nat. Resour. Res. 2025, 34, 1743–1771. [Google Scholar] [CrossRef]
- Gong, L.; Gao, X.Z.; Qu, F.T.; Zhang, Y.S.; Zhang, G.Y.; Zhu, J. Reservoir quality and controlling mechanism of the Upper Paleogene fine-grained sandstones in lacustrine basin in the hinterlands of northern Qaidam Basin, NW China. J. Earth Sci. 2023, 34, 806–823. [Google Scholar] [CrossRef]
- Cao, Z.; Liu, G.D.; Liu, Z.X.X.; Yuan, Y.F.; Wang, P.; Niu, Z.C.; Zhang, J.Y. Research status on tight oil and its prospects. Nat. Gas Geosci. 2014, 25, 1499–1508. (In Chinese) [Google Scholar] [CrossRef]
- Higgs, K.E.; Zwingmann, H.; Reyes, A.G.; Funnell, R.H. Diagenesis, porosity evolution, and petroleum emplacement in tight gas reservoirs, Taranaki basin, New Zealand. J. Sediment. Res. 2007, 77, 1003–1025. [Google Scholar] [CrossRef]
- Desbois, G.; Urai, J.L.; Kukla, P.A.; Konstanty, J.; Baerle, C. High-resolution 3D fabric and porosity model in a tight gas sandstone reservoir: A new approach to investigate microstructures from mm-to nm-scale combing argon beam cross sectioning and SEM imaging. J. Pet. Sci. Eng. 2011, 78, 243–257. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.W.; Wang, Z.; Chen, J.; Pang, X.J.; Wang, S.C.; Zhou, Z.L.; He, Z.B.; Qin, Z.Q.; Fan, X.Q. A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Purcell, W.R. Capillary Pressures—Their measurement using mercury and the calculation of permeability therefrom. Trans. AIME 1949, 186, 39–48. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal sandstone pores: Implications for conductivity and pore formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Liu, X.F.; Wang, J.F.; Lin, G.; Hu, F.L.; Li, C.L.; Li, X.; Yu, J.; Xu, H.J.; Lu, S.F.; Xue, Q.Z. Pore-scale characterization of tight sandstone in Yanchang Formation Ordos Basin China using micro-CT and SEM imaging from nm to cm-scale. Fuel 2017, 209, 254–264. [Google Scholar] [CrossRef]
- Zhang, C.M.; Chen, Z.B.; Zhang, Z.S.; Li, J.; Ling, H.; Sun, B.D. Based on NMR T2 study on pore fractal structure of reservoir rock based on spectrum distribution. J. Oil Gas Technol. 2007, 4, 80–86. (In Chinese) [Google Scholar]
- Guo, X.B.; Huang, Z.L.; Zhao, L.B.; Han, W.; Ding, C.; Sun, X.W.; Yan, R.T.; Zhang, T.H.; Yang, X.J.; Wang, R.M. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Broseta, D.; Barré, L.; Vizika, O. Capillary condensation in a fractal porous medium. Phys. Rev. Lett. 2001, 86, 5313. [Google Scholar] [CrossRef]
- Li, K.W.; Horne, R.N. Fractal modeling of capillary pressure curves for the Geysers rocks. Geothermics 2006, 35, 198–207. [Google Scholar] [CrossRef]
- Giri, A.; Tarafdar, S.; Gouze, P.; Dutta, T. Fractal pore structure of sedimentary rocks: Simulation in 2-D using a relaxed bidisperse ballistic deposition model. J. Appl. Geophys. 2012, 87, 40–45. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.W. Fractal analysis of tight gas sandstones using high-pressure mercury intrusion techniques. J. Nat. Gas Sci. Eng. 2015, 24, 185–196. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Li, W.F. Fractal dimensions of shale. J. Pet. Sci. Eng. 2016, 30, 578–582. [Google Scholar] [CrossRef]
- Kulesza, S.; Bramowicz, M. A comparative study of correlation methods for determination of fractal parameters in surface characterization. Appl. Surf. Sci. 2014, 293, 196–201. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W. H. Freeman: New York, NY, USA, 1977. [Google Scholar]
- Cai, J.C.; Wei, W.; Hu, X.Y.; Wood, D.A. Electrical conductivity models in saturated porous media: A review. Earth Sci. Rev. 2017, 171, 419–433. [Google Scholar] [CrossRef]
- Xie, S.Y.; Cheng, Q.M.; Ling, Q.C.; Li, B.; Bao, Z.Y.; Fan, P. Fractal and multifractal analysis of carbonate pore-scale digital images of petroleum reservoirs. Mar. Pet. Geol. 2010, 27, 476–485. [Google Scholar] [CrossRef]
- Hu, Q.H.; Ewing, R.P.; Dultz, C.S. Low pore connectivity in natural rock. J. Contam. Hydrol. 2012, 133, 76–83. [Google Scholar] [CrossRef]
- Hao, R.L.; Huang, W.H.; Bo, J.; Yuan, L. Fractal characteristics and main controlling factors of high-quality tight sandstone reservoirs in the southeastern Ordos Basin. Pet. Geol. 2024, 35, 631–641. [Google Scholar] [CrossRef]
- Jiao, Y.X. Sedimentary Characteristics and Study of the Formation Conditions of Fine-Grained Mixed Sedimentary Rocks in the Second Member of Kongdian Formation in Cangdong Sag. Master Thesis, China University of Petroleum (East China), Dongying, China, 2017. (In Chinese). [Google Scholar]
- Liu, Z.C.; Zhou, Y.W.; Yang, P.; Shao, H.F.; Mu, L.G.; Lin, L.; Yuan, X.H. The reservoir control mechanism by fault-sand coupling in faulted basin and its exploration discovery: A case study of the member 2 of Kongdian Formation in Nanpi slope of Cangdong Sag, Bohai Gulf, China. J. Chengdu Univ. Technol. 2020, 47, 645–651. (In Chinese) [Google Scholar] [CrossRef]
- Xu, Z.X.; Zhang, Y.J.; Wang, J.F.; Liu, H.T.; Jiang, W.Y. Quantitative characterization of pore structure of the second member of Kongdian Formation tight reservoirs in Cangdong sag. Nat. Gas Geosci. 2016, 27, 102–110. (In Chinese) [Google Scholar] [CrossRef]
- Deng, Y.; Pu, X.G.; Chen, S.Y.; Yan, J.H.; Shi, Z.N.; Zhang, W.; Han, W.Z. Analysis on reservoir characteristics and main controlling factors of fine-grained migmatite—Taking Kong 2 member of Cangdong sag in Bohai Bay Basin as an example. J. China Univ. Min. Technol. 2019, 48, 1301–1316. (In Chinese) [Google Scholar]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.T.; Wang, X.R. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. On the geometry of homogenous turbulence, with stress on the fractal dimension of the iso-surfaces of scalars. J. Fluid Mech. 2006, 72, 401–416. [Google Scholar] [CrossRef]
- Shao, X.H.; Pang, X.Q.; Li, H.; Zhang, X. Fractal analysis of pore network in tight gas sandstones using NMR method: A case study from the Ordos basin, China. Energy Fuels 2017, 31, 10358–10368. [Google Scholar] [CrossRef]
- Wang, W.R.; Yue, D.L.; Eriksson, K.A.; Qu, X.F.; Li, W.; Lv, M.; Zhang, J.Q.; Zhang, X.T. Quantification and prediction of pore structures in tight oil reservoirs based on multifractal dimensions from integrated pressure and rate controlled porosimetry for the upper Triassic Yanchang Formation, Ordos Basin, China. Energy Fuels 2020, 34, 4366–4383. [Google Scholar] [CrossRef]
- Chen, F.Y.; Zhou, Y.; Yang, D.J.; Wan, H.F. Study of pore structure of tight sandstone reservoir based on fractal theory: A case study from Chang 7 tight sandstone of Yanchang formation in Qingcheng area, Ordos Basin. J. China Univ. Min. Technol. 2022, 51, 944–958. (In Chinese) [Google Scholar] [CrossRef]
- Li, K.W. Analytical derivation of Brooks-Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Z.B.; Xu, S.; Li, Y.H.; Zhu, Y.S.; Huang, X.Y. Fractal characteristics and its controlling factors of pore-throat with different scales of in tight sandstones of the Yanchang Formation in Ordos Basin. Pet. Geol. Exp. 2022, 44, 33–40. (In Chinese) [Google Scholar]
- Harmann, D.J.; Beaumont, E.A. Predicting Reservoir System Quality and Performance. In Exploring for Oil and Gas Traps, AAPG Treatise of Petroleum Geology, Handbook of Petroleum Geology; Beaumont, E.A., Foster, N.H., Eds.; AAPG: Tulsa, OK, USA, 1999; pp. 438–456. [Google Scholar]
- Chang, B.; Tong, Q.; Cao, C.; Zhang, Y.D. Effect of pore-throat structure on movable fluid and gas–water seepage in tight sandstone from the southeastern Ordos Basin, China. Sci. Rep. 2025, 15, 7714. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Wang, X.Y.; Wang, S.D.; Wang, H.Y. Pore structure analysis of tight sandstone based on nuclear magnetic resonance and fractal techniques. Acta Geophys. 2025. [Google Scholar] [CrossRef]







| Experimental Method | Instrument Name/Model | Manufacture | City and Country |
|---|---|---|---|
| HPMI | AutoPore IV 9505 | Micromeritics Instrument Corporation | Norcross, GA, USA |
| CRMI | Coretest ASPE-730 | Coretest Systems Inc. | Roseville, CA, USA |
| Micro CT | Carl Zeiss Xradia 520 Versa | Carl Zeiss AG | Pleasanton, CA, USA |
| SEM | TM4000plus | Hitachi | Tokyo, Japan |
| NMR | MARAN DRX 2 | Oxford Instruments plc | Abingdon, Oxfordshire, UK |
| XRD | D8 ADVANCE | Bruker | Karlsruhe, Germany |
| Pore Structure Type | Sample No. | Depth /m | Porosity /% | Permeability /mD | Ra /μm | Rp /μm | R50 /μm | Sp | Skp | D | α | SHgmax /% | We /% | Pd /Mpa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ⅰ | KN6-2 | 3750.30 | 11.78 | 8.155 | 1.587 | 0.488 | 0.507 | 2.431 | 0.589 | 4.496 | 0.307 | 94.332 | 28.19 | 0.463 |
| KN6-1 | 3746.00 | 9.97 | 2.6099 | 1.585 | 0.539 | 0.555 | 2.028 | 0.525 | 3.38 | 0.34 | 98.319 | 29.164 | 0.464 | |
| X8 | 3484.20 | 8.19 | 0.355 | 1.577 | 0.442 | 0.232 | 2.584 | 0.305 | 6.404 | 0.28 | 89.353 | 29.597 | 0.466 | |
| Y21 | 3511.60 | 11.44 | 0.31 | 1.579 | 0.445 | 0.458 | 1.98 | 0.481 | 3.968 | 0.282 | 96.988 | 24.034 | 0.465 | |
| X10-2 | 3547.80 | 7.86 | 0.281 | 2.844 | 0.685 | 0.366 | 3.446 | 0.507 | 6.186 | 0.241 | 71.048 | 21.052 | 0.258 | |
| X9 | 3522.70 | 6.91 | 0.271 | 1.578 | 0.457 | 0.466 | 2.145 | 0.495 | 4.137 | 0.289 | 90.079 | 24.111 | 0.466 | |
| Ⅱ | W26-1 | 3623.30 | 11.31 | 0.078 | 0.533 | 0.19 | 0.145 | 2.176 | 0.451 | 12.204 | 0.356 | 90.497 | 33.008 | 1.379 |
| W26-2 | 3634.30 | 12.54 | 0.044 | 0.269 | 0.091 | 0.085 | 1.707 | 0.418 | 18.029 | 0.338 | 94.668 | 32.115 | 2.737 | |
| Ⅲ | X10-1 | 3533.85 | 4.32 | 0.021 | 0.268 | 0.063 | 0.028 | 2.132 | 0.036 | 39.109 | 0.235 | 83.928 | 41.565 | 2.746 |
| Pore Structure Type | Sample No. | Depth /m | Porosity /% | Permeability /mD | Rt /μm | Rp /μm | η | Rmax /μm | Sf /% | Sp /% | St /% | ε | λ | Pd /MPa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | KN6-2 | 3750.30 | 11.78 | 8.155 | 1.116 | 190.579 | 197.033 | 5.568 | 56.102 | 19.046 | 37.056 | 0.514 | 2.766 | 0.132 |
| KN6-1 | 3746.00 | 9.97 | 2.6099 | 1.113 | 190.225 | 196.131 | 2.082 | 65.413 | 26.650 | 38.763 | 0.688 | 10.797 | 0.353 | |
| X8 | 3484.20 | 8.19 | 0.355 | 1.562 | 185.848 | 131.349 | 1.667 | 47.218 | 8.642 | 38.576 | 0.224 | 11.490 | 0.441 | |
| Y21 | 3511.60 | 11.44 | 0.31 | 1.234 | 189.573 | 171.072 | 1.581 | 73.849 | 26.937 | 46.912 | 0.574 | 20.714 | 0.465 | |
| X10-2 | 3547.80 | 7.86 | 0.281 | 1.621 | 192.413 | 129.019 | 1.525 | 70.423 | 29.156 | 41.267 | 0.707 | 17.422 | 0.482 | |
| X9 | 3522.70 | 6.91 | 0.271 | 1.188 | 190.889 | 185.782 | 1.503 | 60.060 | 17.757 | 42.303 | 0.420 | 13.976 | 0.489 | |
| II | W26-1 | 3623.30 | 11.31 | 0.078 | 0.468 | 196.453 | 411.507 | 0.929 | 50.312 | 5.895 | 44.417 | 0.133 | 30.275 | 0.791 |
| W26-2 | 3634.30 | 12.54 | 0.044 | 7.000 | 194.318 | 436.071 | 0.745 | 42.446 | 0.860 | 41.586 | 0.021 | 33.796 | 0.986 | |
| III | X10-1 | 3533.85 | 4.32 | 0.021 | 16.250 | 205.313 | 100.000 | 0.560 | 31.031 | 0.387 | 30.644 | 0.013 | 25.372 | 1.312 |
| Sample No. | Depth /m | Porosity /% | Permeability /mD | Dh1 | R2 | Dh2 | R2 | Dh3 | R2 | Dh4 | R2 | rh1/μm | rh2/μm | rh3/μm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KN6-2 | 3750.30 | 11.78 | 8.155 | 2.1881 | 0.8922 | 3.3166 | 0.9836 | 2.0786 | 0.9041 | 2.8283 | 0.3564 | |||
| KN6-1 | 3746.00 | 9.97 | 2.6099 | 0.9903 | 0.9617 | 2.1224 | 0.9817 | 3.3166 | 0.9836 | 2.0803 | 21.3951 | 2.8587 | 0.3596 | |
| X8 | 3484.20 | 8.19 | 0.355 | 2.6176 | 0.9985 | 2.1791 | 0.9826 | 4.0343 | 0.9329 | 2.1547 | 0.8453 | 21.3932 | 1.5768 | 0.5398 |
| Y21 | 3511.60 | 11.44 | 0.31 | 2.1676 | 0.9686 | 3.3166 | 0.9836 | 2.091 | 0.8451 | 2.8431 | 0.3589 | |||
| X10-2 | 3547.80 | 7.86 | 0.281 | 2.542 | 0.9803 | 2.1542 | 0.9514 | 3.3166 | 0.9836 | 2.0657 | 0.8899 | 21.3920 | 2.8442 | 0.3583 |
| X9 | 3522.70 | 6.91 | 0.271 | 2.6776 | 0.9999 | 2.1413 | 0.9661 | 3.6906 | 0.9818 | 2.0424 | 0.6481 | 21.3932 | 2.8496 | 0.3578 |
| W26-1 | 3623.30 | 11.31 | 0.078 | 2.6541 | 0.9908 | 2.0768 | 0.9583 | 3.3166 | 0.9836 | 2.1456 | 0.8847 | 21.3951 | 1.0845 | 0.5329 |
| W26-2 | 3634.30 | 12.54 | 0.044 | 2.1077 | 0.9603 | 3.3166 | 0.9836 | 2.1316 | 0.87 | 0.5405 | 0.0667 | |||
| X10-1 | 3533.85 | 4.32 | 0.021 | 2.6002 | 0.9647 | 2.1059 | 0.9349 | 3.3166 | 0.9836 | 2.3355 | 0.9569 | 21.4051 | 0.3585 | 0.0890 |
| Sample No. | Depth /m | Porosity /% | Permeability /mD | Dc1 | R2 | Dc2 | R2 | Dc3 | R2 | Dc4 | R2 | rc1/μm | rc2/μm | rc3/μm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KN6-2 | 3750.30 | 11.78 | 8.155 | 3.5696 | 0.9509 | 2.4013 | 0.9951 | 3.3481 | 0.9785 | 2.2406 | 0.9416 | 11.1097 | 1.8374 | 0.6875 |
| KN6-1 | 3746.00 | 9.97 | 0.634 | 2.7259 | 0.9941 | 2.39 | 0.9613 | 3.7054 | 0.9992 | 2.3605 | 0.9852 | 7.0058 | 2.5205 | 0.5507 |
| X8 | 3484.20 | 8.19 | 0.355 | 2.7805 | 0.9949 | 2.321 | 0.9948 | 3.33398 | 0.9882 | 2.4025 | 0.9822 | 8.6380 | 2.5128 | 1.2133 |
| Y21 | 3511.60 | 11.44 | 0.31 | 2.8106 | 0.9922 | 2.288 | 0.9898 | 3.7311 | 0.9892 | 2.2346 | 0.9357 | 8.6273 | 2.0721 | 0.9800 |
| X10-2 | 3547.80 | 7.86 | 0.281 | 2.7979 | 0.9945 | 2.4157 | 0.9962 | 3.2486 | 0.9817 | 2.1377 | 0.9317 | 8.8572 | 2.5275 | 0.9808 |
| X9 | 3522.70 | 6.91 | 0.271 | 2.7336 | 0.9983 | 2.3638 | 0.9956 | 3.0984 | 0.992 | 2.2798 | 0.9572 | 8.7925 | 2.5255 | 0.6780 |
| W26-1 | 3623.30 | 11.31 | 0.078 | 2.6914 | 0.9813 | 2.1379 | 0.9613 | 3.7054 | 0.9992 | 2.3605 | 0.9852 | 6.9818 | 0.6874 | 0.3820 |
| W26-2 | 3634.30 | 12.54 | 0.044 | 2.6328 | 0.9875 | 2.1261 | 0.9586 | 3.2778 | 0.8876 | 5.9017 | 0.3123 | |||
| X10-1 | 3533.85 | 4.32 | 0.021 | 2.5986 | 0.9795 | 2.1011 | 0.9575 | 2.941 | 0.9768 | 5.9932 | 0.3112 |
| Sample No. | Depth /m | Porosity /% | Permeability /mD | D1 | R2 | D2 | R2 | D3 | R2 | D4 |
|---|---|---|---|---|---|---|---|---|---|---|
| KN6-2 | 3750.30 | 11.78 | 8.155 | 3.5188 | 0.9999 | 2.3907 | 0.9938 | 3.5301 | 0.9999 | 2.0819 |
| KN6-1 | 3746.00 | 9.97 | 2.6099 | 2.7259 | 0.9941 | 2.39 | 0.9983 | 3.4401 | 0.9859 | 2.0815 |
| X8 | 3484.20 | 8.19 | 0.355 | 2.7216 | 0.9900 | 2.306 | 0.9974 | 2.8979 | 0.9773 | 2.1040 |
| Y21 | 3511.60 | 11.44 | 0.31 | 2.7331 | 0.9836 | 2.2648 | 0.9912 | 3.0423 | 0.9885 | 2.1296 |
| X10-2 | 3547.80 | 7.86 | 0.281 | 2.7254 | 0.9861 | 2.3084 | 0.9696 | 2.9274 | 0.9205 | 2.1114 |
| X9 | 3522.70 | 6.91 | 0.271 | 2.6901 | 0.9949 | 2.3586 | 0.9911 | 3.043 | 0.9853 | 2.1468 |
| W26-1 | 3623.30 | 11.31 | 0.078 | 2.6914 | 0.9813 | 2.1415 | 0.9561 | 3.4873 | 0.9966 | 2.1405 |
| W26-2 | 3634.30 | 12.54 | 0.044 | 2.6744 | 0.9923 | 2.1379 | 0.9519 | 3.2071 | 0.9319 | 2.1193 |
| X10-1 | 3533.85 | 4.32 | 0.021 | 2.6462 | 0.9860 | 2.1123 | 0.9500 | 2.7826 | 0.9733 | 2.3086 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Han, G.; Liu, Y.; Mou, L.; Wang, K.; Yang, P.; Yan, K. Fractal Characteristics and Controlling Factors of Pore-Throat Structure in Tight Sandstone Reservoirs: A Case Study of the 2nd Member of the Kongdian Formation in the Nanpi Slope, Cangdong Sag, Bohai Bay Basin. Fractal Fract. 2025, 9, 608. https://doi.org/10.3390/fractalfract9090608
Zhou Y, Han G, Liu Y, Mou L, Wang K, Yang P, Yan K. Fractal Characteristics and Controlling Factors of Pore-Throat Structure in Tight Sandstone Reservoirs: A Case Study of the 2nd Member of the Kongdian Formation in the Nanpi Slope, Cangdong Sag, Bohai Bay Basin. Fractal and Fractional. 2025; 9(9):608. https://doi.org/10.3390/fractalfract9090608
Chicago/Turabian StyleZhou, Yong, Guomeng Han, Yanxin Liu, Liangang Mou, Ke Wang, Peng Yang, and Kexin Yan. 2025. "Fractal Characteristics and Controlling Factors of Pore-Throat Structure in Tight Sandstone Reservoirs: A Case Study of the 2nd Member of the Kongdian Formation in the Nanpi Slope, Cangdong Sag, Bohai Bay Basin" Fractal and Fractional 9, no. 9: 608. https://doi.org/10.3390/fractalfract9090608
APA StyleZhou, Y., Han, G., Liu, Y., Mou, L., Wang, K., Yang, P., & Yan, K. (2025). Fractal Characteristics and Controlling Factors of Pore-Throat Structure in Tight Sandstone Reservoirs: A Case Study of the 2nd Member of the Kongdian Formation in the Nanpi Slope, Cangdong Sag, Bohai Bay Basin. Fractal and Fractional, 9(9), 608. https://doi.org/10.3390/fractalfract9090608







