Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis
Abstract
1. Introduction
2. Materials and Methods
- (1)
- Adjustments to effective stress due to evolving pore pressure.
- (2)
- Updates to permeability in response to damage accumulation.
2.1. Governing Equations
- (1)
- Probability density functions describing the heterogeneity of mineral mechanical properties (such as elastic modulus and strength) [64]:
- (2)
- Damage evolution equation and failure criteria:
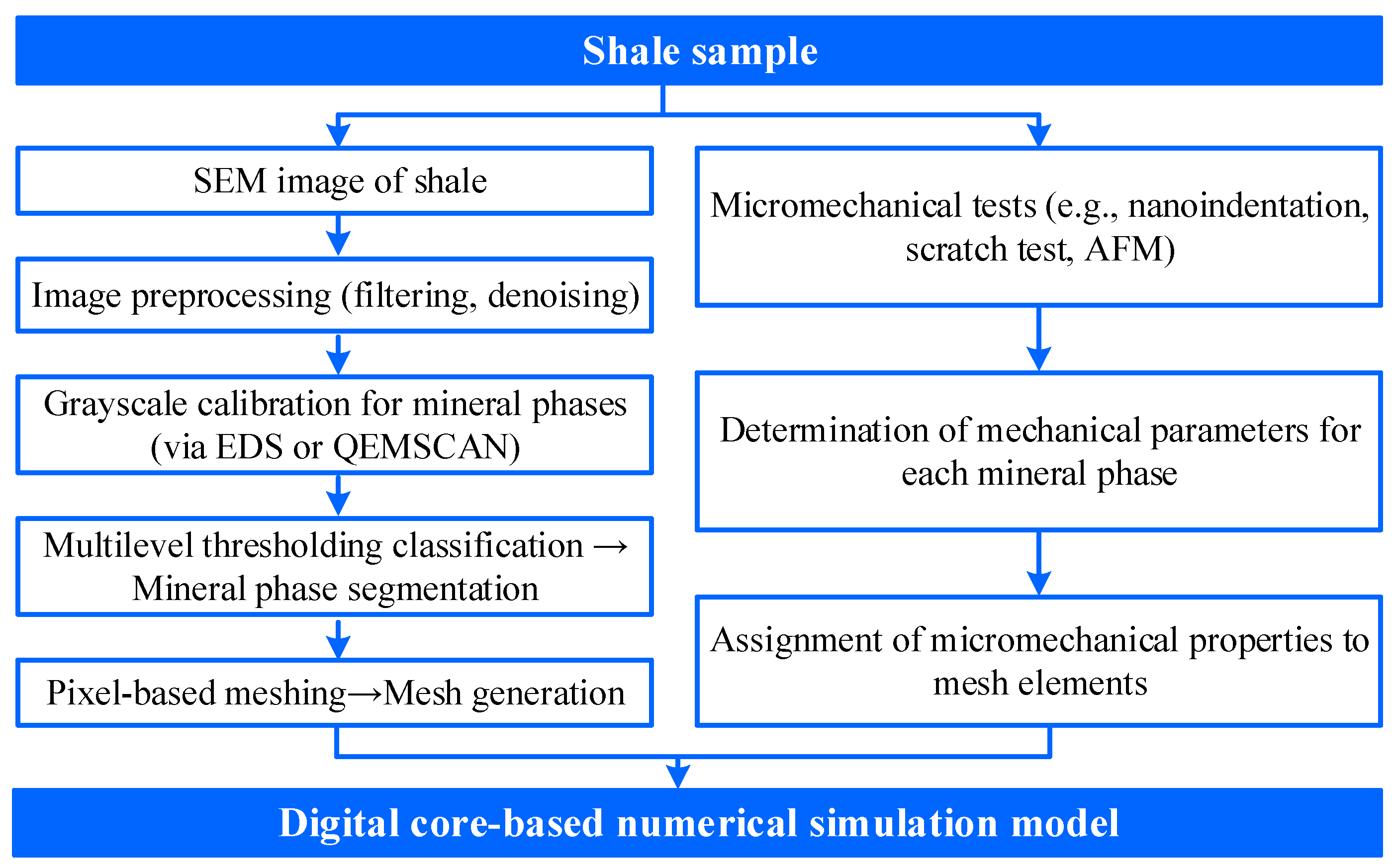
2.2. Model Construction Method
2.3. Mechanical Property Assignment Based on Nanoindentation
3. Generation of Shale Models
3.1. Models with Different Brittleness Indexes
3.2. Models with Different Natural Fracture Densities
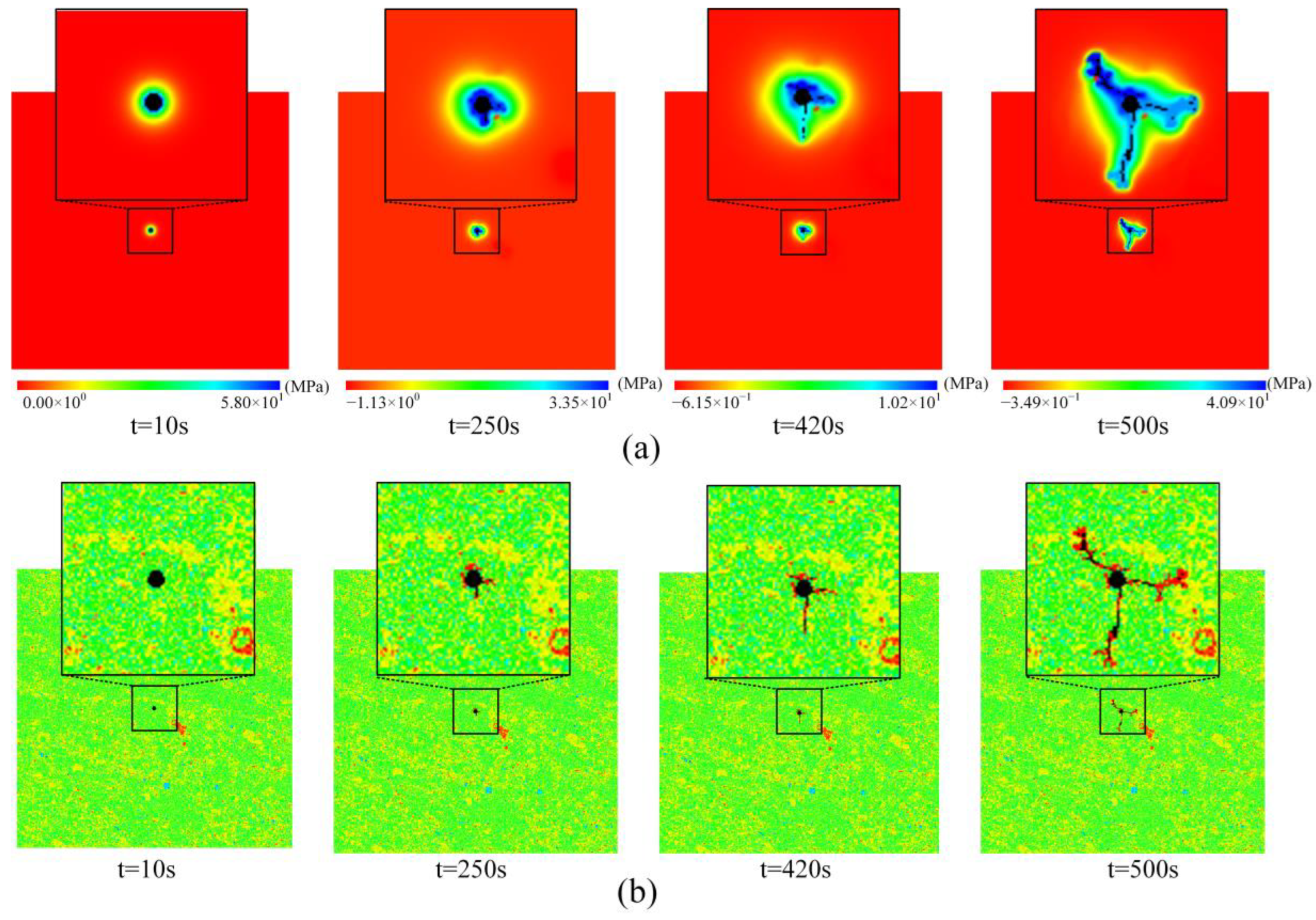
4. Results and Analysis
4.1. Effects of BI on Fracture Propagation Characteristics
4.1.1. Fracture Geometry Analysis Under Different BI Values
4.1.2. Fracture Effectiveness Index Analysis Under Different BI Values
4.1.3. Fracture Propagation Direction Analysis Under Different BI Values
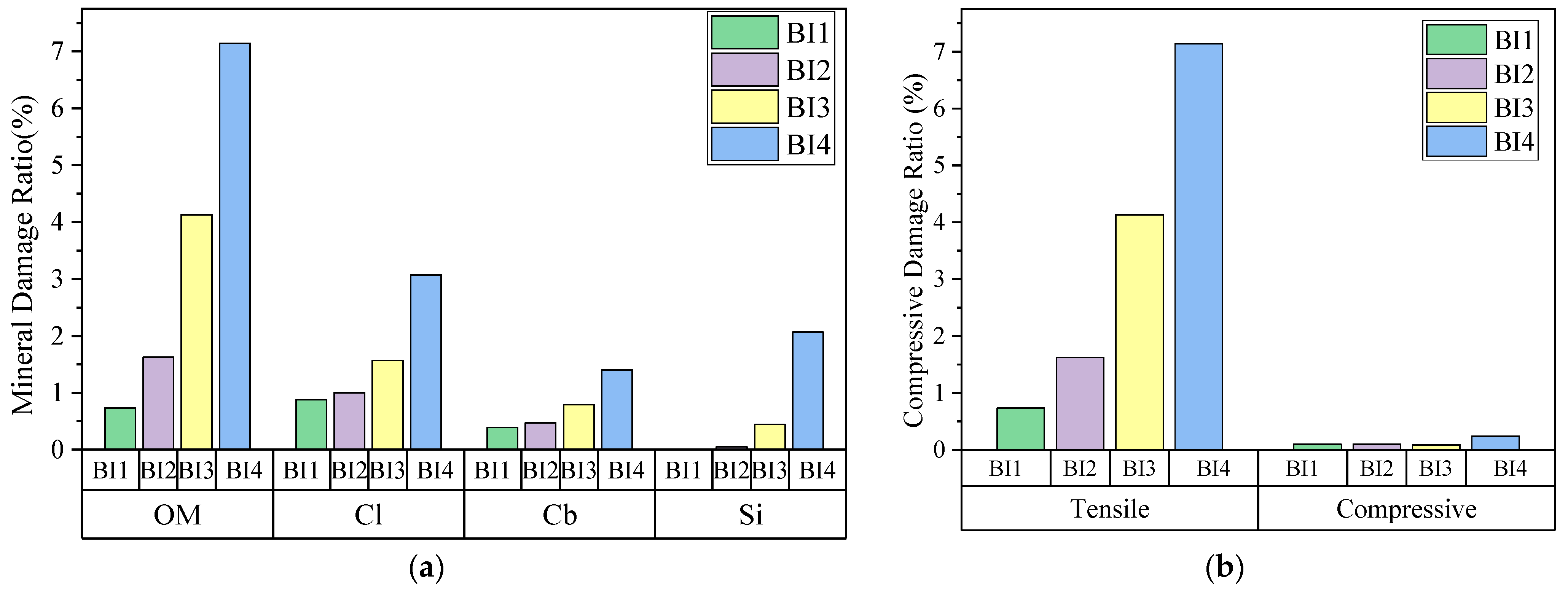
4.1.4. Mineral Damage Behavior Analysis Under Different BI Values
4.2. Effects of NFD on Fracture Propagation Characteristics
4.2.1. Fracture Geometry Analysis Under Varying NFD Values
4.2.2. Fracture Effectiveness Index Analysis Under Varying NFD Values
4.2.3. Fracture Propagation Direction Analysis Under Varying NFD Values
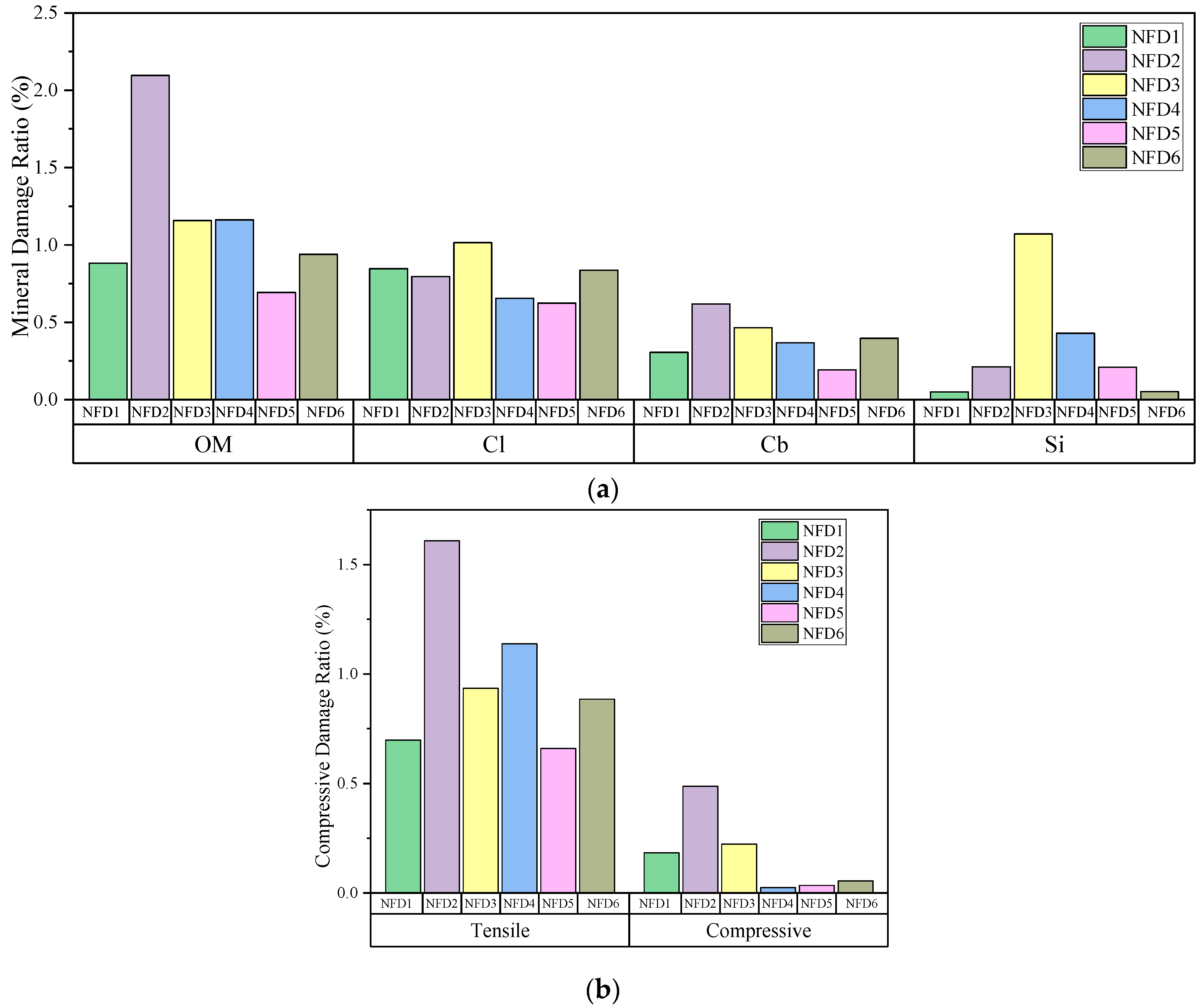
4.2.4. Mineral Damage Behavior Analysis Under Varying NFD Values
5. Discussion
6. Conclusions
- (1)
- In highly brittle shale, fractures initiate, branch, and interconnect more easily, forming complex multidirectional networks that improve reservoir stimulation and flow capacity. The fracture effectiveness index shows a linear positive correlation with the brittleness index.
- (2)
- Natural fracture density has a nonlinear effect on fracture propagation. Moderate fracture density (approximately 8–10%) improves connectivity and network complexity, enhancing fracturing efficiency. However, when the natural fracture density exceeds approximately 10%, excessive density may lead to energy dissipation, fracture shielding, and limited propagation, which can reduce stimulation performance. Overall, the fracture effectiveness index correlates positively with natural fracture density.
- (3)
- Fracture propagation paths are jointly controlled by the spatial distribution of brittle minerals and natural fractures. Local concentrations of brittle minerals or dense natural fractures can cause deflection, intersection, or termination of fractures. This reflects a coupled control mechanism of brittleness-induced and structure-guided deflection, which, together with in situ stress, determines fracture patterns and directions.
- (4)
- Both the brittleness index and natural fracture density significantly affect mineral damage behavior. Higher brittleness increases the damage rate across all mineral types. Changes in fracture density cause nonlinear variations in mineral response. Organic matter is the most sensitive, mainly failing in tension. Silicates follow, while clays and carbonates exhibit higher stability and adaptability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BI | Brittleness index, dimensionless |
| Cb | Carbonate minerals |
| Cl | Clay minerals |
| FEI | Fracture effectiveness index |
| HF | Hydraulic fracture |
| NF | Natural fracture |
| NFD | Natural fracture density |
| OM | Organic matter |
| SRA | Stimulated reservoir area, μm2 |
| Si | Silicate minerals |
| Cf | Conductivity correction factor |
| d | Fractal dimension, dimensionless |
| D | Damage variable, dimensionless |
| Di | Mineral Fractal Dimension, i = OM, Cl, Cb, Si |
| E0 | Initial elastic modulus of the element, Pa |
| G | Shear modulus, Pa |
| g | Gravitational acceleration, m/s2 |
| H | Hydraulic head, m |
| I | Unit tensor, dimensionless |
| Current permeability, mD | |
| Initial permeability, mD | |
| kD | Damage rate coefficient, dimensionless |
| Lef | Effective fracture length, μm |
| Ltotal | Total fracture length, μm |
| m | Degree of material homogeneity |
| Pore pressure, Pa | |
| Volume source, s−1 | |
| V | Volume of an element, m2 |
| Vi | Mineral volume fraction, i = OM, Cl, Cb, Qzt, Si |
| x | Specific value of an element |
| x0 | Mean value of the meso-elements |
| Biot’s coefficient, dimensionless | |
| Empirical coefficient, dimensionless | |
| Strain tensor, dimensionless | |
| Volumetric strain, dimensionless | |
| First principal strain, dimensionless | |
| Third principal strain, dimensionless | |
| Compressive strain at elastic limit, dimensionless | |
| Tensile strain at elastic limit, dimensionless | |
| Ultimate tensile strain, dimensionless | |
| Path deflection coefficient, dimensionless | |
| Fluid viscosity, Pa·s | |
| Poisson’s ratio, dimensionless | |
| Density of the fracturing fluid, kg/m3 | |
| Stress tensor, Pa | |
| Uniaxial compressive strength, Pa | |
| Maximum effective principal stress, Pa | |
| Minimum effective principal stress, Pa | |
| Residual compressive strength, Pa | |
| Residual tensile strength, Pa | |
| Average effective stress, Pa |
References
- Gates, I.; Vishkai, M. On multistage hydraulic fracturing in tight gas reservoirs: Montney Formation, Alberta, Canada. J. Pet. Sci. Eng. 2019, 174, 1127–1141. [Google Scholar] [CrossRef]
- Boak, J.; Kleinberg, R. Shale gas, tight oil, shale oil and hydraulic fracturing. In Future Energy, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 67–95. [Google Scholar] [CrossRef]
- Lu, J.; Li, L.; Yang, F.; Zhang, Z.; Lu, M. Finite element simulation and stimulated reservoir volume optimization of hydraulic fracture propagation in heterogeneous formations based on flow-stress-damage coupling. Phys. Fluids 2025, 37, 036604. [Google Scholar] [CrossRef]
- Gong, X.; Ma, X.; Liu, Y. Analysis of geological factors affecting propagation behavior of fracture during hydraulic fracturing shale formation. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 102. [Google Scholar] [CrossRef]
- Gong, X.; Ma, X.; Liu, Y.; Li, G. Advances in Hydraulic Fracture Propagation Research in Shale Reservoirs. Minerals 2022, 12, 1438. [Google Scholar] [CrossRef]
- Zhuo, R.; Ma, X.; Li, J.; Zhang, S.; Zou, Y.; Ma, J. Study on the Effect of Fluid Viscosity and Injection Rate on the Geometry of Hydraulic Fractures Penetrating Through Laminae Planes and the Proppant Distribution in Deep Shale Oil Reservoirs. Rock. Mech. Rock. Eng. 2024, 58, 2763–2780. [Google Scholar] [CrossRef]
- Fallahzadeh, S.; Hossain, M.; Cornwell, A.; Rasouli, V. Near Wellbore Hydraulic Fracture Propagation from Perforations in Tight Rocks: The Roles of Fracturing Fluid Viscosity and Injection Rate. Energies 2017, 10, 359. [Google Scholar] [CrossRef]
- Wu, J.; Li, X.; Wang, Y. Insight into the Effect of Natural Fracture Density in a Shale Reservoir on Hydraulic Fracture Propagation: Physical Model Testing. Energies 2023, 16, 612. [Google Scholar] [CrossRef]
- Zhang, D.; Ranjith, P.G.; Perera, M.S.A. The brittleness indices used in rock mechanics and their application in shale hydraulic fracturing: A review. J. Pet. Sci. Eng. 2016, 143, 158–170. [Google Scholar] [CrossRef]
- Li, T.; Yao, M.; Xia, Y.; Feng, X.; Cong, W.; Shi, Y.; Tang, C.A. The Influences of Mineral Components and Pore Structure on Hydraulic Fracture Propagation in Shale. Rock. Mech. Rock. Eng. 2024, 58, 2929–2952. [Google Scholar] [CrossRef]
- Nagaso, M.; Mikada, H.; Takekawa, J. Mechanism of complex fracture creation in hydraulic fracturing. In Proceedings of the 20th International Symposium on Recent Advances in Exploration Geophysics (RAEG 2016), Chiba City, Japan, 24 May 2016; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2016; pp. 1–5. [Google Scholar]
- Huo, Z.; Zhang, J.; Li, P.; Tang, X.; Yang, X.; Qiu, Q.; Dong, Z.; Li, Z. An improved evaluation method for the brittleness index of shale and its application—A case study from the southern north China basin. J. Nat. Gas. Sci. Eng. 2018, 59, 47–55. [Google Scholar] [CrossRef]
- Zeng, F.; Gong, G.; Zhang, Y.; Guo, J.; Jiang, J.; Hu, D.; Chen, Z. Fracability evaluation of shale reservoirs considering rock brittleness, fracture toughness, and hydraulic fracturing-induced effects. Geoenergy Sci. Eng. 2023, 229, 212069. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y.; Zhang, J.; Li, P.; Tang, X.; Li, Z.; Dong, Z.; Xu, L.; Zhao, X. Formation conditions and evolution of fractures in multiple tight rocks: Implications for unconventional reservoir exploitation. J. Pet. Sci. Eng. 2021, 200, 108354. [Google Scholar] [CrossRef]
- Khan, J.A.; Padmanabhan, E.; Ul Haq, I.; Franchek, M.A. Hydraulic fracturing with low and high viscous injection mediums to investigate net fracture pressure and fracture network in shale of different brittleness index. Geomech. Energy Environ. 2023, 33, 100416. [Google Scholar] [CrossRef]
- Lan, R.; Jinzhou, Z.; Yongquan, H. Hydraulic Fracture Extending into Network in Shale: Reviewing Influence Factors and Their Mechanism. Sci. World J. 2014, 2014, 847107. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.G.; Dou, F. A numerical investigation for the impacts of shale matrix heterogeneity on hydraulic fracturing with a two-dimensional particle assemblage simulation model. J. Nat. Gas. Sci. Eng. 2022, 104, 104678. [Google Scholar] [CrossRef]
- Liu, H.; Song, H.; Chen, J.; Wang, R.; Wu, Z.; Wang, W.; Wang, S. Fracture Propagation Modes of Lower Cambrian Shale Filled with Different Quartz Contents under Seepage-Stress Coupling. Geofluids 2022, 2022, 1051284. [Google Scholar] [CrossRef]
- Sun, W.; Liang, B.; Hao, J.; Zhao, H.; Hou, M.; Liu, Q. Study on the Fracture Extension Pattern of Shale Reservoir Fracturing under the Influence of Mineral Content. ACS Omega 2024, 9, 32525–32535. [Google Scholar] [CrossRef]
- Sui, H.; Hu, R.; Gao, W.; Xu, D.; Iqbal, J. Effect of Brittle Mineral Size on Hydraulic Fracture Propagation in Shale Gas Reservoir. Geofluids 2019, 1, 9147048. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez, M.; Shojaei, A. Overview of numerical models for interactions between hydraulic fractures and natural fractures: Challenges and limitations. Comput. Geotech. 2016, 71, 361–368. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, S.; Ma, X.; Zhou, T.; Zeng, B. Numerical investigation of hydraulic fracture network propagation in naturally fractured shale formations. J. Struct. Geol. 2016, 84, 1–13. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Wei, S.; Zhang, Z.; Yang, P.; Song, S. Sensitivity analysis on the effect of natural fractures and injected fluid on hydraulic fracture propagation in a fractured reservoir. Eng. Fract. Mech. 2022, 263, 108288. [Google Scholar] [CrossRef]
- Chong, Z.; Li, X.; Chen, X.; Zhang, J.; Lu, J. Numerical Investigation into the Effect of Natural Fracture Density on Hydraulic Fracture Network Propagation. Energies 2017, 10, 914. [Google Scholar] [CrossRef]
- Yoshioka, K.; Hofmann, H.; Liang, Y.; Luo, Y.; Li, X. Phase-Field Modelling of Interactions Between Hydraulic Fractures and Natural Fractures. Rock. Mech. Rock. Eng. 2022, 55, 6227–6247. [Google Scholar] [CrossRef]
- Wang, J.; Xie, H.-P.; Matthai, S.K.; Hu, J.-J.; Li, C.-B. The role of natural fracture activation in hydraulic fracturing for deep unconventional geo-energy reservoir stimulation. Pet. Sci. 2023, 20, 2141–2164. [Google Scholar] [CrossRef]
- Xie, J.; Huang, H.; Ma, H.; Zeng, B.; Tang, J.; Yu, W.; Wu, K. Numerical investigation of effect of natural fractures on hydraulic-fracture propagation in unconventional reservoirs. J. Nat. Gas. Sci. Eng. 2018, 54, 143–153. [Google Scholar] [CrossRef]
- Zheng, H.; Li, F.; Wang, D. Numerical Investigation of Complex Hydraulic Fracture Propagation in Shale Formation. Processes 2024, 12, 2630. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Xue, Y.; Fu, J.; Zhu, J.; Zhao, H.; Wang, L. The Influence of the Distribution Characteristics of Complex Natural Fracture on the Hydraulic Fracture Propagation Morphology. Front. Earth Sci. 2022, 9, 784931. [Google Scholar] [CrossRef]
- Wang, L.; Yang, C.; Chang, X.; Zeng, Y.; Zhenkun, H.; Zhou, J.; Liu, L. Effect of natural filling fracture on the cracking process of shale Brazilian disc containing a central straight notched flaw. J. Pet. Sci. Eng. 2021, 196, 107993. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Z.; Wang, M. Hydro-mechanical coupled mechanisms of hydraulic fracture propagation in rocks with cemented natural fractures. J. Pet. Sci. Eng. 2018, 163, 421–434. [Google Scholar] [CrossRef]
- Wang, W.-H.; Olson, J.; Wu, K. Characterization of hydraulic fracture geometry in shale rocks through physical modeling. Int. J. Fract. 2019, 216, 71–85. [Google Scholar] [CrossRef]
- Geng, Y.; Liu, Z.; Wang, L.; Wang, S.; Zhao, H.; Zhang, G.; Tao, S.; Chen, M.; Li, W. Effect of Random Natural Fractures on Hydraulic Fracture Propagation Geometry in Fractured Carbonate Rocks. Rock. Mech. Rock. Eng. 2018, 51, 491–511. [Google Scholar] [CrossRef]
- Meng, S.; Zhang, Z.; Xu, W.; Yu, H.; Wu, H.; Liu, H. A mixed phase-field model for fracture propagation behavior in Gulong shale with complex wavy bedding. J. Rock. Mech. Geotech. Eng. 2025; in press. [Google Scholar]
- Hu, Y.; Hurst, A.; Gan, Q.; Elsworth, D. Hydraulic fracture propagation and interaction with natural fractures by coupled hydro-mechanical modeling. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 8, 4. [Google Scholar] [CrossRef]
- Dahi-Taleghani, A.; Olson, J. Numerical Modeling of Multistranded-Hydraulic-Fracture Propagation: Accounting for the Interaction Between Induced and Natural Fractures. SPE J. 2009, 16, 575–581. [Google Scholar] [CrossRef]
- Sun, P.; Ge, L.; Liu, Y.; Li, B.; Nie, X. Modeling of multi-mineral-component digital core based on Res-Unet. J. Geophys. Eng. 2023, 20, 483–493. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J.; Huang, Z.; Liu, F.; Yang, Y. Digital core reconstruction based on discrete element and Markov chain-Monte Carlo methods. Geoenergy Sci. Eng. 2024, 236, 212422. [Google Scholar] [CrossRef]
- Yasin, Q.; Liu, B.; Sun, M.; Sohail, G.M.; Ismail, A.; Wood, D.A.; Yang, Z. Digital core modeling for multimineral segmentation of lacustrine shale oil using FE-SEM and KiU-Net. Fuel 2025, 398, 135474. [Google Scholar] [CrossRef]
- Aslannezhad, M.; Sayyafzadeh, M.; Tang, D.; Iglauer, S.; Keshavarz, A. Application of digital core analysis to improve reservoir characterisation and modelling: The Otway formation as a case study. Int. J. Greenh. Gas. Control 2025, 141, 104316. [Google Scholar] [CrossRef]
- Fu, Y.; Zhai, Q.; Yuan, G.; Wang, Z.; Cheng, Y.; Wang, M.; Wu, W.; Ni, G. Multi-scale nonlinear reservoir flow simulation based on digital core reconstruction. Geoenergy Sci. Eng. 2024, 242, 213218. [Google Scholar] [CrossRef]
- Lin, R.; Ren, L.; Zhao, J.; Tan, X.; Rasouli, V.; Wang, X.; Wu, J.; Song, Y.; Shen, C. Stress and pressure dependent permeability of shale rock: Discrete element method (DEM) simulation on digital core. J. Pet. Sci. Eng. 2022, 208, 109797. [Google Scholar] [CrossRef]
- Kazak, A.; Chugunov, S.; Chashkov, A. Integration of Large-Area Scanning-Electron-Microscopy Imaging and Automated Mineralogy/Petrography Data for Selection of Nanoscale Pore-Space Characterization Sites. SPE Reserv. Eval. Eng. 2018, 21, 821–836. [Google Scholar] [CrossRef]
- Yan, W.; Chi, P.; Golsanami, N.; Sun, J.; Xing, H.; Li, S.-Z.; Dong, H. Analysis of reconstructed multi-source and multi-scale 3D digital rocks based on the cycle-consistent generative adversarial network method. Geophys. J. Int. 2023, 235, 736–749. [Google Scholar] [CrossRef]
- Wang, S.; Tan, M.; Wu, H.; Li, Y.; Xie, G.; Zhang, L. A Digital Rock Physics-Based Multiscale Multicomponent Model Construction of Hot-Dry Rocks and Microscopic Analysis of Acoustic Properties under High-Temperature Conditions. SPE J. 2022, 27, 3119–3135. [Google Scholar] [CrossRef]
- Ji, L.; Lin, M.; Cao, G.; Jiang, W. A multiscale reconstructing method for shale based on SEM image and experiment data. J. Pet. Sci. Eng. 2019, 179, 586–599. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, B.; Zhang, S.; Ma, X.; Hao, L.; Zhang, S.; Shi, S.-Z. Parameter Sensitivity Analysis of the Hydraulic Fracture Growth Geometry in a Deep Shale Oil Formation: An Experimental Study. Geofluids 2022, 2022, 6878626. [Google Scholar] [CrossRef]
- Li, Z.; Li, L.; Huang, B.; Zhang, L.; Li, M.; Zuo, J.; Li, A.; Yu, Q. Numerical investigation on the propagation behavior of hydraulic fractures in shale reservoir based on the DIP technique. J. Pet. Sci. Eng. 2017, 154, 302–314. [Google Scholar] [CrossRef]
- Li, Z.; Li, L.; Li, M.; Zhang, L.; Zhang, Z.; Huang, B.; Tang, C.a. A numerical investigation on the effects of rock brittleness on the hydraulic fractures in the shale reservoir. J. Nat. Gas. Sci. Eng. 2018, 50, 22–32. [Google Scholar] [CrossRef]
- Zhao, H.; Zou, L.; Liu, Y.; Wang, J.; Xie, X.; Li, S.; Qin, L. A Dynamic Propagation Numerical Model of Hydraulic Fracture Interactions with Pre-Existing Complex Natural Fractures. Processes 2024, 12, 899. [Google Scholar] [CrossRef]
- Firoozabadi, A.; Wu, T. Fracture Toughness and Surface Energy Density of Kerogen by Molecular Dynamics Simulations in Tensile Failure. J. Phys. Chem. C 2020, 124, 15895–15901. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, D.; Rui, Z.; Meng, S.; Tao, J.; Yang, L.; Liu, X. Study on dynamic fracture growth mechanism of continental shale under compression failure. Gas. Sci. Eng. 2023, 114, 204983. [Google Scholar] [CrossRef]
- Erhu, B.; Song, Y.; Lu, W.; He, C. Numerical Simulation of the Influence of Natural Fractures on Hydraulic Fracture Propagation. Geofluids 2020, 1, 8878548. [Google Scholar] [CrossRef]
- Hu, Y.; Gan, Q.; Hurst, A.; Elsworth, D. Investigation of coupled hydro-mechanical modelling of hydraulic fracture propagation and interaction with natural fractures. Int. J. Rock Mech. Min. Sci. 2023, 169, 105418. [Google Scholar] [CrossRef]
- Lee, Y.H.; Carr, J.R.; Barr, D.J.; Haas, C.J. The fractal dimension as a measure of the roughness of rock discontinuity profiles. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1990, 27, 453–464. [Google Scholar] [CrossRef]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D Roughness Characterization. Rock. Mech. Rock. Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Y. Application of Fractals to Evaluate Fractures of Rock Due to Mining. Fractal Fract. 2022, 6, 96. [Google Scholar] [CrossRef]
- Lv, W.; Yan, G.; Liu, Y.; Liu, X.; Du, D.; Wang, R. Effect of fractal fractures on permeability in three-dimensional digital rocks. Fractals 2019, 27, 1940015. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, H.; Li, N. Pore Structure Characterization Using Fractal Theory and 3D Digital Core. In Springer Series in Geomechanics and Geoengineering, Proceedings of the International Field Exploration and Development Conference 2020. IFEDC 2020, Chengdu, China, 23–25 September 2020; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Liu, H.; Xie, H.; Wu, F.; Li, C.; Gao, R. A novel box-counting method for quantitative fractal analysis of three-dimensional pore characteristics in sandstone. Int. J. Min. Sci. Technol. 2024, 34, 479–489. [Google Scholar] [CrossRef]
- Li, T.; Li, L.; Tang, C.A.; Zhang, Z.; Li, M.; Zhang, L.; Li, A. A coupled hydraulic-mechanical-damage geotechnical model for simulation of fracture propagation in geological media during hydraulic fracturing. J. Pet. Sci. Eng. 2019, 173, 1390–1416. [Google Scholar] [CrossRef]
- Dang-Trung, H.; Keilegavlen, E.; Berre, I. Numerical modeling of wing crack propagation accounting for fracture contact mechanics. Int. J. Solids Struct. 2020, 204–205, 233–247. [Google Scholar] [CrossRef]
- Wang, L.; Vuik, C.; Hajibeygi, H. A stabilized mixed-FE scheme for frictional contact and shear failure analyses in deformable fractured media. Eng. Fract. Mech. 2022, 267, 108427. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Yang, T.H.; Li, L.C. Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock. Mech. 2002, 39, 477–489. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Tang, C.A.; Li, H.X.; Xu, T.; Zhang, Y. Numerical simulation of 3-d failure process in heterogeneous rocks. Int. J. Rock. Mech. Min. Sci. 2004, 41, 323–328. [Google Scholar] [CrossRef]
- Zhou, L.; Hou, M.Z. A new numerical 3D-model for simulation of hydraulic fracturing in consideration of hydro-mechanical coupling effects. Int. J. Rock. Mech. Min. Sci. 2013, 60, 370–380. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Hoboken, NJ, USA, 1980; Volume 13, pp. 455–458. [Google Scholar]
- Li, L.; Meng, Q.; Wang, S.; Li, G.; Tang, C. A numerical investigation of the hydraulic fracturing behaviour of conglomerate in Glutenite formation. Acta Geotech. 2013, 8, 597–618. [Google Scholar] [CrossRef]
- Xia, Y.; Zhou, H.; Zhang, C.; He, S.; Gao, Y.; Wang, P. The evaluation of rock brittleness and its application: A review study. Eur. J. Environ. Civil. Eng. 2022, 26, 239–279. [Google Scholar] [CrossRef]
- Rickman, R.; Mullen, M.; Petre, E.; Grieser, B.; Kundert, D. A Practical Use of Shale Petrophysics for Stimulation Design Optimization: All Shale Plays Are Not Clones of the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21 August–24 September 2008; p. SPE–115258-MS, ISBN 978-1-55563-147-5. [Google Scholar] [CrossRef]
- Jarvie, D.M.; Hill, R.J.; Ruble, T.E.; Pollastro, R.M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermogenic shale-gas assessment. AAPG Bull. 2007, 91, 475–499. [Google Scholar] [CrossRef]
- Zhou, C.; Sun, Z.; Xiao, Y.; Huang, G.; Kuang, D.; Li, M. Study on Brittleness Characteristics and Fracturing Crack Propagation Law of Deep Thin-Layer Tight Sandstone in Longdong, Changqing. Processes 2023, 11, 2636. [Google Scholar] [CrossRef]
- Zhao, Y.; Gou, X. A brittleness evaluation method based on breaking energy theory for tight reservoir in Dagang Oilfield. J. Pet. Explor. Prod. Technol. 2020, 10, 1689–1698. [Google Scholar] [CrossRef]
- Du, J.; Cai, J.; Long, S.; Gao, B.; Feng, D.; Peng, Z.; Zeng, X. The Control of Diagenesis and Mineral Assemblages on Brittleness of Mudstones. Front. Earth Sci. 2021, 9, 758046. [Google Scholar] [CrossRef]
- Lu, S.; Zhi, Q.; Lin, Z.; Wang, J.; Zhang, P.; Huang, H. Evaluation of Lacustrine Shale Brittleness and Its Controlling Factors: A Case Study from the Jurassic Lianggaoshan Formation, Sichuan Basin. Processes 2023, 11, 439. [Google Scholar] [CrossRef]
- Liu, B.; Wang, S.; Liu, X.; Fu, X.; Bai, Y.; Ke, X.; Pan, Z. Mechanical characteristics and factors controlling brittleness of organic-rich continental shales. J. Pet. Sci. Eng. 2020, 194, 107464. [Google Scholar] [CrossRef]
- Xiong, D.; Ma, X. Influence of natural fractures on hydraulic fracture propagation behaviour. Eng. Fract. Mech. 2022, 276, 108932. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, F.; Qiao, Y.; Ren, D.; Liu, Y.; Bai, J. Study on Shear & Tensile Activation of Hydraulic Fracturing in Natural Fractured Reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 10–12 October 2023; p. SPE-215378-MS. [Google Scholar] [CrossRef]
- Nagel, N.; Zhang, F.; Sanchez-Nagel, M.; Lee, B.; Garcia, X. Fracture Network Connectivity—A Key To Hydraulic Fracturing Effectiveness and Microseismicity Generation. In Effective and Sustainable Hydraulic Fracturing; Jeffrey, R.G., McLennan, J., Bunger, A., Eds.; IntechOpen: Rijeka, Croatia, 2013. [Google Scholar] [CrossRef]
- Wang, H. Hydraulic fracture propagation in naturally fractured reservoirs: Complex fracture or fracture networks. J. Nat. Gas. Sci. Eng. 2019, 68, 102911. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, B.; Guo, T.; Wang, H.; Chen, M.; Li, W.; Qu, Z.; Zheng, H. Research on fracture propagation of hydraulic fracturing in a fractured shale reservoir using a novel CDEM-based coupled HM model. Comput. Geotech. 2024, 168, 106170. [Google Scholar] [CrossRef]


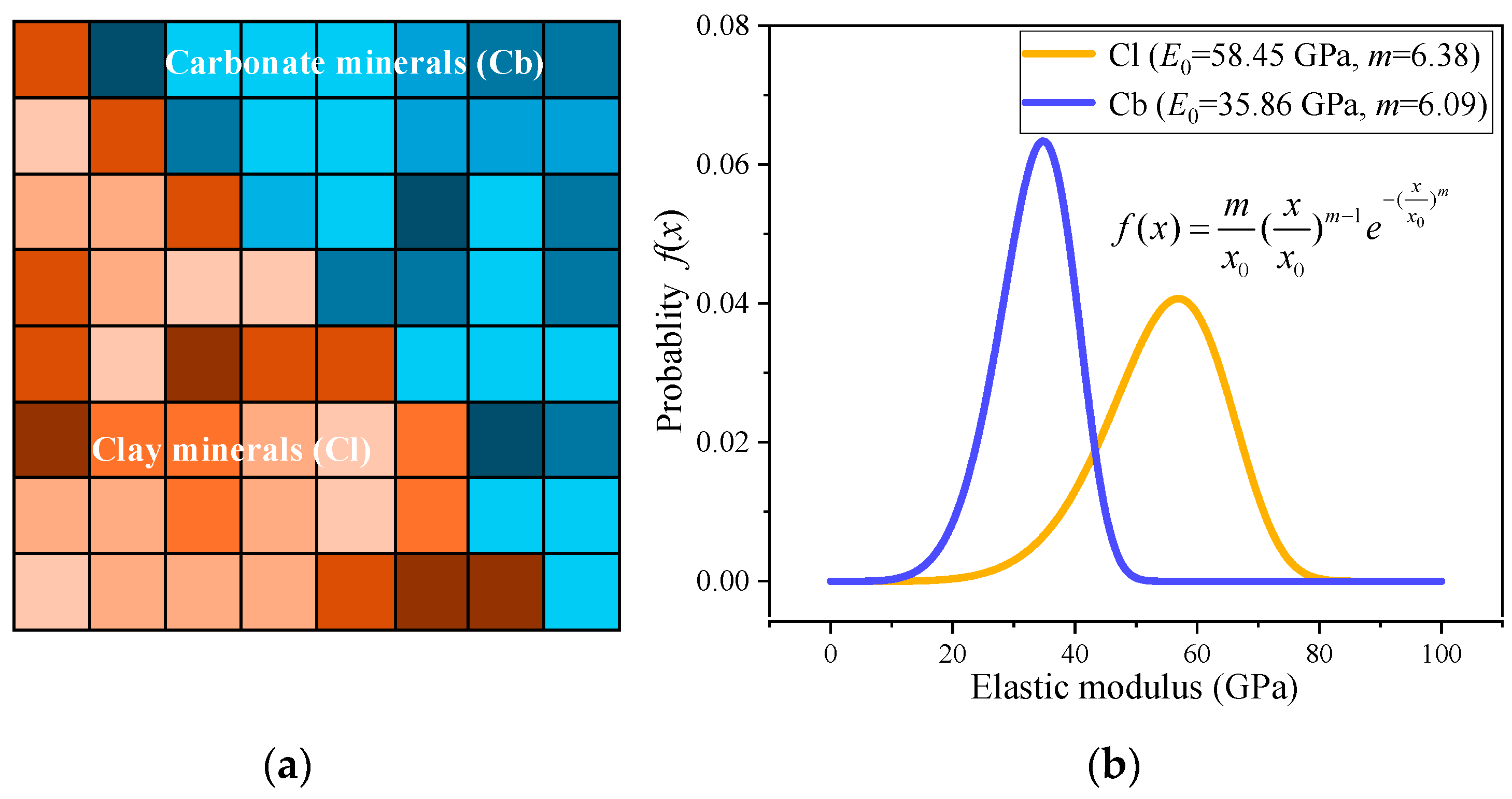




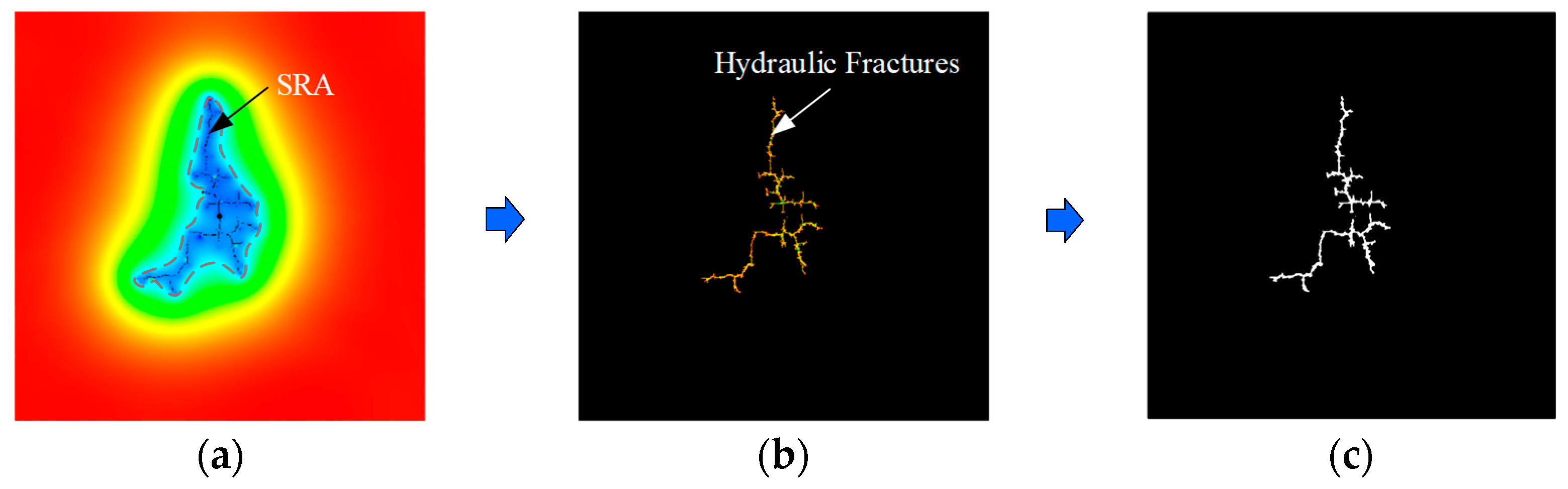





| Mineral Type | E0 (GPa) | (MPa) | k (mD) | |||
|---|---|---|---|---|---|---|
| Carbonate minerals | 58.45 | 6.38 | 315.44 | 4.21 | 0.28 | 6.2 × 10−4 |
| Silicate minerals | 95.49 | 9.43 | 507.68 | 9.73 | 0.07 | 6.2 × 10−4 |
| Clay matrix | 35.86 | 6.09 | 143.85 | 1.73 | 0.34 | 6.2 × 10−3 |
| Organic matter | 8.05 | 2.15 | 94.48 | 2.09 | 0.14 | 6.2 × 10−2 |
| Model ID | DOM | VOM(%) | DCl | VCl (%) | DCb | VCb(%) | DSi | VSi (%) | BI(%) |
|---|---|---|---|---|---|---|---|---|---|
| BI1 | 1.03 | 0.38 | 1.79 | 34.67 | 1.82 | 64.13 | 1.09 | 0.81 | 64.94 |
| BI2 | 1.14 | 0.79 | 1.81 | 34.61 | 1.83 | 63.7 | 1.1 | 2.07 | 65.77 |
| BI3 | 1.05 | 0.43 | 1.78 | 29.33 | 1.82 | 69.38 | 1.09 | 0.87 | 70.25 |
| BI4 | 1.16 | 0.8 | 1.76 | 25.6 | 1.8 | 73.03 | 1.02 | 0.58 | 73.61 |
| Model ID | DOM | VOM (%) | DCl | VCl (%) | DCb | VCb (%) | DSi | VSi (%) | BI (%) |
|---|---|---|---|---|---|---|---|---|---|
| NFD1 | 1.55 | 7.97 | 1.8 | 80.61 | 1.6 | 8.34 | 1.3 | 3.07 | 11.80 |
| NFD2 | 1.6 | 8.23 | 1.76 | 87.86 | 1.41 | 2.81 | 1.11 | 1.09 | 3.9 |
| NFD3 | 1.55 | 10.03 | 1.79 | 69.02 | 1.68 | 15.51 | 1.39 | 5.44 | 21.50 |
| NFD4 | 1.66 | 11.13 | 1.85 | 76.83 | 1.64 | 9.97 | 1.24 | 2.07 | 12.13 |
| NFD5 | 1.65 | 11.36 | 1.84 | 76.47 | 1.63 | 9.96 | 1.26 | 2.21 | 12.63 |
| NFD6 | 1.71 | 14.79 | 1.87 | 70.01 | 1.67 | 11.49 | 1.33 | 3.7 | 15.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, J.; Li, T.; Liang, Z.; Meng, S.; Zheng, L.; Wu, N. Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis. Fractal Fract. 2025, 9, 535. https://doi.org/10.3390/fractalfract9080535
Liu X, Zhang J, Li T, Liang Z, Meng S, Zheng L, Wu N. Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis. Fractal and Fractional. 2025; 9(8):535. https://doi.org/10.3390/fractalfract9080535
Chicago/Turabian StyleLiu, Xin, Jiaqi Zhang, Tianjiao Li, Zhengzhao Liang, Siwei Meng, Licai Zheng, and Na Wu. 2025. "Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis" Fractal and Fractional 9, no. 8: 535. https://doi.org/10.3390/fractalfract9080535
APA StyleLiu, X., Zhang, J., Li, T., Liang, Z., Meng, S., Zheng, L., & Wu, N. (2025). Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis. Fractal and Fractional, 9(8), 535. https://doi.org/10.3390/fractalfract9080535







