A Multi-Dimensional Feature Extraction Model Fusing Fractional-Order Fourier Transform and Convolutional Information
Abstract
1. Introduction
- (1)
- A Fractional-Order Fourier Transform (FrFT) module based on the Chirp-Z algorithm approximation of the learnable order is introduced. The fractional-order Fourier transform module can provide more flexible frequency domain sensing capabilities. By introducing a learnable parameter to control the “order” of the transformation, the model can automatically adjust the optimal degree of frequency domain projection during the training process. This approach enhances the model’s ability to perceive multi-scale and non-stationary signals, effectively improves the expressive power of feature extraction, and is especially suitable for dealing with data scenarios with complex pattern distributions.
- (2)
- A custom convolution module is incorporated to extract local features using convolutional layers. The custom convolution module can effectively capture texture and shape changes within a localized region, which is especially important for processing images or spatial data.
- (3)
- Combining three different types of feature extraction methods (attention mechanism, convolutional network, and fractional-order Fourier transform) to extract features from input data from different perspectives, the model integrates different information from the three branches. The three-branch fusion approach not only preserves the characteristics of each branch, but also combines their strengths, and improves the model’s ability to handle complex data.
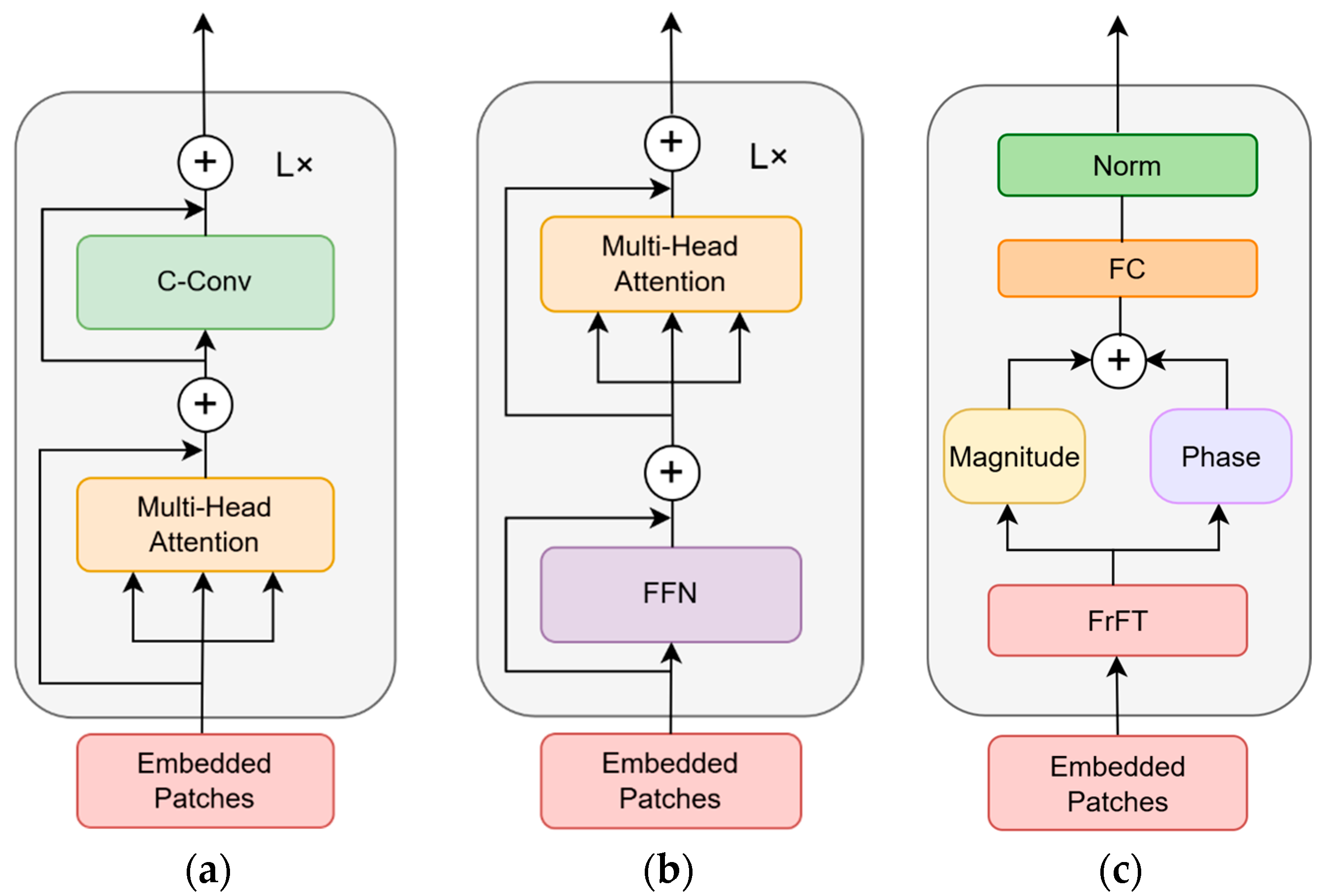
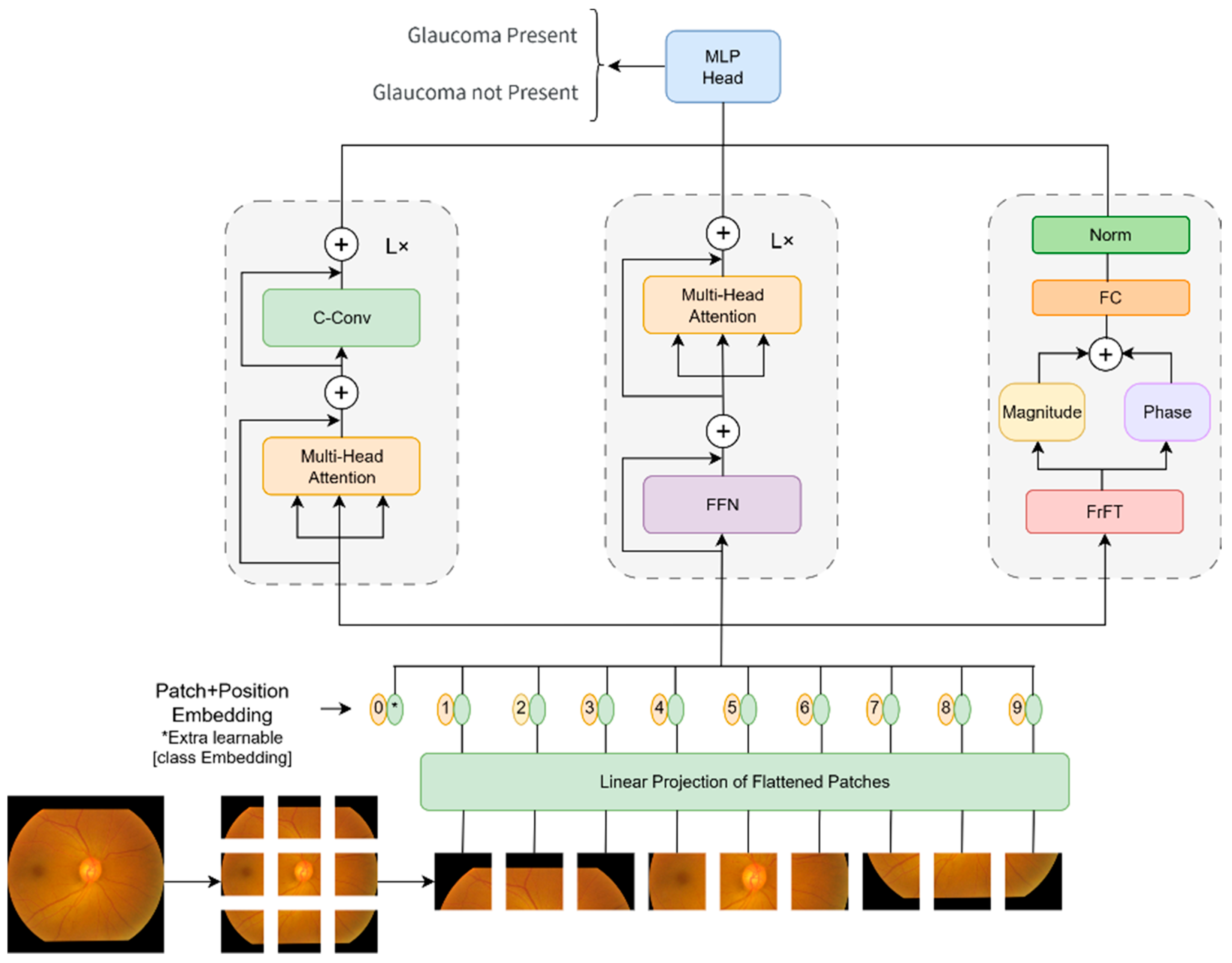
2. Fractional Convolution Vision Transformer Model
2.1. Vision Transformer
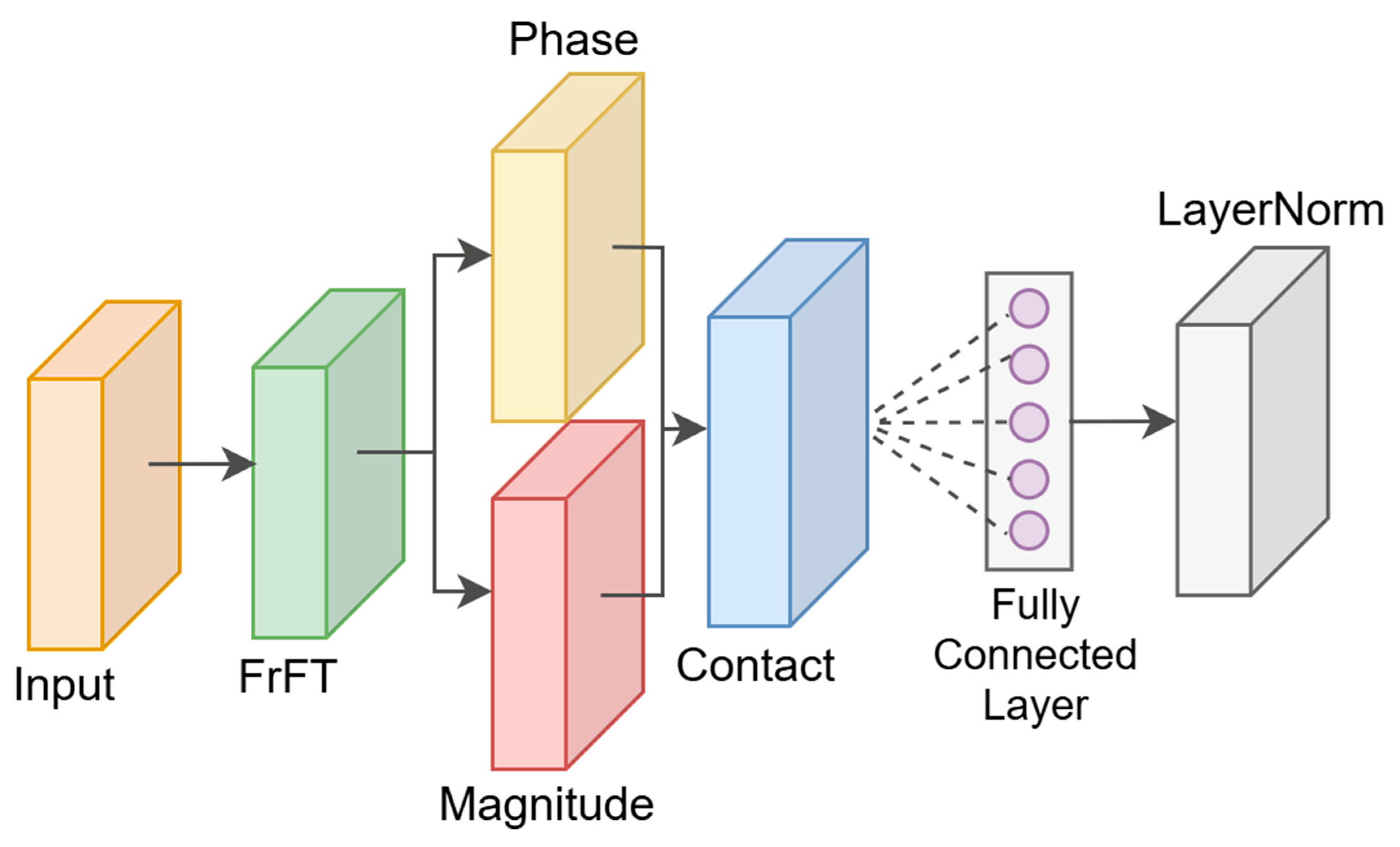
2.2. Fractional-Order Fourier Transform Module
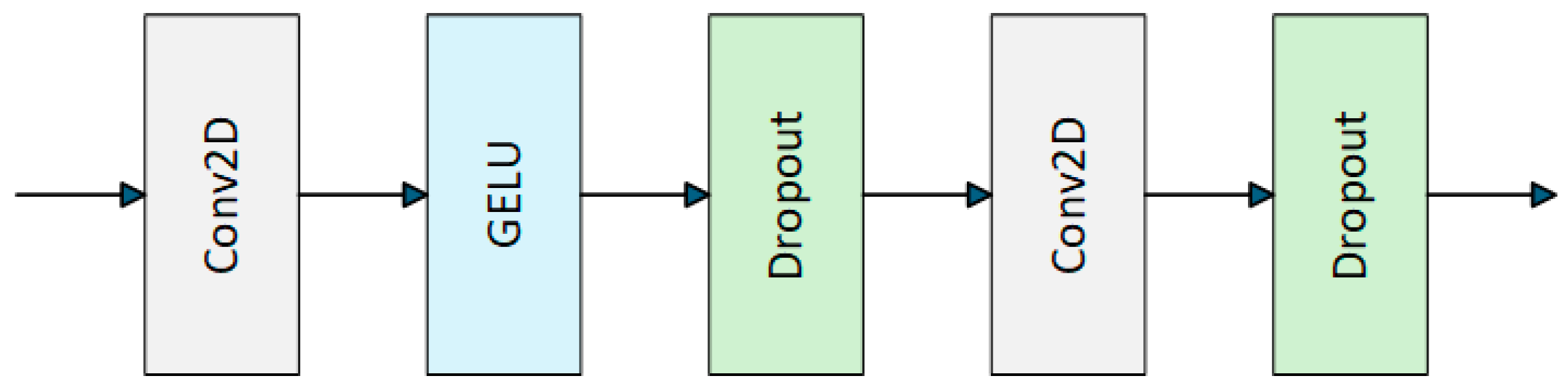
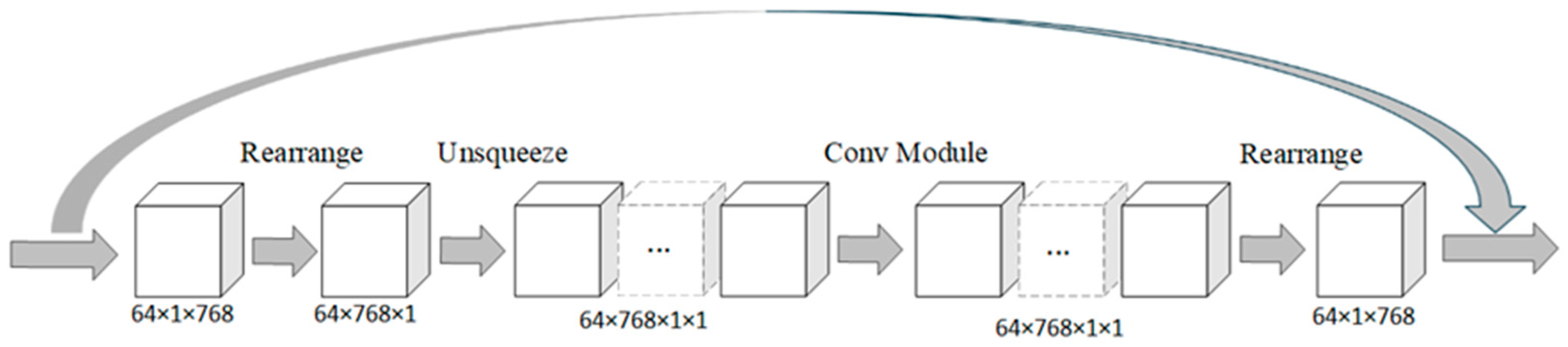
2.3. Customized Convolution Module
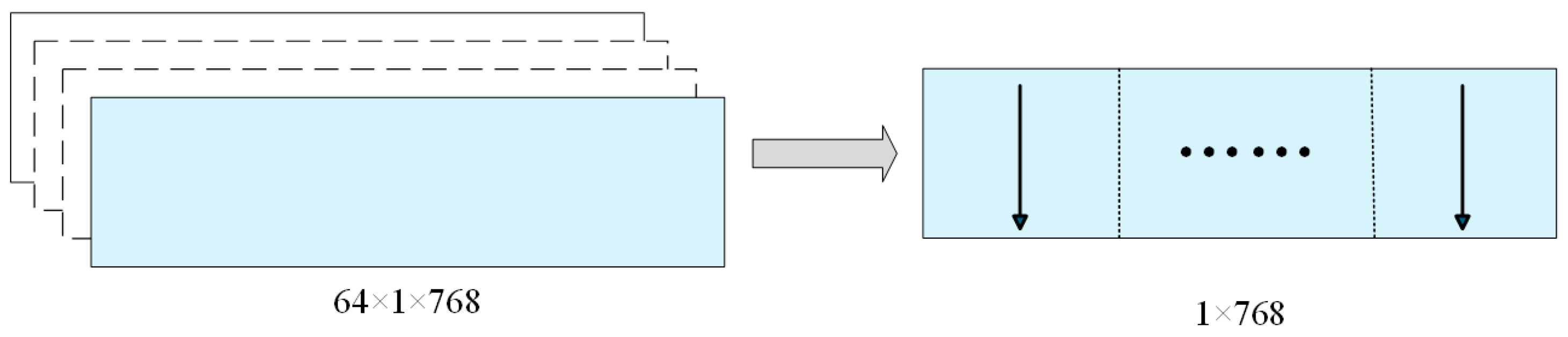
2.4. Three-Branch Module
2.5. FCViT Model
3. Experimental Section
3.1. Common Experimental Models
3.2. Datasets
3.3. Performance Indicator Test
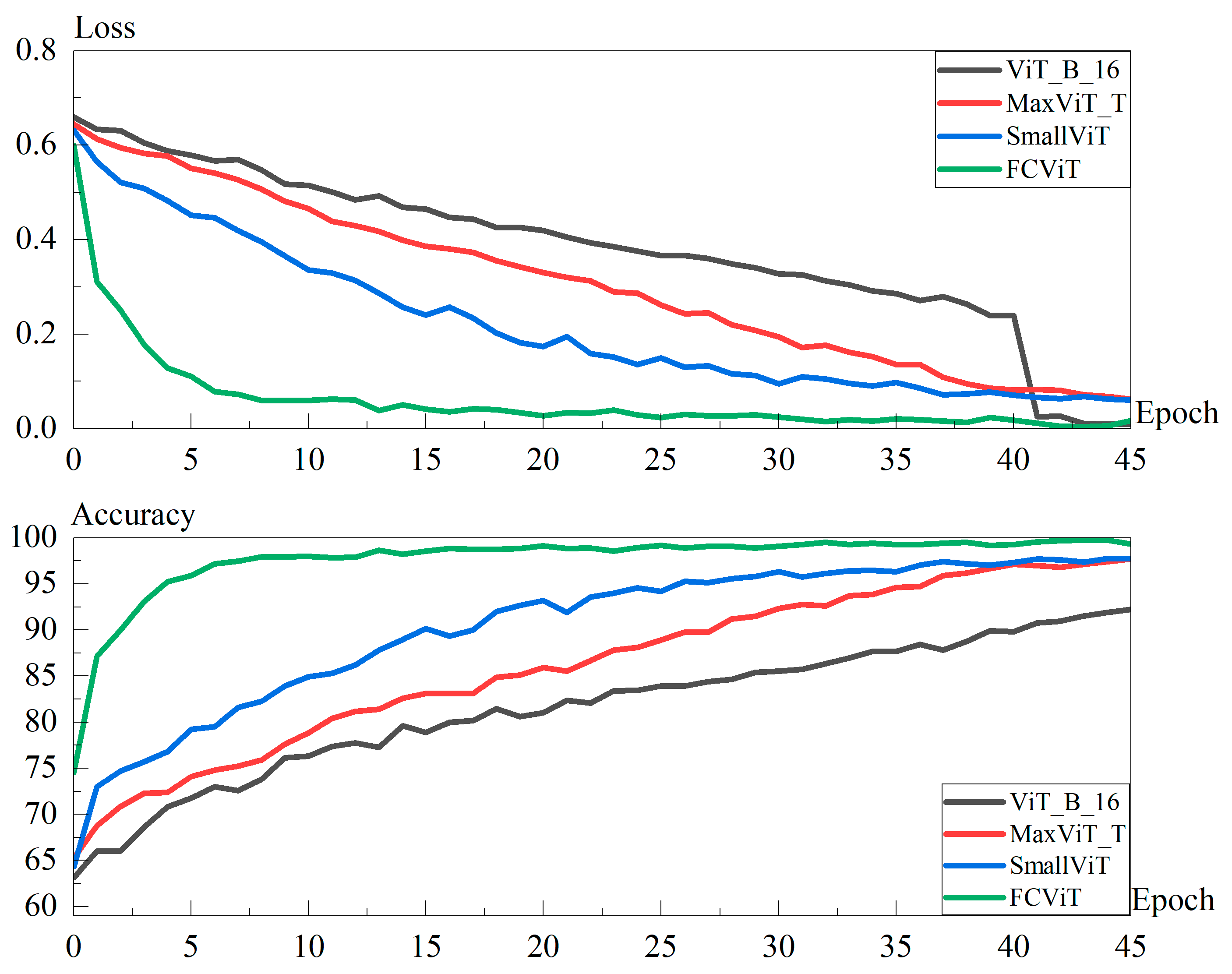
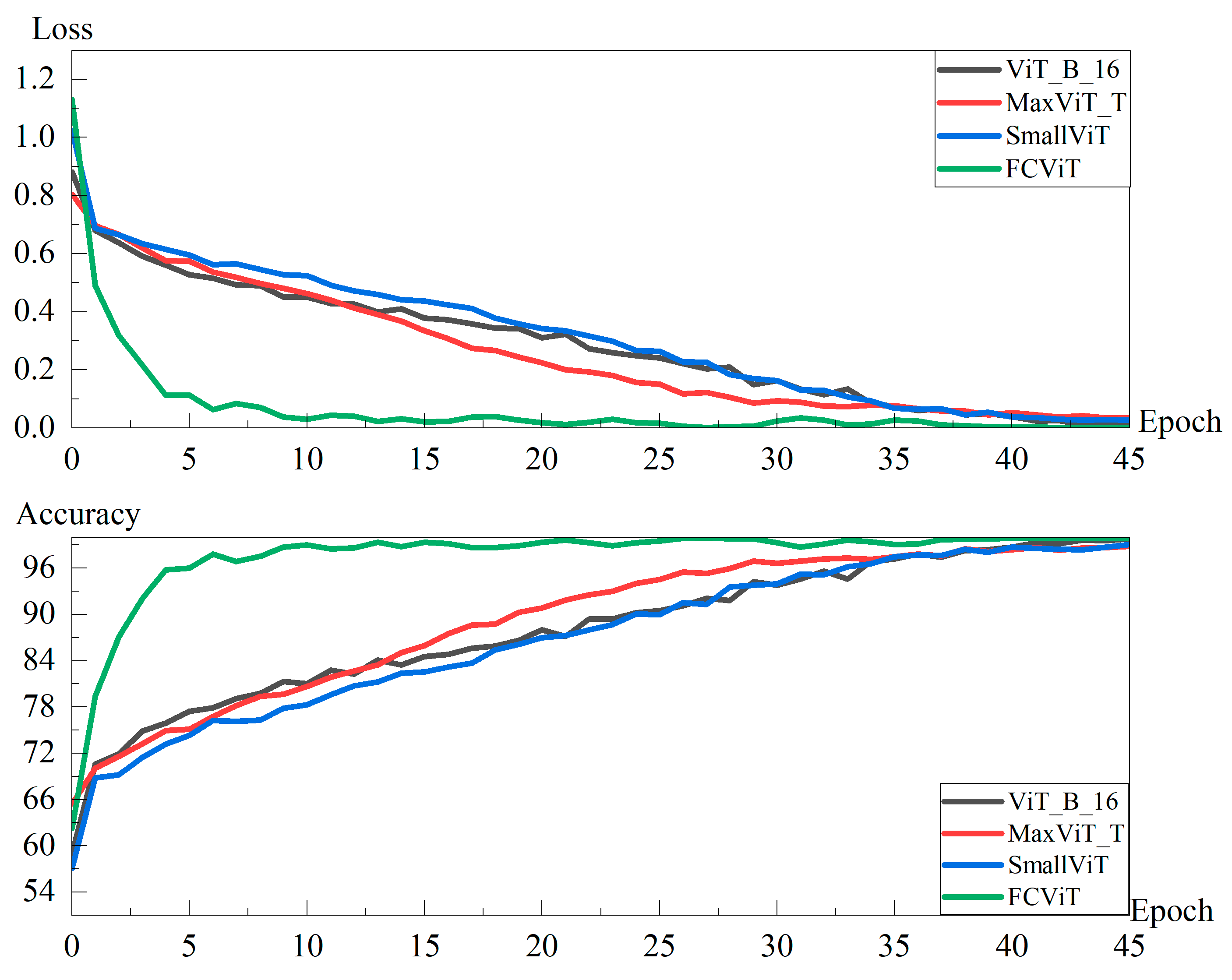
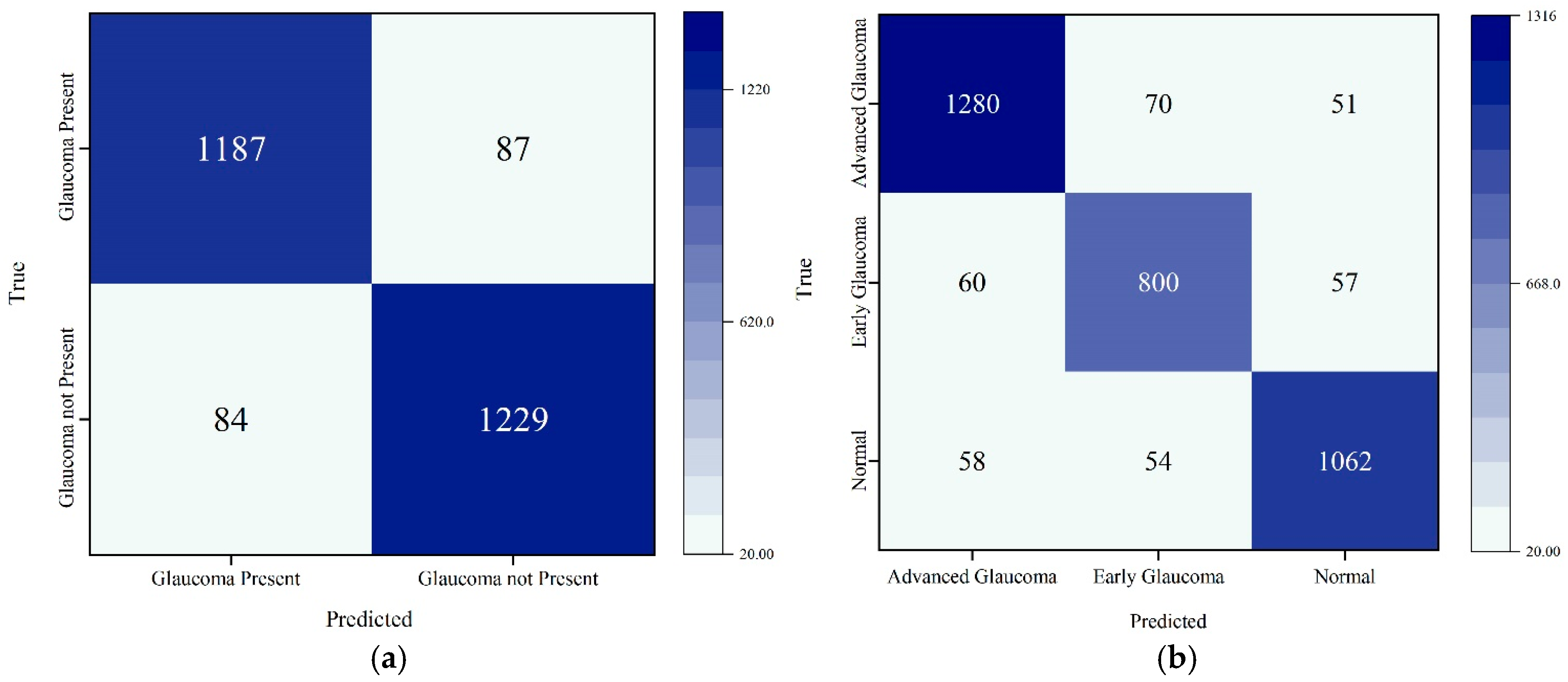
3.4. Experimental Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ViT | Vision Transformer |
| CLS token | Classification Token |
| MLP | Multilayer Perceptron |
| GELU | Gaussian Error Linear Unit |
| FCViT | Fourier Convolution Vision Transformer |
| FFT | Fast Fourier Transform |
| FrFT | Fractional-Order Fourier Transform |
| HDV1 | Harvard Dataverse-V1 |
| C-Conv | Custom Convolutional |
| FFN | Feed-Forward Network |
References
- van Le, C. Unveiling Global Discourse Structures: Theoretical Analysis and NLP Applications in Argument Mining. arXiv 2025, arXiv:2502.08371. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comp. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training. Available online: https://gwern.net/doc/www/s3-us-west-2.amazonaws.com/d73fdc5ffa8627bce44dcda2fc012da638ffb158.pdf (accessed on 28 March 2025).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Yang, J.; Li, C.; Zhang, P.; Dai, X.; Xiao, B.; Yuan, L.; Gao, J. Focal self-attention for local-global interactions in vision transformers. arXiv 2021, arXiv:2107.00641. [Google Scholar]
- Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.R.; Xu, D. Swin unetr: Swin transformers for semantic segmentation of brain tumors in MRI images. In International MICCAI Brainlesion Workshop; Springer: Cham, Switzerland, 2021; pp. 272–284. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 213–229. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T.Y. Do transformers really perform badly for graph representation? Adv. Neural Inf. Process. Syst. 2021, 34, 28877–28888. [Google Scholar]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 7262–7272. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. BEiT: BERT Pre-Training of Image Transformers. arXiv 2022, arXiv:2106.08254. [Google Scholar] [CrossRef]
- Fein-Ashley, J.; Feng, E.; Pham, M. HVT: A Comprehensive Vision Framework for Learning in Non-Euclidean Space. arXiv 2024, arXiv:2409.16897. [Google Scholar] [CrossRef]
- Alotaibi, A.; Alafif, T.; Alkhilaiwi, F.; Alatawi, Y.; Althobaiti, H.; Alrefaei, A.; Hawsawi, Y.; Nguyen, T. ViT-DeiT: An ensemble model for breast cancer histopathological images classification. In Proceedings of the 1st International Conference on Advanced Innovations in Smart Cities (ICAISC), Jeddah, Saudi Arabia, 23–25 January 2023; pp. 1–6. [Google Scholar]
- Krishnan, K.S.; Krishnan, K.S. Vision Transformer Based COVID-19 Detection Using Chest X-Rays. IEEE Conference Publication. In Proceedings of the 2021 6th International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 7–9 October 2021; Available online: https://ieeexplore.ieee.org/document/9609375.
- Wang, L.L.; Lo, K.; Chandrasekhar, Y.; Reas, R.; Yang, J.; Burdick, D.; Eide, D.; Funk, K.; Katsis, Y.; Kinney, R.; et al. CORD-19: The COVID-19 Open Research Dataset. arXiv 2024, arXiv:2004.10706. [Google Scholar] [CrossRef]
- Wu, X.; Tao, R.; Hong, D.; Wang, Y. The FrFT convolutional face: Toward robust face recognition using the fractional Fourier transform and convolutional neural networks. Sci. China Inf. Sci. 2020, 63, 119103_1–119103_3. [Google Scholar] [CrossRef]
- Barshan, B.; Ayrulu, B. Fractional Fourier transform pre-processing for neural networks and its application to object recognition. Neural Netw. 2002, 15, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Kiefer, R.; Abid, M.; Steen, J.; Ardali, M.R.; Amjadian, E. A Catalog of Public Glaucoma Datasets for Machine Learning Applications: A detailed description and analysis of public glaucoma datasets available to machine learning engineers tackling glaucoma-related problems using retinal fundus images and OCT images. In Proceedings of the 7th International Conference on Information System and Data Mining (ICISDM), Atlanta, GA, USA, 10–12 May 2023; pp. 24–31. [Google Scholar] [CrossRef]
- Acharya, U.R.; Ng, E.Y.K.; Eugene, L.W.J.; Noronha, K.P.; Min, L.C.; Nayak, K.P.; Bhandary, S.V. Decision support system for the glaucoma using Gabor transformation. Biomed. Signal Process. Control 2015, 15, 18–26. [Google Scholar] [CrossRef]

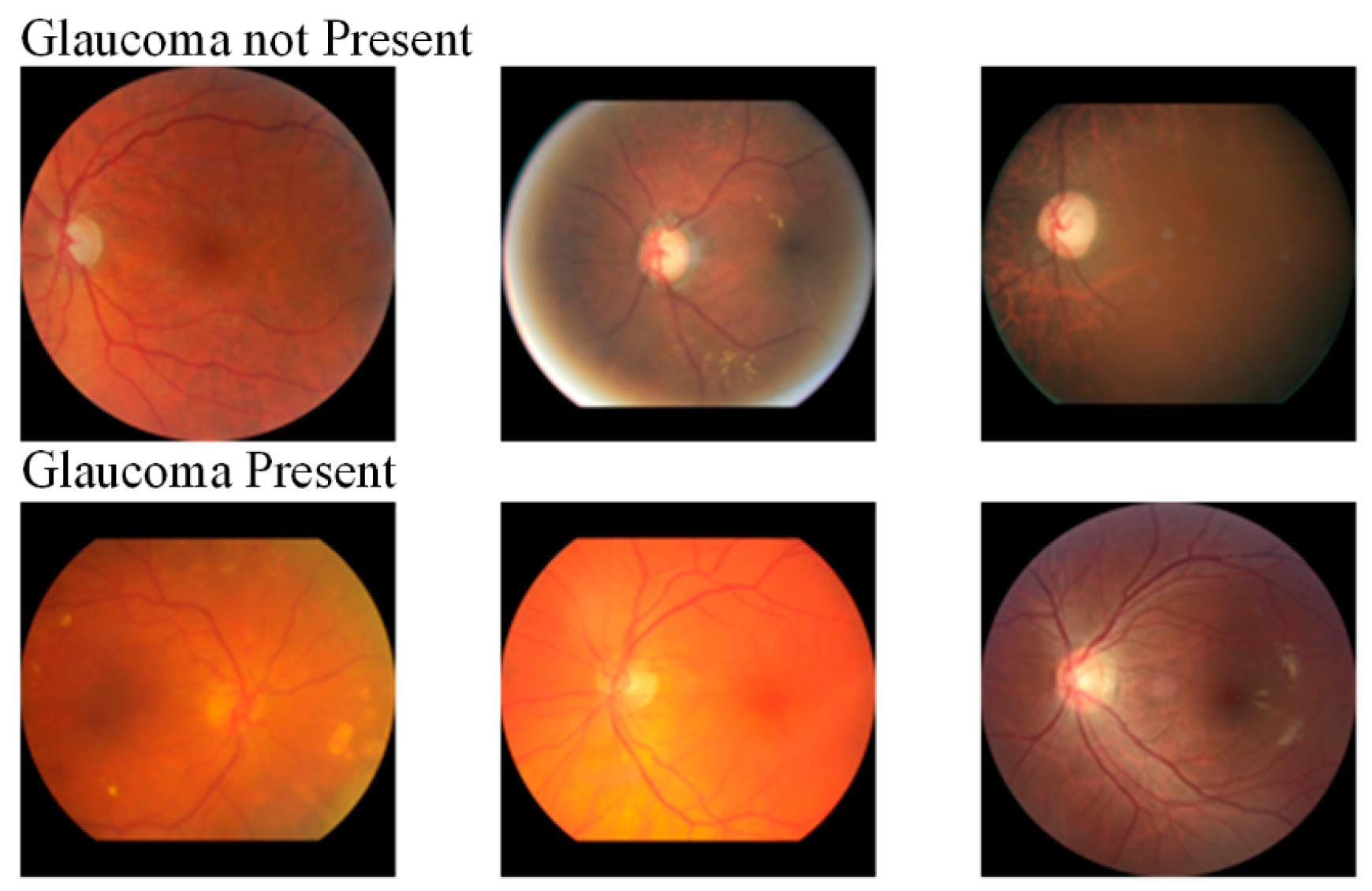
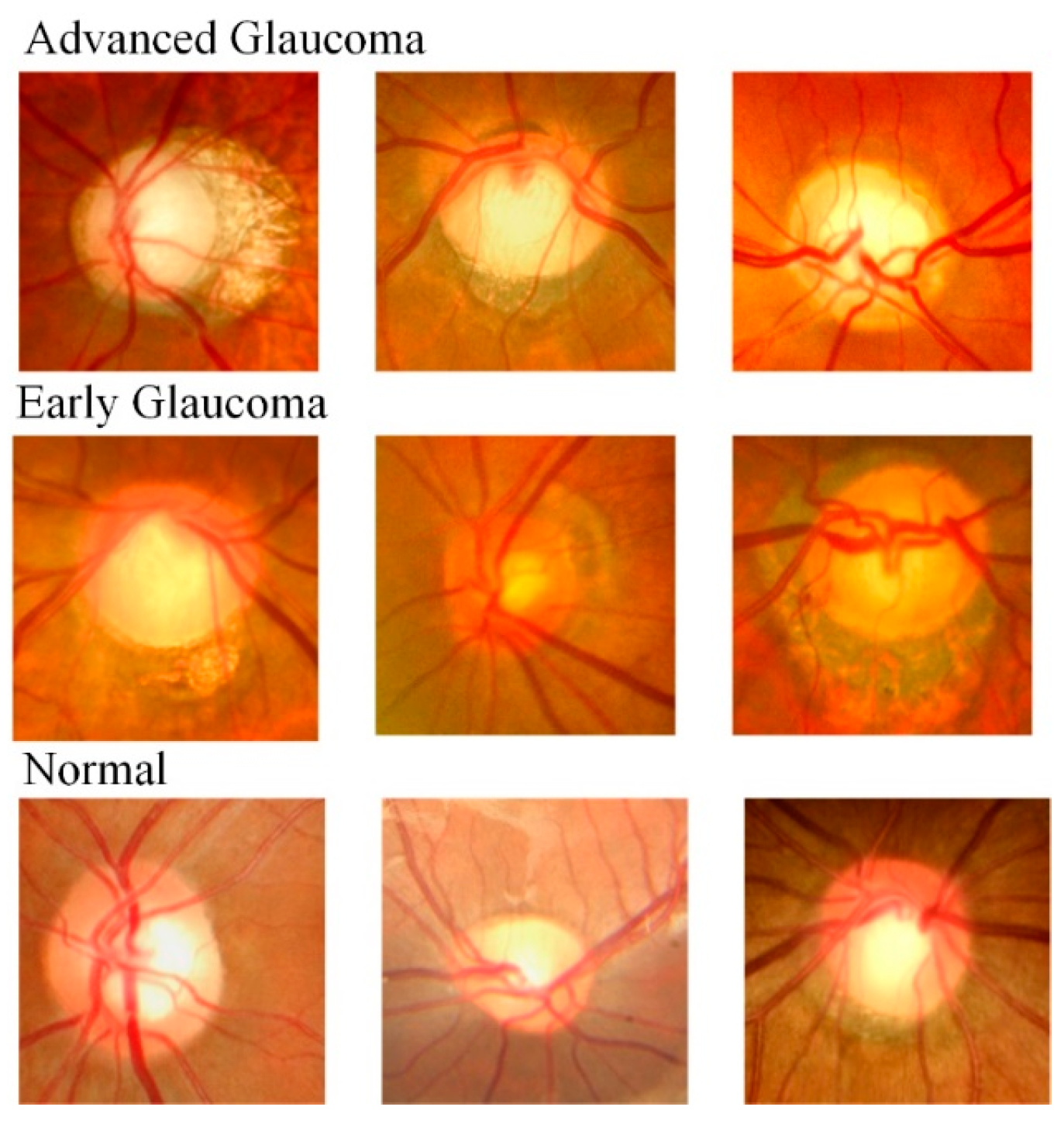


| Dataset | Class Name | Total | Category |
|---|---|---|---|
| Standardized fundus blue light | Glaucoma Present | 5293 | 2 |
| Glaucoma Not Present | 3328 | ||
| HDV1 | Advanced Glaucoma | 4670 | 3 |
| Early Glaucoma | 2890 | ||
| Normal | 3940 |
| Model | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Loss |
|---|---|---|---|---|---|
| MobileV2 | 84.73 | 83.56 | 82.91 | 83.20 | 0.513 |
| MobileV3_Small | 85.25 | 84.01 | 84.58 | 83.71 | 0.525 |
| MobileV3_Large | 84.37 | 83.91 | 83.80 | 83.83 | 0.520 |
| EfficientNet_B0 | 84.81 | 84.80 | 84.68 | 83.09 | 0.506 |
| EfficientNet_B1 | 87.08 | 85.98 | 85.60 | 85.97 | 0.391 |
| ResNet18 | 88.02 | 87.41 | 84.51 | 85.03 | 0.429 |
| ResNet34 | 87.17 | 88.36 | 87.59 | 87.31 | 0.512 |
| ResNet50 | 88.44 | 88.25 | 87.36 | 87.04 | 0.447 |
| ShuffleNetV2 | 85.16 | 84.23 | 83.26 | 82.52 | 0.468 |
| SqueezeNet | 87.69 | 85.49 | 85.71 | 85.02 | 0.396 |
| VGG11 | 85.40 | 86.40 | 86.16 | 86.28 | 0.451 |
| VGG13 | 86.90 | 87.36 | 86.14 | 86.63 | 0.445 |
| ViT_B_16 | 87.31 | 86.59 | 86.52 | 86.29 | 0.461 |
| MaxViT_T | 86.12 | 88.97 | 85.19 | 84.58 | 0.430 |
| SmallViT | 85.74 | 84.80 | 83.62 | 83.21 | 0.539 |
| FCViT | 93.52 | 93.32 | 92.79 | 93.04 | 0.249 |
| Model | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Loss |
|---|---|---|---|---|---|
| MobileV2 | 77.44 | 75.80 | 75.43 | 75.56 | 0.580 |
| MobileV3_Small | 78.78 | 77.30 | 76.98 | 77.11 | 1.208 |
| MobileV3_Large | 77.73 | 76.95 | 76.35 | 76.43 | 1.079 |
| EfficientNet_B0 | 78.08 | 76.98 | 76.30 | 76.47 | 0.597 |
| EfficientNet_B1 | 77.39 | 75.78 | 74.31 | 74.74 | 0.539 |
| ResNet18 | 84.72 | 84.18 | 83.01 | 83.38 | 0.544 |
| ResNet34 | 85.42 | 84.84 | 83.29 | 83.82 | 0.740 |
| ResNet50 | 84.66 | 83.90 | 83.43 | 83.56 | 0.724 |
| ConvNeXt | 80.95 | 80.66 | 79.03 | 79.35 | 0.479 |
| ShuffleNetV2 | 77.71 | 76.15 | 75.09 | 75.43 | 0.508 |
| SqueezeNet | 78.57 | 77.131 | 76.15 | 76.38 | 0.509 |
| VGG11 | 85.21 | 84.94 | 83.48 | 83.96 | 0.476 |
| VGG13 | 85.15 | 84.24 | 83.69 | 83.85 | 0.476 |
| VGG16 | 84.34 | 83.14 | 82.71 | 82.89 | 0.514 |
| ViT_B_16 | 91.04 | 90.26 | 90.26 | 90.24 | 0.380 |
| MaxViT_T | 90.66 | 89.69 | 89.80 | 89.70 | 0.317 |
| SmallViT | 85.18 | 84.24 | 83.59 | 83.73 | 0.634 |
| FCViT | 94.21 | 93.73 | 93.67 | 93.68 | 0.237 |
| MaxViT_T | SmallViT | ViT_B_16 | FCViT | |
|---|---|---|---|---|
| Epoch Time | 112.083 | 163.473 | 177.986 | 197.484 |
| Parameter (M) | 30.391 | 85.612 | 57.300 | 117.508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Zhou, W.; Yang, J.; Shao, Y.; Zhang, L.; Mao, Z. A Multi-Dimensional Feature Extraction Model Fusing Fractional-Order Fourier Transform and Convolutional Information. Fractal Fract. 2025, 9, 533. https://doi.org/10.3390/fractalfract9080533
Sun H, Zhou W, Yang J, Shao Y, Zhang L, Mao Z. A Multi-Dimensional Feature Extraction Model Fusing Fractional-Order Fourier Transform and Convolutional Information. Fractal and Fractional. 2025; 9(8):533. https://doi.org/10.3390/fractalfract9080533
Chicago/Turabian StyleSun, Haijing, Wen Zhou, Jiapeng Yang, Yichuan Shao, Le Zhang, and Zhiqiang Mao. 2025. "A Multi-Dimensional Feature Extraction Model Fusing Fractional-Order Fourier Transform and Convolutional Information" Fractal and Fractional 9, no. 8: 533. https://doi.org/10.3390/fractalfract9080533
APA StyleSun, H., Zhou, W., Yang, J., Shao, Y., Zhang, L., & Mao, Z. (2025). A Multi-Dimensional Feature Extraction Model Fusing Fractional-Order Fourier Transform and Convolutional Information. Fractal and Fractional, 9(8), 533. https://doi.org/10.3390/fractalfract9080533





