Fractal Evolution Characteristics of Weakly Cemented Overlying Rock Fractures in Extra-Thick Coal Seams Mining in Western Mining Areas

Abstract

Coal mining disturbance induces progressive damage and fracturing in overlying rock (OLR), forming a complex fracture network. This process triggers groundwater depletion, ecological degradation, and severely compromises mine safety. Based on field drilling sampling and mechanical experiments, this paper reveals the occurrence properties and characteristics of weakly cemented overlying rock (WCOLR). At the same time, similar simulation experiments, DIC speckle analysis system, and fractal theory are used to explain the development and evolution mechanism of mining-induced fractures under this special geological condition. The OLR fracture is determined based on the grid fractal dimension (D) distribution. A stress arch-bed separation (BS) co-evolution model is established based on dynamic cyclic BS development and stress arch characteristics, enabling identification of BS horizons. The results show that the overlying weak and extremely weak rock accounts for more than 90%. During the process of longwall face (LF) advancing, the D undergoes oscillatory evolution through five distinct stages: rapid initial growth, constrained slow growth under thick, soft strata (TSS), dimension reduction induced by fracturing and compaction of TSS, secondary growth from newly generated fractures, and stabilization upon reaching full extraction. Grid-based D analysis further categorizes fracture zones, indicating a water conducting fracture zone (WCFZ) height of 160~180 m. Mining-induced fractures predominantly concentrate at dip angles of 0–10°, 40–50°, and 170–180°. Horizontally BS fractures account for 70.2% of the total fracture population, vertically penetrating fractures constitute 13.1% and transitional fractures make up the remaining 16.7%. The stress arch height is 314.4 m, and the stable BS horizon is 260 m away from the coal seam. Finally, an elastic foundation theory-based model was used to predict BS development under top-coal caving operations. This research provides scientific foundations for damage-reduced mining in ecologically vulnerable Western China coalfields.

1. Introduction

Coal mining disturbance induces OLR damage, surface subsidence, and ground fissures in mining areas. Effective control of mining-induced damage in ecologically fragile regions constitutes a core research focus of green mining [1,2,3,4]. With the shift of the center of gravity of coal in China to the west, the mining height and intensity of coal seams are gradually increasing, and the engineering geological conditions are becoming increasingly complicated. Xinjiang mining areas feature extensively distributed coal seam thickness typically exceeding 20 m, where WCOLR predominates due to specific stratigraphic deposition. This WCOLR exhibits low strength, water-induced slaking susceptibility, and poor cementation. Mining-induced fracture evolution and ground pressure characteristics in these strata differ significantly from eastern China coalfields [5]. Consequently, investigating OLR failure mechanisms and fracture evolution under high-intensity mining in western WCOLR has emerged as a critical research priority.

Under the disturbance of coal seam mining, the breakage strata cannot bear the load of OLR, but deflect to the unexcavated coal bodies on both sides to form a stress arch structure, thus maintaining the overall stability of OLR [6,7,8]. According to the difference between the OLR combination and the medium characteristics of rock and soil, the arch shell can be divided into a loose layer arch and a bedrock arch [6,9]. Wang et al. [2,10] established mechanical models of unconsolidated arch structures through physical simulations, proposing WCFZ prediction methods based on their load-bearing characteristics. At the same time, due to the difference in geological conditions between the eastern and western mining areas, many scholars have conducted a lot of research on the evolution characteristics of OLR fractures in western mining areas based on theoretical analysis, physically similar simulation, numerical simulation, and field measurement. Wang et al. [11] revealed the characteristics of overburden surface damage under the action of multiple control layers. Zhang et al. [12] developed spatial structural models revealing periodic weighting mechanisms through numerical simulations. Li et al. [13] demonstrated key strata control on subsidence patterns using XT-DIC monitored simulations. Dong et al. [14] proposed trapezoidal fracture models for WCOLR validated through microseismic monitoring.

At the same time, with the development of China’s coal mining technology, the Xinjiang mining area has become an important coal base in China. The Jurassic coal-bearing strata in the mining area have the characteristics of late diagenesis, low physical and mechanical strength, easy mud disintegration when meeting water, and obvious weak cementation characteristics [5,15]. Under these conditions, Zhang et al. [16] found weak strata inhibit WCFZ propagation, exhibiting “macro-large-small” failure structures. Guo et al. [17] discussed the crushing and swelling characteristics of WCOLR through theoretical analysis, and combined with similar simulation and numerical simulation, analyzed the characteristics of repeated mining OLR and surface subsidence. Xu et al. [15,18] established the quantitative relationship between the bearing strength of the masonry beam and the height of the caving zone according to the change in the caving zone height. Li et al. [19] used the UDEC numerical simulation method and thought that the overall shape of the WCFZ in the extra-thick WCOLR presents triangular characteristics. Based on the thick plate theory, a prediction model of the development height of WCFZ in extra-thick WCOLR was established.

Different sedimentary environments and geological evolution lead to the alternate occurrence of soft and hard strata in OLR, which will inevitably form a dynamic BS in the process of mining damage transmission. BS within caving/fracture zones constitutes dry BS, whereas bending zone BS poses flooding risks. Water-bearing BS represents key targets for grouting-based control [20,21]. BS types are classified as elastically supported or unsupported based on stress states [21]. He et al. [3] proposed a theoretical method to identify the dynamic position and pore diameter of BS based on the improved key strata theory. Zhai et al. [22] and Jiang et al. [23], based on similar simulation tests and theoretical analysis, quantitatively characterized the evolution process of BS under the influence of extra-thick conglomerate strata and predicted the space capacity of grouting BS based on elastic foundation beam theory. Yao et al. [24] analyzed BS spatial evolution using UDEC numerical simulation and MatchID-2D strain measurement, which suggests that the evolution process of BS is mainly influenced by the bending and sinking forms of key strata. Dai et al. [25] established optimal grouting timing through fractal dimension analysis. Where thick competent strata are absent, significant BS development is constrained. Ma et al. [26,27] studied the effect of multi-BS grouting to control surface subsidence based on a similar model and numerical simulation, revealing the formation process of BS. Guo et al. [28,29] proposed multi-level grouting schemes based on elastic foundation beam analyses of protective layer stability.

In summary, current research predominantly addresses OLR movement patterns in coal mines with competent roof strata, while investigations into mining-induced fracture evolution within WCOLR, lacking distinct thick hard strata, remain limited. Based on this, this paper examines the 1101 LF at Xinjiang’s Zhundong Second Mine through integrated theoretical analysis and physical simulations. Employing fractal theory, we reveal fracture evolution laws and damage transmission characteristics under these geological conditions, elucidating BS development mechanisms. Furthermore, a stress arch-BS co-evolution model is established based on dynamic cyclic BS processes and stress arch characteristics, enabling quantification of stable BS horizons. Finally, elastic foundation beam theory derives stable BS volumes under top-coal caving operations, providing scientific foundations for mining damage mitigation in WCOLR of Western China coalfields.

2. Engineering Background

2.1. General Situation of Zhundong Mining Area

Zhundong Coalfield is located in the east of the Junggar Basin (as shown in Figure 1), accounting for 17.8% of Xinjiang’s coal reserves and 7% of the national coal reserves. The maximum thickness of a single-layer coal seam can reach 80 m, and the average thickness of a minable coal seam is 43 m. It is an important development area of Xinjiang’s energy industry. Within this coalfield, the Dajing mining area extends along the southern piedmont of the Cramaili Mountains, bounded westward by the Zhangpenggou anticlinal axis and eastward by the Jiangjunmiao anticline. This NNW-SSE trending basin spans 85 km longitudinally and 10–28 km latitudinally, encompassing 1340.86 km². The general terrain of the mining area is a gently inclined slope with a high point in the north and a low point in the south, and most areas are relatively flat. The coal-bearing strata in the mining area are the Jurassic Xishanyao Formation, and the main recoverable coal seam is B1. The total thickness of the recoverable coal seam is 1.12~79.84 m, with an average of 41.40 m. The strike of strata in the main part is nearly east–west, and the dip angle is nearly horizontal.

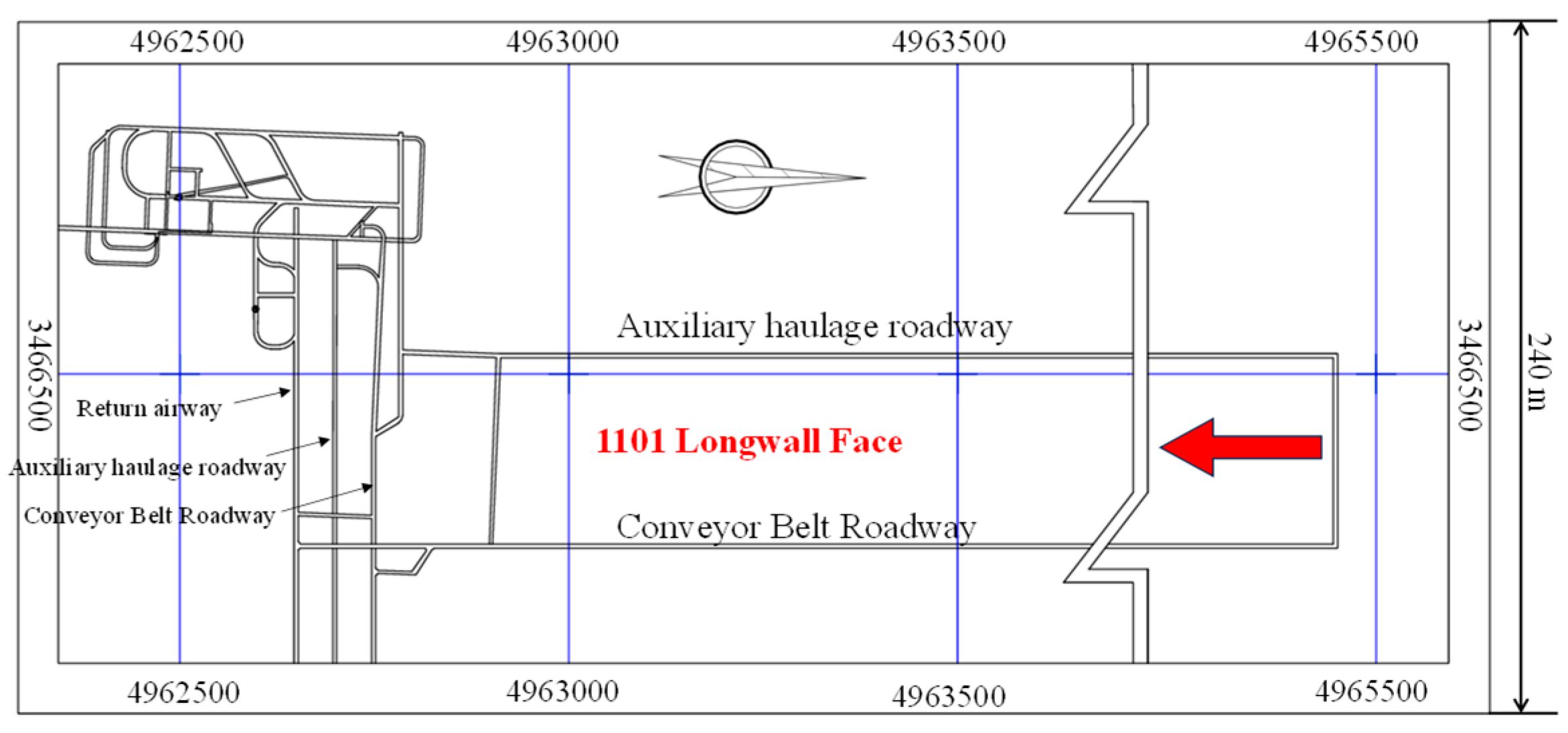
2.2. General Situation of 1101 LF

The 1101 LF is the first mining face in panel 11, with a width of 240 m, a strike length of 2570 m, and a coal seam thickness of 54 m. The layered fully mechanized top-coal caving mining method is adopted, which is divided into upper, middle, and lower layers, each layer is 18 m. The first mining layer is the upper layer, with a normal mining height of 4.5 m and a caving height of 13.5 m. The cutting–caving ratio is 1:3. The roof is managed by the full caving method, and the layout diagram of the LF is shown in Figure 2. The 1101 LF is buried at a depth of 518~544 m, and the roof is mainly composed of WCOLR, such as fine sandstone, siltstone, and mudstone.

2.3. Characteristics of Weakly Cemented Overlying Rock in the Mine Field

China’s western coalfields predominantly feature coal resources within Cretaceous and Jurassic strata, characterized by distinct diagenetic environments, geological ages, and sedimentary histories. Coal seams in these regions exhibit roof and floor strata composed of mudstone, shale, and alternating mudstone–sandstone sequences. These formations are collectively termed WCOLR [5]. The coal-bearing strata in the Zhundong mining field are Lower Jurassic Badaowan Formation (J₁b), Middle Jurassic Xishanyao Formation (J₂x), and Middle and Upper Jurassic Shishugou Formation (J_2–3sh), among which the main coal-bearing strata are Middle Jurassic Xishanyao Formation (J₂x). To characterize lithology and thickness distribution of OR at Zhundong No. 2 Mine, full-depth drilling (0–544 m) sampled roof strata above the 1101 LF (Figure 3). Drill logs were compiled following lithological consolidation principles (Figure 4), enabling comprehensive analysis of WCOLR failure mechanisms in Xinjiang mining conditions.

In the mine water prevention and control regulations, according to the engineering practice and the uniaxial compressive strength of rock, the OLR of coal seam roof is divided into four types: hard, medium–hard, weak, and extremely weak [30]. To illustrate the occurrence characteristics of OLR in 1101 LF, the physical and mechanical strength of rock samples with different burial depths was measured, and the specific results are shown in Figure 5. According to the physical and mechanical test data of rock samples, the general compressive strength, tensile strength, and elastic modulus of rock strata are less than 20 MPa, 2 MPa, and 5 GPa, respectively. Among them, weak and extremely weak strata account for more than 90%, and only two groups of samples show the characteristics of medium–hard strata. According to the borehole histogram, their thicknesses are only 5.2 m and 8.32 m, which are 84.6 m and 16.38 m away from the coal seam, respectively. In addition, there were many TSS with a thickness of 29.9~57.63 m, and the main lithology is siltstone and silty mudstone. To sum up, the mechanical parameters of the mine strata were lower than those of similar strata in the central and eastern mining areas. These strata macroscopically have loose, scattered, and weak characteristics such as low strength, poor cohesiveness, easy weathering, small faults, and undeveloped joint bedding [5,15], which were the typical WCOLR.

3. Similar Simulation Research of Mining Fractures Evolution of Weakly Cemented Overlying Rock

3.1. Similar Simulation Scheme

To reveal the development law of mining fractures and the spatial evolution characteristics of BS in the fully mechanized top-coal caving mining process of extra-thick coal seam, this paper takes the 1101 LF as the engineering background and uses a large-scale plane similarity simulation test system to carry out simulation research. According to the similarity theory [7,31,32], the geometric similarity ratio is 1:400, the bulk weight similarity ratio is 5:8, the stress similarity ratio is 3:1000, and the time similarity ratio is 1:32. The size of the similar material experimental model is 3000 mm × 300 mm × 1440 mm, as shown in Figure 6a. Pure fine river sand with a diameter of less than 3 mm is selected as the aggregate, gypsum powder, and industrial light calcium carbonate as the cementing materials, and the mechanical properties of different rock strata were simulated by changing the content of the cementing materials. Spreading mica powder between strata reflects the layer effect between adjacent strata and prevents the OLR from collapsing as a whole during the advancing process of the LF. After the model is naturally dried, take out the mold, brush white latex paint on its surface, and draw spots evenly with black pigment. The bottom and left, and right sides of the model were rigidly fixed. According to the time similarity ratio, an excavation shall be conducted at intervals of 15 min. According to the actual advancing speed (5 m/d), the unit mining distance is 1.25 cm. In order to reduce the impact of boundary effects on model excavation, 375 mm coal pillars were left on both sides of the model. In the process of model advancement, a fixed-height camera is used to continuously photograph the position of the speckle pattern. The XTDIC (version 9.0.0) non-contact strain analysis software is used to visually monitor the strain and deformation characteristics of rock strata, as shown in Figure 6b. It should be noted that the hydro-mechanical properties of weakly cemented rock strata exhibit significant deterioration upon water exposure; hydrogeochemical processes are inevitably bound to drive alterations in fracture propagation within overlying rock sequences. However, due to the limitations of similar simulation devices, it is difficult to simulate water seepage in aquifers.

3.2. Evolution Characteristics of Mining Fractures in WCOLR

In this paper, the Adobe Photoshop 2020 software is used to sketch the photos of the OLR fracture network with different advancing distances, and ImageJ (version 1.51) software is imported for graying, binarization, and noise reduction. Black and white were used to represent fractures and rock strata, respectively. Finally, the fractal dimension (D) is calculated by Fractal Box Count in ImageJ to reflect the randomness and complexity of OLR fracture expansion under mining disturbance [25,32].

The strain and D processing results during the evolution of OLR fractures are shown in Figure 7. In the early stage of mining on the LF, due to the relatively soft overall rock layer, the rock layer undergoes micro-strain under its own weight, and fractures begin to develop synchronously. When the fracture develops below the TSS-1, due to its large thickness and relatively strong deformation resistance, only part of it is broken, and the D is 1.41, as shown in Figure 7b. Due to the creep characteristics of the TSS-1, a “trapezoid-like” BS is formed in its gradual failure process. When the TSS-1 is completely broken, the lower BS is compacted, and the longitudinal fracture develops further upward, and the D develops to 1.5, which increases by 6.38%. The BS conducts upward synchronously, showing an inverted triangle shape, with a maximum height of about 6.4 m, as shown in Figure 7d.

As the LF continues to advance, the mining damage continues to increase upward, the OLR collapses and compacts the lower block, resulting in an “ I-shaped ” new BS at a height of 140 m from the coal seam, with a height is 7.2 m. At this time, the fractal dimension is reduced to 1.35, a decrease of 4.26%. With the gradual upward fracture of OLR, the “I-shaped” BS tends to be closed. The D is 1.37, with an increase of 1.48%. Synchronously, a new BS with a height of 5.1 m is generated at a distance of 170 m from the coal seam, as shown in Figure 7e,f.

As shown in Figure 7g,h, due to the continuous accumulation and conduction of mining damage, the upper strata were continuously broken, and the D increases to 1.43. Due to the further compaction of the caving block below, the maximum BS height gradually expanded to 6 m. At the same time, a “crescent-shaped” BS appeared under the TSS-2. With the increase in the exposed distance of TSS-2, the lower BS is gradually closed, and the “crescent-shaped” BS continues to expand, gradually forming an “inverted trapezoid-like” shape space with curved boundary, with the maximum height of about 4.8 m. The upper part of TSS-2 is bent and deformed synchronously with the surface, and the interlayer micro-strain phenomenon occurs. At this time, the overall fracture network of OLR remains stable, and the D is stable at 1.43.

The distribution of the OLR fracture network represents the occupancy characteristics of regenerated fractures in two-dimensional space, which continuously changes with the increase in the advancing distance of the LF [33]. The evolution process of the fractal dimension of mining fractures in the OLR is shown in Figure 8. As shown in the figure, the fractal dimension of the fracture network in mining-disturbed rock masses exhibits an overall increasing trend with advancing distance. However, due to the influence of TSS, the fractal dimension undergoes fluctuations governed by the fracturing and subsequent compaction of these strata. Based on the evolution of the fractal dimension, the process can be categorized into five distinct stages: initial rapid growth, inhibited slow growth under TSS, dimension reduction induced by fracturing and compaction of TSS, secondary growth from newly generated fractures, and stabilization upon reaching full mining.

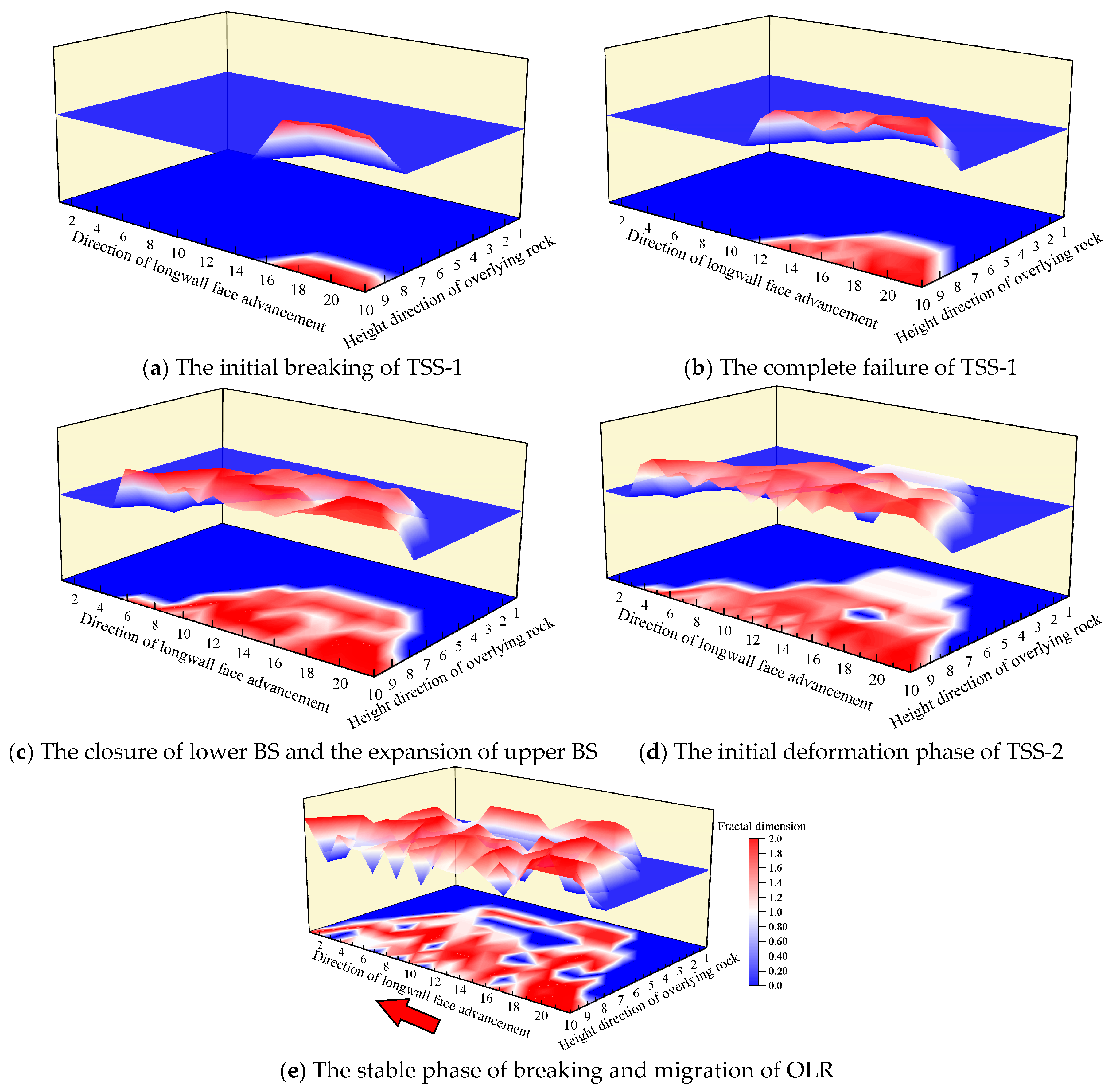
3.3. Distribution Characteristics of Fractal Dimension of WCOLR

After the OLR movement is stable, the fractured field is selected for grid division [31,32]. The field is divided into 22 grids in the horizontal direction and 10 grids in the vertical direction. The grid length and width are both 10 cm. The bottom of the grid is the coal floor, and the top of the grid is the bottom of the TSS-3, as shown in Figure 9. Using MATLAB (version: R2018b) software to quantitatively characterize the fractal dimension of each grid, in order to reveal the complexity of fracture morphology within the OLR mining damage field, as shown in Figure 10.

The spatial evolution law of the fractal dimension of the OLR fracture field is shown in Figure 10. During the LF advance, the spatiotemporal evolution of the OLR fracture field exhibits a characteristic sequence: fracture initiation; rapid development; near-field compaction, far-field propagation; and overall compaction. Under the influence of high-intensity mining disturbance, the extent of OLR damage progressively expands. Concurrently, horizontally BS fractures and vertically penetrating fractures interweave, forming a complex OLR fracture network. Compaction of fractures above the goaf, coupled with enhanced fracture development, propagation, and connectivity due to stress concentration at the LF boundaries, results in more pronounced fractal characteristics within these regions. Spatially, the OLR fracture network evolves driven by mining-induced damage propagation, extending upwards from the base and inwards from the periphery. Its expansion morphology transitions from an arch shape to a trapezoidal configuration, propagating deeper into the strata. The fractal dimension of the OLR fracture network fluctuates and evolves with the advance time, showing a self-fast and slow trend.

As can be seen from Figure 9 and Figure 10e, the fracture at the boundary of LF is fully developed and the penetration is relatively high, which is an active area for fracture expansion. In the advancing direction, the horizontal and vertical fractures run through within the grid-17~22 in the open-cut area, and the development complexity is the highest. In the grid-4~16, the fractures were closed due to the compaction of the overlying caving rock, and the complexity is relatively lower. Only one high-angle extended fracture is distributed with the grid-1~3 of the mining stoppage area on the LF. Therefore, the OLR fracture network can be divided into boundary fracture penetration area and middle compaction fracture transition area in the advancing direction. In the vertical direction, there are no fractures in grid-1, and the horizontal fractures were mainly distributed in grid-2~5. Within the range of grid-6, there is a staggered development of horizontal and vertical fractures, but mainly micro-fractures with relatively low complexity. It is believed to be a transitional zone between fracture zone and bedding subsidence zones. However, longitudinally penetrating fractures and horizontal closed fractures were mainly distributed in the area of grid-7~10. Therefore, the fracture zone can be identified according to the vertical fractal dimension distribution characteristics of OLR. Above all, the WCFZ height is 160–180 m.

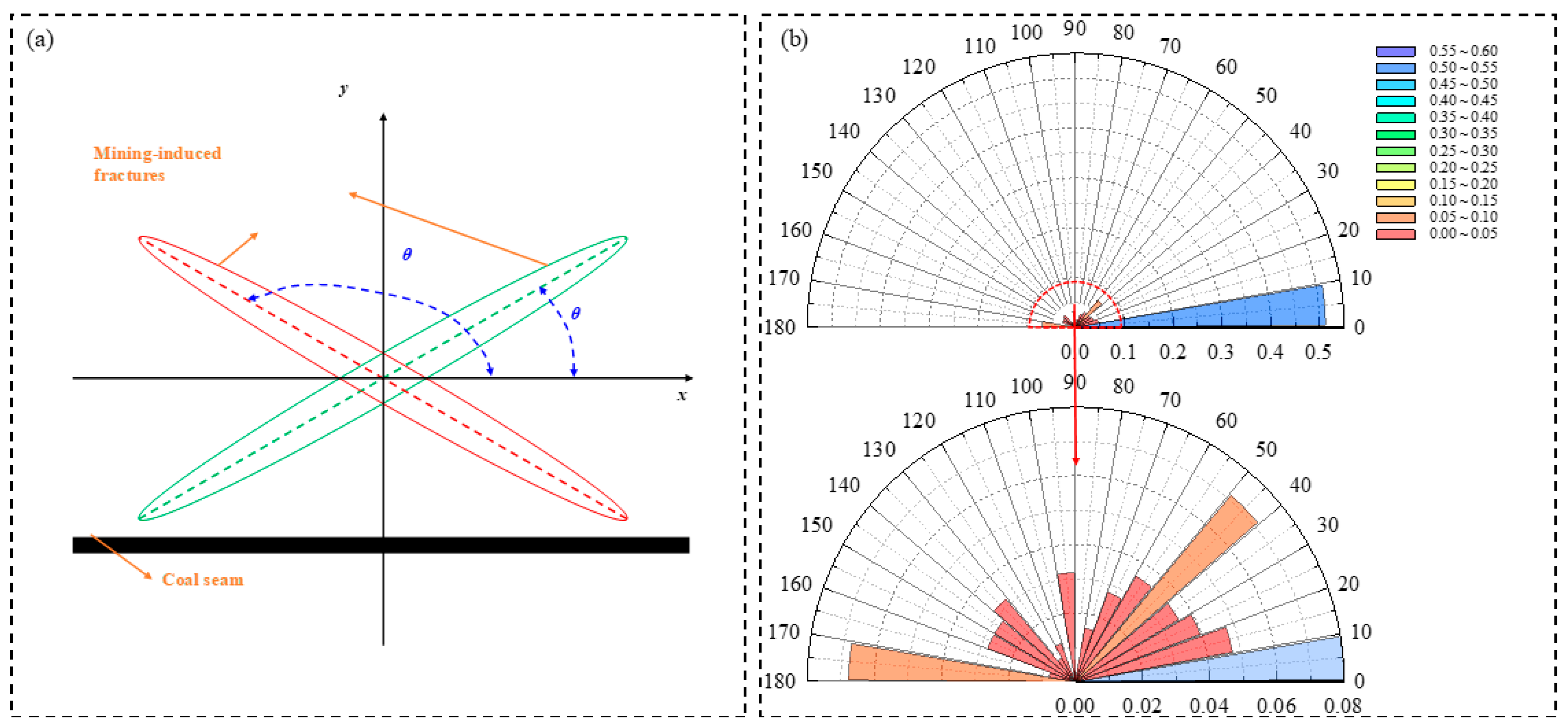
3.4. Distribution Characteristics of the Crack Angles

The development angle of OLR fractures can effectively reflect the evolution characteristics of water channels, which is an important quantitative indicator of the evolution of OLR fracture networks [31,34]. This study simplifies mining-induced fractures into an ideal ellipse, with the x-axis parallel to the grid lines, and the angle between the long axis and the origin of the coordinates considered as the development angle of fractures [31], as shown in Figure 11a. Due to the periodicity of mining induced fracture angles, the range of fracture angles is set to 0–180° [31]. Using MATLAB, automated identification and quantification of fracture dip angles and densities within the OLR (Figure 7h) were performed. The resulting fracture distribution is presented as a rose diagram in Figure 11b. Due to the presence of BS, fracture dip angles are predominantly concentrated within the ranges of 0–10°, 40–50°, and 170–180°. Based on dip angle, mining-induced fractures are classified as follows: fractures within 0–30° and 150–180° are defined as horizontally BS fractures; those within 50–130° are classified as vertically penetrating fractures; and fractures at other angles are categorized as transitional fractures. Horizontally BS fractures account for 70.2% of the total fracture population, vertically penetrating fractures constitute 13.1%, and transitional fractures make up 16.7%. This indicates that the OLR fracture network is primarily composed of horizontally bed-separation fractures (water storage spaces) and vertically penetrating fractures (water-conducting pathways). Owing to the constraining effect of weak rock strata on fracture development and the compaction characteristics of fractured OLR, vertically penetrating fractures exhibit limited development within the interior of the goaf.

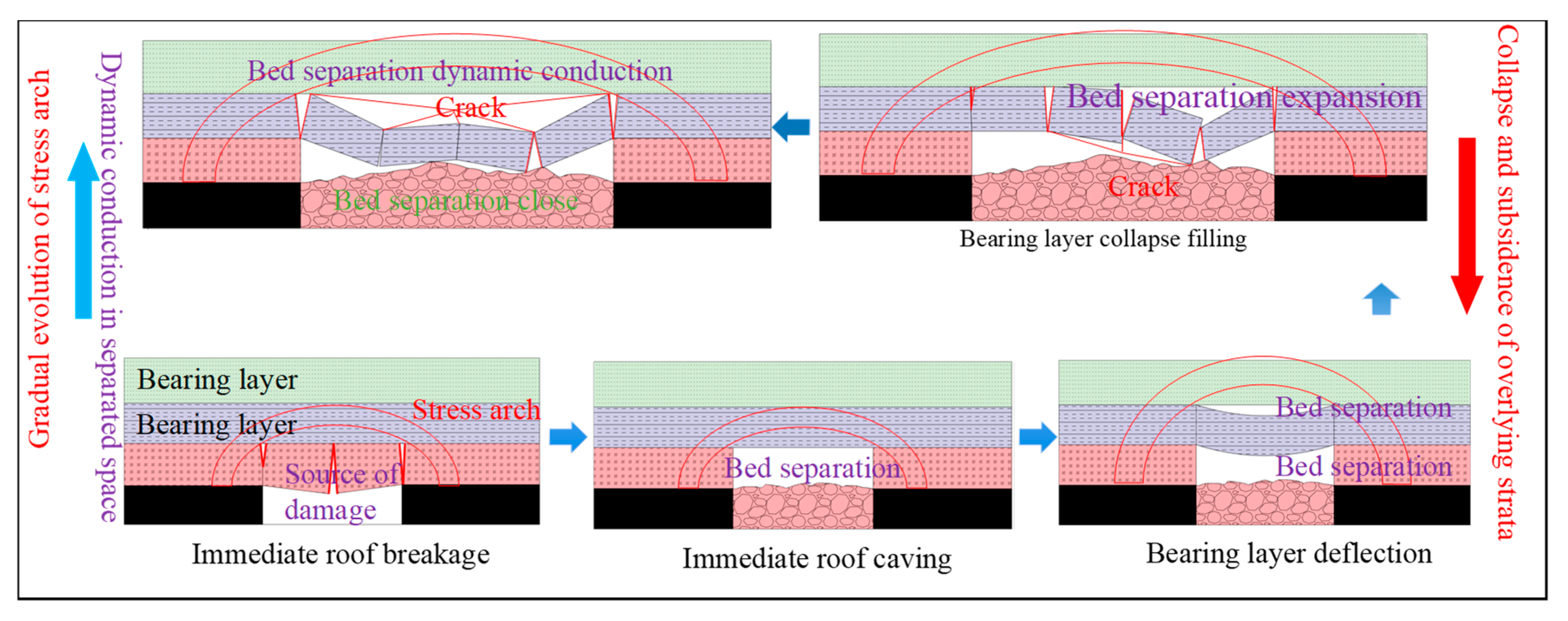
4. The Dynamic Evolution Mechanism of Bed Separation of Weakly Cemented Overlying Rock

4.1. The Co-Development Evolution Model of Stress Arch-BS

After the coal seam roof is disturbed by mining, when its hanging distance reaches the critical value, the rock layer breaks. The breakage rock layer cannot bear the load of the OLR, it deflects towards the unexcavated coal on both sides, forming a stress concentration zone, namely the stress arch structure [9]. Because the stress arch bears the load of OLR [2,6,7,9], the strata in the fractured arch were bent and deformed under the action of self-weight and compressive stress conducted by the fractured rock beam. Due to the difference in strata lithology and the small tensile and shear strength of the weak plane between layers, when the bending stiffness of adjacent lower strata is less than that of the upper strata, they will be grouped and settled, and the normal tension will occur on the weak plane between layers to form BS [3,20,21,23,28,29]. As the LF continues to advance, the upper strata gradually flex, and the BS gradually closes. When the upper strata reach the limit caving step, the strata break and compact the goaf, while the lower BS closes and a new higher BS is formed, and the stress arch upward develops synchronously. Due to the dissipation of mining damage, when the residual mining damage is not enough to cause the OLR to break, the OLR failure will stop. Due to the self-stabilizing ability of the stress arch, the high-level BS also stabilizes synchronously, thus forming a dynamic cycle of initial development, expansion, compression, closure, and high-level conduction of the BS, as shown in Figure 12.

4.2. The Evolution Characteristics of the Stress Arch of WCOLR

Mining disturbance in soft strata causes fracturing, forming discrete rock blocks. These blocks interact through mutual extrusion, leading to the formation of a stress arch structure [35,36]. In this study, a mechanical model of a symmetrical three-hinged arch along the strike is established, considering a unit width along the dip. The boundary conditions were replaced by trapezoidal loads, which provide a more realistic representation. The established mechanical model is shown in Figure 13a.

As shown in Figure 13, the arch is subject to a lateral load increasing uniformly with depth and a simplified vertical load. A lateral stress T acts at the top of the arch. The vertical reaction force at the arch foot is denoted F_H, the horizontal reaction force is F_L, the vault height is h₀, and the height from the coal seam to the surface is H.

Since the bending moment and shearing force are zero everywhere along the theoretical arch axis, the OLR stress is entirely transferred as compressive stress acting on the rock mass. This allows the rock mass to achieve its maximum bearing capacity. According to the characteristics of the reasonable arch axis, the bending moment of any point k should be 0. Therefore, considering an arbitrary point k at position (l_k, h_k), the bending moment at k is:

$${\displaystyle \sum M_k=0}$$

(1)

The moment equation can be expressed as:

$$F_H{l}_k-F_L{h}_k={\displaystyle {\int }_0^{h_k}{q}_l(h_k-h)}dh+{\displaystyle {\int }_0^{l_k}{q}_h(l_k-l)dl}$$

(2)

Among them:

$$q_l=\lambda \gamma g(H-h)$$

(3)

$$q_h=\gamma gH-{\displaystyle \frac{\gamma g{h}_0}{L}}l$$

(4)

The vertical reaction force F_H at the arch foot can be simplified as:

$$F_H=\gamma gLH$$

(5)

From the condition of force balance in the horizontal direction:

$$T={\displaystyle {\int }_0^{h_0}{q}_{l}dh+fL{q}_h}$$

(6)

From Equation (6), the horizontal reaction force at the arch foot can be obtained as follows:

$$F_L=fL\gamma g(H-h_0)$$

(7)

where f is the friction coefficient of coal and rock mass, and the assigned value is related to the hardness of coal and rock mass. Generally, the harder the rock mass is, the greater its value is.

By bringing Equations (3)–(5) and (7) into Equation (2), the implicit equation F (l_k, h_k) of the reasonable arch axis of the stress arch can be obtained after finishing:

$$F(l_k,h_k)=-{\displaystyle \frac{h_0{l_k}^3}{6L}}+{\displaystyle \frac{H}{2}}{l_k}^2-\lambda \left({\displaystyle \frac{1}{6}}{h_k}^3-{\displaystyle \frac{H}{2}}{h_k}^2\right)-LH{l}_k+fL(H-h_0)h_k=0$$

(8)

Bringing the vault parameters (l_k = L, h_k = h₀) into Equation (8), we can obtain the rise-to-span ratio equation F (L, h₀) of the pressure arch as follows:

$$-{\displaystyle \frac{H{L}^2}{2}}-{\displaystyle \frac{h_0{L}^2}{6}}+f{h}_0(H-h_0)L+\lambda \left({\displaystyle \frac{H{h}_0^2}{2}}-{\displaystyle \frac{h_0^3}{6}}\right)=0$$

(9)

where arch span $2L = 2M\mathit{tan}(45° - {\displaystyle \frac{{\phi }_0}{2}})+ D_c$, M is mining height, m. φ₀ is the internal friction angle of coal and rock mass. D_c is the advancing distance of the LF, m.

According to Equation (9), when the φ₀ = 22°, M = 18 m, H = 525 m, the $\lambda$ = 1.2, and the coal and rock mass friction coefficient f = 0.1, the calculated stress arch development height is h₀ = 121.3 m for a critical span D_c = 240 m. According to the similar simulation results, the stress arch development height h₀ =314.4 m after OLR migration stabilizes, as shown in Figure 14.

4.3. Dynamic Identification of BS of WCOLR

Rock mechanics laboratory testing revealed no distinct thick–hard rock strata within the OLR, precluding a complete application of the key strata theory for layer differentiation. According to Figure 4, there are multiple TSS with the thickness of 30~50 m in the OLR. These layers exhibit a significant bearing capacity relative to thinner strata. The key strata theory considers only the load difference between adjacent strata, neglecting the additional mechanical influence exerted by strata above the (n + 1)th strata [3,28,29]. Therefore, based on the modified key strata approach, this study conducts full-sequence mechanical analysis from the immediate roof to the stress arch to ensure accurate identification of BS [3,21,28,29]. Remove ineffective BS within the WCFZ, a stable BS horizon persists at 260.43 m above the coal seam in weakly cemented OLR under fully mechanized top-coal caving mining, which is consistent with physical simulation validation.

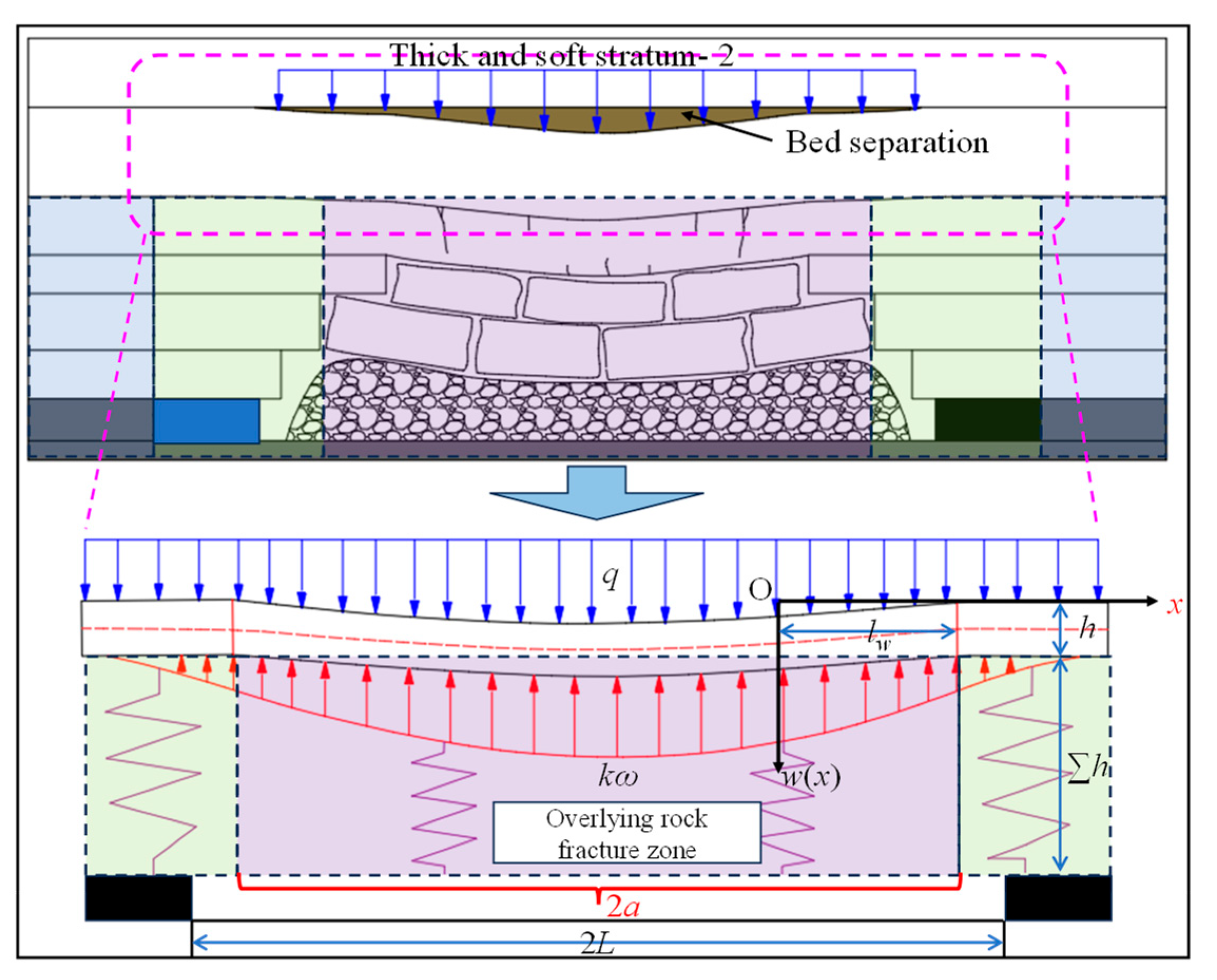
5. Theoretical Model of the Spatial Evolution of Grouting Bed Separation

Similar physical simulations and theoretical analysis confirm that TSS-2 undergoes synchronous bending deformation with surface subsidence. A stable BS persists beneath this stratum, establishing the underlying void space as the critical zone for grouting-based subsidence mitigation [25,26,37]. Theoretical prediction of this BS thus provides the foundation for mining damage control through BS grouting. According to the principle of space conservation [22], the maximum BS height can be calculated by the following formula:

$$S=M_d+\left(1-K_f+K_f\eta \right)\bullet M_f-{\displaystyle \sum _{p=1}^n{h}_i}\bullet (K_p-1)$$

(10)

where M_d is the top coal caving mining height, m. M_f is the height of coal discharge on the fully mechanized top coal face, m. K_f is the residual dilatancy coefficient of top coal. η is the top coal caving rate. Under the condition of top coal caving mining, considering the different recovery rates of cutting coal and caving coal, the total recovery rate is 85%. K_p is the residual dilatancy coefficient of the overlying p-th stratum of the coal seam. S is the maximum height of grouting-BS, m.

The protective layer undergoes bending deformation due to reactive support from the caved rock mass. In the middle of the goaf, due to compaction, it is in a straight state. Simultaneously, bending deformation occurs along the LF boundary and above coal pillars. However, fixed-beam structural models inadequately represent stope boundary deformation [38]. Therefore, this study predicts BS grouting capacity using Winkler elastic foundation beam theory [38]. The mechanical model is shown in Figure 15. In the figure, l_w is the bending length of the rock beam; 2a is the BS span; 2L is the advancing distance; k is the elastic foundation coefficient of the goaf; ${\displaystyle \sum h}$ is the total thickness of the foundation.

The governing deflection equation for the protective layer under self-weight loading is [23,38]:

$$EI{\displaystyle \frac{d^{4}w}{d{x}^4}}+kw=q (0\le x\le l_w)$$

(11)

where $k={\displaystyle \frac{E}{h}}$; EI is the flexural rigidity of the section of the stratum, N·m².

From Equation (11):

$$EI{w}^4(x)+kw(x)=\gamma h$$

(12)

where $\gamma$ is the OLR bulk density, kg/m³; h is the thickness of rock strata, m.

$$w(x)=\exp (\beta x)(A\cos \beta x+B\sin \beta x)+\exp (-\beta x)(C\cos \beta x+D\sin \beta x)+{\displaystyle \frac{q}{k}}(0\le x\le l_w)$$

(13)

where $\beta$ is the characteristic parameter of the elastic foundation beam, m⁻¹; $\beta =\sqrt[4]{{\displaystyle \frac{k}{4EI}}}$.

According to the theory of rock movement, it can be assumed that the range outside the boundary angle of rock movement is not affected by mining on the LF [37]. When $x\to \infty$, $\lim w\left(x\right)\to 0$, $\lim e^{\beta x}\to 0$, $\lim e^{-\beta x}\to 0$. The deflection of an elastic foundation beam can be expressed [23]:

$$w(x)=\exp (-\beta x)(C\cos \beta x+D\sin \beta x)$$

(14)

According to the boundary conditions, when x = 0, w(0) = S, ${\displaystyle \frac{dw(x)}{dx}}=0$.

By combining Equation (14), we can obtain:

C = D = S.

Therefore, the deflection expression of the protective layer is:

$$w(x)=S\bullet \exp (-\beta x)(\cos \beta x+\sin \beta x)(0\le x\le l_w)$$

(15)

By integrating Equation (15), we can obtain:

$$D_{l{c}_1}={\displaystyle \frac{S}{\beta }}\left[1-e^{-\beta l_w}\cos (\beta l_w)\right]$$

(16)

where $l_w=({\displaystyle \sum h+h})(\cot \phi -\cot \alpha )$, φ is the fully mining angle; α is the breaking angle.

Meanwhile,

$$a=L-({\displaystyle \sum h+h})\cot \alpha$$

(17)

Therefore, the spatial area of grouting-BS can be expressed by the following formula:

$$D_{lc}=2[S(a-l_w)+D_{l{c}_1}]$$

(18)

Substitute Equations (10), (16), and (17) into Equation (18), the expression for the spatial area of grouting BS under top coal caving mining can be derived. Due to the limitations of two-dimensional physical similarity simulation test conditions, this study only conducted two-dimensional spatial calculations.

Above all, the grouting-BS is influenced by mining height, caving height, and residual dilatancy coefficient of coal and rock strata, and is also related to the ultimate span of the bearing layer, basic characteristic parameters, fully mining angle φ and breaking angle α. According to similar simulation results, the advancing distance (2L) of the LF is 760 m, the OLR breaking angle and full mining angle are 65° and 42°, respectively, and the characteristic parameters β are 1.32 m⁻¹. According to Equations (10) and (18), the maximum area of the grouting BS at the base of TSS-2 is calculated to be 680.8 m².

6. Conclusions

(1)

Drilling data from the 1101 LF in Xinjiang Zhundong mining area reveal strata dominated by silty mudstone and siltstone. The compressive strength is typically less than 20 MPa, the tensile strength is generally less than 2 MPa, and the elastic modulus is generally less than 5 GPa. The proportion of weak to extremely weak strata is exceeding 90%. Macroscopically, characterized by low strength, poor cementation, susceptibility to weathering, and underdeveloped structural features such as small faults, joints, and bedding planes, this rock mass demonstrates typical attributes of a WCOLR.

(2)

Fractal dimension quantifies OLR mining-induced fracture evolution characteristics. During the LF advancing, the fractal dimension undergoes oscillatory evolution through five distinct stages: rapid initial growth, constrained slow growth under TSS, dimension reduction induced by fracturing and compaction of TSS, secondary growth from newly generated fractures, and stabilization upon reaching full extraction. Grid-based fractal dimension analysis further categorizes fracture zones, indicating a WCFZ height of 160~180 m.

(3)

Under the influence of high-intensity mining disturbance, the extent of OLR damage progressively expands. The horizontally BS fractures and vertically penetrating fractures interweave, forming a complex OLR fracture network. During LF advancing, the spatiotemporal evolution of the fracture field follows the sequence: fracture initiation, rapid development and evolution, near-field compaction, far-field propagation, and overall compaction. Mining-induced fractures predominantly concentrate at dip angles of 0–10°, 40–50°, and 170–180°. Horizontally BS fractures account for 70.2% of the total fracture population, vertically penetrating fractures constitute 13.1% and transitional fractures make up the remaining 16.7%.

(4)

Based on the elastic foundation beam theory, the theoretical prediction model of grouting BS under top-coal caving operations is established. The maximum cross-sectional area of BS is 680.8 m². These results provide theoretical foundations for subsidence-reduction grouting technologies.

(5)

Due to the limitations of two-dimensional physical similarity simulation test conditions, this study only analyzed the characteristics of BS and fracture evolution in the direction of LF advancement. In order to more accurately reveal the damage law of WCOLR, it is necessary to further study the evolution mechanism of fractures in WCOLR in western mining areas in the future.