A Kangaroo Escape Optimizer-Enabled Fractional-Order PID Controller for Enhancing Dynamic Stability in Multi-Area Power Systems

Abstract

In this study, we propose a novel metaheuristic algorithm named Kangaroo Escape optimization Technique (KET), inspired by the survival-driven escape strategies of kangaroos in unpredictable environments. The algorithm integrates a chaotic logistic energy adaptation strategy to balance a two-phase exploration process—zigzag motion and long-jump escape—and an adaptive exploitation phase with local search guided by either nearby elite solutions or random peers. A unique decoy drop mechanism is introduced to prevent premature convergence and ensure dynamic diversity. KET is applied to optimize the parameters of a fractional-order Proportional Integral Derivative (PID) controller for Load Frequency Control (LFC) in interconnected power systems. The designed fractional-order PID controller-based KET optimization extends the conventional PID by introducing fractional calculus into the integral and derivative terms, allowing for more flexible and precise control dynamics. This added flexibility enables enhanced robustness and tuning capability, particularly useful in complex and uncertain systems such as modern power systems. Comparative results with existing state-of-the-art algorithms demonstrate the superior robustness, convergence speed, and control accuracy of the proposed approach under dynamic scenarios. The proposed KET-fractional order PID controller offers 29.6% greater robustness under worst-case conditions and 36% higher consistency across multiple runs compared to existing techniques. It achieves optimal performance faster than the Neural Network Algorithm (NNA), achieving its best Integral of Time Absolute Error (ITAE) value within the first 20 iterations, demonstrating its superior learning rate and early-stage search efficiency. In addition to LFC, the robustness and generality of the proposed KET were validated on a standard speed reducer design problem, demonstrating superior optimization performance and consistent convergence when compared to several recent metaheuristics.

1. Introduction

Maintaining the dynamic stability of electrical power networks requires robust control mechanisms, among which the Load Frequency Regulator (LFR) plays a pivotal role. It is primarily responsible for ensuring the balance between power generation and consumption across multiple interconnected areas, especially under varying load conditions. The reliable operation of such multi-area systems is inherently dependent on the continuous and effective functioning of LFR mechanisms [1].

In today’s increasingly complex and large-scale modern power systems, ensuring grid stability and operational reliability is more critical than ever. These attributes are fundamental to delivering a consistent and high-quality electricity supply, which is vital for both residential and industrial consumers. As the infrastructure of power networks continues to expand, with the integration of renewable sources, decentralization, and variable demand profiles, the task of maintaining frequency stability becomes significantly more challenging. Consequently, LFR has emerged as a core focus area, addressing one of the most pressing issues in modern power system operation [2]. Additionally, conventional generation units often face limitations such as high maintenance costs, reduced operational efficiency, and environmental constraints, further elevating the necessity for effective LFR strategies. This need becomes even more pronounced under dynamic scenarios where load demands fluctuate frequently, network topologies evolve, and generation units vary in size and capacity [3]. Historically, Proportional-Integral-Derivative (PID) controllers have been widely adopted for load frequency regulation due to their simplicity and effectiveness in well-defined conditions. However, in the face of increasingly nonlinear, time-varying, and uncertain operating environments, these traditional control strategies show their limitations. The conventional PID-based approaches struggle to maintain the required performance and adaptability in highly dynamic and interconnected power systems, underscoring the urgent need for more advanced and flexible control solutions [4].

A variety of control strategies have been proposed for LFR, including conventional approaches such as Proportional-Integral (PI), Integral-Derivative (ID) [5], and PID [6] controllers. These methods aim to minimize fluctuations in both tie-line power exchange and system frequency across interconnected areas. While traditional controllers have proven effective in many cases, they often face limitations in handling complex or uncertain environments. To enhance performance, some studies have explored the use of fuzzy logic-based controllers [7]. Although this approach can improve regulation quality, it is often complex to implement and does not always guarantee consistent success in dynamic operating conditions. In recent years, soft computing techniques have gained popularity as promising alternatives for solving LFR challenges in multi-area power systems. Several works have focused on optimizing conventional integer-order PID controllers using advanced metaheuristic algorithms, such as the Teaching–Learning-Based Optimization (TLBO)-tuned PID [8] and the Bacterial Foraging Optimization (BFO)-based PID controller [9]. Moreover, more advanced and intelligent control strategies, including fuzzy logic systems [10] and Model Predictive Control (MPC) [11], have been employed to address the nonlinear characteristics of LFR and to maintain system stability under parametric uncertainties and variable operating conditions. Moreover, the Particle Swarm Optimizer (PSO)–Artificial Hummingbird Algorithm (PSO-AHA) approach with PID controllers has been employed on a two-area thermal tie-line interconnected system as manifested in [12]. An examination of LFR in a multiple-source power network has been conducted, adopting an improved parameter-based controller and a differential evolution method in [13,14]. In [15], a PID controller with Grey Wolf Optimization Algorithm is used for the LFR of an interconnected power generating system.

To successfully maintain the nominal values of tie-line interchange power and system frequency, even in the case of a system breakdown, several control systems have been brought forward in the past few decades. Using a gate-controlled series capacitor, a high-voltage direct current connection, and distributed producing resources, the LFR of a Multi-Area Power Grid (M-APG) was investigated in the studies [16,17]. To optimize PI, PID, and fractional order PID controller settings, a variety of methods have been developed, including the genetic algorithm [18], the binary particle search optimization [19], constrained population external optimization [20], hybrid gravitational search optimizer—binary particle search optimizer [19], Bonobo optimizer [21], and Water Cycle Algorithm (WCA) [22].

Additionally, fractional order calculus has been implemented recently. Since they eliminate the constraints imposed by their traditional equivalents, these controllers are computationally more potent in improving performance than conventional approaches, and it has been established that they can generate notable efficiency gains [23,24]. In [25], a fractional-order PID controller based on Yin-Yang-Pair optimization is introduced to maximize solar power harvesting from the photovoltaic arrays. In order to manage the uncertainties brought on by parametric, load, and renewable source variations, the adaptive FO-fuzzy-PID controller optimized by the TLBO algorithm is proposed, with all controller parameters simultaneously adjusted [26]. To illustrate the superiority of FO, an LFC strategy using FO controllers has been provided and contrasted with conventional approaches, where the proportion of integral and derivative parts falls within [0, 1] [27,28]. One recent development in this approach is that the fractional integral and derivative components can be any real number for the differentiator and integrator orders, revealing superior dynamic response and outstanding resilience to parameter uncertainties and outside disturbances [29,30].

While a great deal of research has been devoted to LFR in interconnected power systems, several important challenges are still unresolved. Controllers like PI and PID, and their numerous variants, remain widely used because they are simple and straightforward to implement. However, their ability to adapt to the increasingly complex realities of modern power systems, such as nonlinear behavior, time-varying parameters, and uncertain operating conditions, is quite limited. In response, researchers have turned to soft computing methods and bio-inspired optimization algorithms, which have led to noticeable improvements in controller performance and tuning accuracy. Still, these methods often struggle with slow convergence, a tendency to get trapped in local optima, and difficulty balancing exploration with exploitation—issues that become more pronounced in large or highly complex search spaces. The use of fractional-order PID controllers has emerged as a promising direction, offering improved flexibility and robustness thanks to their ability to account for the system’s memory and dynamic behavior. However, in most cases, the tuning of these advanced controllers is still handled using basic or traditional optimization tools, which are often not capable of fully leveraging the potential of fractional calculus. Moreover, many studies fall short in providing comprehensive evaluations of these techniques against more recent and competitive optimization algorithms, especially under varying load conditions or scenarios that involve disturbances and uncertainties. This leaves a significant gap in our understanding of how these methods perform in realistic, dynamic environments.

This study aims to address these gaps by proposing a novel bio-inspired Kangaroo Escape optimization Technique (KET) to optimize the parameters of a fractional-order PID controller for enhanced LFR performance in a two-area thermal power system. The introduced KET is developed by mimicking the real-life escape behaviors of kangaroos in natural environments. The algorithm features adaptive decision-making mechanisms based on energy-driven movement, chaotic dynamics, and switching strategies between long jumps and zigzag patterns, combined with selective local search through safer area exploration and decoy drop behaviors. The primary contributions of this research can be summarized as follows:

• A novel KET is proposed, inspired by kangaroo survival behavior, which dynamically balances exploration and exploitation through an adaptive chaotic energy model; this is further enhanced by biologically inspired mechanisms such as decoy drop and safer area selection to improve local search accuracy and avoid premature convergence.
• The proposed KET is applied to tune the parameters of a fractional-order PID controller for LFR in interconnected Multi-Area Power Grids (M-APGs). This integration leverages the advantages of fractional calculus to improve dynamic response and robustness.
• The proposed fractional-order PID controller via KET is evaluated and compared against several well-established optimization algorithms such as PSO, Differential Evolution (DE), Jaya optimization algorithm (JAYA), and Neural Network Algorithm (NNA)-based fractional-order PID tuning. Performance is assessed using key metrics like ITAE, settling time, maximum overshoot, and maximum undershoot.
• Simulation results confirm that the proposed controller significantly enhances frequency stability and tie-line power regulation, outperforming benchmark methods in terms of convergence speed and overall system robustness.
• The proposed KET, tested using the speed reducer design problem, demonstrated its generality and performance by achieving the least statistical metrics among all competing methods.

2. Proposed KET: A Novel Metaheuristic Inspired by the Survival-Driven Escape Strategies of Kangaroos

This section introduces a novel Kangaroo Escape optimization Technique (KET), a bio-inspired metaheuristic optimization that mimics the survival instincts and evasive behaviors of kangaroos in the wild. Drawing on kangaroos’ instinctive responses—such as zigzagging under threat, long jumps to evade predators, and the use of decoys—the algorithm effectively balances exploration and exploitation in the search space. The key behavioral elements modeled in KET include the following:

(i)

Zigzag Motion: Erratic changes in direction to evade predators;

(ii)

Long Jumps: Large, rapid movements to escape poor conditions;

(iii)

Decoy Drops: Misdirection tactics to confuse threats and maintain diversity;

(iv)

Energy-Based Decisions: Adaptive strategy based on internal energy dynamics, influenced by chaos.

2.1. Initialization

The initial population, represented as a group of kangaroos, is randomly distributed across the solution landscape. Each kangaroo’s position X_j is a vector in a D-dimensional decision space:

$$X_j=\left(\left(Up-Low\right)\times rand\left(1,D\right)\right)+Low\hspace{1em}j=1:N$$

(1)

where Low and Up define the lower and upper limits of the design variables, respectively. The D-dimensional decision space is specified as [Low, Up]^D. The fitness of each kangaroo is then evaluated based on the objective of optimization.

2.2. Adaptive Energy of Kangaroos

KET presents a chaotic logistic map to simulate fluctuating energy levels of kangaroos over iterations. This mimics real-world biological rhythms and environmental stress. The energy Energy_j(time) of each kangaroo at iteration (time) is calculated using

$$\lambda \left(time+1\right)=4\times \left(1-\lambda \left(time\right)\right)\times \lambda \left(time\right)\hspace{1em}\mathit{where}, \lambda \left(time=0\right)=7/10$$

(2)

$$Energ{y}_j\left(time\right)=\left(1-\left({\displaystyle \frac{time}{tim{e}^{\mathit{max}}}}\times r_{1,j}\right)\right)\times \left(\left(5\times \lambda \left(time\right)/100\right)+0.95\right)\hspace{1em}j=1:N$$

(3)

where r_1,j is a uniformly distributed random number generated individually for each kangaroo, and time^max is the maximum number of iterations. In the early iterations, the model assigns high energy levels to reflect the kangaroo’s vigorous escape behavior, promoting rapid and wide-ranging exploration.

2.3. Strategy 1: Escape via Zigzagging

When energy is low, kangaroos execute zigzag movements to explore the surrounding area. This is modeled by rotating their direction vectors by a random angle θ

$$\theta ={\theta }^{\mathit{max}}\times \left(2\times r_2-1\right)$$

(4)

$$V_r=\mathit{sin}\left(\theta \right)\times U\times ‖V_j‖+\mathit{cos}\left(\theta \right)\times V_j$$

(5)

where θ^max is the maximum permissible movement angle (θ^max is 30°) and r₂ is a random number. The scaling coefficient is β, and the rotated direction vector towards the best at the moment is V_r.

In Equation (5), U is defined as a unit vector that is perpendicular to V_j, the vector pointing toward the current best solution. Including this perpendicular component is important because it allows the algorithm to create zigzag movements rather than straight-line paths, effectively mimicking the unpredictable, evasive behavior of kangaroos and helping the search escape local optima. Additionally, V_j is the direction vector to the global best (X_Leader), which is defined as follows, and U is an orthogonal unit vector.

$$V_j=X_{Leader}-X_j$$

(6)

where X_Leader is the position of the agent (kangaroo) with the lowest value of the objective function (i.e., best fitness) among all individuals in the population at the current iteration. As a result, the kangaroo’s new location may be modified as follows:

$$Xne{w}_j=X_j+\left(\mathit{sin}\left(\theta \right)\times \beta \times \left(V_r\circ \mathbb{N}\left(1,D\right)\right)\right)$$

(7)

The zigzagging step size (β = 50%) is represented by β, a D-dimensional random vector with a Gaussian distribution; element-wise multiplication is indicated by ∘.

2.4. Strategy 2: Escape via Long Jumping

With higher energy, kangaroos perform long-distance leaps to explore distant parts of the search space

$$Xne{w}_j=2\times \left(X_j\circ Deco{y}_{drop}\right)\circ \mathbb{N}\left(1,D\right)+X_j$$

(8)

where Decoy_drop is the term used to describe the kangaroo’s decoy drop action. This mechanism enables global exploration and helps escape from local optima.

In Equation (8), we use a constant multiplier of 2 in the long-jump step to increase the step size during the global search phase. This helps the agents explore a wider area by allowing them to move farther from their current positions, which enhances diversity and introduces more randomness, especially useful in the early stages of optimization. Through empirical testing, we found that using a factor of 2 strikes a good balance between strong exploration and maintaining stable convergence behavior.

2.5. Energy-Based Switching Mechanism

The KET enables each kangaroo to adaptively select its movement strategy—either zigzagging escape or long jumping—based on its current energy level (Energy_j(time)), which evolves throughout the optimization process. A probabilistic threshold mechanism is employed, where energy is compared against a benchmark value (Energy_threshold), set at 50%. If the kangaroo’s energy falls below this threshold, it favors the zigzag escape pattern to perform localized exploration. Conversely, when energy exceeds the threshold, it adopts long jump behavior to explore distant and potentially optimal regions. This dynamic strategy-switching mechanism allows KET to maintain an effective balance between exploration and exploitation across iterations.

2.6. Strategy 3: Safe Zone Search with Decoy Drop

In the absence of immediate threats, kangaroos search for safe and resource-rich zones. This process is guided by one of three modes:

(i)

Explorative Mode—A random kangaroo position is chosen;

(ii)

Exploitative Mode—A local best position is selected;

(iii)

Deep Exploitative Mode—The global best is used. The update rule integrates a decoy drop mask

$$Xne{w}_j=Deco{y}_{drop}\circ \mathbb{N}\left(1,D\right)\circ \left(X_j-X_{Safe}\right)+X_{Safe}$$

(9)

where X_Safe represents the position of a selected kangaroo deemed to be in a safer location. This mechanism enables partial position updates, mimicking the way kangaroos subtly adjust their paths while remaining concealed. The decoy drop mechanism enhances population diversity and helps prevent premature convergence by introducing controlled randomness. Inspired by real-world kangaroo defense behaviors, such as creating misleading tracks, making diversionary movements, or kicking sand to confuse predators, this strategy enables escape toward safer or more optimal regions. Mathematically, the decoy drop mechanism is modeled as follows:

$$Deco{y}_{drop}=\left\{\begin{array}{cc}round\left({\left[U_1\left(0,1\right)\right]}_{1\times D}\circ {\left[U_2\left(0,1\right)\right]}_{1\times D}\right)& if r_3\ge 2/3\\ round\left({\left[U_1\left(0,1\right)\right]}_{1\times D}\right)& if 1/3<r_3<2/3\\ {\left[\begin{array}{ccccc}1& 1& .& .& 1\end{array}\right]}_{1\times D}& Else\end{array}\right.$$

(10)

The decoy drop mechanism operates as a probabilistic gating strategy designed to enhance the adaptability of the KET. It controls the extent to which candidate solutions are updated. This mechanism supports diversity preservation, prevents premature convergence, and encourages exploratory behavior in the population, particularly helpful in avoiding entrapment in local optima. By occasionally misleading the search direction, it allows the algorithm to escape from suboptimal regions and maintain a dynamic search trajectory.

As shown in Equation (10), the structure of the decoy mask is determined by the value of a random variable r₃, which is drawn uniformly from the interval [0, 1]. While r₃ does not explicitly appear within the equation itself, it functions as a conditional strategy variable that governs which one of the three masking strategies is activated.

• If r₃ ≥ 2/3, the first case is selected, in which the mask is generated by taking the elementwise (Hadamard) product of two random binary vectors, rounded to the nearest integer. This results in a sparser and more irregular mask that promotes high diversity.
• If 1/3 < r₃ < 2/3, the second masking strategy is activated, involving a single random binary vector, again rounded, producing a more moderate selection pattern for updating candidate solutions.
• If r₃ ≤ 1/3, the default case is applied, where the mask is a vector of ones, meaning no decoy drop is applied, and the update proceeds in full.

This conditional behavior introduces a level of stochastic control over the algorithm’s exploitation-exploration balance. It simulates the natural uncertainty and deceptive tactics observed in real-world kangaroo behavior, thereby strengthening the algorithm’s ability to maintain search momentum in both early and later phases of optimization.

2.7. Boundary Handling and Memory Updating

To ensure solution feasibility, the algorithm enforces boundary constraints

$$Xne{w}_j=\mathit{max}\left(Low,\mathit{min}\left(Up,Xne{w}_j\right)\right)$$

(11)

Accordingly, the new fitness value f(Xnew_i) is evaluated for each updated position. Only improvements are retained, allowing kangaroos to learn from their most successful experiences while discarding less effective solutions. This adaptive memory mechanism ensures that the search process continually evolves toward better regions of the solution space, as formulated below:

$$X_j\left(time+1\right)=\left\{\begin{array}{cc}{Xnew}_j& if f\left(Xne{w}_j\right)\le f\left(X_j\left(time\right)\right)\\ X_j\left(time\right)& Else\end{array}\right.$$

(12)

Only movements that lead to improved fitness are retained, and the best-known positions are stored and updated. These steps are repeated iteratively until a maximum number of iterations is reached.

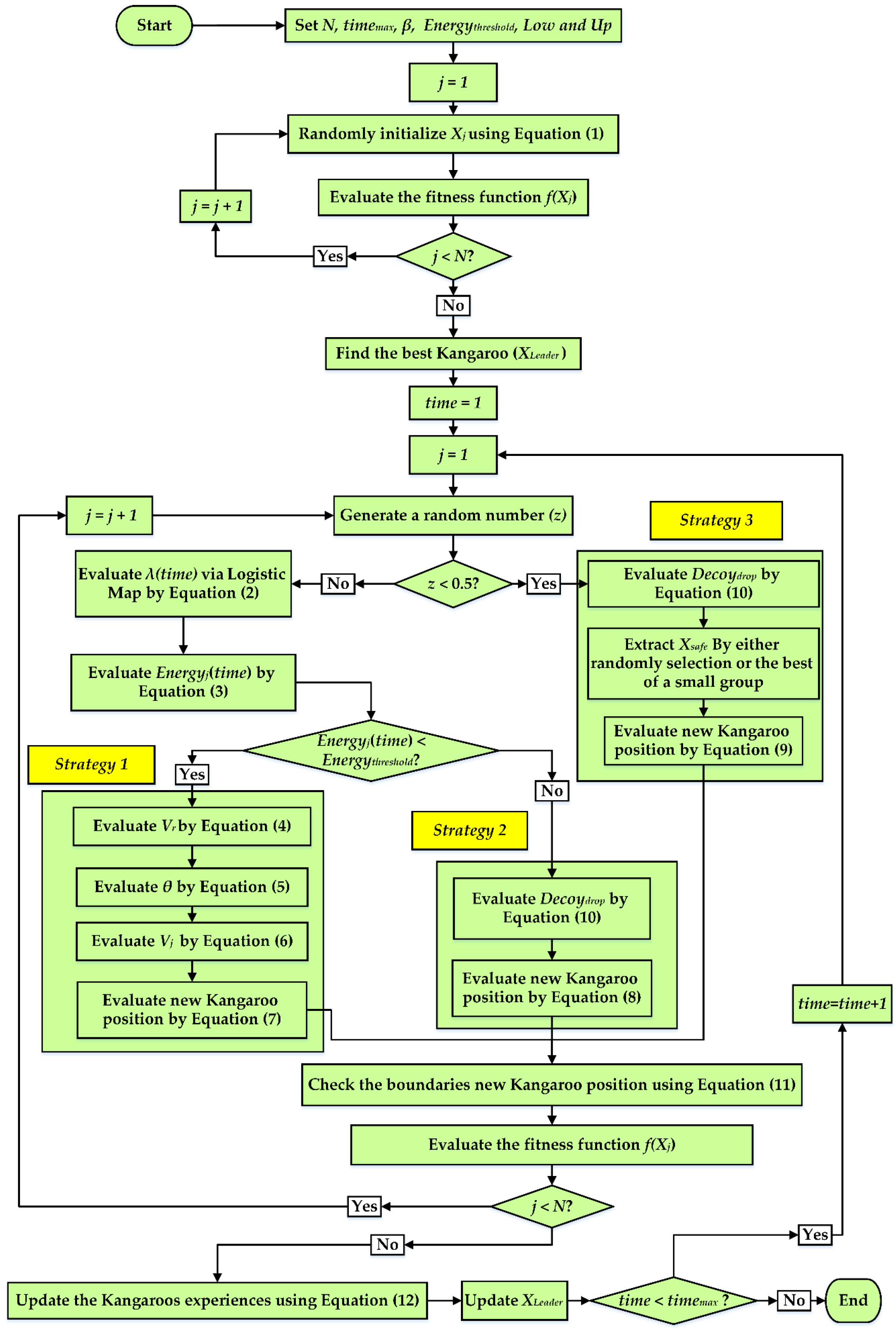
The entire optimization cycle is visualized in Figure 1, illustrating the interplay between exploration and exploitation phases within the KET framework.

As shown in Figure 1, the selection and alternation of the three KET strategies in the numerical simulations are not arbitrary but are systematically governed by the conditional logic. At each iteration and for every kangaroo, a random number z ∈ [0, 1] is generated to determine which movement strategy will be applied. If z < 0.5, the algorithm activates strategy 3: safe zone search with decoy drop. This strategy allows the kangaroo to move toward a safe solution (e.g., best-so-far or a trusted peer) with a probabilistic masking mechanism that introduces partial misleading steps, enhancing diversification and avoiding premature convergence.

However, if z ≥ 0.5, then either strategy 1: long jump or strategy 2: zigzag movement is selected based on the kangaroo’s energy level, which is dynamically calculated in Equation (3). If the energy level is greater than or equal to 0.5, the kangaroo is considered energetic and is assigned strategy 1: long jump, which encourages exploration by moving toward randomly chosen peers over longer distances. Conversely, the kangaroo uses strategy 2: zigzag movement, which introduces erratic, locally biased steps that simulate evasive or unpredictable behavior around the current best solution.

This adaptive strategy-switching mechanism ensures that the algorithm dynamically balances exploration and exploitation based on the agent’s state and progression through the search process. This design is a key factor behind KET’s demonstrated robustness and effectiveness in the simulations presented.

3. Problem Formulation

3.1. M-APG Model

In this study, the analyzed M-APG consists of two interconnected non-reheat thermal generating units, each representing a separate control area. As depicted in Figure 2, the main functional components for each area include a speed governor, turbine, and synchronous generator. The system is built on non-reheat thermal stations in accordance with the modeling conventions described in [31]. In the schematic representation, the power demand variations in areas 1 and 2 are denoted by ∆P_D1 and ∆P_D2, respectively. Similarly, the tie-line power exchange deviation is indicated by ∆P_TIE, while the control input signals from the governors are labeled as u₁ and u₂. These variables collectively represent the system’s inputs and serve as crucial indicators of the system’s dynamic response to load perturbations.

On the output side, frequency deviations in each area are expressed as ∆f₁ and ∆f₂, while Area Control Errors (AREs), which quantify the mismatch between scheduled and actual power interchange, are symbolized by ARE₁ and ARE₂. These signals provide feedback for regulatory mechanisms to restore balance under fluctuating conditions, as elaborated in [32,33]. Moreover, several parameters govern the system’s dynamic behavior. The time constants for turbines, governors, and power systems in both areas are denoted as T_t1, T_t2, T_g1, T_g2, T_P1, and T_P2, all measured in seconds. These constants dictate the responsiveness of individual components to disturbances. In addition, the system gain coefficients KP₁ and KP₂, along with the governor speed regulation parameters R₁ and R₂, define the proportional influence of frequency changes on mechanical power output and control input sensitivity in each respective area.

3.2. Objective Function

The growing adoption of fractional-order PID controllers in modern control systems is largely attributed to their enhanced robustness and superior performance when compared to conventional PID controllers. By introducing non-integer (fractional) orders into the proportional (P), integral (I), and derivative (D) components, fractional-order PID controllers offer a refined and more flexible alternative to the classical PID structure. This fractional extension enables more precise control over complex systems, particularly those exhibiting nonlinear dynamics, time delays, or fractional-order behaviors, thereby expanding the controller’s degrees of freedom.

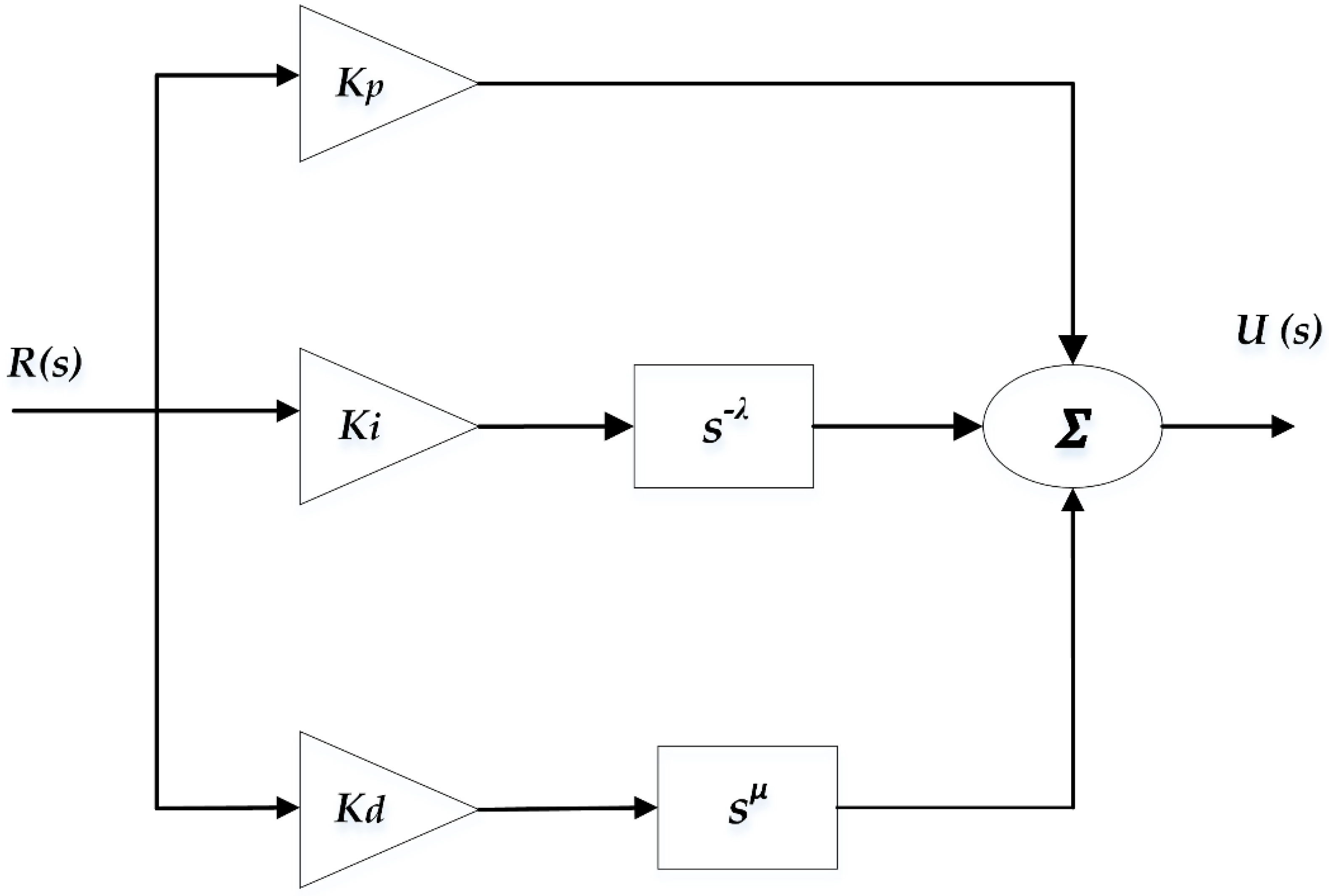
Unlike their integer-order counterparts, fractional-order PID controllers possess non-local dynamic properties, meaning their response is influenced not just by the present state but also by the history of the system error. This memory enhances their ability to manage uncertainty and disturbances in dynamic environments. The functional structure of the fractional-order PID controller is illustrated in Figure 2, and its mathematical representation is defined by the transfer function Gc(s), as shown in Equation (13). In this formulation, Y(s) and R(s) denote the Laplace transforms of the controller’s output and the reference (error) signal, respectively [34].

$$Gc(s)=Y(s)/R(s)=K_p+K_d\times s^{\mu }+K_i\times s^{-\lambda }$$

(13)

The controller parameters include the following:

• Kp: the proportional gain;
• K_d: the derivative gain;
• μ: the fractional order of differentiation;
• K_i: the integral gain;
• λ: the fractional order of integration.

$$Gc(t)=\left(K_p+K_i{D}^{-\lambda }+K_d{D}^{\mu }\right)\times e(t),$$

(14)

The error signal, denoted as e(t), represents the difference between the system’s reference input r(t) and its actual output response y(t). In the context of LFR, a widely used metric to quantify this error is the Area Regulator Error (ARE). This measure accounts for both frequency deviations and tie-line power changes in each control area, and is represented by the area-specific errors ARE₁ and ARE₂, as defined in [35]

$${{\displaystyle ARE}}_1={{\displaystyle B}}_1\Delta {{\displaystyle f}}_1+\Delta {{\displaystyle P}}_{TIE}$$

(15)

$${{\displaystyle ARE}}_2={{\displaystyle B}}_2\Delta {{\displaystyle f}}_2+{{\displaystyle a}}_{12}\Delta {{\displaystyle P}}_{TIE}$$

(16)

Fractional calculus provides a wide variety of definitions for fractional derivatives and integrals, each with distinct theoretical properties and practical implications. Among the most widely used are the Caputo, Grünwald–Letnikov, and Riemann–Liouville formulations [36]. The Caputo derivative is often favored in physical modeling due to its compatibility with classical initial conditions (i.e., integer-order derivatives of known functions) [37]. The Grünwald–Letnikov approach is valued for its direct numerical approximability, often used in discrete implementations [38]. In contrast, the Riemann–Liouville definition, which is adopted in this study, is rooted in a strong mathematical foundation and is particularly suitable for frequency-domain analysis and controller synthesis, especially in continuous-time systems [36].

As presented in Equation (17), the design of the fractional-order PID controller (${}_{a}D_t^x$) incorporates fractional calculus principles. These fractional-order operators enable the controller to process the error signal with memory-dependent dynamics, offering greater flexibility and performance in handling complex system behaviors. In the formulation of the fractional-order operations within the controller, the variables t and a represent the upper and lower bounds, respectively, over which the fractional differentiation or integration is applied. The expression R(a) refers to the real part of the fractional-order value. To implement the fractional operators, the Riemann–Liouville approximation method is employed, as detailed in [39]. This method allows the computation of non-integer order derivatives or integrals by discretizing the operation over a defined interval. Specifically, the approximation relies on the integer part of the fractional order x, which must be a whole number, while the fractional component accounts for the order’s non-integer behavior.

$${}_{a}D_t^{x}e\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-x\right)}}{\displaystyle \frac{d^n}{d{t}^n}}{\displaystyle \underset{a}{\overset{t}{\int }}{\left(t-\tau \right)}^{n-x-1}e\left(\tau \right)d\tau },$$

(17)

where $\Gamma (n-x)=(n-x-1)!$; $n=\left[x\right]+1$ and should be an integer, $\left[x\right]$ signifies the integer portion of x

$${}_{a}D_t^{x}e\left(t\right)={\displaystyle \frac{1}{\Gamma \left(1-x\right)}}{\displaystyle \underset{a}{\overset{t}{\int }}{\left(t-\tau \right)}^{-x}e\left(\tau \right)d\tau },$$

(18)

where the x represents fractional-order and $x\in \left[0,1\right]$.

The optimization process is designed to minimize the Integral of Time Absolute Error (ITAE), which is selected as the objective function (OB_F) for tuning the parameters of the fractional-order PID controller. This criterion ensures improved dynamic response by penalizing sustained deviations in frequency and tie-line power.

$$O{B}_F={\displaystyle \underset{0}{\overset{t_{sim}}{\int }}\left(\left|\Delta f_1\right|+\left|\Delta f_2\right|+\left|\Delta P_{TIE}\right|\right)}\times t\times dt$$

(19)

Figure 3 displays the model of a fractional-order PID controller [40]. The optimization is carried out subject to predefined constraints, which typically include physical system limits, controller parameter bounds, and stability requirements, to ensure feasible and reliable operation.

$$K{p}_{Area,Min}\le K{p}_{Area}\le K{p}_{Area,Max},\hspace{1em}Area=1 or 2$$

(20)

$$K{i}_{Area,Min}\le K{i}_{Area}\le K{i}_{Area,Max},\hspace{1em}Area=1 or 2$$

(21)

$$K{d}_{Area,Min}\le K{d}_{Area}\le K{d}_{Area,Max},\hspace{1em}Area=1 or 2$$

(22)

$${\lambda }_{Area,Min}\le {\lambda }_{Area}\le {\lambda }_{Area,Max},\hspace{1em}Area=1 or 2$$

(23)

$${\mu }_{Area,Min}\le {\mu }_{Area}\le {\mu }_{Area,Max},\hspace{1em}Area=1 or 2$$

(24)

In the context of constraints on the fractional-order PID controller parameters defined in Equations (20)–(24), K_P indicates the proportional gain; K_i indicates the integral gain; K_d indicates the derivative gain, and the fractional orders of integration is symbolized by λ while differentiation is symbolized by μ to ensure the system remains stable and responsive under varying load conditions, Also, the subscript symbol Area refers to the Area while the subscript symbols Area,Min and Area,Max represent the specified minimum and maximum value of the regarding parameter in each Area.

In this study, the fractional derivative (λ₁, λ₂) and integral (μ₁, μ₂) orders of the fractional-order PID controller besidethe other parameters (K_P1, K_i1, K_d1, n₁, K_P2, K_i2, K_d2, n₂) are treated as decision variables within the optimization process. The proposed KET was employed to simultaneously optimize all twelve fractional-order PID parameters (six parameters to each Area), proportional (K_P), integral (K_i), derivative (K_d) and filter (n), as well as the fractional orders λ and μ. At each iteration of the algorithm, a candidate set of controller parameters is passed to a MATLAB R2017b/Simulink simulation model, which evaluates the system’s dynamic performance using the ITAE as the objective function. The resulting ITAE value is then returned to the optimization algorithm to guide the search. This closed-loop process continues until convergence is achieved, meaning the values of parameters used in the final controller are those that yield the best stability in the simulated multi-area power system.

4. Simulation Results

In this section, the proposed KET is applied with the goal of minimizing the ITAE, as defined in Equation (19). To evaluate its effectiveness, three distinct test scenarios are considered, each involving specific load disturbances. The system data used for these simulations are sourced from references [41,42] as outlined in Appendix A.

For comparison, several recently developed optimization algorithms, namely Artificial Rabbit Optimizer (ARO), PSO, DE, NNA, JAYA, and SAMPE-JAYA, are included in the study. Each simulation is run with a fixed population size of 10 agents, and the number of iterations is capped at 100. To ensure a fair and consistent comparison across all methods, the total number of function evaluations is set to 1000 for each algorithm. After 20 independent runs using these conditions, the best performance result for each technique is recorded. The analysis is conducted across three load scenarios: a step change in load (SCL) in Area 1 (Case 1), an SCL in Area 2 (Case 2), and simultaneous SCLs in both areas (Case 3).

4.1. Case 1

The effectiveness of the proposed KET-optimized fractional-order PID controller is initially examined within a M-APG framework. To simulate a realistic operating disturbance, a SCL of 0.1 per unit (pu) is applied to Area 1 at time t = 0 s. This test scenario allows for a detailed assessment of the controller’s dynamic behavior under sudden demand fluctuations.

The controller parameters for this scenario, specifically the fractional orders λ, μ, K_p, K_i, and K_d are presented in

Table 1. Controller parameters along with the corresponding performance results for Case 1.

Algorithm		Proposed KET+ Fractional Order PID	NNA+Fractional Order PID	JAYA+PIDn	PSO+PIDn	ARO+PIDn	SAMPE-JAYA+PIDn
Controller Parameters	KP1	2.674531	2.864494	1.8394	1.9602	1.875133	1.8066
	Ki1	4	3.999996	3	3	2.997462	2.9895
	Kd1	1.000001	0.839761	0.5806	0.6083	0.578319	0.5654
	n1	0.754982	-	72.985	385.58	115.132	88.111
	λ1	1	0.999999	-	-	-	-
	μ1	3.999951	0.999933	-	-	-	-
	KP2	0.000212	0.046009	1.4843	2.9756	2.979045	2.1364
	Ki2	3.998922	0.000801	0.4306	1.5561	0.729651	0.4187
	Kd2	3.998807	0.149124	1.0095	2.6638	1.050161	1.7534
	n2	0.669206	-	425.37	497.92	15.40281	146.04
	λ2	2.674531	0.010384	-	-	-	-
	μ2	4	0.999999	-	-	-	-
ITAE Value		0.05363897	0.059063	0.0770	0.0769	0.075401	0.0769
ITAE Improvement %		-	9.18%	30.34%	30.25%	28.86%	30.25%

, accompanied by the resulting performance metrics for each area. For comparative analysis, the table also includes ITAE values from several recently published optimization-based control strategies. These include the (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn) and (SAMPE-JAYA+PIDn) controllers, which have reported ITAE values of 0.059063, 0.0770, 0.0769, 0.075401, and 0.0769, respectively.

By contrast, the proposed KET-fractional order PID controller achieves a superior ITAE value of 0.0536, outperforming all compared techniques. These results translate into relative improvements of 9.18%, 30.34%, 30.25%, 28.86%, and 30.25%, respectively, when compared with (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn) and (SAMPE-JAYA+PIDn) controllers. This clearly highlights the enhanced tuning capability and dynamic response of the KET, confirming its potential as a robust and efficient tool for load frequency control in complex power systems.

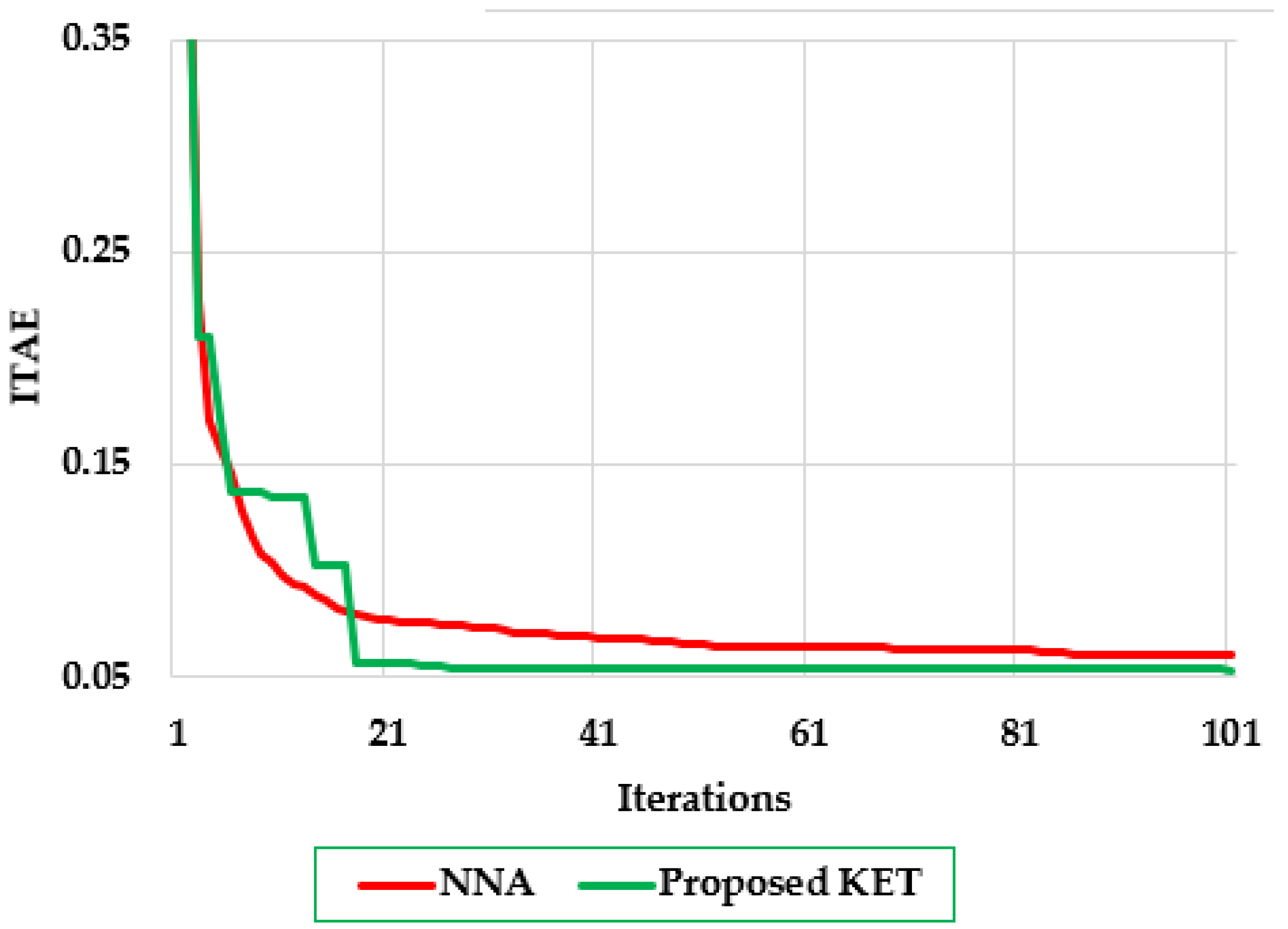
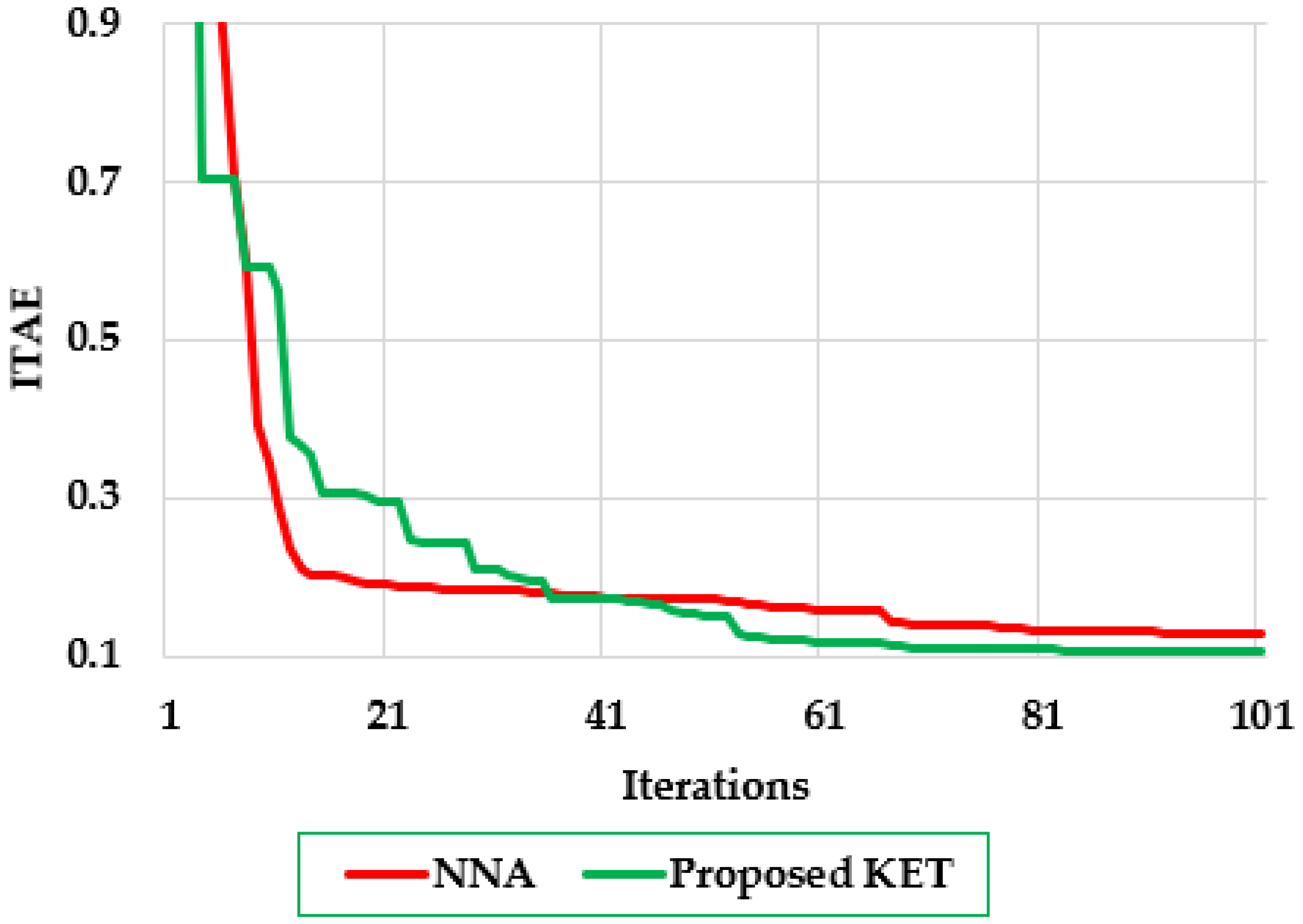
Figure 4 presents the convergence behavior of the proposed KET compared to the NNA [43] during the tuning process of a fractional-order PID controller, as measured by the ITAE. As shown, both algorithms begin with a relatively high ITAE value (~0.35), reflecting the poor initial solution quality. The KET (green curve) demonstrates faster convergence, reaching an ITAE below 0.06 within the first 20 iterations, with noticeable performance jumps in early stages. In contrast, the NNA algorithm (red curve) shows a more gradual and smoother convergence pattern, requiring more iterations to approach the same ITAE level. Both methods plateau after iteration 40, but the KET consistently maintains a lower ITAE throughout the simulation. The KET exhibits superior convergence efficiency, consistently lower ITAE throughout the simulation, indicating strong exploratory capabilities early in the search process and effective local exploitation later on. The sharper drop in ITAE values within the first 20 iterations indicates KET’s rapid discovery of promising regions in the search space.

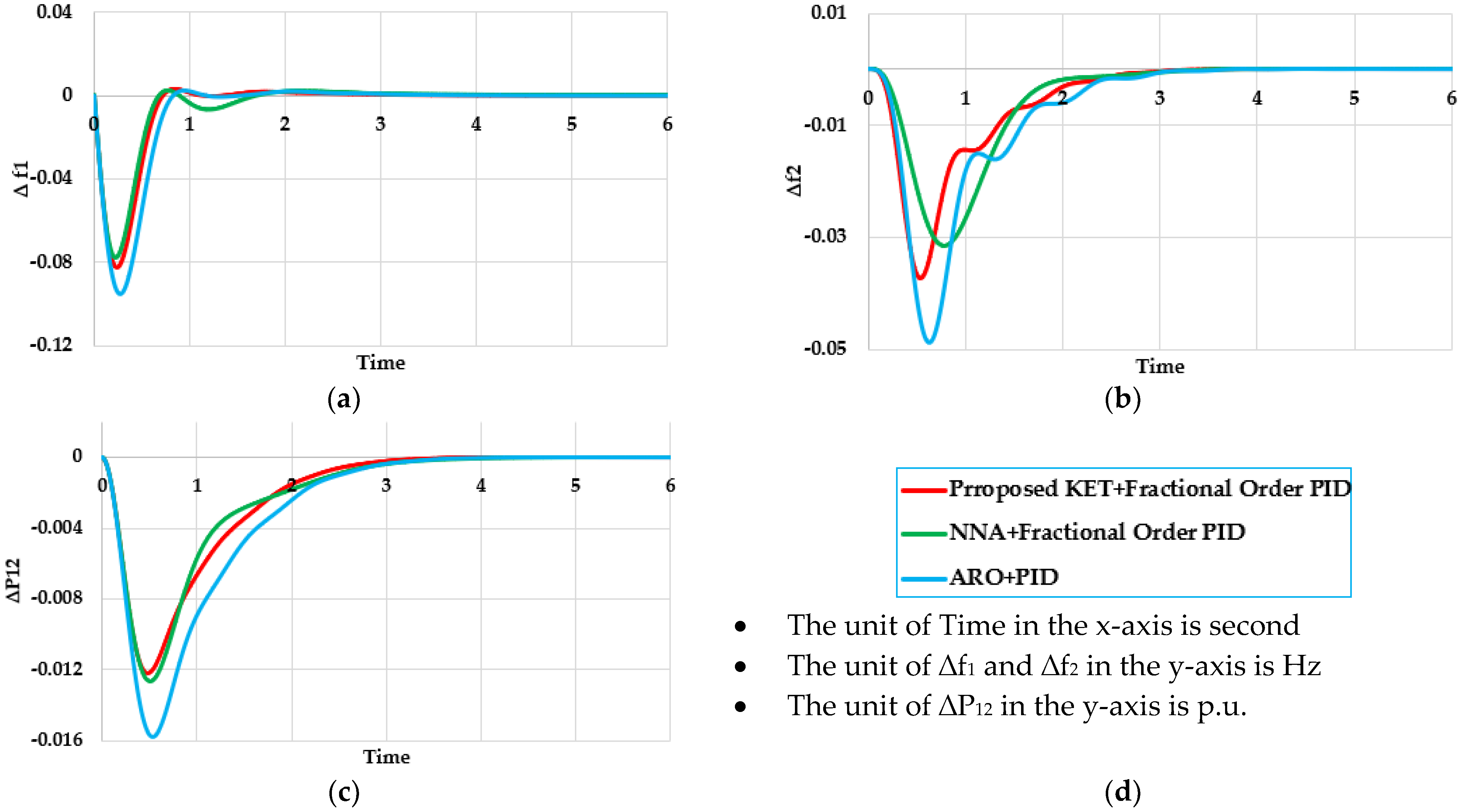
Figure 5 illustrates the dynamic responses of frequency and tie-line power in Area 1 using three different controllers: (NNA+Fractional Order PID), (ARO+PIDn) and the proposed (KET+Fractional Order PID) controllers. The simulation tables present a comprehensive evaluation of all six control methods, whereas this figure illustrates only the top three performers. As shown, the KET-tuned fractional-order PID controller demonstrates strong capability in suppressing frequency deviations and regulating tie-line power, even under varying power outputs. It maintains stable transient performance and adapts effectively to load changes, ensuring consistent control behavior throughout the disturbance period. Complementing the graphical results,

Table 2. Comparison of SET, MUT, and MOT for Case 1.

Approach	$\mathbf{\Delta }\mathit{P}$			$\mathbf{\Delta }{\mathit{f}}_2$			$\mathbf{\Delta }{\mathit{f}}_1$
	MUT	MOT	SET	MUT	MOT	SET	MUT	MOT	SET
Proposed KET+ Fractional Order PID	−0.0119	8.89 × 10−6	2.8875	−0.0361	2.35 × 10−5	2.6922	−0.0819	0.0029	1.8921
NNA+Fractional Order PID	−0.0127	6.47 × 10−7	3.2203	−0.0314	6.32 × 10−6	3.0024	−0.0775	0.0021	2.4628
ARO+PIDn	−0.0158	1.08 × 10−5	3.0594	−0.0487	5.7 × 10−5	2.9014	−0.0953	0.0025	2.1957

provides a quantitative comparison of the Maximum Undershoot (MUT), Settling Time (SET), and Maximum Overshoot (MOT) for all three control approaches. Among them, the proposed (KET+Fractional Order PID) controller achieves the shortest settling times in both frequency and power transfer responses, measured at 2.8875 s, 2.6922 s, and 1.8921 s, clearly outperforming both (NNA+Fractional Order PID) and (ARO+PIDn) controllers in terms of dynamic response speed and stability.

4.2. Case 2

In this instance, Area 2 is subjected to an SCL of 0.1 per unit (pu) at time t = 0 s in order to replicate a genuine operating disturbance. The controller parameters for this scenario are presented in

Table 3. Controller parameters along with the corresponding performance results for Case 2.

Algorithm		Proposed KET+ Fractional Order PID	NNA+Fractional Order PID	JAYA+PIDn	PSO+PIDn	ARO+PIDn	SAMPE-JAYA+PIDn
Controller Parameters	KP1	2.12244	3.1637	2.017	2.2948	2.794512	2.7421
	Ki1	3.441717	0.1092	1.9978	1.1983	0.509808	0.3762
	Kd1	0.874426	0.9775	2.403	1.0794	0.995084	3
	n1	2.719018	-	57.928	500	15.03582	307.57
	λ1	0.639415	1.2028	-	-	-	-
	μ1	2.636113	0.9403	-	-	-	-
	KP2	3.999745	3.0919	1.9102	2.2328	1.865161	1.9881
	Ki2	1.00001	4	3	2.9705	2.997782	2.9963
	Kd2	0.751156	0.8851	0.6106	0.6757	0.576527	0.5997
	n2	1	-	372.48	136.77	166.8088	500
	λ2	2.12244	1	-	-	-	-
	μ2	3.441717	1	-	-	-	-
ITAE Value		0.053522	0.056735	0.0780	0.0816	0.075409	0.0770
ITAE Improvement %		-	5.66%	31.38%	34.41%	29.02%	30.49%

, including the ITAE values from several recently published optimization-based control strategies. These include the (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn), and (SAMPE-JAYA+PIDn) controllers, which have reported ITAE values of 0.056735, 0.0780, 0.0816, 0.075409, and 0.077, respectively. On the other hand, the proposed KET-fractional order PID controller achieves a superior ITAE value of 0.05352, outperforming all compared techniques. These results translate into relative improvements of 5.66%, 31.38%, 34.41%, 29.02% and 30.49%, respectively, when compared with (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn), and (SAMPE-JAYA+PIDn) controllers. This clearly highlights the enhanced tuning capability and dynamic response of the KET, confirming its potential as a robust and efficient tool for load frequency control in complex power systems.

For this case, Figure 6 presents the convergence behavior of the proposed KET compared to the NNA [43] during the tuning process of a fractional-order PID controller, as measured by the ITAE. As shown, the proposed KET exhibits better convergence efficiency after the 50th iteration, consistently lower ITAE throughout the simulation.

Figure 7 illustrates the stability responses due to SCL in Area 2, including both frequency and tie-line power deviations, under the control of (proposed KET+Fractional Order PID), ((NNA+Fractional Order PID), and (ARO+PIDn) controllers. The results clearly show that the KET-tuned fractional-order PID controller delivers superior performance in regulating frequency and tie-line power, even when power output conditions vary. Despite these fluctuations, the KET-based controller maintains robust transient behavior, demonstrating its ability to quickly and accurately respond to changes in load demand while preserving system stability.

4.3. Case 3

In this instance, Areas a and 2 are subjected to an SCL of 0.1 per unit (pu) at time t = 0 s. The controller parameters for this scenario are presented in

Table 4. Controller parameters along with the corresponding performance results for Case 3.

Algorithm		Proposed KET+ Fractional Order PID	NNA+Fractional Order PID	JAYA+PIDn	PSO+PIDn	ARO+PIDn	SAMPE-JAYA+PIDn
Controller Parameters	KP1	2.010182	3.501814	2.1068	1.7764	1.820495	1.8022
	Ki1	3.111396	3.879404	2.9333	3	2.994891	2.6685
	Kd1	1.001229	0.587896	1.4944	0.9385	0.577278	0.6436
	n1	0.603423	-	85.067	392.86	67.01898	138.3
	λ1	0.999839	0.981918	-	-	-	-
	μ1	2.211087	1.021741	-	-	-	-
	KP2	3.999882	2.008655	1.1472	1.562	1.565437	1.7795
	Ki2	1.001595	4	2.9487	2.5835	2.989529	2.859
	Kd2	0.571789	0.863688	0.4789	0.6575	0.462035	0.4627
	n2	0.999903	-	489.58	500	448.9027	340.75
	λ2	2.010182	0.829761	-	-	-	-
	μ2	3.111396	0.992725	-	-	-	-
ITAE Value		0.10782	0.129195	0.2272	0.2354	0.146308	0.1726
ITAE Improvement %		-	16.54%	52.54%	54.20%	26.31%	37.53%

, including the ITAE values from several recently published optimization-based control strategies. These include the (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn), and (SAMPE-JAYA+PIDn) controllers, which have reported ITAE values of 0.129195, 0.2272, 0.2354, 0.146308, and 0.1726, respectively. The proposed KET-fractional order PID controller achieves a superior ITAE value of 0.10782, outperforming all compared techniques. These results translate into relative improvements of 16.54%, 52.54%, 54.20%, 26.31%, and 37.53%, respectively, when compared with (NNA+Fractional Order PID), (JAYA+PIDn), (PSO+PIDn), (ARO+PIDn), and (SAMPE-JAYA+PIDn) controllers. This clearly highlights the enhanced tuning capability and dynamic response of the KET, confirming its potential as a robust and efficient tool for load frequency control in complex power systems.

Figure 8 presents the convergence behavior of the proposed KET compared to the NNA [43] during the tuning of a fractional-order PID controller, using the ITAE as the performance metric. The green curve, representing KET, shows a rapid improvement in performance, especially noticeable after the midpoint of the iterations. While both algorithms begin to plateau around iteration 60, KET consistently achieves a lower ITAE value across the entire simulation. This trend reflects the superior convergence capability of the KET, demonstrating strong exploratory behavior during the initial search phase and effective fine-tuning in later iterations through local exploitation.

Figure 9 displays the frequency and tie-line power responses, along with the overall stability behavior in Area 2, for three different controllers (proposed KET+Fractional Order PID), (NNA+Fractional Order PID), and (ARO+PIDn). As evident from the results, the KET-tuned fractional-order PID controller demonstrates effective regulation of both frequency deviations and tie-line power fluctuations, even under varying power output conditions. Moreover, it maintains strong transient performance, quickly adapting to load changes and ensuring system stability throughout the disturbance period.

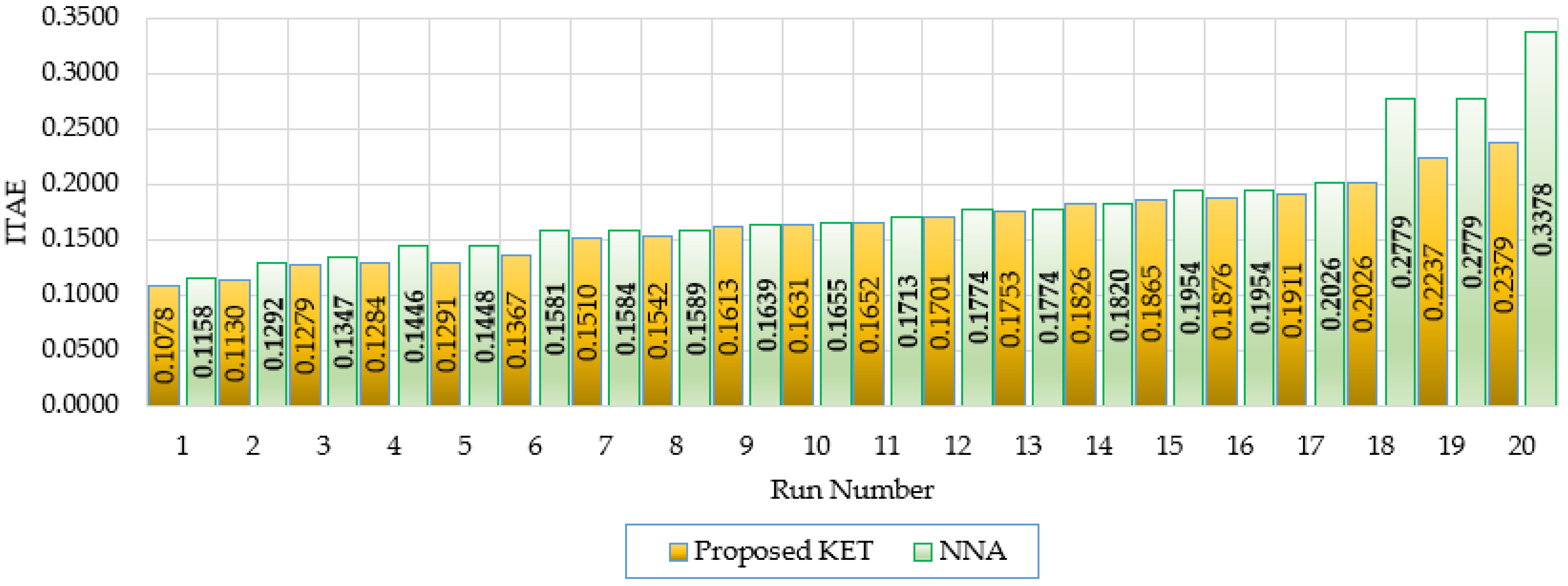
Figure 10 displays the results of 20 independent simulation runs, comparing the ITAE performance of the proposed KET against the NNA for tuning a fractional-order PID controller. As shown, the best ITAE achieved by KET is 0.1078, compared to 0.1158 from NNA, marking a 6.89% improvement. Also, the average ITAE across all runs is 0.1648 for KET versus 0.1775 for NNA, showing a consistent 7.2% improvement in overall performance. Moreover, the worst ITAE value for KET is 0.2379, significantly better than NNA’s 0.3378, reflecting a 29.58% improvement in worst-case behavior. Additionally, the standard deviation of ITAE in KET runs is 0.0351, which is lower than the 0.0550 of NNA, representing a 36.17% improvement in consistency. These results highlight the robustness and reliability of the proposed KET in optimizing the fractional-order PID controller. Not only does KET outperform NNA in the best-case scenario, but it also shows a tighter performance spread, indicating greater stability and repeatability across multiple runs.

The differences observed in the outcomes of independent KET simulations, even when applied to the same system configuration with identical parameters (as listed in Appendix A), are a natural consequence of the stochastic nature of the algorithm. KET, like most metaheuristic optimization techniques, incorporates random variables in various stages of the search process (e.g., random initialization, probabilistic movement strategies, and masking mechanisms). As a result, each run begins with a different set of initial solutions and follows a distinct search trajectory, leading to slight variations in the final output. This behavior is typical of population-based stochastic algorithms and highlights the importance of performing multiple independent runs to evaluate the robustness and consistency of the optimizer.

4.4. Validations Through Comparative Analysis with Other Controllers

To further validate the performance and robustness of the proposed KET-tuned fractional-order PID controller, a comparative analysis was conducted against a range of existing control strategies, both classical and modern. These include PI- and PID-based controllers optimized by well-known methods such as the Firefly Algorithm (FA), Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO), Bacterial Foraging Optimization (BFOA), and their hybrid variants. Additionally, the comparison includes the PID-ARO and the more recent fractional-order PID-NNA controller. The detailed performance metrics, summarized in

Table 5. Performance comparison of different optimization techniques based on ITAE and SET metrics.

Controller	Optimization Approach	SET (s)			Objective Value
		∆f1	∆f2	∆PTIE	ITAE
PI	Conventional [42]	45	45.01	28.27	3.5795
	Firefly Algorithm [42]	7.11	7.22	5.62	0.8695
	Bacterial Forage Optimization [42]	5.52	7.09	6.35	1.8379
	Genetic Algorithm [42]	10.59	11.39	9.37	2.7475
	Differential Evolution [41]	8.96	8.16	5.75	0.9911
	Hybrid Bacterial Forage Optimization-Particle Swarm Optimizer [44]	7.39	7.65	5.73	1.1865
	Particle Swarm Optimizer [44]	7.37	7.82	5.0	1.2142
PID	Artificial Rabbit Algorithm [45]	2.195834	2.901341	3.059294	0.0953
	Firefly Algorithm [42]	4.25	5.49	4.78	0.4714
Fractional-order PID	Neural Network Algorithm [43]	2.4628	3.0024	3.2203	0.059063
	Kangaroo Escape optimization Technique	1.8924	2.6922	2.8875	0.05363897

, clearly indicate that the proposed KET-based controller outperforms all other techniques in terms of both the ITAE and settling time (SET). As shown, the ITAE value achieved by KET is 0.0536, which is lower than those reported by any of the previously tested methods. In terms of settling times, the proposed controller demonstrates superior responsiveness, achieving (i) 1.8924 s for frequency deviation in Area 1, (ii) 2.6922 s for frequency deviation in Area 2, and (iii) 2.8875 s for tie-line power deviation. These results confirm the KET controller’s ability to minimize both transient deviations and the total error accumulation over time more effectively than other algorithms.

The study utilizes simulation-based analysis to develop a fractional-order PID controller that can be technically implemented in real-world multi-area power systems, including the M-APG configuration. The KET is used offline to optimize controller parameters, relying on executing a fractional-order PID control law with fixed parameters for real-time control implementation.

To show the implementation feasibility of the KET-tuned controller, contemporary control hardware, including digital signal processors or even Programmable Logic Control (PLC)-based platforms, can support this architecture, particularly when fractional operators are approximated using rational transfer functions. Also, the suggested controller’s PID-based structure is in line with standard generator control architectures, which makes it easy to integrate with little to no changes. These considerations confirm the practical feasibility of using the KET-tuned controller in operating thermal power plants or other grid-connected producing units. Future work may explore hardware-in-the-loop (HIL) testing [46] or experimental validation to further demonstrate its applicability under real-world conditions.

4.5. Comparative Validation and Robustness Assessment of the KET Using the Speed Reducer Design Benchmark

To comprehensively assess the effectiveness, robustness, and competitive edge of the proposed KET, a comparative evaluation was carried out against a set of recently developed and well-established optimization techniques. The algorithms considered in this benchmark study include the following:

• Mantis Shrimp Optimization Algorithm, 2025, (MShoa) [47];
• Water Uptake and Transport in Plants algorithm, 2025, (WUTP) [48];
• Rime Optimization Algorithm, 2023, (RIME) [49,50,51];
• Walrus Optimizer, 2023, (WO) [52];
• PSO [53]—widely acknowledged in the literature.

The performance of these algorithms was evaluated on the Speed Reducer Design problem, a widely recognized benchmark in industrial design optimization [54]. This problem involves minimizing the weight of a speed reducer used in small aircraft engines, subject to a set of nonlinear constraints. The mathematical formulation of the problem consists of an objective function and multiple constraints, as defined by Equations (25)–(37).

Minimize

$$\begin{array}{l}F\left(x\right)=0.7854x_1{x}_2^2\left(14.9334x_3+3.3333x_3^2-43.0934\right)\\ +7.4777\left(x_6^3+x_7^3\right)+0.7854\left(x_4{x}_6^2+x_5{x}_7^2\right)-1.508x_1\left(x_6^2+x_7^2\right)\end{array}$$

(25)

Subject to

$$G_1\left(x\right)=27-x_1{x}_3{x}_2^2\le 0$$

(26)

$$G_2\left(x\right)=397.5-x_1{x}_2^2{x}_3^2\le 0$$

(27)

$$G_3\left(x\right)=1.93-x_2{x}_3{x}_4^{-3}{x}_6^4\le 0$$

(28)

$$G_4\left(x\right)=1.93-x_2{x}_3{x}_5^{-3}{x}_7^4\le 0$$

(29)

$$G_5\left(x\right)={\displaystyle \frac{10}{x_6^3}}\times {\left(16.91\times {10}^6+{\left(745{\displaystyle \frac{x_4}{x_2{x}_3}}\right)}^2\right)}^{-2}-1100\le 0$$

(30)

$$G_6\left(x\right)={\displaystyle \frac{10}{x_7^3}}\times {\left(157.5\times {10}^6+{\left(745{\displaystyle \frac{x_5}{x_2{x}_3}}\right)}^2\right)}^{-2}-850\le 0$$

(31)

$$G_7\left(x\right)=x_2{x}_3-40\le 0$$

(32)

$$G_8\left(x\right)=5-{\displaystyle \frac{x_1}{x_2}}\le 0$$

(33)

$$G_9\left(x\right)={\displaystyle \frac{x_1}{x_2}}-12\le 0$$

(34)

$$G_{10}\left(x\right)=1.5x_6-x_4+1.9\le 0$$

(35)

$$G_{11}\left(x\right)=1.1x_7-x_5+1.9\le 0$$

(36)

$$\begin{array}{l}0.7\le x_1\le 0.8, 17\le x_2\le 28, 2.6\le x_3\le 3.6, \\ 7.3\le x_4\le 8.3, 7.3\le x_5\le 8.3, 2.9\le x_6\le 3.9, 5\le x_7\le 5.5\end{array}$$

(37)

All six algorithms were implemented using standardized control parameter settings as shown in

Table 6. The proposed KET, RIME, WO, MShoa, WUTP, and PSO parameter settings.

Applied Algorithm	Parameters
RIME	Soft-rime parameters W = 5; Number of rime agents = 50; Maximum number of iterations = 300
PSO	Number of particles = 50; Cognitive parameter c1 = 2; Social parameter c2 = 2; Maximum number of iterations = 300
MShoa	Number of mantis shrimps = 50; Maximum number of iterations = 300
WO	Proportion of females p = 0.4; Number of males = 20; Number of females = 20; Number of children = 10; Maximum number of iterations = 300
WUTP	Number of particles = 50; Alternate parameter p = 0.5; Water density rho = 1000; eta = 0.0018; Gravitational force g = 9.81; Radial hydraulic conductivity Lp = 10−9; Diffusivity coefficient D = 10−9; Hydraulic conductivity K = 10−9; a = 1; Maximum number of iterations = 300
Proposed KET	Number of kangaroos = 50; Maximum number of iterations = 300

, and each was executed for 50 independent runs to ensure statistical robustness. The corresponding optimal design parameters and resulting objective function values (fabrication cost) are presented in

Table 7. Optimal results of the proposed KET, RIME, WO, MShoa, WUTP, and PSO for speed reducer design problem.

Control Parameters	RIME	PSO	MShoa	WO	WUTP	Proposed KET
x1	3.5	3.5	3.5051	3.5001	3.5	3.5
x2	0.7	0.7	0.7	0.7	0.7	0.7
x3	17	17	17.0275	17	17	17
x4	7.3	7.3	7.9325	7.3	7.3	7.3
x5	7.7332	7.7153	8.1195	7.7249	7.7153	7.7153
x6	3.3506	3.3505	3.4305	3.3506	3.3505	3.3505
x7	5.2867	5.2867	5.3161	5.2867	5.2867	5.2867
F(x)	2994.8939	2994.4245	3055.7906	2994.6967	2994.4254	2994.4245

.

The outcomes presented in Table 7 reveal that the proposed KET, RIME, WO, WUTP, and PSO achieve nearly identical optimal values for the control parameters (x₁ to x₇), with minor variations observed in x₃, x₄, and x₅. The proposed KET, WUTP, and PSO converge to the best fabrication cost (F(x)) of 2994.4245, slightly outperforming RIME (2994.8939) and WO (2994.6967), while MShoa lags with a higher cost of 3055.7906. This suggests that KET, alongside PSO and WUTP, provides a highly competitive best solution for this benchmark.

Table 8. Statistical indices of the proposed KET, RIME, WO, MShoa, WUTP, and PSO for speed reducer design.

Statistical Indices	RIME	PSO	MShoa	WO	WUTP	Proposed KET
Minimum Fitness	2994.894	2994.425	3055.791	2994.697	2994.425	2994.425
Mean Fitness	3000.489	3073.803	3270.337	2998.55	2997.196	2994.769
Maximum Fitness	3012.789	3197.598	3664.256	3007.862	3032.007	2999.523
Standard deviation	4.6605	62.7313	150.1988	3.4732	9.2744	0.9185
CPU time(s)	0.4018	0.3495	0.599	0.3876	0.4706	0.4163
Constraints Validation	100%	100%	100%	100%	100%	100%

offers a deeper statistical insight, highlighting KET’s superiority in consistency and efficiency. KET records the lowest mean fitness (2994.769), maximum fitness (2999.523), and standard deviation (0.9185), indicating exceptional stability across runs compared to PSO (standard deviation 62.7313) and MShoa (150.1988). The CPU time for the proposed KET (0.4163 s) is reasonable, falling between the fastest (PSO at 0.3495 s) and slowest (MShoa at 0.599 s), suggesting a balanced computational efficiency. All algorithms successfully met the constraints 100% of the time, affirming their feasibility.

In terms of average fitness, the KET outperformed all competitors, with improvement percentages of 0.19%, 2.57%, 8.43%, 0.13%, and 0.08% when compared to RIME, PSO, MShoa, WO, and WUTP, respectively. The maximum (worst-case) cost achieved by KET (2999.523) was also the lowest among all, indicating strong convergence stability and reduced performance variability. The KET reduced the worst-case cost by 0.64%, 6.37%, 18.18%, 0.28%, and 1.07%, respectively, over RIME, PSO, MShoa, WO, and WUTP. Even more significantly, the KET achieved the least standard deviation of just 0.9185. This reflects a performance consistency improvement of 80.29% over RIME, 98.54% over PSO, 99.39% over MShoa, 73.56% over WO, and 90.10% over WUTP. These findings confirm the superior reliability of KET in generating consistent and near-optimal results across repeated trials, making it a highly robust optimization tool for complex engineering problems.

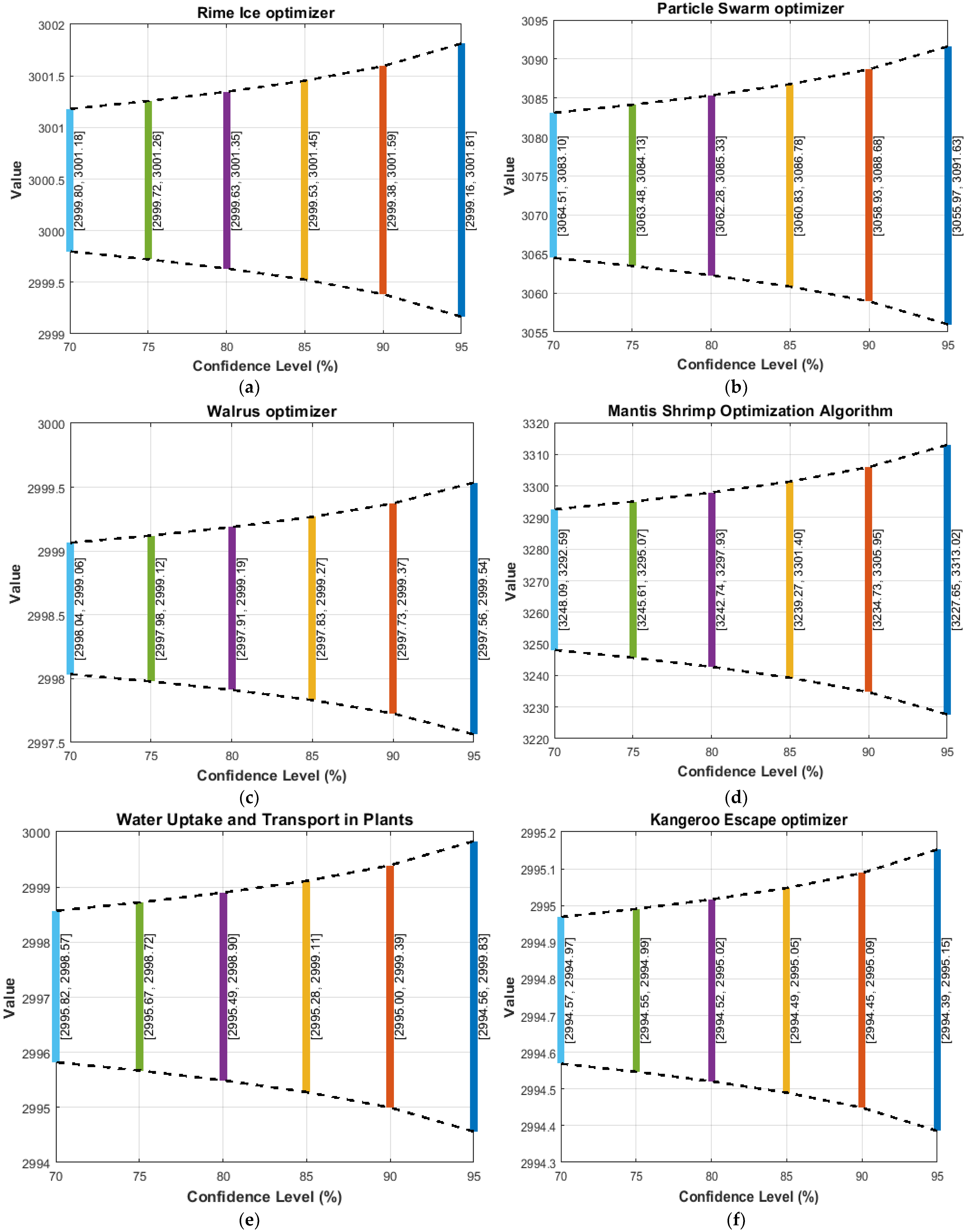
Figure 11a–f illustrates the distribution of fitness scores across various confidence intervals (95%, 90%, 85%, 80%, 75%, 70%) for each algorithm. The KET plot (f) shows a tight clustering of fitness scores, particularly at higher confidence levels (e.g., 95% and 90%), reflecting its robustness and reliability. In contrast, MShoa (d) exhibits a wider spread, indicating greater variability, while PSO (b) and WUTP (e) show moderate dispersion. RIME (a) and WO (c) perform reasonably but do not match KET’s consistency, especially at lower confidence intervals.

5. Conclusions

This study introduced a novel biologically inspired optimization algorithm, the Kangaroo Escape optimization Technique (KET), to enhance the performance of fractional-order PID controllers in Load Frequency Regulation (LFR) applications for multi-area power systems. Drawing inspiration from kangaroo escape behaviors, such as zigzagging motion, long-distance jumping, and decoy dropping, the KET was designed to achieve an adaptive and dynamic balance between exploration and exploitation in the optimization process. Through extensive simulations under three distinct test scenarios (SCL in Area 1, Area 2, and both), the proposed KET-tuned fractional-order PID controller consistently outperformed several state-of-the-art algorithms, including NNA, JAYA, ARO, PSO, DE, and SAMPE-JAYA. It achieved significant improvements in ITAE, settling time, and system stability metrics across all tested cases. Furthermore, convergence analysis and statistical validation demonstrated the superior speed, robustness, and reliability of the proposed method. The results confirm that KET is a powerful and efficient alternative for optimizing control parameters in complex, dynamic, and uncertain power system environments. Future work may extend this approach to renewable-integrated microgrids, incorporate cyber-physical constraints, or explore hybrid versions of KET with other heuristic techniques to further boost performance in high-dimensional control applications. To further establish the efficacy and generalizability of the proposed KET, an additional benchmark based on the speed reducer design was conducted. KET outperformed 50 independent trials in average and worst-case performance, demonstrating strong convergence behavior and robustness, with the lowest standard deviation. These results suggest that KET might be a useful tool for a wider range of limited engineering optimization challenges.

The proposed method for adjusting fractional-order PID controllers shows promise in simulation but requires further research. Renewable energy source integration, alternative formulations, and scalability of the KET algorithm can be explored for real-world validation and application in complex power systems. Moreover, adaptive or hybrid extensions of KET, such as combining it with machine learning models or other metaheuristic techniques, could be developed to enhance convergence behavior and solution quality. Finally, applying KET to other nonlinear and high-dimensional control applications beyond power systems may help generalize its utility and reveal additional strengths or limitations.