Effects of Organic Matter Volume Fraction and Fractal Dimension on Tensile Crack Evolution in Shale Using Digital Core Numerical Models
Abstract
1. Introduction
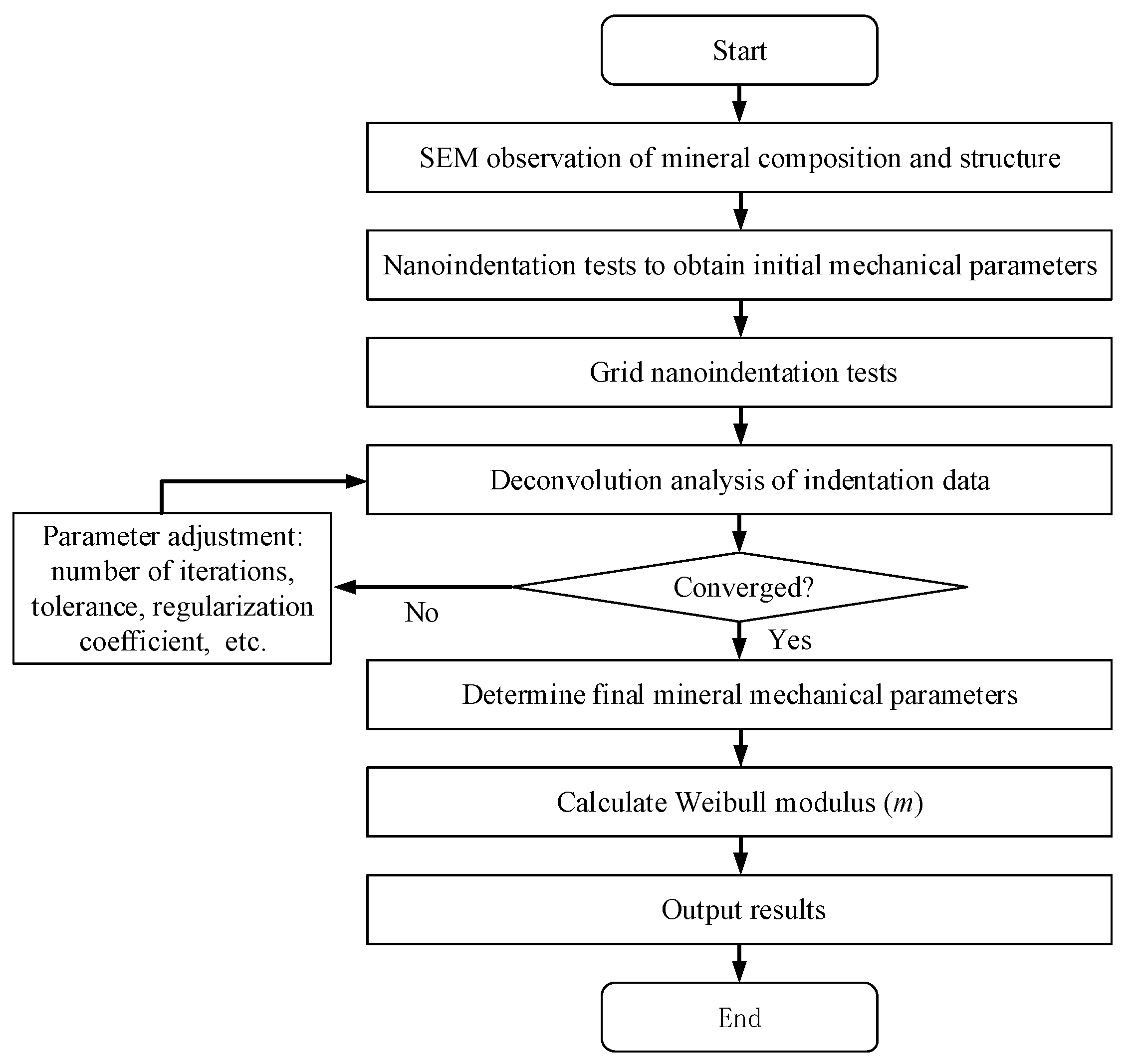
2. Methods and Models
2.1. Elastic–Brittle Damage Constitutive Model Considering Heterogeneity of Mineral Materials
2.1.1. Damage Evolution
2.1.2. Failure Criterion
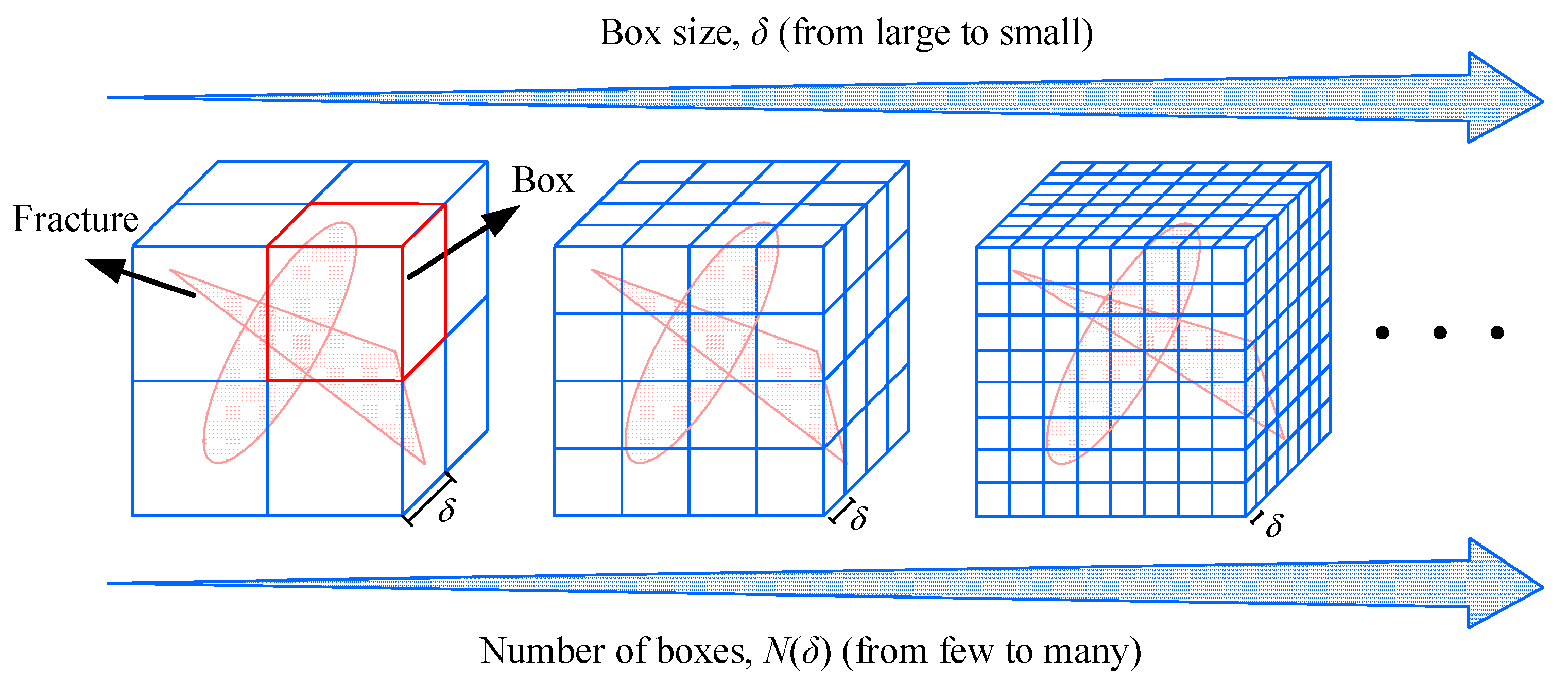
2.2. Construction of Digital Core Numerical Model
2.2.1. Scanning
2.2.2. Median Filtering
2.2.3. Threshold Segmentation
2.2.4. Reconstruction Principle of Digital Core Model
2.2.5. Digital Core Numerical Model
3. Uniaxial Tensile Simulations of Digital Core Numerical Model
3.1. Evolution Process of Tensile Cracks
3.2. Dynamic Evolution Characteristics of Tensile Stress and Damage Variable
3.3. Acoustic Emission Analysis
4. The Influence of Organic Matter Volume Fraction and Fractal Dimension
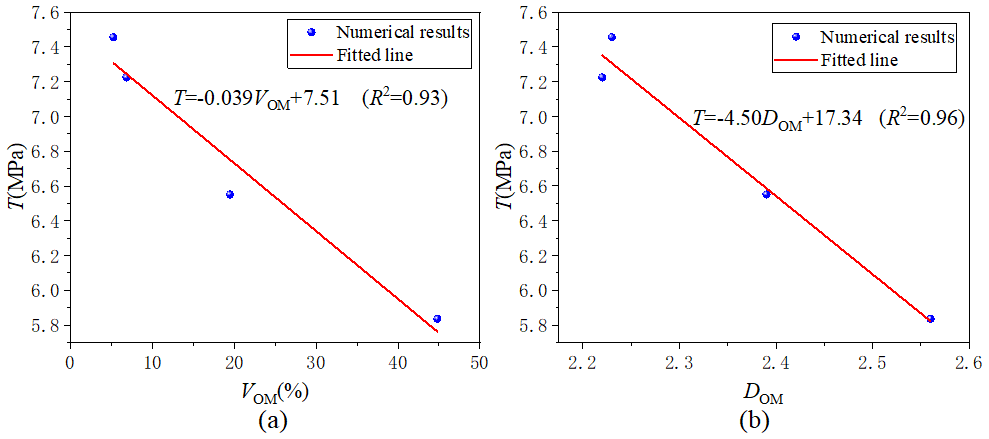
4.1. Tensile Strength
4.2. Characteristic Parameters of Tensile Cracks
5. Analysis of Tensile Fracture Mechanism
5.1. Dynamic Evolution of Microfracture Mechanisms
5.2. Comparison with SEM Scanning Test Results
6. Conclusions
- (1)
- The volume fraction and spatial distribution of organic matter have a significant impact on the location of tensile failure. Tensile cracks tend to initiate at interfaces between minerals with large differences in elastic modulus. When the angle between the normal of organic-matter-filled cracks and the direction of applied tensile stress is smaller, cracks are more likely to initiate and propagate along these organic-matter-filled interfaces.
- (2)
- Under tensile loading, as both the volume fraction and fractal dimension of organic matter increase, the uniaxial tensile strength, global damage variable, unit damage variable, and total number of acoustic emissions all decrease progressively. However, when the volume fractions are approximately equal, specimens with a higher fractal dimension exhibit greater tensile strength, damage variables, and unit damage variables. Therefore, both the volume fraction and fractal dimension of organic matter can be used to predict the tensile strength and damage characteristics of shale specimens.
- (3)
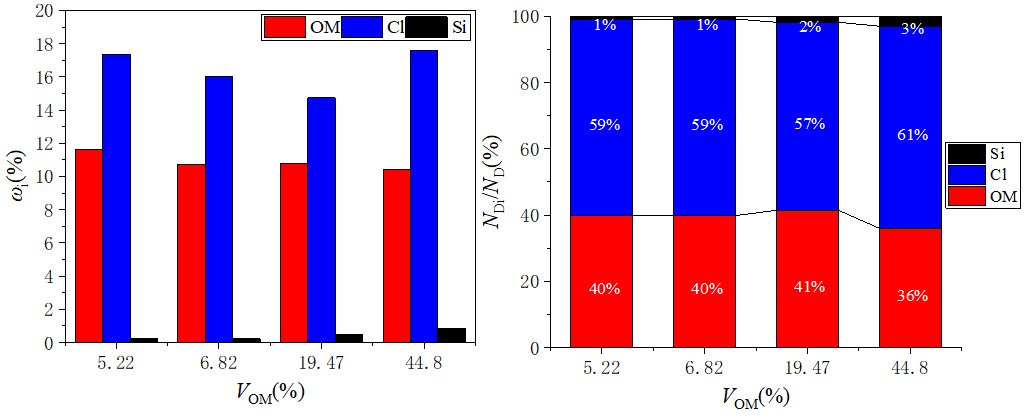
- For organic-rich shale formations primarily composed of clay minerals, organic matter, and silicates, the tensile failure behavior of different mineral phases is governed by both their mechanical properties and spatial distribution. In our digital core simulations under uniaxial tensile loading, the clay matrix exhibits the highest overall failure rate, followed by organic matter, while silicate minerals show the lowest. However, this trend does not reflect intrinsic material weakness alone. The higher failure rate of clay is primarily due to its dominant volume fraction and widespread interfacial contact with both stronger and softer phases. Organic matter displays intermediate failure behavior, which transitions from brittle to ductile as its volume fraction and structural continuity increase. Although silicate minerals rarely fail directly due to their high tensile strength, their stiffness contrast may induce stress concentrations in adjacent regions. Notably, the sequence of failure typically initiates in the clay matrix, progresses through the organic matter, and affects silicate minerals only minimally at the final stages of loading. Crack propagation preferentially occurs at mechanically heterogeneous interfaces.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cl | Clay Matrix |
| FIB-SEM | Focused Ion Beam Scanning Electron Microscopy |
| OM | Organic Matter |
| ROI | Regions of Interest |
| Si | Silicate Mineral |
References
- Goral, J.; Deo, M.; McLennan, J.; Huang, H.; Mattson, E. Macro- and micro-compression testing of shales. J. Pet. Sci. Eng. 2020, 191, 107034. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Yang, C.; Zheng, Y.; Jiang, W.; Menegon, L.; Renard, F.; Peng, P.; Xiong, Y. Upscaling the creep behavior of clay-rich and quartz-rich shales from nanoindentation measurements: Application to the Wufeng-Longmaxi shale, China. Int. J. Rock Mech. Min. Sci. 2023, 171, 105580. [Google Scholar] [CrossRef]
- Yan, D.; Zhao, L.; Wang, Y.; Zhang, Y.; Cai, Z.; Song, X.; Zhang, F.; Geng, J. Heterogeneity indexes of unconventional reservoir shales: Quantitatively characterizing mechanical properties and failure behaviors. Int. J. Rock Mech. Min. Sci. 2023, 171, 105577. [Google Scholar] [CrossRef]
- Guan, Y.; Cui, Z.; Zhou, W. Reconstruction in off-axis digital holography based on hybrid clustering and the fractional Fourier transform. Opt. Laser Technol. 2025, 186, 112622. [Google Scholar] [CrossRef]
- Ni, Z.L.; Ma, J.S.; Liu, Y.; Li, B.H.; Nazarov, A.A.; Li, H.; Yuan, Z.P.; Ling, Z.C.; Wang, X.X. Numerical Analysis of Ultrasonic Spot Welding of Cu/Cu Joints. J. Mater. Eng. Perform. 2025, 1–12. [Google Scholar] [CrossRef]
- Yali, D. High-temperature deformation measurement using optical imaging digital image correlation: Status, challenge and future. Chin. J. Aeronaut. 2025, 38, 103472. [Google Scholar] [CrossRef]
- Zhang, H.H.; Jia, Z.L.; Zhang, P.F.; Liu, Y.; Jiang, L.J.; Ding, D.Z. Electromagnetic-Circuital-Thermal-Mechanical Multiphysics Numerical Simulation Method for Microwave Circuits. IEEE J. Multiscale Multiphysics Comput. Tech. 2024, 9, 129–141. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z. Review of Numerical Modeling Based on Digital Image Processing for Rock Mechanics Applications. Chinese Chin. J. Rock Mech. Eng 2020, 39, 3286–3296. (In Chinese) [Google Scholar]
- Tang, C.A. Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. Sci. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Tang, C.; Ma, T.; Ding, X. On stress-forecasting strategy of earthquakes from stress buildup, stress shadow and stress transfer (SSS) based on numerical approach. Earthq. Sci. 2009, 22, 53–62. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.; Lee, P.; Tsui, Y.; Liu, H. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part II: Constraint, slenderness and size effect. Int. J. Rock Mech. Min. Sci. 2000, 37, 571–583. [Google Scholar] [CrossRef]
- Tang, C.A.; Liu, H.; Lee, P.; Tsui, Y.; Tham, L.G. Numerical studies of the inuence of microstructure on rock failure in uniaxial compression part I: Eect of heterogeneity. Int. J. Rock Mech. Min. Sci. 2000, 37, 555–569. [Google Scholar] [CrossRef]
- Tang, C.A.; Xu, T.; Yang, T.H.; Liang, Z.Z. Numerical investigation of the mechanical behavior of rock under confining pressure and pore pressure. Int. J. Rock Mech. Min. Sci. 2004, 41, 336–341. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Pan, C.; Li, X.; He, L.; Li, J. Study on the effect of micro-geometric heterogeneity on mechanical properties of brittle rock using a grain-based discrete element method coupling with the cohesive zone model. Int. J. Rock Mech. Min. Sci. 2021, 140, 104680. [Google Scholar] [CrossRef]
- Liu, G.; Cai, M.; Huang, M. Mechanical properties of brittle rock governed by micro-geometric heterogeneity. Comput. Geotech. 2018, 104, 358–372. [Google Scholar] [CrossRef]
- Gao, F.; Stead, D.; Elmo, D. Numerical simulation of microstructure of brittle rock using a grain-breakable distinct element grain-based model. Comput. Geotech. 2016, 78, 203–217. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Li, Q.; Xing, H.; Liu, J.; Liu, X. A review on hydraulic fracturing of unconventional reservoir. Petroleum 2015, 1, 8–15. [Google Scholar] [CrossRef]
- Wang, G.; Shen, J.; Liu, S.; Jiang, C.; Qin, X. Three-dimensional modeling and analysis of macro-pore structure of coal using combined X-ray CT imaging and fractal theory. Int. J. Rock Mech. Min. Sci. 2019, 123, 104082. [Google Scholar] [CrossRef]
- Chen, B.; Xiang, J.; Latham, J.-P. Influence of inter-grain cementation stiffness on the effective elastic properties of porous Bentheim sandstone. J. Rock Mech. Geotech. Eng. 2022, 15, 573–583. [Google Scholar] [CrossRef]
- Chen, B.; Xiang, J.; Latham, J.-P.; Bakker, R.R. Grain-scale failure mechanism of porous sandstone: An experimental and numerical FDEM study of the Brazilian Tensile Strength test using CT-Scan microstructure. Int. J. Rock Mech. Min. Sci. 2020, 132, 104348. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, X.-P. Establishment of numerical cracking constitutive models using 3D reconstruction and X-ray CT images of geomaterials. Int. J. Mech. Sci. 2020, 183, 105814. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, Z.Q.; Hu, Y.Z. In situ X-ray micro-CT for investigation of damage evolution in black shale under uniaxial compression. Environ. Earth Sci. 2018, 77, 1–12. [Google Scholar] [CrossRef]
- Eliyahu, M.; Emmanuel, S.; Day-Stirrat, R.J.; Macaulay, C.I. Mechanical properties of organic matter in shales mapped at the nanometer scale. Mar. Pet. Geol. 2015, 59, 294–304. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, J.; Li, P.; Tang, X.; Yang, X.; Qiu, Q.; Dong, Z.; Li, Z. An improved evaluation method for the brittleness index of shale and its application—A case study from the southern north China basin. J. Nat. Gas Sci. Eng. 2018, 59, 47–55. [Google Scholar] [CrossRef]
- Bennett, K.C.; Berla, L.A.; Nix, W.D.; Borja, R.I. Instrumented nanoindentation and 3D mechanistic modeling of a shale at multiple scales. Acta Geotech. 2015, 10, 1–14. [Google Scholar] [CrossRef]
- Bobko, C.P.; Gathier, B.; Ortega, J.A.; Franz, J.; Ulm, F.J.; Borges, L.; Abousleiman, Y.N. The nanogranular origin of friction and cohesion in shale—A strength homogenization approach to interpretation of nanoindentation results. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1854–1876. [Google Scholar] [CrossRef]
- Yang, C.; Xiong, Y.; Wang, J.; Li, Y.; Jiang, W. Mechanical characterization of shale matrix minerals using phase-positioned nanoindentation and nano-dynamic mechanical analysis. Int. J. Coal Geol. 2020, 229, 103571. [Google Scholar] [CrossRef]
- Gerke, K.M.; Korostilev, E.V.; Romanenko, K.A.; Karsanina, M.V. Going submicron in the precise analysis of soil structure: A FIB-SEM imaging study at nanoscale. Geoderma 2021, 383, 114739. [Google Scholar] [CrossRef]
- Tang, X.; Jiang, Z.; Jiang, S.; Li, Z. Heterogeneous nanoporosity of the Silurian Longmaxi Formation shale gas reservoir in the Sichuan Basin using the QEMSCAN, FIB-SEM, and nano-CT methods. Mar. Pet. Geol. 2016, 78, 99–109. [Google Scholar] [CrossRef]
- Gou, Q.; Xu, S.; Hao, F.; Yang, F.; Zhang, B.; Shu, Z.; Zhang, A.; Wang, Y.; Lu, Y.; Cheng, X.; et al. Full-scale pores and micro-fractures characterization using FE-SEM, gas adsorption, nano-CT and micro-CT: A case study of the Silurian Longmaxi Formation shale in the Fuling area, Sichuan Basin, China. Fuel 2019, 253, 167–179. [Google Scholar] [CrossRef]
- Kelly, S.; El-Sobky, H.; Torres-Verdín, C.; Balhoff, M.T. Assessing the utility of FIB-SEM images for shale digital rock physics. Adv. Water Resour. 2016, 95, 302–316. [Google Scholar] [CrossRef]
- Saif, T.; Lin, Q.; Butcher, A.R.; Bijeljic, B.; Blunt, M.J. Multi-scale multi-dimensional microstructure imaging of oil shale pyrolysis using X-ray micro-tomography, automated ultra-high resolution SEM, MAPS Mineralogy and FIB-SEM. Appl. Energy 2017, 202, 628–647. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; He, D.; Sun, P.; Zou, X. Full-scale nanopore system and fractal characteristics of clay-rich lacustrine shale combining FE-SEM, nano-CT, gas adsorption and mercury intrusion porosimetry. Appl. Clay Sci. 2020, 196, 105758. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, S.; Lu, S.; He, Z.; Li, D.; Wang, Z.; Xiao, D. Investigation of mechanical properties of bedded shale by nanoindentation tests: A case study on Lower Silurian Longmaxi Formation of Youyang area in southeast Chongqing, China. Pet. Explor. Dev. 2019, 46, 177–185. (In Chinese) [Google Scholar] [CrossRef]
- Li, T.; Li, L.; Tang, C.A.; Zhang, Z.; Li, M.; Zhang, L.; Li, A. A coupled hydraulic-mechanical-damage geotechnical model for simulation of fracture propagation in geological media during hydraulic fracturing. J. Pet. Sci. Eng. 2019, 173, 1390–1416. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Yang, T.H.; Li, L.C. Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock Mech. 2002, 39, 477–489. [Google Scholar] [CrossRef]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Liang, Z.Z.; Xing, H.; Wang, S.Y.; Williams, D.J.; Tang, C.A. A three-dimensional numerical investigation of the fracture of rock specimens containing a pre-existing surface flaw. Comput. Geotech. 2012, 45, 19–33. [Google Scholar] [CrossRef]
- Zhou, W.; Yan, G.; Yang, R. Elasto brittle damage model for rockmass based on field tests in Laxiwa arch dam site. Chin. J. Geotech. Eng. 1998, 20, 57–60. (In Chinese) [Google Scholar]
- Rankine, W.J.M. A Manual of Applied Mechanics; C. Griffin and Company, Ltd.: London, UK, 1901. [Google Scholar]
- Liu, X.; Meng, S.-W.; Liang, Z.-Z.; Tang, C.; Tao, J.-P.; Tang, J.-Z. Microscale crack propagation in shale samples using focused ion beam scanning electron microscopy and three-dimensional numerical modeling. Pet. Sci. 2023, 20, 1488–1512. [Google Scholar] [CrossRef]
- Ren, Y.; Chua, C.-S.; Ho, Y.-K. Motion detection with nonstationary background. Mach. Vis. Appl. 2003, 13, 332–343. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 52–66. [Google Scholar] [CrossRef]
- Li, X.; Wei, W.; Wang, L.; Cai, J. Fractal Dimension of Digital 3D Rock Models with Different Pore Structures. Energies 2022, 15, 7461. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour. Res. 1990, 26, 1047–1054. [Google Scholar] [CrossRef]
- Wang, Y. Numerical modelling of heterogeneous rock breakage behaviour based on texture images. Miner. Eng. 2015, 74, 130–141. [Google Scholar] [CrossRef]
- Tan, X.; Konietzky, H.; Chen, W. Numerical Simulation of Heterogeneous Rock Using Discrete Element Model Based on Digital Image Processing. Rock Mech. Rock Eng. 2016, 49, 4957–4964. [Google Scholar] [CrossRef]




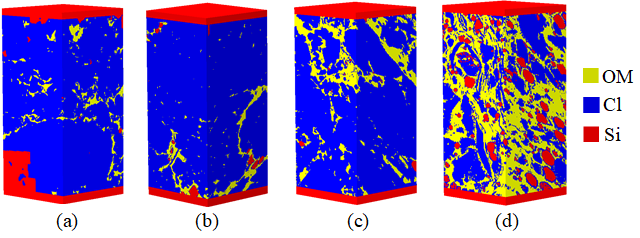
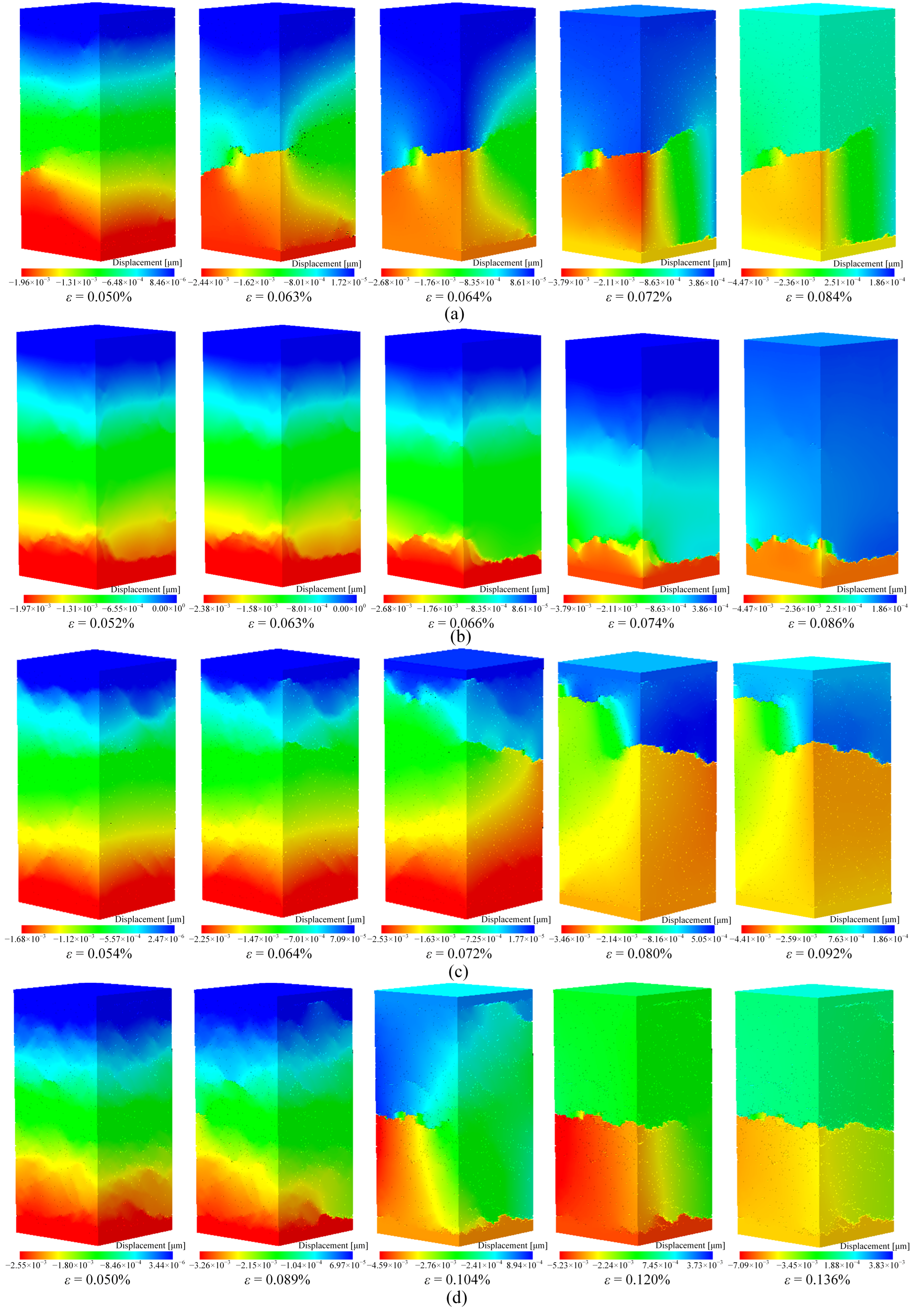


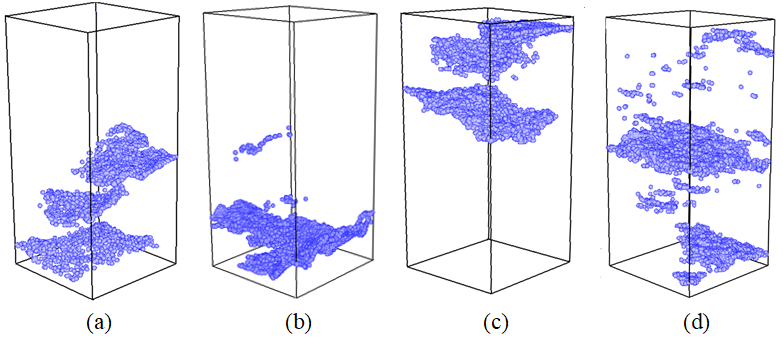




| Model No. | VSi | DSi | VOM | DOM | VCl | DCl |
|---|---|---|---|---|---|---|
| WM1 | 2.30% | 1.83 | 5.22% | 2.23 | 92.43% | 2.32 |
| WM2 | 0.83% | 1.87 | 6.82% | 2.22 | 92.35% | 1.92 |
| WM3 | 1.24% | 1.89 | 19.47% | 2.39 | 79.27% | 2.43 |
| WM4 | 12.24% | 2.27 | 44.80% | 2.56 | 42.87% | 2.59 |
| Mineral Type | Silicate Mineral | Clay Mineral | Organic Matter |
|---|---|---|---|
| Heterogeneity coefficient of elastic modulus | 9.43 | 6.09 | 2.15 |
| Elastic modulus (Gpa) | 95.49 | 35.86 | 8.05 |
| Heterogeneity coefficient of uniaxial compressive strength | 9.73 | 1.73 | 2.09 |
| Uniaxial compressive strength (Mpa) | 507.68 | 143.85 | 94.48 |
| Poisson’s ratio | 0.07 | 0.34 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, Y.; Li, T.; Liang, Z.; Meng, S.; Zheng, L. Effects of Organic Matter Volume Fraction and Fractal Dimension on Tensile Crack Evolution in Shale Using Digital Core Numerical Models. Fractal Fract. 2025, 9, 518. https://doi.org/10.3390/fractalfract9080518
Liu X, Wang Y, Li T, Liang Z, Meng S, Zheng L. Effects of Organic Matter Volume Fraction and Fractal Dimension on Tensile Crack Evolution in Shale Using Digital Core Numerical Models. Fractal and Fractional. 2025; 9(8):518. https://doi.org/10.3390/fractalfract9080518
Chicago/Turabian StyleLiu, Xin, Yuepeng Wang, Tianjiao Li, Zhengzhao Liang, Siwei Meng, and Licai Zheng. 2025. "Effects of Organic Matter Volume Fraction and Fractal Dimension on Tensile Crack Evolution in Shale Using Digital Core Numerical Models" Fractal and Fractional 9, no. 8: 518. https://doi.org/10.3390/fractalfract9080518
APA StyleLiu, X., Wang, Y., Li, T., Liang, Z., Meng, S., & Zheng, L. (2025). Effects of Organic Matter Volume Fraction and Fractal Dimension on Tensile Crack Evolution in Shale Using Digital Core Numerical Models. Fractal and Fractional, 9(8), 518. https://doi.org/10.3390/fractalfract9080518







