Wirtinger-Type Inequalities Involving Tempered Ψ-Fractional Derivatives with Applications

Abstract

In this work, we explore Wirtinger-type inequalities involving tempered Ψ-Caputo fractional derivatives by utilizing Taylor’s formula. We establish more general inequalities for the same operator in $L_p$ norms for $p>1$ by using Hölder’s inequality. Special cases are discussed in the form of remarks by highlighting their relationships with the existing literature. The derived results are also verified through illustrative examples, including tables and graphs. Moreover, applications of the obtained inequalities are discussed in the context of arithmetic and geometric means.

1. Introduction

An essential field of mathematical analysis, fractional calculus has existed as long as classical differential calculus. As scholars explored the various applications of fractional derivatives and integrals in different fields, the scientific investigations of these concepts attracted significant attention in the 20th century. These applications include bioengineering [1], control theory [2], atmospheric and statistical physics [3], optimization, viscoelasticity [4], and electrical and mechanical engineering [5]. There are various definitions and interpretations of fractional integrals and derivatives in the literature. In both simulation and applied studies, the Riemann–Liouville [6], Caputo [6], Hadamard [7], Caputo–Hadamard [8], and Hilfer [9] are regarded as some of the most essential and often employed formulations. In addition to classical operators, fractional derivatives such as the tempered Riemann–Liouville [10], tempered Caputo [10], Ψ-Riemann–Liouville [6], Ψ-Caputo [11], and tempered Ψ-Caputo fractional derivatives [12] have been established to offer more flexibility in modeling. The investigation of inequalities is crucial in multiple fields, especially optimization, integral estimation, and special means. Over the last few decades, extensive research has led to significant advances in fractional integral inequalities. Some of these contributions can be found in [13,14,15]. Furthermore, fractional inequalities are employed in many disciplines within mathematics and science, including optimization, image and signal processing, and probability theory. The Wirtinger inequality, named after Wilhelm Wirtinger, is one of the most well-known inequalities in this field of research. It was first used in 1904 in the context of the isoperimetric inequality. The significance of this outcome lies in the ability of the Wirtinger inequality to link the integral of the square of a function to the integral of the square of its derivative. As in [16], if the function ${\rm Y}\in C^1[\nu ,\kappa ]$ satisfies ${\rm Y}(\nu )={\rm Y}(\kappa )=0$, then

$$\begin{array}{c}\hfill {\int }_{\nu }^{\kappa }{{\rm Y}}^2(h)dh\le {\int }_{\nu }^{\kappa }{({{\rm Y}}^{\prime }(h))}^{2}dh.\end{array}$$

(1)

Beesack extended the aforementioned inequality in [17], as follows.

If ${\rm Y}\in C^2[\nu ,\kappa ]$ with ${\rm Y}(\nu )={\rm Y}(\kappa )=0$, then the following inequality holds:

$$\begin{array}{c}\hfill {\int }_{\nu }^{\kappa }{{\rm Y}}^4(h)dh\le {\displaystyle \frac{4}{3}}{\int }_{\nu }^{\kappa }{({{\rm Y}}^{\prime }(h))}^{4}dh.\end{array}$$

(2)

A variety of issues related to series convergence and identifying the smallest eigenvalues of differential operators are influenced by the interpretation by Beesack and other experts. The first eigenvalue of the Laplace operator is the optimal constant in the Poincare inequality [18]. This inequality is considered a generalization of the Wirtinger inequality. Additionally, Bottcher and Widom analyzed a series of constants that originate in specific cases in their work [19], concentrating particularly on identifying the best possible constant in the Wirtinger–Sobolev inequality. They established a consistent connection between the square of the higher-order derivatives of a function and the integral of the square of the function. Samet Erden developed Wirtinger-type inequalities that are applicable to higher-order differential functions in [20]. Meanwhile, Robert Osserman examined the isoperimetric inequality extensively in [21], covering its refinement, enhanced generalization, and innovative applications. The generalized formulations of the Wirtinger inequality in n-dimensional space were revealed by C.A. Swanson in [22]. In [23], Horst Alzer presented improved variants of the Wirtinger inequality in continuous and discrete forms. Furthermore, in [24], Mohammad W. Alomari established Beesack–Wirtinger-type inequalities for absolutely continuous functions with derivatives in $L_p$ spaces $(p>1)$. Numerous modified Wirtinger-type inequalities were proposed by Sarikaya in [25].

Theorem 1. 

Consider a function ${\rm Y}\in C^1[\nu ,\kappa ]$ such that ${\rm Y}(\nu )={\rm Y}(\kappa )=0$ and ${{\rm Y}}^{\prime }\in L_2[\nu ,\kappa ]$. Then, the following inequality holds:

$${\int }_{\nu }^{\kappa }{[{\rm Y}(h)]}^{2}dh\le {\displaystyle \frac{{(\kappa -\nu )}^2}{6}}{\int }_{\nu }^{\kappa }{\left[{{\rm Y}}^{\prime }(h)\right]}^{2}dh.$$

(3)

Large gaps between the zeros of the Riemann zeta function have been identified via Wirtinger-type inequalities, as established by Samir H. Saker in [26], and similar inequalities have been used in the analysis of time-delay systems by Seuret et al. in [27]. Many researchers have studied Wirtinger-type inequalities in both classical and fractional contexts. Such inequalities involving classical form were examined by Samet Erden in [28]. Later, Erden et al. expanded these inequalities by incorporating Caputo and Riemann–Liouville fractional derivatives in [29]. Furthermore, Samraiz et al. established related inequalities for the Caputo–Hadamard and Hadamard fractional derivatives in [30].

Motivated by previous studies and the various applications of fractional calculus, the objective of this work is to establish a new class of inequalities involving the tempered Ψ-Caputo fractional differential operator, specifically Wirtinger-type inequalities. This operator offers greater flexibility for applications by extending both tempered and Ψ-Caputo fractional operators. To our knowledge, no results are available in the literature for Wirtinger-type inequalities involving tempered Ψ-Caputo fractional derivatives. Therefore, this paper fills the gap by applying Hölder’s inequality to establish new inequalities of this form. It is expected that these outcomes could be beneficial for statistical modeling and mathematical analysis. Furthermore, it is expected that the findings of this work will encourage further investigation into inequalities associated with the tempered Ψ-Caputo fractional operator.

In this paper, we present a novel class of Wirtinger-type inequalities involving tempered Ψ-Caputo fractional derivatives. Specifically, we establish generalized inequalities that extend the classical and fractional Wirtinger inequalities to this more general operator. The paper is organized as follows.

The first section presents the introduction, outlining the background, motivation, and importance of the study. Section 2 offers definitions, notations, and results related to the tempered Ψ-Caputo fractional operator. In Section 3, we derive Wirtinger-type inequalities involving tempered Ψ-Caputo fractional derivatives, supported by examples and relevant remarks. The applications of these inequalities, particularly in the contexts of arithmetic and geometric mean inequalities, are explored in Section 4. Finally, Section 5 provides concluding remarks and summarizes the main results.

2. Preliminaries

We begin by presenting the essential definitions and results necessary for our study. Throughout the article, the terms $C^m[\nu ,\kappa ]$, $L_p[\nu ,\kappa ]$, $\lambda$, and $\alpha$ represent the space of m-times continuously differentiable functions on the interval $[\nu ,\kappa ]$, the space of p-integrable functions for $p>1$, the tempering parameter, and the order of fractional operators, respectively. Following [10], we present the definition of tempered Riemann–Liouville fractional integrals.

Definition 1. 

Let ${\rm Y}(h)$ be a piecewise continuous, real-valued, and integrable function on $(\nu ,\kappa )$. The left- and right-sided tempered Riemann–Liouville fractional integrals of order $\alpha >0$ with $\lambda \ge 0$ are defined as follows:

$$\begin{array}{cc}\hfill {}_{\nu }I^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{}_{\nu }I^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{(h-u)}^{\alpha -1}{e}^{-\lambda (h-u)}{\rm Y}(u)du,\hfill \\ \hfill I_{\kappa }^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{I}_{\kappa }^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{{(-1)}^m}{\Gamma (\alpha )}}{\int }_h^{\kappa }{(u-h)}^{\alpha -1}{e}^{-\lambda (u-h)}{\rm Y}(u)du,\hfill \end{array}$$

where ${}_{\nu }I^{\alpha }$ and $I_{\kappa }^{\alpha }$ are left- and right-sided Riemann–Liouville fractional derivatives defined in [6].

$$\begin{array}{cc}\hfill & {}_{\nu }I^{\alpha }{\rm Y}(h)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{(h-u)}^{\alpha -1}{\rm Y}(u)du,\hfill \\ \hfill & I_{\kappa }^{\alpha }{\rm Y}(h)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_h^{\kappa }{(u-h)}^{\alpha -1}{\rm Y}(u)du.\hfill \end{array}$$

The definition of tempered Riemann–Liouville fractional derivatives is presented here, according to [10].

Definition 2. 

For $m-1<\alpha <m$, $m\in \mathbb{N}$, and $\lambda \ge 0$, the tempered Riemann–Liouville fractional derivatives of order α are defined as

$$\begin{array}{cc}\hfill {}_{\nu }D^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{}_{\nu }D^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{e^{-\lambda h}}{\Gamma (m-\alpha )}}{\displaystyle \frac{d^m}{d{h}^m}}{\int }_{\nu }^h{(h-u)}^{m-\alpha -1}{e}^{\lambda u}{\rm Y}(u)du,\hfill \\ \hfill D_{\kappa }^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{D}_{\kappa }^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{{(-1)}^m{e}^{-\lambda h}}{\Gamma (m-\alpha )}}{\displaystyle \frac{d^m}{d{h}^m}}{\int }_h^{\kappa }{(u-h)}^{m-\alpha -1}{e}^{\lambda u}{\rm Y}(u)du,\hfill \end{array}$$

where ${}_{\nu }D^{\alpha }$ and $D_{\kappa }^{\alpha }$ are Riemann–Liouville fractional derivatives as defined in [6].

$$\begin{array}{cc}\hfill & {}_{\nu }D^{\alpha }(e^{\lambda h}{\rm Y}(h))={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\displaystyle \frac{d^m}{d{h}^m}}{\int }_{\nu }^h{(h-u)}^{m-\alpha -1}{e}^{\lambda u}{\rm Y}(u)du,\hfill \\ \hfill & D_{\kappa }^{\alpha }(e^{\lambda h}{\rm Y}(h))={\displaystyle \frac{{(-1)}^m}{\Gamma (m-\alpha )}}{\displaystyle \frac{d^m}{d{h}^m}}{\int }_h^{\kappa }{(u-h)}^{m-\alpha -1}{e}^{\lambda u}{\rm Y}(u)du.\hfill \end{array}$$

As in [6], the tempered Caputo fractional derivatives are presented here.

Definition 3. 

Let $m-1<\alpha <m$, $m\in \mathbb{N}$, and $\lambda \ge 0$; then, the left- and right-sided tempered Caputo fractional derivatives of order α are defined below:

$$\begin{array}{cc}\hfill {}_{\nu }{}^c\mathfrak{D}^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{}_{\nu }{}^c\mathfrak{D}^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{e^{-\lambda h}}{\Gamma (m-\alpha )}}{\int }_{\nu }^h{(h-u)}^{m-\alpha -1}{\displaystyle \frac{d^m}{d{u}^m}}(e^{\lambda u}{\rm Y}(u))du,\hfill \\ \hfill {}^c\mathfrak{D}_{\kappa }^{\alpha ,\lambda }{\rm Y}(h)& =e^{-\lambda h}{}^c\mathfrak{D}_{\kappa }^{\alpha }(e^{\lambda h}{\rm Y}(h))\hfill \\ & ={\displaystyle \frac{{(-1)}^m{e}^{-\lambda h}}{\Gamma (m-\alpha )}}{\int }_h^{\kappa }{(u-h)}^{m-\alpha -1}{\displaystyle \frac{d^m}{d{u}^m}}(e^{\lambda u}{\rm Y}(u))du,\hfill \end{array}$$

where ${}_{\nu }{}^c\mathfrak{D}^{\alpha }$ and ${}^c\mathfrak{D}_{\kappa }^{\alpha }$ denote the Caputo fractional derivatives defined here according to [6].

$$\begin{array}{cc}\hfill & {}_{\nu }{}^c\mathfrak{D}^{\alpha }(e^{\lambda h}{\rm Y}(h))={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\int }_{\nu }^h{(h-u)}^{m-\alpha -1}{\displaystyle \frac{d^m}{d{u}^m}}(e^{\lambda u}{\rm Y}(u))du,\hfill \\ \hfill & {}^c\mathfrak{D}_{\kappa }^{\alpha }(e^{\lambda h}{\rm Y}(h))={\displaystyle \frac{{(-1)}^m}{\Gamma (m-\alpha )}}{\int }_h^{\kappa }{(u-h)}^{m-\alpha -1}{\displaystyle \frac{d^m}{d{u}^m}}(e^{\lambda u}{\rm Y}(u))du.\hfill \end{array}$$

According to [6], the definitions of Ψ-Riemann–Liouville fractional derivatives and integrals are provided here, where we analyze the fractional operators involving a kernel based on another function.

Definition 4. 

For a finite or infinite interval $(\nu ,\kappa )$ $(-\infty \le \nu <\kappa \le \infty )$, assume an integrable function Υ defined on $I=[\nu ,\kappa ]$. Suppose that $\mathrm{\Psi }\in C^1(I)$ is an increasing and positive monotone function such that ${\mathrm{\Psi }}^{\prime }(h)\ne 0$ for all $h\in I$. Then, the left-sided Ψ-Riemann–Liouville fractional integral of order $\alpha >0$ is defined as

$$\begin{array}{c}\hfill {}_{\nu }I^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(h)-\mathrm{\Psi }(u))}^{\alpha -1}{\rm Y}(u)du,\end{array}$$

and the right-sided Ψ-Riemann–Liouville fractional integral of order $\alpha >0$ is defined as

$$\begin{array}{c}\hfill I_{\kappa }^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(u)-\mathrm{\Psi }(h))}^{\alpha -1}{\rm Y}(u)du.\end{array}$$

Definition 5. 

The left- and right-sided Ψ-Riemann–Liouville fractional derivatives of order $\alpha >0$ are defined as follows:

$$\begin{array}{cc}\hfill {}_{\nu }D^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)& ={\left({\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{}_{\nu }I^{m-\alpha ,\mathrm{\Psi }}{\rm Y}(h)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\left({\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(h)-\mathrm{\Psi }(u))}^{m-\alpha -1}{\rm Y}(u)du,\hfill \\ \hfill D_{\kappa }^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)& ={\left(-{\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{I}_{\kappa }^{m-\alpha ,\mathrm{\Psi }}{\rm Y}(h)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\left(-{\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(u)-\mathrm{\Psi }(h))}^{m-\alpha -1}{\rm Y}(u)du.\hfill \end{array}$$

The definition reduces to standard fractional derivatives for particular choices of the function $\mathrm{\Psi }$. The Hadamard fractional derivative, as presented in [7], is obtained by choosing $\mathrm{\Psi }(h)=logh$ and the Riemann–Liouville fractional derivative, as defined in [6], by setting $\mathrm{\Psi }(h)=h$.

As introduced in [11], the definition of Ψ-Caputo fractional derivatives is presented below.

Definition 6. 

Consider ${\rm Y},\mathrm{\Psi }\in C^m(I)$ such that Ψ is increasing and ${\mathrm{\Psi }}^{\prime }(h)\ne 0$ for all $h\in I$, where I is the interval $[\nu ,\kappa ]$. The left-sided Ψ-Caputo fractional derivative of order $\alpha >0$ is defined as

$$\begin{array}{cc}\hfill {}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)& ={}_{\nu }I^{m-\alpha ,\mathrm{\Psi }}{\left({\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{\rm Y}(h)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(h)-\mathrm{\Psi }(u))}^{m-\alpha -1}{{\rm Y}}_{\mathrm{\Psi }}^{\left[m\right]}(u)du.\hfill \end{array}$$

The right-sided Ψ-Caputo fractional derivative of order $\alpha >0$ is given by

$$\begin{array}{cc}\hfill {}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi }}{\rm Y}(h)& =I_{\kappa }^{m-\alpha ,\mathrm{\Psi }}{\left(-{\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{\rm Y}(h)\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (m-\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(u)-\mathrm{\Psi }(h))}^{m-\alpha -1}{(-1)}^m{{\rm Y}}_{\mathrm{\Psi }}^{\left[m\right]}(u)du,\hfill \end{array}$$

where $m=\left[\alpha \right]+1$. For simplicity, we use the abbreviated form

$$\begin{array}{c}\hfill {{\rm Y}}_{\mathrm{\Psi }}^{\left[m\right]}(h)={\left({\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m{\rm Y}(h).\end{array}$$

By substituting $\mathrm{\Psi }(h)=h$, the definition reduces to the classical Caputo fractional derivative, as defined in [6], and by letting $\mathrm{\Psi }(h)=logh$, the definition yields the Caputo–Hadamard fractional derivative, as presented in [8].

Following [12], we now present a new type of fractional integral, called tempered $\mathrm{\Psi }$-fractional integral.

Definition 7. 

Consider the real function ${\rm Y}(h)$, which is continuous on $[\nu ,\kappa ]$. Suppose that $\mathrm{\Psi }(h)\in C^1[\nu ,\kappa ]$ is an increasing differentiable function such that ${\mathrm{\Psi }}^{\prime }(h)\ne 0$ for all $h\in [\nu ,\kappa ]$, and $\lambda \ge 0$. Then, the left- and right-sided tempered Ψ-fractional integrals of order $\alpha >0$ are defined as

$$\begin{array}{cc}\hfill {}_{\nu }I^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)& =e^{-\lambda \mathrm{\Psi }(h)}{}_{\nu }I^{\alpha ,\mathrm{\Psi }}(e^{\lambda \mathrm{\Psi }(h)}{\rm Y}(h))\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(u){[\mathrm{\Psi }(h)-\mathrm{\Psi }(u)]}^{\alpha -1}{e}^{-\lambda [\mathrm{\Psi }(h)-\mathrm{\Psi }(u)]}{\rm Y}(u)du,\hfill \\ \hfill I_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)& =e^{-\lambda \mathrm{\Psi }(h)}{I}_{\kappa }^{\alpha ,\mathrm{\Psi }}(e^{\lambda \mathrm{\Psi }(h)}{\rm Y}(h))\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(u){[\mathrm{\Psi }(u)-\mathrm{\Psi }(h)]}^{\alpha -1}{e}^{-\lambda [\mathrm{\Psi }(u)-\mathrm{\Psi }(h)]}{\rm Y}(u)du.\hfill \end{array}$$

Here, we present the definition of tempered Ψ-Caputo fractional derivatives, as introduced in [12].

Definition 8. 

Suppose that $\mathrm{\Psi }\in C^m[\nu ,\kappa ]$ is an increasing differentiable function and ${\mathrm{\Psi }}^{\prime }(h)\ne 0$ for all $h\in [\nu ,\kappa ]$. Let $m-1<\alpha <m$ and $\lambda \ge 0$. Then, the left- and right-sided tempered Ψ-Caputo fractional derivatives of order $\alpha >0$ are defined as follows:

$$\begin{array}{cc}\hfill & {}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)={\displaystyle \frac{e^{-\lambda \mathrm{\Psi }(h)}}{\Gamma (m-\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(h)-\mathrm{\Psi }(u))}^{m-\alpha -1}{{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[m\right]}(u)du,\hfill \\ \hfill & {}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)={\displaystyle \frac{e^{-\lambda \mathrm{\Psi }(h)}}{\Gamma (m-\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(u){(\mathrm{\Psi }(u)-\mathrm{\Psi }(h))}^{m-\alpha -1}{(-1)}^m{{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[m\right]}(u)du,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[m\right]}(h)={\left({\displaystyle \frac{1}{{\mathrm{\Psi }}^{\prime }(h)}}{\displaystyle \frac{d}{dh}}\right)}^m(e^{\lambda \mathrm{\Psi }(h)}{\rm Y}(h)).\end{array}$$

The definition of tempered Ψ-Caputo fractional derivatives extends several well-known fractional derivatives. For instance, when the tempering parameter $\lambda =0$, we obtain Ψ-Caputo fractional derivatives. Similarly, by setting $\lambda =0$, and $\mathrm{\Psi }(h)=h$, we arrive at the Caputo fractional derivatives. Also, by setting $\lambda =0$, and $\mathrm{\Psi }(h)=logh$, we obtain the Caputo–Hadamard fractional derivatives.

The following result corresponds to Theorem 1 introduced by Medved et al. in [12].

Theorem 2. 

If the assumptions in Definition (7) and (8) are satisfied, then the following identities hold:

$$\begin{array}{c}\hfill {\rm Y}(h)={}_{\nu }I^{\alpha ,\mathrm{\Psi },\lambda }[{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)]+e^{-\lambda \mathrm{\Psi }(h)}\sum _{i=0}^{m-1}{C}_i(h){[\mathrm{\Psi }(h)-\mathrm{\Psi }(\nu )]}^i,\end{array}$$

(4)

$$\begin{array}{c}\hfill {\rm Y}(h)=I_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }[{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)]+e^{-\lambda \mathrm{\Psi }(h)}\sum _{i=0}^{m-1}{C}_i(h){[\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(h)]}^i,\end{array}$$

(5)

where the coefficients $C_i(h)$ are given by

$$\begin{array}{c}\hfill C_i(h)={\displaystyle \frac{{{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[m\right]}(h)}{i!}}.\end{array}$$

By merging the flexibility of the Ψ-fractional framework with the tempering effect, the tempered Ψ-Caputo fractional derivative offers a more precise model for memory-dependent phenomena over finite ranges. It addresses the limitations of classical fractional derivatives by capturing decay behavior more accurately and providing control over long-term dependence. This makes it an effective tool for analyzing complex dynamic systems with tempered memory effects, anomalous dispersion, and viscoelasticity. In particular, this article explores the application of this derivative in deriving Wirtinger-type inequalities.

3. Main Results

Wirtinger-type inequalities involving tempered Ψ-Caputo fractional derivatives are discussed in this section. Several particular cases are presented by exploring the relationship among various types of fractional derivatives. The key identities stated in (4) and (5) are employed to derive the results.

Theorem 3. 

Let ${\rm Y},\mathrm{\Psi }\in C^m[\nu ,\kappa ]$, where $m=\lceil \alpha \rceil$, $\alpha \ge 1$. Assume that ${}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)$, ${}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)\in L_2[\nu ,\kappa ]$, and ${{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\nu )={{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\kappa )=0$, for all $t=0,1,\dots ,m-1$.

Let $U={sup}_{h\in [\nu ,\kappa ]}{\mathrm{\Psi }}^{\prime }(h)$. Then, we have the following inequality:

$$\begin{array}{cc}\hfill {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{2}dh& \le {\displaystyle \frac{{\mathit{U}}^2{(\kappa -\nu )}^2}{6{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^2\right]d\tau .\hfill \end{array}$$

(6)

Idea of the proof. The proof begins by expressing the function ${\rm Y}(h)$ in integral form with its left- and right-sided tempered Ψ-Caputo fractional integrals. The Cauchy–Schwarz inequality is applied for estimating these representations, supposing that ${\rm Y}(h)$ and its generalized fractional derivatives vanish at the endpoints. After integrating the resulting expressions over subintervals, the integrals are rearranged by applying the Dirichlet formula. A change of variable is applied to adjust the interval, and the order of integration is changed to separate the fractional terms. Lastly, by setting suitable bounds to the associated weight function, the desired inequality is obtained.

Proof. 

First, we take the absolute values of (4) and (5) under the condition ${{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\nu )={{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\kappa )=0$. Next, we apply the Cauchy–Schwarz inequality to the resulting expressions.

$$\begin{array}{cc}\hfill {|{\rm Y}(h)|}^2& ={\left|{\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(s)e^{-\lambda (\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}{(\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}^{\alpha -1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)ds\right|}^2\hfill \\ & \le \left[{\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}{\left({\int }_{\nu }^h|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|ds\right)}^2\right]\hfill \\ & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}(h-\nu )\left[{\int }_{\nu }^h{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{2}ds\right],\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill {|{\rm Y}(h)|}^2& ={\left|{\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(s)e^{-\lambda (\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}{(\mathrm{\Psi }(s)-\mathrm{\Psi }(h))}^{\alpha -1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)ds\right|}^2\hfill \\ & \le \left[{\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}{\left({\int }_h^{\kappa }{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|ds\right)}^2\right]\hfill \\ & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\left(\kappa -h\right)\left[{\int }_h^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{2}ds\right].\hfill \end{array}$$

(8)

By integrating (7) with respect to h over the interval $[\nu ,\sigma \nu +(1-\sigma )\kappa ]$, where $\sigma \in [0,1]$, and applying Dirichlet’s formula, we obtain the following:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }(h-\nu ){\int }_{\nu }^h{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{2}dsdh\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^2{\int }_s^{\sigma \nu +(1-\sigma )\kappa }(h-\nu )dhds\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^2}{2{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^2({(\kappa -\nu )}^2{(1-\sigma )}^2-{(s-\nu )}^2)ds.\hfill \end{array}$$

(9)

Then, by applying Dirichlet’s formula after integrating (8) over the interval $[\sigma \nu +(1-\sigma )\kappa ,\kappa ]$, we derive

$$\begin{array}{cc}\hfill & {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }(\kappa -h){\int }_h^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{2}dsdh\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\kappa }^{\sigma \nu +(1-\sigma )\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^2{\int }_s^{\sigma \nu +(1-\sigma )\kappa }(\kappa -h)dhds\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^2}{2{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^2\left({(\kappa -\nu )}^2{\sigma }^2-{(\kappa -s)}^2\right)ds.\hfill \end{array}$$

(10)

Then, by applying the change of variable $s=\rho \nu +(1-\rho )\kappa$ to (9) and (10), we obtain the expressions in their modified form:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\sigma }^1[{(1-\sigma )}^2-{(1-\rho )}^2]{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{2}d\rho ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_0^{\sigma }[{\sigma }^2-{\rho }^2]{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{2}d\rho .\hfill \end{array}$$

The following expression is obtained by combining the two inequalities above and integrating with respect to $\sigma$ over the interval [0, 1].

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times [{\int }_0^1{\int }_{\sigma }^1[{(1-\sigma )}^2-{(1-\rho )}^2]{{|}_{\nu }^c{\mathfrak{D}}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )|}^{2}d\rho d\sigma \hfill \\ \hfill & +{\int }_0^1{\int }_0^{\sigma }[{\sigma }^2-{\rho }^2]{|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )|}^{2}d\rho d\sigma ].\hfill \end{array}$$

(11)

By changing the order of integration, we obtain

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times [{\int }_0^1{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^2{\int }_0^{\rho }[{(1-\sigma )}^2-{(1-\rho )}^2]d\sigma d\rho \hfill \\ \hfill & +{\int }_0^1{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^2{\int }_{\rho }^1[{\sigma }^2-{\rho }^2]d\sigma d\rho ].\hfill \end{array}$$

Furthermore, we arrive at

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{2}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2}{{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times [{\int }_0^1{S}_1(\rho ){\left|{}_{\nu }{}^c\mathfrak{D}_{\nu +}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{2}d\rho \hfill \\ \hfill & +{\int }_0^1{S}_2(\rho ){\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }(\rho \nu +(1-\rho )\kappa )\right|}^{2}d\rho ],\hfill \end{array}$$

(12)

where

$$\begin{array}{c}\hfill S_1(\rho )={\displaystyle \frac{1}{3}}-{\displaystyle \frac{{(1-\rho )}^3}{3}}-\rho {(1-\rho )}^2,\end{array}$$

and

$$\begin{array}{c}\hfill S_2(\rho )={\displaystyle \frac{1}{3}}-{\displaystyle \frac{{\rho }^3}{3}}-{\rho }^2(1-\rho ).\end{array}$$

We obtain (6) by substituting $\tau =\rho \nu +(1-\rho )\kappa$ in (12) and by observing that for $\rho \in [0,1]$, the maximum values of the functions $S_1(\rho )$ and $S_2(\rho )$ are both ${\displaystyle \frac{1}{3}}$. □

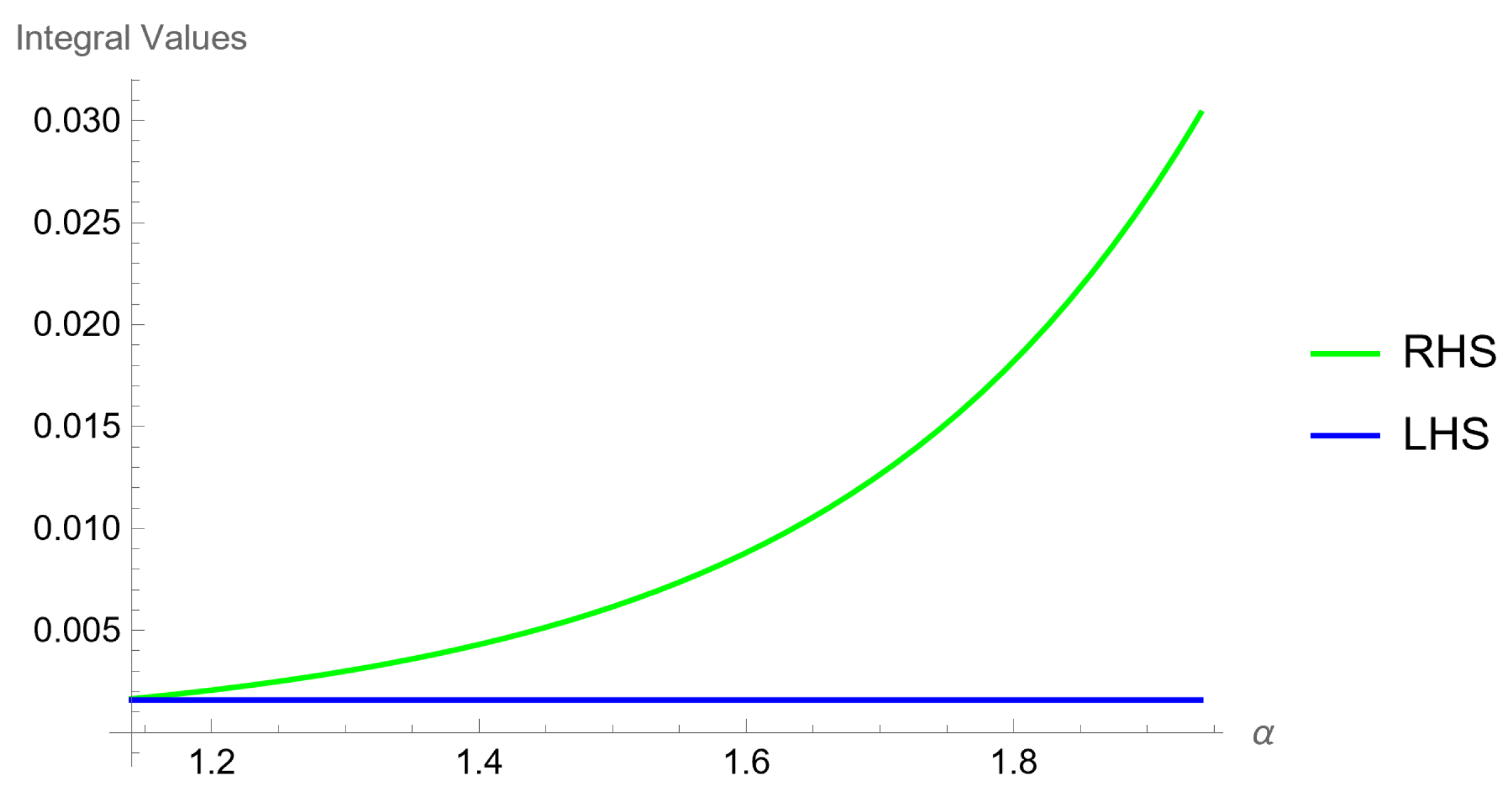
Example 1. 

Let ${\rm Y}(h)={(h-1)}^m{(2-h)}^m$ and $\mathrm{\Psi }(h)=h$ be two functions defined on the interval $[1,2]$, satisfying the conditions of the theorem, such that ${{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(1)={{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(2)=0$ for $t=0,1,\dots ,m-1$. If we assume that $m=2$, $\alpha =1.5$, $\lambda =1$, and $\mathit{U}=1$, then we obtain

$$\begin{array}{c}\hfill {\int }_1^2{|{\rm Y}(h)|}^{2}dh=0.0015873.\end{array}$$

We proceed with the following steps in our calculation to determine the value of the right-hand side of (6).

$$\begin{array}{cc}\hfill {}_1{}^c\mathfrak{D}^{1.5,1}{\rm Y}(h)& =0.56419e^{-h}[1.77245e^h(-1.4375+12h-9.5h^2+h^4)-e^h((6+4h-11h^2\hfill \\ & +2h^3+h^4)Gamma[0.5,-1+h]-2(2-11h+3h^2+2h^3)Gamma[1.5,-1+h]\hfill \\ & -11Gamma[2.5,-1+h]+6hGamma[2.5,-1+h]+6h^{2}Gamma[2.5,-1+h]\hfill \\ & -2Gamma[3.5,-1+h]-4hGamma[3.5,-1+h]+Gamma[4.5,-1+h]\left)\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {}^c\mathfrak{D}_2^{1.5,1}{\rm Y}(h)& =0.56419e^{-h}[(-3.25594\ast {10}^{-16})e^h(-1.4375+12h-9.5h^2+h^4)\hfill \\ & -{\displaystyle \frac{1}{{(2-h)}^{1.5}}}{e}^h{(-2+h)}^{1.5}((6+4h-11h^2+2h^3+h^4)Gamma[0.5,-2+h]\hfill \\ & -2(2-11h+3h^2+2h^3)Gamma[1.5,-2+h]-11Gamma[2.5,-2+h]\hfill \\ & +6hGamma[2.5,-2+h]+6h^{2}Gamma[2.5,-2+h]-2Gamma[3.5,-2+h]\hfill \\ & -4hGamma[3.5,-2+h]+Gamma[4.5,-2+h])].\hfill \end{array}$$

From the calculation, we obtain

$$\begin{array}{c}\hfill {\int }_1^2\left[{|}_1^c{\mathfrak{D}}^{1.5,1}{{\rm Y}(h)|}^2+{{|}^c{\mathfrak{D}}_2^{1.5,1}{\rm Y}(h)|}^2\right]dh=0.214638.\end{array}$$

Also, by using the assumptions on the parameters, we can write

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{U}}^2{(2-1)}^2}{6{[\Gamma (1.5)]}^2}}{e}^{-2}{(\mathrm{\Psi }(2)-\mathrm{\Psi }(1))}^{2(1.5)-2}=0.028719.\end{array}$$

By substituting these values into the right-hand side of (6), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\mathit{U}}^2{(2-1)}^2}{6{[\Gamma (1.5)]}^2}}{e}^{-2}{(\mathrm{\Psi }(2)-\mathrm{\Psi }(1))}^{2(1.5)-2}{\int }_1^2\left[{|}_1^c{\mathfrak{D}}^{1.5,1}{{\rm Y}(h)|}^2+{{|}^c{\mathfrak{D}}_2^{1.5,1}{\rm Y}(h)|}^2\right]dh\hfill \\ \hfill & =0.028719\ast 0.214638\hfill \\ \hfill & =0.00616421.\hfill \end{array}$$

The validity of inequality (6) is confirmed by mathematical calculations, which offer

$$\begin{array}{c}\hfill 0.0015873\le 0.00616421.\end{array}$$

Figure 1 displays the corresponding graphs of (6) for $\mathrm{\Psi }(h)=h$ over the interval $[1,2]$ for some values of $\alpha$, while Table 1 presents the associated numerical values.

Figure 1. The graphical representation of inequality (6) with $\mathrm{\Psi }(h)=h$ over the interval $[1,2]$ for different values of $\alpha$.

Table 1. The left- and right-hand side values of inequality (6) for different choices of the parameter α.

α	1.14	1.34	1.54	1.74	1.94
Left side	0.0015873	0.0015873	0.0015873	0.0015873	0.0015873
Right side	0.00164705	0.0034747	0.00711157	0.0146234	0.0303739

Discussion. The purpose of the example above is to demonstrate the validity of Theorem 3. The functions and parameters are chosen in accordance with the hypotheses of the theorem, satisfying all required conditions. The calculations and graphs were obtained using Wolfram Mathematica 13.2, and it is clearly observable that as $\alpha$ increases, the right-hand side values also increase. This behavior is expected, as the constant on the right-hand side includes power and exponential terms.

Additionally, it is observed that the right-hand side is significantly larger than the left-hand side. This indicates that although the inequality provides a valid upper bound, it may not be very tight. This occurs because the inequality is constructed to be valid for a wide class of functions, not just the specific one used in this example. However, the result remains useful, and future studies could aim to refine the constants or establish sharper bounds for specific cases.

Remark 1. 

The result for the Ψ-Caputo fractional derivative can be obtained by setting $\lambda =0$ in Theorem 3.

Remark 2. 

The result for the Caputo–Hadamard fractional derivative can be obtained by setting $\lambda =0$ and $\mathrm{\Psi }(h)=logh$ into Theorem 3, as established by Samraiz et al. in [30].

Remark 3. 

By choosing $\lambda =0$ and $\mathrm{\Psi }(h)=h$ in Theorem 3, we recover the result for the Caputo fractional derivatives, presented by Erden et al. in [29].

Theorem 4. 

Suppose that the functions ${\rm Y},\mathrm{\Psi }\in C^m[\nu ,\kappa ]$, where $m\in \mathbb{N}\setminus \left\{0\right\}$ with $m=\lceil \alpha \rceil$, and assume that ${}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)$, ${}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(h)$ belong to $L_p[\nu ,\kappa ]$ for $(p>1)$. If $\alpha \ge 1$ and ${{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\nu )={{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(\kappa )=0$ for all $t=0,1,\dots ,m-1$, then the inequality

$$\begin{array}{cc}\hfill {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{p}dh& \le {\displaystyle \frac{{\mathit{U}}^p{(\kappa -\nu )}^p}{p(p+1){[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^p+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^p\right]d\tau ,\hfill \end{array}$$

(13)

holds.

Proof. 

To begin the proof, we first take the absolute values of (4) and (5) and then apply the Cauchy–Schwarz inequality on the resulting expressions with the indices p and ${\displaystyle \frac{p}{p-1}}$ to obtain the following:

$$\begin{array}{cc}\hfill {|{\rm Y}(h)|}^p& ={\left|{\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_{\nu }^h{\mathrm{\Psi }}^{\prime }(s)e^{-\lambda (\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}{(\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}^{\alpha -1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)ds\right|}^p\hfill \\ & \le \left[{\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}{\left({\int }_{\nu }^h|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|ds\right)}^p\right]\hfill \\ & \le {\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}{(h-\nu )}^{p-1}\left[{\int }_{\nu }^h{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{p}ds\right],\hfill \end{array}$$

(14)

and

$$\begin{array}{cc}\hfill {|{\rm Y}(h)|}^p& ={\left|{\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_h^{\kappa }{\mathrm{\Psi }}^{\prime }(s)e^{-\lambda (\mathrm{\Psi }(h)-\mathrm{\Psi }(s))}{(\mathrm{\Psi }(s)-\mathrm{\Psi }(h))}^{\alpha -1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)ds\right|}^p\hfill \\ & \le \left[{\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}{\left({\int }_h^{\kappa }{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|ds\right)}^p\right]\hfill \\ & \le {\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}{\left(\kappa -h\right)}^{p-1}\left[{\int }_h^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{p}ds\right].\hfill \end{array}$$

(15)

By using Dirichlet’s formula and integrating (14) with respect to h over the interval $[\nu ,\sigma \nu +(1-\sigma )\kappa ]$, where $\sigma \in [0,1]$, we obtain the following expression:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{(h-\nu )}^{p-1}{\int }_{\nu }^h{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{p}dsdh\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^p{\int }_s^{\sigma \nu +(1-\sigma )\kappa }{(h-\nu )}^{p-1}dhds\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^p}{p{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^p\left({(\kappa -\nu )}^p{(1-\sigma )}^p-{(s-\nu )}^p\right)ds.\hfill \end{array}$$

(16)

By integrating (15) over the interval $[\sigma \nu +(1-\sigma )\kappa ,\kappa ]$ and using Dirichlet’s formula, we derive

$$\begin{array}{cc}\hfill & {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{(\kappa -h)}^{p-1}{\int }_h^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^{p}dsdh\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\kappa }^{\sigma \nu +(1-\sigma )\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^p{\int }_s^{\sigma \nu +(1-\sigma )\kappa }{(\kappa -h)}^{p-1}dhds\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{U}}^p}{p{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{{|}^c{\mathfrak{D}}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(s)|}^p\left({(\kappa -\nu )}^p{\sigma }^p-{(\kappa -s)}^p\right)ds.\hfill \end{array}$$

(17)

The expressions are then further simplified by using the change of variable $s=\rho \nu +(1-\rho )\kappa$ in (16) and (17), i.e.,

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\sigma \nu +(1-\sigma )\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{2{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_{\sigma }^1[{(1-\sigma )}^p-{(1-\rho )}^p]{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{p}d\rho ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{\sigma \nu +(1-\sigma )\kappa }^{\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{p{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times {\int }_0^{\sigma }[{\sigma }^p-{\rho }^p]{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{p}d\rho .\hfill \end{array}$$

By combining the above two inequalities and integrating the resulting expression over the interval [0, 1] with respect to $\sigma$, we get

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{p{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times [{\int }_0^1{\int }_{\sigma }^1[{(1-\sigma )}^p-{(1-\rho )}^p]{{|}_{\nu }^c{\mathfrak{D}}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )|}^{p}d\rho d\sigma \hfill \\ \hfill & +{\int }_0^1{\int }_0^{\sigma }[{\sigma }^p-{\rho }^p]{|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )|}^{p}d\rho d\sigma ].\hfill \end{array}$$

(18)

By changing the order of integration, one obtains the following result:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{p{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times [{\int }_0^1{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^p{\int }_0^{\rho }[{(1-\sigma )}^p-{(1-\rho )}^p]d\sigma d\rho \hfill \\ \hfill & +{\int }_0^1{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^p{\int }_{\rho }^1[{\sigma }^p-{\rho }^p]d\sigma d\rho ].\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{p}dh\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^p}{{[\Gamma (\alpha )]}^p}}{e}^{-p\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{p\alpha -p}\hfill \\ \hfill & \times [{\int }_0^1{S}_3(\rho ){\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\rho \nu +(1-\rho )\kappa )\right|}^{p}d\rho \hfill \\ \hfill & +{\int }_0^1{S}_4(\rho ){\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }(\rho \nu +(1-\rho )\kappa )\right|}^{p}d\rho ],\hfill \end{array}$$

(19)

where

$$\begin{array}{c}\hfill S_3(\rho )={\displaystyle \frac{1}{p+1}}-{\displaystyle \frac{{(1-\rho )}^{p+1}}{p+1}}-\rho {(1-\rho )}^p,\end{array}$$

and

$$\begin{array}{c}\hfill S_4(\rho )={\displaystyle \frac{1}{p+1}}-{\displaystyle \frac{{\rho }^{p+1}}{p+1}}-{\rho }^p(1-\rho ).\end{array}$$

By applying the change of variable $\tau =\rho \nu +(1-\rho )\kappa$ in (19) and observing that the maximum value of the functions $S_3(\rho )$ and $S_4(\rho )$ is ${\displaystyle \frac{1}{p+1}}$ for $\rho \in [0,1]$, we arrive at (13). □

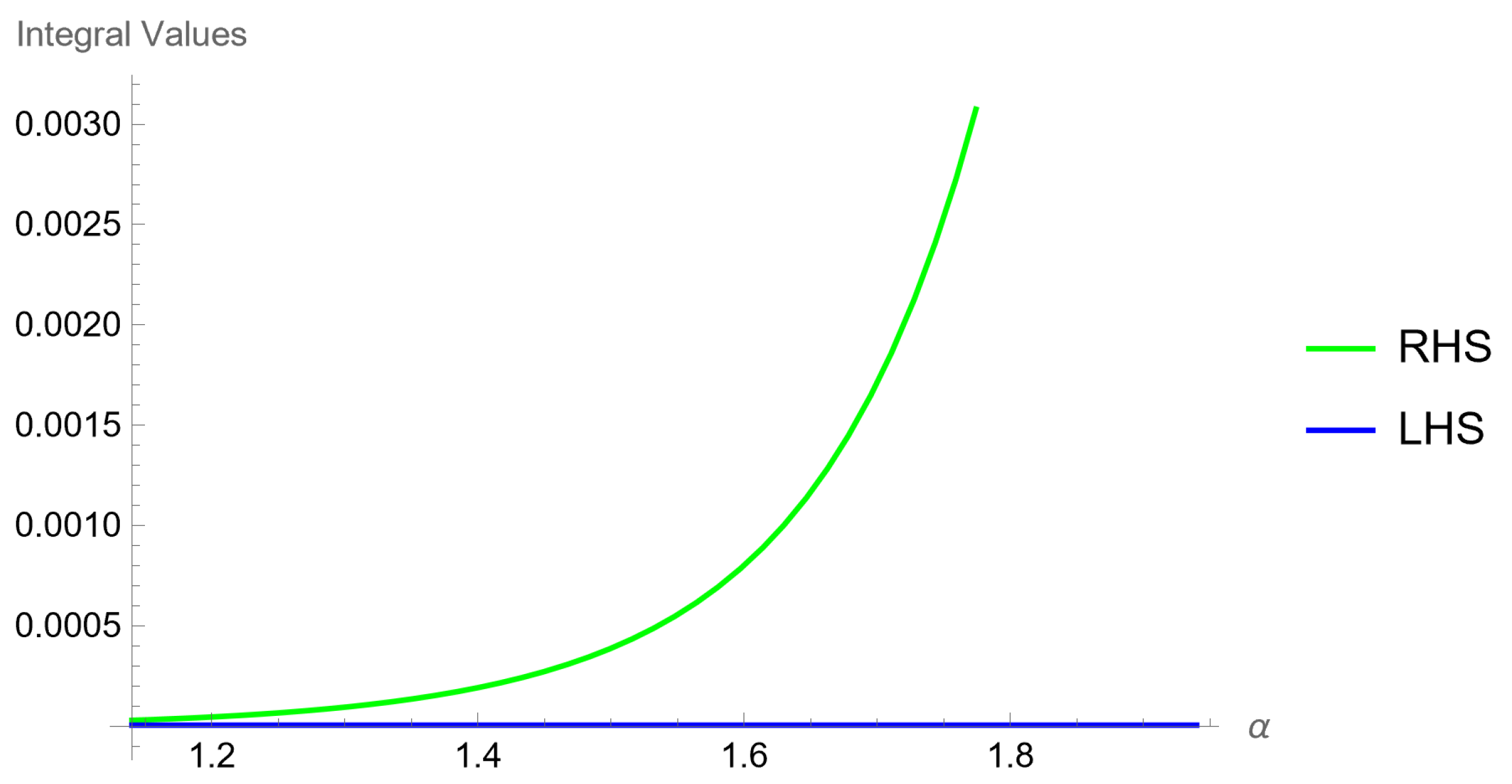
Example 2. 

Consider the functions ${\rm Y}(h)={(h-1)}^m{(2-h)}^m$ and $\mathrm{\Psi }(h)=h$ on the interval $[1,2]$, which satisfy the conditions of the theorem, such that ${{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(1)={{\rm Y}}_{\mathrm{\Psi },\lambda }^{\left[t\right]}(2)=0$ for all $t=0,1,\dots ,m-1$. Let $m=2$, $\alpha =1.5,$$\lambda =1$ and $\mathit{U}=1$. Then, we obtain

$$\begin{array}{c}\hfill {\int }_1^2{|{\rm Y}(h)|}^{4}dh=0.00000457059.\end{array}$$

Hence, 0.0000832501 is the left-hand side value of (13).

We proceed with the following steps to evaluate the right-hand side of (13):

$$\begin{array}{cc}\hfill {}_1{}^c\mathfrak{D}^{1.5,1}{\rm Y}(h)& =0.56419e^{-h}[1.77245e^h(-1.4375+12h-9.5h^2+h^4)-e^h((6+4h-11h^2\hfill \\ & +2h^3+h^4)Gamma[0.5,-1+h]-2(2-11h+3h^2+2h^3)Gamma[1.5,-1+h]\hfill \\ & -11Gamma[2.5,-1+h]+6hGamma[2.5,-1+h]+6h^{2}Gamma[2.5,-1+h]\hfill \\ & -2Gamma[3.5,-1+h]-4hGamma[3.5,-1+h]+Gamma[4.5,-1+h]\left)\right],\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {}^c\mathfrak{D}_2^{1.5,1}{\rm Y}(h)& =0.56419e^{-h}[(-3.25594\ast {10}^{-16})e^h(-1.4375+12h-9.5h^2+h^4)\hfill \\ & -{\displaystyle \frac{1}{{(2-h)}^{1.5}}}{e}^h{(-2+h)}^{1.5}((6+4h-11h^2+2h^3+h^4)Gamma[0.5,-2+h]\hfill \\ & -2(2-11h+3h^2+2h^3)Gamma[1.5,-2+h]-11Gamma[2.5,-2+h]\hfill \\ & +6hGamma[2.5,-2+h]+6h^{2}Gamma[2.5,-2+h]-2Gamma[3.5,-2+h]\hfill \\ & -4hGamma[3.5,-2+h]+Gamma[4.5,-2+h])].\hfill \end{array}$$

By combining theses results, we obtain

$$\begin{array}{c}\hfill {\int }_1^2\left[|{}_1{}^c\mathfrak{D}^{1.5,1}{{\rm Y}(h)|}^4+{|{}^c\mathfrak{D}_2^{1.5,1}{\rm Y}(h)|}^4\right]dh=0.035332.\end{array}$$

Moreover, using the assumed parameters values, we can write

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mathit{U}}^4{(2-1)}^4}{20{[\Gamma (1.5)]}^4}}{(\mathrm{\Psi }(2)-\mathrm{\Psi }(1))}^{4(1.5)-4}=0.0109699.\end{array}$$

By substituting these values into the right-hand side of (13), we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\mathit{U}}^4{(2-1)}^4}{20{[\Gamma (1.5)]}^4}}{(\mathrm{\Psi }(2)-\mathrm{\Psi }(1))}^{4(1.5)-4}{\int }_1^2\left[|{}_1{}^c\mathfrak{D}^{1.5,1}{{\rm Y}(h)|}^4+{|{}^c\mathfrak{D}_2^{1.5,1}{\rm Y}(h)|}^4\right]dh\hfill \\ \hfill & =0.0109699\ast 0.035332\hfill \\ \hfill & =0.000387588.\hfill \end{array}$$

Thus, the numerical result confirms that

$$\begin{array}{c}\hfill 0.00000457059\le 0.000387588.\end{array}$$

This relation demonstrates the validity of (13).

Figure 2 illustrates the graphs corresponding to inequality (13) for $\mathrm{\Psi }(h)=h$ over the interval $[1,2]$, for several values of the parameter $\alpha$, while Table 2 provides the associated numerical values.

Figure 2. The graph of inequality (13) with $\mathrm{\Psi }(h)=h$ over the interval $[1,2]$ for different values of $\alpha$.

Table 2. The left- and right-hand sides of (13) for different values of the parameter α.

α	1.14	1.34	1.54	1.74	1.94
Left side	0.00000457	0.00000457	0.00000457	0.00000457	0.00000457
Right side	0.0000285097	0.000125172	0.000516443	0.00234213	0.0119992

Discussion. The purpose of the aforementioned example is to demonstrate the validity of Theorem 4. Functions and parameters were chosen to satisfy the conditions of the theorem. Using Wolfram Mathematica, the calculations and graphs were generated. The results clearly indicate that the values on the right-hand side increase as $\alpha$ increases. Additionally, we observe that the right-hand side is significantly larger than the left-hand side. This shows that although the inequality provides a valid upper bound, it may not be very tight. This happens because the inequality has been constructed to be valid for various types of functions, not only the one given in the example. While the result remains useful, further studies may aim to improve the constants or develop sharper bounds for specific cases.

Remark 4. 

By replacing $p=4$, $\lambda =0$, and $\mathrm{\Psi }(h)=logh$ in Theorem 4, we recover [30] (Remark 2.2):

$$\begin{array}{cc}\hfill {\int }_{\nu }^{\kappa }{|{\rm Y}(h)|}^{4}dh& \le {\displaystyle \frac{{\mathit{U}}^4{(\kappa -\nu )}^4}{20{[\Gamma (\alpha )]}^4}}{e}^{-4\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{4\alpha -4}\hfill \\ & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^4+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\tau )\right|}^4\right]d\tau .\hfill \end{array}$$

Remark 5. 

Setting $p=2$ in Theorem 4 yields (6).

Remark 6. 

By substituting $\lambda =0$ into Theorem 4, we obtain the result corresponding to the Ψ-Caputo fractional derivatives.

Remark 7. 

If we substitute $\lambda =0$ and $\mathrm{\Psi }(h)=logh$ into Theorem 4, we recover the result for the Caputo–Hadamard fractional derivatives, established by Samraiz et al. in [30].

Remark 8. 

By taking $\lambda =0$ and $\mathrm{\Psi }(h)=h$ in Theorem 4, we obtain the result for the Caputo fractional derivatives, as derived by Erden et al. in [29].

4. Generalized Wirtinger Inequalities with Applications to Arithmetic–Geometric Mean Inequality

In this section, we present fundamental inequalities that provide tighter bounds for functions involving both integer-order and fractional derivatives, particularly in systems with memory effects and nonlocal behavior. Within the framework of the tempered Ψ-Caputo fractional derivative, these results enhance flexibility in modeling memory effects and domain scaling, by incorporating features from both Wirtinger-type and arithmetic–geometric mean inequalities. These inequalities are useful tools for advancing research on complex dynamical systems in both applied and theoretical contexts due to their broad applicability in the investigation of fractional differential equations and control problems. We begin by recalling the following elementary inequalities from [31], which are essential to deriving the results presented in this section. For real numbers $L_1,L_2,\dots ,L_m\ge 0$ with $m\ge 1$, we have the following inequalities:

$$\begin{array}{c}\hfill {\left(\prod _{i=1}^m{L}_i\right)}^{{\displaystyle \frac{1}{m}}}\le {\displaystyle \frac{1}{m}}\sum _{i=1}^m{L}_i,\end{array}$$

(20)

and

$$\begin{array}{c}\hfill {\left(\sum _{i=1}^m{L}_i\right)}^2\le m\sum _{i=1}^m{L}_i^2.\end{array}$$

(21)

The theorems presented below have geometric-type expressions on the left-hand side and arithmetic-type relations on the right-hand side.

Theorem 5. 

Let the function $\Phi (\xi )$ be a real-valued, non-negative, and continuous function defined on the interval $I=[\nu ,\kappa ]$. Suppose that ${\rm Y}(\xi )$ satisfies ${}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi ),{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\in C^{m-1}(I)$ and $D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi ),D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )$ are absolutely continuous for all $\xi \in I$, where $i=1,2,\dots m$. If, in addition, ${\rm Y}(\nu )={\rm Y}(\kappa )=0$, then the following inequality holds:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|\Phi (\xi )|}^2\left[{\left(\prod _{i=1}^m{|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right)}^{{\displaystyle \frac{2}{m}}}+{\left(\prod _{i=1}^m{|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right)}^{{\displaystyle \frac{2}{m}}}\right]d\xi \hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2{(\kappa -\nu )}^2}{6m{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right]d\xi \hfill \\ \hfill & \times \left[\sum _{i=1}^m\right({\int }_{\nu }^{\kappa }|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^{2}d\xi {\int }_{\nu }^{\kappa }{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \hfill \\ \hfill & +{\int }_{\nu }^{\kappa }|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^{2}d\xi {\int }_{\nu }^{\kappa }{|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \left)\right].\hfill \end{array}$$

(22)

Proof. 

We begin the proof by stating the following identities, which are easily derived:

$$\begin{array}{cc}\hfill & {[D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )]}^2=2{\int }_{\nu }^{\xi }[D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )][D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )]d\varkappa ,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {[D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )]}^2=-2{\int }_{\xi }^{\kappa }[D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )][D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )]d\varkappa ,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & {[D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )]}^2=2{\int }_{\nu }^{\xi }[D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )][D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )]d\varkappa ,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & {[D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )]}^2=-2{\int }_{\xi }^{\kappa }[D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )][D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )]d\varkappa ,\hfill \end{array}$$

(26)

for $\xi \in I$ and $i=1,2,\dots ,m$. The inequality below is obtained by adding (23) and (24):

$$\begin{array}{c}\hfill |D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^2\le {\int }_{\nu }^{\kappa }|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^2{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi .\end{array}$$

(27)

Similarly, by adding (25) and (26), we obtain the following inequality:

$$\begin{array}{c}\hfill |D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^2\le {\int }_{\nu }^{\kappa }|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^2{|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi .\end{array}$$

(28)

By applying the elementary inequalities given in (20) and (21), along with the Cauchy–Schwarz inequality, to (27), we obtain

$$\begin{array}{cc}\hfill & {\left[\prod _{i=1}^m{|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right]}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\left[\prod _{i=1}^m\left({\int }_{\nu }^{\kappa }|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )||D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi \right)\right]}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left({\int }_{\nu }^{\kappa }|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )||D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi \right)\right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{1}{m^2}}\left[m\sum _{i=1}^m{\left({\int }_{\nu }^{\kappa }|D^{i-1}{c}_{\nu }{\mathfrak{D}}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )||D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi \right)}^2\right]\hfill \\ \hfill & \le {\displaystyle \frac{1}{m}}\left[\sum _{i=1}^m\right(\left({\int }_{\nu }^{\kappa }{|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\hfill \\ \hfill & \times \left({\int }_{\nu }^{\kappa }{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\left)\right].\hfill \end{array}$$

(29)

Similarly, from (28), we derive

$$\begin{array}{cc}\hfill & {\left[\prod _{i=1}^m{|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right]}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{m}}\left[\sum _{i=1}^m\right(\left({\int }_{\nu }^{\kappa }{|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\hfill \\ \hfill & \times \left({\int }_{\nu }^{\kappa }{|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\left)\right].\hfill \end{array}$$

(30)

By combining (29) and (30), we arrive at

$$\begin{array}{cc}\hfill & {\left[\prod _{i=1}^m{|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right]}^{{\displaystyle \frac{2}{m}}}+{\left[\prod _{i=1}^m{|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right]}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{m}}\left[\sum _{i=1}^m\right(\left({\int }_{\nu }^{\kappa }{|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\left({\int }_{\nu }^{\kappa }{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\hfill \\ \hfill & +\left({\int }_{\nu }^{\kappa }{|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\left({\int }_{\nu }^{\kappa }{|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\left)\right].\hfill \end{array}$$

(31)

By integrating (31) over the interval $[\nu ,\kappa ]$, after multiplying by ${|\Phi (\xi )|}^2$, and then by utilizing (6), we arrive at (22). □

Remark 9. 

The following Wirtinger-type inequality is obtained by setting $m=1$ in (22):

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|\Phi (\xi )|}^2\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^4+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^4\right]d\xi \hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{U}}^2{(\kappa -\nu )}^2}{6{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right]d\xi \hfill \\ \hfill & [\left({\int }_{\nu }^{\kappa }{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^{2}d\xi {\int }_{\nu }^{\kappa }{\left|D{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^{2}d\xi \right)\hfill \\ \hfill & +\left({\int }_{\nu }^{\kappa }{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^{2}d\xi {\int }_{\nu }^{\kappa }{\left|D{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^{2}d\xi \right)].\hfill \end{array}$$

Theorem 6. 

Under the conditions defined in Theorem 5, we derive the following inequality:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|\Phi (\xi )|}^2\left[{\left(\prod _{i=1}^m\left|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|\right)}^{{\displaystyle \frac{2}{m}}}+{\left(\prod _{i=1}^m\left|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|\right)}^{{\displaystyle \frac{2}{m}}}\right]d\xi \hfill \\ \hfill & \le {\displaystyle \frac{{(\kappa -\nu )}^3}{4m}}{\displaystyle \frac{{\mathit{U}}^2}{6{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right]d\xi \hfill \\ & \times {\int }_{\nu }^{\kappa }\left[\sum _{i=1}^m\left({\left|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right)\right]d\xi .\hfill \end{array}$$

(32)

Proof. 

Clearly, the following identities hold:

$$\begin{array}{cc}\hfill & D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )d\xi ={\int }_{\nu }^{\xi }{D}^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )d\varkappa ,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )d\xi =-{\int }_{\xi }^{\kappa }{D}^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )d\varkappa ,\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )d\xi ={\int }_{\nu }^{\xi }{D}^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )d\varkappa ,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )d\xi =-{\int }_{\xi }^{\kappa }{D}^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\varkappa )d\varkappa ,\hfill \end{array}$$

(36)

for $\xi \in I$ and $i=1,2,\dots m$. Using identities (33)–(36), we obtain the following:

$$\begin{array}{c}\hfill |D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\le {\displaystyle \frac{1}{2}}{\int }_{\nu }^{\kappa }|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi ,\end{array}$$

(37)

$$\begin{array}{c}\hfill |D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\le {\displaystyle \frac{1}{2}}{\int }_{\nu }^{\kappa }|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi ,\end{array}$$

(38)

for $\xi \in I$ and $i=1,2,\dots m$. Now, considering (37), by applying the Cauchy–Schwarz inequality along with identities (20) and (21), we obtain the following:

$$\begin{array}{cc}\hfill & {\left(\prod _{i=1}^m|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\right)}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\left[\prod _{i=1}^m\left({\displaystyle \frac{1}{2}}{\int }_{\nu }^{\kappa }|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi \right)\right]}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{4}}{\left[{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left({\int }_{\nu }^{\kappa }|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|d\xi \right)\right]}^2\hfill \\ \hfill & \le {\displaystyle \frac{\kappa -\nu }{4m}}\sum _{i=1}^m\left({\int }_{\nu }^{\kappa }{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^{2}d\xi \right)\hfill \\ \hfill & ={\displaystyle \frac{\kappa -\nu }{4m}}{\int }_{\nu }^{\kappa }\left(\sum _{i=1}^m{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right)d\xi .\hfill \end{array}$$

(39)

By using a similar method to (38), we derive the following:

$$\begin{array}{cc}\hfill & {\left(\prod _{i=1}^m|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\right)}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\displaystyle \frac{\kappa -\nu }{4m}}{\int }_{\nu }^{\kappa }\left(\sum _{i=1}^m{|D^i{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right)d\xi .\hfill \end{array}$$

(40)

By adding (39) and (40), we obtain

$$\begin{array}{cc}\hfill & {\left(\prod _{i=1}^m|D^{i-1}{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\right)}^{{\displaystyle \frac{2}{m}}}+{\left(\prod _{i=1}^m|D^{i-1}{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|\right)}^{{\displaystyle \frac{2}{m}}}\hfill \\ \hfill & \le {\displaystyle \frac{\kappa -\nu }{4m}}{\int }_{\nu }^{\kappa }\left[\sum _{i=1}^m\left(|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{{\rm Y}(\xi )|}^2+{|D^i{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )|}^2\right)\right]d\xi .\hfill \end{array}$$

(41)

By multiplying both sides of (41) by ${|\Phi (\xi )|}^2$, integrating over the interval $[\nu ,\kappa ]$, and then using (6), we obtain (32). □

Remark 10. 

Setting $m=1$ in (32), we attain the following Wirtinger-type inequality:

$$\begin{array}{cc}\hfill & {\int }_{\nu }^{\kappa }{|\Phi (\xi )|}^2\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right]d\xi \hfill \\ \hfill & \le {\displaystyle \frac{{(\kappa -\nu )}^3}{4}}{\displaystyle \frac{{\mathit{U}}^2}{6{[\Gamma (\alpha )]}^2}}{e}^{-2\lambda (\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}{(\mathrm{\Psi }(\kappa )-\mathrm{\Psi }(\nu ))}^{2\alpha -2}\hfill \\ \hfill & \times {\int }_{\nu }^{\kappa }\left[{\left|{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right]d\xi \hfill \\ \hfill & {\int }_{\nu }^{\kappa }\left[\left({\left|D{}_{\nu }{}^c\mathfrak{D}^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2+{\left|D{}^c\mathfrak{D}_{\kappa }^{\alpha ,\mathrm{\Psi },\lambda }{\rm Y}(\xi )\right|}^2\right)\right]d\xi .\hfill \end{array}$$

5. Conclusions

This study developed a new class of Wirtinger-type inequalities involving the tempered Ψ-Caputo fractional derivatives, proposed within the framework of $L_2$ and $L_p$ spaces for $p>1$. The research is motivated by recent developments in fractional calculus, specifically in the study of tempered and Ψ-fractional operators. Our approach utilized various types of integral inequalities, including Hölder’s inequality, to establish the key results. Several special cases were explored, followed by remarks that highlighted their significance with respect to existing factional operators. We offered illustrative examples, graphical plots, and numerical tables to strengthen the theoretical results. These examples demonstrate how the proposed inequalities behave under different parameter choices. Further, we investigated applications of inequalities involving arithmetic and geometric means, highlighting the scientific importance of the results. In general, by providing a broad and flexible framework for tempered Ψ-Caputo fractional operator, this study expands the theory of fractional inequalities. Furthermore, this framework may also be extended by incorporating other fractional operators or by exploring its potential in the analysis of fractional differential equations.