Finite-Time Stability of Equilibrium Points of Nonlinear Fractional Stochastic Differential Equations
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. Finite-Time Equilibrium Point
3.2. Finite-Time Stability
- (i) Finite-time attractiveness in probability: For all , the first hitting time satisfies .
- (ii) Stability in probability: For every pair of and , there exists a constant such that
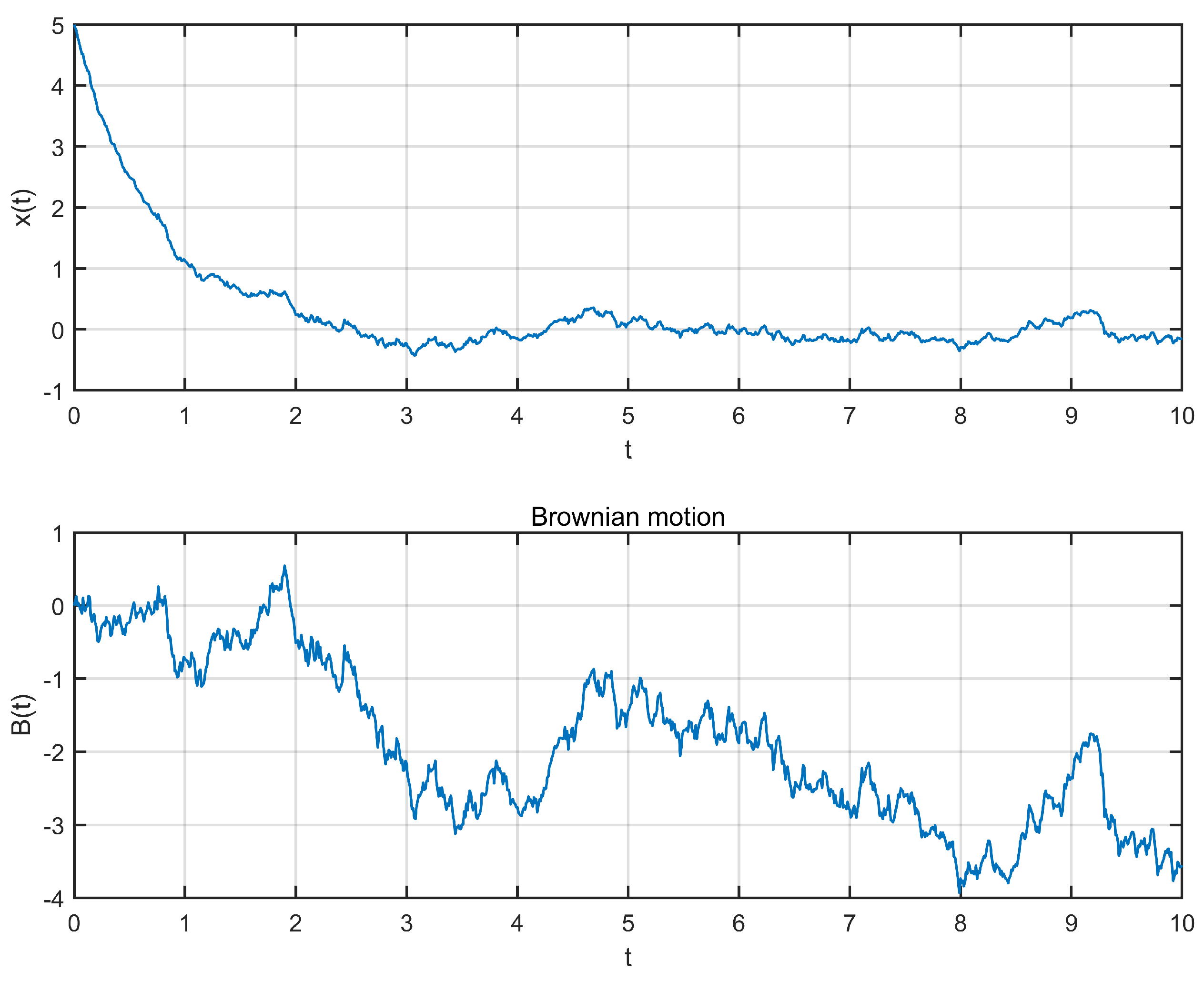
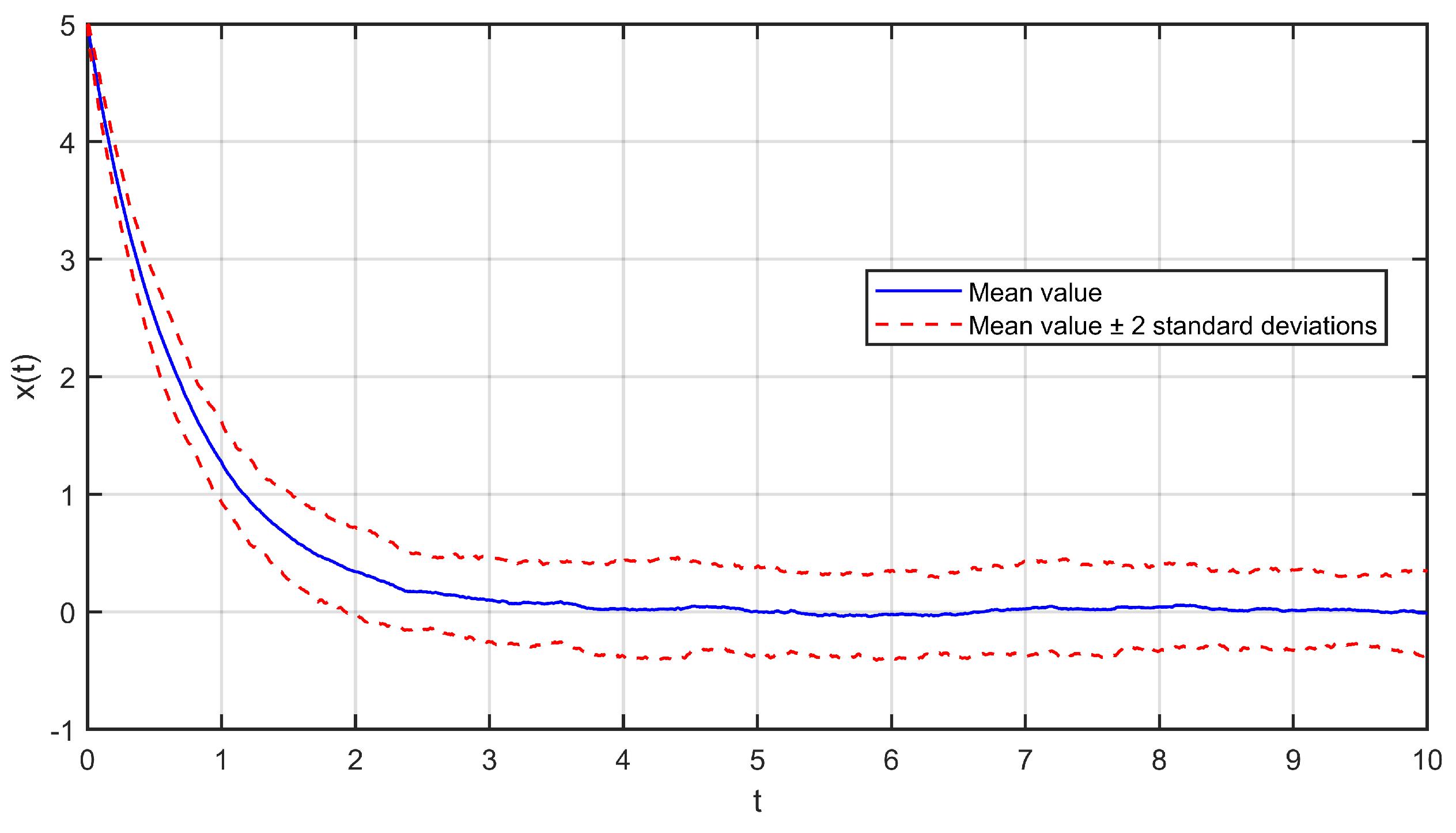
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayour, B.; Torres, D.F.M. Existence of solution to a local fractional nonlinear differential equation. J. Comput. Appl. Math. 2017, 312, 127–133. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Zhang, L. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2016. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Luo, D.; Wang, J.; Shen, D. Learning formation control for fractional-order multiagent systems. Math. Methods Appl. Sci. 2018, 41, 5003–5014. [Google Scholar] [CrossRef]
- Luo, D.; Wang, J.; Shen, D. PDα-ype distributed learning control for nonlinear fractional-order multi-agent systems. Math. Methods Appl. Sci. 2019, 42, 4543–4553. [Google Scholar] [CrossRef]
- Abuasbeh, K.; Mahmudov, N.I.; Awadalla, M. Fractional stochastic integro-differential equations with nonintantaneous impulses: Existence, approximate controllability and stochastic iterative learning control. Fractal Fract. 2023, 7, 87. [Google Scholar] [CrossRef]
- Luo, D.; Wang, J.; Shen, D. Consensus tracking problem for linear fractional multi-agent sytems with initial state error. Nonlinear Anal. Model. Control 2020, 25, 766–785. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Application, 2nd ed.; Horwood Publishing Limited: Chichester, UK, 2007. [Google Scholar]
- Sakthivel, R.; Revathi, P.; Ren, Y. Existence of solutions for nonlinear fractional stochastic differential equations. Nonlinear Anal. Theory Methods Appl. 2013, 81, 70–86. [Google Scholar] [CrossRef]
- Doan, T.S.; Huong, P.T.; Kloeden, P.E. Asymptotic separation between solutions of Caputo fractional stochastic differential equations. Stat. Probab. Lett. 2018, 36, 654–664. [Google Scholar]
- Anh, P.T.; Doan, T.S.; Huong, P.T. A variation of constant formula for Caputo fractional stochastic differential equations. Stat. Probab. Lett. 2019, 145, 351–358. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, S.; Guo, Z.; Yan, X. A note on the continuity for Caputo fractional stochastic differential equations. Chaos 2020, 30, 073106. [Google Scholar] [CrossRef]
- Alanzi, A.; Alshqaq, S.; Fakhfakh, R.; Makhlouf, A.B. Existence and uniqueness results for a class of fractional integro-stochastic differential equations. Fractal Fract. 2025, 9, 42. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, X.; Wang, H. Well-posedness and regularity of Caputo–Hadamard fractional stochastic differential equations. Z. Angew. Math. Phys. 2021, 72, 141. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, J. On the stability of solutions to conformable stochastic differential equations. Miskolc Math. Notes 2020, 21, 509–523. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, J.; O’Regan, D. Existence and stability of solutions to neutral conformable stochastic functional differential equations. Qual. Theory Dyn. Syst. 2022, 21, 7. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, J. Stability of solutions of Caputo fractional stochastic differential equations. Nonlinear Anal. Model. Control 2021, 26, 581–596. [Google Scholar] [CrossRef]
- Xiao, G.; Fečkan, M.; Wang, J. On the averaging principle for stochastic differential equations involving Caputo fractional derivative. Chaos 2022, 32, 101105. [Google Scholar] [CrossRef]
- Blouhi, T.; Albala, H.; Ladrani, F.; Cherif, A.; Moumen, A.; Zennir, K.; Bouhali, K. Averaged systems of stochastic differential equations with Lévy noise and fractional Brownian motion. Fractal Fract. 2025, 9, 419. [Google Scholar] [CrossRef]
- Chadha, A.; Bora, S.N. Existence and exponential stability for neutral stochastic fractional differential equations with impulses driven by Poisson jumps. Stochastics 2018, 5, 663–681. [Google Scholar] [CrossRef]
- Nguye, D. Asymptotic behavior of linear fractional stochastic differential equations with time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1–7. [Google Scholar] [CrossRef]
- Yin, J.; Khoo, S.; Man, Z.; Yu, X. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Xiao, G.; Ren, L.; Zhu, Q.; Wang, J. Adaptive Predefined-time consensus control for stochastic multi-agent systems. Int. J. Robust Nonlinear Control 2025, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, D.; Chen, Y.Q.; Podlubny, I.; Zhang, C. Finite energy Lyapunov function candidate for fractional order general nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104886. [Google Scholar] [CrossRef]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2013, 50, 547–551. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Sánchez-Orta, A.; Parra-Vega, V. A general result on non-existence of finite-time stable equilibria in fractional-order systems. J. Frankl. Inst. 2018, 356, 268–275. [Google Scholar] [CrossRef]
- Wei, Y.; Cao, J.; Chen, Y.; Wei, Y. The proof of Lyapunov asymptotic stability theorems for Caputo fractional order systems. Appl. Math. Lett. 2022, 129, 107961. [Google Scholar] [CrossRef]
- Panda, S.K.; Vijayakumar, V. Results on finite time stability of various fractional order systems. Chaos Solitons Fractals 2023, 174, 113906. [Google Scholar] [CrossRef]
- Feng, Z.; Xiang, Z. Finite-time stability of fractional-order nonlinear systems. Chaos 2024, 34, 023105. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, S.; Zhang, W. Predefined-time stabilization for nonlinear stochastic Itô systems. Sci. China Inf. Sci. 2023, 66, 182202. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, G.; Ren, L.; Liu, R. Finite-Time Stability of Equilibrium Points of Nonlinear Fractional Stochastic Differential Equations. Fractal Fract. 2025, 9, 510. https://doi.org/10.3390/fractalfract9080510
Xiao G, Ren L, Liu R. Finite-Time Stability of Equilibrium Points of Nonlinear Fractional Stochastic Differential Equations. Fractal and Fractional. 2025; 9(8):510. https://doi.org/10.3390/fractalfract9080510
Chicago/Turabian StyleXiao, Guanli, Lulu Ren, and Rui Liu. 2025. "Finite-Time Stability of Equilibrium Points of Nonlinear Fractional Stochastic Differential Equations" Fractal and Fractional 9, no. 8: 510. https://doi.org/10.3390/fractalfract9080510
APA StyleXiao, G., Ren, L., & Liu, R. (2025). Finite-Time Stability of Equilibrium Points of Nonlinear Fractional Stochastic Differential Equations. Fractal and Fractional, 9(8), 510. https://doi.org/10.3390/fractalfract9080510





