Large Deviation Principle for Hilfer Fractional Stochastic McKean–Vlasov Differential Equations

Abstract

This paper studies the large deviation principle (LDP) of a class of Hilfer fractional stochastic McKean–Vlasov differential equations with multiplicative noise. Firstly, by making use of the Laplace transform and its inverse transform, the solution of the equation is derived. Secondly, considering the equivalence between the LDP and the Laplace principle (LP), the weak convergence method is employed to prove that the equation satisfies the LDP. Finally, through specific example, it is elaborated how to utilize the LDP to analyze the behavioral characteristics of the system under small noise perturbation.

1. Introduction

In recent years, mathematical models involving fractional derivatives have received much attention from scholars. Compared to traditional models of integer order, fractional order models are more precise and have greater practical significance [1,2,3,4]. At the same time, the introduction of random factors can effectively describe the uncertainties and complexities of the real world. As a special class of stochastic equations, McKean–Vlasov stochastic differential equations (SDEs) have coefficients that depend on the solution process and its probability distribution. This feature makes them an important tool for studying interacting particle systems, and they are widely used in financial engineering, quantum mechanics, and stochastic control [5].

The LDP mainly focuses on the exponential estimation of the probability of the occurrence of a rare (tail) event $\mathbb{B}$. That is, when $ϵ\to 0$, it examines whether or not the speed at which $\mathbf{P}(X^{ϵ}\in \mathbb{B})\to 0$ decays is exponential. The LDP is a hot topic studied by many modern scholars. It has important and profound applications in many fields, such as probability theory [6], information theory [7], etc., and there are currently a great many rich research results in the literature. Dupuis and Ellis [8] combined the technique of stochastic control with the concept of large deviations and constructed a weak convergence technique. By using the weak convergence method, Mo et al. [9] established the LDP of SDEs with delay, Li [10] studied the LDP of mean-reflecting SDEs with jumps, Hong et al. [11] studied the LDP of McKean–Vlasov quasilinear stochastic evolution equations, Shruthi et al. [12] studied the LDP of stochastic functional differential equations with nonlocal conditions, Fan et al. [13] studied the LDP of a class of McKean–Vlasov SDEs driven by fractional Brownian motion, Yang et al. [14] studied the LDP of slow-fast rough differential equations under controlled rough paths, and Yang et al. [15] studied the LDP for multi-scale McKean–Vlasov systems with jumps.

However, the above-mentioned literatures all focus on studying the LDP of integerorder SDEs, while there are relatively few pieces of literature on the study of the large deviation of fractional-order SDEs. Suivinthra et al. [16] studied the LDP of nonlinear fractional stochastic integral differential equations, Siva et al. [17] studied the LDP of stochastic neutral fractional functional differential equations with multiplicative noise, and Ranjani et al. [18] established the LDP for stochastic fractional pantograph differential equations. As far as we know, although the research on fractional SDEs is quite extensive nowadays, the establishment of the LDP for fractional stochastic McKean–Vlasov differential equations is relatively scarce.

Therefore, based on the above discussion, this paper considers the following Hilfer fractional stochastic McKean–Vlasov differential equation:

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\kappa ,\varkappa }X\left(t\right)=AX\left(t\right)+b\left(t,X\left(t\right),L_{X\left(t\right)}\right)+\sigma \left(t,X\left(t\right),L_{X\left(t\right)}\right)\frac{\mathrm{d}W\left(t\right)}{\mathrm{d}t},t\in J^{\prime }=(0,T],\hfill \\ I_{0^{+}}^{1-\gamma }X\left(0\right)=X_0,\gamma =\kappa +\varkappa -\kappa \varkappa ,\hfill \end{array}\right.$$

(1)

where $D_{0^{+}}^{\kappa ,\varkappa }$ is the Hilfer fractional derivative, parameter $\kappa (0⩽\kappa ⩽1)$, and order $\varkappa ({\displaystyle \frac{1}{2}}<\varkappa <1)$, $I_{0^{+}}^{1-\gamma }$ stands for the $1-\gamma$ order Riemann–Liouville (R-L) fractional integral. A is an m-dimensional matrix and ${\left\{W\left(t\right)\right\}}_{t\in J}$ is the d-dimensional standard Brownian motion in the probability space with the $\sigma$-algebra flow $\left(\Omega ,\mathcal{F},\mathbf{P};{\left\{{\mathcal{F}}_t\right\}}_{t\in J}\right)$, where $J=[0,T]$. $L_{X\left(t\right)}$ is taken as the distribution of the stochastic process $X\left(t\right)$. In addition, Borel measurable functions b: $J\times {\mathbb{R}}^m\times {\mathcal{P}}_2\left({\mathbb{R}}^m\right)\to {\mathbb{R}}^m$ and $\sigma$: $J\times {\mathbb{R}}^m\times {\mathcal{P}}_2\left({\mathbb{R}}^m\right)\to {\mathbb{R}}^{m\times d}$ are continuous; ${\mathcal{P}}_2\left({\mathbb{R}}^m\right)$ will be given in Section 2.

The structural plan of this paper is as follows. In Section 2, the preliminary knowledge about the LDP is introduced. In Section 3, the LDP of model (1) with multiplicative noise is proved by weak convergence. A case is designed according to model to illustrate the main results of this paper in Section 4.

2. Preliminaries

This section will expound on the definitions, assumptions, and theorems required in the subsequent proof process.

Let $\mathcal{P}\left({\mathbb{R}}^m\right)$ represents the totality of probability distributions on ${\mathbb{R}}^m$ and ${\mathcal{P}}_2\left({\mathbb{R}}^m\right):=\{u\in \mathcal{P}\left({\mathbb{R}}^m\right),u\left({|·|}^2\right)={\int }_{{\mathbb{R}}^m}{\left|x\right|}^{2}u\left(dx\right)<\infty \}$. We endow ${\mathcal{P}}_2\left({\mathbb{R}}^m\right)$ with the ${\mathbb{L}}^2$-Wasserstein metric, which is defined as

$$\begin{array}{c}\hfill {\mathbb{W}}_2(u,v)=\underset{\pi \in \Pi (u,v)}{inf}{\left({\int }_{{\mathbb{R}}^m\times {\mathbb{R}}^m}{|x-y|}^2\pi (dx,dy)\right)}^{{\displaystyle \frac{1}{2}}},\forall u,v\in {\mathcal{P}}_2\left({\mathbb{R}}^m\right),\end{array}$$

where $\Pi (u,v)$ represents the set of all probability measures that are couplings of u and v, that is, all the probability measures on ${\mathbb{R}}^m\times {\mathbb{R}}^m$ whose marginal distributions are u and v. Thus, ${\mathcal{P}}_2\left({\mathbb{R}}^m\right)$ is a Polish space and ${\mathbb{W}}_2$ is a complete metric on ${\mathcal{P}}_2\left({\mathbb{R}}^m\right)$.

Note 1.

From the above, it can be seen that for any ${\mathbb{R}}^m$-valued random variables X and Y, there is

$$\begin{array}{c}\hfill {\mathbb{W}}_2{(L_X,L_Y)}^2⩽\mathbf{E}\left({|X-Y|}^2\right).\end{array}$$

Definition 1

(see [19]). The R-L fractional integral of order $p>0$ with the lower limit b for a function $f:[b,\infty )\to \mathbb{R}$ is defined as

$$\begin{array}{c}\hfill I_{b^{+}}^{p}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(p\right)}}{\int }_b^t{\displaystyle \frac{f\left(s\right)}{{(t-s)}^{1-p}}}\mathrm{d}s,t>b,\end{array}$$

where $\Gamma (·)$ is the Gamma function.

Definition 2

(see [20]). The Hilfer fractional derivative of order $0⩽\kappa ⩽1$ and $0<\varkappa <1$ is defined as

$$\begin{array}{c}\hfill D_{b^{+}}^{\kappa ,\varkappa }f\left(t\right)=I_{b^{+}}^{\kappa (1-\varkappa )}{\displaystyle \frac{d}{dt}}{I}_{b^{+}}^{(1-\kappa )(1-\varkappa )}f\left(t\right).\end{array}$$

The main goal is to derive the explicit integral expression of the solution to system (1) by using the Laplace transform and its inverse transform, and this expression is defined as the solution to system (1). Consider the auxiliary equation:

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\kappa ,\varkappa }X\left(t\right)=AX\left(t\right)+\lambda \left(t\right),t\in J^{\prime },\hfill \\ I_{0^{+}}^{1-\gamma }X\left(0\right)=X_0,\gamma =\kappa +\varkappa -\kappa \varkappa ,\hfill \end{array}\right.$$

(2)

where $\lambda \left(t\right)\in C\left([0,T];{\mathbb{R}}^m\right)$. For any given $T>0$, $C\left([0,T];{\mathbb{R}}^m\right)$ denotes the set of all ${\mathbb{R}}^m$-valued continuous functions on $[0,T]$.

By applying the inverse operation of the Hilfer derivative (fractional integral $I_{0^{+}}^{\varkappa })$, transform (2) into an integral form:

$$\begin{array}{cc}\hfill X\left(t\right)={\displaystyle \frac{t^{\gamma -1}}{\Gamma \left(\gamma \right)}}{X}_0& +I_{0^{+}}^{\varkappa }\left(AX\left(t\right)+\lambda \left(t\right)\right).\hfill \end{array}$$

(3)

We apply the Laplace transform to (3). By using $\mathcal{L}\left\{t^{\gamma -1}\right\}=\Gamma \left(\gamma \right)s^{-\gamma }$, $\mathcal{L}\left\{I_{0^{+}}^{\varkappa }\lambda \left(t\right)\right\}=s^{-\varkappa }\mathcal{L}\left\{\lambda \left(t\right)\right\}=s^{-\varkappa }\overline{\lambda }\left(s\right)$ and $\mathcal{L}\left\{AX\left(t\right)\right\}=A\mathcal{L}\left\{X\left(t\right)\right\}=A\overline{X}\left(s\right)$, we can get

$$\begin{array}{c}\hfill \overline{X}\left(s\right)=X_0{s}^{-\gamma }+s^{-\varkappa }\left(A\overline{X}\left(s\right)+\overline{\lambda }\left(s\right)\right).\end{array}$$

Next, we derive the explicit solution for $\overline{X}\left(s\right)$ as follows:

$$\begin{array}{cc}\hfill \overline{X}\left(s\right)-s^{-\varkappa }A\overline{X}\left(s\right)& =X_0{s}^{-\gamma }+s^{-\varkappa }\overline{\lambda }\left(s\right),\hfill \\ \hfill \overline{X}\left(s\right)\left(I-s^{-\varkappa }A\right)& =X_0{s}^{-\gamma }+s^{-\varkappa }\overline{\lambda }\left(s\right),\hfill \\ \hfill \overline{X}\left(s\right)\left(s^{\varkappa }I-A\right)& =X_0{s}^{\varkappa -\gamma }+\overline{\lambda }\left(s\right),\hfill \\ \hfill \overline{X}\left(s\right)& ={\left(s^{\varkappa }I-A\right)}^{-1}\left(X_0{s}^{\varkappa -\gamma }+\overline{\lambda }\left(s\right)\right),\hfill \end{array}$$

(4)

combined with the inverse distribution law of matrix ${\left(s^{\varkappa }I-A\right)}^{-1}{s}^{\varkappa }={\left(I-A{s}^{-\varkappa }\right)}^{-1}$; (4) is rewritten as

$$\begin{array}{c}\hfill \overline{X}\left(s\right)=s^{-\gamma }{\left(I-A{s}^{-\varkappa }\right)}^{-1}{X}_0+s^{-\varkappa }{\left(I-A{s}^{-\varkappa }\right)}^{-1}\overline{\lambda }\left(s\right).\end{array}$$

In the end, the Mittag–Leffler function and its Laplace transform are introduced:

$$\begin{array}{cc}\hfill E_{\varkappa ,\gamma }\left(z\right)& =\sum _{i=0}^{\infty }{\displaystyle \frac{z^i}{\Gamma (i\varkappa +\gamma )}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathcal{L}}^{-1}\left\{s^{-\gamma }{\left(I-A{s}^{-\varkappa }\right)}^{-1}\right\}& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\mathcal{L}}^{-1}\left\{s^{-\varkappa }{\left(I-A{s}^{-\varkappa }\right)}^{-1}\right\}& =t^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{t}^{\varkappa }\right).\hfill \end{array}$$

(7)

For (6), expand $s^{-\gamma }{\left(I-A{s}^{-\varkappa }\right)}^{-1}$ based on the knowledge of matrix series, apply the inverse Laplace transform, and combine it with (5) to derive (6). The specific process is as follows:

$$\begin{array}{cc}\hfill s^{-\gamma }{\left(I-A{s}^{-\varkappa }\right)}^{-1}& =s^{-\gamma }\sum _{k=0}^{\infty }{\left(A{s}^{-\varkappa }\right)}^k=\sum _{k=0}^{\infty }{A}^k{s}^{-\varkappa k-\gamma },\hfill \\ \hfill {\mathcal{L}}^{-1}\left\{A^k{s}^{-\varkappa k-\gamma }\right\}& =A^k{\displaystyle \frac{t^{\varkappa k+\gamma -1}}{\Gamma (\varkappa k+\gamma )}},\hfill \\ \hfill \sum _{k=0}^{\infty }{A}^k{\displaystyle \frac{t^{\varkappa k+\gamma -1}}{\Gamma (\varkappa k+\gamma )}}& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right).\hfill \end{array}$$

Similarly, by adopting the above derivation idea, we can prove that (7) holds.

Let $s^{-\varkappa }{\left(I-A{s}^{-\varkappa }\right)}^{-1}=F\left(s\right)$; using (7) and convolution theorems ${\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}=f\left(t\right)$, ${\mathcal{L}}^{-1}\left\{G\left(s\right)\right\}=g\left(t\right)$, and ${\mathcal{L}}^{-1}\left\{F\left(s\right)G\left(s\right)\right\}={\int }_0^{t}f(t-s)g\left(s\right)\mathrm{d}s$, we can get

$$\begin{array}{c}\hfill {\mathcal{L}}^{-1}\left\{s^{-\varkappa }{\left(I-A{s}^{-\varkappa }\right)}^{-1}\overline{\lambda }\left(s\right)\right\}={\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\lambda \left(s\right)\mathrm{d}s.\end{array}$$

Thus, the solution of Equation (2) is

$$\begin{array}{cc}\hfill X\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\lambda \left(s\right)\mathrm{d}s.\hfill \end{array}$$

Similarly, We define the solution to system (1) as follows.

Definition 3.

If $X\left(t\right)$ satisfies the following equation:

$$\begin{array}{cc}\hfill X\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,X\left(s\right),L_{X\left(s\right)}\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X\left(s\right),L_{X\left(s\right)}\right)\mathrm{d}W\left(s\right),\hfill \end{array}$$

(8)

then the ${\mathbb{R}}^m$-valued stochastic process $\left\{X\right(t),0⩽t⩽T\}$ is called the solution to system (1).

Regarding the proof of the existence and uniqueness of this solution, the proof process in [21] can be referred to, and will not be repeated here.

Define the weighted space of a continuous function

$$\begin{array}{c}\hfill C_{1-\gamma }[0,T]=\left\{f:(0,T]\to {\mathbb{R}}^m:x^{1-\gamma }f\left(x\right)\in C[0,T]\right\},0⩽1-\gamma <1;\end{array}$$

its modulus is ${\parallel f\parallel }_{C_{1-\gamma }}={sup}_{x\in [0,T]}\left|x^{1-\gamma }f\left(x\right)\right|$.

Next, some important concepts and results of the LDP will be presented.

Suppose that $\{X^{ϵ},ϵ>0\}$ is a family of random variables defined in the complete probability space $\left(\Omega ,\mathcal{F},\mathbf{P}\right)$ and taking values in $\mathbb{E}$, where $\mathbb{E}$ represents a Polish space, that is, a complete and separable metric space.

Definition 4

(Rate Function [8]). Function $I:\mathbb{E}\to [0,+\infty ]$ is lower semi-continuous, then the function I is called a rate function. If for each real number $N<\infty$, the level set $K_N:=\{f\in \mathbb{E}:I\left(f\right)⩽N\}$ is a compact subset of $\mathbb{E}$, then I is called a good rate function.

Definition 5

(LDP [8]). Let I be a rate function defined on $\mathbb{E}$. Assume the family of $\mathbb{E}$-valued random variables $\left\{X^{ϵ}\right\}$ satisfies the following two conditions:

$\left(i\right)$ For every closed subset $\mathcal{H}$ on space $\mathbb{E}$

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}supϵlog\mathbf{P}(X^{ϵ}\in \mathcal{H})⩽-\underset{x\in \mathcal{H}}{inf}I\left(x\right).\end{array}$$

$\left(ii\right)$ For every open subset $\mathcal{G}$ on space $\mathbb{E}$

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}infϵlog\mathbf{P}(X^{ϵ}\in \mathcal{G})⩾-\underset{x\in \mathcal{G}}{inf}I\left(x\right).\end{array}$$

The conditions $\left(i\right)$ and $\left(ii\right)$ are the upper and lower bound of large deviation, respectively. Then $\left\{X^{ϵ}\right\}$ is said to satisfy the LDP with the rate function I.

Definition 6

(LP [8]). Let I be a rate function on $\mathbb{E}$. For all real-valued bounded continuous functions h on $\mathbb{E}$, we have

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}ϵlog\mathbf{E}\left\{exp[-{\displaystyle \frac{1}{ϵ}}h\left(X^{ϵ}\right)]\right\}=-\underset{f\in \mathbb{E}}{inf}\left\{h\left(f\right)+I\left(f\right)\right\},\end{array}$$

then $\left\{X^{ϵ}\right\}$ is said to satisfy the LP with the rate function I.

According to Theorems 1.2.1 and 1.2.3 in [8], the equivalent results of the LDP and the LP are presented as follows.

Theorem 1.

For the rate function I on $\mathbb{E}$, the family of random variables $\left\{X^{ϵ}\right\}$ satisfies the LP, if and only if, for the same rate function I, $\left\{X^{ϵ}\right\}$ satisfies the LDP.

In order to further obtain the desired results, we assume that the following conditions hold:

$\left({\mathsf{A}}_1\right)$ There exists a positive constant $K_1$, for ∀$x,y\in {\mathbb{R}}^m$, ∀$u,v\in {\mathcal{P}}_2\left({\mathbb{R}}^m\right)$, and $t\in J$, such that

$$\begin{array}{c}\hfill {|b(t,x,u)-b(t,y,v)|}^2\vee {|\sigma (t,x,u)-\sigma (t,y,v)|}^2⩽K_1^2\left({|x-y|}^2+{\mathbb{W}}_2{\left(u,v\right)}^2\right).\end{array}$$

$\left({\mathsf{A}}_2\right)$ There exists a positive constant $K_2$, for ∀$x\in {\mathbb{R}}^m$, $u\in {\mathcal{P}}_2\left({\mathbb{R}}^m\right)$, and $t\in J$, such that

$$\begin{array}{c}\hfill {\left|b(t,x,u)\right|}^2\vee {\left|\sigma (t,x,u)\right|}^2⩽K_2^2\left[1+|t^{1-\gamma }{x|}^2+u\left({|·|}^2\right)\right].\end{array}$$

3. The LDP with Multiplicative Noise

This section mainly discusses the LDP for a Hilfer fractional stochastic McKean–Vlasov differential equation with multiplicative noise:

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\kappa ,\varkappa }{X}^{ϵ}\left(t\right)=A{X}^{ϵ}\left(t\right)+b\left(t,X^{ϵ}\left(t\right),u_t^{ϵ}\right)+\sqrt{ϵ}\sigma \left(t,X^{ϵ}\left(t\right),u_t^{ϵ}\right)\frac{\mathrm{d}W\left(t\right)}{\mathrm{d}t},t\in J^{\prime },\hfill \\ I_{0^{+}}^{1-\gamma }{X}^{ϵ}\left(0\right)=X_0,\gamma =\kappa +\varkappa -\kappa \varkappa ,\hfill \end{array}\right.$$

(9)

here we define $u_t^{ϵ}=L_{X^{ϵ}\left(t\right)}$.

Definition 7.

If $X^{ϵ}\left(t\right)$ satisfies the following equation:

$$\begin{array}{cc}\hfill X^{ϵ}\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)\mathrm{d}s\hfill \\ \hfill & +\sqrt{ϵ}{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)\mathrm{d}W\left(s\right).\hfill \end{array}$$

(10)

then the ${\mathbb{R}}^m$-valued stochastic process $\{X^{ϵ}\left(t\right),0⩽t⩽T\}$ is called the solution of Equation (9).

Assume that there exists a measurable mapping $G^{ϵ}$ from $C\left([0,T];{\mathbb{R}}^d\right)$ to $C\left([0,T];{\mathbb{R}}^m\right)$. Define $X^{ϵ}=G^{ϵ}\left(W\right)$, then $X^{ϵ}$ is a stochastic process on $C([0,T];{\mathbb{R}}^m)$. Let

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \Lambda =\left\{\psi :\psi \mathrm{is}\mathrm{a}{\mathbb{R}}^d-\mathrm{valued}{\mathcal{F}}_t-\mathrm{predictable}\mathrm{process}\mathrm{and}{\int }_0^T{\left|\psi \left(s\right)\right|}^2\mathrm{d}s<\infty \mathrm{a}.\mathrm{s}.\right\},\hfill \\ \hfill & {\mathbb{S}}_N=\left\{\psi \in {\mathbb{L}}^2([0,T];{\mathbb{R}}^d):{\int }_0^T{\left|\psi \left(s\right)\right|}^2\mathrm{d}s⩽N,\mathrm{for}N>0\right\},\hfill \end{array}\end{array}$$

where ${\mathbb{L}}^2([0,T];{\mathbb{R}}^d)$ is the space of all ${\mathbb{R}}^d$-valued square-integrable functions on $[0,T]$. In addition, ${\mathbb{S}}_N$ endowed with the weak topology is a Polish space. Define

$$\begin{array}{c}\hfill {\Lambda }_N=\left\{\psi \in \Lambda :\psi \left(\omega \right)\in {\mathbb{S}}_N\mathbf{P}-\mathrm{a}.\mathrm{s}.\right\}.\end{array}$$

According to the conclusions of Mataussi [22], the weak convergence method is based on the equivalence between the LP and the LDP. To prove that the LP holds, we only need to verify that the following condition $\left(\mathbb{A}\right)$ is satisfied:

$\left(\mathbb{A}\right)$ Suppose there exists a measurable map $G^0:C([0,T];{\mathbb{R}}^d)\to C([0,T];{\mathbb{R}}^m)$ such that the following two conditions hold:

$\left(a\right)$ For any $N<+\infty$, when $n\to \infty$ and ${\left\{{\psi }_n\right\}}_{n⩾1}\subset {\mathbb{S}}_N$ converges to $\psi$ in ${\mathbb{S}}_N$, then $G^0\left({\int }_0^t{\psi }_n\left(s\right)\mathrm{d}s\right)$→$G^0\left({\int }_0^t\psi \left(s\right)\mathrm{d}s\right)$ in $C([0,T];{\mathbb{R}}^m)$.

$\left(b\right)$ For any $N<+\infty$, when ${\left\{{\psi }_{ϵ}\right\}}_{ϵ>0}\subset {\Lambda }_N$ and any $\delta >0$, we have

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}\mathbf{P}\left(d\left(G^{ϵ}\left(W+{\displaystyle \frac{1}{\sqrt{ϵ}}}{\int }_0^t{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right),G^0\left({\int }_0^t{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right)\right)>\delta \right)=0,\end{array}$$

where $d(·,·)$ denotes the metric in space $C([0,T];{\mathbb{R}}^m)$.

Proposition 1.

Suppose that $\left({\mathsf{A}}_1\right)$–$\left({\mathsf{A}}_2\right)$ hold and denote $L_{X^0\left(t\right)}=u_t^0$, there exists a unique solution ${\left\{X^0\left(t\right)\right\}}_{t\in J^{\prime }}$ such that

(i) 

$t^{1-\gamma }{X}^0\left(t\right)\in C([0,T];{\mathbb{R}}^m)$,

(ii) 

$X^0$ satisfies the following equation

$$\begin{array}{cc}\hfill X^0\left(t\right)=t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0& +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,X^0\left(s\right),u_s^0\right)\mathrm{d}s.\hfill \end{array}$$

(11)

Since $X^0$ is a deterministic path, then $L_{X^0}={\delta }_{X^0\left(t\right)}$, where ${\delta }_{X^0\left(t\right)}$ is the Dirac measure of $X^0\left(t\right)$. Furthermore, as a deterministic process, the time-dependent distribution $u_t^0$ of $X^0\left(t\right)$ satisfies $u_t^0={\delta }_{X^0\left(t\right)}$. According to the property of the Dirac measure, for any function f, it holds that ${\delta }_x\left(f\right)=f\left(x\right)$. In particular, when $f(·)={|·|}^2$, we obtain $u_t^0\left({|·|}^2\right)={\delta }_{X^0\left(t\right)}\left({|·|}^2\right)={\left|X^0\left(t\right)\right|}^2$.

Note 2.

For $\forall t\in J$, there are some positive constants $S_1$, $S_2$, such that

$$\begin{array}{c}\hfill \underset{0⩽\tau ⩽t}{sup}|E_{\varkappa ,\gamma }\left(A{\tau }^{\varkappa }\right)|⩽S_1,\underset{0⩽\tau ⩽t}{sup}\left|E_{\varkappa ,\varkappa }\left(A{(t-\tau )}^{\varkappa }\right)\right|⩽S_2.\end{array}$$

Lemma 1.

Suppose that assumption $\left({\mathsf{A}}_2\right)$ holds. If $X^0\left(t\right)$ is a solution to Equation (11), then

$$\begin{array}{cc}\hfill \underset{0⩽\tau ⩽t}{sup}{\left|{\tau }^{1-\gamma }{X}^0\left(\tau \right)\right|}^2& ⩽\left(2S_1^2{\left|X_0\right|}^2+{\displaystyle \frac{2S_2^2{K}_2^2{T}^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}\right)\hfill \\ \hfill & \times exp\left({\displaystyle \frac{2S_2^2{K}_2^2{T}^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}\left(1+{\displaystyle \frac{T^{2\gamma -2}}{2\gamma -1}}\right)\right)⩽C^{*},t\in [0,T],\hfill \end{array}$$

where $C^{*}$ is a positive constant that depends on $S_1$, $S_2$, ϰ, γ, $K_2$, and T.

Proof. 

Considering ${\left|t^{1-\gamma }{X}^0\left(t\right)\right|}^2$, by using the elementary inequality, $H\ddot{o}lder$ inequality, and $\left({\mathsf{A}}_2\right)$, one has

$$\begin{array}{cc}\hfill & |t^{1-\gamma }{X}^0{\left(t\right)|}^2\hfill \\ \hfill & ⩽2|E_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0{|}^2+2|t^{1-\gamma }{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,X^0\left(s\right),u_s^0\right)\mathrm{d}s{|}^2\hfill \\ \hfill & ⩽2S_1^2{\left|X_0\right|}^2+2S_2^2{t}^{2(1-\gamma )}{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}b\left(s,X^0\left(s\right),u_s^0\right)\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽2S_1^2{\left|X_0\right|}^2+2S_2^2{t}^{2(1-\gamma )}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\mathrm{d}s\right)\left({\int }_0^t|b\left(s,X^0\left(s\right),u_s^0\right){|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽2S_1^2{\left|X_0\right|}^2+2S_2^2{t}^{2(1-\gamma )}{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{K}_2^2{\int }_0^t\left[1+|s^{1-\gamma }{X}^0{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]\mathrm{d}s\hfill \\ \hfill & ⩽2S_1^2|X_0{|}^2+2S_2^2{K}_2^2{\displaystyle \frac{t^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}+2S_2^2{K}_2^2{\displaystyle \frac{t^{2(\varkappa -\gamma )+1}}{2\varkappa -1}}{\int }_0^t{\left|s^{1-\gamma }{X}^0\left(s\right)\right|}^2\left(1+s^{2(\gamma -1)}\right)\mathrm{d}s.\hfill \end{array}$$

Let $H\left(t\right)={sup}_{0⩽\tau ⩽t}{\left|{\tau }^{1-\gamma }{X}^0\left(\tau \right)\right|}^2$, then

$$\begin{array}{c}\hfill H\left(t\right)⩽2S_1^2{\left|X_0\right|}^2+2S_2^2{K}_2^2{\displaystyle \frac{T^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}+2S_2^2{K}_2^2{\displaystyle \frac{T^{2(\varkappa -\gamma )+1}}{2\varkappa -1}}{\int }_0^{t}H\left(s\right)\left(1+s^{2(\gamma -1)}\right)\mathrm{d}s.\end{array}$$

By using the Gronwall inequality and further simplifying, we can get

$$\begin{array}{c}\hfill H\left(t\right)⩽\left(2S_1^2{\left|X_0\right|}^2+2S_2^2{K}_2^2{\displaystyle \frac{T^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}\right)\times exp\left(2S_2^2{K}_2^2{\displaystyle \frac{T^{2(\varkappa -\gamma +1)}}{2\varkappa -1}}\left(1+{\displaystyle \frac{T^{2\gamma -2}}{2\gamma -1}}\right)\right).\end{array}$$

□

Since $|X^0{\left(s\right)|}^2=s^{2(\gamma -1)}{\left|s^{1-\gamma }{X}^0\left(s\right)\right|}^2$, then ${sup}_{0⩽\tau ⩽t}{\left|X^0\left(\tau \right)\right|}^2⩽C^{\prime }$. $C^{\prime }$ is a positive constant that depends on $S_1$, $S_2$, $\varkappa$, $\gamma$, $K_2$, and T.

To prove the LDP, the main task is to verify the sufficient conditions for the validity of the LP. First, to prove condition $\left(a\right)$, we introduce the skeleton equation related to (9):

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\kappa ,\varkappa }{Z}^{\psi }\left(t\right)=A{Z}^{\psi }\left(t\right)+b\left(t,Z^{\psi }\left(t\right),u_t^0\right)+\sigma \left(t,Z^{\psi }\left(t\right),u_t^0\right)\psi \left(t\right),t\in J^{\prime },\hfill \\ I_{0^{+}}^{1-\gamma }{Z}^{\psi }\left(0\right)=X_0,\hfill \end{array}\right.$$

(12)

where $\psi \in {\mathbb{L}}^2\left(J;{\mathbb{R}}^d\right)$; solution $Z^{\psi }$ is denoted as

$$\begin{array}{cc}\hfill Z^{\psi }\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\psi \left(s\right)\mathrm{d}s.\hfill \end{array}$$

(13)

Lemma 2.

Suppose that assumption $\left({\mathsf{A}}_2\right)$ holds. If $Z^{\psi }\left(t\right)$ is a solution to (12), then

$$\begin{array}{cc}\hfill \underset{0⩽\tau ⩽t}{sup}{\left|{\tau }^{1-\gamma }{Z}^{\psi }\left(\tau \right)\right|}^2& ⩽\left(3S_1^2{\left|X_0\right|}^2+3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}\left(1+C^{\prime }\right)\left(T+N\right)\right)\hfill \\ \hfill & \times exp\left(3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}\left(T+N\right)\right)⩽\widehat{C},t\in [0,T].\hfill \end{array}$$

In addition, $\widehat{C}$ is a positive constant dependent on $T,N,\varkappa ,\gamma ,S_1,S_2,K_2$.

Proof. 

Considering $t^{1-\gamma }{Z}^{\psi }\left(t\right)$:

$$\begin{array}{cc}\hfill t^{1-\gamma }{Z}^{\psi }\left(t\right)& =E_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+t^{1-\gamma }{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\mathrm{d}s\hfill \\ \hfill & +t^{1-\gamma }{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\psi \left(s\right)\mathrm{d}s.\hfill \end{array}$$

By using the elementary inequality, the $H\ddot{o}lder$ inequality, and $\left({\mathsf{A}}_2\right)$, we have

$$\begin{array}{cc}\hfill & |t^{1-\gamma }{Z}^{\psi }{\left(t\right)|}^2\hfill \\ \hfill & ⩽3|E_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0{|}^2+3|t^{1-\gamma }{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\mathrm{d}s{|}^2\hfill \\ \hfill & +3|t^{1-\gamma }{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\psi \left(s\right)\mathrm{d}s{|}^2\hfill \\ \hfill & ⩽3S_1^2{|X_0|}^2+3S_2^2{t}^{2(1-\gamma )}{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & +3S_2^2{t}^{2(1-\gamma )}{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\psi \left(s\right)\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽3S_1^2{|X_0|}^2+3S_2^2{t}^{2(1-\gamma )}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\mathrm{d}s\right)\left({\int }_0^t{|b\left(s,Z^{\psi }\left(s\right),u_s^0\right)|}^2\mathrm{d}s\right)\hfill \\ \hfill & +3S_2^2{t}^{2(1-\gamma )}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\mathrm{d}s\right)\left({\int }_0^t|\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\psi \left(s\right){|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽3S_1^2{|X_0|}^2+3S_2^2{t}^{2(1-\gamma )}{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{K}_2^2{\int }_0^t\left[1+|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]\mathrm{d}s\hfill \\ \hfill & +3S_2^2{t}^{2(1-\gamma )}{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{K}_2^2{\int }_0^t\left[1+|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]{|\psi \left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & ⩽3S_1^2{|X_0|}^2+3S_2^2{K}_2^2{\displaystyle \frac{t^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^t\left(1+|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2+\underset{0⩽s⩽t}{sup}{|X^0\left(s\right)|}^2\right)\mathrm{d}s\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{t^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^t\left(1+|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2+\underset{0⩽s⩽t}{sup}{|X^0\left(s\right)|}^2\right){|\psi \left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & ⩽3S_1^2{|X_0|}^2+3S_2^2{K}_2^2{\displaystyle \frac{t^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}\left(1+C^{\prime }\right)\left(t+N\right)\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{t^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^t{|s^{1-\gamma }{Z}^{\psi }\left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{t^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^t|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2{|\psi \left(s\right)|}^2\mathrm{d}s.\hfill \end{array}$$

(14)

Let $K\left(t\right)={sup}_{0⩽\tau ⩽t}{|{\tau }^{1-\gamma }{Z}^{\psi }\left(\tau \right)|}^2$, and (14) can be rearranged as

$$\begin{array}{cc}\hfill K\left(t\right)& ⩽3S_1^2{|X_0|}^2+3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}\left(1+C^{\prime }\right)\left(T+N\right)\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^{t}K\left(s\right)\left(1+{|\psi \left(s\right)|}^2\right)\mathrm{d}s.\hfill \end{array}$$

By applying the Gronwall inequality, we can finally get

$$\begin{array}{cc}\hfill \underset{0⩽\tau ⩽t}{sup}{|{\tau }^{1-\gamma }{Z}^{\psi }\left(\tau \right)|}^2& ⩽\left(3S_1^2{|X_0|}^2+3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}\left(1+C^{\prime }\right)\left(T+N\right)\right)\hfill \\ \hfill & \times exp\left(3S_2^2{K}_2^2{\displaystyle \frac{T^{2\left(\varkappa -\gamma \right)+1}}{2\varkappa -1}}{\int }_0^t\left(1+{|\psi \left(s\right)|}^2\right)\mathrm{d}s\right).\hfill \end{array}$$

□

Lemma 3.

For any $N<+\infty$, when $n\to \infty$ and ${\left\{{\psi }_n\right\}}_{n⩾1}\subset {\mathbb{S}}_N$ converges to ψ in ${\mathbb{S}}_N$, then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\underset{0⩽\tau ⩽t}{sup}|G^0\left({\int }_0^{\tau }{\psi }_n\left(s\right)\mathrm{d}s\right)-G^0\left({\int }_0^{\tau }\psi \left(s\right)\mathrm{d}s\right)|=0,t\in [0,T].\end{array}$$

Proof. 

For any sequence ${\psi }_n\in {\mathbb{S}}_N$, ${\psi }_n$ converges to $\psi$ in ${\mathbb{L}}^2(J;{\mathbb{R}}^d)$. Let $Z^{{\psi }_n}=G^0\left({\int }_0^t{\psi }_n\left(s\right)\mathrm{d}s\right)$ be the solution to Equation (12), which is obtained by replacing $\psi$ with ${\psi }_n$:

$$\begin{array}{cc}\hfill Z^{{\psi }_n}\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right){\psi }_n\left(s\right)\mathrm{d}s.\hfill \end{array}$$

(15)

Now it is proven that $Z^{{\psi }_n}$ converges to $Z^{\psi }$ in $C([0,T];{\mathbb{R}}^m)$. For $t\in [0,T]$, combining (13) and (15), there is

$$\begin{array}{cc}\hfill & Z^{{\psi }_n}\left(t\right)-Z^{\psi }\left(t\right)\hfill \\ \hfill & ={\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[\sigma \left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\right]{\psi }_n\left(s\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\left[{\psi }_n\left(s\right)-\psi \left(s\right)\right]\mathrm{d}s\hfill \\ \hfill & =\sum _{i=1}^3{Q}_i\left(t\right).\hfill \end{array}$$

(16)

Firstly, by applying the $H\ddot{o}lder$ inequality and $\left({\mathsf{A}}_1\right)$, we derive the estimates for $|Q_1\left(t\right){|}^2$ and $|Q_2\left(t\right){|}^2$:

$$\begin{array}{cc}\hfill & |Q_1\left(t\right){|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\right]\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\times \left({\int }_0^t{\left|b\left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-b\left(s,Z^{\psi }\left(s\right),u_s^0\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t{|Z^{{\psi }_n}\left(s\right)-Z^{\psi }\left(s\right)|}^2\mathrm{d}s,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & |Q_2\left(t\right){|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[\sigma \left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\right]{\psi }_n\left(s\right)\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & \times \left({\int }_0^t{\left|\left[\sigma \left(s,Z^{{\psi }_n}\left(s\right),u_s^0\right)-\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\right]{\psi }_n\left(s\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t|Z^{{\psi }_n}\left(s\right)-Z^{\psi }{\left(s\right)|}^2{\left|{\psi }_n\left(s\right)\right|}^2\mathrm{d}s.\hfill \end{array}$$

(18)

Finally, consider $|Q_3\left(t\right){|}^2$; using the $H\ddot{o}lder$ inequality and $\left({\mathsf{A}}_1\right)$, we have

$$\begin{array}{cc}\hfill & |Q_3\left(t\right){|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\left[{\psi }_n\left(s\right)-\psi \left(s\right)\right]\right|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\times \left({\int }_0^t{\left|\sigma \left(s,Z^{\psi }\left(s\right),u_s^0\right)\left[{\psi }_n\left(s\right)-\psi \left(s\right)\right]\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_2^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left[1+|s^{1-\gamma }{Z}^{\psi }{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]{|{\psi }_n\left(s\right)-\psi \left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & ⩽S_2^2{K}_2^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right){\int }_0^t{|{\psi }_n\left(s\right)-\psi \left(s\right)|}^2\mathrm{d}s.\hfill \end{array}$$

(19)

Take the modulus of (16) and let $D_n\left(t\right)={sup}_{0⩽\tau ⩽t}{|Z^{{\psi }_n}\left(\tau \right)-Z^{\psi }\left(\tau \right)|}^2$. Substituting the expressions in (17)–(19), the following equation holds:

$$\begin{array}{cc}\hfill D_n\left(t\right)& ⩽3S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t{D}_n\left(s\right)\mathrm{d}s+3S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t{D}_n\left(s\right){|{\psi }_n\left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right){\int }_0^t{|{\psi }_n\left(s\right)-\psi \left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & ⩽3S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t{D}_n\left(s\right)\left(1+|{\psi }_n{\left(s\right)|}^2\right)\mathrm{d}s\hfill \\ \hfill & +3S_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right){\int }_0^t{|{\psi }_n\left(s\right)-\psi \left(s\right)|}^2\mathrm{d}s.\hfill \end{array}$$

Using the Gronwall inequality, one has

$$\begin{array}{cc}\hfill D_n\left(t\right)& ⩽\left(3S_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right){\int }_0^t{|{\psi }_n\left(s\right)-\psi \left(s\right)|}^2\mathrm{d}s\right)\hfill \\ \hfill & \times exp\left(3S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(T+N\right)\right).\hfill \end{array}$$

Since ${\psi }_n$ converges to $\psi$ in ${\mathbb{L}}^2(J;{\mathbb{R}}^d)$, combined with (19), then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\underset{0⩽\tau ⩽t}{sup}{|Q_3\left(\tau \right)|}^2=0.\end{array}$$

Therefore, we can get

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\underset{0⩽\tau ⩽t}{sup}{|Z^{{\psi }_n}\left(\tau \right)-Z^{\psi }\left(\tau \right)|}^2=0.\end{array}$$

Thus, $G^0\left({\int }_0^t{\psi }_n\left(s\right)\mathrm{d}s\right)$→$G^0\left({\int }_0^t\psi \left(s\right)\mathrm{d}s\right)$ in $C([0,T];{\mathbb{R}}^m)$. □

In order to prove condition $\left(b\right)$, we introduce the following lemma.

Lemma 4.

Suppose that conditions $\left({\mathsf{A}}_1\right)$ and $\left({\mathsf{A}}_2\right)$ hold. If $X^{ϵ}\left(t\right)$ is the solution to Equation (9), then it satisfies

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|X^{ϵ}\left(\tau \right)-X^0\left(\tau \right)|}^2\right)=0.\end{array}$$

Proof. 

Combining (10) and (11), we get

$$\begin{array}{cc}\hfill X^{ϵ}\left(t\right)-X^0\left(t\right)& ={\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)-b\left(s,X^0\left(s\right),u_s^0\right)\right]\mathrm{d}s\hfill \\ \hfill & +\sqrt{ϵ}{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)\mathrm{d}W\left(s\right)\hfill \\ \hfill & =\sum _{i=1}^2{L}_i\left(t\right).\hfill \end{array}$$

For $|L_1{\left(t\right)|}^2$, by using the $H\ddot{o}lder$ inequality and $\left({\mathsf{A}}_1\right)$, then

$$\begin{array}{cc}\hfill & |L_1{\left(t\right)|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)-b\left(s,X^0\left(s\right),u_s^0\right)\right]|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\times \left({\int }_0^t{\left|b\left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)-b\left(s,X^0\left(s\right),u_s^0\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(|X^{ϵ}\left(s\right)-X^0{\left(s\right)|}^2+{\mathbb{W}}_2{\left(u_s^{ϵ},u_s^0\right)}^2\right)\mathrm{d}s\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(|X^{ϵ}\left(s\right)-X^0{\left(s\right)|}^2+\mathbf{E}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right)\mathrm{d}s.\hfill \end{array}$$

From this, we can obtain

$$\begin{array}{c}\hfill \mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|L_1\left(\tau \right)|}^2\right)⩽2S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\mathbf{E}{\int }_0^t{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\mathrm{d}s.\end{array}$$

For $|L_2{\left(t\right)|}^2$, we apply the Burkholder–Davis–Gundy (B-D-G) inequality [23] and $\left({\mathsf{A}}_1\right)$; we have

$$\begin{array}{cc}\hfill & \mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|L_2\left(\tau \right)|}^2\right)\hfill \\ \hfill & ⩽ϵ\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}|{\int }_0^{\tau }{(\tau -s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(\tau -s)}^{\varkappa }\right)\left[\sigma \left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,X^0\left(s\right),u_s^0\right)\right]\mathrm{d}W\left(s\right){|}^2\right)\hfill \\ \hfill & +ϵ\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}|{\int }_0^{\tau }{(\tau -s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(\tau -s)}^{\varkappa }\right)\sigma \left(s,X^0\left(s\right),u_s^0\right)\mathrm{d}W\left(s\right){|}^2\right)\hfill \\ \hfill & ⩽ϵC_2\mathbf{E}\left({\int }_0^t|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[\sigma \left(s,X^{ϵ}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,X^0\left(s\right),u_s^0\right)\right]{|}^2\mathrm{d}s\right)\hfill \\ \hfill & +ϵC_2\mathbf{E}\left({\int }_0^t|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^0\left(s\right),u_s^0\right){|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽ϵC_2{S}_2^2{K}_1^2\mathbf{E}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\left(|X^{ϵ}\left(s\right)-X^0{\left(s\right)|}^2+{\mathbb{W}}_2{\left(u_s^{ϵ},u_s^0\right)}^2\right)\mathrm{d}s\right)\hfill \\ \hfill & +ϵC_2{S}_2^2{K}_2^2\mathbf{E}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\left[1+|s^{1-\gamma }{X}^0{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]\mathrm{d}s\right)\hfill \\ \hfill & ⩽2ϵC_2{S}_2^2{K}_1^2\mathbf{E}{\int }_0^t{(t-s)}^{2\varkappa -2}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & +ϵC_2{S}_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{*}+C^{\prime }\right),\hfill \end{array}$$

where $C_2$ is the B-D-G constant.

Let $Y\left(t\right)=\mathbf{E}\left({sup}_{0⩽\tau ⩽t}{|X^{ϵ}\left(\tau \right)-X^0\left(\tau \right)|}^2\right)$; then,

$$\begin{array}{cc}\hfill Y\left(t\right)& ⩽4S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^{t}Y\left(s\right)\mathrm{d}s\hfill \\ \hfill & +4ϵC_2{S}_2^2{K}_1^2{\int }_0^t{(t-s)}^{2\varkappa -2}Y\left(s\right)\mathrm{d}s\hfill \\ \hfill & +2ϵC_2{S}_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{*}+C^{\prime }\right).\hfill \end{array}$$

Using the Gronwall inequality and further simplifying, one has

$$\begin{array}{cc}\hfill Y\left(t\right)& ⩽\left(2ϵC_2{S}_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{*}+C^{\prime }\right)\right)\hfill \\ \hfill & \times exp\left(4S_2^2{K}_1^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(T+ϵC_2\right)\right).\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|X^{ϵ}\left(\tau \right)-X^0\left(\tau \right)|}^2\right)=0.\end{array}$$

□

To prove condition $\left(b\right)$, consider the following perturbed stochastic control equation:

$$\begin{array}{cc}\hfill X^{{\psi }_{ϵ}}\left(t\right)& =t^{\gamma -1}{E}_{\varkappa ,\gamma }\left(A{t}^{\varkappa }\right)X_0+{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)b\left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right){\psi }_{ϵ}\left(s\right)\mathrm{d}s\hfill \\ \hfill & +\sqrt{ϵ}{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)\mathrm{d}W\left(s\right).\hfill \end{array}$$

(20)

Define

$$\begin{array}{c}\hfill X^{{\psi }_{ϵ}}(·)=G^{ϵ}\left(W(·)+{\displaystyle \frac{1}{\sqrt{ϵ}}}{\int }_0^{·}{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right).\end{array}$$

Lemma 5.

Suppose that $\left({\mathsf{A}}_1\right)$−$\left({\mathsf{A}}_2\right)$ hold; for any $N<+\infty$, when ${\left\{{\psi }_{ϵ}\right\}}_{ϵ>0}\subset {\Lambda }_N$ and any $\delta >0$, we have

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}\mathbf{P}\left(d\left(G^{ϵ}\left(W+{\displaystyle \frac{1}{\sqrt{ϵ}}}{\int }_0^t{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right),G^0\left({\int }_0^t{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right)\right)>\delta \right)=0.\end{array}$$

Proof. 

Let $Z^{{\psi }_{ϵ}}=G^0\left({\int }_0^t{\psi }_{ϵ}\left(s\right)\mathrm{d}s\right)$ be the solution to Equation (12), which is obtained by replacing $\psi$ with ${\psi }_{ϵ}$. Combining (12) and (20), we have

$$\begin{array}{cc}\hfill & X^{{\psi }_{ϵ}}\left(t\right)-Z^{{\psi }_{ϵ}}\left(t\right)\hfill \\ \hfill & ={\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-b\left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]\mathrm{d}s\hfill \\ \hfill & +{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]{\psi }_{ϵ}\left(s\right)\mathrm{d}s\hfill \\ \hfill & +\sqrt{ϵ}{\int }_0^t{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)\mathrm{d}W\left(s\right)\hfill \\ \hfill & =\sum _{i=1}^3{M}_i\left(t\right).\hfill \end{array}$$

For $|M_1{\left(t\right)|}^2$, $|M_2{\left(t\right)|}^2$, using the $H\ddot{o}lder$ inequality and (${\mathsf{A}}_1$), we have

$$\begin{array}{cc}\hfill & |M_1{\left(t\right)|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[b\left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-b\left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & \times \left({\int }_0^t{\left|b\left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-b\left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+{\mathbb{W}}_2{\left(u_s^{ϵ},u_s^0\right)}^2\right)\mathrm{d}s\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+\mathbf{E}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right)\mathrm{d}s.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & |M_2{\left(t\right)|}^2\hfill \\ \hfill & ⩽{\left({\int }_0^t|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\left[\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]{\psi }_{ϵ}\left(s\right)|\mathrm{d}s\right)}^2\hfill \\ \hfill & ⩽\left({\int }_0^t{\left|{(t-s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(t-s)}^{\varkappa }\right)\right|}^2\mathrm{d}s\right)\hfill \\ \hfill & \times \left({\int }_0^t|\left[\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]{\psi }_{ϵ}\left(s\right){|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left[|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+{\mathbb{W}}_2{\left(u_s^{ϵ},u_s^0\right)}^2\right]{|{\psi }_{ϵ}\left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & ⩽S_2^2{K}_1^2{\displaystyle \frac{t^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+\mathbf{E}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right){|{\psi }_{ϵ}\left(s\right)|}^2\mathrm{d}s.\hfill \end{array}$$

For $|M_3{\left(t\right)|}^2$, using the B-D-G inequality, $H\ddot{o}lder$ inequality, and $\left({\mathsf{A}}_1\right)$-$\left({\mathsf{A}}_2\right)$, we can get

$$\begin{array}{cc}\hfill & \mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|M_3\left(\tau \right)|}^2\right)\hfill \\ \hfill & ⩽ϵ\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}|{\int }_0^{\tau }{(\tau -s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(\tau -s)}^{\varkappa }\right)\left[\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]\mathrm{d}W\left(s\right){|}^2\right)\hfill \\ \hfill & +ϵ\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}|{\int }_0^{\tau }{(\tau -s)}^{\varkappa -1}{E}_{\varkappa ,\varkappa }\left(A{(\tau -s)}^{\varkappa }\right)\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\mathrm{d}W\left(s\right){|}^2\right)\hfill \\ \hfill & ⩽ϵC_2{S}_2^2\mathbf{E}\left({\int }_0^t|{(t-s)}^{\varkappa -1}\left[\sigma \left(s,X^{{\psi }_{ϵ}}\left(s\right),u_s^{ϵ}\right)-\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right)\right]{|}^2\mathrm{d}s\right)\hfill \\ \hfill & +ϵC_2{S}_2^2\mathbf{E}\left({\int }_0^t|{(t-s)}^{\varkappa -1}\sigma \left(s,Z^{{\psi }_{ϵ}}\left(s\right),u_s^0\right){|}^2\mathrm{d}s\right)\hfill \\ \hfill & ⩽ϵC_2{S}_2^2{K}_1^2\mathbf{E}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\left(|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+{\mathbb{W}}_2{\left(u_s^{ϵ},u_s^0\right)}^2\right)\mathrm{d}s\right)\hfill \\ \hfill & +ϵC_2{S}_2^2{K}_2^2\mathbf{E}\left({\int }_0^t{(t-s)}^{2\varkappa -2}\left[1+|s^{1-\gamma }{Z}^{{\psi }_{ϵ}}{\left(s\right)|}^2+u_s^0\left({|·|}^2\right)\right]\mathrm{d}s\right)\hfill \\ \hfill & ⩽ϵC_2{S}_2^2{K}_1^2\mathbf{E}{\int }_0^t{(t-s)}^{2\varkappa -2}\left(|X^{{\psi }_{ϵ}}\left(s\right)-Z^{{\psi }_{ϵ}}{\left(s\right)|}^2+\mathbf{E}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right)\mathrm{d}s\hfill \\ \hfill & +ϵC_2{S}_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right).\hfill \end{array}$$

Let $M\left(t\right)=\mathbf{E}\left({sup}_{0⩽\tau ⩽t}{|X^{{\psi }_{ϵ}}\left(\tau \right)-Z^{{\psi }_{ϵ}}\left(\tau \right)|}^2\right)$, then

$$\begin{array}{cc}\hfill M\left(t\right)& ⩽{\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(M\left(s\right)+\mathbf{E}\underset{0⩽s⩽t}{sup}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right)\mathrm{d}s\hfill \\ \hfill & +{\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa -1}}{2\varkappa -1}}{\int }_0^t\left(M\left(s\right)+\mathbf{E}\underset{0⩽s⩽t}{sup}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right){|{\psi }_{ϵ}\left(s\right)|}^2\mathrm{d}s\hfill \\ \hfill & +3ϵC_2{S}_2^2{K}_1^2{\int }_0^t{(t-s)}^{2\varkappa -2}\left(M\left(s\right)+\mathbf{E}\underset{0⩽s⩽t}{sup}{|X^{ϵ}\left(s\right)-X^0\left(s\right)|}^2\right)\mathrm{d}s\hfill \\ \hfill & +3ϵC_2{S}_2^2{K}_2^2{\displaystyle \frac{T^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right).\hfill \end{array}$$

Using the Gronwall inequality and further simplifying it, we can get

$$\begin{array}{cc}\hfill & M\left(t\right)\hfill \\ \hfill & ⩽({\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa }}{2\varkappa -1}}\mathbf{E}\underset{0⩽\tau ⩽t}{sup}|X^{ϵ}\left(\tau \right)-X^0{\left(\tau \right)|}^2+{\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa -1}N}{2\varkappa -1}}\mathbf{E}\underset{0⩽\tau ⩽t}{sup}{|X^{ϵ}\left(\tau \right)-X^0\left(\tau \right)|}^2\hfill \\ \hfill & +{\displaystyle \frac{3ϵC_2{S}_2^2{K}_1^2{T}^{2\varkappa -1}}{2\varkappa -1}}\mathbf{E}\underset{0⩽\tau ⩽t}{sup}{|X^{ϵ}\left(\tau \right)-X^0\left(\tau \right)|}^2+{\displaystyle \frac{3ϵC_2{S}_2^2{K}_2^2{T}^{2\varkappa -1}}{2\varkappa -1}}\left(1+C^{\prime }+\widehat{C}\right))\hfill \\ \hfill & \times exp\left({\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa }}{2\varkappa -1}}+{\displaystyle \frac{3S_2^2{K}_1^2{T}^{2\varkappa -1}N}{2\varkappa -1}}+{\displaystyle \frac{3ϵC_2{S}_2^2{K}_1^2{T}^{2\varkappa -1}}{2\varkappa -1}}\right).\hfill \end{array}$$

When $ϵ\to 0$, combining with Lemma 4, we can deduce

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|X^{{\psi }_{ϵ}}\left(\tau \right)-Z^{{\psi }_{ϵ}}\left(\tau \right)|}^2\right)=0.\end{array}$$

For any $\delta >0$, by the Chebyshev inequality, one has

$$\begin{array}{c}\hfill \mathbf{P}\left(\underset{0⩽\tau ⩽t}{sup}|X^{{\psi }_{ϵ}}\left(\tau \right)-Z^{{\psi }_{ϵ}}\left(\tau \right)|>\delta \right)⩽{\displaystyle \frac{1}{{\delta }^2}}\mathbf{E}\left(\underset{0⩽\tau ⩽t}{sup}{|X^{{\psi }_{ϵ}}\left(\tau \right)-Z^{{\psi }_{ϵ}}\left(\tau \right)|}^2\right).\end{array}$$

Based on the above results, when $ϵ\to 0$, ${lim}_{ϵ\to 0}\mathbf{P}\left(d\left(X^{{\psi }_{ϵ}},Z^{{\psi }_{ϵ}}\right)>\delta \right)=0$. Therefore, condition $\left(b\right)$ is proven. □

It follows from Lemmas 3 and 5 that $\left\{X^{ϵ}\right\}$ satisfies the LP. Based on the equivalence between the LP and the LDP, we can conclude that the following theorem holds.

Theorem 2.

For any $ϵ>0$, let $X^{ϵ}=G^{ϵ}\left(W\right)$ and assume that conditions $\left({\mathsf{A}}_1\right)$–$\left({\mathsf{A}}_2\right)$ and $\left(\mathbb{A}\right)$ hold. Then, $\left\{X^{ϵ}\right\}$ satisfies the LDP in $C_{1-\gamma }([0,T];{\mathbb{R}}^m)$ with the rate function

$$\begin{array}{c}\hfill I\left(f\right)=\underset{\psi \in {\mathbb{L}}^2([0,T];{\mathbb{R}}^d),f=G^0\left({\int }_0^{·}\psi \left(s\right)\mathrm{d}s\right)}{inf}\left\{{\displaystyle \frac{1}{2}}{\int }_0^T|{\psi \left(s\right)|}^2\mathrm{d}s\right\},\end{array}$$

where $inf(\varnothing )=\infty$.

4. Model Application

To better understand the specific application of our work, in this section we will design a practical example based on the characteristics of model (1) to illustrate how to apply the LDP of the Hilfer fractional stochastic McKean–Vlasov differential equation to a specific system.

In this section, we consider that there are two competitive waterfowl populations, Egret $\left(X_1\right)$ and Goshawk $\left(X_2\right)$, in a wetland ecosystem, and their dynamic density is affected by limited natural resources, intra-population, and inter-population competition and random climate change. We use fractional derivatives to describe the historical dependence of population dynamics. The following Hilfer fractional stochastic differential equation is considered:

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\kappa ,\varkappa }X\left(t\right)=AX\left(t\right)+b\left(t,X\left(t\right),u_t\right)+\sigma \left(t,X\left(t\right),u_t\right)\frac{\mathrm{d}W\left(t\right)}{\mathrm{d}t},t\in J^{\prime },\hfill \\ I_{0^{+}}^{1-\gamma }X\left(0\right)=X_0,\gamma =\kappa +\varkappa -\kappa \varkappa ,\hfill \end{array}\right.$$

(21)

where $\kappa =0.5,\varkappa =0.75$, $\gamma =0.5+0.75-0.5\times 0.75=0.875$. The state variable $X\left(t\right)={\left(X_1\left(t\right),X_2\left(t\right)\right)}^T$ and initial condition $\left(X_1\left(0\right),X_2\left(0\right)\right)$ = ${(1.2,0.8)}^T$, which means that the density of egrets is 1.2/${\mathrm{km}}^2$ and goshawks is 0.8/${\mathrm{km}}^2$ at the initial moment. The matrix $A=\left(\begin{array}{cc}-0.2& 0\\ 0& -0.2\end{array}\right)$ is the natural decay rate matrix, which indicates the population decay caused by the limitation of natural resources. Consider the nonlinear interaction term

$$b\left(t,X\left(t\right),u_t\right)=t^{1-\gamma }\left(\begin{array}{c}0.3X_1-0.1\mathbf{E}\left[X_1\right]-0.05X_2\\ 0.5X_2+0.05\mathbf{E}\left[X_2\right]-0.08X_1\end{array}\right),$$

where the time factor $t^{1-\gamma }$ means that with the increase of time, the influence of cluster effect and competition effect will gradually increase. The positive feedback terms of $0.3X_1$ and $0.5X_2$ respectively represent the cluster effect of egrets and goshawks to promote the reproductive rate, while $-0.1\mathbf{E}\left[X_1\right]$ means that when the overall population density is too high, the mortality rate will increase due to habitat congestion, and $-0.05X_2$ means that goshawks and egrets compete for the same food resources (such as fish), and the growth rate of egrets will decrease by 5% for every increase of goshawk density per/${\mathrm{km}}^2$. On the contrary, the item of $+0.05\mathbf{E}\left[X_2\right]$ means that a certain degree of population aggregation may reduce the risk of predation (such as group vigilance). The item of $-0.08X_1$ means that egrets have stronger competition inhibition on goshawks by occupying habitats (such as nesting sites), and the growth rate of goshawks will decrease by 8% for every increase in egret density. The multiplicative noise intensity

$$\sigma \left(t,X\left(t\right),u_t\right)=\left(\begin{array}{cc}{\sigma }_{11}& {\sigma }_{12}\\ {\sigma }_{21}& {\sigma }_{22}\end{array}\right)=\left(\begin{array}{cc}0.05+0.1t^{1-\gamma }{X}_1& 0.03t^{1-\gamma }{X}_2\\ 0.03t^{1-\gamma }{X}_1& 0.1+0.05t^{1-\gamma }{X}_2\end{array}\right)$$

can be used to describe the influence of random factors such as environment and individuals on the population. For example, in the egret noise item $\left({\sigma }_{11}\right)$, 0.05 represents constant environmental disturbance and $0.1X_1$ means that the higher the population density, the more intense the competition among individuals will be, leading to the amplification of environmental fluctuation. And $t^{1-\gamma }$ means that the intensity of noise term increases slowly with time, which is used to simulate the long-term cumulative effect of the ecological community. The cross noise term $({\sigma }_{12},{\sigma }_{21})$ indicates that the competition between two groups leads to the mutual influence of environmental disturbance.

Next, we need to verify whether or not the coefficients in the example satisfy the assumptions $\left({\mathsf{A}}_1\right)$ and $\left({\mathsf{A}}_2\right)$. First, we check whether or not the nonlinear term b and the noise term $\sigma$ in condition $\left({\mathsf{A}}_1\right)$ satisfy the Lipschitz condition. For

$$b\left(t,x,u\right)-b\left(t,y,v\right)=t^{1-\gamma }\left(\begin{array}{c}0.3\Delta x_1-0.1\Delta {\mathbf{E}}_1-0.05\Delta x_2\\ 0.5\Delta x_2+0.05\Delta {\mathbf{E}}_2-0.08\Delta x_1\end{array}\right),$$

where $\Delta x_i=x_i-y_i$, $\Delta {\mathbf{E}}_i={\mathbf{E}}_u\left(x_i\right)-{\mathbf{E}}_v\left(x_i\right)$. Applying the elementary inequality to $|b\left(t,x,u\right)-b\left(t,y,v\right){|}^2$, we can obtain

$$\begin{array}{c}\hfill |b\left(t,x,u\right)-b\left(t,y,v\right){|}^2⩽3t^{0.25}\times \left(0.0964\Delta {x_1}^2+0.2525\Delta {x_2}^2+0.01\Delta {{\mathbf{E}}_1}^2+0.0025\Delta {{\mathbf{E}}_2}^2\right).\end{array}$$

(22)

Moreover, since $\Delta {x_1}^2+\Delta {x_2}^2={|x-y|}^2$ and $|{\mathbf{E}}_u\left(x_i\right)-{\mathbf{E}}_v\left(x_i\right)|⩽{\mathbb{W}}_2(u,v)$, (22) can be transformed into

$$\begin{array}{c}\hfill |b\left(t,x,u\right)-b\left(t,y,v\right){|}^2⩽3t^{0.25}\times \left({0.3489|x-y|}^2+0.0125{\mathbb{W}}_2{(u,v)}^2\right).\end{array}$$

Similarly,

$$\sigma \left(t,x,u\right)-\sigma \left(t,y,v\right)=\left(\begin{array}{cc}0.1t^{1-\gamma }\Delta x_1& 0.03t^{1-\gamma }\Delta x_2\\ 0.03t^{1-\gamma }\Delta x_1& 0.05t^{1-\gamma }\Delta x_2\end{array}\right).$$

For $|\sigma \left(t,x,u\right)-\sigma \left(t,y,v\right){|}^2$, then

$$\begin{array}{cc}\hfill |\sigma \left(t,x,u\right)-\sigma \left(t,y,v\right){|}^2& ={\left(0.1t^{0.125}\Delta x_1\right)}^2+{\left(0.03t^{0.125}\Delta x_2\right)}^2\hfill \\ \hfill & +{\left(0.03t^{0.125}\Delta x_1\right)}^2+{\left(0.05t^{0.125}\Delta x_2\right)}^2\hfill \\ \hfill & =t^{0.25}\left(0.0109\Delta {x_1}^2+0.0034\Delta {x_2}^2\right)\hfill \\ \hfill & ⩽t^{0.25}\times 0.0143{|x-y|}^2.\hfill \end{array}$$

Requirement: $K_1^2=max\left(1.0467T^{0.25},0.0375T^{0.25},0.0143T^{0.25}\right)$; if $T=1$, then $K_1\approx 1.023$. Under the model parameters, the Lipschitz constant of the nonlinear term b and the noise term $\sigma$ satisfy $K_1\approx 1.023$, then $\left({\mathsf{A}}_1\right)$ holds. Finally, verify whether or not b and $\sigma$ satisfy $\left({\mathsf{A}}_2\right)$. To calculate $|b\left(t,x,u\right){|}^2$ and expand it by using the elementary inequality, we can get

$$\begin{array}{cc}\hfill |b\left(t,x,u\right){|}^2& =t^{2(1-\gamma )}\left[{\left(0.3x_1-0.1{\mathbf{E}}_u\left(x_1\right)-0.05x_2\right)}^2+{\left(0.5x_2+0.05{\mathbf{E}}_u\left(x_2\right)-0.08x_1\right)}^2\right]\hfill \\ \hfill & ⩽3t^{2(1-\gamma )}\left[0.0964x_1^2+0.2525x_2^2+0.01{\mathbf{E}}_u\left(x_1^2\right)+0.0025{\mathbf{E}}_u\left(x_2^2\right)\right].\hfill \end{array}$$

Due to ${u(|·|}^2)={\mathbf{E}}_u[x_1^2+x_2^2]$, it is further simplified as

$$\begin{array}{cc}\hfill |b\left(t,x,u\right){|}^2& ⩽3t^{2(1-\gamma )}\left[{0.3489|x|}^2{+0.0125u(|·|}^2)\right]\hfill \\ \hfill & ⩽1.0467|t^{1-\gamma }{x|}^2{+0.0375u(|·|}^2).\hfill \end{array}$$

For ${|\sigma (t,x,u)|}^2={\left(0.05+0.1t^{1-\gamma }{x}_1\right)}^2+{\left(0.03t^{1-\gamma }{x}_2\right)}^2+{\left(0.03t^{1-\gamma }{x}_1\right)}^2+{\left(0.1+0.05t^{1-\gamma }{x}_2\right)}^2$, using Young inequality, we can obtain ${|\sigma (t,x,u)|}^2⩽0.0175+0.0193{|t^{1-\gamma }x|}^2$. To make $\left({\mathsf{A}}_2\right)$ hold, it is necessary to satisfy $K_2^2=max\left(1.0467,0.0375,0.0175,0.0193\right)$; then, $K_2\approx 1.023$. Therefore, when $K_1=K_2\approx 0.87$, both $\left({\mathsf{A}}_1\right)$ and $\left({\mathsf{A}}_2\right)$ are satisfied.

To analyze the changes of egret and goshawk population densities under different noise disturbances, we first draw the deterministic and stochastic paths of the two species under noise $ϵ=0.1$ with the above parameter settings, and the results are shown in Figure 1. It shows the deterministic path (blue solid line) and stochastic path (red curve) of Egret $\left(X_1\right)$ and Goshawk $\left(X_2\right)$ with time under noise $ϵ=0.1$, respectively. It can be seen that the noise intensity at this time has a great influence on the population density of the two birds. At the initial stage, the stochastic path fluctuates around the deterministic path, but with the passage of time it deviates from the deterministic path and shows strong randomness.

Figure 1. The deterministic and stochastic paths of the evolution of Egret $\left(X_1\right)$ and Goshawk $\left(X_2\right)$ with time under noise $ϵ=0.1$. The time-step is ${10}^{-2}$.

For Figure 1, we can observe that the "stochastic path" exhibits significant instability compared to the “deterministic path". There are two main reasons for this: first, as $X_i\left(t\right)$ changes, $\sigma (t,X,u_t)$ grows proportionally to the state variables, thus amplifying small perturbations; second, $b(t,X,u_t)$ depends on $\mathbf{E}\left(X_i\right)$, and the random perturbations in $X^{ϵ}\left(t\right)$ will alter the instantaneous distribution $u_t^{ϵ}$, which in turn generates perturbations and causes the initial deviation to expand continuously. Therefore, even with a noise level of $ϵ=0.1$, the stochastic path will show a significant deviation from the deterministic path after $t>0.4$. The environmental randomness is amplified through population density dependence and group effects, leading to path instability.

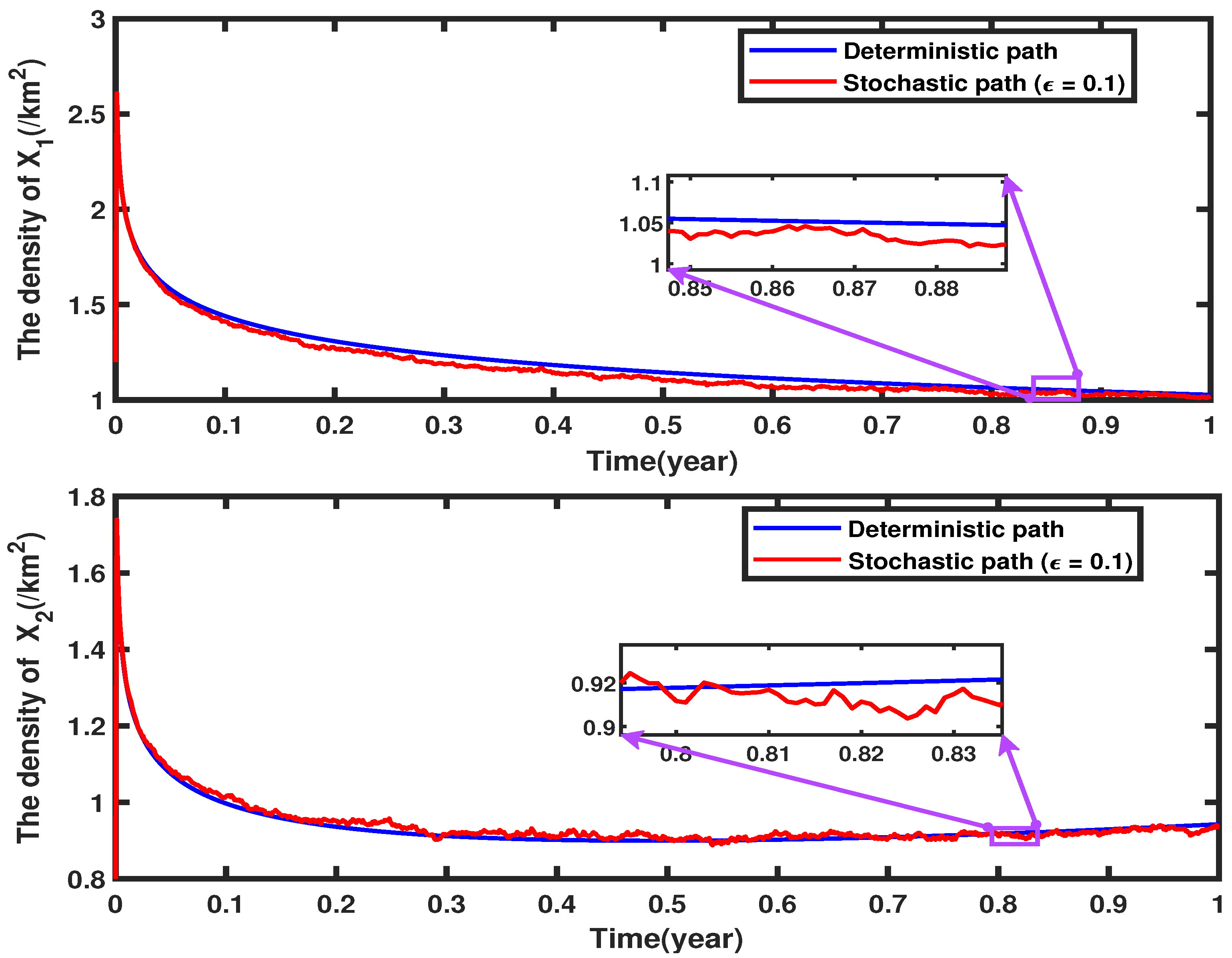
Based on the LDP, we are more concerned about the evolution of two populations under small noise disturbance, so we set a small noise $ϵ=0.001$ to study, and we draw Figure 2 while keeping other parameters unchanged. Figure 2 shows the certainty (blue solid line) and random path (red curve) of the evolution of Egret $\left(X_1\right)$ and Goshawk $\left(X_2\right)$ with time under noise $ϵ=0.001$, respectively. It can be seen that the stochastic paths of $X_1$ and $X_2$ almost coincide with the deterministic paths in the case of small noise, which indicates that the behavior of the system is mainly dominated by the deterministic part, and the random disturbance has little influence on the two bird populations.

Figure 2. The deterministic and stochastic paths of the evolution of Egret $\left(X_1\right)$ and Goshawk $\left(X_2\right)$ with time under noise $ϵ=0.001$. The time-step is ${10}^{-2}$.

Figure 1 and Figure 2 show the density changes of egrets and goshawks under environmental noise intensities 0.1 and 0.001, respectively. While stochastic noise clearly induces deviations from deterministic paths, we have not yet quantified the risk of population density fluctuations caused by random environmental factors. To address this, we employ the LDP to analyze the fluctuation risk of competitive populations in wetland ecosystems. Specifically, the probability that the stochastic path $X^{ϵ}\left(t\right)$ deviates from the deterministic path $X^0\left(t\right)$ by exceeding a threshold $\delta$ satisfies

$$\begin{array}{c}\hfill \underset{ϵ\to 0}{lim}ϵlog\mathbf{P}\left(\underset{t\in [0,T]}{sup}|X^{ϵ}\left(t\right)-X^0\left(t\right)|>\delta \right)=-I\left(\delta \right),\end{array}$$

(23)

where the rate function $I\left(\delta \right)$ is defined by the variational problem

$$I\left(\delta \right)=\underset{\psi \in {\mathcal{A}}_{\delta }}{inf}\left\{{\displaystyle \frac{1}{2}}{\int }_0^T{|\psi \left(s\right)|}^2\mathrm{d}s\right\},$$

where ${\mathcal{A}}_{\delta }$ is the set of all control processes $\psi$ that satisfy the conditions

$${\mathcal{A}}_{\delta }=\left\{\psi \in {\mathbb{L}}^2\left([0,T];{\mathbb{R}}^d\right)|\underset{t\in [0,T]}{sup}|Z^{\psi }\left(t\right)-X^0\left(t\right)|\ge \delta \right\},$$

and $Z^{\psi }\left(t\right)$ is the solution of the controlled skeleton Equation (12).

Secondly, taking the egret population as an example, we use the LDP to estimate the probability that the population density of egrets is less than 1/${\mathrm{km}}^2$ (initial 1.2/${\mathrm{km}}^2$) within one year under the influence of random factors, and this event is recorded as $\mathbb{B}=\{X_1^{ϵ}\left(1\right)<1\}$. The deterministic path of egret population density is $X_1^0\left(1\right)$ at t = 1 (year), and the deviation threshold corresponding to the target event is $\delta =X_1^0\left(1\right)-1$. Therefore, according to (23), the probability of this event can be expressed as follows:

$$\begin{array}{c}\hfill \mathbf{P}(X_1^{ϵ}\left(1\right)<1)=\mathbf{P}\left(X_1^{ϵ}\left(1\right)-X_1^0\left(1\right)<-\delta \right)\approx {\mathrm{e}}^{{\displaystyle \frac{-I\left(\delta \right)}{ϵ}}},\end{array}$$

where the rate function $I\left(\delta \right)={inf}_{\psi \in {\mathcal{A}}_{\delta }}\left\{{\displaystyle \frac{1}{2}}{\int }_0^1{|\psi \left(s\right)|}^2\mathrm{d}s|Z_1^{\psi }\left(1\right)\le 1\right\}$.

We use the Monte Carlo method to generate 200 independent random paths. Through repeated random experiments, we count the probability that the egret density is lower than the threshold when the noise is $ϵ$ = 0.1, 0.01, and 0.001. The calculated results are $\mathbf{P}(X_1^{0.1}\left(1\right)<1)=0.335$, $\mathbf{P}(X_1^{0.01}\left(1\right)<1)=0.09$ and $\mathbf{P}(X_1^{0.001}\left(1\right)<1)=0$. The results show that the egret population has strong stability in weak noise environments, but if the noise intensity increases (such as environmental pollution), the risk of population density decline will greatly increase. This indicates that the instability will increase with the enhancement of noise intensity.

5. Discussion and Outlook

This paper systematically investigates the establishment and application of the LDP for a class of Hilfer fractional stochastic McKean–Vlasov differential equations. The combination of fractional derivatives and McKean–Vlasov can better reflect the real dynamics in fields such as physics and biology. Taking competitive populations in wetland ecology as an example, the LDP is used to quantify the probability of the probability of the population density falling below the threshold, indicating that ecological risks increase significantly under strong noise. In ecosystems, financial markets, and power systems, the rate function I is used to quantify the occurrence probability of critical events (such as population collapse, market crash, and power grid frequency deviation), thereby optimizing regulation strategies.

Although this paper establishes the LDP for Hilfer fractional stochastic McKean–Vlasov equations and provides application examples, the research still has the following limitations: the coefficients satisfy the global Lipschitz condition, but non-Lipschitz continuous systems may exist in practical applications; the model is applicable to Gaussian noise and cannot handle non-Gaussian noise (such as Lévy jump processes); in the ecological case, static parameters are assumed, and the impact of time-varying environmental factors on population dynamic changes is not considered.

Based on the above limitations, future work can be carried out in the following directions: studying the LDP of the system under the local Lipschitz condition; establishing the LDP driven by non-Gaussian noise; introducing time-varying parameters into ecosystem models to analyze the impact of climate change on the risk of population extinction.