Soliton Dynamics of the Nonlinear Kodama Equation with M-Truncated Derivative via Two Innovative Schemes: The Generalized Arnous Method and the Kudryashov Method

Abstract

The primary aim of this research article is to investigate the soliton dynamics of the M-truncated derivative nonlinear Kodama equation, which is useful for optical solitons on nonlinear media, shallow water waves over complex media, nonlocal internal waves, and fractional viscoelastic wave propagation. We utilized two recently developed analytical techniques, the generalized Arnous method and the generalized Kudryashov method. First, the nonlinear Kodama equation is transformed into a nonlinear ordinary differential equation using the homogeneous balance principle and a traveling wave transformation. Next, various types of soliton solutions are constructed through the application of these effective methods. Finally, to visualize the behavior of the obtained solutions, three-dimensional, two-dimensional, and contour plots are generated using Maple (2023) mathematical software.

1. Introduction

Nonlinear wave models such as nonlinear Schrodinger (NLS) [1] and Korteweg-de Vries (KdV) [2] play an important role in optics and fluid dynamics. Extensions made in these equations, such as Kodama or Hirota, incorporate high-order dispersion, which enables us to describe the short light pulses more precisely. However, utilizing fractional derivatives, such as Riemann–Liouville fractional derivatives [3], the M-truncated derivative [4], and conformable fractional derivatives [5,6], allow the model to incorporate an effect that depends on the past, like memory, which fades over time. Complex fractional partial differential equations (CFPDEs) are used in many areas like communication, physics, biology, engineering, geophysics, and chemistry [7,8]. In physics, CFPDEs help us to describe actions that incorporate diffusion and memory. In communication systems [9], CFPDEs can be used to filter and improve the signals. They help to construct models that speculate on the change in the market. Besides these areas, CFPDEs are also very useful in other fields of study.

The nonlinear Kodama equation with the M-truncated derivative (NLKE-MTD) is a unique type of CFPDE, described as follows [10]:

$$i{T}_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }\mathcal{Q}+{\mathcal{Q}}_{\mathcal{XX}}++{\delta }_1{\left|\mathcal{Q}\right|}^2\mathcal{Q}+i{\delta }_2{\left|\mathcal{Q}\right|}^2{\mathcal{Q}}_{\mathcal{X}}+i{\delta }_3{\mathcal{Q}}^2{\mathcal{Q}}_{\mathcal{X}}=0,$$

(1)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }(·)$ depicts the M-truncated derivative; its interpretation and properties will be detailed in Section 2. $\mathcal{Q}=\mathcal{Q}(\mathcal{X},\mathcal{T})$ represents the complex function. $\left({\mathcal{Q}}_{\mathcal{XX}}\right)$ is a second-order dispersion term that spreads the wave packet, $\left({\delta }_1\right|\mathcal{Q}{|}^2\mathcal{Q})$ is the cubic nonlinearity that stabilizes the dispersion to generate solitons, $\left(i{\delta }_2\right|\mathcal{Q}{|}^2{\mathcal{Q}}_{\mathcal{X}})$ is a self-steepening term that shifts the pulse peak, and $\left(i{\delta }_3{\mathcal{Q}}^2{\mathcal{Q}}_{\mathcal{X}}\right)$ is a non-Hermitian term that enables non-conservative energy change. $\gamma$ and $\theta$ control the robustness and type of memory. ${\delta }_1$ (the strength of cubic nonlinearity), ${\delta }_2$, and ${\delta }_3$ (the magnitude of nonlinear effects) are random constants. i represents the imaginary unit fulfilling $i^2=-1$.

The NLKE-MTD Equation (1) can be reduced to other, different models by choosing specific parameter values and derivative terms. Setting $T_{\mathcal{X}}^{3\theta }\to 0,{\delta }_2={\delta }_3=0$, Equation (1) reduces to the Space–Time Fractional nonlinear Schrodinger (STF-NLS) equation [11].

$$i{T}_{\mathcal{T}}^{\gamma }\mathcal{Q}+T_{\mathcal{X}}^{2\theta }\mathcal{Q}+{\delta }_1{\left|\mathcal{Q}\right|}^2\mathcal{Q}=0.$$

(2)

where the notation $T_X^{3\theta }\to 0$ indicates the suppression of third-order dispersion effects in the generalized form of the Kodama equation, even though Equation (1) explicitly displays only second-order dispersion ($Q_{\mathcal{XX}}$). This reduction step is standard when deriving the fractional NLS limits (Equations (2) and (3)). Incorporating $0<\gamma ,\theta <1$ and retaining all other terms in Equation (1) will yield the Space–Time Fractional Hirota (STF-H) equation [12].

$$i{T}_{\mathcal{T}}^{\gamma }\mathcal{Q}+T_{\mathcal{X}}^{2\theta }\mathcal{Q}+i{T}_{\mathcal{X}}^{3\theta }\mathcal{Q}+{\delta }_1{\left|\mathcal{Q}\right|}^2\mathcal{Q}+i{\delta }_2{\left|\mathcal{Q}\right|}^2{T}_{\mathcal{X}}^{\theta }\mathcal{Q}+i{\delta }_3{\mathcal{Q}}^2{T}_{\mathcal{X}}^{\theta }\mathcal{Q}=0.$$

(3)

Equation (1) can be transformed into the Space–Time Fractional Chen–Lee–Liu (STF-CLL) equation [13] by inserting $T_{\mathcal{X}}^{3\theta }\to 0,{\delta }_3=0,{\delta }_2\ne 0$ into Equation (1).

$$i{T}_{\mathcal{T}}^{\gamma }\mathcal{Q}+T_{\mathcal{X}}^{2\theta }\mathcal{Q}+{\delta }_1{\left|\mathcal{Q}\right|}^2\mathcal{Q}+i{\delta }_2{\left|\mathcal{Q}\right|}^2{T}_{\mathcal{X}}^{\theta }\mathcal{Q}=0.$$

(4)

Inserting $Q\in \mathbb{R},{\delta }_1={\delta }_2=0$ and dropping the i structure in Equation (1) yields the Space–Time Fractional Modified KdV (STF-mKdV) equation [14].

$$T_{\mathcal{T}}^{\gamma }\mathcal{Q}+T_{\mathcal{X}}^{3\theta }\mathcal{Q}+{\delta }_3{\mathcal{Q}}^2{T}_{\mathcal{X}}^{\theta }\mathcal{Q}=0.$$

(5)

The Space–Time Fractional KdV (STF-KdV) equation [15] can be obtained from Equation (1) by incorporating ${\delta }_3=0$ further in Equation (5).

$$T_{\mathcal{T}}^{\gamma }\mathcal{Q}+T_{\mathcal{X}}^{2\theta }\mathcal{Q}+{\delta }_1\mathcal{Q}{T}_{\mathcal{T}}^{\theta }\mathcal{Q}=0.$$

(6)

Li et al. [16] constructed the solitary waves of Equation (1) via the (G’/G)-expansion method. The solitary wave solutions of the stochastic nonlinear Kodama (SNLK) equation utilize the mapping and (G’/G) expansion method in [17] by Algolam. Obeidat et al. [18], along with collaborators, worked on the dynamical behavior, including bifurcation, chaotic behavior, and solitary wave solutions, of the SNLK equation. Hosseini et al. [19] performed Lie symmetry, bifurcation analysis, solitary wave solution, and sensitivity analysis on the NLK equation. The solitary wave solutions of Equation (1) were obtained using the Jacobi elliptic function method and the generalized Riccati equation method in [10] by Mohammad.

In this paper, we aimed to construct the solitary wave solution of Equation (1) via two novel techniques: the Arnous method and the new Kudryashov method. In the literature, no one had previously constructed as many precise solitary waves as we did in this paper, demonstrating the novelty and the importance of our work and methods to the scientific world.

This paper is arranged as follows: In Section 2, NLKE-MTD is converted into a nonlinear ordinary differential equation (NLPDE) with the aid of traveling wave transformation. In Section 3, the Arnous method is applied to Equation (1) to construct the solitary wave solutions for NLKE-MTD and plot the solution. In Section 4, the new Kudryashov method is applied to obtain and plot the optical solution of Equation (1). Section 6 concludes our article.

2. Preliminary

2.1. Mathematical Formulation of M-Truncated Fractional Derivative

Definition 1.

Let $f:[0,+\infty )\to (-\infty ,+\infty )$. For $0<\gamma \le 1$, the M-truncated fractional derivative is represented as follows [20]:

$$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }f\left(\mathcal{T}\right)=\underset{h\to 0}{lim}{\displaystyle \frac{f\left(\mathcal{T}{E}_{\mathcal{K},\theta }\left(h{\mathcal{T}}^{1-\gamma }\right)\right)-f\left(\mathcal{T}\right)}{h}},\theta \in (0,+\infty ),$$

(7)

where the constant γ denotes the order of the fractional derivative. The function $E_{\mathcal{K},\theta }\left(\mathcal{T}\right)$ represents a truncated Mittag-Leffler function, described as follows [21]:

$$E_{\mathcal{K},\theta }\left(\mathcal{T}\right)=\sum _{n=0}^{\mathcal{K}}{\displaystyle \frac{{\mathcal{T}}^n}{\Gamma (\theta n+1)}},\mathcal{T}\in \mathbb{C},$$

(8)

Here, $\mathbb{C}$ denotes a complex number.

Remark 1.

Fundamental properties of MTD [22]:

(i)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }(af+bg)=a{T}_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }f+b{T}_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }g$;

(ii)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }\left(f\right)\left(\mathcal{T}\right)={\displaystyle \frac{{\mathcal{T}}^{1-\theta }}{\Gamma (\theta +1)}}{\displaystyle \frac{df}{dt}}$;

(iii)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }\left(fg\right)=f{T}_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }g+g{T}_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }f$;

(iv)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }(f\circ g)\left(\mathcal{T}\right)=f^{\prime }\left(g\left(\mathcal{T}\right)\right)T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }g\left(\mathcal{T}\right)$;

(v)

$T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }{\mathcal{T}}^{\gamma }={\displaystyle \frac{\gamma }{\Gamma (\theta +1)}}{\mathcal{T}}^{\gamma -\gamma }$.

2.2. Traveling Wave Transformation and Reduction of Governing Model

Consider a complex partial differential equation governed by the M-truncated fractional derivative operator.

$$\mathbf{P}(\mathcal{T},\mathcal{X},T_{\mathcal{K},\mathcal{T}}^{\gamma ,\theta }\mathcal{Q},{\mathcal{Q}}_{\mathcal{X}},{\mathcal{Q}}_{\mathcal{XX}},\cdots )=0,$$

(9)

Here, $\mathcal{Q}=\mathcal{Q}(\mathcal{X},\mathcal{T})$ is the unknown function. To simplify the equation, we apply a fractional-order traveling wave transformation, which has the following form:

$$\mathcal{Q}(\mathcal{X},\mathcal{T})=\Delta \left(\xi \right)e^{i\eta },\xi ={\varphi }_1\mathcal{X}+{\displaystyle \frac{\Gamma (\theta +1){\varphi }_2}{\gamma }}{\mathcal{T}}^{\gamma },\eta ={\rho }_1\mathcal{X}+{\displaystyle \frac{\Gamma (\theta +1){\rho }_2}{\gamma }}{\mathcal{T}}^{\gamma },$$

(10)

Here, ${\varphi }_1$, ${\varphi }_2$, ${\rho }_1$, and ${\rho }_2$ are nonzero arbitrary constants. Inserting Equation (10) back into Equation (9), a nonlinear ordinary differential equation can be constructed as follows:

$$\mathbf{Q}(\Delta ,{\displaystyle \frac{d\Delta }{d\xi }},{\displaystyle \frac{d^2\Delta }{d{\xi }^2}},{\displaystyle \frac{d^3\Delta }{d{\xi }^3}},\cdots )=0.$$

(11)

where $U\left(\xi \right)$ represents the unknown function. Inserting Equation (10) into Equation (1) and splitting into the real and imaginary parts yields the following:

$$\begin{array}{cc}\hfill & \mathrm{Real}\mathrm{part}:({\varphi }_1^2-3{\delta }_1{\rho }_1{\varphi }_1^2){\Delta }^{″}+({\delta }_1{\rho }_1^3-{\rho }_2-{\rho }_1^2)\Delta +({\delta }_1-{\delta }_2{\rho }_1+{\delta }_3{\rho }_1){\Delta }^3=0,\hfill \\ \hfill & \mathrm{Imaginary}\mathrm{part}:{\delta }_1{\varphi }_1^3{\Delta }^{‴}+({\varphi }_2+2{\rho }_1{\varphi }_1-3{\delta }_1{\rho }_1^2{\varphi }_1){\Delta }^{\prime }+{\varphi }_1({\delta }_2+{\delta }_3){\Delta }^2{\Delta }^{\prime }=0.\hfill \end{array}$$

(12)

Upon integrating Equation (12) concerning $\xi$ and setting the integration constant to zero to satisfy the boundary conditions, ${\Delta }^{\prime }\left(\xi \right)\to 0$ as $\left|\xi \right|\to \infty$. This condition avoids the unbounded solutions, which are consistent with the physical behavior of the derivative vanishing at infinity. The real part of Equation (12) imposes the parameter constraints through Equation (14). At the end we get the following:

$${\delta }_1{\varphi }_1^3{\Delta }^{″}+({\varphi }_2+2{\rho }_1{\varphi }_1-3{\delta }_1{\rho }_1^2{\varphi }_1)\Delta +{\displaystyle \frac{{\varphi }_1({\delta }_2+{\delta }_3)}{3}}{\Delta }^3=0.$$

(13)

Therefore, Equation (13) corresponds to the first equation in Equation (12), and it must satisfy the following conditions:

$${\displaystyle \frac{{\varphi }_1^2-3{\delta }_1{\rho }_1{\varphi }_1^2}{{\delta }_1{\varphi }_1^3}}={\displaystyle \frac{{\delta }_1{\rho }_1^3-{\rho }_2-{\rho }_1^2}{{\varphi }_2+2{\rho }_1{\varphi }_1-3{\delta }_1{\rho }_1^2{\varphi }_1}}={\displaystyle \frac{3({\delta }_1-{\delta }_2{\rho }_1+{\delta }_3{\rho }_1)}{{\varphi }_1({\delta }_2+{\delta }_3)}}.$$

(14)

If the above conditions are satisfied, then Equation (13) can be written as follows:

$${\Delta }^{″}+{\aleph }_2{\Delta }^3+{\aleph }_1\Delta =0,$$

(15)

where ${\aleph }_2={\displaystyle \frac{{\delta }_2+{\delta }_3}{3{\delta }_1{\varphi }_1^2}}$ and ${\aleph }_1={\displaystyle \frac{{\varphi }_2+2{\rho }_1{\varphi }_1-3{\delta }_1{\rho }_1^2{\varphi }_1}{{\delta }_1{\varphi }_1^3}}$.

3. Generalized Arnous Method

The core steps of the generalized Arnous (GA) method are as follows [23]:

• Step 01: The (GA) method provides the solution of Equation (15), as follows:

$$\Delta \left(\xi \right)={\alpha }_0+\sum _{1=1}^N{\displaystyle \frac{{\alpha }_i+{\beta }_i{\mathfrak{P}}^{\prime }{\left(\xi \right)}^i}{\mathfrak{B}{\left(\xi \right)}^i}}.$$

(16)

where (for i = 1, 2, …, N) ${\alpha }_0$,${\alpha }_i$,${\beta }_i$ are real constants, and $\mathfrak{B}\left(\xi \right)$ is a function that verifies the relation as follows:

$${\left[{\mathfrak{B}}^{\prime }\left(\xi \right)\right]}^2=[\mathfrak{B}{\left(\xi \right)}^2-\eta ]ln\left[P\right].$$

(17)

with

$${\mathfrak{B}}^{\left(n\right)}\left(\xi \right)=\left\{\begin{array}{cc}\mathfrak{B}\left(\xi \right)ln{\left(P\right)}^n,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even},\hfill \\ {\mathfrak{B}}^{\prime }\left(\xi \right)ln{\left(P\right)}^{n-1},\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$$

(18)

where $n\ge 2$, and $P\ne 1$. Equation (17) has solutions of the form:

$$\mathfrak{B}\left(\xi \right)=Hln\left(P\right)P^{\xi }+{\displaystyle \frac{\eta }{4Hln\left(P\right)P^{\xi }}}.$$

(19)

where H and $\eta$ are arbitrary parameters.

• Step 02: By balancing the nonlinear term and the term with the highest-order derivative in Equation (15), the positive integer N is determined for Equation (16).
• Step 03: After inserting Equations (17) and (20) into Equation (15) and since ${\mathfrak{B}}^i\left(\xi \right)\ne 0$, as a result of this substitution, we get a polynomial of ${\displaystyle \frac{1}{\mathfrak{B}\left(\xi \right)}}\left({\displaystyle \frac{{\mathfrak{B}}^{\prime }\left(\xi \right)}{\mathfrak{B}\left(\xi \right)}}\right)$. Equivalently, all terms with the same power are set equal to zero. Then, by solving this set of nonlinear algebraic systems and with the help of Equations (17) and (9), the solutions of Equation (1) can be determined.

SolitaryWave Solution by Generalized Arnous Method

Finding $N=1$ and inserting this value into Equation (16) yields the following:

$$\Delta \left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\alpha }_1}{\mathfrak{B}\left(\xi \right)}}+{\displaystyle \frac{{\beta }_1{\mathfrak{B}}^{\prime }\left(\xi \right)}{\mathfrak{B}\left(\xi \right)}}.$$

(20)

By inserting Equation (20) into Equation (15), together with Equations (15) and (17), we have a polynomial in terms of ${\displaystyle \frac{1}{\mathfrak{B}\left(\xi \right)}}\left({\displaystyle \frac{{\mathcal{B}}^{\prime }\left(\xi \right)}{\mathfrak{B}\left(\xi \right)}}\right)$. This leads to a system of algebraic equations by collecting terms of the same power and setting them to zero. The unknown constants are then determined from this system.

• Set 1.

$$\begin{array}{c}\hfill {\delta }_1=0,{\varphi }_2=-2{\rho }_1{\varphi }_1,{\delta }_3=-{\delta }_2.\end{array}$$

(21)

Inserting set 1 into Equation (20), the resulting solution is expressed as follows:

$$\begin{array}{c}\hfill {\mathcal{Q}}_1\left(\xi \right)={\alpha }_0+{\displaystyle \frac{ln\left(P\right)\left(4{\alpha }_{1}H{P}^{\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+x{\varphi }_1}-{\beta }_1\left(\eta -4H^2{ln}^2\left(P\right)P^{\frac{2\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+2x{\varphi }_1}\right)\right)}{\eta +4H^2{ln}^2\left(P\right)P^{\frac{2\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+2x{\varphi }_1}}}.\end{array}$$

(22)

when we choose B = e and $\eta =4H^2$, Equation (22) will be

$${\mathcal{Q}}_2\left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\alpha }_1\sec \mathrm{h}\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{2H}}+{\beta }_{1}tanh\left(x{\varphi }_1-{\displaystyle \frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }}\right).$$

(23)

when we choose P = e and $\eta =-4H^2$, Equation (22) will be

$${\mathcal{Q}}_3\left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\alpha }_1\csc \mathrm{h}\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{2H}}+{\beta }_{1}coth\left(x{\varphi }_1-{\displaystyle \frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }}\right).$$

(24)

• Set 2.

$$\begin{array}{c}\hfill {\delta }_1=0,{\delta }_3=-{\delta }_2,{\rho }_1=-{\displaystyle \frac{{\varphi }_2}{2{\varphi }_1}}.\end{array}$$

(25)

Inserting set 2 into Equation (20), the resulting solution is expressed as follows:

$$\begin{array}{c}\hfill {\mathcal{Q}}_4\left(\xi \right)={\alpha }_0+{\displaystyle \frac{ln\left(P\right)\left(4{\alpha }_{1}H{P}^{\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+x{\varphi }_1}-{\beta }_1\left(\eta -4H^2{ln}^2\left(P\right)P^{\frac{2\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+2x{\varphi }_1}\right)\right)}{\eta +4H^2{ln}^2\left(P\right)P^{\frac{2\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+2x{\varphi }_1}}}.\end{array}$$

(26)

when we choose P = e and $\eta =4H^2$, Equation (26) will be

$$\begin{array}{cc}\hfill & {\mathcal{Q}}_5\left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\alpha }_1\sec \mathrm{h}\left(\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+x{\varphi }_1\right)}{2H}}\hfill \\ \hfill & +{\beta }_{1}tanh\left({\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+{\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+x{\varphi }_1\right).\hfill \end{array}$$

(27)

when we choose P = e and $\eta =-4H^2$, Equation (26) will be

$$\begin{array}{cc}\hfill & {\mathcal{Q}}_6\left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\alpha }_1\csc \mathrm{h}\left(\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }+x{\varphi }_1\right)}{2H}}\hfill \\ \hfill & +{\beta }_{1}coth\left({\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+{\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+x{\varphi }_1\right).\hfill \end{array}$$

(28)

• Set 3.

$${\alpha }_0=0,\eta =0,{\delta }_1=0,{\varphi }_2=-2{\rho }_1{\varphi }_1.$$

(29)

Inserting set 3 into Equation (20), the resulting solution is expressed as follows:

$${\mathcal{Q}}_7\left(\xi \right)={\displaystyle \frac{{\alpha }_1{P}^{\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }-x{\varphi }_1}}{Hln\left(P\right)}}+{\beta }_{1}ln\left(P\right).$$

(30)

when we choose P = e and $\eta =4H^2$, Equation (30) will be

$${\mathcal{Q}}_8\left(\xi \right)={\beta }_1-{\displaystyle \frac{{\alpha }_{1}sinh\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{H}}+{\displaystyle \frac{{\alpha }_{1}cosh\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{H}}.$$

(31)

when we choose P = e and $\eta$= −4 H, Equation (30) will be

$${\mathcal{Q}}_9\left(\xi \right)={\beta }_1-{\displaystyle \frac{{\alpha }_{1}sinh\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{H}}+{\displaystyle \frac{{\alpha }_{1}cosh\left(x{\varphi }_1-\frac{2\Gamma (\theta +1){\rho }_1{\varphi }_1{t}^{\gamma }}{\gamma }\right)}{H}}.$$

(32)

• Set 4.

$${\alpha }_1=0,{\delta }_1=0,{\varphi }_1=-{\displaystyle \frac{{\varphi }_2}{2{\rho }_1}}.$$

(33)

Inserting set 4 into Equation (20), the resulting solution is expressed as follows:

$${\mathcal{Q}}_{10}\left(\xi \right)={\alpha }_0+{\displaystyle \frac{{\beta }_1\left(H{ln}^2\left(P\right)P^{\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }-\frac{x{\varphi }_2}{2{\rho }_1}}-\frac{\eta P^{\frac{x{\varphi }_2}{2{\rho }_1}-\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}}{4H}\right)}{\frac{\eta P^{\frac{x{\varphi }_2}{2{\rho }_1}-\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}}{4Hln\left(P\right)}+Hln\left(P\right)P^{\frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }-\frac{x{\varphi }_2}{2{\rho }_1}}}}.$$

(34)

when we choose P = e and $\eta =4H^2$, Equation (34) will be

$${\mathcal{Q}}_{11}\left(\xi \right)={\alpha }_0+{\beta }_{1}tanh\left({\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+{\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}-{\displaystyle \frac{x{\varphi }_2}{2{\rho }_1}}\right).$$

(35)

when we choose P = e and $\eta$= −4 H, Equation (34) will be

$${\mathcal{Q}}_{12}\left(\xi \right)={\alpha }_0+{\beta }_{1}coth\left({\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}+{\displaystyle \frac{\Gamma (\theta +1){\varphi }_2{t}^{\gamma }}{\gamma }}-{\displaystyle \frac{x{\varphi }_2}{2{\rho }_1}}\right).$$

(36)

4. Formulation of New Kudryashov Method

Below are the major steps of the new Kudryashov technique (NK) [24].

• Step 01: The NK method constructs the solution of Equation (15) as

$$\Delta \left(\xi \right)=h_0+\sum _{i=1}^N\left({\mathfrak{B}}_i{f}^i\left(\xi \right)\right).$$

(37)

where $c_i$ for (i = 0, 1, 2,...,N) are the constants, $h_N\ne 0$, and $\mathfrak{B}\left(\xi \right)={\displaystyle \frac{1}{c{M}^{\lambda \xi }+d{M}^{-\lambda \xi }}}$ is the solution to the following equation:

$${\mathfrak{B}}^{\prime }{\left(\xi \right)}^2={(\lambda ln\left(E\right)\mathfrak{B}\left(\xi \right))}^2(1-4cd{\mathfrak{B}}^2\left(\xi \right)).$$

(38)

$${\mathfrak{B}}^{″}\left(\xi \right)=({\lambda }^{2}ln{\left(E\right)}^2\mathfrak{B}\left(\xi \right))(1-8cd{\mathfrak{B}}^2\left(\xi \right)).$$

(39)

Here, the constants c, d, $\lambda$, and E are all non-zero, with $1\ne E>0$.

• Step 02: By balancing the nonlinear term and the term with the highest-order derivative in Equation (15), the positive integer N is determined for Equation (37).
• Step 03: After inserting Equation (37) into Equation (15) and since ${\mathfrak{B}}^i\left(\xi \right)\ne 0$, as a result of this substitution, we get a polynomial of ${\displaystyle \frac{1}{\mathfrak{B}\left(\xi \right)}}\left({\displaystyle \frac{{\mathfrak{B}}^{\prime }\left(\xi \right)}{\mathfrak{B}\left(\xi \right)}}\right)$. Equivalently, all terms with the same power are set equal to zero. Then, by solving this set of nonlinear algebraic systems and with the help of Equation (37) and Equation (9), the solutions of Equation (1) can be determined.

Solution by New Kudryashov Method

Finding $N=1$ and inserting this value into Equation (37) yields

$$\Delta \left(\xi \right)=h_0+h_1\mathfrak{B}\left(\xi \right).$$

(40)

By inserting Equation (40) into Equation (15), together with Equation (22) and Equation (40), we have a polynomial in terms of ${\displaystyle \frac{1}{\mathfrak{B}\left(\xi \right)}}\left({\displaystyle \frac{{\mathcal{B}}^{\prime }\left(\xi \right)}{\mathfrak{B}\left(\xi \right)}}\right)$. This leads to a system of algebraic equations by collecting terms of the same power and setting them to zero. The unknown constants are then determined from this system.

• Set 1:

$$h_0=0,h_1=2\sqrt{6}\sqrt{{\displaystyle \frac{{\delta }_{1}cd{\phi }_1}{{\phi }_1\left({\delta }_2+{\delta }_3\right)}}}ln\left(E\right)\lambda {\phi }_1,{\rho }_1={\displaystyle \frac{{\phi }_1+\sqrt{3ln{\left(E\right)}^2{\sigma }^2{\delta }_1^2{\phi }_1^4+3{\delta }_1{\phi }_1{\phi }_2+{\phi }_1^2}}{3{\delta }_1{\phi }_1}}.$$

(41)

• Set 2:

$$\lambda ={\displaystyle \frac{\sqrt{-\frac{-3{\delta }_1{\rho }_1^2{\phi }_1+2{\rho }_1{\phi }_1+{\phi }_2}{{\delta }_1{\phi }_1}}}{{\phi }_{1}ln\left(E\right)}},h_0=0,h_1=2\sqrt{-{\displaystyle \frac{-18cd{\delta }_1{\rho }_1^2{\phi }_1+12cd{\rho }_1{\phi }_1+6cd{\phi }_2}{{\phi }_1\left({\delta }_2+{\delta }_3\right)}}}.$$

(42)

Inserting set 1 into Equation (40), the exact solution can be determined as follows:

$${\mathcal{Q}}_1(\mathcal{X},\mathcal{T})={\displaystyle \frac{2\sqrt{6}\sqrt{\frac{{\delta }_{1}cd{\phi }_1}{{\phi }_1\left({\delta }_2+{\delta }_3\right)}}ln\left(E\right)\lambda {\phi }_1}{c{E}^{\lambda \xi }+d{E}^{-\lambda \xi }}}.$$

(43)

Inserting set 2 into Equation (40), the exact solution can be determined as follows:

$${\mathcal{Q}}_2(\mathcal{X},\mathcal{T})={\displaystyle \frac{2\sqrt{-\frac{-18cd{\delta }_1{\rho }_1^2{\phi }_1+12cd{\rho }_1{\phi }_1+6cd{\phi }_2}{{\phi }_1\left({\delta }_2+{\delta }_3\right)}}}{c{E}^{\lambda \xi }+d{E}^{-\lambda \xi }}}.$$

(44)

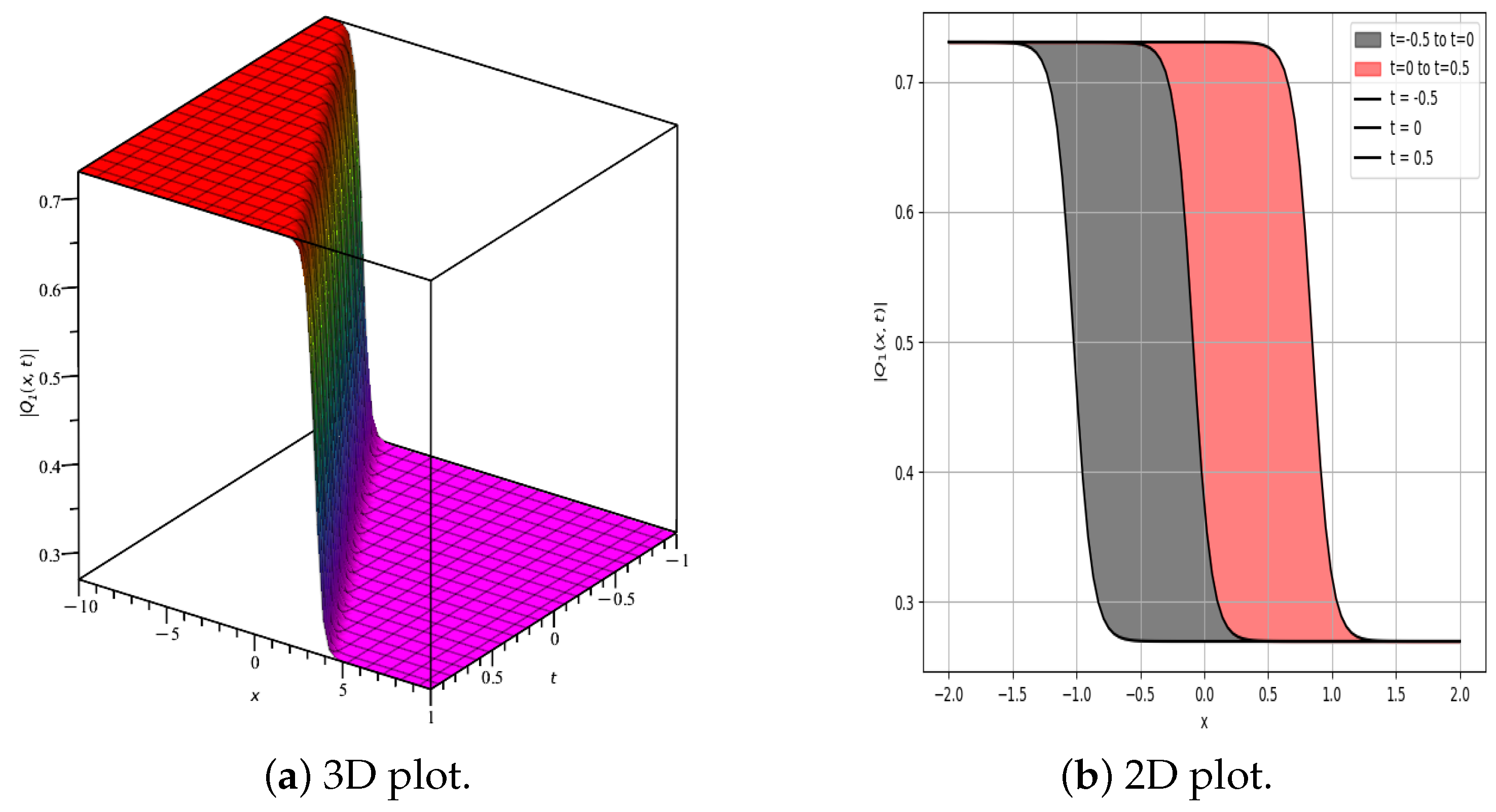
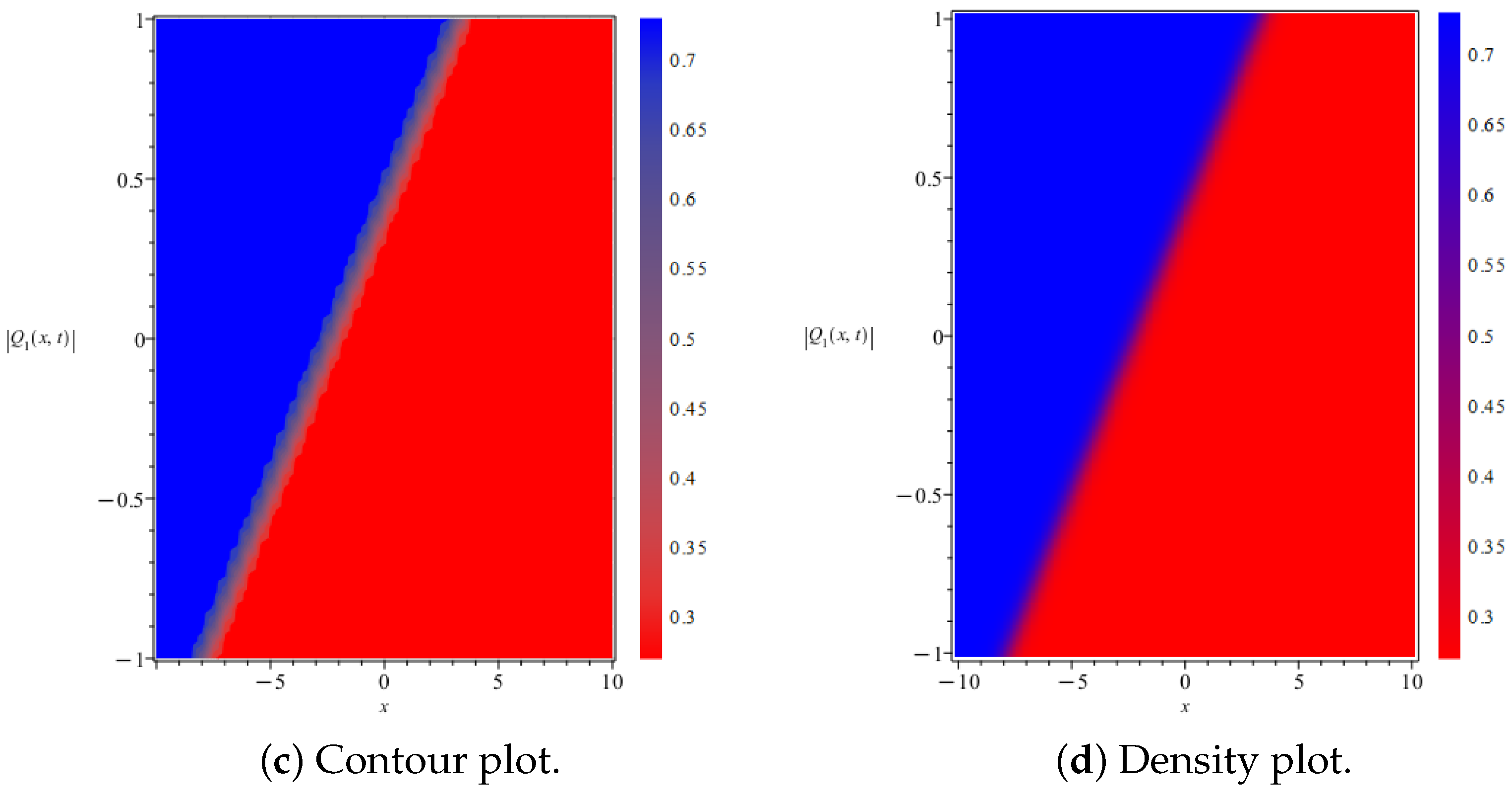
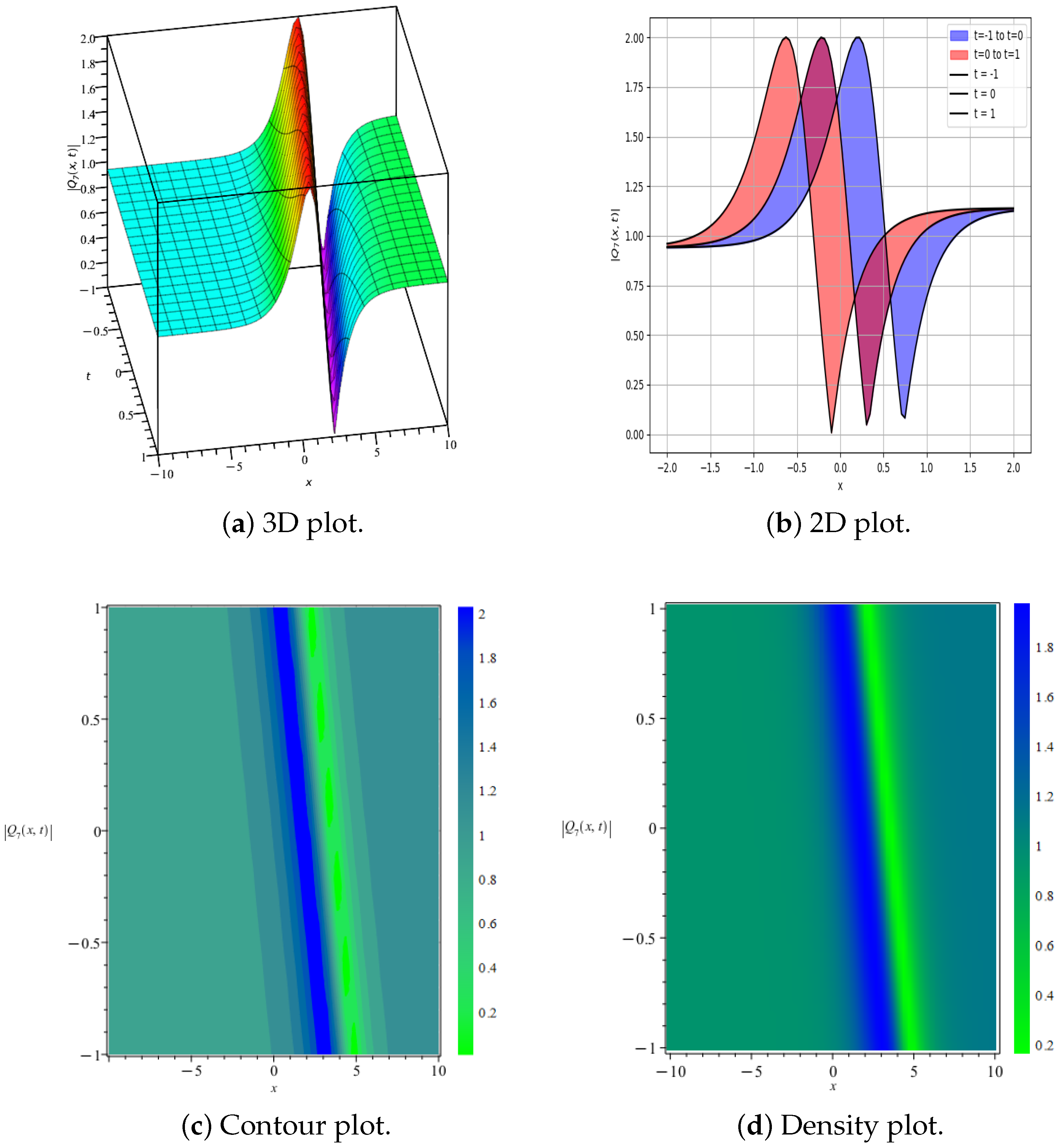
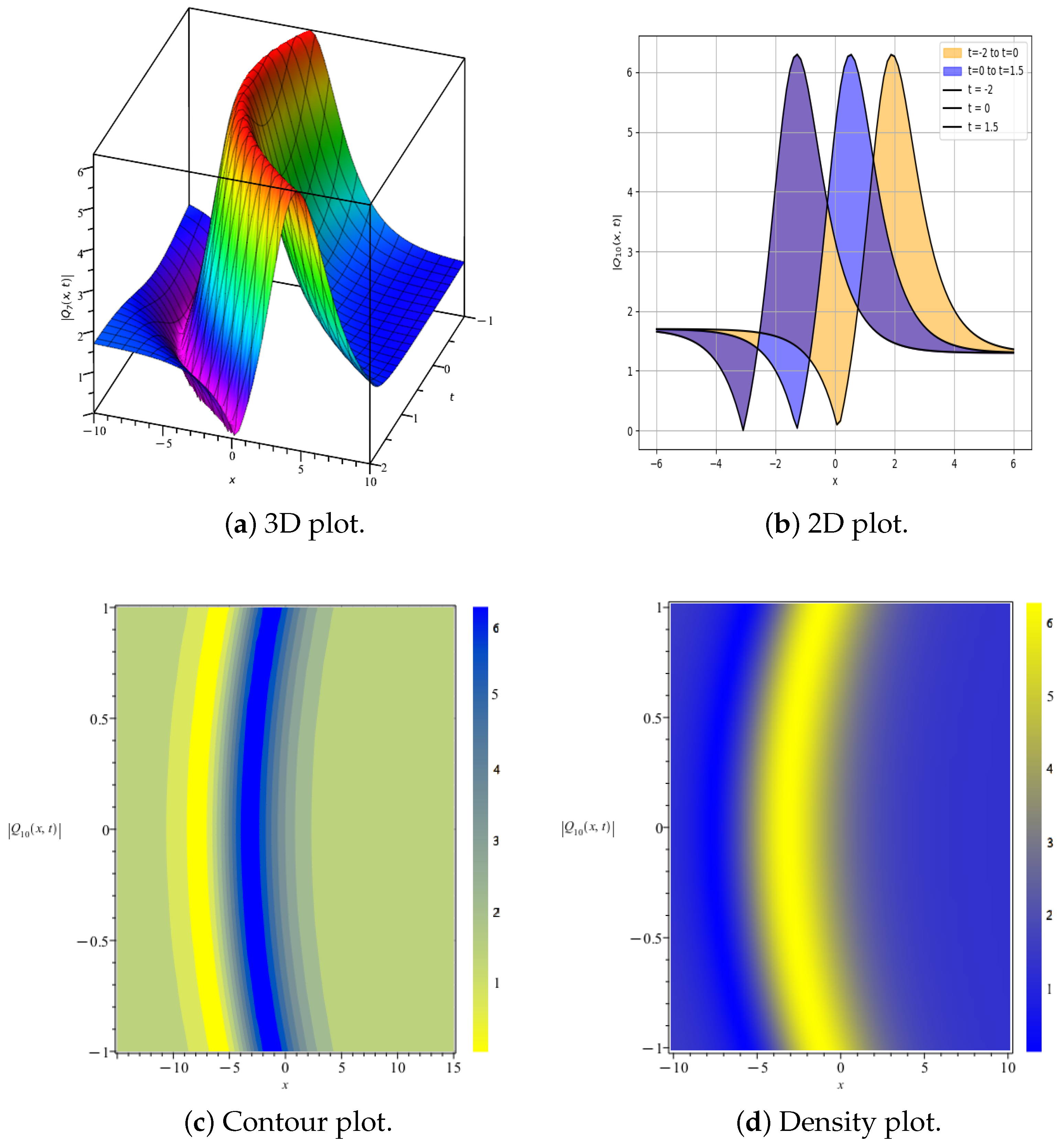
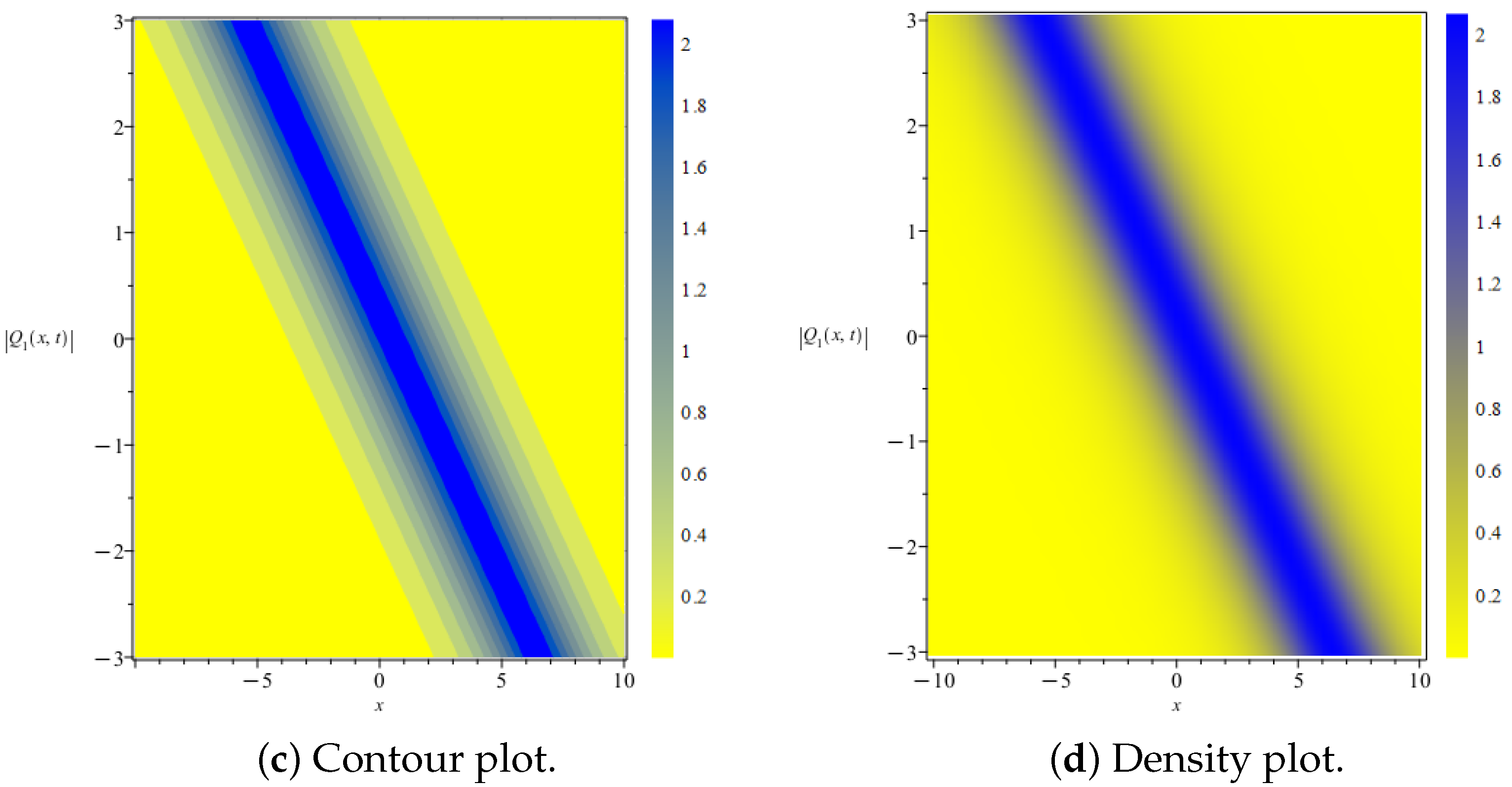
5. Results and Discussion

In this section, we have selected specific values for the physical parameters to illustrate the significance of the new optical solutions in relation to the current governing equation. The effect of both parameters x and t on the existing soliton solutions is portrayed through two-dimensional (2D) and three-dimensional (3D) graphs. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 present 3D, 2D, and contour graphs illustrating the behavior of the current solutions. Figure 1 provides a detailed visualization of the kink-type soliton solution $|{\mathcal{Q}}_1(\mathcal{X},\mathcal{T})|$ for varying values of the temporal parameter t and ${\alpha }_0=0.5,{\alpha }_1=3,{\beta }_1=0.1,P=0.1,H=4,{\varphi }_1=0.01,$$\gamma =0.99,\Gamma =2,{\varphi }_2=2,\eta =0.01,\theta =0.4,{\rho }_1=1.$ A kink soliton is a topological soliton that represents a smooth but localized change from one asymptotic state to another, typically moving through space with constant shape and speed. It connects two different constant values of a field at spatial infinity and is non-periodic and stable. The soliton profile exhibits a smooth, monotonic rise, demonstrating its stability and persistent structure over time. The resulting profile becomes noticeably sharper and more abrupt, with enhanced gradient steepness and increased localization. This reflects the influence of fractional-order dynamics in intensifying nonlinear effects and compressing the soliton structure. Figure 2 illustrates the spatiotemporal dynamics of the multiple dark-bright soliton solution of $|{\mathcal{Q}}_7(\mathcal{T},\mathcal{X})|$, illustrating its evolution for varying values of the temporal parameter t and ${\alpha }_0=0.1,{\alpha }_1=1,{\beta }_1=1.5,P=0.5,H=exp\left(1.5\right),{\varphi }_1=1.5,\gamma =0.99,\Gamma =1,{\varphi }_2=1,$$\eta =0.3,\theta =1.$ A dark–bright soliton is a combination of a dark soliton and a bright soliton. It has the characteristics of both solutions. The soliton maintains a well-defined structure as it propagates, combining localized dips and peaks, a signature of the mixed dark–bright soliton class. Figure 3 illustrates the spatiotemporal dynamics of the bright soliton solution of $|{\mathcal{Q}}_{10}(\mathcal{T},\mathcal{X})|$, illustrating its evolution with varying values of the temporal parameter t and ${\alpha }_0=0.2,{\alpha }_1=2,{\beta }_1=1.5,H=1,{\varphi }_1=1,\gamma =2,\Gamma =1,{\varphi }_2=1,\eta =0.1,\theta =1,$${\rho }_1=1,{\delta }_2=exp\left(1\right).$ Bright solitons are characterized by localized peaks in intensity, emerging from a zero or near-zero background due to the interplay of dispersion and nonlinearity. Similarly, Figure 4 represents the bright soliton using suitable parametric values$:{\delta }_1=-1.5,{\delta }_2=0.8,{\delta }_3=0.5,{\varphi }_1=1,{\varphi }_2=1,c=1,d=0.5,E=0.5,\lambda =1,$$\Gamma =1,\theta =1,\gamma =0.99$ of the solution $|{\mathcal{Q}}_1(\mathcal{T},\mathcal{X}|)$. Figure 5 represents the dark soliton using suitable parametric values$:{\delta }_1=-1.5,{\delta }_2=0.8,{\delta }_3=0.5,{\varphi }_1=3,{\varphi }_2=2.5,$$c=1,d=1,E=0.5,\lambda =1,\Gamma =1,\theta =1,\gamma =0.99,{\rho }_1=-0.3$. of the solution $|{\mathcal{Q}}_2(\mathcal{T},\mathcal{X}|)$. A dark soliton is a type of localized wave solution that appears as a dip or notch in the amplitude of a continuous wave background. It is a stable, self-reinforcing structure that occurs in nonlinear dispersive media.

6. Conclusions

This study investigated the M-truncated nonlinear Kodama equation, incorporating spatio-temporal dispersion effects within the context of nonlinear optics, shallow water waves over complex media, nonlocal internal waves, and fractional viscoelastic wave propagation. A variety of novel optical soliton solutions—such as bright solitons, kink waves, dark–bright solitons, and periodic wave solutions—were derived using the generalized Arnous method, which is constrained by the need for balanced polynomial forms, and a new variant of the Kudryashov method, which is limited to rational function-type solution structures. To visualize the dynamics of these solutions, we present comprehensive graphical representations, including two-dimensional, three-dimensional, and contour plots, illustrating the amplitude behavior of the M-truncated nonlinear Kodama equation. By selecting appropriate physical parameters, we uncovered a wide range of solution behaviors. Furthermore, we explored the impact of variations in the temporal parameter and the M-truncated fractional-order derivative on the structure and evolution of solutions. These results highlight the efficacy and practicality of the proposed methods for solving both integer- and fractional-order differential equations. The analytical solutions obtained offer valuable insights into the dynamics of complex optical systems. In future research, the methodology can be extended to other nonlinear equations involving M-truncated order derivatives.