A Novel Fractional Order Multivariate Partial Grey Model and Its Application in Natural Gas Production
Abstract
1. Introduction
2. Literature Review
2.1. Introduction to Three Types of Natural Gas Production Prediction Methods
2.2. Research on Grey Prediction Model and Its Application in Natural Gas Production Prediction
2.3. Research Limitations, Contributions, and Structure of This Paper
- Given the spatiotemporal and nonlinear characteristics of natural gas production data, this paper utilizes the advantages of partial differentiation to effectively capture details and features in the data. Fractional order damping accumulation can improve model accuracy and effectively compensate for the phenomenon of inaccurate results caused by data fluctuations. A new fractional order multivariate biased grey prediction model is established.
- In terms of model structure, the classic grey prediction model is extended from ordinary differential form to partial differential form, and the fractional order accumulation principle is integrated into the partial grey prediction model to expand the structure of the classic grey prediction model. This improvement enables the model to more effectively capture various complex features such as time and space of data, improve model accuracy, and greatly broaden the structural framework and scope of application of the grey prediction model.
- In terms of application practice, this study applies the newly constructed partial grey prediction to the field of natural gas production forecasting. Based on the selection of oil, raw coal, and electricity production as the relevant series, the validity of the model is analysed in-depth through seven specific cases in three categories. The results showed that the average relative error of the new model was around 1% in all seven cases, and its prediction performance is significantly better than the other five grey prediction models. In addition, the model has successfully achieved an accurate forecast of natural gas production for the next nine months.
3. Modelling Partial Grey Differential Equations in First-Order Individual Variables
3.1. Grey Differential Equation Model with First-Order Individual Variables
3.2. Modelling Partial Grey Differential Equations in First-Order Individual Variables
- (1)
- (2)
3.3. Modelling Steps and Modelling Process for the DPGMC(1,N,ζ)
4. Effectiveness Analysis of DPGMC(1,N,ζ)
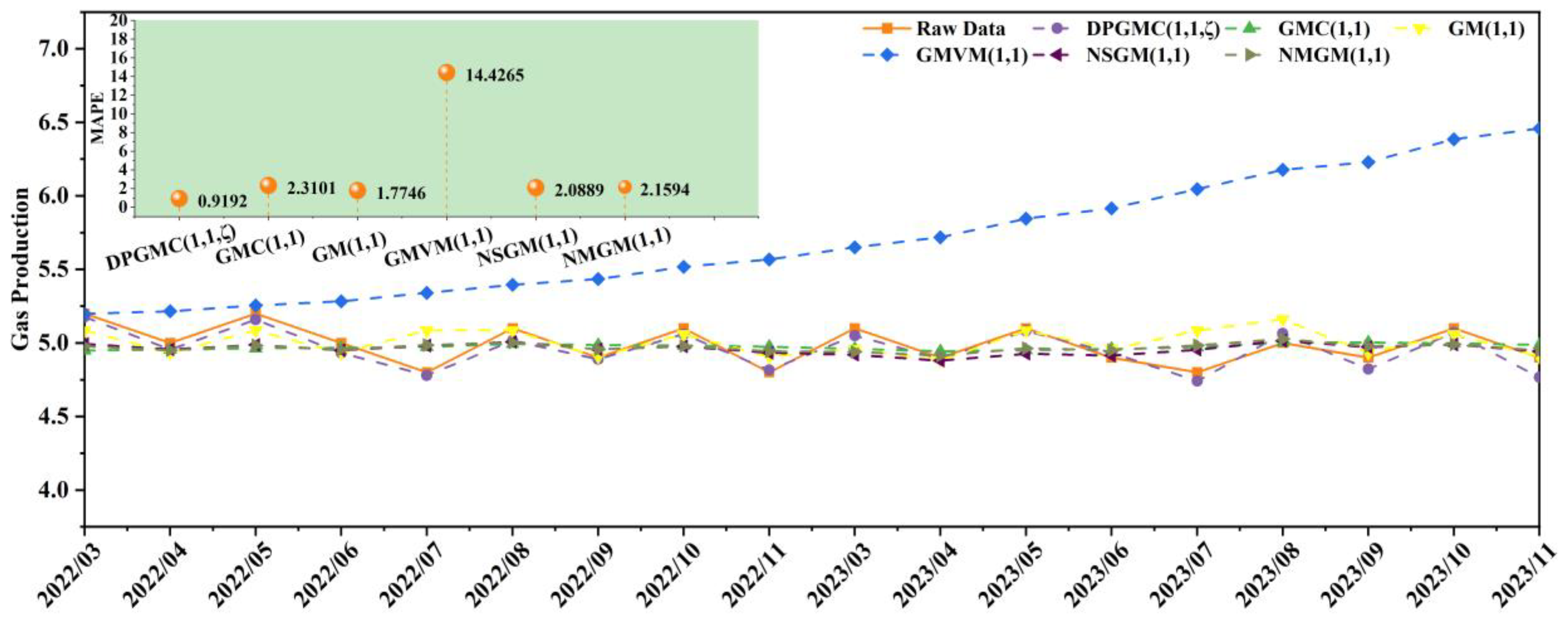
4.1. Analysis of the Effectiveness of the First Category DPGMC(1,N,ζ)
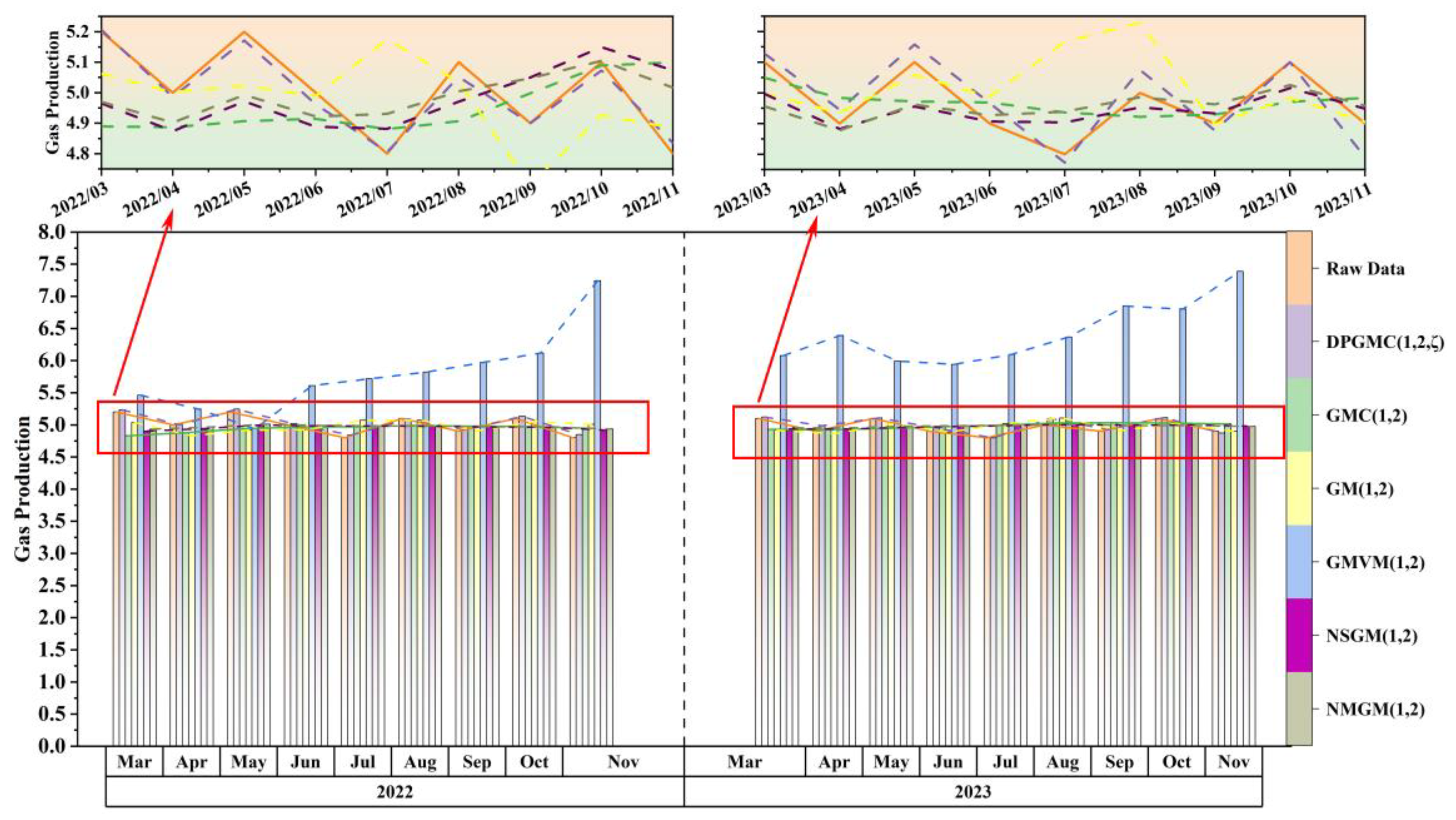
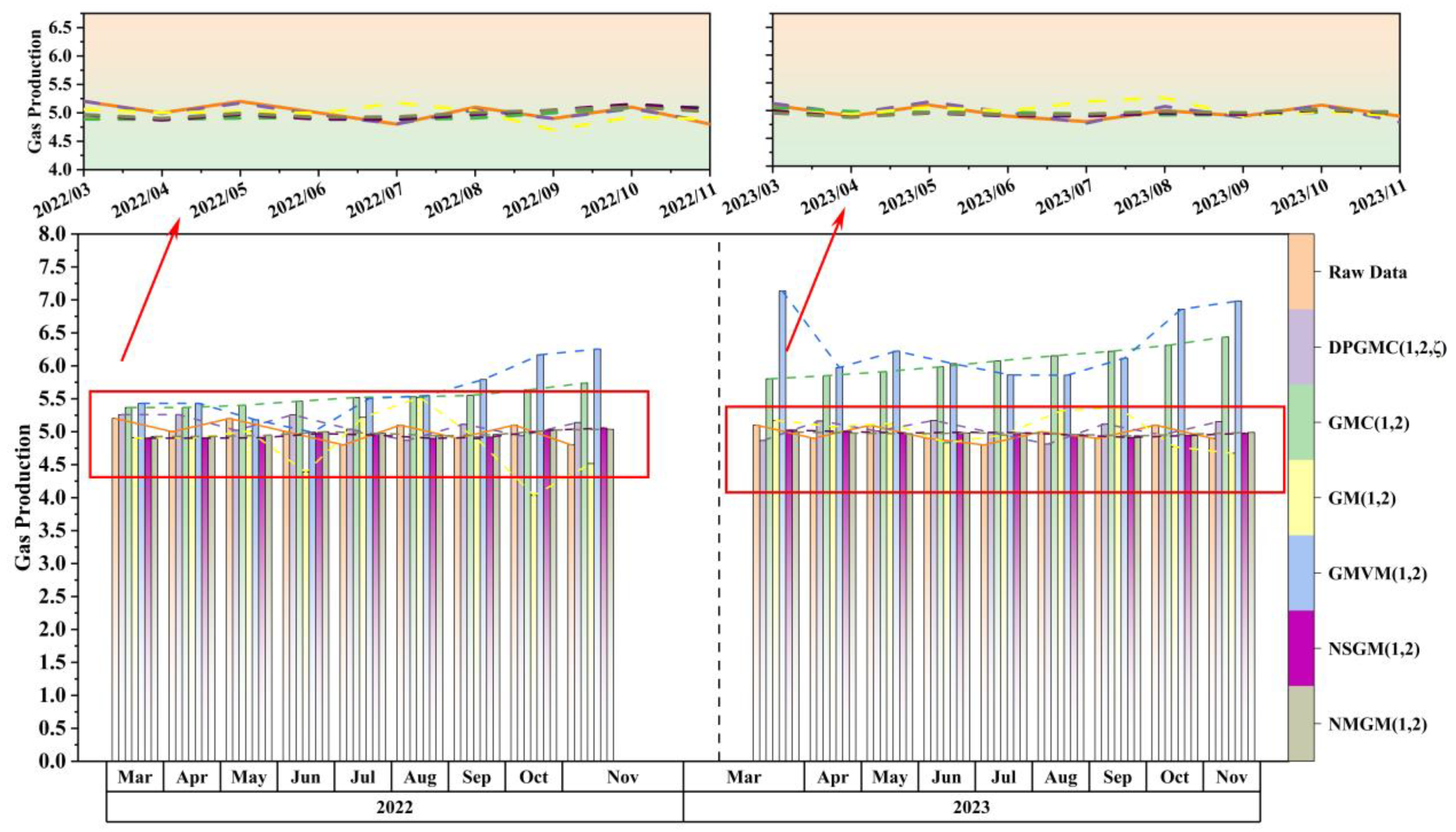
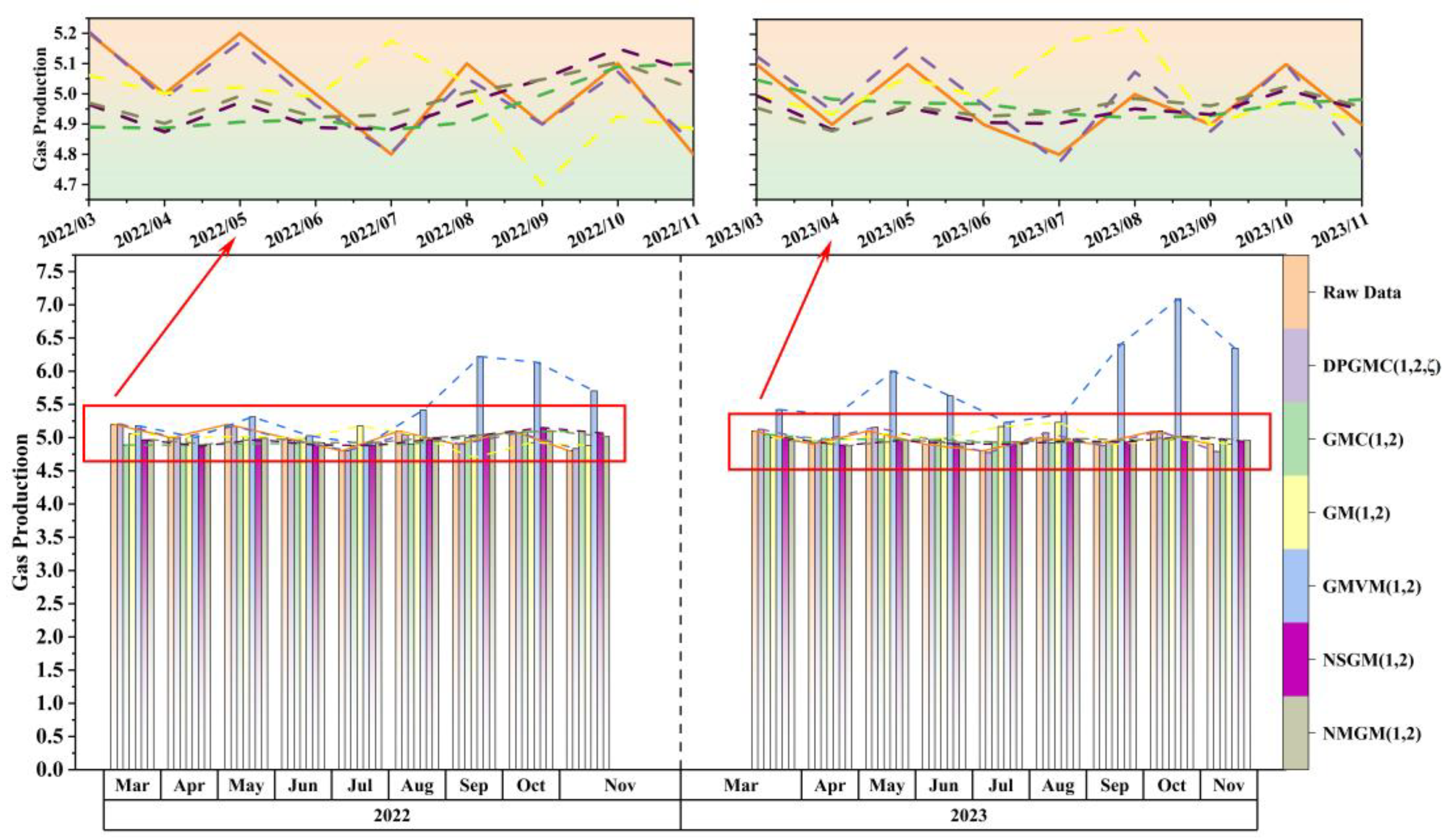
4.2. Effectiveness Analysis of the Second Category DPGMC(1,N,ζ)
4.3. Effectiveness Analysis of the Third Category DPGMC(1,N,ζ)
4.4. Summary of Effectiveness Analysis of Three Categories of DPGMC(1,N,ζ)
5. Application of DPGMC(1,N,ζ)
- (1)
- Dynamically adjust production plans and conduct equipment maintenance in advance from January to February before peak periods occur in these months to ensure that production equipment is in optimal condition during peak months. At the same time, utilise low season months to conduct in-depth maintenance and technological upgrades on equipment. Improve the efficiency of natural gas exploration, control open costs, and optimise development plans.
- (2)
- Data-driven decision-making, dynamically guiding and adjusting production strategies based on forecast results, establishing emergency data-driven mechanisms with surrounding provinces, coordinating exports in months of excess production, and complementing supply in months of shortage. At the same time, responding to seasonal fluctuations in natural gas demand based on forecast results, enhancing natural gas peak shaving capabilities, and ensuring stable supply.
- (3)
- Promote the complementary and coordinated development of natural gas and other energy sources. With the development of clean energy in Qinghai Province, the proportion of natural gas in the energy structure may change. Therefore, the energy structure should be adjusted promptly according to market demand, and the production forecast results provide an important basis for the development planning and investment decisions of the shale gas industry.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Liang, K.; Zhang, G.S.; Li, Z.; Ding, L.; Su, J.; Zhu, S.; Ge, S.; Liu, J. Research on the development strategy of Chinese natural gas under the constraint of carbon peaking and carbon neutral. Strateg. Study CAE 2021, 23, 33. [Google Scholar] [CrossRef]
- Zou, C.; Zhao, Q.; Chen, J.; Li, J.; Yang, Z.; Sun, Q.; Lu, J.; Zhang, G. Natural gas in China: Development trend and strategic forecast. Nat. Gas Ind. B 2018, 5, 380–390. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Fu, L.B.; Xu, J.Q. Application and comparison of two production decline models in shale gas wells and tight gas wells. Pet. Geol. Recovery Effic. 2021, 28, 6. [Google Scholar] [CrossRef]
- Chen, Y.R.; Yu, G.; Zou, Y.H.; Fang, Y. Optimization of natural gas production prediction method based on index and multiple correction coefficient. Nat. Gas Technol. Econ. 2021, 15, 83. [Google Scholar] [CrossRef]
- Chen, J.S.; Cao, J.Z.; Han, H.B.; Nian, J.; Guo, L. Adaptability analysis of commonly used production prediction models for shale oil and gas well. Unconv. Oil Gas 2019, 6, 48–57. [Google Scholar] [CrossRef]
- Wang Yu Li, Z.P.; Liu, C. Prediction for coal bed gas output based on fractal and ARIMA. Nat. Gas Oil 2011, 29, 45–48+87. [Google Scholar] [CrossRef]
- Manowska, A.; Rybak, A.; Dylong, A.; Pielot, J. Forecasting of natural gas consumption in pol and based on ARIMA-LSTM hybrid model. Energies 2021, 14, 8597. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, S.; Zhang, D.; Liu, C. An adsorbed gas estimation model for shale gas reservoirs via statistical learning. Appl. Energy 2017, 197, 327–341. [Google Scholar] [CrossRef]
- Smajla, I.; Vulin, D.; Sedlar, D.K. Short-term forecasting of natural gas consumption by determining the statistical distribution of consumption data. Energy Rep. 2023, 10, 2352–2360. [Google Scholar] [CrossRef]
- Kani, A.H.; Abbasspour, M.; Abedi, Z. Estimation of demand function for natural gas in Iran: Evidences based on smooth transition regression models. Econ. Model. 2014, 36, 341–347. [Google Scholar] [CrossRef]
- Zhou, Q.Q.; Duan, H.M.; Xie, D.R. A multivariate partial grey prediction model based on second-order traffic flow kinematics equation and its application. J. Comput. Appl. Math. 2025, 463, 116505. [Google Scholar] [CrossRef]
- Ji, L.; Li, J.H.; Xiao, J.L. Application of random forest algorithm in the multistage fracturing stimulation of shale gas field. Pet. Geol. Oilfield Dev. Daqing 2020, 39, 168–174. [Google Scholar] [CrossRef]
- Qiao, W.; Liu, W.; Liu, E. A combination model based on wavelet transform for predicting the difference between monthly natural gas production and consumption of U.S. Energy 2021, 235, 121216. [Google Scholar] [CrossRef]
- Zhu, H.; Kong, D.Q.; Qian, X. Method for predicting shale gas production based on ATD-BP neural network. Sci. Technol. Eng. 2017, 17, 128–132. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting monthly gas field production based on the CNN-LSTM model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Anđelković, A.S.; Bajatović, D. Integration of weather forecast and artificial intelligence for a short-term city-scale natural gas consumption prediction. J. Clean. Prod. 2020, 266, 122096. [Google Scholar] [CrossRef]
- Chen, R.X.; Xiao, X.P.; Gao, M.Y.; Ding, Q. A novel mixed frequency sampling discrete grey model for forecasting hard disk drive failure. ISA Trans. 2024, 147, 304–327. [Google Scholar] [CrossRef]
- Li, X.M.; Li, N.; Ding, S.; Cao, Y.; Li, Y. A novel data-driven seasonal multivariable grey model for seasonal time series forecasting. Inf. Sci. 2023, 642, 119165. [Google Scholar] [CrossRef]
- Ye, L.L.; Xie, N.M.; Boylan, J.E.; Shang, Z. Forecasting seasonal demand for retail: A Fourier time-varying grey model. Int. J. Forecast. 2024, 40, 1467–1485. [Google Scholar] [CrossRef]
- Zeng, B.; Li, H.; Mao, C.W.; Wu, Y. Modeling, prediction and analysis of new energy vehicle sales in China using a variable-structure grey model. Expert Syst. Appl. 2023, 213, 118879. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.S.; Ye, L.L.; Wang, L.; Zhou, Y.; Luo, Y. A novel self-adaptive fractional grey Euler model with dynamic accumulation order and its application in energy production prediction of China. Energy 2023, 265, 126384. [Google Scholar] [CrossRef]
- Duan, H.M.; Wang, G.; Song, Y.X.; Chen, H. A novel grey multivariable time-delayed model and its application in predicting oil production. Eng. Appl. Artif. Intell. 2024, 139, 109505. [Google Scholar] [CrossRef]
- Wang, J.J.; Ye, L.; Ding, X.Y.; Dang, Y. A novel seasonal grey prediction model with time-lag and interactive effects for forecasting the photovoltaic power generation. Energy 2024, 304, 131939. [Google Scholar] [CrossRef]
- Zhang, R.Y.; Mao, S.Y.; Kang, Y.X. A novel traffic flow prediction model: Variable order fractional grey model based on an improved grey evolution algorithm. Expert Syst. Appl. 2023, 224, 119943. [Google Scholar] [CrossRef]
- Zhao, K.; Yu, S.J.; Wang, L.F. Carbon emissions prediction considering environment protection investment of 30 provinces in China. Environ. Res. Sect. A 2024, 244, 117914. [Google Scholar] [CrossRef]
- Gao, M.Y.; Yang, H.L.; Xiao, Q.Z.; Goh, M. A novel method for carbon emission forecasting based on Gompertz’s law and fractional grey model: Evidence from American industrial sector. Renew. Energy 2022, 181, 803–819. [Google Scholar] [CrossRef]
- Xiao, Q.Z.; Shan, M.Y.; Gao, M.Y.; Xiao, X.; Guo, H. Evaluation of the coordination between China’s technology and economy using a grey multivariate coupling model. Technol. Econ. Dev. Econ. 2021, 27, 24–44. [Google Scholar] [CrossRef]
- Han, S.; Chen, M.G.; Su, W.; Xiao, Y.; Wu, Z.; Chen, J.; Wang, L. Prediction method and application of single shale gas well production in Weiyuan block, Sichuan basin. Spec. Oil Gas Reserv. 2022, 29, 141. [Google Scholar] [CrossRef]
- Zeng, B.; Ma, X.; Zhou, M. A new-structure grey Verhulst model for China’s tight gas production forecasting. Appl. Soft Comput. 2020, 96, 106600. [Google Scholar] [CrossRef]
- Ma, X.; Deng, Y.; Ma, M. A novel kernel ridge grey system model with generalized Morlet wavelet and its application in forecasting natural gas production and consumption. Energy 2024, 287, 129630. [Google Scholar] [CrossRef]
- Ding, S. A novel self-adapting intelligent grey model for forecasting China’s natural-gas demand. Energy 2018, 162, 393–407. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, X.; Li, W.; Wu, W.; Tu, D. Forecasting manufacturing industrial natural gas consumption of China using a novel time-delayed fractional grey model with multiple fractional order. Comput. Appl. Math. 2020, 39, 4915–4921. [Google Scholar] [CrossRef]
- Duan, H.M.; Wang, G. Partial differential grey model based on control matrix and its application in short-term traffic flow prediction. Appl. Math. Model. 2023, 116, 763–785. [Google Scholar] [CrossRef]
- Tien, T.L. The indirect measurement of tensile strength of material by the grey prediction model GMC(1,n). Meas. Sci. Technol. 2005, 16, 1322–1328. [Google Scholar] [CrossRef]
- Deng, J.L. The control problems of grey systems. Syst. Control Lett. 1982, 5, 288–294. [Google Scholar] [CrossRef]
- Jiang, H.; Kong, P.; Hu, Y.C.; Jiang, P. Forecasting China’s CO2 emissions by considering interaction of bilateral FDI using the improved grey multivariable Verhulst model. M Environment. Dev. Sustain. 2021, 23, 225–240. [Google Scholar] [CrossRef]
- Wang, Z.X.; Jv, Y.Q. A non-linear systematic grey model for forecasting the industrial economy-energy-environment system. Technol. Forecast. Soc. Change 2021, 167, 120707. [Google Scholar] [CrossRef]
- Zeng, B.; Duan, H.M.; Zhou, Y.F. A new multivariable grey prediction model with structure compatibility. Appl. Math. Model. 2019, 75, 385–397. [Google Scholar] [CrossRef]
- Krishnamoorthy, U.; Karthika, V.; Mathumitha, M.K.; Panchal, H.; Jatti, V.K.S.; Kumar, A. Learned prediction of cholesterol and glucose using ARIMA and LSTM models—A comparison. Results Control Optim. 2024, 14, 100362. [Google Scholar] [CrossRef]




| Number | Abbreviation | Definition |
|---|---|---|
| 1 | GM(1,1) | Grey model with one variable and one first order equation |
| 2 | GMC(1,N) | A first-order n-variable grey differential equation model [34] |
| 3 | GM(1,N) | Grey model of the first order with n variables [35] |
| 4 | GMVM(1,N) | The grey multivariable Verhulst model [36] |
| 5 | NSGM(1,N) | The new structured grey model [37] |
| 6 | NMGM(1,N) | Novel multi-variable grey model [38] |
| 7 | DPGMC(1,N,ζ) | The damping fractional order multivariate partial grey prediction model |
| Month | Natural Gas Production | Crude Oil Production | Raw Coal Production | Electric Power Generation |
|---|---|---|---|---|
| Mar. 2021 | 5.6 | 19.9 | 76.4 | 65.6 |
| Apr. 2021 | 5.4 | 19.2 | 83.8 | 84.4 |
| May. 2021 | 5.5 | 19.9 | 88.3 | 70.3 |
| Jun. 2021 | 5.3 | 19.2 | 102.9 | 72.9 |
| Jul. 2021 | 5.4 | 19.9 | 86.4 | 89.6 |
| Aug. 2021 | 4.7 | 19.9 | 84.0 | 84.5 |
| Sep. 2021 | 4.4 | 19.2 | 98.9 | 67.1 |
| Oct. 2021 | 4.7 | 19.9 | 116.7 | 72.3 |
| Nov. 2021 | 5.1 | 19.2 | 111.5 | 77.3 |
| Mar. 2022 | 5.2 | 20.0 | 67.5 | 73.4 |
| Apr. 2022 | 5.0 | 19.4 | 53.5 | 78.8 |
| May. 2022 | 5.2 | 20.0 | 42.1 | 70.2 |
| Jun. 2022 | 5.0 | 19.4 | 73.3 | 77.7 |
| Jul. 2022 | 4.8 | 20.0 | 75.1 | 82.8 |
| Aug. 2022 | 5.1 | 20.0 | 75.2 | 71.2 |
| Sep. 2022 | 4.9 | 19.3 | 74.9 | 55.5 |
| Oct. 2022 | 5.1 | 19.9 | 76.5 | 64.0 |
| Nov. 2022 | 4.8 | 19.3 | 97.1 | 70.9 |
| Mar. 2023 | 5.1 | 19.5 | 67.0 | 76.7 |
| Apr. 2023 | 4.9 | 19.2 | 70.7 | 76.7 |
| May. 2023 | 5.1 | 20.0 | 63.4 | 73.1 |
| Jun. 2023 | 4.9 | 19.5 | 60.9 | 75.9 |
| Jul. 2023 | 4.8 | 20.0 | 63.7 | 82.0 |
| Aug. 2023 | 5.0 | 20.3 | 67.3 | 82.0 |
| Sep. 2023 | 4.9 | 19.4 | 70.5 | 70.2 |
| Oct. 2023 | 5.1 | 19.9 | 69.3 | 68.7 |
| Nov. 2023 | 4.9 | 19.3 | 73.2 | 72.6 |
| Month | ||||||||
|---|---|---|---|---|---|---|---|---|
| DPGMC(1,1,ζ) ζ = 0.0178 | GMC(1,1) | GM(1,1) | GMVM(1,1) | NSGM(1,1) | NMGM(1,1) | LSTM | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 4.5860 |
| Apr. 2021 | 5.4 | 5.4000 | 5.3221 | 1.9171 | 5.3003 | 5.4420 | 5.6043 | 5.9785 |
| May. 2021 | 5.5 | 5.5000 | 5.3027 | 4.7737 | 5.2531 | 5.3151 | 5.3132 | 4.5090 |
| Jun. 2021 | 5.3 | 5.3000 | 5.2666 | 6.8709 | 5.2309 | 5.1924 | 5.1285 | 6.2710 |
| Jul. 2021 | 5.4 | 5.4000 | 5.2309 | 6.6953 | 5.2087 | 5.1218 | 5.0441 | 4.5351 |
| Aug. 2021 | 4.7 | 4.7000 | 5.2106 | 6.6617 | 5.2019 | 5.0701 | 4.9989 | 6.5843 |
| Sep. 2021 | 4.4 | 4.4000 | 5.1794 | 7.5430 | 5.2437 | 5.0061 | 4.9543 | 4.9369 |
| Oct. 2021 | 4.7 | 4.7000 | 5.1194 | 8.6381 | 5.3428 | 4.9279 | 4.9063 | 6.3443 |
| Nov. 2021 | 5.1 | 5.1000 | 5.0469 | 8.2215 | 5.4148 | 4.8746 | 4.8854 | 4.8361 |
| Mar. 2022 | 5.2 | 5.2211 | 5.0144 | 5.1461 | 5.2924 | 4.9015 | 4.9293 | 6.2642 |
| Apr. 2022 | 5.0 | 4.9813 | 5.0312 | 4.0544 | 5.2393 | 4.9446 | 4.9720 | 5.0140 |
| May. 2022 | 5.2 | 5.2277 | 5.0703 | 3.1641 | 5.1728 | 4.9963 | 5.0109 | 6.1109 |
| Jun. 2022 | 5.0 | 5.0008 | 5.0937 | 5.2229 | 5.4071 | 4.9881 | 4.9935 | 5.1525 |
| Jul. 2022 | 4.8 | 4.8233 | 5.0891 | 5.2986 | 5.4849 | 4.9789 | 4.9813 | 6.0543 |
| Aug. 2022 | 5.1 | 5.0711 | 5.0827 | 5.2712 | 5.5599 | 4.9715 | 4.9743 | 5.0913 |
| Sep. 2022 | 4.9 | 4.9099 | 5.0763 | 5.2260 | 5.6388 | 4.9661 | 4.9706 | 5.9866 |
| Oct. 2022 | 5.1 | 5.1209 | 5.0687 | 5.3188 | 5.7489 | 4.9594 | 4.9665 | 5.1058 |
| Nov. 2022 | 4.8 | 4.8377 | 5.0421 | 6.7273 | 6.1502 | 4.9219 | 4.9381 | 5.9004 |
| Mar. 2023 | 5.1 | 5.2085 | 5.0224 | 4.6431 | 5.8386 | 4.9395 | 4.9599 | 5.1154 |
| Apr. 2023 | 4.9 | 5.0095 | 5.0253 | 4.8921 | 5.9923 | 4.9475 | 4.9678 | 5.7983 |
| May. 2023 | 5.1 | 5.2083 | 5.0312 | 4.3842 | 5.9578 | 4.9653 | 4.9815 | 5.1734 |
| Jun. 2023 | 4.9 | 5.0088 | 5.0457 | 4.2087 | 5.9939 | 4.9831 | 4.9924 | 5.7112 |
| Jul. 2023 | 4.8 | 4.8096 | 5.0604 | 4.3999 | 6.1411 | 4.9928 | 4.9952 | 5.2856 |
| Aug. 2023 | 5.0 | 5.1101 | 5.0699 | 4.6470 | 6.3259 | 4.9948 | 4.9922 | 5.5445 |
| Sep. 2023 | 4.9 | 4.9103 | 5.0738 | 4.8668 | 6.5241 | 4.9913 | 4.9864 | 5.3726 |
| Oct. 2023 | 5.1 | 5.1103 | 5.0760 | 4.7834 | 6.6227 | 4.9904 | 4.9846 | 5.4490 |
| Nov. 2023 | 4.9 | 4.8110 | 5.0761 | 5.0521 | 6.8713 | 4.9837 | 4.9787 | 5.4437 |
| MAPE (%) | 0.9507 | 2.6117 | 10.6134 | 18.2251 | 2.3439 | 2.2724 | 11.0028 | |
| MAE | 0.0474 | 0.1288 | 0.5293 | 0.9009 | 0.1174 | 0.1137 | 0.5439 | |
| MSE | 0.0040 | 0.0232 | 0.6023 | 1.0985 | 0.0188 | 0.0174 | 0.4775 | |
| 0.7563 | −0.4029 | −35.4246 | −65.4012 | −0.1382 | −0.0490 | −27.8616 | ||
| RMSE | 0.0635 | 0.1523 | 0.7763 | 1.0481 | 0.1372 | 0.1317 | 0.6910 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,1,ζ) ζ = 0.9000 | GMC(1,1) | GM(1,1) | GMVM(1,1) | NSGM(1,1) | NMGM(1,1) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 4.8564 | 4.2758 | 5.2770 | 5.3342 | 5.5273 |
| May. 2021 | 5.5 | 5.5000 | 4.8806 | 5.1209 | 5.2388 | 5.2693 | 5.2927 |
| Jun. 2021 | 5.3 | 5.3000 | 4.8934 | 4.8830 | 5.2080 | 5.1501 | 5.1076 |
| Jul. 2021 | 5.4 | 5.4000 | 4.9088 | 5.0590 | 5.1871 | 5.1268 | 5.0621 |
| Aug. 2021 | 4.7 | 4.7000 | 4.9387 | 5.0589 | 5.1739 | 5.1087 | 5.0372 |
| Sep. 2021 | 4.4 | 4.4000 | 4.9378 | 4.8810 | 5.1647 | 5.0257 | 4.9672 |
| Oct. 2021 | 4.7 | 4.7000 | 4.9427 | 5.0589 | 5.1702 | 5.0304 | 4.9850 |
| Nov. 2021 | 5.1 | 5.1000 | 4.9408 | 4.8810 | 5.1738 | 4.9651 | 4.9386 |
| Mar. 2022 | 5.2 | 5.1762 | 4.9484 | 5.0843 | 5.1980 | 4.9933 | 4.9773 |
| Apr. 2022 | 5.0 | 4.9555 | 4.9545 | 4.9318 | 5.2151 | 4.9560 | 4.9504 |
| May. 2022 | 5.2 | 5.1586 | 4.9641 | 5.0843 | 5.2552 | 4.9863 | 4.9838 |
| Jun. 2022 | 5.0 | 4.9320 | 4.9665 | 4.9318 | 5.2833 | 4.9506 | 4.9540 |
| Jul. 2022 | 4.8 | 4.7799 | 4.9732 | 5.0843 | 5.3409 | 4.9821 | 4.9858 |
| Aug. 2022 | 5.1 | 5.0143 | 4.9938 | 5.0843 | 5.3951 | 5.0065 | 5.0032 |
| Sep. 2022 | 4.9 | 4.8891 | 4.9859 | 4.9064 | 5.4345 | 4.9564 | 4.9566 |
| Oct. 2022 | 5.1 | 5.0602 | 4.9820 | 5.0589 | 5.5176 | 4.9767 | 4.9792 |
| Nov. 2022 | 4.8 | 4.8149 | 4.9742 | 4.9064 | 5.5675 | 4.9334 | 4.9434 |
| Mar. 2023 | 5.1 | 5.0503 | 4.9595 | 4.9572 | 5.6506 | 4.9195 | 4.9398 |
| Apr. 2023 | 4.9 | 4.8916 | 4.9433 | 4.8810 | 5.7183 | 4.8792 | 4.9138 |
| May. 2023 | 5.1 | 5.0821 | 4.9503 | 5.0843 | 5.8455 | 4.9267 | 4.9637 |
| Jun. 2023 | 4.9 | 4.9338 | 4.9594 | 4.9572 | 5.9153 | 4.9143 | 4.9510 |
| Jul. 2023 | 4.8 | 4.7403 | 4.9704 | 5.0843 | 6.0462 | 4.9540 | 4.9841 |
| Aug. 2023 | 5.0 | 5.0638 | 5.0019 | 5.1606 | 6.1770 | 5.0143 | 5.0264 |
| Sep. 2023 | 4.9 | 4.8218 | 5.0031 | 4.9318 | 6.2298 | 4.9723 | 4.9774 |
| Oct. 2023 | 5.1 | 5.0698 | 4.9978 | 5.0589 | 6.3844 | 4.9890 | 4.9906 |
| Nov. 2023 | 4.9 | 4.7660 | 4.9863 | 4.9064 | 6.4587 | 4.9429 | 4.9497 |
| MAPE (%) | 0.9192 | 2.3101 | 1.7746 | 14.4265 | 2.0889 | 2.1594 | |
| MAE | 0.0458 | 0.1156 | 0.0878 | 0.7132 | 0.1048 | 0.1081 | |
| MSE | 0.0031 | 0.0178 | 0.0147 | 0.7169 | 0.0154 | 0.0158 | |
| 0.8147 | −0.0752 | 0.1140 | −42.3333 | 0.0684 | 0.0422 | ||
| RMSE | 0.0554 | 0.1334 | 0.1211 | 0.8467 | 0.1241 | 0.1259 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,1,ζ) ζ = 0.7151 | GMC(1,1) | GM(1,1) | GMVM(1,1) | NSGM(1,1) | NMGM(1,1) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 5.3818 | 3.7821 | 5.2706 | 5.3673 | 5.5417 |
| May. 2021 | 5.5 | 5.5000 | 5.3835 | 5.3309 | 5.2321 | 5.3095 | 5.3183 |
| Jun. 2021 | 5.3 | 5.3000 | 5.4212 | 5.2045 | 5.2021 | 5.2453 | 5.1753 |
| Jul. 2021 | 5.4 | 5.4000 | 5.4070 | 6.1805 | 5.1916 | 5.0820 | 5.0129 |
| Aug. 2021 | 4.7 | 4.7000 | 5.3547 | 5.7842 | 5.1833 | 4.9836 | 4.9419 |
| Sep. 2021 | 4.4 | 4.4000 | 5.3628 | 4.5831 | 5.1605 | 5.0195 | 4.9826 |
| Oct. 2021 | 4.7 | 4.7000 | 5.4103 | 4.9346 | 5.1671 | 5.0141 | 4.9818 |
| Nov. 2021 | 5.1 | 5.1000 | 5.4318 | 5.2750 | 5.1877 | 4.9764 | 4.9578 |
| Mar. 2022 | 5.2 | 5.1762 | 5.4507 | 5.0087 | 5.1964 | 4.9718 | 4.9621 |
| Apr. 2022 | 5.0 | 4.9577 | 5.4680 | 5.3772 | 5.2405 | 4.9321 | 4.9392 |
| May. 2022 | 5.2 | 5.1451 | 5.4945 | 4.7903 | 5.2394 | 4.9571 | 4.9664 |
| Jun. 2022 | 5.0 | 4.9336 | 5.5285 | 5.3021 | 5.3119 | 4.9275 | 4.9468 |
| Jul. 2022 | 4.8 | 4.7812 | 5.5279 | 5.6501 | 5.3952 | 4.8696 | 4.9113 |
| Aug. 2022 | 5.1 | 5.0219 | 5.5444 | 4.8586 | 5.3794 | 4.8998 | 4.9454 |
| Sep. 2022 | 4.9 | 4.8754 | 5.6423 | 3.7872 | 5.3050 | 5.0288 | 5.0394 |
| Oct. 2022 | 5.1 | 5.0449 | 5.7727 | 4.3672 | 5.4103 | 5.0769 | 5.0542 |
| Nov. 2022 | 4.8 | 4.8085 | 5.8687 | 4.8381 | 5.5285 | 5.0699 | 5.0303 |
| Mar. 2023 | 5.1 | 5.0635 | 5.9352 | 5.2339 | 5.6617 | 5.0256 | 4.9890 |
| Apr. 2023 | 4.9 | 4.8939 | 5.9897 | 5.2339 | 5.7493 | 4.9898 | 4.9648 |
| May. 2023 | 5.1 | 5.1080 | 6.0590 | 4.9882 | 5.7938 | 4.9846 | 4.9676 |
| Jun. 2023 | 4.9 | 4.9283 | 6.1373 | 5.1793 | 5.9263 | 4.9618 | 4.9561 |
| Jul. 2023 | 4.8 | 4.7343 | 6.1965 | 5.5955 | 6.1299 | 4.9027 | 4.9205 |
| Aug. 2023 | 5.0 | 5.0432 | 6.2420 | 5.5955 | 6.2570 | 4.8548 | 4.8997 |
| Sep. 2023 | 4.9 | 4.8406 | 6.3247 | 4.7903 | 6.1621 | 4.8944 | 4.9433 |
| Oct. 2023 | 5.1 | 5.0804 | 6.4550 | 4.6880 | 6.2352 | 4.9366 | 4.9758 |
| Nov. 2023 | 4.9 | 4.7653 | 6.5900 | 4.9541 | 6.4264 | 4.9448 | 4.9765 |
| MAPE (%) | 0.8624 | 18.4241 | 7.9274 | 14.1216 | 2.3354 | 2.3263 | |
| MAE | 0.0430 | 0.9126 | 0.3934 | 0.6975 | 0.1170 | 0.1164 | |
| MSE | 0.0028 | 1.0040 | 0.2438 | 0.6851 | 0.0193 | 0.0174 | |
| 0.8307 | −59.6868 | −13.7351 | −41.0168 | −0.1651 | −0.0527 | ||
| RMSE | 0.0529 | 1.0020 | 0.4937 | 0.8337 | 0.1388 | 0.1320 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,2,ζ) ζ = 0.8734 | GMC(1,2) | GM(1,2) | GMVM(1,2) | NSGM(1,2) | NMGM(1,2) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 5.0003 | 4.2089 | 5.3210 | 5.4388 | 5.6012 |
| May. 2021 | 5.5 | 5.5000 | 4.9732 | 5.2639 | 5.2600 | 5.3175 | 5.3160 |
| Jun. 2021 | 5.3 | 5.3000 | 4.9329 | 5.0249 | 5.2614 | 5.1875 | 5.1240 |
| Jul. 2021 | 5.4 | 5.4000 | 4.9091 | 5.1014 | 5.2382 | 5.1229 | 5.0459 |
| Aug. 2021 | 4.7 | 4.7000 | 4.9198 | 5.0895 | 5.2459 | 5.0756 | 5.0043 |
| Sep. 2021 | 4.4 | 4.4000 | 4.8962 | 4.9931 | 5.3993 | 5.0034 | 4.9510 |
| Oct. 2021 | 4.7 | 4.7000 | 4.8589 | 5.2409 | 5.6992 | 4.9324 | 4.9104 |
| Nov. 2021 | 5.1 | 5.1000 | 4.8177 | 5.0514 | 5.9142 | 4.8718 | 4.8820 |
| Mar. 2022 | 5.2 | 5.2356 | 4.8299 | 5.0367 | 5.4608 | 4.9050 | 4.9324 |
| Apr. 2022 | 5.0 | 4.9979 | 4.8788 | 4.8302 | 5.2478 | 4.9413 | 4.9684 |
| May. 2022 | 5.2 | 5.2430 | 4.9390 | 4.9192 | 4.9400 | 4.9979 | 5.0126 |
| Jun. 2022 | 5.0 | 5.0176 | 4.9660 | 4.9219 | 5.6115 | 4.9845 | 4.9901 |
| Jul. 2022 | 4.8 | 4.8393 | 4.9707 | 5.0719 | 5.7166 | 4.9821 | 4.9849 |
| Aug. 2022 | 5.1 | 5.0903 | 4.9883 | 5.0724 | 5.8207 | 4.9800 | 4.9818 |
| Sep. 2022 | 4.9 | 4.9238 | 4.9804 | 4.9056 | 5.9710 | 4.9662 | 4.9689 |
| Oct. 2022 | 5.1 | 5.1334 | 4.9744 | 5.0548 | 6.1166 | 4.9638 | 4.9694 |
| Nov. 2022 | 4.8 | 4.8470 | 4.9489 | 5.0084 | 7.2429 | 4.9200 | 4.9349 |
| Mar. 2023 | 5.1 | 5.1215 | 4.9303 | 4.9163 | 6.0758 | 4.9346 | 4.9550 |
| Apr. 2023 | 4.9 | 4.9847 | 4.9268 | 4.8626 | 6.3920 | 4.9350 | 4.9571 |
| May. 2023 | 5.1 | 5.1087 | 4.9451 | 5.0178 | 5.9908 | 4.9608 | 4.9803 |
| Jun. 2023 | 4.9 | 4.9503 | 4.9705 | 4.8881 | 5.9415 | 4.9758 | 4.9883 |
| Jul. 2023 | 4.8 | 4.7979 | 4.9933 | 5.0192 | 6.0961 | 4.9925 | 4.9977 |
| Aug. 2023 | 5.0 | 5.0994 | 5.0289 | 5.1067 | 6.3659 | 5.0055 | 5.0036 |
| Sep. 2023 | 4.9 | 4.9263 | 5.0318 | 4.9089 | 6.8499 | 4.9947 | 4.9884 |
| Oct. 2023 | 5.1 | 5.1124 | 5.0261 | 5.0215 | 6.8014 | 4.9970 | 4.9893 |
| Nov. 2023 | 4.9 | 4.8727 | 5.0130 | 4.8978 | 7.3875 | 4.9822 | 4.9752 |
| MAPE (%) | 0.6530 | 2.6438 | 2.2076 | 23.3142 | 2.3165 | 2.2437 | |
| MAE | 0.0325 | 0.1326 | 0.1101 | 1.1527 | 0.1161 | 0.1122 | |
| MSE | 0.0017 | 0.0244 | 0.0205 | 1.7536 | 0.0185 | 0.0171 | |
| 0.8970 | −0.4751 | −0.2371 | −105.0031 | −0.1202 | −0.0317 | ||
| RMSE | 0.0413 | 0.1562 | 0.1431 | 1.3242 | 0.1361 | 0.1306 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,2,ζ) ζ = 0.6213 | GMC(1,2) | GM(1,2) | GMVM(1,2) | NSGM(1,2) | NMGM(1,2) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 5.4719 | 3.3740 | 5.3189 | 5.4456 | 5.6010 |
| May. 2021 | 5.5 | 5.5000 | 5.4715 | 5.5741 | 5.2632 | 5.3542 | 5.3438 |
| Jun. 2021 | 5.3 | 5.3000 | 5.4834 | 5.8037 | 5.2615 | 5.2487 | 5.1658 |
| Jul. 2021 | 5.4 | 5.4000 | 5.4570 | 6.2538 | 5.2171 | 5.0943 | 5.0156 |
| Aug. 2021 | 4.7 | 4.7000 | 5.4158 | 5.8223 | 5.2126 | 4.9984 | 4.9470 |
| Sep. 2021 | 4.4 | 4.4000 | 5.4096 | 5.0243 | 5.3805 | 4.9945 | 4.9539 |
| Oct. 2021 | 4.7 | 4.7000 | 5.4072 | 5.5266 | 5.6485 | 4.9426 | 4.9209 |
| Nov. 2021 | 5.1 | 5.1000 | 5.3732 | 5.7196 | 5.8065 | 4.8801 | 4.8884 |
| Mar. 2022 | 5.2 | 5.2598 | 5.3676 | 4.9060 | 5.4310 | 4.9025 | 4.9281 |
| Apr. 2022 | 5.0 | 5.0225 | 5.4018 | 5.0076 | 5.1809 | 4.9089 | 4.9466 |
| May. 2022 | 5.2 | 5.2562 | 5.4628 | 4.3851 | 4.9910 | 4.9732 | 5.0006 |
| Jun. 2022 | 5.0 | 5.0385 | 5.5195 | 5.2172 | 5.5049 | 4.9486 | 4.9736 |
| Jul. 2022 | 4.8 | 4.8683 | 5.5293 | 5.5186 | 5.5480 | 4.8995 | 4.9371 |
| Aug. 2022 | 5.1 | 5.1159 | 5.5509 | 4.8901 | 5.7919 | 4.9207 | 4.9574 |
| Sep. 2022 | 4.9 | 4.9391 | 5.6322 | 4.0335 | 6.1672 | 5.0212 | 5.0268 |
| Oct. 2022 | 5.1 | 5.1402 | 5.7367 | 4.5169 | 6.2535 | 5.0562 | 5.0358 |
| Nov. 2022 | 4.8 | 4.8658 | 5.8016 | 5.1721 | 7.1353 | 5.0236 | 4.9950 |
| Mar. 2023 | 5.1 | 5.1670 | 5.8501 | 5.0770 | 5.9739 | 5.0025 | 4.9803 |
| Apr. 2023 | 4.9 | 5.0092 | 5.9097 | 5.1274 | 6.2233 | 4.9808 | 4.9678 |
| May. 2023 | 5.1 | 5.1714 | 5.9840 | 4.8325 | 6.0322 | 4.9909 | 4.9809 |
| Jun. 2023 | 4.9 | 4.9893 | 6.0738 | 4.9505 | 5.8608 | 4.9874 | 4.9811 |
| Jul. 2023 | 4.8 | 4.8118 | 6.1524 | 5.3199 | 5.8574 | 4.9489 | 4.9562 |
| Aug. 2023 | 5.0 | 5.1194 | 6.2194 | 5.3689 | 6.1158 | 4.9133 | 4.9376 |
| Sep. 2023 | 4.9 | 4.9502 | 6.3112 | 4.7718 | 6.8594 | 4.9428 | 4.9661 |
| Oct. 2023 | 5.1 | 5.1529 | 6.4382 | 4.6740 | 6.9831 | 4.9762 | 4.9898 |
| Nov. 2023 | 4.9 | 4.8786 | 6.5692 | 4.9389 | 7.2853 | 4.9781 | 4.9858 |
| MAPE (%) | 1.1135 | 17.6279 | 6.8397 | 22.2456 | 2.4293 | 2.3169 | |
| MAE | 0.0555 | 0.8728 | 0.3408 | 1.1007 | 0.1216 | 0.1158 | |
| MSE | 0.0039 | 0.9352 | 0.1844 | 1.6421 | 0.0193 | 0.0170 | |
| 0.7623 | −55.5327 | −10.1480 | −98.2617 | −0.1689 | −0.0291 | ||
| RMSE | 0.0627 | 0.9671 | 0.4294 | 1.2814 | 0.1391 | 0.1305 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,2,ζ) ζ = 0.4363 | GMC(1,2) | GM(1,2) | GMVM(1,2) | NSGM(1,2) | NMGM(1,2) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 5.0016 | 4.2726 | 5.2852 | 5.3840 | 5.5468 |
| May. 2021 | 5.5 | 5.5000 | 4.9679 | 5.0992 | 5.2560 | 5.3742 | 5.3696 |
| Jun. 2021 | 5.3 | 5.3000 | 4.9701 | 4.8934 | 5.2252 | 5.2243 | 5.1514 |
| Jul. 2021 | 5.4 | 5.4000 | 4.9009 | 5.2378 | 5.1370 | 5.0864 | 5.0153 |
| Aug. 2021 | 4.7 | 4.7000 | 4.8372 | 5.1756 | 5.0911 | 5.0140 | 4.9633 |
| Sep. 2021 | 4.4 | 4.4000 | 4.8439 | 4.8180 | 5.1755 | 4.9744 | 4.9398 |
| Oct. 2021 | 4.7 | 4.7000 | 4.8912 | 5.0271 | 5.1695 | 5.0204 | 4.9900 |
| Nov. 2021 | 5.1 | 5.1000 | 4.8846 | 4.9421 | 5.0545 | 4.8971 | 4.8953 |
| Mar. 2022 | 5.2 | 5.2054 | 4.8899 | 5.0613 | 5.1767 | 4.9652 | 4.9702 |
| Apr. 2022 | 5.0 | 4.9861 | 4.8863 | 5.0020 | 5.0031 | 4.8739 | 4.9017 |
| May. 2022 | 5.2 | 5.1713 | 4.9067 | 5.0224 | 5.3136 | 4.9719 | 4.9931 |
| Jun. 2022 | 5.0 | 4.9622 | 4.9145 | 4.9886 | 5.0297 | 4.8884 | 4.9221 |
| Jul. 2022 | 4.8 | 4.8054 | 4.8807 | 5.1757 | 4.8970 | 4.8819 | 4.9305 |
| Aug. 2022 | 5.1 | 5.0522 | 4.9063 | 5.0346 | 5.4149 | 4.9704 | 5.0046 |
| Sep. 2022 | 4.9 | 4.8996 | 4.9980 | 4.6977 | 6.2207 | 5.0496 | 5.0474 |
| Oct. 2022 | 5.1 | 5.0727 | 5.0891 | 4.9261 | 6.1322 | 5.1496 | 5.1046 |
| Nov. 2022 | 4.8 | 4.8351 | 5.0995 | 4.8850 | 5.7034 | 5.0726 | 5.0164 |
| Mar. 2023 | 5.1 | 5.1278 | 5.0490 | 4.9973 | 5.4233 | 4.9968 | 4.9558 |
| Apr. 2023 | 4.9 | 4.9455 | 4.9837 | 4.9348 | 5.3394 | 4.8825 | 4.8781 |
| May. 2023 | 5.1 | 5.1576 | 4.9718 | 5.0577 | 6.0024 | 4.9555 | 4.9616 |
| Jun. 2023 | 4.9 | 4.9664 | 4.9686 | 4.9876 | 5.6272 | 4.9067 | 4.9273 |
| Jul. 2023 | 4.8 | 4.7729 | 4.9363 | 5.1660 | 5.2298 | 4.9035 | 4.9384 |
| Aug. 2023 | 5.0 | 5.0747 | 4.9219 | 5.2285 | 5.3558 | 4.9525 | 4.9861 |
| Sep. 2023 | 4.9 | 4.8775 | 4.9295 | 4.8974 | 6.4082 | 4.9332 | 4.9624 |
| Oct. 2023 | 5.1 | 5.1000 | 4.9708 | 4.9833 | 7.0872 | 5.0156 | 5.0252 |
| Nov. 2023 | 4.9 | 4.7903 | 4.9833 | 4.9057 | 6.3451 | 4.9484 | 4.9582 |
| MAPE (%) | 0.7072 | 2.5213 | 2.4869 | 13.3693 | 2.1880 | 2.0976 | |
| MAE | 0.0352 | 0.1263 | 0.1233 | 0.6642 | 0.1096 | 0.1048 | |
| MSE | 0.0020 | 0.0237 | 0.0275 | 0.7785 | 0.0174 | 0.0155 | |
| 0.8785 | −0.4299 | −0.6649 | −46.0577 | −0.0531 | 0.0615 | ||
| RMSE | 0.0448 | 0.1538 | 0.1660 | 0.8823 | 0.1320 | 0.1246 | |
| Month | |||||||
|---|---|---|---|---|---|---|---|
| DPGMC(1,3,ζ) ζ = 0.9900 | GMC(1,3) | GM(1,3) | GMVM(1,3) | NSGM(1,3) | NMGM(1,3) | ||
| Mar. 2021 | 5.6 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 | 5.6000 |
| Apr. 2021 | 5.4 | 5.4000 | 5.0734 | 4.2107 | 5.3169 | 5.4243 | 5.5829 |
| May. 2021 | 5.5 | 5.5000 | 5.0184 | 5.2433 | 5.2642 | 5.3824 | 5.3694 |
| Jun. 2021 | 5.3 | 5.3000 | 4.9901 | 5.0157 | 5.2599 | 5.2324 | 5.1535 |
| Jul. 2021 | 5.4 | 5.4000 | 4.9095 | 5.1678 | 5.2066 | 5.0926 | 5.0165 |
| Aug. 2021 | 4.7 | 4.7000 | 4.8462 | 5.1325 | 5.1962 | 5.0145 | 4.9596 |
| Sep. 2021 | 4.4 | 4.4000 | 4.8345 | 4.9569 | 5.3640 | 4.9728 | 4.9356 |
| Oct. 2021 | 4.7 | 4.7000 | 4.8469 | 5.2098 | 5.6078 | 4.9779 | 4.9483 |
| Nov. 2021 | 5.1 | 5.1000 | 4.8149 | 5.0582 | 5.7339 | 4.8635 | 4.8710 |
| Mar. 2022 | 5.2 | 5.2238 | 4.8217 | 5.0325 | 5.4092 | 4.9267 | 4.9451 |
| Apr. 2022 | 5.0 | 4.9915 | 4.8455 | 4.8682 | 5.1519 | 4.8759 | 4.9181 |
| May. 2022 | 5.2 | 5.2089 | 4.8953 | 4.9115 | 5.0251 | 4.9765 | 5.0058 |
| Jun. 2022 | 5.0 | 5.0082 | 4.9183 | 4.9453 | 5.4484 | 4.9108 | 4.9473 |
| Jul. 2022 | 4.8 | 4.8182 | 4.8896 | 5.1092 | 5.4635 | 4.8955 | 4.9408 |
| Aug. 2022 | 5.1 | 5.0906 | 4.9118 | 5.0540 | 5.7654 | 4.9629 | 4.9931 |
| Sep. 2022 | 4.9 | 4.8925 | 4.9881 | 4.8234 | 6.2331 | 5.0395 | 5.0370 |
| Oct. 2022 | 5.1 | 5.1072 | 5.0653 | 5.0028 | 6.2924 | 5.1176 | 5.0764 |
| Nov. 2022 | 4.8 | 4.8299 | 5.0644 | 4.9896 | 7.0310 | 5.0450 | 4.9984 |
| Mar. 2023 | 5.1 | 5.0779 | 5.0188 | 4.9363 | 5.9176 | 4.9909 | 4.9609 |
| Apr. 2023 | 4.9 | 4.9408 | 4.9698 | 4.8857 | 6.1296 | 4.9064 | 4.9083 |
| May. 2023 | 5.1 | 5.1072 | 4.9679 | 5.0140 | 6.0482 | 4.9669 | 4.9718 |
| Jun. 2023 | 4.9 | 4.9078 | 4.9770 | 4.9071 | 5.8288 | 4.9364 | 4.9527 |
| Jul. 2023 | 4.8 | 4.7862 | 4.9588 | 5.0580 | 5.7566 | 4.9298 | 4.9554 |
| Aug. 2023 | 5.0 | 5.0431 | 4.9532 | 5.1390 | 6.0054 | 4.9595 | 4.9823 |
| Sep. 2023 | 4.9 | 4.9376 | 4.9596 | 4.8976 | 6.8459 | 4.9506 | 4.9712 |
| Oct. 2023 | 5.1 | 5.1095 | 4.9930 | 4.9954 | 7.0521 | 5.0171 | 5.0183 |
| Nov. 2023 | 4.9 | 4.8625 | 5.0012 | 4.8984 | 7.2136 | 4.9670 | 4.9705 |
| MAPE (%) | 0.3821 | 2.6781 | 2.3823 | 21.5136 | 2.2198 | 2.1290 | |
| MAE | 0.0189 | 0.1343 | 0.1188 | 1.0649 | 0.1111 | 0.1064 | |
| MSE | 0.0005 | 0.0265 | 0.0229 | 1.5653 | 0.0177 | 0.0157 | |
| 0.9683 | −0.5996 | −0.3883 | −93.6203 | −0.0716 | 0.0533 | ||
| RMSE | 0.0229 | 0.1627 | 0.1513 | 1.2511 | 0.1331 | 0.1251 | |
| Month | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|
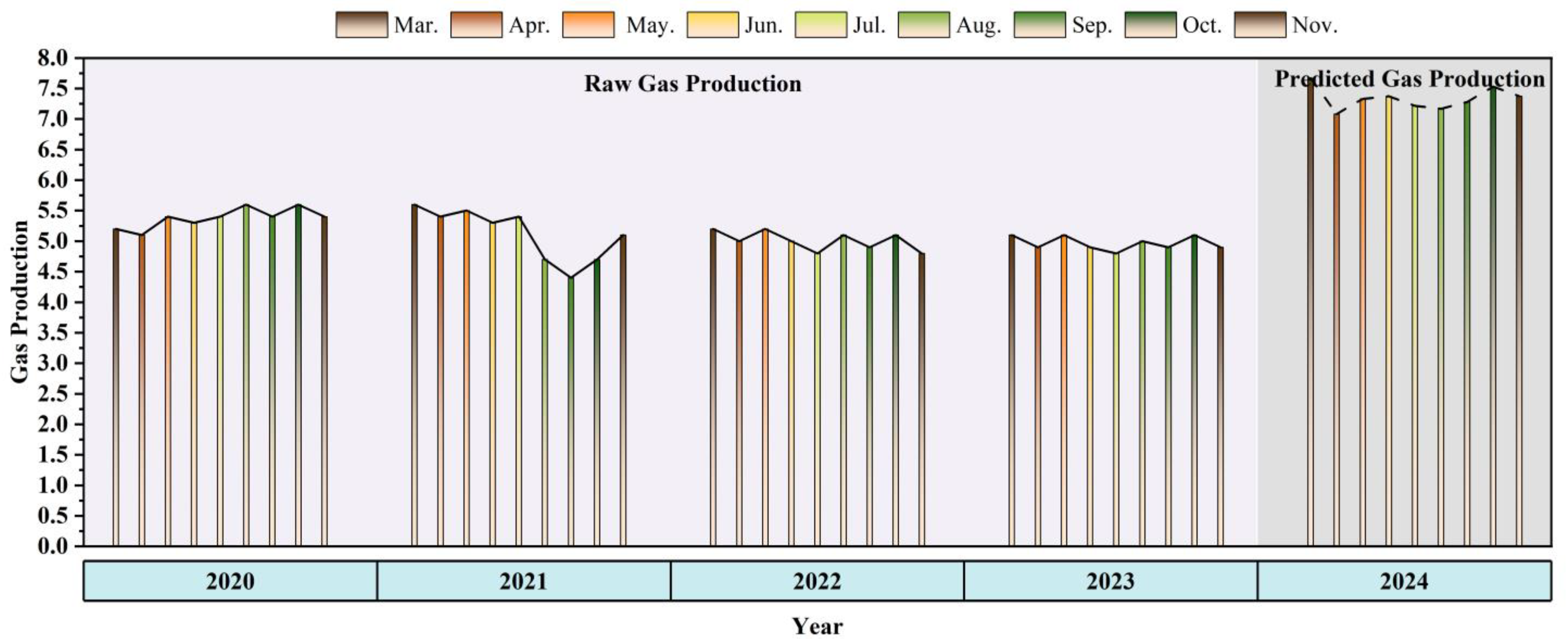
| Nature Gas Production | 7.6703 | 7.0827 | 7.3308 | 7.3726 | 7.2158 | 7.1693 | 7.2791 | 7.5310 | 7.3757 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Duan, H.; Chen, H. A Novel Fractional Order Multivariate Partial Grey Model and Its Application in Natural Gas Production. Fractal Fract. 2025, 9, 422. https://doi.org/10.3390/fractalfract9070422
Li H, Duan H, Chen H. A Novel Fractional Order Multivariate Partial Grey Model and Its Application in Natural Gas Production. Fractal and Fractional. 2025; 9(7):422. https://doi.org/10.3390/fractalfract9070422
Chicago/Turabian StyleLi, Hui, Huiming Duan, and Hongli Chen. 2025. "A Novel Fractional Order Multivariate Partial Grey Model and Its Application in Natural Gas Production" Fractal and Fractional 9, no. 7: 422. https://doi.org/10.3390/fractalfract9070422
APA StyleLi, H., Duan, H., & Chen, H. (2025). A Novel Fractional Order Multivariate Partial Grey Model and Its Application in Natural Gas Production. Fractal and Fractional, 9(7), 422. https://doi.org/10.3390/fractalfract9070422






