A Novel Nonlinear Different Fractional Discrete Grey Multivariate Model and Its Application in Energy Consumption

Abstract

With global energy demand escalating and climate change posing unprecedented challenges, accurate forecasting of regional energy consumption has emerged as a cornerstone for national energy planning and sustainable development strategies. This study develops a novel nonlinear different fractional discrete grey multivariate model (NDFDGM(r_i,N)). This model improves the shortcomings of the conventional GM(1,N) in handling nonlinear relationships and variable differences by introducing different fractional order accumulation and nonlinear logarithmic conditioning terms. In addition, the Firefly Algorithm (FA) was utilized to optimize the model’s hyperparameters, significantly enhancing the prediction accuracy. Through empirical analysis of energy consumption data in China’s eastern, central and western regions and across the country, it has been confirmed that the NDFDGM model outperforms others during both the simulation and forecasting phases, and its predicted MAPE values are, respectively, 1.4585%, 1.4496%, 2.0673% and significantly lower than that of compared models. The findings indicate that this model can effectively capture the complex characteristics of energy consumption, and its prediction results offer a solid scientific foundation for guiding energy strategies and shaping policy decisions. Finally, this paper conducts extrapolation and predictive analysis using the NDFDGM(r_i,N) to explore the development trends of energy consumption in the whole country in the coming three years and puts forward energy policy suggestions for different regions to promote the optimization and sustainable development of the energy structure.

1. Introduction

Against the backdrop of ever-increasing global energy requirements and progressively intensifying climate change concerns, the accurate projection of regional energy consumption patterns has evolved into an indispensable element within the framework of national energy policy development and the implementation of sustainable growth strategies across diverse geographical contexts. China, as the world’s largest developing nation, has seen a substantial rise in energy demand driven by its rapid economic expansion. The energy resource endowments and industrial structures in different regions vary greatly, resulting in significant temporal and spatial differentiation in energy consumption. Many policy documents attach great importance to the significance of efficient energy utilization and scientific planning. The “14th Five-Year Plan for the Modern Energy System” explicitly states that the intelligence level of the energy system should be enhanced, and the analysis, prediction and warning of the energy supply and demand situation should be intensified [1]. All these have provided policy guidance and practical demands for regional energy consumption prediction research. Therefore, accurately grasping the spatio-temporal differentiation characteristics of regional energy consumption and precisely predicting its development trend is of great significance for China to improve energy allocation, ensure energy security, promote coordinated regional development, and achieve the “dual carbon” goals [2].

There are many research methods in the field of prediction. This study mainly selects to conduct prediction research by applying the relevant methods of grey system theory. Grey System Theory, developed by Deng Julong, is a framework designed primarily to address systems characterized by uncertainty and partially known information [3]. This theory focuses on those “small sample” and “poor information” uncertain systems. The key lies in exploring the internal laws of the data by performing generation processing on the original data and forming a grey model for prediction [4,5]. The grey system theory, with its unique data processing methods and modelling approaches, provides a new channel for addressing the prediction challenges of complex systems and has thus been fully implemented in many fields [6]. Energy consumption prediction is one of these fields [7,8,9].

The traditional grey multivariate model GM(1,N) belongs to the category of grey system theory and is a key model for multifactor prediction [10]. This model is based on many correlated variables and weakens the randomness of the data through cumulative generation operations to form a first-order linear differential equation model, showing the dynamic connections among the variables [11], thereby performing predictions on the target variables [12]. At present, this model has been widely applied in the prediction research of various fields. For example, in the field of engineering, considering the characteristic of numerous unforeseen risk factors in highway projects, Tang Li utilized GM(1,N) to construct a risk cost estimation model for sensitivity analysis. Compared with traditional models, the analysis results of GM(1,N) are more direct and objective, which is conducive to cost savings and risk avoidance [13]. In the field of transportation, Chen Yufei et al. established a prediction model based on the number of deaths in road traffic accidents as an indicator. Through comparison, it was found that the model had relatively high accuracy [14]. In the field of talent demand, Ma Weimin et al. established a talent demand prediction model based on data such as the industrial growth rate and the number of job demands of the software and information service industry in Zhuhai City, using the GM(1,N) model. After verification, this model has guiding significance for the prediction of industrial talents [15]. In terms of regional energy consumption prediction, the GM(1,N) model has also achieved certain applications because it can comprehensively consider many influencing factors [16] such as economic growth, industrial structure [17], population size, etc., and has not very high requirements for sample data [18]. Some scholars predict energy consumption in specific regions through the GM(1,N) model [8,19,20]. For example, Wei Long used the improved GM(1,N) model to predict energy consumption in Jiangsu Province, providing a referential basis for regional energy planning [21].

However, due to the computational error in the modelling process of GM(1,N), researchers improved the traditional GM(1,N) model in order to overcome this problem and improve the prediction accuracy [22]. Firstly, the traditional GM(1,N) model assumes that the variables have a linear relationship. However, in reality, the variable relationships are intricate [23], and the nonlinear characteristics are significant, which seriously affects the accuracy of the model’s prediction. In view of the deficiencies of the GM(1,N) model in handling nonlinear relations, some scholars have attempted to make improvements from the grey model itself. They introduced nonlinear functions to preprocess the original data, mine the nonlinear features in the data, and enable the model to better fit the nonlinear relationships among the variables in the system. For example, by performing logarithmic transformation, exponential transformation and other methods on the data, scholars implement data preprocessing techniques that optimize the distribution characteristics of the input variables, thereby improving the model’s predictive performance on complex datasets [24]. On the other hand, in the cumulative generation process of the traditional GM(1,N) model, the same first-order cumulative order is adopted for all variables, without considering the differences in the variation laws of different variables themselves, making it difficult to accurately depict the complex dynamic relationships among variables. Aiming at the deficiency of the single accumulation process of the model, scholars first thought of improving the first-order accumulation to the fractional-order accumulation, endowing the variables with more refined accumulation parameters, so as to make the prediction accuracy of the model better [25]. With the deepening of research, many scholars have proposed many improved accumulation operators at present, further enriching the accumulation operations in the modelling process [26]. Furthermore, some scholars have proposed an improved method of variable cumulative order. According to the variation characteristics of different variables, different cumulative orders are assigned to them. For variables with relatively stable changes, a lower cumulative order is adopted; For variables with large fluctuations and complex changes, a higher cumulative order is assigned [27]. The above-mentioned multiple methods have achieved the optimization of the grey model’s fitting degree to the actual system, which can reflect the relationship between variables more accurately and successfully improve the reliability of the model’s prediction.

In addition to the grey prediction model, models such as neural networks [28] and support vector machines [29] are also widely used in regional energy consumption prediction [30,31,32]. Neural networks, especially BP neural networks [33], have strong self-learning, self-adaptation and nonlinear mapping capabilities [34]. For instance, scholar Wang designed a traffic control protocol for wireless network communication ports and constructed a traffic composite control mechanism using BP neural networks, achieving effective management of communication port traffic [35]. He et al. obtained the influencing factors of output power by analyzing the principle of wind power generation, and then accurately predicted wind power based on BP neural network algorithm, etc. [36]. Support vector machine, relying on statistical learning theory, performs well in small sample, nonlinear and high-dimensional pattern recognition problems [37]. Zhou used the SVM model to predict coal consumption. The research finds that in recent years, with the adjustment of the industrial structure in this region, the trend of coal consumption has become complex [38]. Feng selected data such as coal consumption data of the past 15 years, indicators related to industrial structure adjustment, and the implementation intensity of environmental protection policies as samples, and made predictions through the SVM model. The prediction results accurately reflected the trend of coal consumption in this region rising first and then declining under the influence of industrial structure adjustment and environmental protection policies [39]. It has provided strong support for formulating the development plan of the coal industry and the energy transition strategy in this region.

To sum up, many achievements have been made in the research of regional energy consumption prediction. The grey multivariate prediction model and its improved forms, neural networks, support vector machines and other models each have their own uses. However, the energy consumption system is complex and changeable, and there is still some room for improvement in current research. Therefore, this study will be committed to improving the several deficiencies mentioned above and establishing a new fractional-order discrete grey multivariate prediction model for the prediction of regional energy consumption in China. This paper’s novel aspects and contributions are outlined as follows:

(1)

The model is mainly improved in the accumulation method, breaking through the limitation that the accumulation order of the dependent variable and the independent variable is the same in the previous fractional accumulation, and endowing different sequences with different accumulation orders.

(2)

Although the traditional grey model (such as GM(1,N)) can deal with multi-variable problems, its linear structure is difficult to describe the nonlinear interaction between variables. Therefore, a nonlinear logarithmic adjustment term is introduced in this paper to make up for the shortcomings of the model in nonlinear prediction.

(3)

The parameters of the traditional grey model are usually set manually or through simple search, which is prone to fall into local optimum. This paper adopts the Firefly Algorithm for global optimization, solving the problem that the selection of model hyperparameters relies on experience. This algorithm has prominent advantages compared with commonly used.

The contents of the upcoming sections of this paper are summarized as follows. Section 2 explains the modelling process of a novel nonlinear different fractional discrete grey multivariate model and outlines the details the technique used for estimating its parameters. In Section 3, the Firefly Algorithm is briefly described, highlighting its role in fine-tuning the model’s hyperparameters. Section 4 tests the proposed model with energy consumption cases in China’s central, eastern and western regions to illustrate the validity of the model. Section 5 is to apply the NDFDGM(r_i,N) to the national energy consumption prediction for empirical analysis and conduct extrapolation and predictive analysis using the NDFDGM(r_i,N) to explore the development trends of energy consumption in the whole country in the coming three years. Section 6 mainly puts forward relevant policy recommendations aimed at guiding regional energy development in China, based on the insights gained from this research. Lastly, Section 7 encapsulates the key findings and conclusions drawn from the study and proposes future work which focuses on the key discussions of the model’s limitations and the directions for improvement.

2. Nonlinear Different Fractional Discrete Grey Multivariate Model NDFDGM(r_i,N)

2.1. The Principle of Fractional Accumulation

Definition 1.

Suppose the original non-negative sequence $x^{(0)}=\{x^{(0)}(1),x^{(0)}(2),\dots ,x^{(0)}(n)\}$, the r-order cumulative generation sequence $x^{(r)}(k)$ can be calculated by the following equation:

$$x^{(r)}(k)={\displaystyle \sum _{i=1}^k\left(\begin{array}{c}k-i+r-1\\ k-i\end{array}\right)} x^{(0)}(i)$$

(1)

where $\left(\begin{array}{c}k-i+r-1\\ k-i\end{array}\right)={\displaystyle \frac{(k-i+r-1)\dots (r+1)r}{(k-i)!}}$. r is a fractional cumulative parameter, and its value range is from 0 to 1.

Definition 2.

Assuming a non-negative original sequence $x^{(0)}=\{x^{(0)}(1),x^{(0)}(2),\dots ,x^{(0)}(n)\}$, the r-order inverse accumulation generated sequence $x^{(-r)}(k)$ can be calculated by:

$$x^{(-r)}(k)={\displaystyle \sum _{i=1}^k\left(\begin{array}{c}k-i-r-1\\ k-i\end{array}\right)} x^{(0)}(i)$$

(2)

By observing Definitions 1 and 2, it can be found that the calculation formula for r-order accumulation is similar to that for r-order inverse accumulation, and the following relationship exists between the two:

$${[x^{(r)}(k)]}^{(-r)}={\displaystyle \sum _{i=1}^k\left(\begin{array}{c}k-i-r-1\\ k-i\end{array}\right)} x^{(r)}(i)=x^{(0)}(k)$$

(3)

To sum up, it is found that Equation (3) plays a significant role in restoring the predicted values of the original sequence during the modelling process.

2.2. The Modelling Process of the Nonlinear Different Fractional Discrete Grey Multivariate Model NDFDGM(r_i,N)

The nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N) is an optimized form of the traditional GM(1,N) model. By adding the power exponent of the influencing factors and introducing the time adjustment term into the model, and then optimizing the accumulation method from the first-order accumulation of all sequences to the fractional-order accumulation of the dependent variable, the aim is to enhance the nonlinear expression ability of the model and further improve the predictive ability of the grey multivariate model. The specific modelling process is as follows.

Suppose the non-negative sequence $x_1^{(0)}=\{x_1^{(0)}(1),x_1^{(0)}(2),\dots ,x_1^{(0)}(n)\}$ is the system characteristic sequence, that is, the sequence of dependent variables, and the corresponding sequence of related factors is $x_i^{(0)}=\{x_i^{(0)}(1),x_i^{(0)}(2),\dots ,x_i^{(0)}(n)\}$, $i=2,3,\dots ,N$. Then the r-order cumulative sequence $x_1^{(r)}(k)$ of the dependent variable sequence $x_1^{(0)}(k)$ can be calculated through Equation (1).

The expression of the traditional GM(1,N) model is as follows:

$${\displaystyle \frac{d{x}_1^{(1)}(t)}{dt}}+a{x}_1^{(1)}(t)={\displaystyle \sum _{i=2}^N{b}_i{x}_i^{(1)}(t)}$$

(4)

where $a$ is the development coefficient and $b_i$ is the adjustment coefficient of $x_i$. After assigning different fractional accumulation parameters to the dependent variable and the independent variable and introducing the time adjustment term into the model, its expression is transformed into:

$${\displaystyle \frac{d{x}_1^{(r_1)}(t)}{dt}}+a{x}_1^{(r_1)}(t)={\displaystyle \sum _{i=2}^N{a}_i[x_i^{(r_i)}(t)}]+b_1{[\ln (t)]}^{\beta }+b_2$$

(5)

where $\ln (t)$ is the logarithmic conditioning term we add, and at the same time, to enhance the model’s ability to handle nonlinear problems, an index $\beta$ is assigned to this term.

The following discretizes the model. The discrete grey model can be constructed using the approximation of the derivative. Therefore, the first-order derivative ${\displaystyle \frac{d{x}_1^{(r_1)}(t)}{dt}}$ in Formula (5) can be approximately expressed as:

$${\displaystyle \frac{d{x}_1^{(r_1)}(t)}{dt}}\approx \underset{\mathrm{\Delta }t\to 1}{\lim }{\displaystyle \frac{x_1^{(r_1)}(t)-x_1^{(r_1)}(t-\mathrm{\Delta }t)}{\mathrm{\Delta }t}}=x_1^{(r_1)}(t)-x_1^{(r_1)}(t-1)$$

After sorting, Formula (5) becomes:

$$x_1^{(r_1)}(t)=\rho x_1^{(r_1)}(t-1)+{\displaystyle \sum _{i=2}^N{\tau }_i{x}_i^{(r_i)}(t)}+{\xi }_1{[\ln (t)]}^{\beta }+{\xi }_2$$

(6)

where $\rho ={\displaystyle \frac{1}{1+a}}$, ${\tau }_i={\displaystyle \frac{a_i}{1+a}}$, ${\xi }_i={\displaystyle \frac{b_i}{1+a}}$.

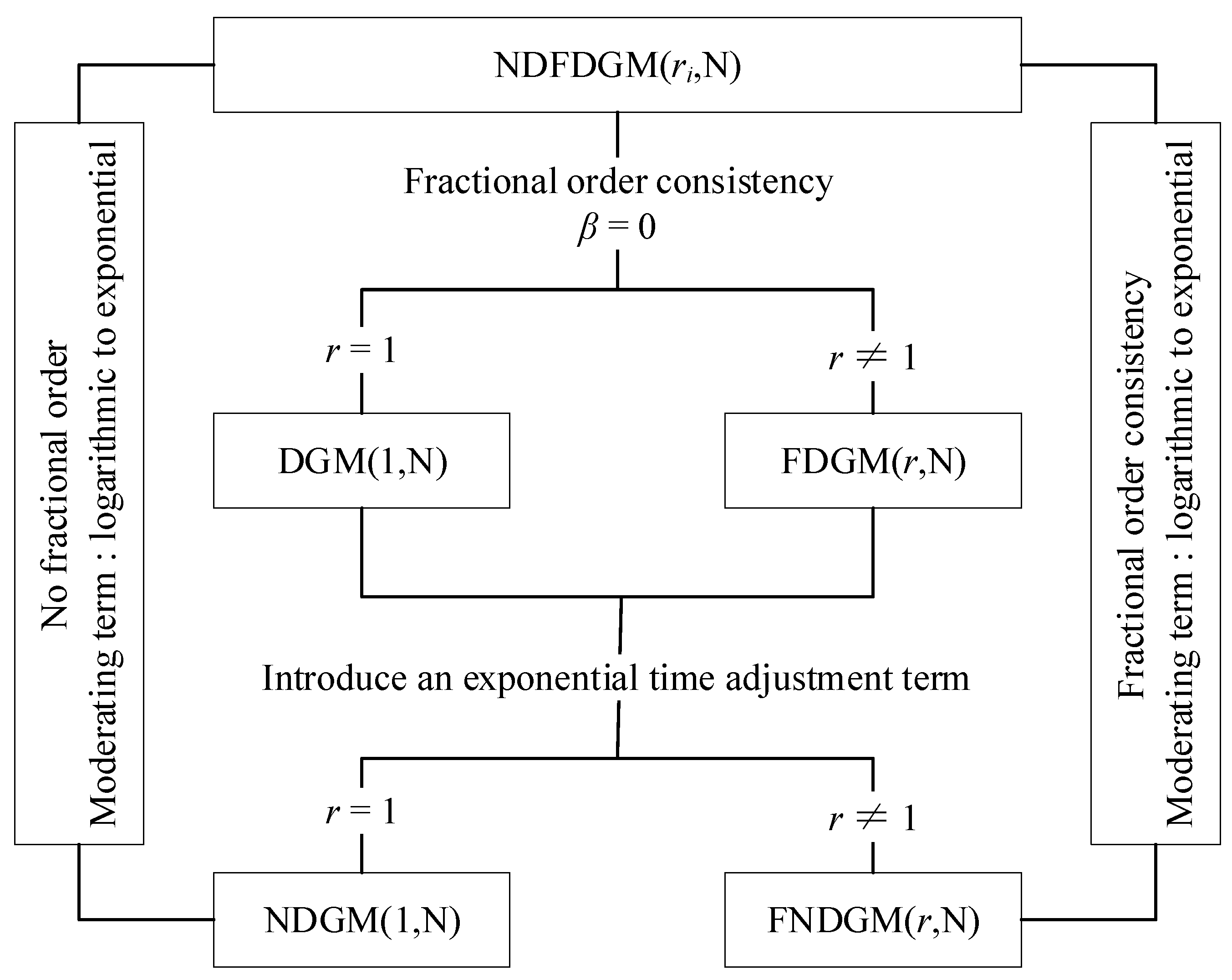
To sum up, Equation (6) is the expression of the nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N). In order to clarify the mathematical structure and evolution mechanism of the NDFDGM model more clearly, its model degradation tree is shown in Figure 1, systematically presenting the progressive relationship among models under different parameter Settings.

It can be seen from Figure 1 that the main innovation point of the model proposed in this paper compared with other basic models lies in: (1) The consistency problem of fractional parameters of variables; (2) The form of the adjustment term. When there are no fractional and nonlinear adjustment terms, the model degenerates into the most fundamental DGM(1,N). When the fractional order is consistent and there is no linear moderating term, the model degenerates into FDGM(r,N). When there is no fractional order and the moderating term is exponential, the model degenerates into NDGM(1,N). When the fractional order is consistent and the moderating term is exponential, the model degenerates into FNDGM(r,N). To sum up, in this paper, DGM(1,N), FDGM(r,N), NDGM(1,N), and FNDGM(r,N) are selected as comparison models to verify the prediction performance of the proposed NDFDGM(r_i,N) model.

2.3. The Solution Process of the Nonlinear Different Fractional Discrete Grey Multivariate Model NDFDGM(r_i,N)

From the above derivation, it can be known that if the parameters of the nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N) are known, the solution of the model can be obtained and the final prediction result can be obtained. The parameters of the NDFDGM(r_i,N) model mainly include: (1) The inherent parameters $P={(\rho ,{\tau }_1,{\tau }_2,\cdots ,{\tau }_N,{\xi }_1,{\xi }_2)}^{\mathrm{T}}$ of the model; (2) Model hyperparameters, namely the fractional-order cumulative parameter r and nonlinear parameters. This chapter mainly discusses the solution methods of the inherent parameters of the model.

The inherent parameters $P={(\rho ,{\tau }_1,{\tau }_2,\cdots ,{\tau }_N,{\xi }_1,{\xi }_2)}^{\mathrm{T}}$ of the model can be obtained by the ordinary least square method.

$$\widehat{P}={(\widehat{\rho },{\widehat{\tau }}_1,{\widehat{\tau }}_2,\cdots ,{\widehat{\tau }}_N,{\widehat{\xi }}_1,{\widehat{\xi }}_2)}^T={(B^{T}B)}^{-1}{B}^{T}Y$$

(7)

where

$$B=\left[\begin{array}{cccccc}{x}_1^{(r_1)}(1)& x_2^{(r_2)}(2)& \cdots & x_N^{(r_N)}(2)& {(\ln 2)}^{\beta }& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_1^{(r_1)}(n-1)& x_2^{(r_2)}(n)& \cdots & x_N^{(r_N)}(n)& {(\ln n)}^{\beta }& 1\end{array}\right],Y=\left[\begin{array}{c}{x}_1^{(r_1)}(2)\\ ⋮\\ x_1^{(r_1)}(n)\end{array}\right].$$

In conclusion, the solution of the model parameters $P={(\rho ,{\tau }_1,{\tau }_2,\cdots ,{\tau }_N,{\xi }_1,{\xi }_2)}^{\mathrm{T}}$ has been completed. From Equation (7), we can obtain the estimated parameter vector of the model. Therefore, if we want to find the time response function of the NDFDGM(r_i,N) model, we only need to find the recursive formula. The time response of the nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N) can be recursively derived through Equation (6).

Theory 1.

Suppose a non-negative sequence $x_i^{(0)}$ is given. After obtaining the corresponding fractional accumulation generated sequence $x_i^{(r_i)}$ through Equation (1), the time response function used to predict the dependent variable sequence $x_1^{(r_1)}$ can be expressed in the following form:

$${\widehat{x}}_1^{(r_1)}(t)={\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}$$

(8)

 and its corresponding cumulative reduction expression is:

$${\widehat{x}}_1^{(0)}(t)={\displaystyle \sum _{i-1}^t\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)}\left\{{\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\right\}$$

(9)

Proof. 

From Equation (6), we can conclude:

$$x_1^{(r_1)}(t-1)=\rho x_1^{(r_1)}(t-2)+{\displaystyle \sum _{i=2}^N{\tau }_i{x}_i^{(r_i)}(t-1)}+{\xi }_1{[\ln (t-1)]}^{\beta }+{\xi }_2$$

$$x_1^{(r_1)}(t-2)=\rho x_1^{(r_1)}(t-3)+{\displaystyle \sum _{i=2}^N{\tau }_i{x}_i^{(r_i)}(t-2)}+{\xi }_1{[\ln (t-2)]}^{\beta }+{\xi }_2$$

By analogy, we have:

$$\begin{array}{l}{\widehat{x}}_1^{(r_1)}(t)=\widehat{\rho }{\widehat{x}}_1^{(r_1)}(t-1)+{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i{x}_i^{(r_i)}(t)}+{\widehat{\xi }}_1{[\ln (t)]}^{\beta }+{\widehat{\xi }}_2\\ \hspace{1em}\hspace{1em}\hspace{1em}=\widehat{\rho }\left\{\widehat{\rho }{\widehat{x}}_1^{(r_1)}(t-2)+{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i{x}_i^{(r_i)}(t-1)}+{\widehat{\xi }}_1{[\ln (t-1)]}^{\beta }+{\widehat{\xi }}_2\right\}+{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i{x}_i^{(r_i)}(t)}+{\widehat{\xi }}_1{[\ln (t)]}^{\beta }+{\widehat{\xi }}_2\\ \hspace{1em}\hspace{1em}\hspace{1em}={\widehat{\rho }}^2{\widehat{x}}_1^{(r_1)}(t-2)+{\widehat{\rho }}^1\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i{x}_i^{(r_i)}(t-1)}+{\widehat{\xi }}_1{[\ln (t-1)]}^{\beta }+{\widehat{\xi }}_2\right\}+{\widehat{\rho }}^0\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i{x}_i^{(r_i)}(t-0)}+{\widehat{\xi }}_1{[\ln (t-0)]}^{\beta }+{\widehat{\xi }}_2\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}=\cdots ={\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\end{array}$$

Finally, perform fractional cumulative reduction based on Equation (3), thereby obtaining:

$$\begin{array}{l}{\widehat{x}}_1^{(0)}(t)={[{\widehat{x}}_1^{(0)}(t)]}^{(-r)}={\displaystyle \sum _{i=1}^k\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)} {\widehat{x}}_1^{(r)}(t)\\ \hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \sum _{i-1}^t\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)}\left\{{\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\right\}\end{array}$$

Therefore, Equations (8) and (9) have been proved. □

2.4. The Unbiasedness of the Nonlinear Different Fractional Discrete Grey Multivariate Model NDFDGM(r_i,N)

Conducting unbiased analysis on the proposed nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N) is crucial for ensuring the reliability and accuracy of the model. Unbiasedness is a fundamental characteristic, which reflects the model’s ability to provide estimates and predictions without systematic errors. By conducting unbiased analysis, we can verify whether there are any consistency biases in the parameter estimation and prediction of the model, and thereby establish its credibility and robustness. In the following section, we will provide the proof of unbiasedness to verify the validity and feasibility of the model proposed in this paper.

Theory 2.

Suppose there exists a time series ${\{x_1^{(r_1)}(t)\}}_{t=1}^n$ that satisfies ${\widehat{x}}_1^{(r_1)}(t)={\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}$, $P={(\rho ,{\tau }_1,{\tau }_2,\dots ,{\tau }_N,{\xi }_1,{\xi }_2)}^{\mathrm{T}}$is a given parameter set. Then the output sequence ${\widehat{x}}_1^{(0)}(t)$ of the nonlinear different fractional discrete grey multivariate model NDFDGM(r_i,N) must satisfy ${\widehat{x}}_1^{(0)}(t)=x_1^{(0)}(t)$.

Proof. 

According to the hypothetical situation, we can obtain:

$$\begin{array}{c}{x}_1^{(r_1)}(t)-\rho x_1^{(r_1)}(t-1)={\rho }^{t-1}{x}_1^{(r_1)}(1)-\rho [{\rho }^{t-2}{x}_1^{(r_1)}(1)]+{\displaystyle \sum _{q=0}^{t-2}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q)}+{\xi }_1{[\ln (t-q)]}^{\beta }+{\xi }_2\right\}}\\ \hspace{1em}-\rho \left\{{\displaystyle \sum _{q=0}^{t-3}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q-1)}+{\xi }_1{[\ln (t-q-1)]}^{\beta }+{\xi }_2\right\}}\right\}\end{array}$$

In which ${\rho }^{t-1}{x}_1^{(r_1)}(1)-\rho [{\rho }^{t-2}{x}_1^{(r_1)}(1)]=0$; ${\displaystyle \sum _{q=0}^{t-2}{\rho }^q\cdot {\xi }_2}-\rho \cdot {\displaystyle \sum _{q=0}^{t-3}{\rho }^q\cdot {\xi }_2}={\xi }_2$, then:

$$\begin{array}{l}{x}_1^{(r_1)}(t)-\rho x_1^{(r_1)}(t-1)={\displaystyle \sum _{q=0}^{t-2}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q)}+{\xi }_1{[\ln (t-q)]}^{\beta }\right\}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\rho \left\{{\displaystyle \sum _{q=0}^{t-3}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q-1)}+{\xi }_1{[\ln (t-q-1)]}^{\beta }\right\}}\right\}+{\xi }_2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t)}+{\xi }_1{(\ln t)}^{\beta }+{\xi }_2\end{array}$$

In conclusion, the above equation is consistent with the model expression, and the above equation can also be written as $BP=Y$; therefore, we have $P=\stackrel{⏜}{P}$, then:

$$\begin{array}{l}{\widehat{x}}_1^{(r_1)}(t)={\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\\ \hspace{1em}\hspace{1em}\hspace{1em}={\rho }^{t-1}{x}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q)}+{\xi }_1{[\ln (t-q)]}^{\beta }+{\xi }_2\right\}}\\ \hspace{1em}\hspace{1em}\hspace{1em}=x_1^{(r_1)}(t)\end{array}$$

Namely:

$$\begin{array}{l}{\widehat{x}}_1^{(0)}(t)={[{\widehat{x}}_1^{(0)}(t)]}^{(-r)}={\displaystyle \sum _{i=1}^k\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)} {\widehat{x}}_1^{(r)}(t)\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\displaystyle \sum _{i-1}^t\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)}\left\{{\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\right\}\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}={\displaystyle \sum _{i-1}^t\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)}\left\{{\rho }^{t-1}{x}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\rho }^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\tau }_i\cdot x_i^{(r_i)}(t-q)}+{\xi }_1{[\ln (t-q)]}^{\beta }+{\xi }_2\right\}}\right\}\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}=x_1^{(0)}(t)\end{array}$$

In this way, the proof is completed. □

3. Search for the Fractional Parameter $r_i$ and Nonlinear Parameter $\beta$ of the Nonlinear Different Fractional Discrete Grey Multivariate Model NDFDGM(r_i,N)

Except for the parameter vector P, both the fractional order r_i and the nonlinear parameter $\beta$ have significant influences on the prediction performance and accuracy of the model. This chapter mainly discusses the optimization process of fractional cumulative parameters r_i and nonlinear parameter $\beta$. Due to the existence of hyperparameters, it is difficult to solve this model by traditional methods. Therefore, this paper chooses to use the Firefly Algorithm (FA) to search for the optimal value of parameters (the situation of parameter settings is as follows: Population size = 50; Maximum iterations = 1000; Initial attractiveness coefficient = 1.0; Randomization disturbance factor = 0.5; Step attenuation coefficient = 0.98; Distance attenuation factor = 1.0; Dimensionality = 4; Parameter variables include $r_1$, $r_2$, $r_3$, $\beta$).

To ensure optimal model performance, the hyperparameters should be calibrated to minimize the model’s fitting error. Accordingly, this study adopts an optimization framework centred on minimizing the Mean Absolute Percentage Error (MAPE) to maximize the predictive accuracy of the proposed model given the available data. Formally, this reduces to solving a constrained optimization problem, where (1) the objective function seeks to minimize the model’s simulation error (quantified by MAPE) by adjusting the hyperparameters. (2) The constraints are derived from the structural assumptions and modelling procedures inherent to the proposed framework.

This approach ensures that the model not only achieves the best possible fit to the training data but also adheres to its theoretical foundations. The optimization problem is transformed into mathematical language as follows:

$$\underset{(r_i, \beta )}{\min }MAPE={\displaystyle \frac{1}{n-1}}{\displaystyle \sum _{t=2}^n\left|\frac{{\widehat{x}}_1^{(0)}(t)-x_1^{(0)}(t)}{x_1^{(0)}(t)}\right|}\times 100\%$$

(10)

$$s.t.\left\{\begin{array}{l}\widehat{P}={(\widehat{\rho },{\widehat{\tau }}_1,{\widehat{\tau }}_2,\dots ,{\widehat{\tau }}_N,{\widehat{\xi }}_1,{\widehat{\xi }}_2)}^T={(B^{T}B)}^{-1}{B}^{T}Y\\ r_i\in [0,1],i=1,2,3; \beta \in [-5,5]\\ {\widehat{x}}_1^{(0)}(t)={\displaystyle \sum _{i-1}^t\left(\begin{array}{c}t-i-r-1\\ t-i\end{array}\right)}{\widehat{x}}_1^{(r_1)}(t)\\ {\widehat{x}}_1^{(r_1)}(t)={\widehat{\rho }}^{t-1}{\widehat{x}}_1^{(r_1)}(1)+{\displaystyle \sum _{q=0}^{t-2}{\widehat{\rho }}^q\cdot \left\{{\displaystyle \sum _{i=2}^N{\widehat{\tau }}_i\cdot x_i^{(r_i)}(t-q)}+{\widehat{\xi }}_1{[\ln (t-q)]}^{\beta }+{\widehat{\xi }}_2\right\}}\end{array}\right.$$

In this paper, the Firefly Algorithm is selected for parameter tuning. FA The firefly algorithm was first proposed by Xin-She Yang from the University of Cambridge in the UK in 2008 [40]. It is an optimization algorithm based on swarm intelligence, and its inspiration comes from the luminescence behaviour and mutual attraction mechanism of fireflies in nature. This algorithm solves the multi-objective optimization problem by simulating the luminance attraction and movement process among individual fireflies. The core idea is to regard each solution in the search space as a firefly. The position of each firefly represents a potential solution, and its brightness indicates the objective function value of that solution. Bright fireflies have a stronger attraction to other fireflies, and the attraction decreases with the increase in distance. This mechanism enables fireflies to dynamically adjust their positions during the search process, thereby gradually approaching the global optimal solution [41]. Therefore, we can summarize the following features. Firstly, by simulating the mutual attraction mechanism among fireflies, FA can explore the solution space on a global scale and avoid getting trapped in local optimal solutions [42]. Secondly, the mathematical model of this algorithm is simple and easy to understand and implement. In addition, through the dynamic adjustment of the step size factor and the light absorption coefficient, the algorithm can balance the capabilities of global search and local search [43]. Furthermore, FA is applicable to both continuous and discrete optimization problems, and is capable of handling multi-objective optimization problems, with strong flexibility [44].

There are already many recent algorithms have been applied for modelling of fractional order system. To further illustrate the rationality of choosing the Firefly algorithm in this paper, the Firefly algorithm is compared with several commonly used meta-heuristic algorithms in multiple dimensions. The specific results are shown in

Table 1. Convergence and Computational Performance Comparison among FA, ALO, GOA and MFO.

Algorithm	Convergence Speed	Multimodal Problem Performance	Parameter Sensitivity	Computational Complexity
Firefly Algorithm (FA)	Fast (Attraction mechanism provides clear search direction; random perturbation avoids stagnation)	Excellent (Dynamic adjustment of search scope enables effective escape from local optima)	$\mathrm{Low} (\mathrm{only} \alpha /\gamma$ needed)	Low (O(N2) with parallel potential)
Ant Lion Optimizer (ALO)	Medium (dependent on parameter adjustment)	Medium (requires niching’s technical assistance)	High (sensitive to trap size)	Medium (O(N2))
Grasshopper Optimization Algorithm (GOA)	Slower (prone to getting stuck in local optimum)	Poor (prone to clustering on a single peak)	High (social factors sensitive)	High (O(N2))
Moth-Flame Optimization (MFO)	Medium (prone to fluctuation in the later stage)	Medium (The number of flames affects diversity)	Medium (convergence parameters sensitive)	Medium (O(N2))

.

In conclusion, FA performs well in model hyperparameter search with its unique global search ability and flexible dynamic adjustment mechanism. Compared with ALO, GOA and MFO, the convergence speed of FA is fast and the Performance of Multimodal Problem is excellent. Moreover, the parameters of FA only need to be adjusted to $\alpha$ and $\gamma$, making it easier to optimize. It also has strong robustness and is not sensitive to the initial solution, maintaining stable performance even in a noisy environment. Furthermore, FA can not only effectively avoid local optimal solutions, but also achieve efficient global search through simple mathematical models [42,45]. This advantage makes it an ideal choice for the optimization of discrete fractional-order grey multivariate prediction models.

By utilizing FA to solve the aforementioned optimization problems, the hyperparameters for modelling can be obtained. It is worth noting that it is particularly important to find the global optimal solution during the experiment. Based on the principle of precision priority, this paper selects the parameter combination that makes the MAPE of the simulated value the smallest as the optimal solution. The pseudocode determined for MPA is shown in Algorithm 1.

Algorithm 1 Optimization of ri and β with Firefly Algorithm

Input: f: Objective function, M: number of fireflies, a0: maximum attractiveness, γ: absorption coefficient, α: step size, T: maximum number of iterations Output: Optimized parameters ri and β 1: Initialize the firefly population xm for m = 1, 2, …, M, according to the search ranges of ri and β 2: Initialize parameters: a0, γ, α 3: For each firefly xm, compute its brightness Im = f(xm) 4: Initialize the global optimal solution x* = argmin(Im) 5. for t = 1 to T do 6:    for m = 1 to M do 7:      for j = 1 to M do 8:        if Ij > Im then $9:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Compute} \mathrm{the} \mathrm{distance} \mathrm{between} \mathrm{fireflies} m \mathrm{and} j: r=\sqrt{{\displaystyle {\sum }_{d=1}^D{(x_{m,d}-x_{j,d})}^2}}$ 10:         Compute the attractiveness: a = a0$e^{-\gamma r^2}$ 11:         Update the position of firefly m: xm = xm + a(xj − xm) + α(rand()−0.5) 12:         Ensure xm remains within the search space (boundary handling) 13:         Compute the light intensity at the new position: Im = f(xm) 14:      end if 15:    end for 16:   end for 17:   Update the global optimal solution x* = argmin(Im) and Update parameter α 18: end for 19: Return: global optimal solution ri and β

To sum up, once the optimal hyperparameters of the model are obtained through the above search process, and combined with Equations (7)–(9), the final prediction result of the model proposed in this paper can be calculated.

Based on the above theoretical derivation, to enhance the visual expression of the model construction process, Figure 2 elaborately depicts the implementation process of the model in the form of a standardized flowchart, gradually analyzes the modelling steps, and fully presents the key steps from data preprocessing, parameter optimization to prediction verification to ensure the transparency and reproducibility of the methodology, thereby providing a clear methodological basis for the subsequent empirical analysis.

4. Model Test

This section presents an empirical evaluation of the nonlinear different fractional discrete grey multivariate model (NDFDGM(r_i,N)) through its application to regional energy consumption patterns across China’s eastern, central, and western regions. To comprehensively assess the model’s performance, we conduct a comparative analysis against established multivariate grey models, including DGM(1, N), FDGM(r, N), NDGM(1, N) and NFDGM(r, N). This systematic comparison serves to validate both the predictive accuracy and theoretical advancement of NDFDGM(r_i,N). In this paper, the data of the original dataset from 2000 to 2019 is selected for training the model. The 2020–2022 data is used as a test set to check the model’s predictive performance. The detailed information of raw datasets is shown in

Table 2. Raw data information of three cases.

NO.	Name	Data Range
		Modelling	Testing
Case 1	The total energy consumption in the eastern region of China	From 2010 to 2019	From 2020 to 2022
Case 2	The total energy consumption in the central region of China
Case 3	The total energy consumption in the western region of China

Data source: China Statistical Yearbook and Statistical Yearbooks of various provinces.

.

4.1. Selection of Model Indicators

In production and daily life, the use of energy has multi-dimensional characteristics, so the factors influencing the total energy consumption are complex and diverse. According to the theory of energy economics, the intricate interdependence between energy systems and socioeconomic progress has been extensively documented in scholarly research. A comprehensive review of academic literature reveals that energy consumption patterns are shaped by multiple interrelated determinants, which leading experts have systematically categorized according to several key dimensions: economic factors, population factors, industrial structure, technological progress and social development. Due to the differences in research perspectives, research objects and methods, the selection of specific indicators in various aspects also varies. From an economic perspective, Gross Domestic Product (GDP) serves as a fundamental metric for assessing economic performance, exhibiting a robust and well-documented interdependence with energy consumption patterns. Population factors also play an important role in energy consumption. The increase in population size directly leads to the rise in energy demand, while changes in population structure, such as ageing, urbanization and changes in family size, may indirectly affect energy consumption by influencing consumption patterns and lifestyles. The industrial structure is another key factor influencing energy consumption. The industrial sector usually has a relatively high energy consumption intensity, so the adjustment of the industrial structure has an important impact on energy consumption. Technological progress is playing an increasingly important role in energy consumption. With the continuous advancement of energy technology, energy utilization efficiency has been significantly improved, thereby reducing energy waste. Meanwhile, technological progress can also influence the total amount of energy consumption by enhancing energy production efficiency and reducing energy costs. The level of social development also has a profound impact on energy consumption. With the development of society, the lifestyles and consumption concepts of residents have changed, which may prompt the adjustment of the energy consumption structure.

In conclusion, based on the above five aspects, this paper selects representative indicators from each aspect, respectively, for grey relational analysis, and screens the indicators with relatively high correlation to the total energy consumption for subsequent modelling. The results of its grey relational analysis are shown in

Table 3. Results of grey relational degree for each indicator.

NO.	GDP	Urbanization Level	Total Population	The Proportion of R&D Expenditure in GDP	The Proportion of the Added Value of the Secondary Industry in GDP	The Proportion of the Added Value of the Tertiary Industry in GDP	The Added Value of the Secondary Industry	The Added Value of the Tertiary Industry
Case 1	$>0.7$	$>0.8$	$>0.8$	$>0.8$	$<0.7$	$>0.7$	$>0.7$	$>0.7$
Case 2	$>0.7$	$>0.8$	$>0.7$	$>0.7$	$<0.7$	$>0.7$	$>0.7$	$>0.7$
Case 3	$>0.7$	$>0.8$	$>0.8$	$>0.8$	$<0.7$	$<0.7$	$>0.7$	$>0.7$

.

According to the results of the grey relational degree, among the three cases, the indicator whose grey relational degree is all greater than 0.8 is only the urbanization level. And the grey relational degrees of GDP, total population, the proportion of R&D expenditure in GDP, the added value of the secondary industry and the added value of the tertiary industry are all above 0.7. After eliminating the multicollinearity influence among the indicators, this paper selects GDP and urbanization level as the influencing factors for the modelling of the prediction model. Due to the different data dimensions of the total energy consumption and the indicators of GDP and urbanization level, there are significant differences in the order of magnitude. Therefore, in order to eliminate the influence brought by the differences in data dimensions and units, this paper first standardizes the data using the maximization method before modelling to improve the predictive performance and generalization ability of the model.

4.2. Case 1: Forecast of the Total Energy Consumption in Eastern China

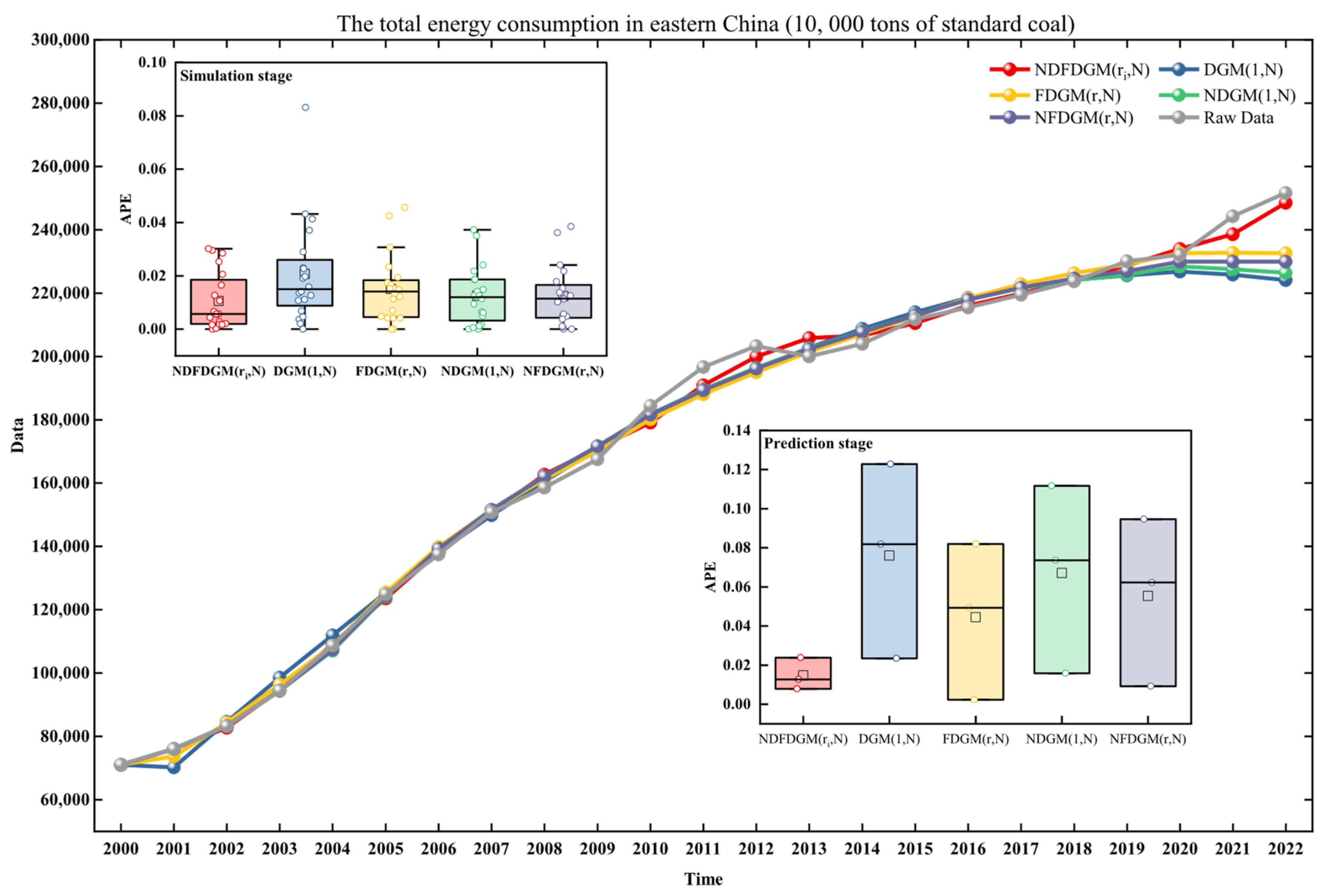
The eastern region serves as China’s primary energy consumption hub, representing a disproportionately large share of national energy demand. This consumption pattern exhibits strong correlation with regional economic development levels, particularly evident in major coastal economic zones. The Beijing-Tianjin-Hebei metropolitan cluster, Yangtze River Delta, and Pearl River Delta regions demonstrate particularly intensive energy usage patterns, reflecting distinct spatial concentration characteristics in China’s energy consumption geography. In conclusion, as the main area of energy consumption, the optimization of the energy structure in the eastern region is of great significance to the national energy transition. The raw data and prediction results of grey models are shown in Figure 3 and evaluation metrics and parameters values are shown in

Table 4. The parameters values and evaluation metrics of the grey models in the energy consumption forecast of the eastern region of China.

Model	Evaluation Metrics		Parameters Values
	MAPEsim (%)	MAPEpre (%)	${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	$\mathit{\beta }$
DGM	2.0377	6.9328	1.0000	1.0000	1.0000	0.0000
FDGM	1.5748	4.1715	0.0712	0.0712	0.0712	0.0000
NDGM	1.3140	6.1551	1.0000	1.0000	1.0000	0.8264
FNDGM	1.2917	5.1415	0.6332	0.6332	0.6332	0.0024
NDFDGM	1.1152	1.4585	0.0001 × 10−2	0.9999	0.9795	2.4427

.

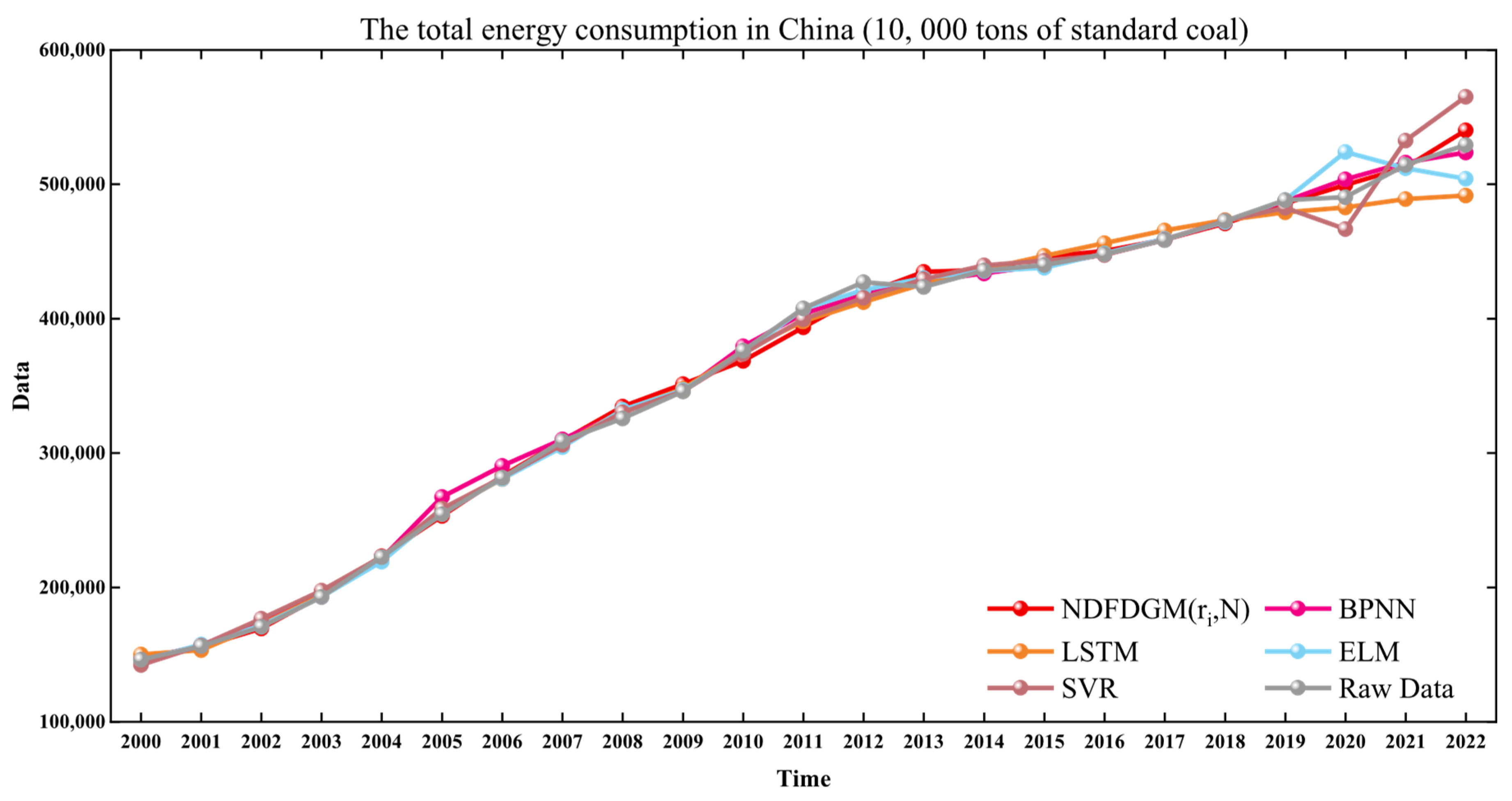
It is found from Figure 3 that, compared with other models, the predicted value curve of the model in this paper is the closest to the trend of the true value curve, which proves that the model has better simulation and prediction performance. From Table 4, we can also further verify this conclusion from the perspective of error. The simulation MAPE of the model in this paper is 1.1152%, and the prediction MAPE is 1.4585%. Compared with the other four models, these two errors are the smallest, which proves that NDFDGM(r_i,N) has small simulation and prediction errors and performs well in the prediction of eastern region’s energy consumption.

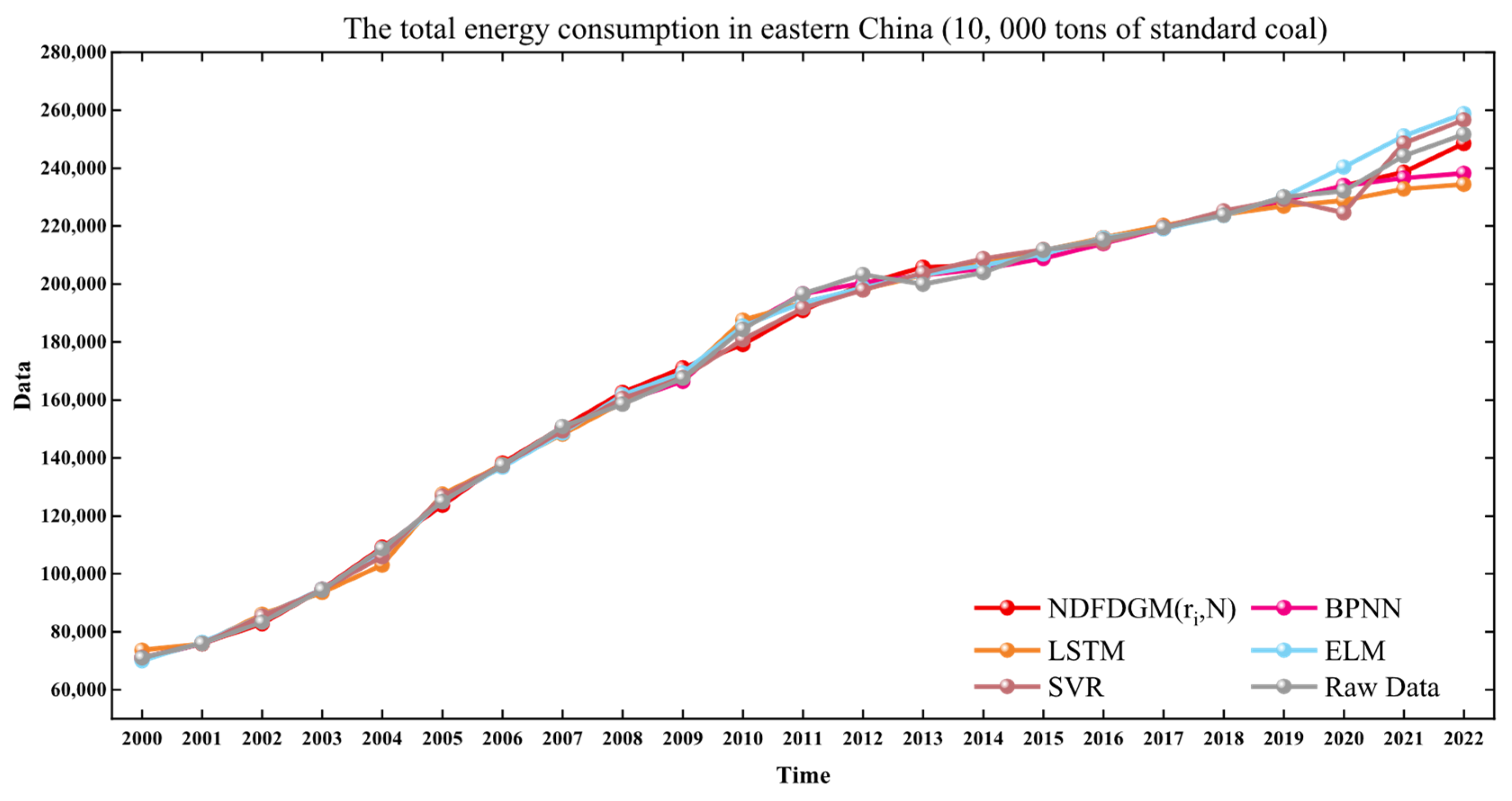
In order to more comprehensively evaluate the advantages and disadvantages of the innovative grey model in this paper, clarify its applicability, and enhance the credibility of the prediction conclusion, it is also necessary to compare this model with non-grey models. This paper selects four commonly used non-grey models: BPNN, LSTM, ELM and SVR for comparison. The prediction curves are shown in Figure 4, and the error situations are presented in

Table 5. The evaluation metrics of the non-grey models in the energy consumption forecast of the eastern region of China.

Model	MAPEsim (%)	MAPEpre (%)
BPNN	31.1060	3.8521
LSTM	1.1379	4.4566
ELM	31.1741	3.0389
SVR	1.1230	2.3292
NDFDGM	1.1152	1.4585

.

It can also be found from Figure 4 that the performance differences of the five models in the prediction stage are relatively obvious. Among them, the prediction curve of NDFDGM is the closest to the true value curve, while the prediction values of BPNN and LSTM are relatively low, and those of ELM and SVR are relatively high. The error data analysis in Table 5 also proves that NDFDGM performs the best. The predicted MAPE of NDFDGM is the smallest, while the MAPE of the other four models is all above 2%.

In conclusion, whether compared with the grey model in terms of difficulty or with the mainstream non-grey models, the NDFDGM in this paper has achieved the highest prediction accuracy, demonstrating its powerful predictive ability and applicability.

4.3. Case 2: Forecast of the Total Energy Consumption in Central China

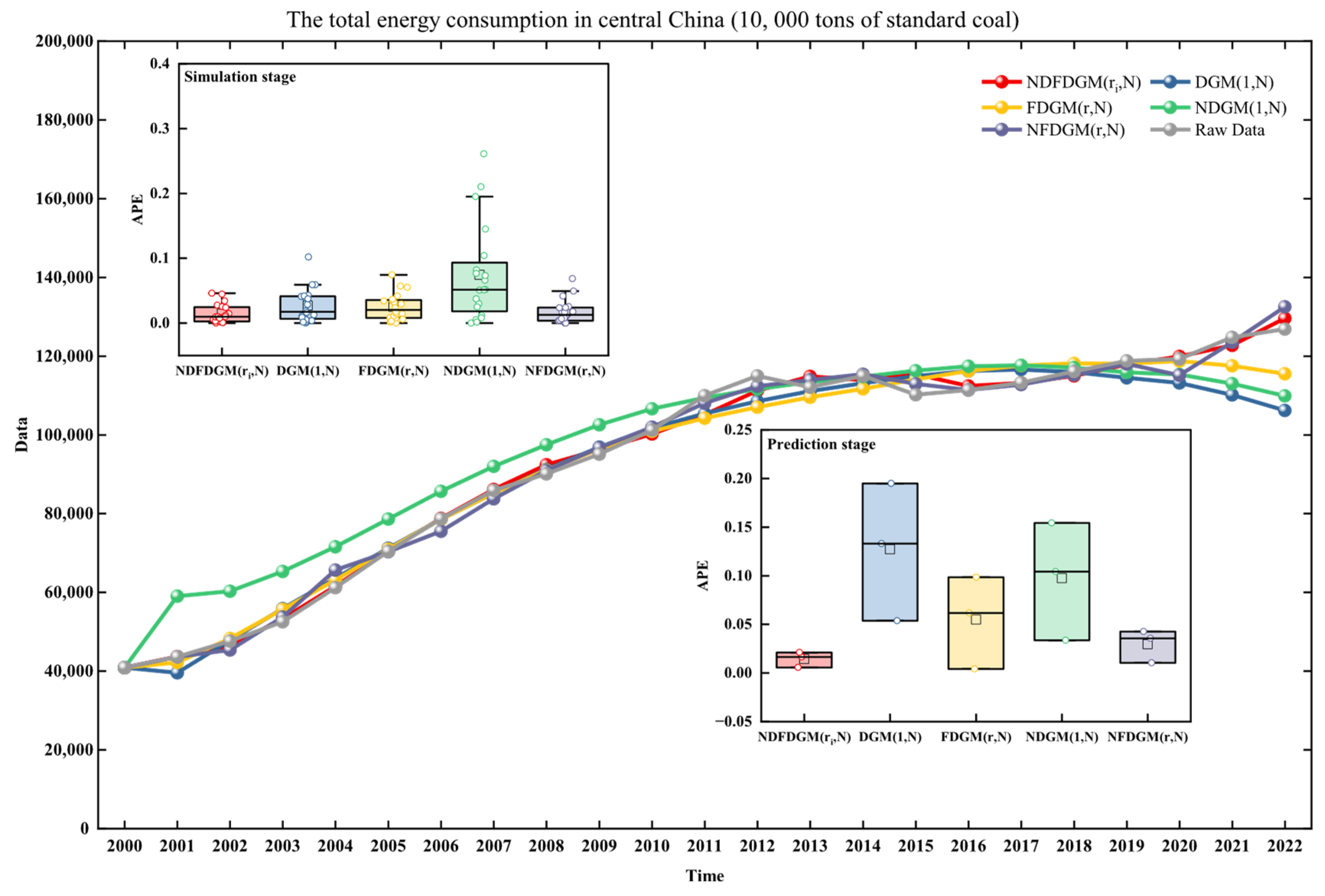
With the advancement of urbanization and industrialization, the energy demand in the central region has continued to increase, but the growth rate has slowed down somewhat. In addition, energy consumption in the central region is closely related to economic growth. As an energy-intensive area and an important hub connecting the east and the west, the prediction of the central region’s total energy consumption is crucial for achieving the “dual carbon” goals, and is conducive to promoting coordinated regional development. The raw data and model prediction results are shown in Figure 5 and evaluation metrics and parameters values are shown in

Table 6. The parameters values and evaluation metrics of the grey models in the energy consumption forecast of the central region of China.

Model	Evaluation Metrics		Parameters Values
	MAPEsim(%)	MAPEpre (%)	${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	$\mathit{\beta }$
DGM	2.6592	11.0475	1.0000	1.0000	1.0000	0.0000
FDGM	2.6304	5.0696	0.1623	0.1623	0.1623	0.0000
NDGM	9.2222	8.6866	1.0000	1.0000	1.0000	0.0001 × 10−2
FNDGM	1.8235	2.9733	0.5906	0.5906	0.5906	0.8004
NDFDGM	1.5164	1.4496	0.0001 × 10−2	0.9999	0.8343	2.2784

.

It can be found from Figure 5 that the predicted value curve of NDGM differs greatly from the true value. The performances of DGM and FDGM are relatively similar, but the predicted value curves of FNDGM and the model NDFDGM in this paper are closer to the true value curves and perform better. From Table 6, we can further analyze the effects of the five models from the perspective of error. The simulation mean absolute percentage error of the model in this paper is 1.5164%, and the prediction mean absolute percentage error is 1.4496%. In terms of simulation performance, the errors of the four models except NDGM are not much different, but the error of NDFDGM is smaller. The errors of the five models in terms of prediction performance vary greatly. The error of DGM is the largest, but the errors of the models NDFDGM in this paper are still the smallest.

The prediction curves comparing the model results of this paper with BPNN, LSTM, ELM and SVR are shown in Figure 6, and the error situations are presented in

Table 7. The evaluation metrics of the non-grey models in the energy consumption forecast of the central region of China.

Model	MAPEsim (%)	MAPEpre (%)
BPNN	28.6381	4.7458
LSTM	2.0005	4.7081
ELM	28.1856	1.8212
SVR	1.6040	7.6863
NDFDGM	1.5164	1.4496

.

Figure 6 shows that SVR fluctuates greatly in the central energy prediction, the overall predicted value of LSTM is relatively low, and the prediction results of ELM and NDFDGM are both relatively close to the true value. Therefore, in order to more accurately compare the prediction performance of ELM and NDFDGM, the errors of each model were calculated (Table 7). From the perspective of errors, it can be clearly stated that the error of NDFDGM is the smallest, about 0.4% lower than that of ELM, while the errors of the other three models are all above 4%. Therefore, it can be indicated that NDFDGM (r_i,N) has a good performance in this case.

4.4. Case 3: Forecast of the Total Energy Consumption in Western China

Geographical limitations and economic development disparities have historically constrained the expansion of energy consumption in China’s western region. Nevertheless, as the national Western Development Strategy gains momentum through sustained policy implementation and infrastructure investments, this region is projected to experience a substantial acceleration in energy demand growth, potentially reshaping its energy consumption trajectory in the coming decades. With the advancement of China’s “dual carbon” goals, the western region, as an area rich in energy resources, has seen the evolution of its energy consumption structure and total amount become a research focus. By predicting the total energy consumption, energy security can be provided for the economic development of the western region and regional coordinated development can be promoted. The raw data and model prediction results are shown in Figure 7 and evaluation metrics and parameters values are shown in

Table 8. The parameters values and evaluation metrics of the models in the energy consumption forecast of the western region of China.

Model	Evaluation Metrics		Parameters Values
	MAPEsim(%)	MAPEpre (%)	${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	$\mathit{\beta }$
DGM	2.0260	2.7848	1.0000	1.0000	1.0000	0.0000
FDGM	2.1327	2.7848	0.9999	0.9999	0.9999	0.0000
NDGM	1.8747	2.8523	1.0000	1.0000	1.0000	0.6652
FNDGM	1.2149	8.0600	0.7723	0.7723	0.7723	0.9999
NDFDGM	0.9041	2.0673	0.0001 × 10−2	0.0001 × 10−2	0.5000	1.9375

.

As can be seen from Figure 7, the results of the five models are relatively close in the simulation stage, but in the prediction stage, the result of FNDGM deviates more from the true value compared with other models. A closer examination of each model’s simulation and forecasting accuracy reveals that, according to the error data in Table 8, the NDFDGM model proposed in this study stands alone in achieving a simulation error below 1%, which is 0.9041%, while the errors of the other four comparison models are all above 1.2%. Except for the relatively high prediction error of FNDGM, the errors of the other models are relatively close. However, the prediction error result of NDFDGM is still the smallest, which is about 0.7% lower than the error results of the other three models.

The prediction curves comparing the model results of this paper with BPNN, LSTM, ELM and SVR are shown in Figure 8, and the error situations are presented in

Table 9. The evaluation metrics of the non-grey models in the energy consumption forecast of the western region of China.

Model	MAPEsim (%)	MAPEpre (%)
BPNN	38.2481	3.5935
LSTM	1.5199	4.0908
ELM	38.2238	3.4140
SVR	0.9235	9.7106
NDFDGM	0.9041	2.0673

.

It can be found from Figure 8 and Table 9 that both NDFDGM and SVR perform well in the fitting stage, but the error of SVR is relatively large in the prediction stage. However, the performance of the other three models, whether in the fitting stage or the prediction stage, is inferior to that of NDFDGM. This significant margin underscores the model’s reliability and effectiveness in forecasting total energy consumption across China’s western region, solidifying its superior performance.

4.5. Short Summary of the Case Studies

Based on the findings discussed earlier, this subsection provides an overview of the accuracy levels demonstrated by the grey models examined in the previous case studies. The performance rankings of these models, alongside those from relevant referenced models for each case, are visualized in Figure 9.

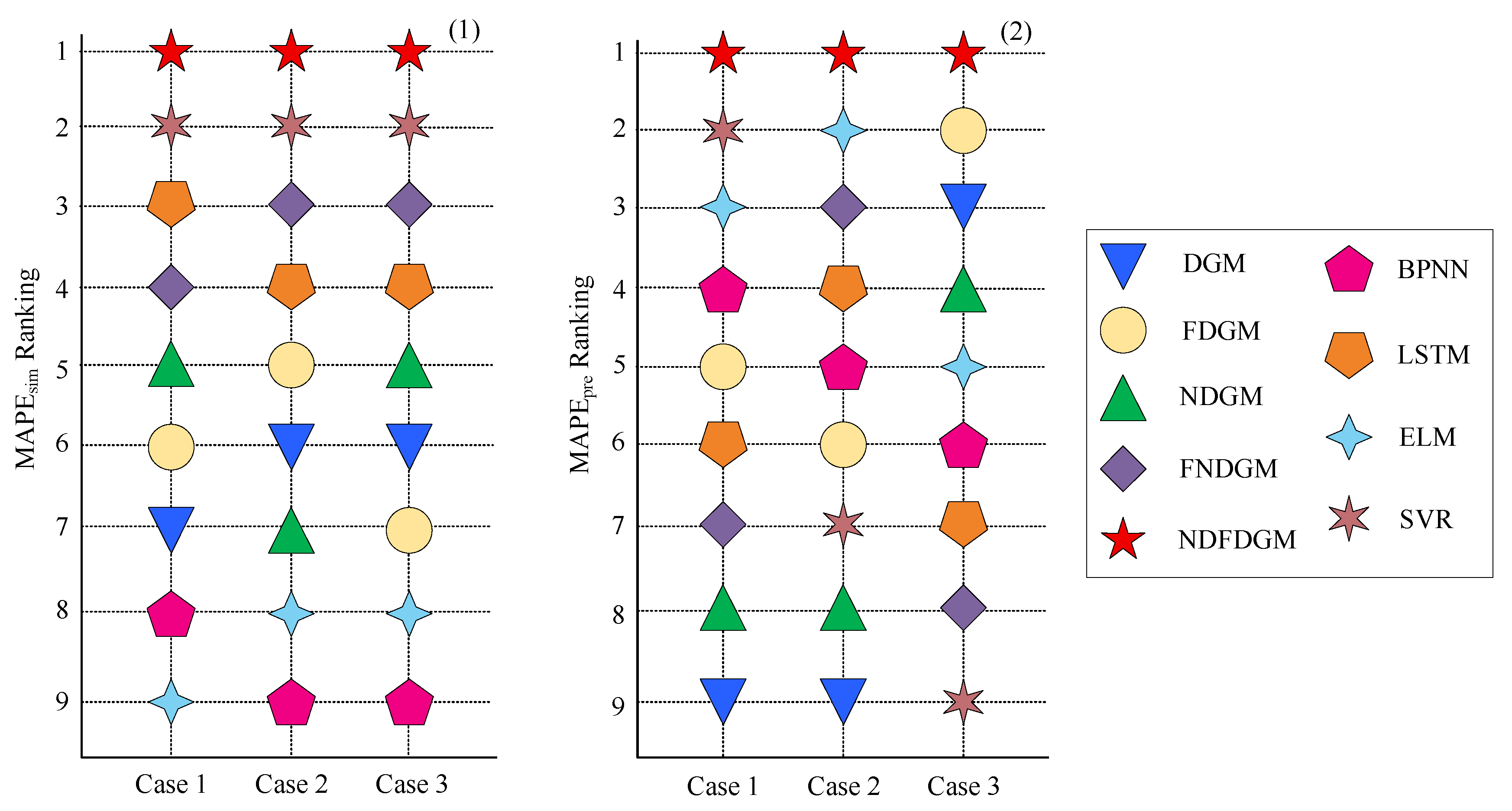
Figure 9 compares the MAPE situations of a total of nine models in the above three cases. Figure 9(1) shows the simulation stage, and Figure 9(2) shows the prediction stage. (1) In the simulation stage, NDFDGM ranked first among the three cases, and ELM (Case 1) and BPNN (Case 2, 3) ranked ninth respectively; (2) In the prediction stage, NDFDGM ranked first among the three cases, and DGM (Case 1, Case 2) and SVR (Case 3) ranked ninth respectively. Based on the comprehensive performance of each model in the two stages, it is found that NDFDGM (indicated by the red five-pointed star) ranked 1 in all cases evaluated by the two error indicators, demonstrating the most outstanding and stable performance. This indicates that the model has always been leading in the MAPE rankings of simulation and prediction, with high simulation and prediction accuracy. The rankings of both other grey models and non-grey models fluctuate greatly under different cases and different types of evaluations. For example, in the grey model, FDGM (indicated by the yellow circle) is named 6 in Case 1, 5 in Case 2, and 7 in Case 3 under the simulation error assessment. Under the prediction error assessment, the ranking is 5 in Case 1, 6 in Case 2, and in Case 3, the ranking is 2. For another example, FNDGM (represented by the purple diamond) performed relatively stably in all cases under the simulation error assessment, with a ranking of 3 in cases 2 and 3, and ranking in Case 1 is 4. However, its performance under the prediction error assessment varied greatly. It ranked 7 in Case 1, 3 in Case 2, and 8 in Case 3. Among the non-grey models, the SVR model (represented by a brown hexagonal star) performed very stably during the simulation stage, ranking 2nd in all three cases, outperforming other grey models in comparison but not exceeding the model proposed in this paper. However, their performance under the evaluation of prediction errors varies greatly. Case 1 ranks second, Case 2 ranks seventh, and Case 3 ranks ninth. In contrast to the SVR model, the ELM model (indicated by the blue four-pointed star) performs poorly in the simulation stage. In the three cases, the simulation error ranks among the bottom two of all models, while the prediction accuracy is at an upper-middle level. However, the error is still higher than that of the NDFDGM model. In summary, it reflects that the adaptability of these four comparison grey models and four comparison non-grey models to case scenarios and simulation or prediction evaluations is different, and their general adaptability is not as good as that of the NDFDGM proposed in this paper.

To verify that the Firefly algorithm used in this paper is the best method for searching the model’s hyperparameters, we also employed three other different intelligent algorithms (ALO, MFO and GOA) to search for the optimal hyperparameters of the model. All of them took the predicted MAPE as the evaluation index. The comparison results obtained are shown in

Table 10. Comparison of the results of four algorithms based on MAPE_pre (%).

Algorithm	Case 1	Case 2	Case 3
FA	1.4585	1.4496	2.0673
ALO	4.4280	7.5310	2.2134
GOA	5.3998	11.1430	4.8629
MFO	1.4499	8.5105	3.6639

.

It can be found through the data comparison in Table 10 that in Case 1, the prediction errors of FA and MFO are relatively close, both being about 1.45%, and they perform better compared to the other two algorithms. In Case 3, FA and ALO performed in the top two positions. The error of FA was approximately 0.15% lower than that of ALO. However, in Case 2, the errors of the four algorithms vary greatly, and the performance of FA is far superior to the other three algorithms. Based on the comprehensive performance of the above three cases, we can conclude that FA is our optimal choice when searching for model hyperparameters.

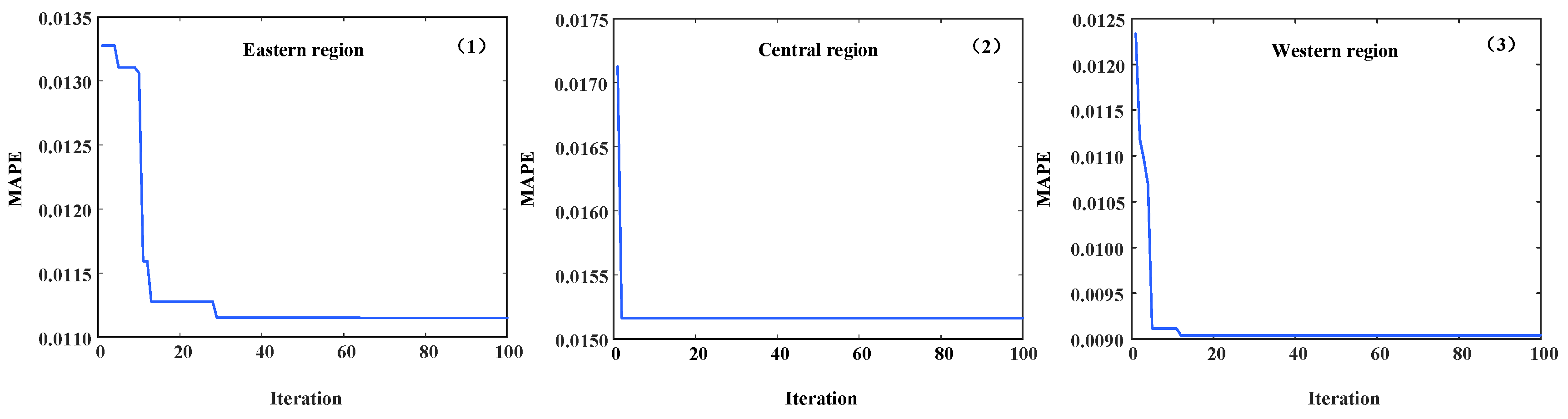
Figure 10 summarizes the FA iteration process of the NDFDGM model in three cases. Figure 10(1) The iterative convergence of FA in Case 1 achieves the minimum error within 30 iterations; Figure 10(2) FA converges to the minimum error within 20 iterations in Case 2; Figure 10(3) In Case 3, the iterative convergence of FA has the smallest error within 20 iterations. In conclusion, it is not difficult to find that FA satisfies the convergence rule in all three cases, proving that FA is applicable to the hyperparameter solution process of the NDFDGM model. Moreover, when the NDFDGM model reaches the minimum MAPE value in the three cases, the number of iterations does not exceed 20 times. This proves that the model can quickly obtain the optimal solution in various data environments. It further proves that the NDFDGM model proposed in this paper has good prediction accuracy and can be applied to the prediction process from multiple angles and in multiple environments. This further verifies the validity of the prediction results of the NDFDGM model in the above three cases.

Therefore, based on the above performances, we can conclude that NDFDGM has obvious advantages over other models in enhancing simulation and prediction accuracy and reducing MAPE. It can be chosen as a better option for the simulation and prediction analysis of relevant total energy consumption data, providing a reference for related research and improving the reliability of the results.

5. Model Application: Forecast of the Total Energy Consumption in China

5.1. The Validity of the NDFDGM(r_i,N) in Total Energy Consumption of China

In the cases of energy use prediction in China’s eastern, central and western regions, the NDFDGM model has shown good predictive ability, laying a solid foundation for subsequent research. Based on these verification results, we further apply the NDFDGM model to the empirical analysis of the total energy consumption prediction across the country. This application not only helps to verify the model’s suitability and precision on a larger scale, but also provides data support for energy planning at the national level. By analyzing the prediction results, we can better understand the energy consumption trends and identify supply-demand dynamics. This understanding offers critical insights for policymakers and industry stakeholders alike, ultimately aiding in the sustainable growth of China’s energy sector. The initial data alongside the model’s forecasted results are illustrated in Figure 11, and the evaluation metrics and parameter values are presented in

Table 11. The parameters values and evaluation metrics of the models in the energy consumption forecast of China.

Model	Evaluation Metrics		Parameters Values
	MAPEsim(%)	MAPEpre (%)	${\mathit{r}}_1$	${\mathit{r}}_2$	${\mathit{r}}_3$	$\mathit{\beta }$
DGM	1.9593	6.8625	1.0000	1.0000	1.0000	0.0000
FDGM	1.7962	4.3526	0.0454	0.0454	0.0454	0.0000
NDGM	1.3140	6.0553	1.0000	1.0000	1.0000	0.6249
FNDGM	1.3068	5.1202	0.7885	0.7885	0.7885	0.0091
NDFDGM	1.0648	1.4244	0.0001 × 10−2	0.8280	0.7878	2.1803

.

It can be seen from the line graph in Figure 11 that although the results of the five models fluctuated slightly in the simulation stage, the overall trend was relatively close to the true value, indicating that the performance of each model in the simulation stage was relatively stable. However, looking at the box plot from the simulation phase, it is clear that the NDFDGM model demonstrates greater stability, with notably lower error margins. In the prediction stage, these models exhibit stark variations in performance. The prediction results of NDFDGM are closer to the true values, while the performance of the other four models is relatively poor. This conclusion can also be verified from the box plot in the prediction stage. The result errors of the other four models are relatively large, while the error of the model proposed in this paper is significantly smaller.

In order to make the above conclusion more persuasive, the simulation errors and prediction errors of each model are precisely calculated to facilitate comparison. The specific results are shown in Table 11. The above conclusion can be verified from the test error. That is, the performances of the five models in the test stage are relatively close and stable. However, the NDFDGM has the best performance and the smallest error, which is more than 0.25% lower than that of the other models. The superior performance of our proposed model becomes even more evident when examining prediction errors. With an error rate of just 1.4244%, which is significantly lower than the error of more than 2.9% of other models, our solution clearly outperforms competing models. This substantial difference leaves no doubt about which approach delivers better results.

To further demonstrate the wide applicability of NDFDGM and enhance the credibility of the model results, it was compared with other prediction models in non-grey fields. The prediction curve is shown in Figure 12, and the error results are presented in

Table 12. The evaluation metrics of the non-grey models in the energy consumption forecast of China.

Model	MAPEsim (%)	MAPEpre (%)
BPNN	31.8430	2.9664
LSTM	1.2856	4.6851
ELM	32.1541	3.9454
SVR	1.1479	5.0499
NDFDGM	1.0648	1.4244

.

It is not difficult to find from the above chart that, compared with the non-grey models, NDFDGM is still the best choice. Although in the simulation stage, the performances of LSTM and SVR are close to that of NDFDGM, in the prediction stage, the errors of other models all exceeded NDFDGM by more than 1.5%, and their performances are not good. Therefore, taking into account the overall performance comprehensively, the NDFDGM innovatively proposed in this paper remains the best choice. In conclusion, we have every reason to believe in the prediction results of NDFDGM and use them as a basis to predict the future trend of energy consumption and make subsequent adjustments.

5.2. Forecast of Total Energy Consumption in China for the Next Three Years

To forecast China’s aggregate energy demand across the forthcoming triennium, it is essential to determine the initial values of future influencing factors. Accordingly, this research develops a multivariate forecasting framework grounded in comprehensive historical datasets encompassing all relevant driving factors, continues with the current scenario of daily energy consumption in China, incorporates the predicted data of influencing factors for the upcoming three-year period, and applies the NDFDGM model for forecasting. The detailed procedure is outlined as follows: First, the future values of the influencing factors are predicted using the traditional GM(1,1) model, with the results presented in

Table 13. Predicted values of influencing factors in the energy consumption of China for next three years.

Year	GDP (100 Million Yuan)	Urbanization Level (%)
2023	1,643,169.19	71.19
2024	1,808,979.82	72.78
2025	1,991,522.25	74.41

. Subsequently, these predicted values are input into the NDFDGM model to estimate China’s total energy consumption for the next three years.

Based on the aforementioned data and analysis, this paper employs the NDFDGM model to forecast China’s aggregate energy demand across the forthcoming triennium, with the results presented in

Table 14. Predicted values of total energy consumption in China for the forthcoming triennium.

Year	2023	2024	2025
Total energy consumption (10,000 tons of standard coal)	581,285.51	617,461.32	659,731.11

.

According to the prediction data analysis results in Table 14, China’s total energy consumption is expected to show a stable growth trend in the next three years (2023–2025). In order to present this changing trend more clearly and intuitively, based on historical data, fitting data and the predicted data in Table 14, this study generated the simulation effect diagram (Figure 13) through the data visualization method. This effect drawing systematically presents the historical variation pattern of China’s total energy consumption, the model fitting effect and the future prediction trend, providing strong graphical support for the research conclusion.

It can also be seen from the trends of the two curves in Figure 13 that the model results in the early fitting stage are basically consistent with the true values, which indirectly proves the credibility of the prediction results. Judging from the extrapolated three-year forecast results, China’s overall energy demand will continue rising at an accelerated pace compared to past years.

Consequently, to guarantee the long-term sustainability of our nation’s energy supply, it is crucial to prioritize energy efficiency and weave it into the fabric of our overarching national development plan. Putting forward scientific, reasonable and forward-looking policy suggestions is not only a key path to achieving energy transformation and green development, but also a crucial enabler for facilitating high-calibre economic growth and achieving the “dual carbon” goals.

6. Policy Suggestions

Building on the findings from the research, this paper proposes targeted policy recommendations from four key perspectives: the eastern, central, western regions, and the nation as a whole. The goal is to refine the energy mix and boost efficiency in how energy is used, ultimately driving balanced regional energy development across China. These steps aim to foster sustainable energy practices nationwide, offering a solid foundation for high-quality economic growth and long-term economic stability.

6.1. Eastern Region: Optimize the Industrial Structure and Promote Green and Low-Carbon Transformation

The eastern region, as the most economically developed area in China, has a total energy consumption and energy consumption intensity both higher than the national average. However, the eastern region still faces problems such as an energy structure that leans towards fossil fuels and relatively low energy utilization efficiency. The NDFDGM model predicts sustained growth in energy demand. Therefore, the eastern region should accelerate the adjustment of its industrial structure, promote the transformation of traditional industries to green and low-carbon industries, focus on developing high-tech industries, services and the digital economy, and reduce its reliance on high energy-consuming and high-polluting industries. In addition, to optimize energy consumption, we must prioritize efficiency by adopting cutting-edge energy-saving technologies. This involves implementing stricter conservation measures across key sectors like construction, transportation, and manufacturing. Additionally, we need to establish robust energy management systems while continuously improving how effectively we harness and use power resources. Secondly, relying on the abundant solar and wind energy resources in the eastern region, we should accelerate the construction of renewable energy bases and gradually replace the dominant position of coal and oil. In addition, when formulating population, economic and industrial policies, the impact on energy consumption should be fully considered to ensure that energy policies are in line with other policy goals.

6.2. Central Region: Strengthen Regional Coordination and Promote the Optimization of the Energy Structure

The central region shows the characteristics of “large total amount and fast growth rate” in terms of energy consumption. The growth of its energy consumption is mainly affected by population growth and changes in economic structure. The NDFDGM(r_i,N) model’s superior predictive performance confirms that population expansion and rapid industrialization are the primary drivers of this surge. The model’s high accuracy validates its ability to capture the region’s energy demand dynamics, which are closely tied to demographic changes and economic structural shifts. Moreover, Energy demand structure in the central region is dominated by coal, with a relatively high energy consumption intensity. And the expansion of energy demand is constrained by two key factors: declining end-use energy intensity and enhanced supply side efficiency gains. This dynamic exists alongside significant regional disparities in resource allocation—while the central region possesses substantial energy reserves, its uneven spatial distribution creates pronounced supply-demand imbalances that challenge sustainable development. Consequently, the central region ought to prioritize refining its energy usage framework by speeding up the shift away from coal and encouraging the adoption of cleaner energy sources like natural gas and electricity. Additionally, efforts should be made to enhance the overall cleanliness of its energy consumption. Second, enhance regional coordination: Promote energy cooperation between central region and eastern as well as western regions, establish a regional energy allocation mechanism, and improve energy utilization efficiency. Third, promote the construction of energy infrastructure: Accelerate the construction of energy transmission channels, enhance energy supply capacity, and alleviate the contradiction between energy availability and demand. Fourth, enhance energy technology innovation: Encourage and support the research and application of energy technologies, promote technological progress in energy, and improve energy utilization efficiency.

6.3. Western Region: Leverage Resource Advantages to Promote Sustainable Energy Development

The West of China boasts an abundance of energy resources, placing it at the forefront of the nation’s most energy-rich regions. With vast reserves of coal, oil, natural gas, and hydroelectric power, these resources stand out at the national level. Despite the relatively modest energy consumption in this region, the pace at which it is increasing is rather swift. According to the results of previous study, this surge in energy usage is predominantly driven by the swelling population and shifting economic dynamics. Meanwhile, the western region’s energy landscape remains heavily reliant on coal, resulting in notably high consumption rates. However, rising efficiency in energy supply and declining end-use intensity are putting a natural brake on unchecked demand growth. Therefore, the western region should take advantage of its rich energy reserves to give full play to its local resource advantages, focus on expanding traditional energy industries. At the same time, it should strive to accelerate the development of renewable energy to achieve diversification of the overall energy structure. In addition, it should actively promote the West–East Gas Pipeline Project to strengthen energy cooperation between the western and central and eastern regions, promote energy transportation eastward, optimize energy utilization efficiency and solve the energy shortage problem in the eastern region. Furthermore, it is necessary to strengthen the construction of energy infrastructure in the western region, accelerate the construction of transmission channels, improve energy supply capabilities and narrow the gap between energy supply and demand.

6.4. National Level: Coordinate Regional Development and Promote the Optimization and Green Transformation of the Energy Structure

In summary, China’s energy use is characterized by its large overall volume, rapid expansion, and a heavy reliance on certain structures. The eastern region has seen a notable decline in energy consumption per unit of output, while the central areas are experiencing relatively swift growth in energy use. Although overall energy consumption in the western region remains comparatively modest, its growth rate is accelerating quickly. As the country’s total energy demand continues to rise, it underscores the need for more robust measures to support economic development, safeguard the environment, and ensure energy security. Accordingly, from a national standpoint, regional coordination is essential to foster balanced growth, refine the energy mix, and advance toward green, low-carbon solutions. Building a more efficient, environmentally friendly, and sustainable energy framework becomes crucial. The following recommendations outline potential avenues for achieving these goals.

First, improve the energy policy system: establish a unified, coordinated and efficient energy policy system, integrating the goals of total energy consumption control, energy structure adjustment, energy technology innovation and energy security guarantee, to ensure that policies do not conflict or overlap and form a synergy.

Second, promote the optimization of the energy structure: we should focus on optimizing the energy mix by fast-tracking the shift away from coal reliance. This involves boosting the share of cleaner energy sources, like natural gas and electricity, within overall energy use. The goal is to steer energy consumption toward cleaner, lower-carbon options. Special attention needs to be given to advancing renewable energy projects and encouraging a more diverse, balanced energy portfolio.

Third, strengthen the construction of energy infrastructure: we must prioritize upgrading our energy infrastructure by speeding up the development of transmission networks to boost supply capacity and ease imbalances between energy demand and availability. Investing in cutting-edge systems like smart grids, energy storage solutions, and the energy internet will optimize efficiency and modernize how we harness and distribute power.

Fourth, promoting coordinated regional development: strengthen energy cooperation among the eastern, central and western regions, promote cross-regional energy allocation mechanisms such as energy transmission to the east and west-to-east power transmission, and facilitate the best possible use and efficient deployment of energy assets.

Fifth, enhance energy technology innovation and talent cultivation: ramp up funding for cutting-edge energy research, accelerate technological advancements, and boost efficiency across energy systems. Meanwhile, efforts should be made to strengthen the cultivation of talents in the energy sector to provide talent support for energy transformation. By fostering a pipeline of skilled professionals and breakthrough technologies, we can drive sustainable progress in the field.

Sixth, enhance efforts to manage overall energy use and carbon output: building on the foundation of regulating total energy consumption, intensify measures to curb carbon emissions, encouraging a separation between energy consumption and emissions growth. The goal is to steer development towards greener, low-carbon pathways.

Seventh, improve the alignment between energy initiatives and other policy areas: when developing strategies related to population, economic development, or industrial growth, it is crucial to thoroughly assess how these policies will influence energy consumption. The aim is to ensure that energy policies complement and reinforce other policymaking efforts, creating a cohesive and synergistic approach.

7. Conclusions

Energy use has dual significance. It not only reflects the quality and efficiency of economic growth, but also plays a key role in maintaining the ecological environment and ensuring social sustainability. Given that energy consumption is influenced by many complex variables within the real-world system, a comprehensive understanding of its potential impact mechanisms remains challenging, making the prediction itself difficult. In order to solve these problems, this study improves the traditional grey prediction model by developing a nonlinear grey model that incorporates multiple influencing factors and can perform dynamic prediction. In order to optimize the hyperparameters of the model and improve the accuracy of energy consumption prediction, the Firefly algorithm is used. Finally, after verifying the effectiveness of the NDFDGM model through energy consumption predictions in central, eastern and western regions of China, the method was further used to predict the country’s overall energy demand, and several important conclusions are reached.

(1)

Model Performance and Advantages: the proposed nonlinear different fractional discrete grey multivariate model (NDFDGM) demonstrates superior performance in predicting regional and national energy consumption compared to traditional models such as DGM, FDGM, NDGM, and FNDGM. By incorporating fractional order accumulation and nonlinear adjustment terms, NDFDGM effectively captures the complex, nonlinear relationships among variables, significantly reducing both simulation and prediction errors. The use of the Firefly Algorithm (FA) for hyperparameter optimization further enhances the model’s accuracy and robustness, ensuring reliable predictions even with limited data.

(2)

Regional Energy Consumption Trends: the application of NDFDGM to China’s eastern, central, and western regions reveals distinct energy consumption patterns. The eastern region, with its high energy intensity, requires structural optimization and green transformation. The central region, characterized by rapid growth, benefits from regional coordination and infrastructure development. The western region, rich in resources, shows potential for sustainable energy expansion. These findings underscore the importance of tailored energy policies to address regional disparities.

(3)

National Forecast and Policy Implications: the model predicts a steady increase in China’s total energy consumption over the next three years, driven by economic growth and urbanization. This trend highlights the urgent need for comprehensive energy policies that prioritize efficiency, clean energy adoption, and regional coordination. The government must balance energy security with environmental goals, leveraging technological innovation and cross-regional collaboration to achieve sustainable development.

(4)

Limitations and Future Work: while NDFDGM offers significant improvements, it still has some limitations in this study. First, the cumulative generation operation used in the model may change the distribution characteristics of the original data to some extent, and then affect the interpretability of the data. This can make it difficult to compare forecast results with actual changes. Secondly, there are multiple methods to choose from in the process of finding the optimal hyperparameters of a model. The method used in this paper is relatively simple and may limit the improvement of the model’s prediction accuracy. In addition, the performance of the model depends on the quality and size of the data, and a small sample size or incomplete data may affect the prediction results. And the uniformity of data sources may also limit the generalization ability of the model. Furthermore, outliers in the data may interfere with the learning process of the model, resulting in a deviation in the model’s understanding of the normal pattern. Missing values may make the model’s information acquisition incomplete in some periods, which in turn affects its grasp of the overall trend and seasonal characteristics. If these issues are not properly addressed, they can have a negative impact on the final model predictions. Therefore, the several limitations above must be addressed to enhance the robustness and applicability of NDFDGM model. Future research could explore its integration with other advanced algorithms or hybrid models to further enhance predictive capabilities. When there are problems in data quality, more refined and effective methods can be adopted in the data preprocessing stage. Methods based on statistical principles or machine learning, such as cluster analysis and boxplot, can be used to accurately identify outliers and reasonably correct or eliminate these outliers, or to identify outliers based on dynamic threshold quantile regression and interpolate the correction with the EM algorithm to make the data more consistent with the normal distribution. When dealing with missing values, appropriate filling methods can be selected according to data characteristics, such as mean filling, linear interpolation, model-based predictive filling, etc., to ensure data integrity and continuity. Additionally, expanding the model’s application to other sectors or global energy systems could provide broader insights. Through continuous technological innovation and method improvement, this model is expected to develop into an important analytical tool in the field of energy forecasting, providing more accurate decision support for the intelligent management and sustainable development of energy systems.