Dynamic Analysis of a Fractional Breast Cancer Model with Incommensurate Orders and Optimal Control
Abstract
1. Introduction
2. Qualitative Analysis of the System
2.1. The Existence of Solution
2.2. The Uniqueness of Solution
2.3. Existence of the Equilibriums
2.4. Stability of the Equilibriums
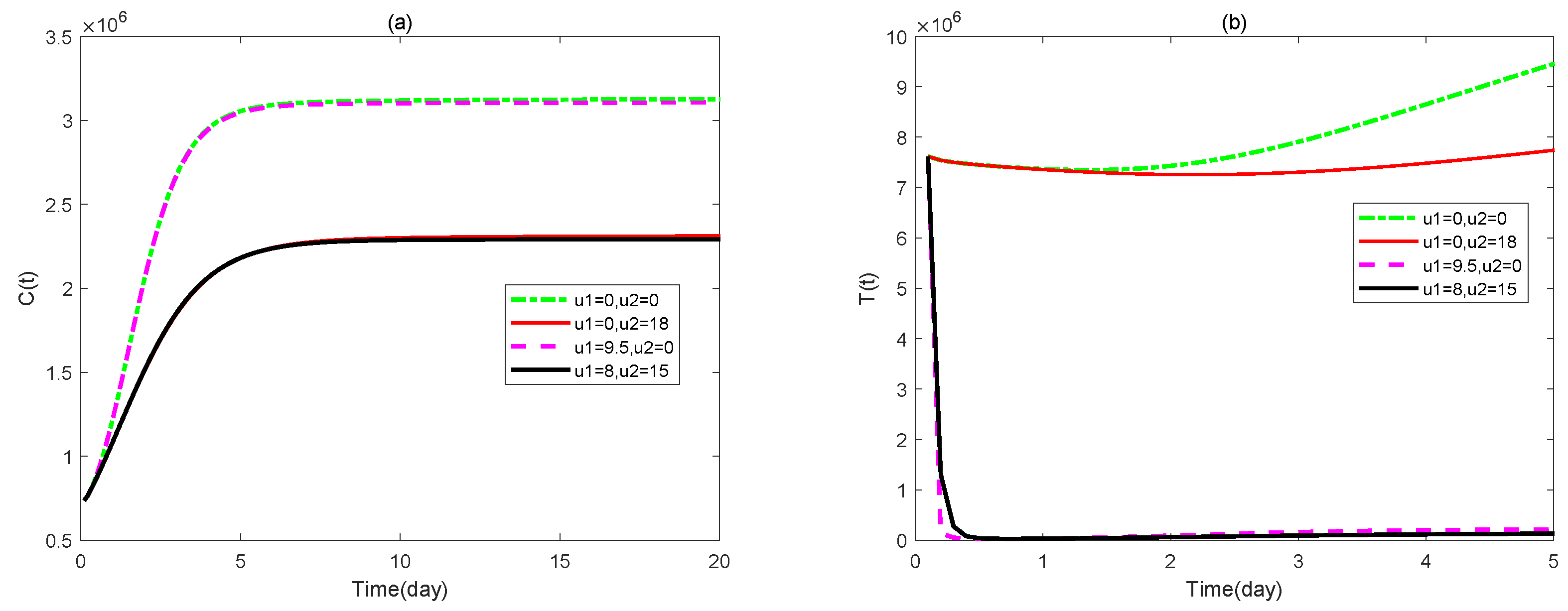
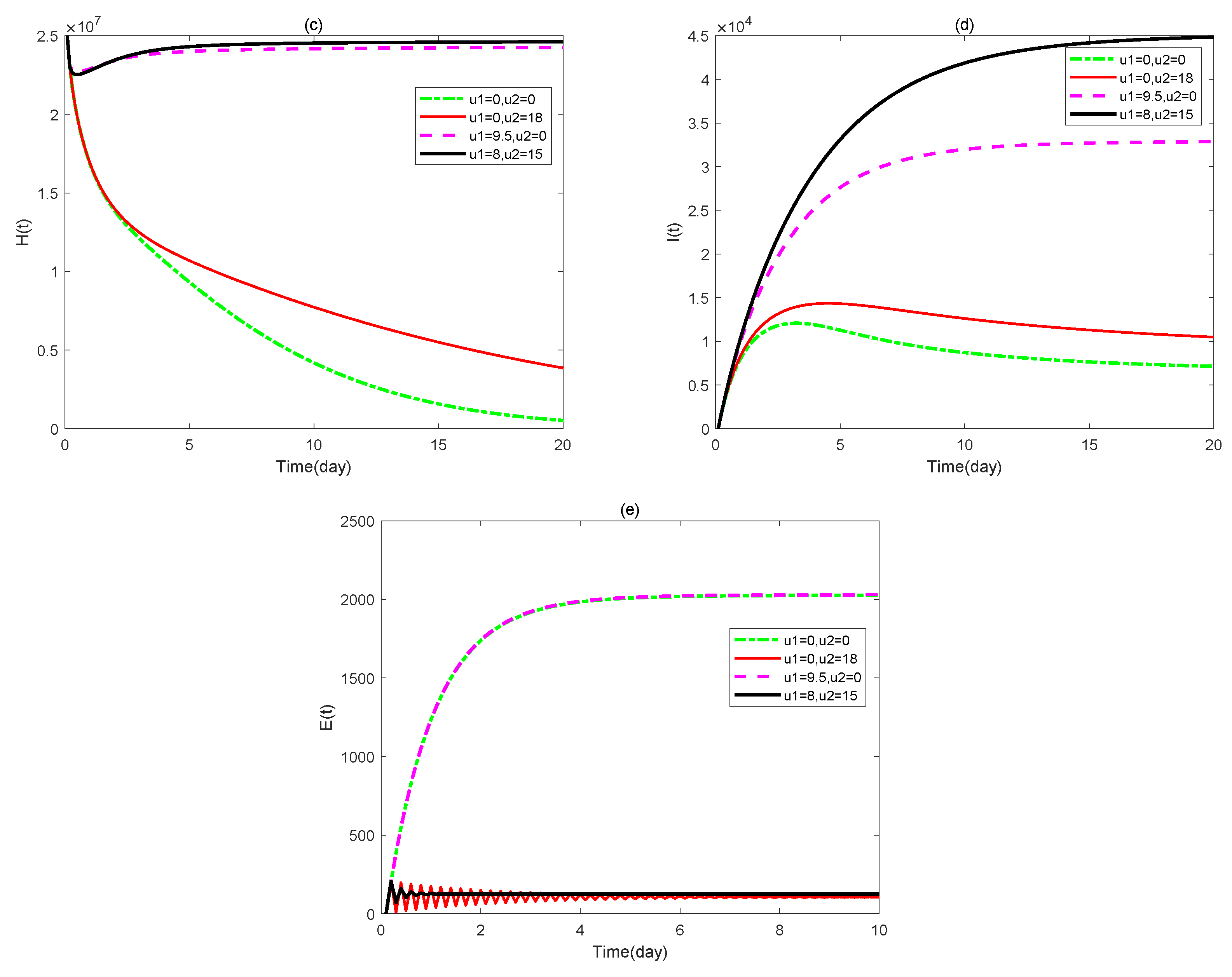
3. Optimal Control Problem of the Model
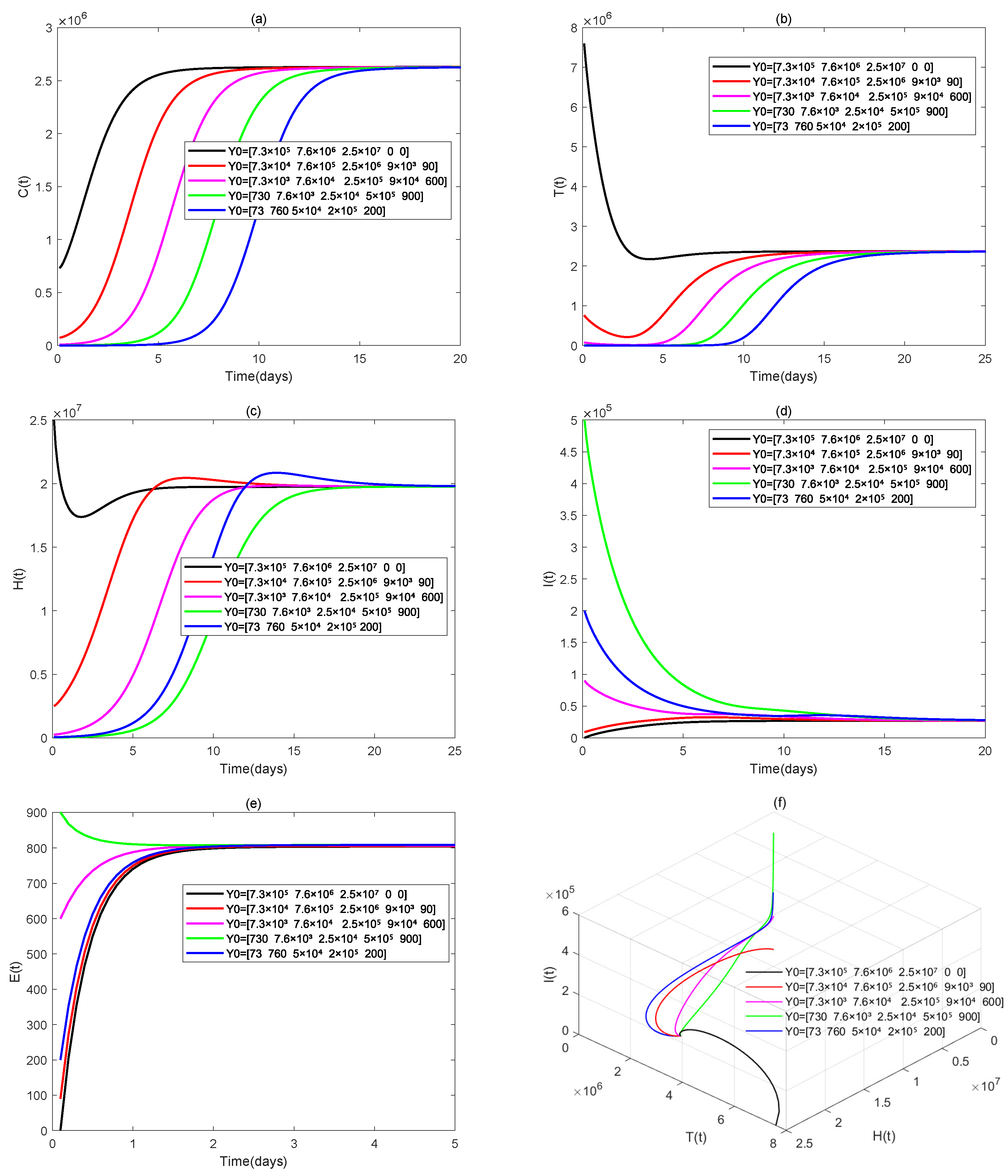
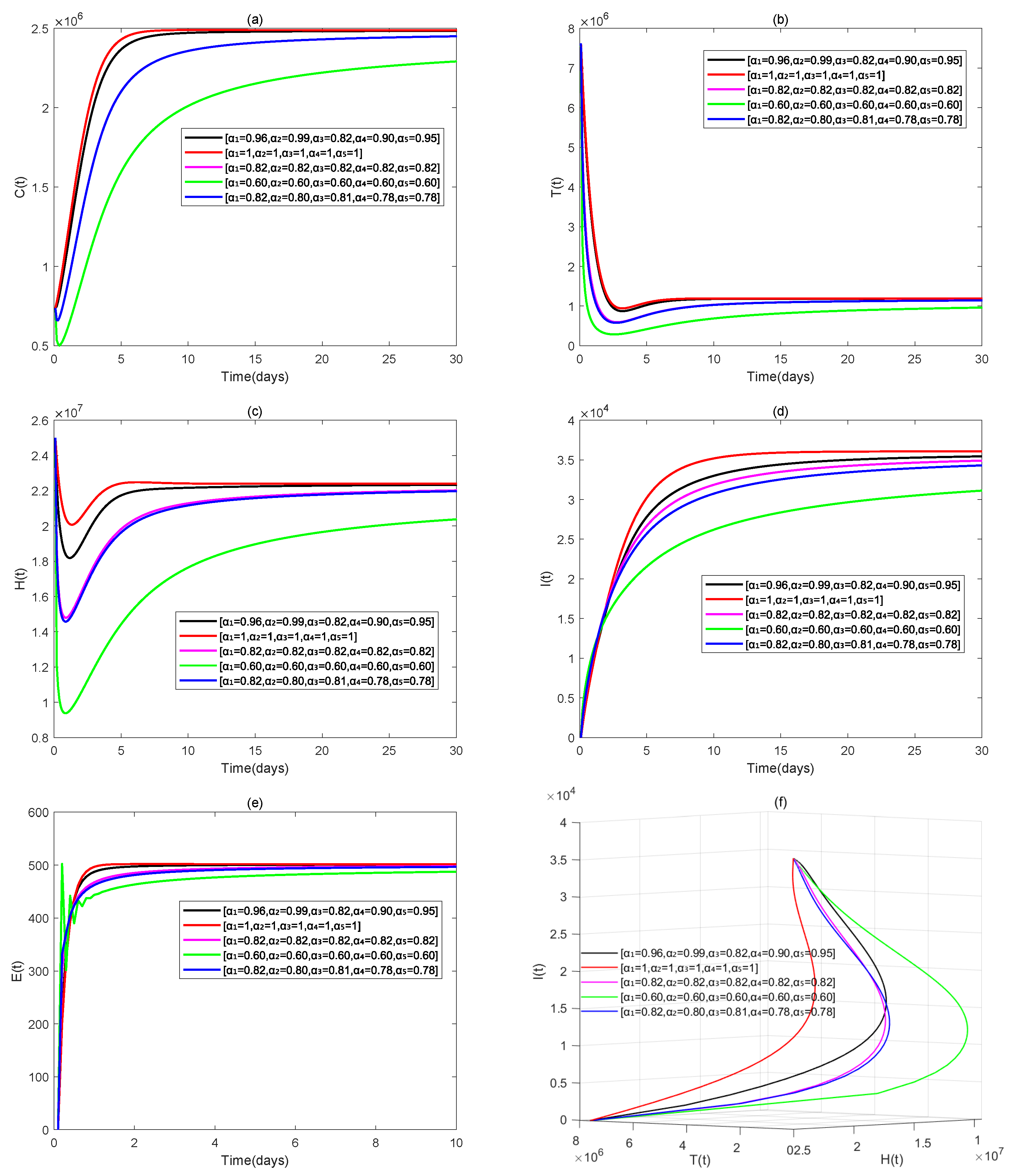
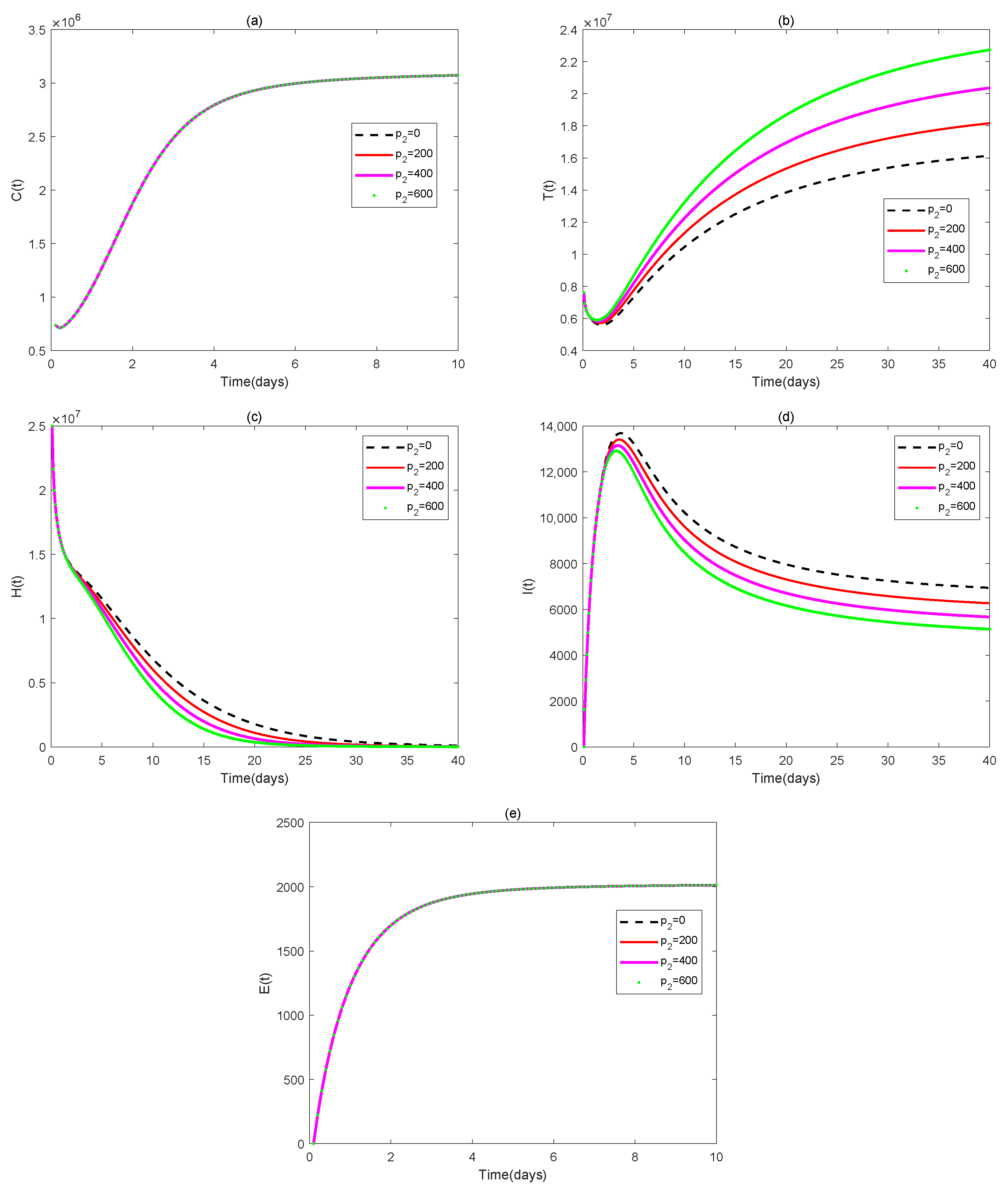
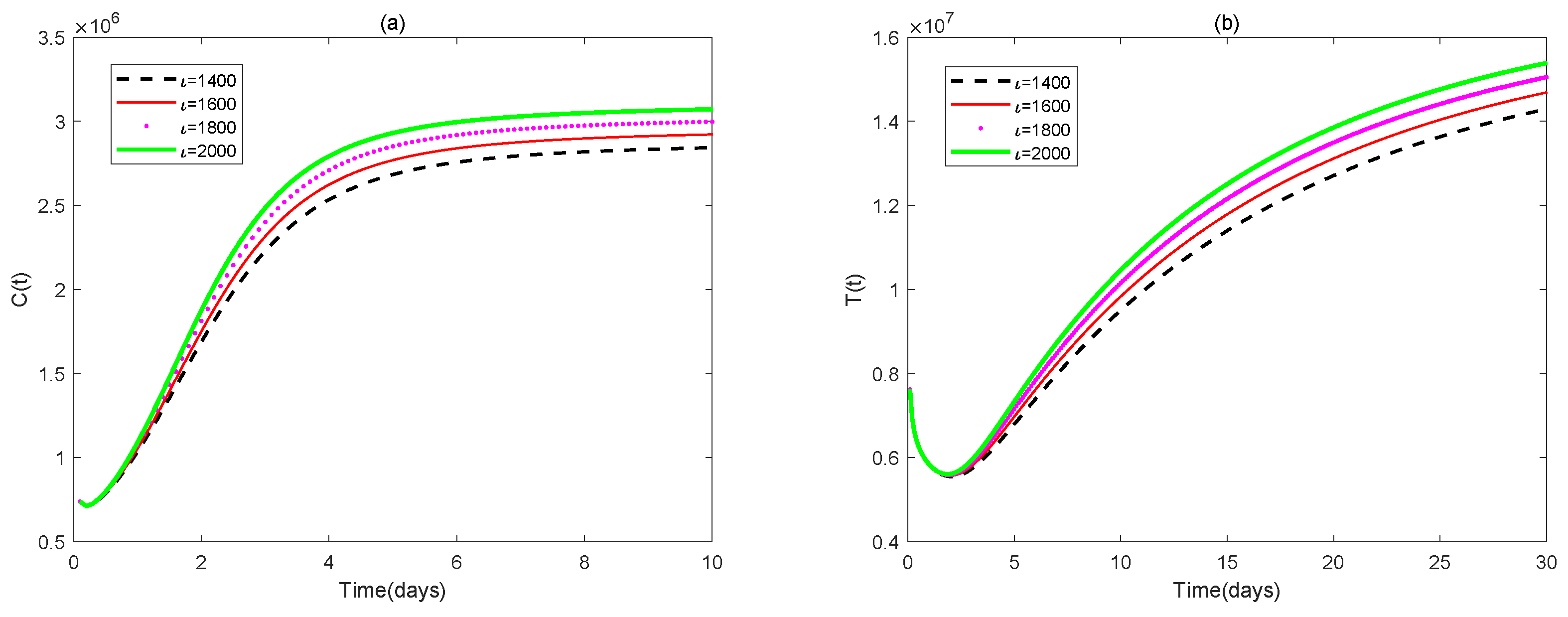
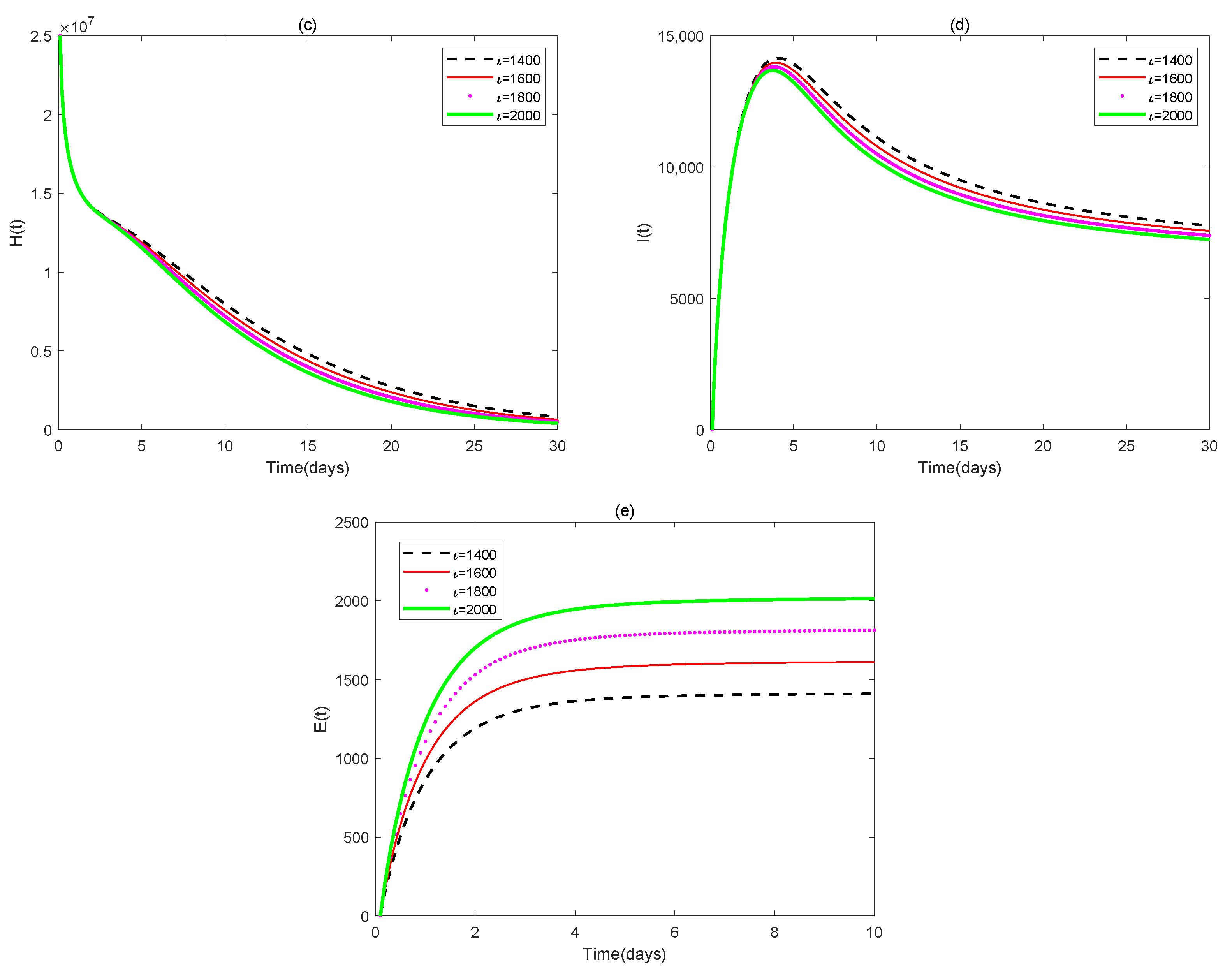
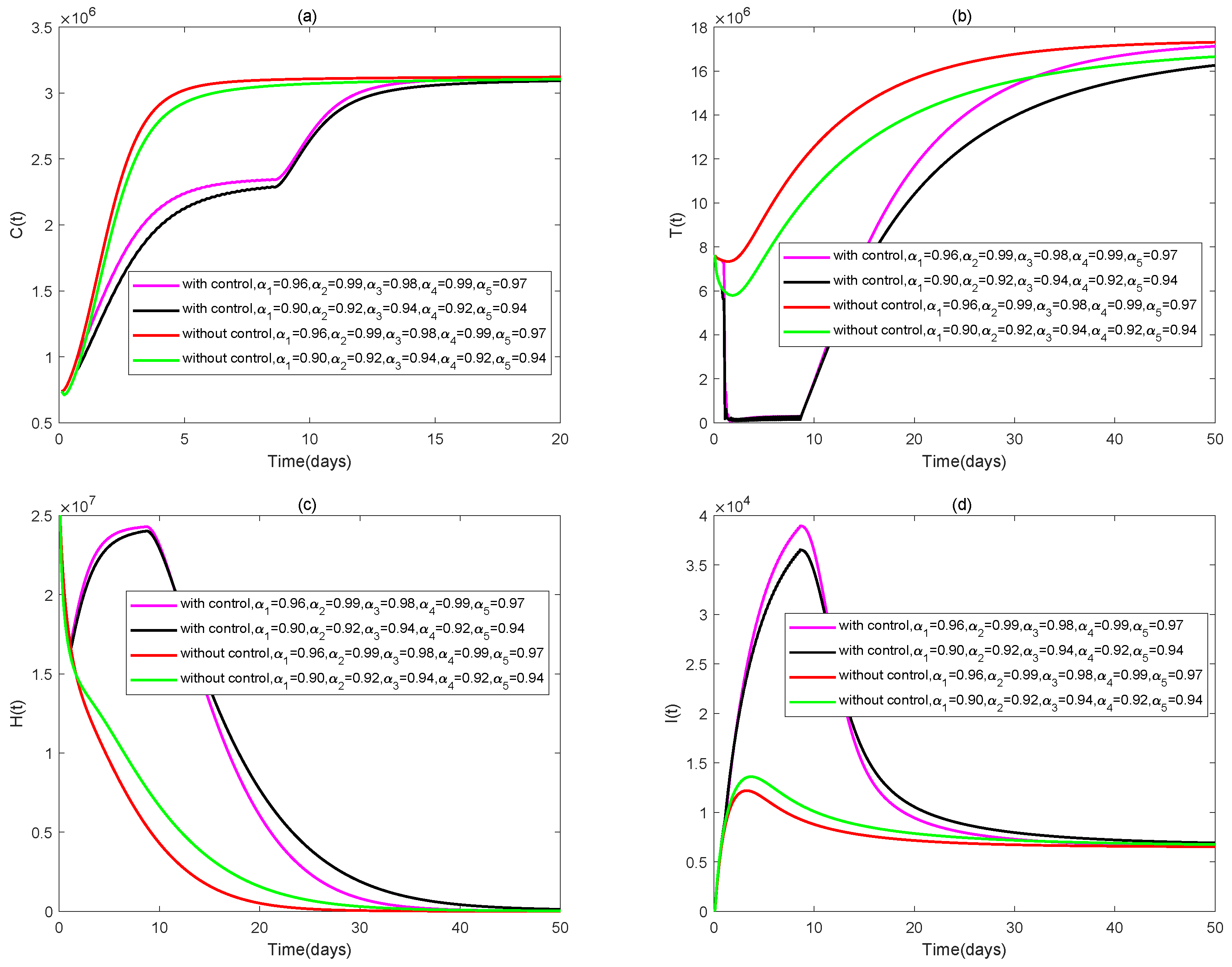
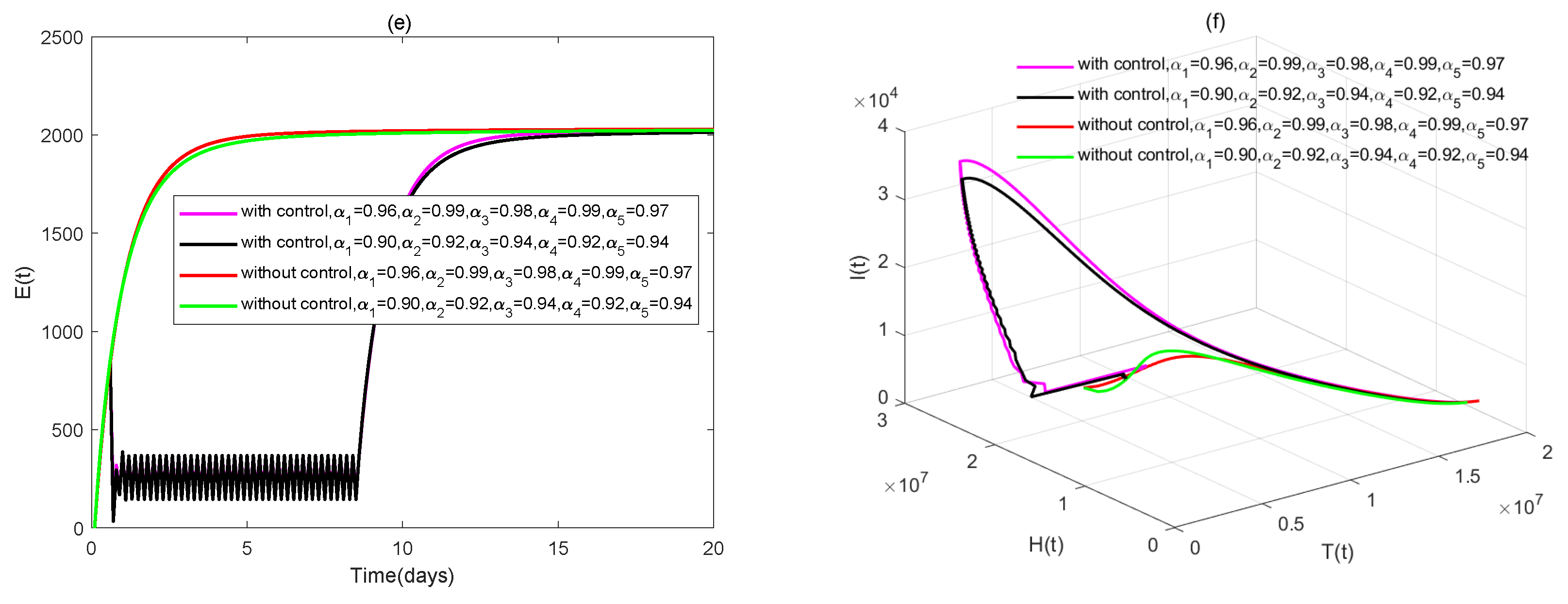
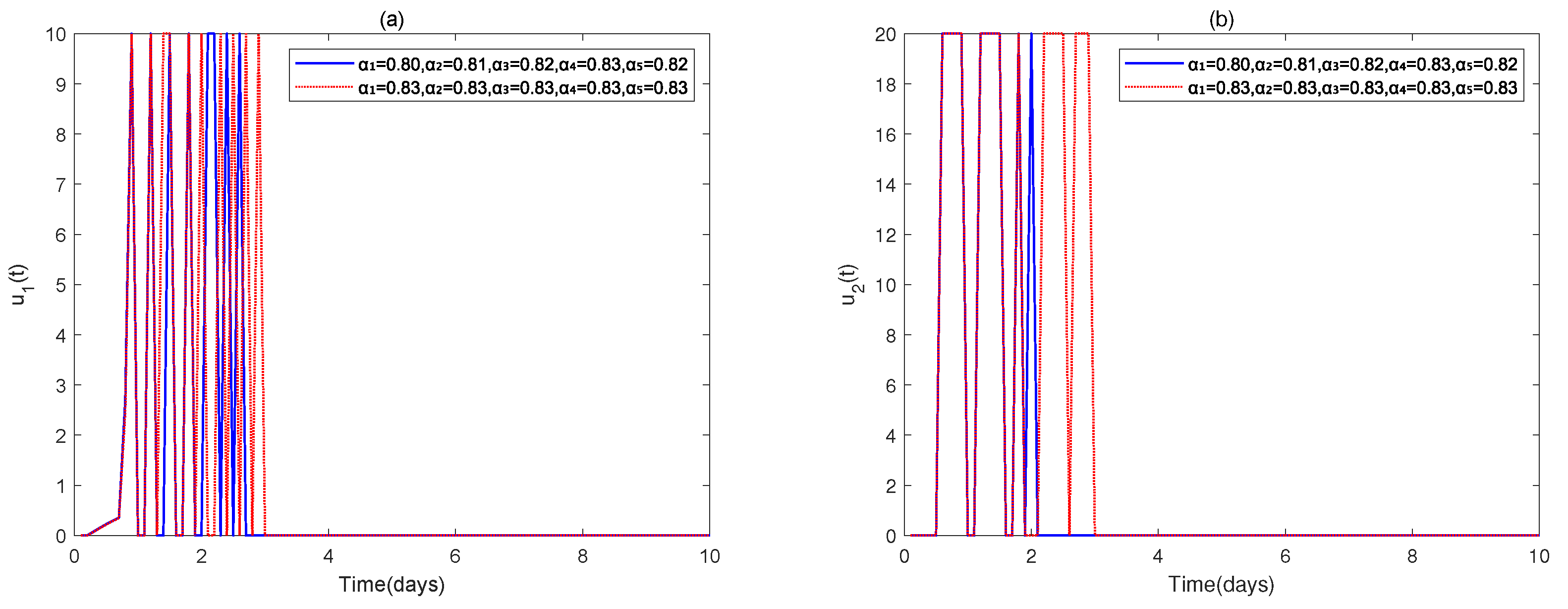
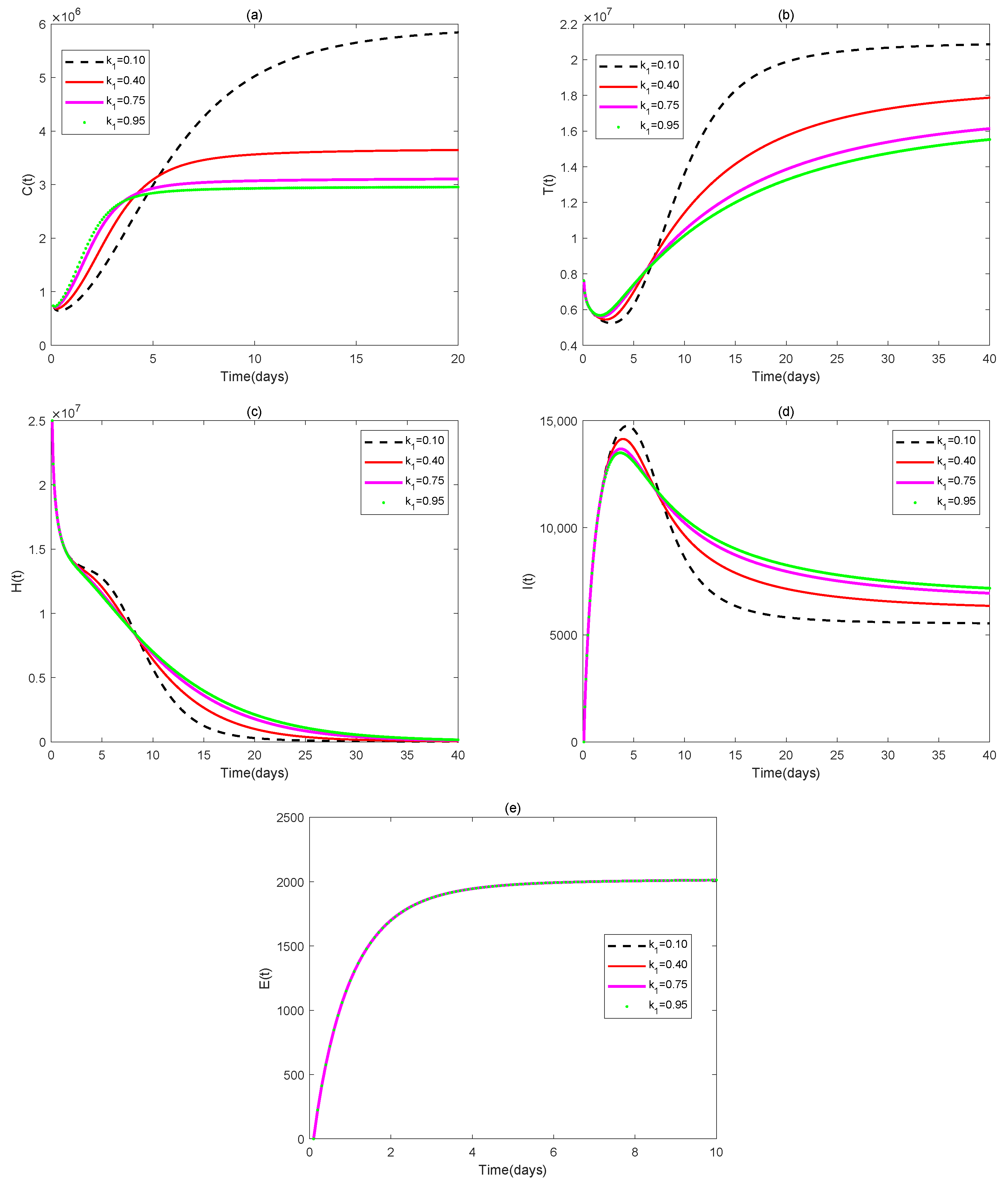
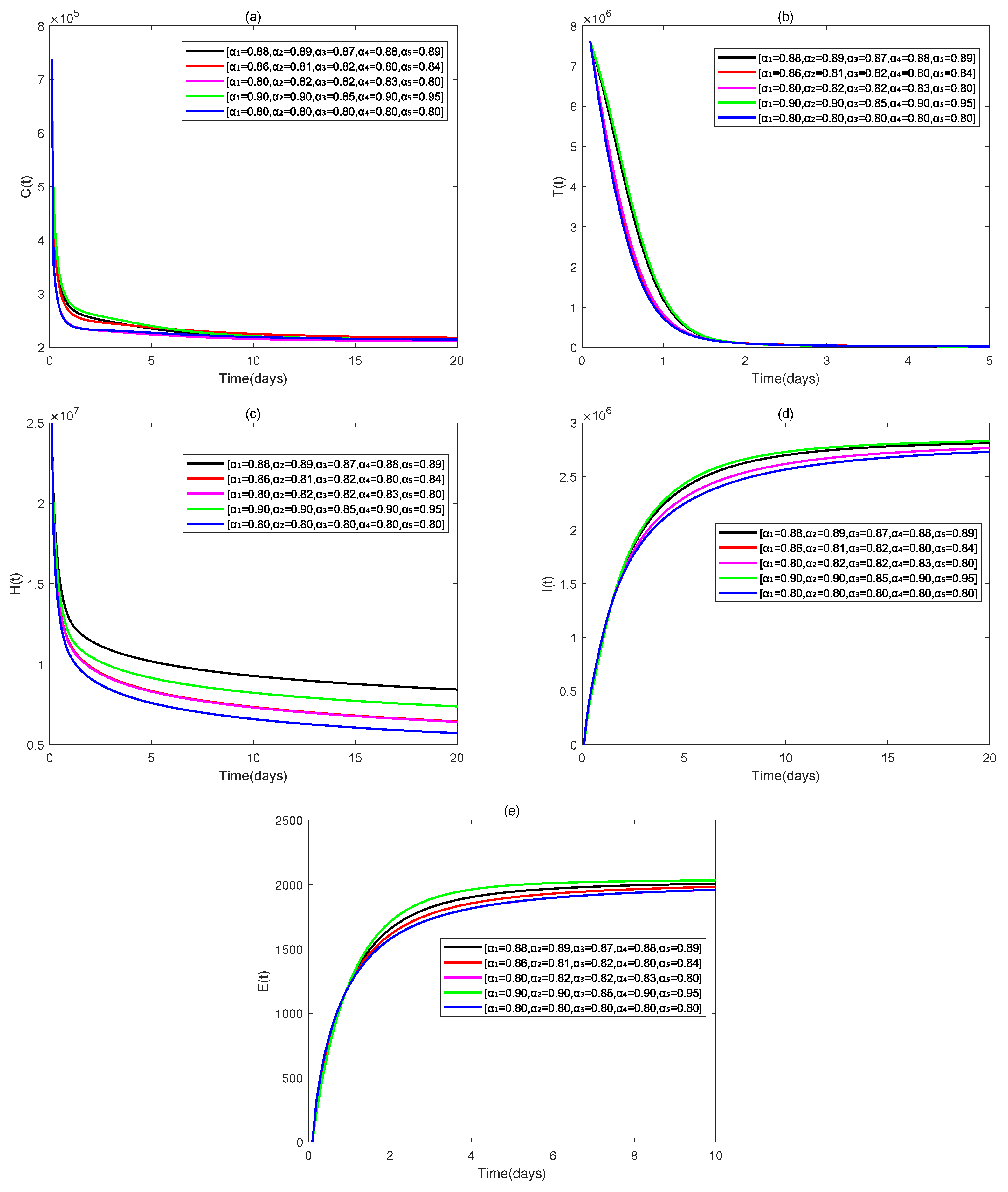
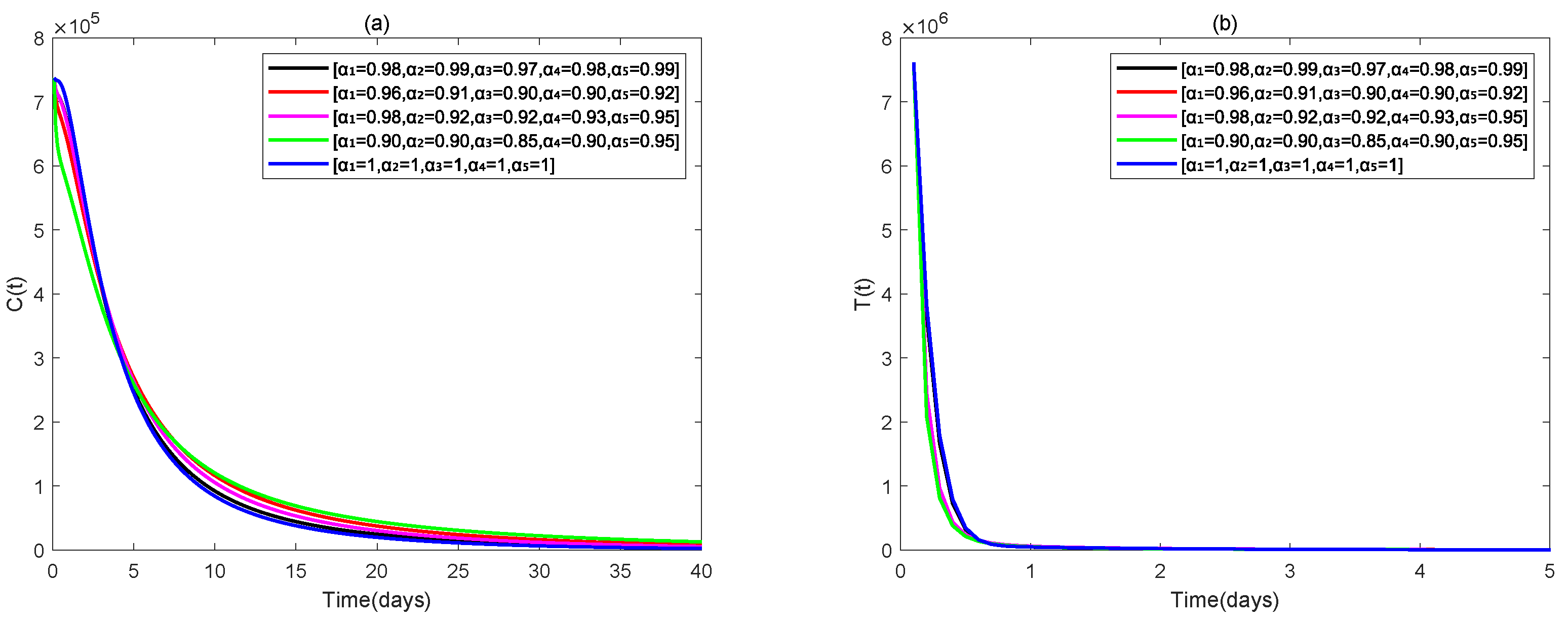
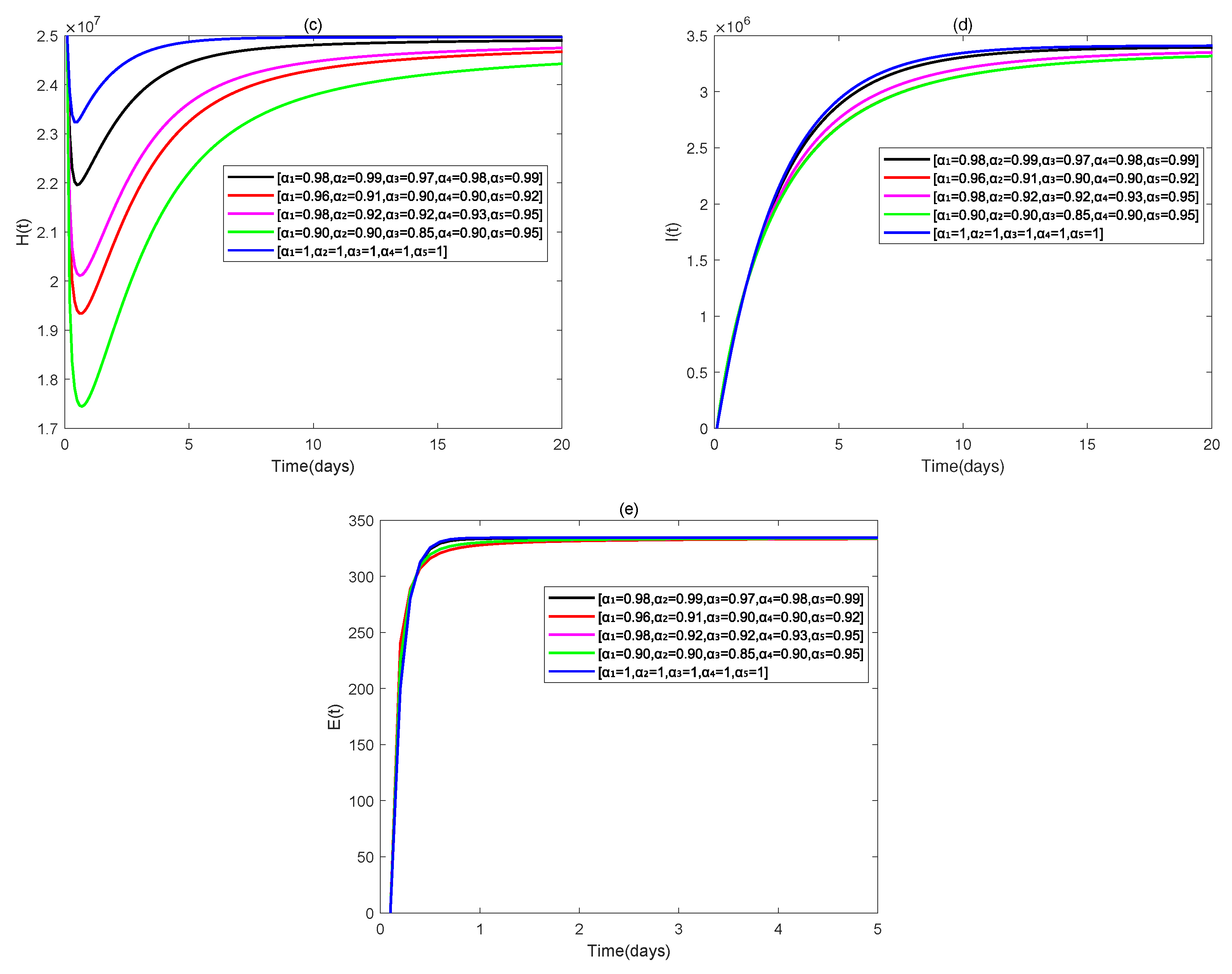
4. Numerical Simulations
5. Discussions and Conclusions
- ⋆
- In this article, we constructed and analyzed a deterministic model. However, in real life, there are numerous random factors, such as fluctuations in environmental conditions and physiological differences among individuals, all of which can have an impact on the development process of the disease.
- ⋆
- In this paper, the Caputo type fractional derivative is used to construct the model. In fact, there are many methods worthy of exploration in the field of fractional order models, such as fractional order systems involving vector order non-singular kernels [39] and generalized fractional order differential equations [40].
- ⋆
- Currently, the theoretical analysis of time delay tumor models mostly focuses on integer order models. However, for fractional-order time delay models, especially the exploration of Hopf bifurcations under different fractional order cases, is relatively scarce. Meanwhile, there are significant differences in the relevant discussions between integer order and fractional-order time delay models, which constitutes a theoretical challenge that can be a key area of research in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kansara, S.; Singh, A. The emerging regulatory roles of non-coding RNAs associated with glucose metabolism in breast cancer. Semin. Cancer Biol. 2023, 95, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zheng, R.; Baade, P.D.; Zhang, S.; Zeng, H.; Bray, F.; Jemal, A.; Yu, X.Q.; He, J. Cancer statistics in China, 2015. CA Cancer J. Clin. 2016, 66, 115–132. [Google Scholar] [CrossRef]
- Fitzmaurice, C.; Dicker, D.; Pain, A.; Hamavid, H.; Moradi-Lakeh, M.; MacIntyre, M.F.; Allen, C.; Hansen, G.; Woodbrook, R.; Wolfe, C.; et al. The global burden of cancer 2013. JAMA Oncol. 2015, 1, 505–527. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Ye, F.; Kong, Y.; Hu, X.; Deng, X.; Xie, J.; Song, C.; Ou, X.; Wu, S.; Wu, L.; et al. The single-cell landscape of intratumoral heterogeneity and the immunosuppressive microenvironment in liver and brain metastases of breast cancer. Adv. Sci. 2023, 10, 2203699. [Google Scholar] [CrossRef]
- Ye, F.; Dewanjee, S.; Li, Y. Advancements in clinical aspects of targeted therapy and immunotherapy in breast cancer. Mol. Cancer 2023, 22, 105. [Google Scholar] [CrossRef]
- Farhan, M.; Shah, Z.; Jan, R.; Islam, S.; Alshehri, M.H.; Ling, Z. A fractional modeling approach for the transmission dynamics of measles with double-dose vaccination. Comput. Methods Biomech. Biomed. Eng. 2025, 28, 511–528. [Google Scholar] [CrossRef]
- El-Houseini, M.E.; Arafat, M.S.; El-Husseiny, A.M.; Kasem, I.M.; El-Habashy, A.H.; Khafagy, M.M.; Radwan, E.M.; Helal, M.H.; Abdellateif, M.S. Biological and molecular studies on specific immune cells treated with checkpoint inhibitors for the thera-personal approach of breast cancer patients (ex vivo study). Oncol. Res. 2022, 29, 319. [Google Scholar] [CrossRef]
- Harbeck, N.; Gnant, M. Breast cancer. Lancet 2017, 389, 1134–1150. [Google Scholar] [CrossRef] [PubMed]
- Fathoni, M.; Gunardi, G.; Kusumo, F.A.; Hutajulu, S.H. Mathematical model analysis of breast cancer stages with side effects on heart in chemotherapy patients.In AIP conference proceedings. AIP Publ. 2019, 2192, 060007. [Google Scholar]
- Mufudza, C.; Sorofa, W.; Chiyaka, E.T. Assessing the effects of estrogen on the dynamics of breast cancer. Comput. Math. Methods Med. 2012, 2012, 473572. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Upadhyay, R.K.; Das, P.; Ghosh, D. Exploring dynamical complexity in a time-delayed tumor-immune model. Chaos 2020, 30, 123118. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, 78–90. [Google Scholar] [CrossRef]
- Alvarez, R.F.; Barbuto, J.A.M.; Venegeroles, R.A. Nonlinear mathematical model of cell-mediated immune response for tumor phenotypic heterogeneity. J. Theor. Biol. 2019, 471, 42–50. [Google Scholar] [CrossRef] [PubMed]
- Frascoli, F.; Kim, P.S.; Hughes, B.D.; Landman, K.A. A dynamical model of tumour immunotherapy. Math. Biosci. 2014, 253, 50–62. [Google Scholar] [CrossRef] [PubMed]
- Yıldız, T.A.; Arshad, S.; Baleanu, D. New observations on optimal cancer treatments for a fractional tumor growth model with and without singular kernel. Chaos Solitons Fractals 2018, 117, 226–239. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Yuste, S.B.; Acedo, L.; Lindenberg, K. Reaction front in an A+B→ C reaction-subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef]
- Chen, W.C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Spanos, P.D.; Malara, G. Random vibrations of nonlinear continua endowed with fractional derivative elements. Procedia Eng. 2017, 199, 18–27. [Google Scholar] [CrossRef]
- Arshad, S.; Baleanu, D.; Huang, J.; Tang, Y.; Al Qurashi, M.M. Dynamical analysis of fractional order model of immunogenic tumors. Adv. Mech. Eng. 2016, 8, 1687814016656704. [Google Scholar] [CrossRef]
- Wang, C.; Wang, G.; Zhang, Y.; Dai, Y.; Yang, D.; Wang, C.; Li, J. Differentiation of benign and malignant breast lesions using diffusion-weighted imaging with a fractional-order calculus model. Eur. J. Radiol. 2023, 159, 110646. [Google Scholar] [CrossRef] [PubMed]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana-Baleanu-Caputo fractional derivative. Adv. Differ. Equ. 2020, 2020, 334. [Google Scholar] [CrossRef]
- Sabir, Z.; Munawar, M.; Abdelkawy, M.A.; Raja, M.A.Z.; Ünlü, C.; Jeelani, M.B.; Alnahdi, A.S. Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks. Fractal Fract. 2022, 6, 184. [Google Scholar] [CrossRef]
- Tang, T.Q.; Jan, R.; Ahmad, H.; Shah, Z.; Vrinceanu, N.; Racheriu, M. A fractional perspective on the dynamics of hiv, considering the interaction of viruses and immune system with the effect of antiretroviral therapy. J. Nonlinear Math. Phys. 2023, 30, 1327–1344. [Google Scholar] [CrossRef]
- Wu, P.; He, Z.; Khan, A. Dynamical analysis and optimal control of an age-since infection HIV model at individuals and population levels. Appl. Math. Model. 2022, 106, 325–342. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, Y. Dynamic analysis and optimal control of a fractional order HIV/HTLV co-infection model with HIV-specific antibody immune response. AIMS Math. 2024, 9, 9455–9493. [Google Scholar] [CrossRef]
- Dai, P.; Song, T.; Liu, J.; He, Z.; Wang, X.; Hu, R.; Yang, J. Therapeutic strategies and landscape of metaplastic breast cancer. Cancer Treat. Rev. 2025, 133, 102885. [Google Scholar] [CrossRef]
- Bitsouni, V.; Tsilidis, V. Mathematical modeling of tumor-immune system interactions: The effect of rituximab on breast cancer immune response. J. Theor. Biol. 2022, 539, 111001. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Li, L. Optimality conditions for fractional variational problems with Caputo-Fabrizio fractional derivatives. Adv. Differ. Equ. 2017, 2017, 357. [Google Scholar] [CrossRef]
- Abernathy, K.; Abernathy, Z.; Baxter, A. Stevens, M. Global dynamics of a breast cancer competition model. Differ. Equ. Dyn. Syst. 2017, 28, 791–805. [Google Scholar] [CrossRef] [PubMed]
- Sols-Prez, J.E.; Gmez-Aguilar, J.F.; Atangana, A. A fractional mathematical model of breast cancer competition model. Chaos Solitons Fractals 2019, 127, 38–54. [Google Scholar] [CrossRef]
- Arpino, G.; Ferrero, J.M.; De la Haba-Rodriguez, J.; Easton, V.; Schuhmacher, C.; Restuccia, E.; Rimawi, M. Abstract S3-04: Primary analysis of PERTAIN: A randomized, two-arm, open-label, multicenter phase II trial assessing the efficacy and safety of pertuzumab given in combination with trastuzumab plus an aromatase inhibitor in first-line patients with HER2-positive and hormone receptor-positive metastatic or locally advanced breast cancer. Cancer Res. 2017, 77, S3-04. [Google Scholar]
- Alshammari, S.; Alshammari, M.; Alabedalhadi, M.; Al-Sawalha, M.M.; Al-Smadi, M. Numerical investigation of a fractional model of a tumor-immune surveillance via Caputo operator. Alex. Eng. J. 2024, 86, 525–536. [Google Scholar] [CrossRef]
- Caputo, M.; Fabricio, M. A new definition of fractional derivative without singu-lar Kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Lozada, J.; Nieto, J.J. Properties of a new fractional derivative without singular Kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Sadki, M.; Danane, J.; Allali, K. Hepatitis C virus fractional-order model: Mathematical analysis. Model. Earth Syst. Environ. 2023, 9, 1695–1707. [Google Scholar] [CrossRef]
- Shiri, B.; Baleanu, D. Numerical solution of some fractional dynamical systems in medicine involving non-singular kernel with vector order. Results Nonlinear Anal. 2019, 2, 160–168. [Google Scholar]
- Baleanu, D.; Shiri, B. Generalized fractional differential equations for past dynamic. AIMS Math. 2022, 8, 14394–14418. [Google Scholar] [CrossRef]
| the density of cancer stem cells | |||
| the density of tumor cells | |||
| the density of healthy cells | |||
| the density of immune cells | |||
| the density of excess estrogen | |||
| the normal rate of division for cancer stem cells | [0.10, 0.95] day−1 | [32] | |
| the normal rate of division for tumor cells | 0.514 day−1 | [32] | |
| q | the normal rate of division for healthy cells | 0.70 day−1 | [33] |
| the carrying capacity of cancer stem cells | cells | [32] | |
| the carrying capacity of tumor cells | cells | [33] | |
| the carrying capacity of healthy cells | cells | [33] | |
| the death rate of cancer stem cells | [33] | ||
| the death rate of tumor cells due to immune | [33] | ||
| cells’ response | |||
| the death rate of immune cells due to tumor | [33] | ||
| cells’ response | |||
| represent the rate at which estrogen helps to | 600 | [33] | |
| proliferate cancer stem cells | |||
| represent the rate at which estrogen helps to | [0, 600] | [32,33] | |
| proliferate tumor cells | |||
| the rate at which healthy cells are lost to DNA | 100 | [33] | |
| mutation by estrogen presence | |||
| the number of cancer stem cells at which the rate | cells | [33] | |
| of absorption is at half its maximum | |||
| the number of tumor cells at which the rate of | cells | [33] | |
| absorption is at half its maximum | |||
| the number of healthy cells at which the rate of | cells | [33] | |
| absorption is at half its maximum | |||
| the normal death rate of tumor cells | 0.01 day−1 | [33] | |
| the normal death rate of immune cells | 0.29 day−1 | [33] | |
| the death rate of healthy cells due to competition | [33] | ||
| with tumor cells | |||
| the source rate of immune cells | [32] | ||
| the immune cells’ response rate | 0.20 | [33] | |
| the immune cells threshold | cells | [32] | |
| the rate of immune suppression by estrogen | 0.20 | [33] | |
| the estrogen threshold | 400 | [33] | |
| the continuous infusion of estrogen | [1400, 2000] | [32,33] | |
| the washout rate of estrogen by the body | 0.97 day−1 | [33] | |
| the absorption rate of estrogen by cancer stem cells | 0.01 day−1 | [33] | |
| the absorption rate of estrogen by tumor cells | 0.01 day−1 | [33] | |
| the absorption rate of estrogen by healthy cells | 0.01 day−1 | [33] | |
| represent the efficacy of Trastuzumab | |||
| represent the efficacy of Aromatase Inhibitors |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Shi, R. Dynamic Analysis of a Fractional Breast Cancer Model with Incommensurate Orders and Optimal Control. Fractal Fract. 2025, 9, 371. https://doi.org/10.3390/fractalfract9060371
Zhao Y, Shi R. Dynamic Analysis of a Fractional Breast Cancer Model with Incommensurate Orders and Optimal Control. Fractal and Fractional. 2025; 9(6):371. https://doi.org/10.3390/fractalfract9060371
Chicago/Turabian StyleZhao, Yanling, and Ruiqing Shi. 2025. "Dynamic Analysis of a Fractional Breast Cancer Model with Incommensurate Orders and Optimal Control" Fractal and Fractional 9, no. 6: 371. https://doi.org/10.3390/fractalfract9060371
APA StyleZhao, Y., & Shi, R. (2025). Dynamic Analysis of a Fractional Breast Cancer Model with Incommensurate Orders and Optimal Control. Fractal and Fractional, 9(6), 371. https://doi.org/10.3390/fractalfract9060371





