The Optimal L2-Norm Error Estimate of a Weak Galerkin Finite Element Method for a Multi-Dimensional Evolution Equation with a Weakly Singular Kernel
Abstract
1. Introduction
- A WG finite element fully discrete scheme is constructed for a multi-dimensional evolution equation with a weakly singular kernel.
- The stability and convergence of the discrete approximation are proved.
2. Weak Galerkin Finite Element Scheme
- such thatwhere is the projection from onto for and is the projection operator from onto for .
- as follows:
3. Stability of Weak Galerkin Finite Element Scheme
4. Convergence of Weak Galerkin Finite Element Scheme
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Chen, H.; Xu, D. A compact difference scheme for an evolution equation with a weakly singular kernel. Numer. Math. Theoret. Meth. Appl. 2012, 5, 559–572. [Google Scholar]
- Chen, C.; Thomée, V.; Wahlbin, L. Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel. Math. Comput. 1992, 58, 587–602. [Google Scholar] [CrossRef]
- Mclean, W.; Thomée, V. Numerical solution of an evolution equation with a positive type memory term. J. Austral. Math. Soc. Ser. B 1993, 35, 23–70. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yang, X. An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space. J. Appl. Math. Comput. 2023, 69, 651–674. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, Y. A fast temporal second-order compact finite difference method for two-dimensional parabolic integro-differential equations with weakly singular kernel. J. Comput. Sci. 2025, 87, 102558. [Google Scholar] [CrossRef]
- Fakhari, H.; Mohebbi, A. Galerkin spectral and finite difference methods for the solution of fourth-order time fractional partial integro-differential equation with a weakly singular kernel. J. Appl. Math. Comput. 2024, 70, 5063–5080. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Huang, Y. An hp-version of the discontinuous Galerkin method for fractional integro-differential equations with weakly singular kernels. BIT Numer. Math. 2024, 64, 27. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhang, Q.; Yuan, G.; Sheng, Z. The finite volume scheme preserving maximum principle for two-dimensional time-fractional Fokker–Planck equations on distorted meshes. Appl. Math. Lett. 2019, 97, 99–106. [Google Scholar] [CrossRef]
- Qiu, W.; Xu, D.; Guo, J.; Zhou, J. A time two-grid algorithm based on finite difference method for the two-dimensional nonlinear time fractional mobile/immobile transport model. Numer. Algor. 2020, 85, 39–58. [Google Scholar] [CrossRef]
- Qiu, W.; Xu, D.; Guo, J. The Crank-Nicolson-type Sinc-Galerkin method for the fourth-order partial integro-differential equation with a weakly singular kernel. Appl. Numer. Math. 2021, 159, 239–258. [Google Scholar] [CrossRef]
- Yan, Y.; Fairweather, G. Orthogonal spline collocation methods for some partial integro-differential equations. SIAM J. Numer. Anal. 1992, 29, 755–768. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, X.; Xu, D. An efficient spline collocation method for a nonlinear fourth-order reaction subdiffusion equation. J. Sci. Comput. 2020, 85, 7. [Google Scholar] [CrossRef]
- Zhao, Y.; Gu, X.; Ostermann, A. A preconditioning technique for an all-at-once system from Volterra subdiffusion equations with graded time steps. J. Sci. Comput. 2021, 88, 11. [Google Scholar] [CrossRef]
- Rostami, Y. Two approximated techniques for solving of system of two-dimensional partial integral differential equations with weakly singular kernels. Comput. Appl. Math. 2021, 40, 217. [Google Scholar] [CrossRef]
- Wang, J.; Ye, X. A weak Galerkin finite element method for second-order elliptic problems. J. Comput. Appl. Math. 2013, 241, 103–115. [Google Scholar] [CrossRef]
- Mu, L.; Wang, J.; Wang, Y.; Ye, X. A computational study of the weak Galerkin method for second order elliptic equations. Numer. Algor. 2012, 63, 753–777. [Google Scholar] [CrossRef]
- Gao, F.; Mu, L. On L2 error estimate for weak Galerkin finte element for parabolic problems. J. Comput. Math. 2014, 32, 195–204. [Google Scholar]
- Li, W.; Gao, F.; Cui, J. A weak Galerkin finite element method for nonlinear convection-diffusion equation. Appl. Math. Comput. 2024, 461, 128315. [Google Scholar] [CrossRef]
- Mu, L.; Wang, J.; Ye, X. Weak Galerkin finite element methods on polytopal Meshes. Int. J. Numer. Anal. Model. 2012, 12, 31–53. [Google Scholar]
- Wang, C.; Ye, X.; Zhang, S. A Modified weak Galerkin finite element method for the Maxwell equations on polyhedral meshes. J. Comput. Appl. Math. 2024, 448, 115918. [Google Scholar] [CrossRef]
- Wang, C. Auto-stabilized weak Galerkin finite element methods on polytopal meshes without convexity constraints. J. Comput. Appl. Math. 2025, 466, 116572. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Zhai, Q.; Zhang, R. A systematic study on weak Galerkin finite element methods for second order elliptic problems. J. Sci. Comput. 2018, 74, 1369–1396. [Google Scholar] [CrossRef]
- Li, D.; Wang, C.; Wang, J.; Ye, X. Generalized weak Galerkin finite element methods for second order elliptic problems. J. Comput. Appl. Math. 2024, 445, 115833. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Dai, X. Weak Galerkin finite element method for the parabolic integro-differential equation with weakly singular kernel. Comput. Appl. Math. 2019, 38, 38. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Chen, H. A weak Galerkin finite element method for multi-term time-fractional diffusion equations. East Asian J. Appl. Math. 2018, 8, 181–193. [Google Scholar]
- Zhou, J.; Xu, D.; Qiu, W.; Qiao, L. An accurate, robust, and efficient weak Galerkin finite element scheme with graded meshes for the time-fractional quasi-linear diffusion equation. Comput. Math. Appl. 2022, 124, 188–195. [Google Scholar] [CrossRef]
- Tang, T. A finite difference scheme for partial integro-differential equations with a weakly singular kernel. Appl. Numer. Math. 1993, 11, 309–319. [Google Scholar] [CrossRef]
- Wheeler, M.F. A priori L2 error estimates for Galerkin approximations to parabolic partial differential equations. SIAM J. Numer. Anal. 1973, 10, 723–759. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, Y.; Xu, Y.; Zhai, Q.; Yue, H. Weak Galerkin finite element method for second order parabolic equations. Int. J. Numer. Anal. Model. 2016, 13, 525–544. [Google Scholar]
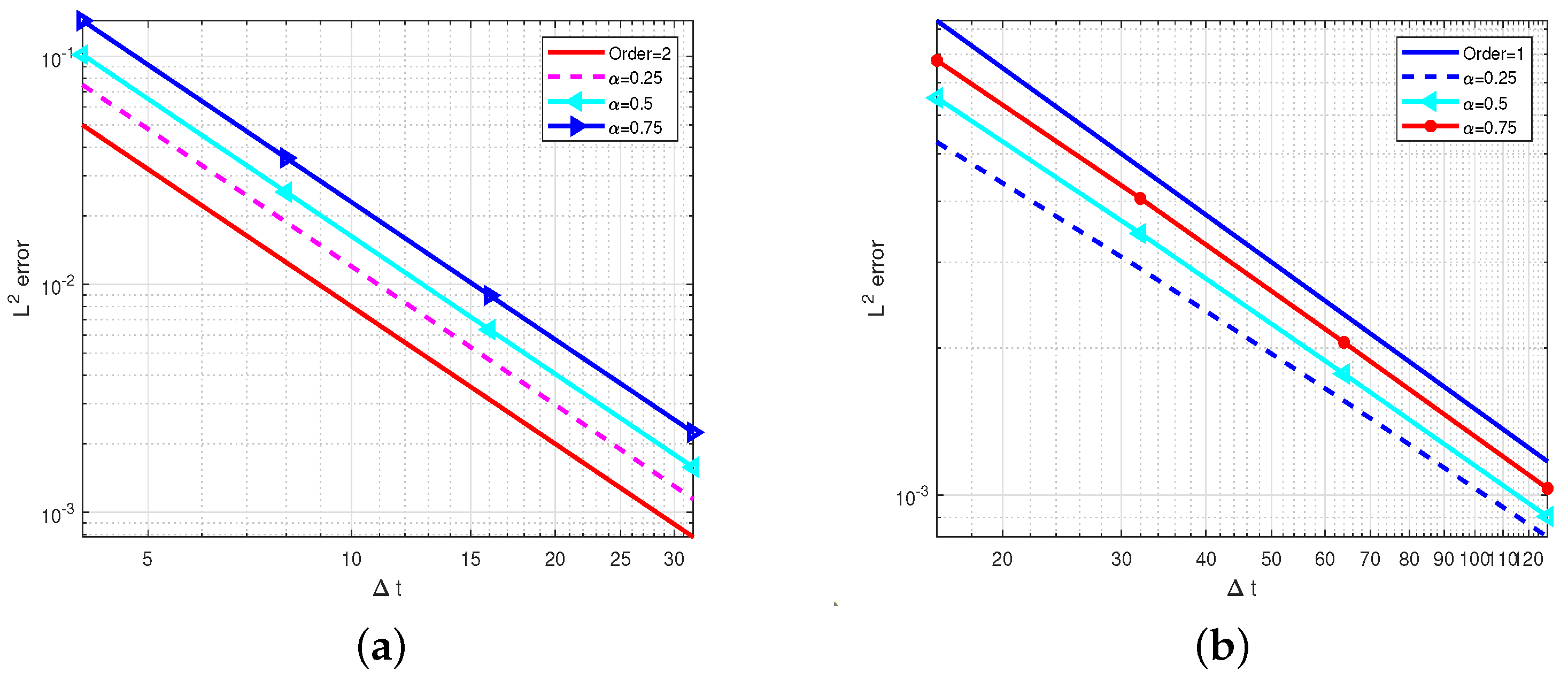
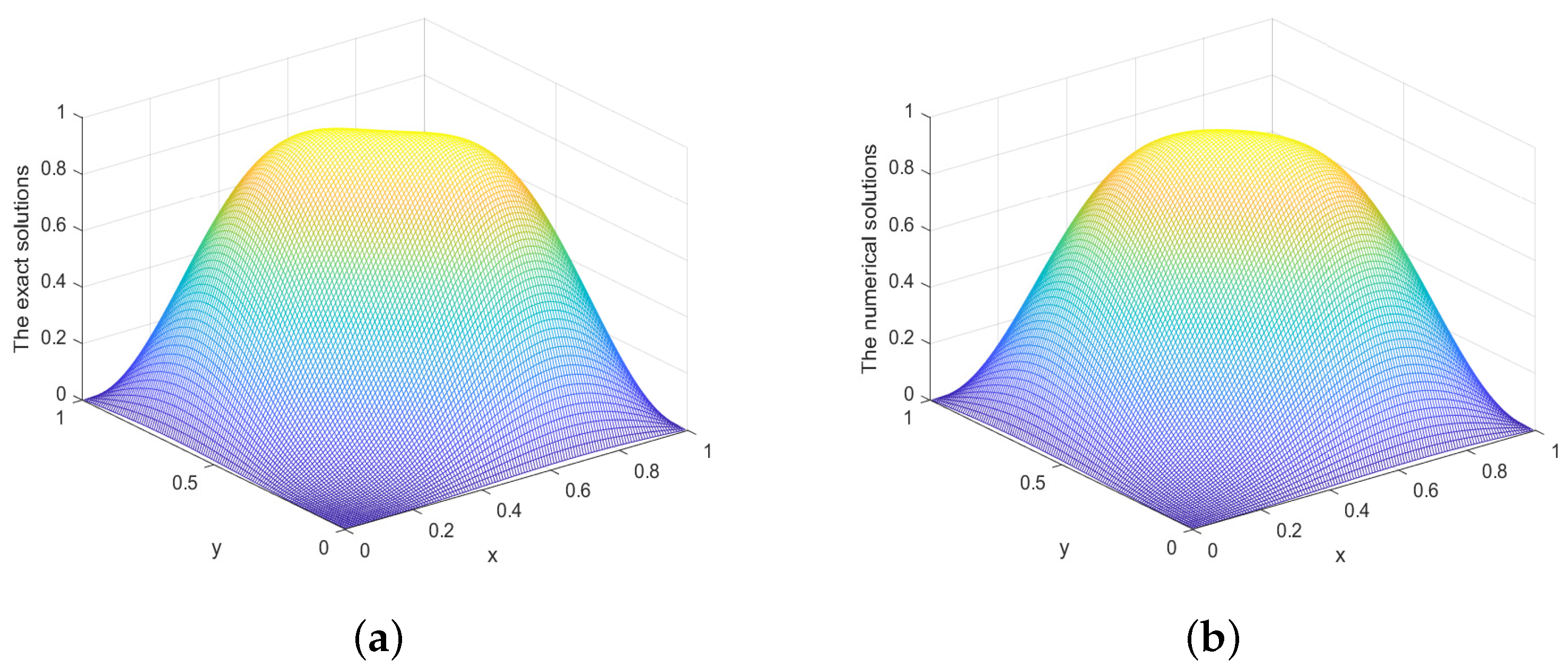
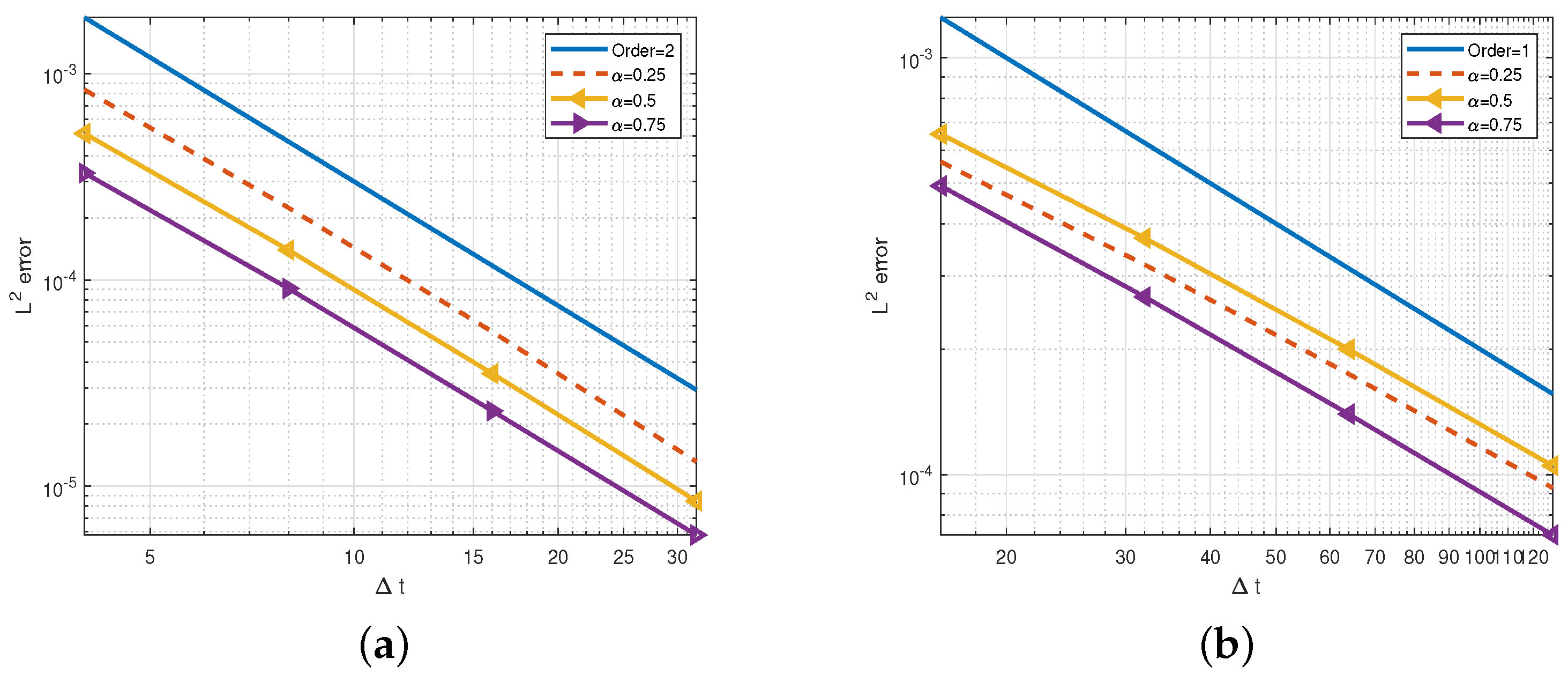
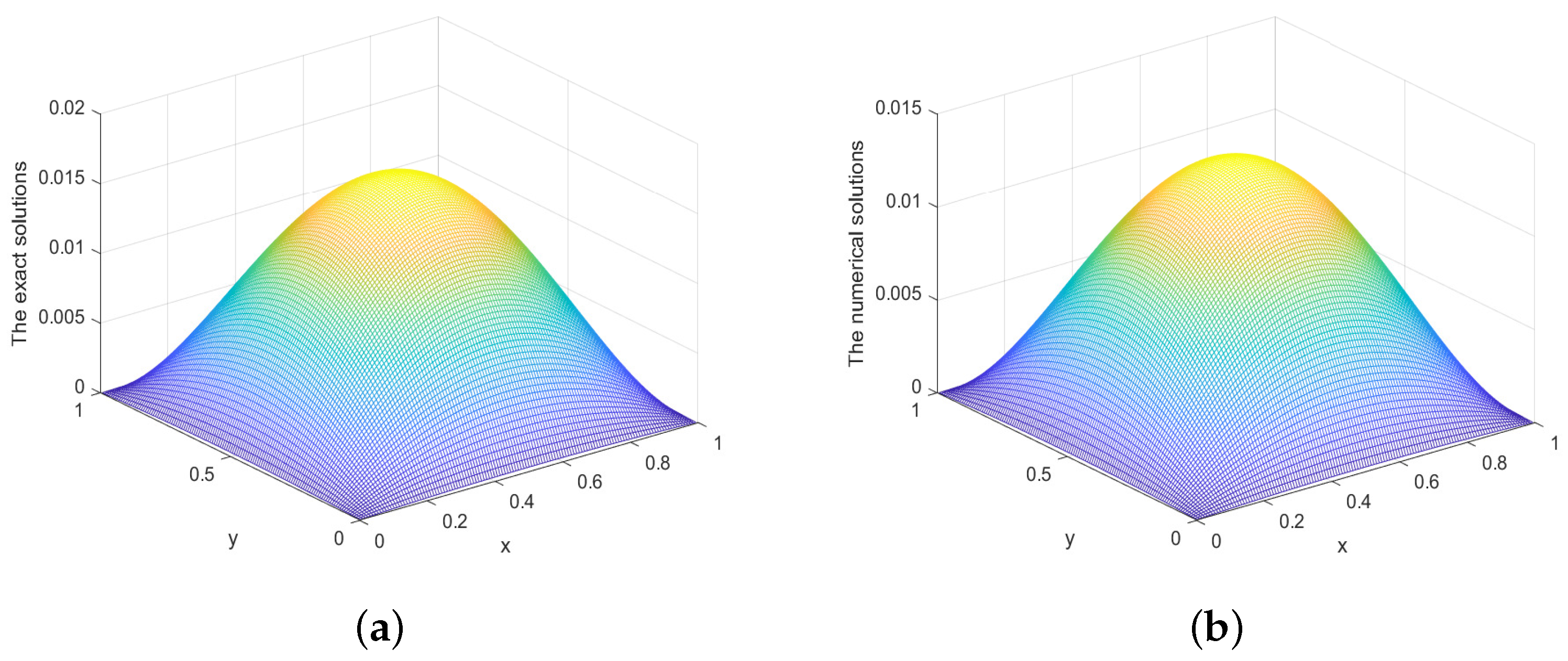
| M | |||
|---|---|---|---|
| 1.500299 3.761225 9.396687 2.340609 | 1.99598 2.00098 2.00527 | ||
| 1.453775 3.634613 9.078598 2.265468 | 1.99993 2.00126 2.00266 | ||
| 1.435374 3.588690 8.966046 2.239688 | 1.99990 2.00091 2.00117 |
| N | |||
|---|---|---|---|
| 8.807003 4.846912 2.599962 1.367762 | 0.86159 0.89858 0.92667 | ||
| 1.050071 5.538527 2.856477 1.457183 | 0.92291 0.95527 0.97106 | ||
| 9.710630 5.066485 2.568006 1.289339 | 0.93858 0.98034 0.99402 |
| M | |||
|---|---|---|---|
| 8.493773 2.244136 5.575981 1.291414 | 1.92025 2.00886 2.11027 | ||
| 5.223547 1.400798 3.496892 8.450654 | 1.89878 2.00210 2.04894 | ||
| 3.364420 9.127113 2.311183 5.849509 | 1.88213 1.98153 1.98224 |
| N | |||
|---|---|---|---|
| 5.631114 3.189182 1.743488 9.295012 | 0.82023 0.87121 0.90745 | ||
| 6.561934 3.695099 1.998514 1.049854 | 0.82851 0.88669 0.92874 | ||
| 4.929918 2.669213 1.396821 7.162491 | 0.88515 0.93427 0.96361 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Zhou, J.; Chen, H. The Optimal L2-Norm Error Estimate of a Weak Galerkin Finite Element Method for a Multi-Dimensional Evolution Equation with a Weakly Singular Kernel. Fractal Fract. 2025, 9, 368. https://doi.org/10.3390/fractalfract9060368
Zhou H, Zhou J, Chen H. The Optimal L2-Norm Error Estimate of a Weak Galerkin Finite Element Method for a Multi-Dimensional Evolution Equation with a Weakly Singular Kernel. Fractal and Fractional. 2025; 9(6):368. https://doi.org/10.3390/fractalfract9060368
Chicago/Turabian StyleZhou, Haopan, Jun Zhou, and Hongbin Chen. 2025. "The Optimal L2-Norm Error Estimate of a Weak Galerkin Finite Element Method for a Multi-Dimensional Evolution Equation with a Weakly Singular Kernel" Fractal and Fractional 9, no. 6: 368. https://doi.org/10.3390/fractalfract9060368
APA StyleZhou, H., Zhou, J., & Chen, H. (2025). The Optimal L2-Norm Error Estimate of a Weak Galerkin Finite Element Method for a Multi-Dimensional Evolution Equation with a Weakly Singular Kernel. Fractal and Fractional, 9(6), 368. https://doi.org/10.3390/fractalfract9060368





