Highly Accurate Numerical Method for Solving Fractional Differential Equations with Purely Integral Conditions
Abstract
1. Introduction
- (i)
- We construct a new class of basis polynomials, IMSC2Ps, and introduce two classes of basis polynomials, MSC2Ps, that satisfy the homogeneous form of the given ICs and IBCs.
- (ii)
- We discuss the establishment of OMs for ODs and CFDs of IMSC2Ps and MSC2Ps, respectively.
- (iii)
- We use the SCM along with the suggested OMs of the derivatives to develop a numerical method to solve the two models of FPDEs presented in Section 3.
2. Basic Definition of Caputo FDs
3. Formulation of FPDEs with IBCs
- Model 1:
- Model 2:
4. An Overview of SC2Ps and MSC2Ps and Introduction to IMSC2Ps
5. OMs for the Derivatives of , and
5.1. OMs for Fds of and
5.2. OM for ODs of
- ;
- ;
- ;
- .
6. Numerical Handling for Model 1 (4) and (5)
6.1. Homogeneous Form of Initial and Purely Integral Conditions (5)
- 1.
- The zeros of and : This approach typically provides optimal convergence properties for spectral methods. The zeros are advantageous as they cluster towards the boundaries of the interval, resulting in better accuracy near the endpoints.
- 2.
- Uniform grid points: This approach provides a straightforward implementation when the distribution of points does not need to be optimized.
6.2. Nonhomogeneous Form of Initial and Purely Integral Conditions (5)
7. Numerical Handling for Model 2 (7) and (8)
7.1. Homogeneous Form of Initial and Purely Integral Conditions (8)
7.2. Nonhomogeneous Form of Initial and Purely Integral Conditions (8)
- 1.
- The assembly of the linear system requires at most operations, leveraging the sparsity. The system exhibits a triangular structure.
- 2.
- The solution of the system is efficiently carried out via forward substitution, with an overall computational cost that is lower than those of dense system solvers.
8. Convergence and Error Estimates for ISC2COMM
9. Numerical Simulations
| ℵ | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|---|---|
| 3.3 × 10−3 | 1.2 × 10−5 | 1.0 × 10−7 | 4.4 × 10−9 | 1.4 × 10−11 | 1.8 × 10−13 | 3.2 × 10−16 | |
| CPU Time | 0.231 | 0.412 | 0.451 | 0.521 | 0.631 | 0.932 | 1.165 |
| 0.1 | 1.4 × |
| 0.2 | 2.6 × |
| 0.3 | 1.5 × |
| 0.4 | 2.2 × |
| 0.5 | 4.1 × |
| 0.6 | 4.9 × |
| 0.7 | 3.5 × |
| 0.8 | 1.2 × |
| 0.9 | 1.5 × |
| ℵ | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
|---|---|---|---|---|---|---|---|---|
| 4.3 × | 7.1 × | 4.4 × | 2.9 × | 1.2 × | 3.9 × | 1.0 × | 1.1 × | |
| CPU Time | 0.131 s | 0.372 | 0.421 | 0.523 | 0.631 | 0.682 | 0.955 | 1.197 |
| 0.1 | 2.4 × |
| 0.2 | 4.0 × |
| 0.3 | 2.5 × |
| 0.4 | 7.1 × |
| 0.5 | 5.1 × |
| 0.6 | 1.1 × |
| 0.7 | 4.2 × |
| 0.8 | 1.3 × |
| 0.9 | 4.3 × |
| ℵ | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
|---|---|---|---|---|---|---|---|---|
| 2.4 × | 1.2 × | 1.0 × | 5.5 × | 1.4 × | 1.7 × | 1.2 × | 1.0 × | |
| CPU Time | 0.133 | 0.380 | 0.434 | 0.541 | 0.662 | 0.702 | 0.878 | 1.229 |
| [17] | ||
|---|---|---|
| 0.1 | 1.1 × | 5.80 × |
| 0.2 | 1.0 × | 5.45 × |
| 0.3 | 2.7 × | 5.06 × |
| 0.4 | 9.0 × | 4.63 × |
| 0.5 | 3.1 × | 4.16 × |
| 0.6 | 9.0 × | 3.63 × |
| 0.7 | 4.2 × | 3.05 × |
| 0.8 | 1.4 × | 2.41 × |
| 0.9 | 2.3 × | 1.69 × |
| ℵ | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
|---|---|---|---|---|---|---|---|
| 2.4 × | 1.2 × | 1.0 × | 5.5 × | 1.4 × | 1.7 × | 8.0 × | |
| CPU Time | 0.333 | 0.552 | 0.581 | 0.622 | 0.682 | 0.714 | 0.893 |
| [17] | ||
|---|---|---|
| 0.1 | 4.1 × | 5.80 × |
| 0.2 | 5.3 × | 5.45 × |
| 0.3 | 1.7 × | 5.06 × |
| 0.4 | 4.2 × | 4.63 × |
| 0.5 | 3.1 × | 4.16 × |
| 0.6 | 3.3 × | 3.63 × |
| 0.7 | 2.5 × | 3.05 × |
| 0.8 | 1.2 × | 2.41 × |
| 0.9 | 2.3 × | 1.69 × |
| ℵ | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|---|---|
| 1.4 × | 1.8 × | 1.1 × | 3.5 × | 2.4 × | 3.8 × | 4.6 × | |
| CPU Time | 0.242 | 0.431 | 0.460 | 0.530 | 0.642 | 0.943 | 1.245 |
| ℵ | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|---|---|
| 3.1 × | 2.7 × | 4.1 × | 1.5 × | 4.4 × | 5.8 × | 1.6 × | |
| CPU Time | 0.251 | 0.471 | 0.490 | 0.530 | 0.681 | 0.983 | 1.278 |
- Array: For creating and manipulating arrays, which are used to hold coefficients and operational matrices throughout the computations.
- NSolve: For finding numerical solutions to nonlinear algebraic equations; it is utilized to compute the zeros of .
- FindRoot: For solving equations by finding roots; it is essential in handling the nonlinear aspects of our system, using a zero initial approximation.
- ChebyshevU: For generating MSC2Ps and IMSC2Ps, which serve as basis functions that provide the foundation for approximating the solution in our collocation method.
- D: To compute ordinary derivatives to determine the defined residuals.
- CaputoD: To compute Caputo fractional derivatives to determine the defined residuals.
- Table: For generating lists and arrays of values based on specified formulas, particularly for collocation points and other parameterized data.
| Algorithm 1 ISC2COMM Algorithm to Solve Model 1 (4) and (5) | |
| Step 1. | Given and . |
| Step 2. | Define the bases and and the matrices , and compute the elements of matrices and . |
| Step 3. | Evaluate the matrices: 1. , 2., 3., |
| Step 4. | Define as in Equation (41). |
| Step 5. | List , defined in Equation (42). |
| Step 6. | Use Mathematica’s built-in numerical solver to obtain the solution to the system of equations in [Output 5]. |
| Step 7. | Evaluate defined in Equation (38) (in the case of homogeneous conditions). |
| Step 8. | Evaluate and defined in Equation (46) (in the case of Nonhomogeneous conditions). |
| Algorithm 2 ISC2COMM Algorithm to Solve Model 2 (7) and (8) | |
| Step 1. | Given and . |
| Step 2. | Define the basis and and the matrices , and compute the elements of matrices and . |
| Step 3. | Evaluate the matrices: 1. , 2. 3. |
| Step 4. | Define as in Equation (50). |
| Step 5. | List , defined in Equation (51). |
| Step 6. | Use Mathematica’s built-in numerical solver to obtain the solution to the system of equations in [Output 5]. |
| Step 7. | Evaluate defined in Equation (47) (in the case of homogeneous conditions). |
| Step 8. | Evaluate and defined in Equation (55) (in the case of Nonhomogeneous conditions). |
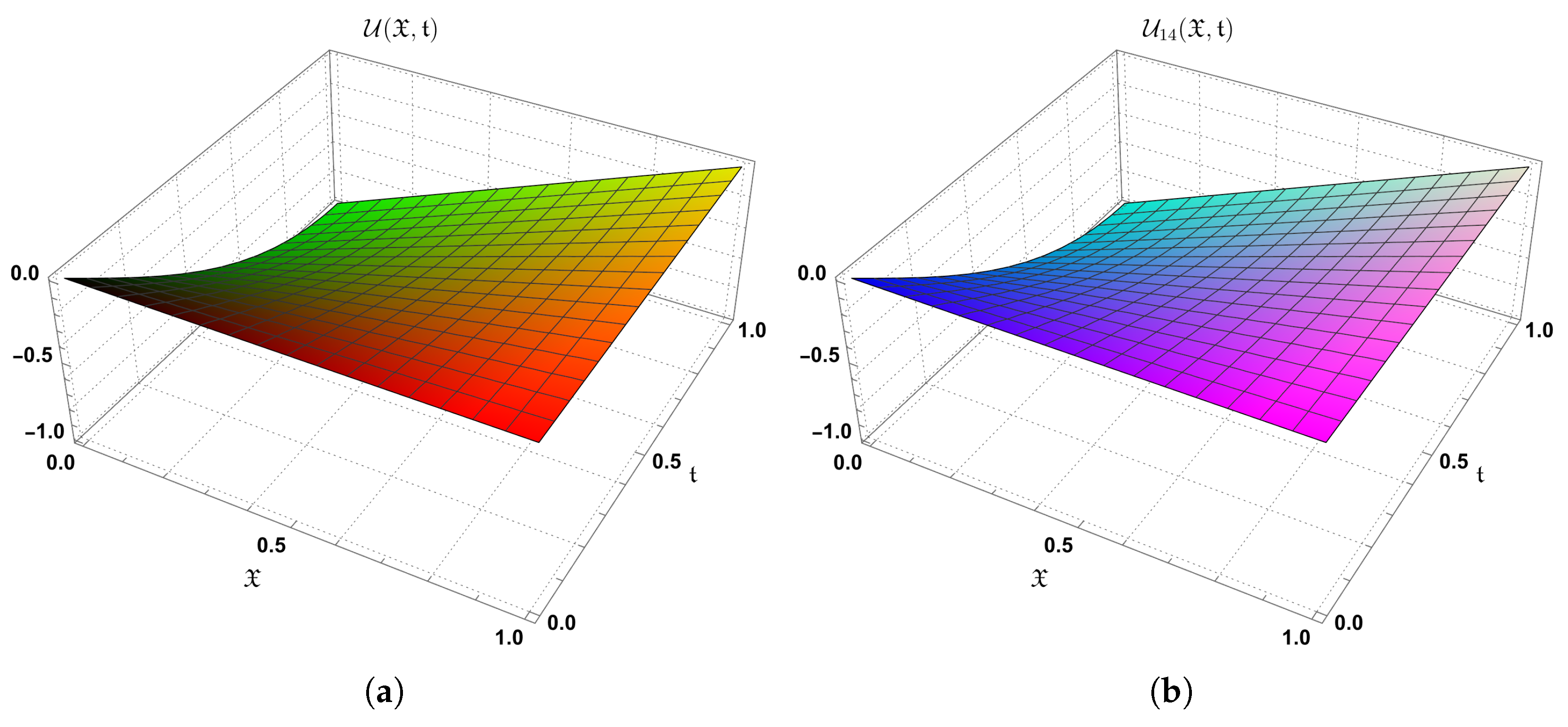

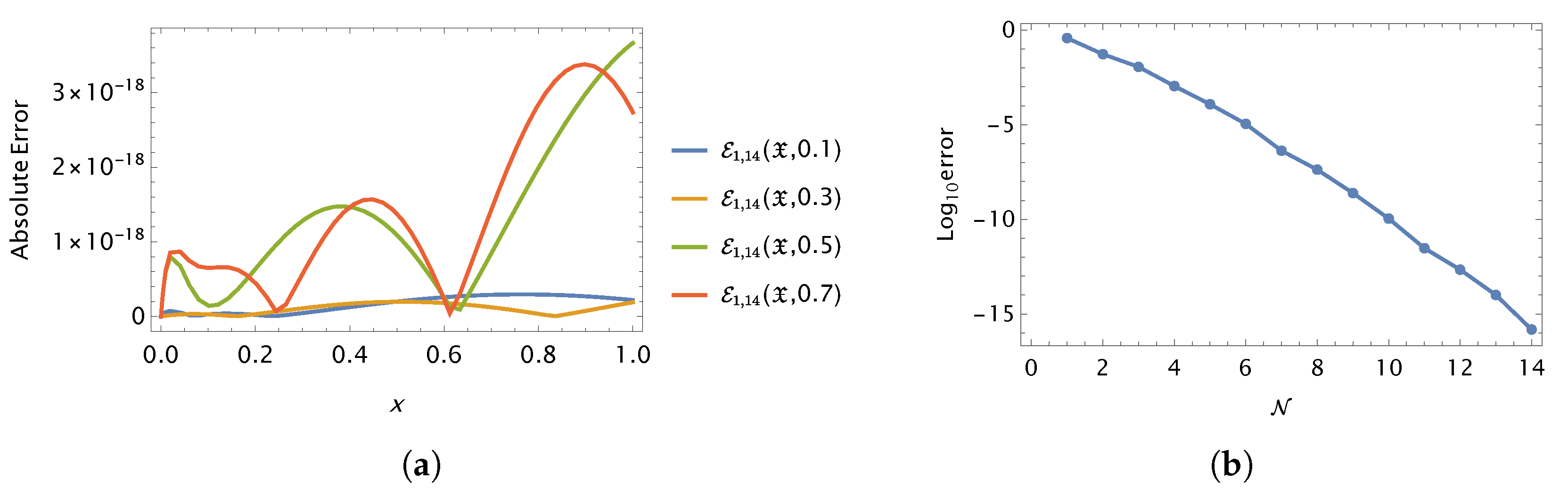
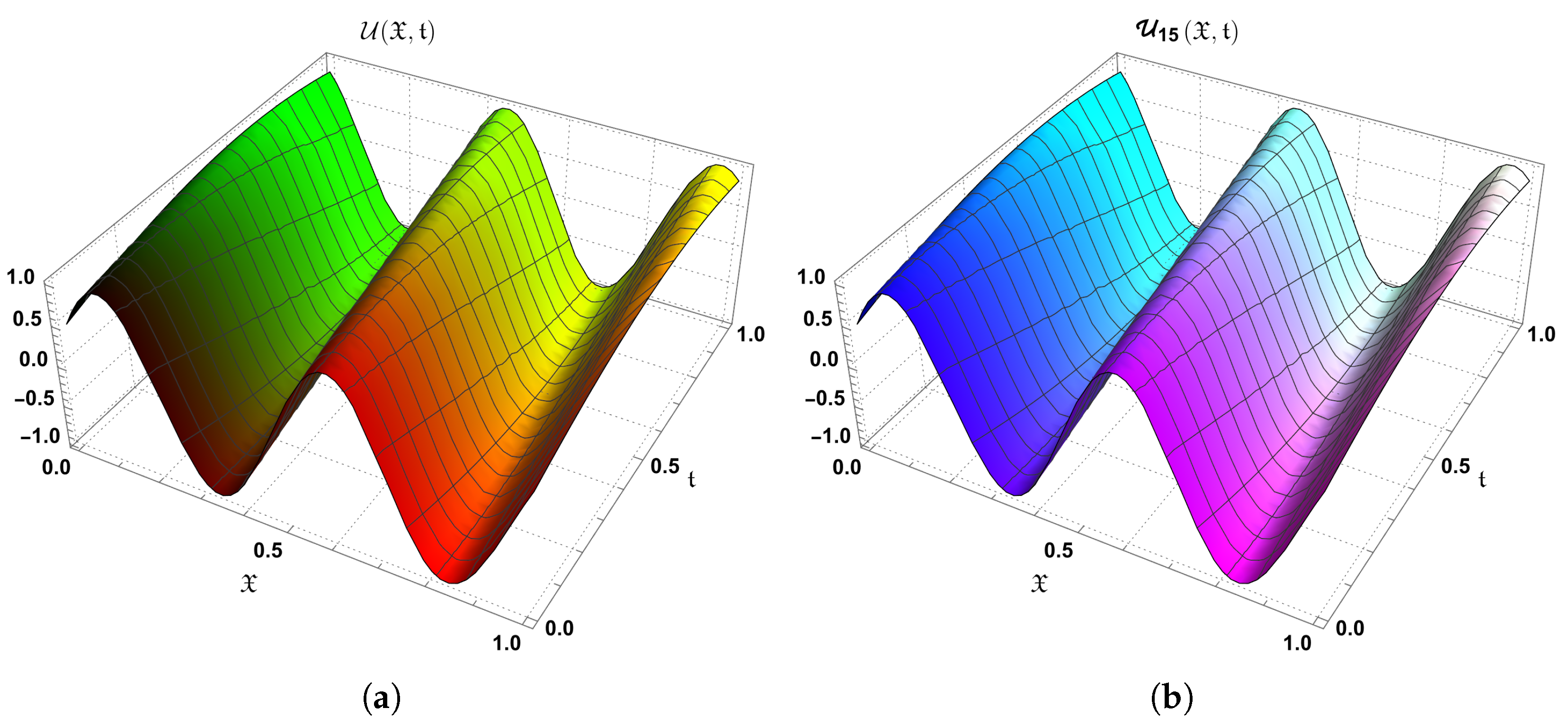
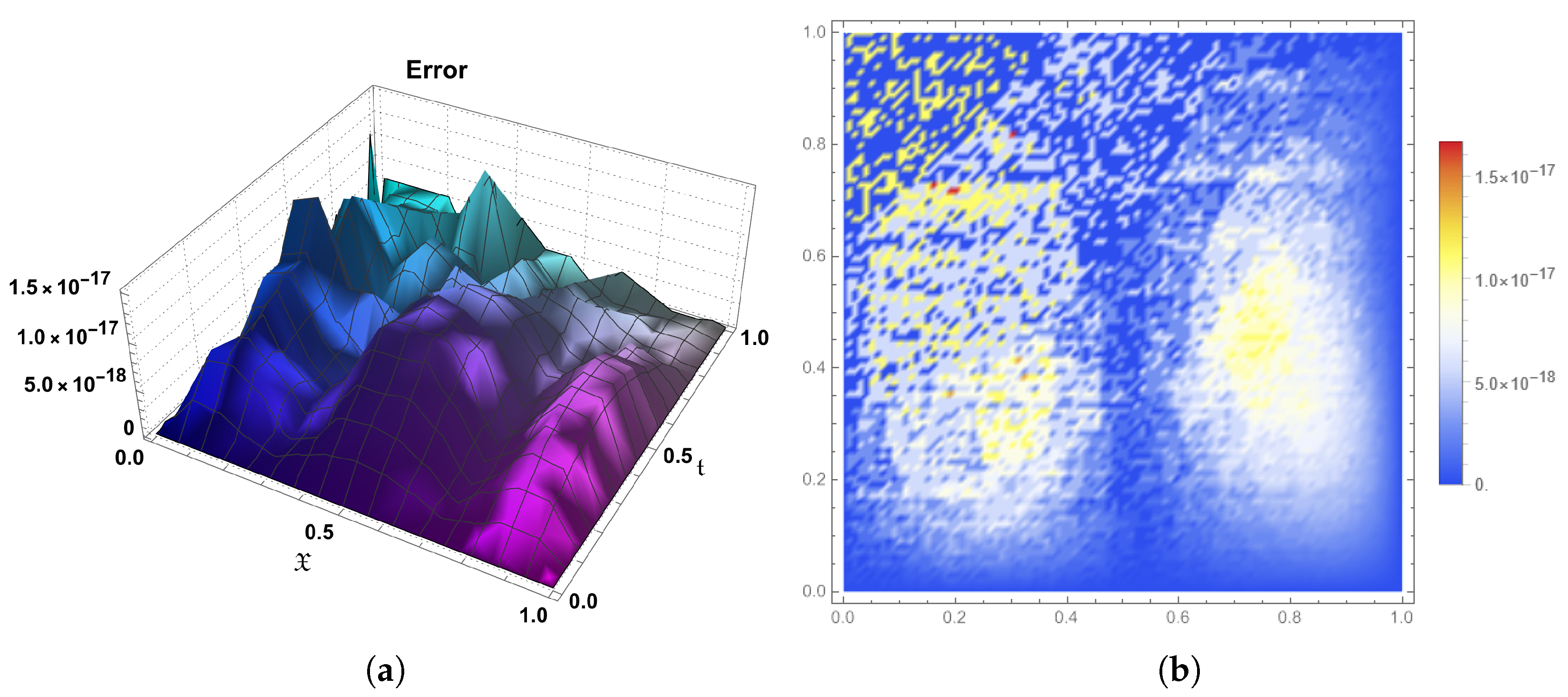

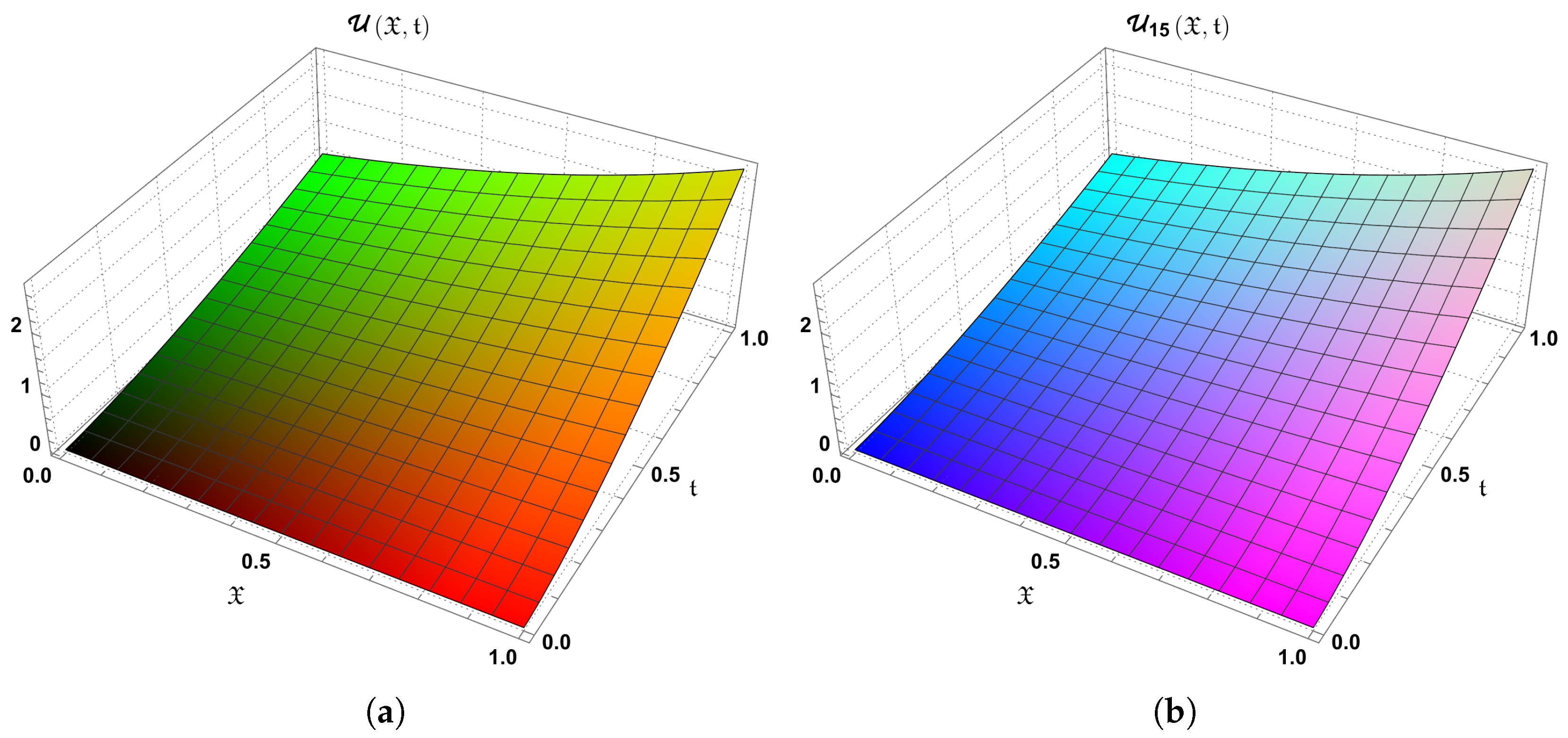
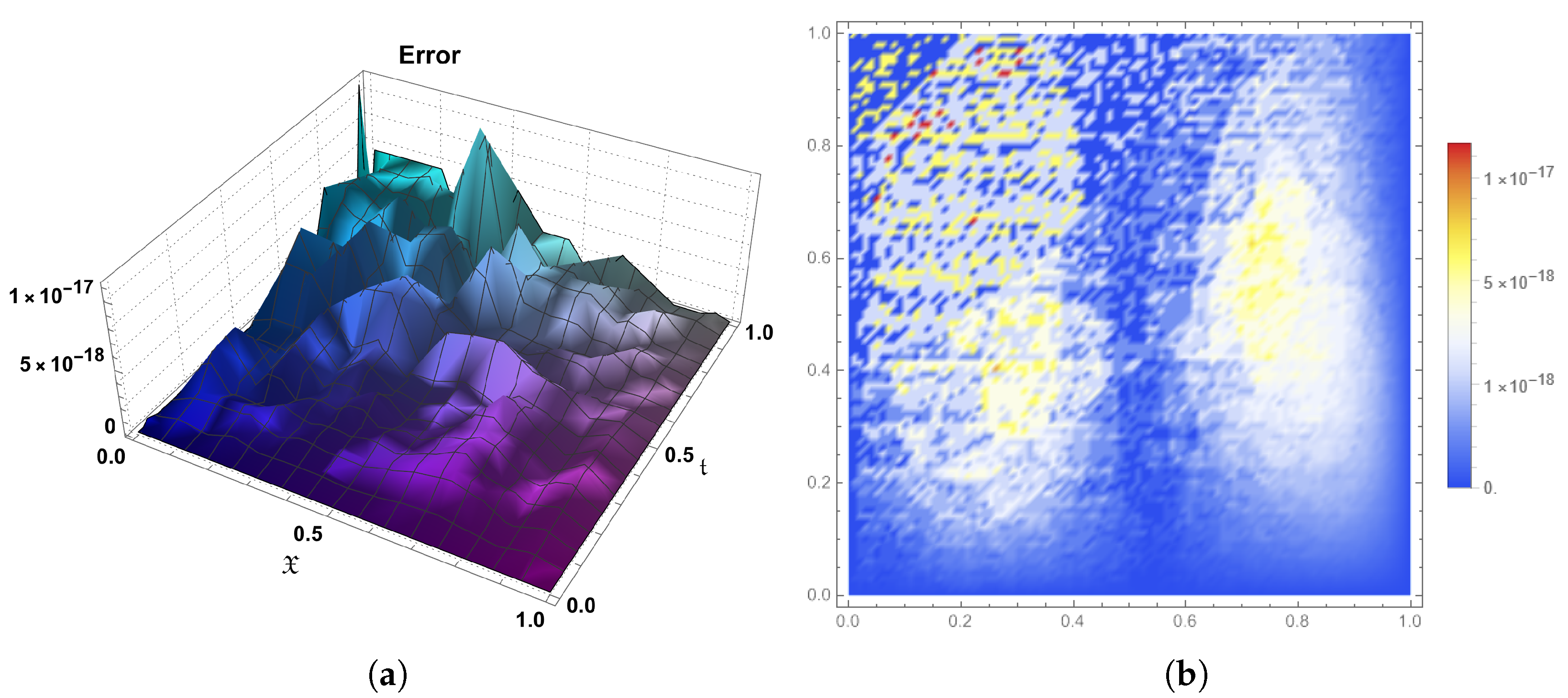


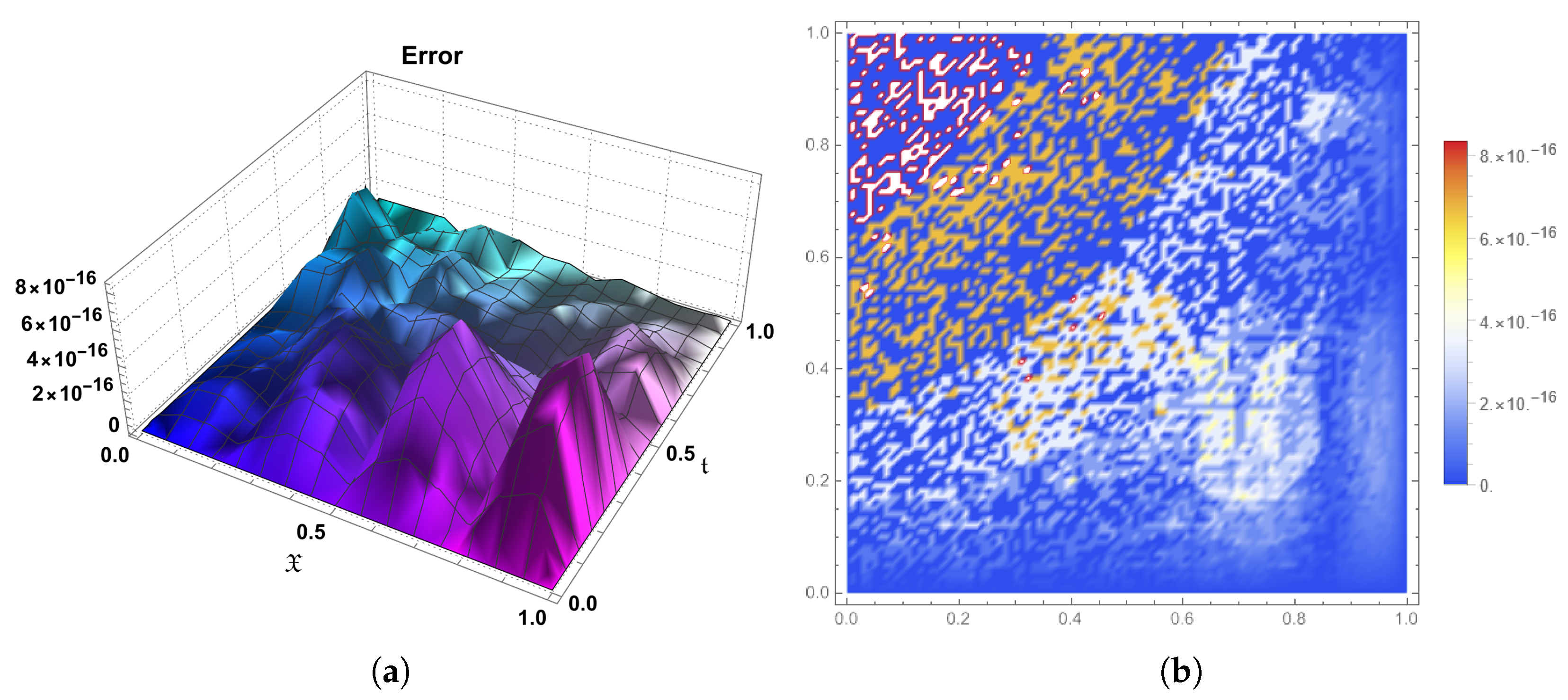


10. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
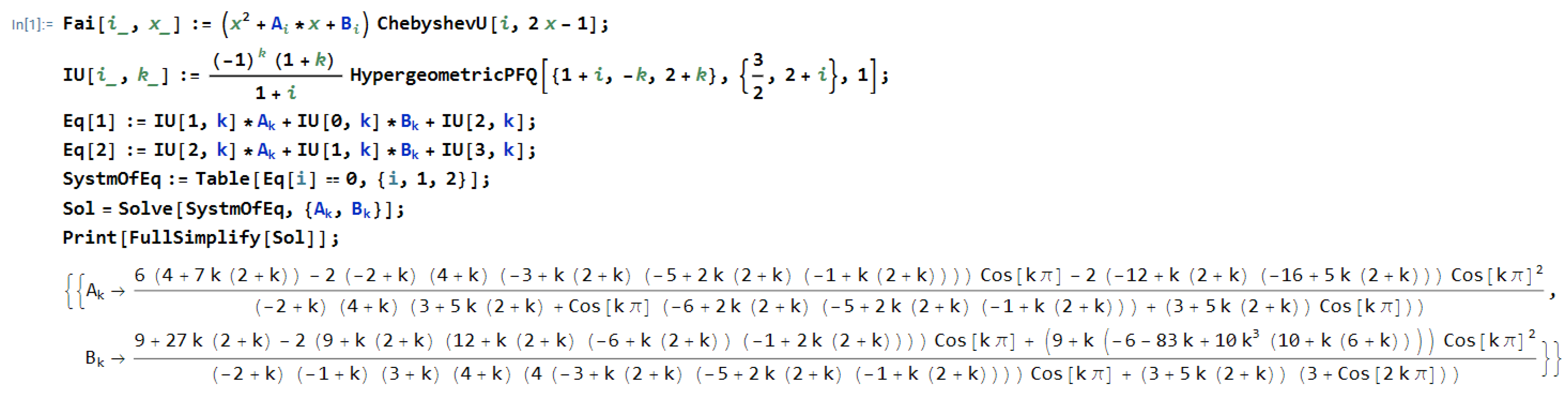
References
- Nigmatullin, R. The realization of the generalized transfer equation in a medium with fractal geometry. Phys. Status Solidi B 1986, 133, 425–430. [Google Scholar] [CrossRef]
- Chen, P.; Ma, W.; Tao, S.; Zhang, K. Blowup and global existence of mild solutions for fractional extended Fisher–Kolmogorov equations. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 641–656. [Google Scholar] [CrossRef]
- Langlands, T.A.M.; Henry, B.I.; Wearne, S.L. Fractional cable equation models for anomalous electrodiffusion in nerve cells: Finite domain solutions. SIAM J. Appl. Math. 2011, 71, 1168–1203. [Google Scholar] [CrossRef]
- Biler, P.; Funaki, T.; Woyczynski, W. Fractal Burgers equations. J. Diff. Equ. 1998, 148, 9–46. [Google Scholar] [CrossRef]
- Cahlon, B.; Kulkarni, D.; Shi, P. Stepwise stability for the heat equation with a nonlocal constraint. SIAM J. Numer. Anal. 1995, 32, 571–593. [Google Scholar] [CrossRef]
- Cannon, J.R. The solution of the heat equation subject to the specification of energy. Q. Appl. Math. 1963, 21, 155–160. [Google Scholar] [CrossRef]
- Choi, Y.; Chan, K. A parabolic equation with nonlocal boundary conditions arising from electrochemistry. Nonlinear Anal. 1992, 18, 317–331. [Google Scholar] [CrossRef]
- Shi, P. Weak solution to an evolution problem with a nonlocal constraint. SIAM J. Math. Anal. 1993, 24, 46–58. [Google Scholar] [CrossRef]
- Samarski, A. Some problems in the modern theory of differential equation. Differ. Uraven 1980, 16, 1221–1228. [Google Scholar]
- Du, J.; Cui, M. Solving the forced Duffing equation with integral boundary conditions in the reproducing kernel space. Int. J. Comput. Math. 2010, 87, 2088–2100. [Google Scholar] [CrossRef]
- Geng, F.; Cui, M. New method based on the HPM and RKHSM for solving forced Duffing equations with integral boundary conditions. J. Comput. Appl. Math. 2009, 233, 165–172. [Google Scholar] [CrossRef]
- Doostdar, M.; Kazemi, M.; Vahidi, A. A numerical method for solving the Duffing equation involving both integral and non-integral forcing terms with separated and integral boundary conditions. Comput. Methods Differ. Equ. 2023, 11, 241–253. [Google Scholar]
- Chen, Z.; Jiang, W.; Du, H. A new reproducing kernel method for Duffing equations. Int. J. Comput. Math. 2021, 98, 2341–2354. [Google Scholar] [CrossRef]
- Bahuguna, D.; Abbas, S.; Dabas, J. Partial functional differential equation with an integral condition and applications to population dynamics. Nonlinear Anal. 2008, 69, 2623–2635. [Google Scholar] [CrossRef]
- Kamynin, L.I. A boundary-value problem in the theory of heat conduction with non-classical boundary conditions. Zh. Vychisl. Mat. Fiz. 1964, 4, 1006–1024. [Google Scholar]
- Balaji, S.; Hariharan, G. An efficient operational matrix method for the numerical solutions of the fractional Bagley–Torvik equation using wavelets. J. Math. Chem. 2019, 57, 1885–1901. [Google Scholar] [CrossRef]
- Brahimi, S.; Merad, A.; Kılıçman, A. Theoretical and Numerical Aspect of Fractional Differential Equations with Purely Integral Conditions. Mathematics 2021, 9, 1987. [Google Scholar] [CrossRef]
- Day, W.A. A decreasing property of solutions of parabolic equations with applications to thermoelasticity. Quart. Appl. Math. 1983, 40, 468–475. [Google Scholar] [CrossRef]
- Martin-Vaquero, J.; Merad, A. Existence, uniqueness and numerical solution of a fractional PDE with integral conditions. Nonlinear Anal. Model. Control. 2019, 24, 368–386. [Google Scholar] [CrossRef]
- Anguraj, A.; Karthikeyan, P. Existence of solutions for fractional semiliear evolution boundary value problem. Commun. Appl. Anal. 2010, 14, 505. [Google Scholar]
- Benchohra, M.; Graef, J.; Hamani, S. Existence results for boundary value problems with non-linear fractional differential equations. Appl. Anal. 2008, 87, 851–863. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. Boundary value problems for fractional diffusion-wave equation. Aust. J. Math. Anal. Appl. 2006, 3, 8. [Google Scholar]
- Amiraliyev, G.; Amiraliyeva, I.; Kudu, M. A numerical treatment for singularly perturbed differential equations with integral boundary condition. Appl. Math. Comput. 2007, 185, 574–582. [Google Scholar] [CrossRef]
- Mashayekhi, S.; Ordokhani, Y.; Razzaghi, M. A hybrid functions approach for the Duffing equation. Phys. Scr. 2013, 88, 025002. [Google Scholar] [CrossRef]
- Ahmed, H. New generalized Jacobi–Galerkin operational matrices of derivatives: An algorithm for solving the time-fractional coupled KdV equations. Bound. Value Probl. 2024, 2024, 144. [Google Scholar] [CrossRef]
- Ahmed, H. Enhanced shifted Jacobi operational matrices of integrals: Spectral algorithm for solving some types of ordinary and fractional differential equations. Bound. Value Probl. 2024, 2024, 75. [Google Scholar] [CrossRef]
- Ahmed, H. Enhanced shifted Jacobi operational matrices of derivatives: Spectral algorithm for solving multiterm variable-order fractional differential equations. Bound. Value Probl. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Ahmed, H. New Generalized Jacobi Polynomial Galerkin Operational Matrices of Derivatives: An Algorithm for Solving Boundary Value Problems. Fractal Fract. 2024, 8, 199. [Google Scholar] [CrossRef]
- Ahmed, H. Highly accurate method for boundary value problems with Robin boundary conditions. J. Nonlinear Math. Phys. 2023, 30, 1239–1263. [Google Scholar] [CrossRef]
- Napoli, A.; Abd-Elhameed, W.M. A new collocation algorithm for solving even-order boundary value problems via a novel matrix method. Mediterr. J. Math. 2017, 14, 170. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Youssri, Y. Spectral solutions for fractional differential equations via a novel Lucas operational matrix of fractional derivatives. Rom. J. Phys. 2016, 61, 795–813. [Google Scholar]
- Loh, J.R.; Phang, C. Numerical solution of Fredholm fractional integro-differential equation with Right-sided Caputo’s derivative using Bernoulli polynomials operational matrix of fractional derivative. Mediterr. J. Math. 2019, 16, 28. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Abd-Elhameed, W.; Ahmed, H.; Youssri, Y. A new generalized Jacobi Galerkin operational matrix of derivatives: Two algorithms for solving fourth-order boundary value problems. Adv. Differ. Equ. 2016, 2016, 1–16. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica Version Number 13.3.1; Wolfram Research, Inc.: Champaign, IL, USA, 2023. [Google Scholar]
- Luke, Y. Special Functions and Their Approximations; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Lakshmikantham, V.; Sen, S.K. Computational Error and Complexity in Science and Engineering; Elsevier: Melbourne, FL, USA, 2005. [Google Scholar]
- Kirk, D.; Wen-Mei, W. Programming Massively Parallel Processors: A Hands-On Approach; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Hafez, R.; Abd-Elhameed, W. A computational strategy for nonlinear time-fractional generalized Kawahara equation using new eighth-kind Chebyshev operational matrices. Phys. Scr. 2024, 99, 045250. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.; Ahmed, H.; Zaky, M.; Hafez, R. A new shifted generalized Chebyshev approach for multi-dimensional sinh-Gordon equation. Phys. Scr. 2024, 99, 095269. [Google Scholar] [CrossRef]
- Ahmed, H. New Generalized Jacobi Galerkin operational matrices of derivatives: An algorithm for solving multi-term variable-order time-fractional diffusion-wave equations. Fractal Fract. 2024, 8, 68. [Google Scholar] [CrossRef]
- Narumi, S. Some formulas in the theory of interpolation of many independent variables. Tohoku Math. J. 1920, 18, 309–321. [Google Scholar]
- Mason, J.; Handscomb, D. Chebyshev Polynomials; Chapman and Hall: New York, NY, USA; CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.M. Highly Accurate Numerical Method for Solving Fractional Differential Equations with Purely Integral Conditions. Fractal Fract. 2025, 9, 407. https://doi.org/10.3390/fractalfract9070407
Ahmed HM. Highly Accurate Numerical Method for Solving Fractional Differential Equations with Purely Integral Conditions. Fractal and Fractional. 2025; 9(7):407. https://doi.org/10.3390/fractalfract9070407
Chicago/Turabian StyleAhmed, Hany M. 2025. "Highly Accurate Numerical Method for Solving Fractional Differential Equations with Purely Integral Conditions" Fractal and Fractional 9, no. 7: 407. https://doi.org/10.3390/fractalfract9070407
APA StyleAhmed, H. M. (2025). Highly Accurate Numerical Method for Solving Fractional Differential Equations with Purely Integral Conditions. Fractal and Fractional, 9(7), 407. https://doi.org/10.3390/fractalfract9070407








