Solitons, Cnoidal Waves and Nonlinear Effects in Oceanic Shallow Water Waves
Abstract
1. Introduction
2. Residual Symmetry and Localization
2.1. Residual Symmetry and Bäcklund Transformation
2.2. Soliton Solutions
3. CRE Solvability and Interaction Solutions
3.1. CRE Solvability
3.2. Solitary Wave and Soliton–Cnoidal Wave Solutions
3.2.1. Solitary Wave Solutions
3.2.2. Soliton–Cnoidal Wave Solutions
4. Exact Solutions of gBBKW Equations by Modified Sardar Sub-Equation Method
4.1. Description of Modified Sardar Sub-Equation Method
4.2. Exact Solutions of gBBKW Equations
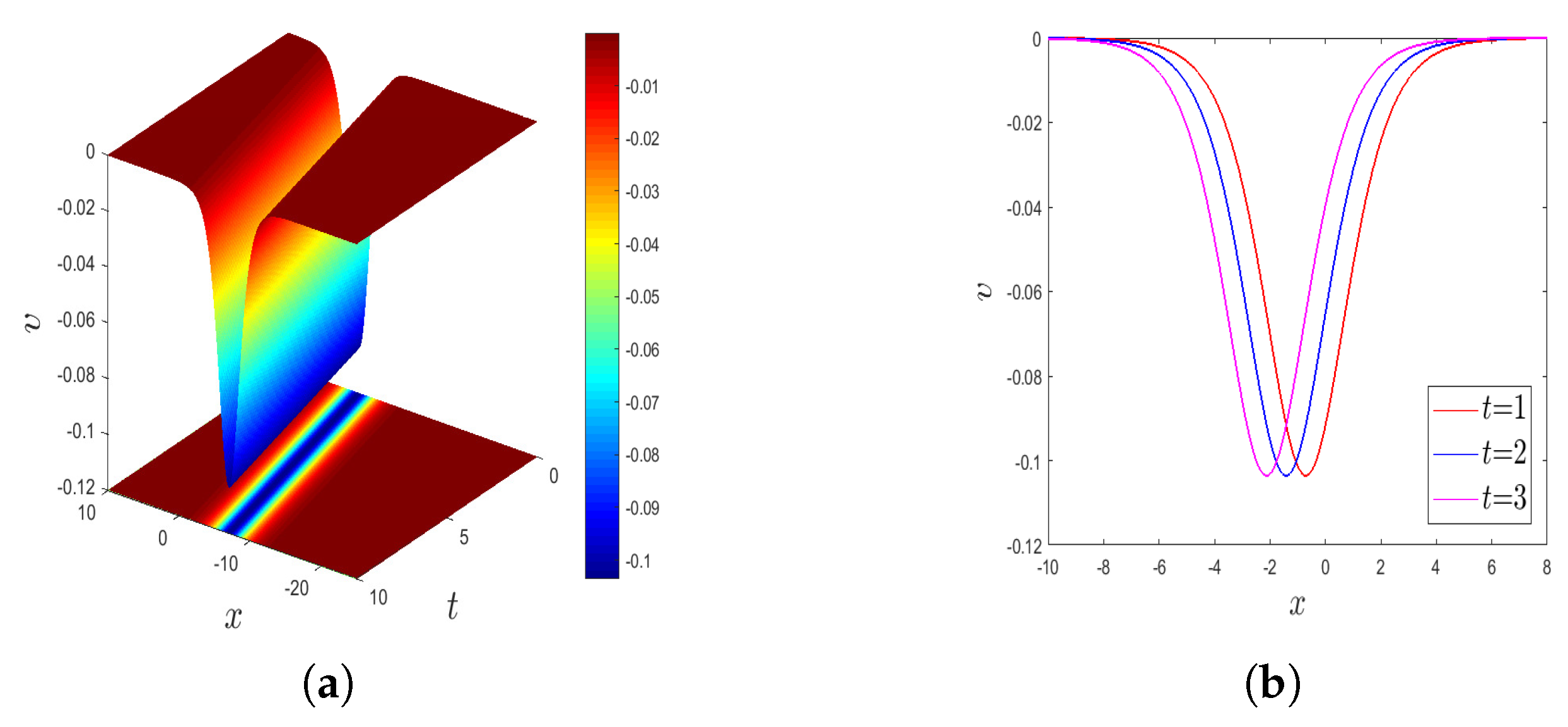
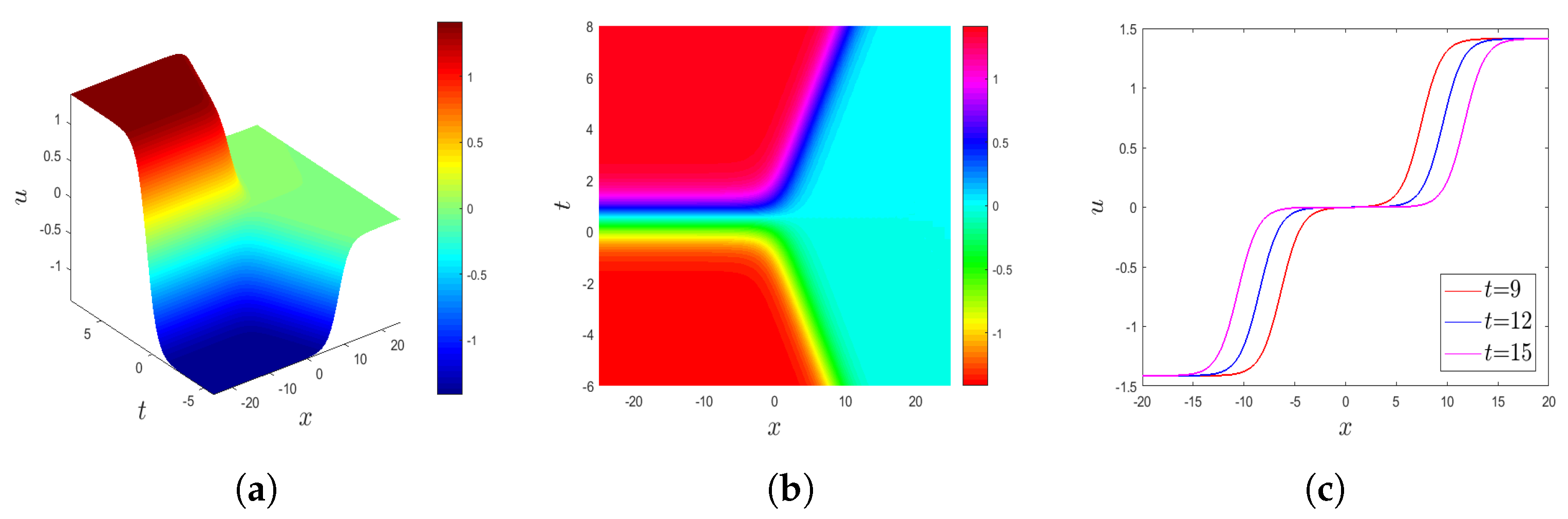
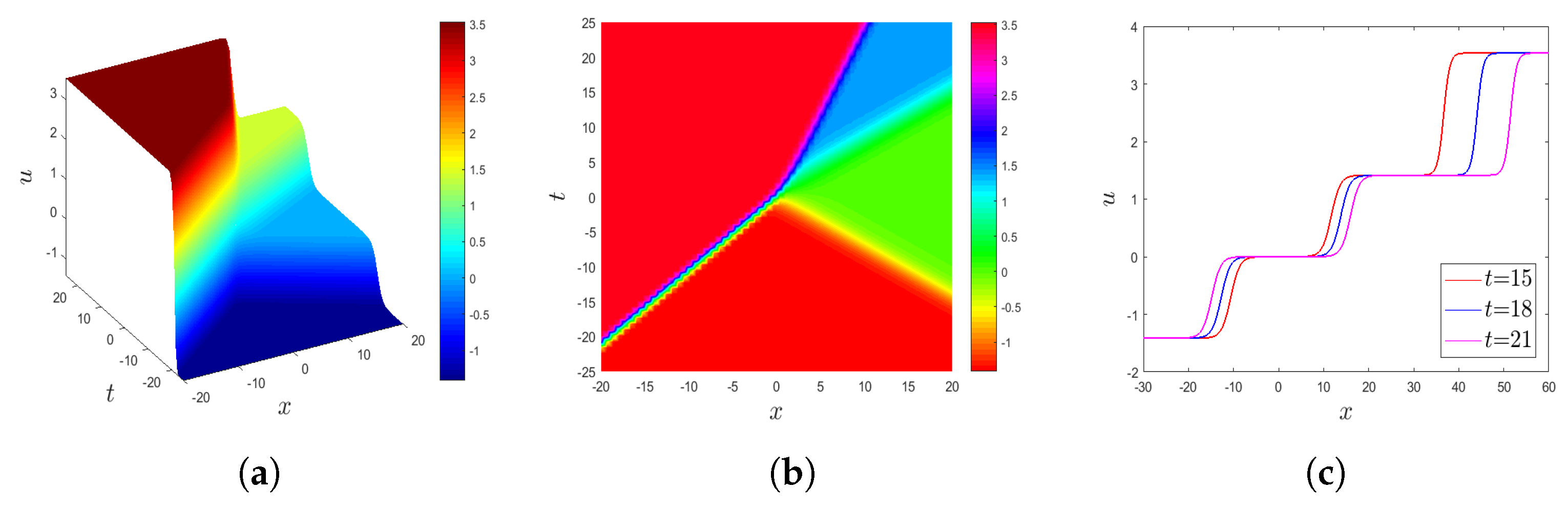
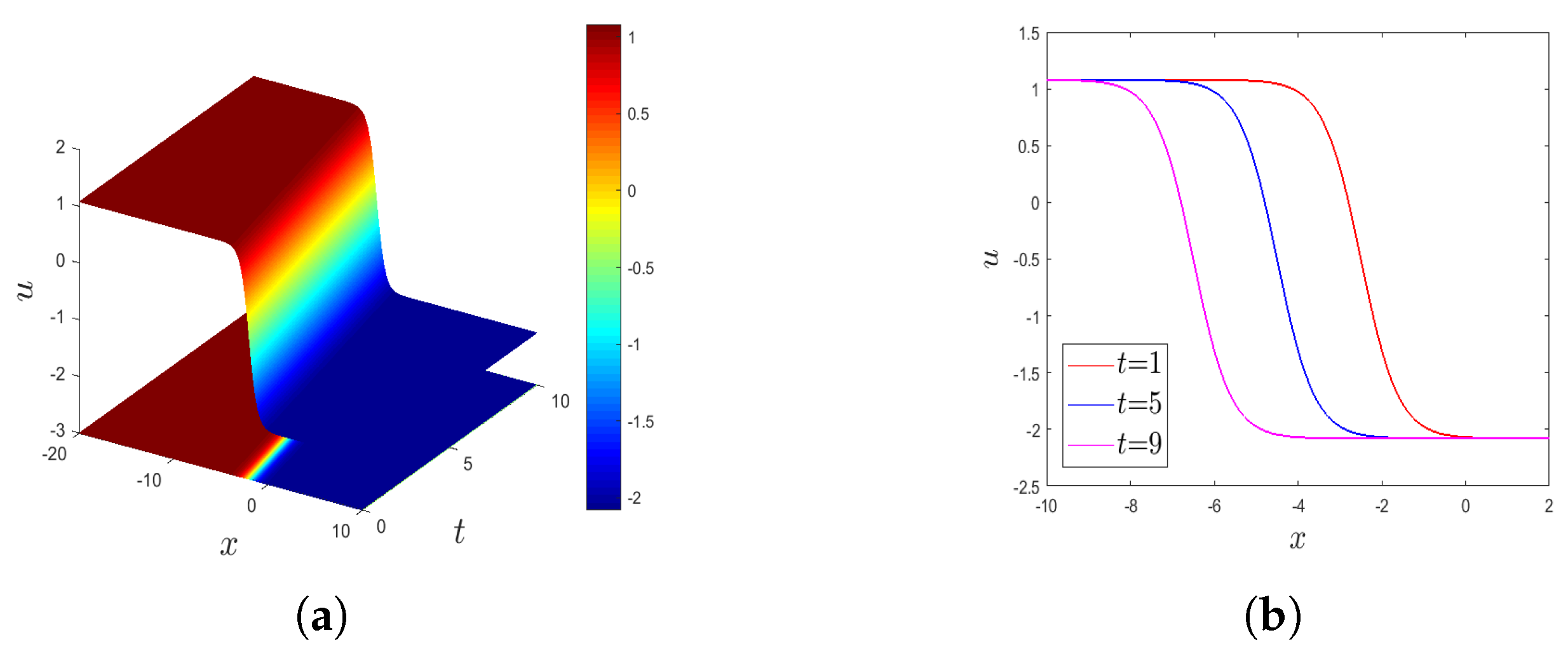
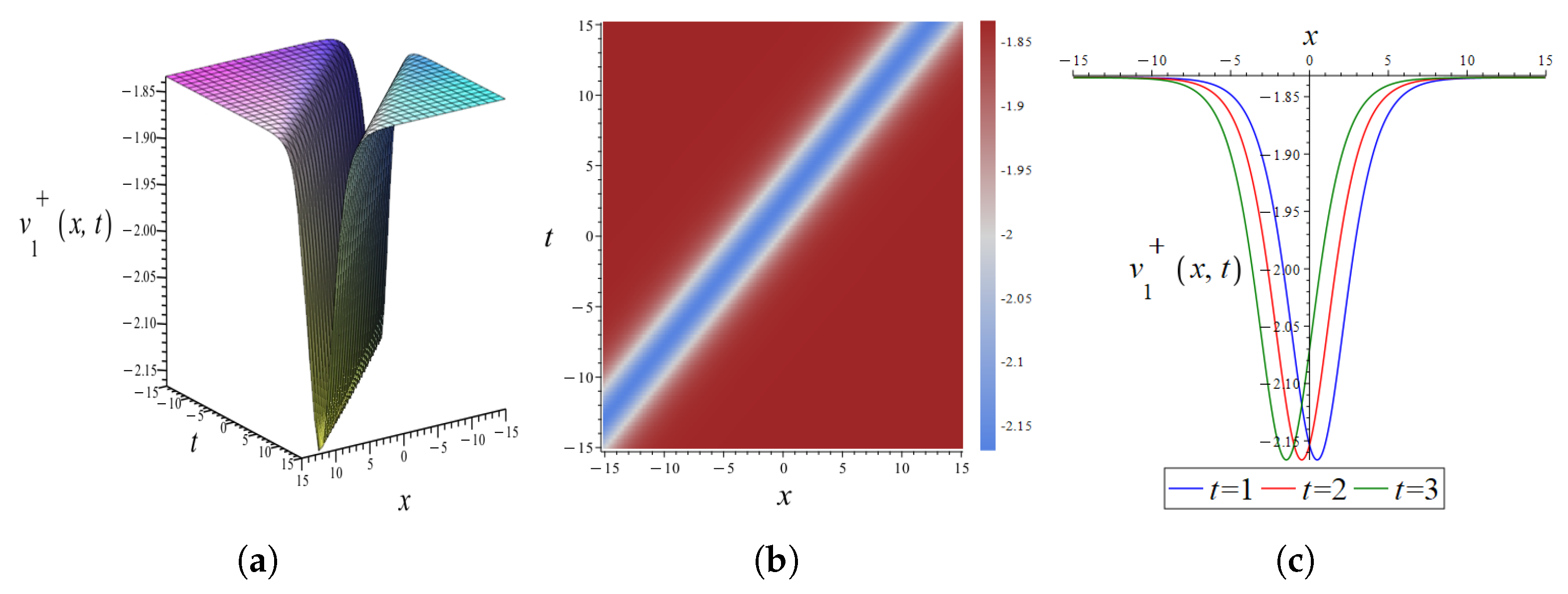
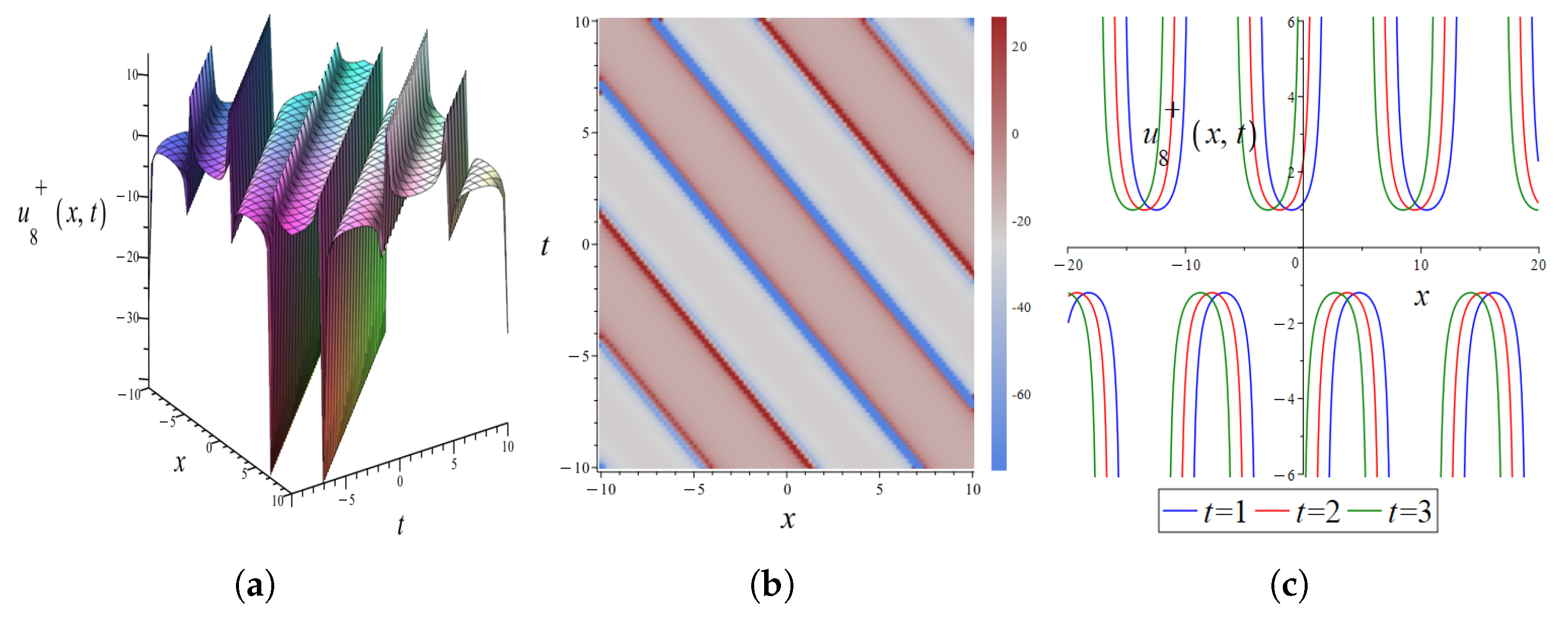
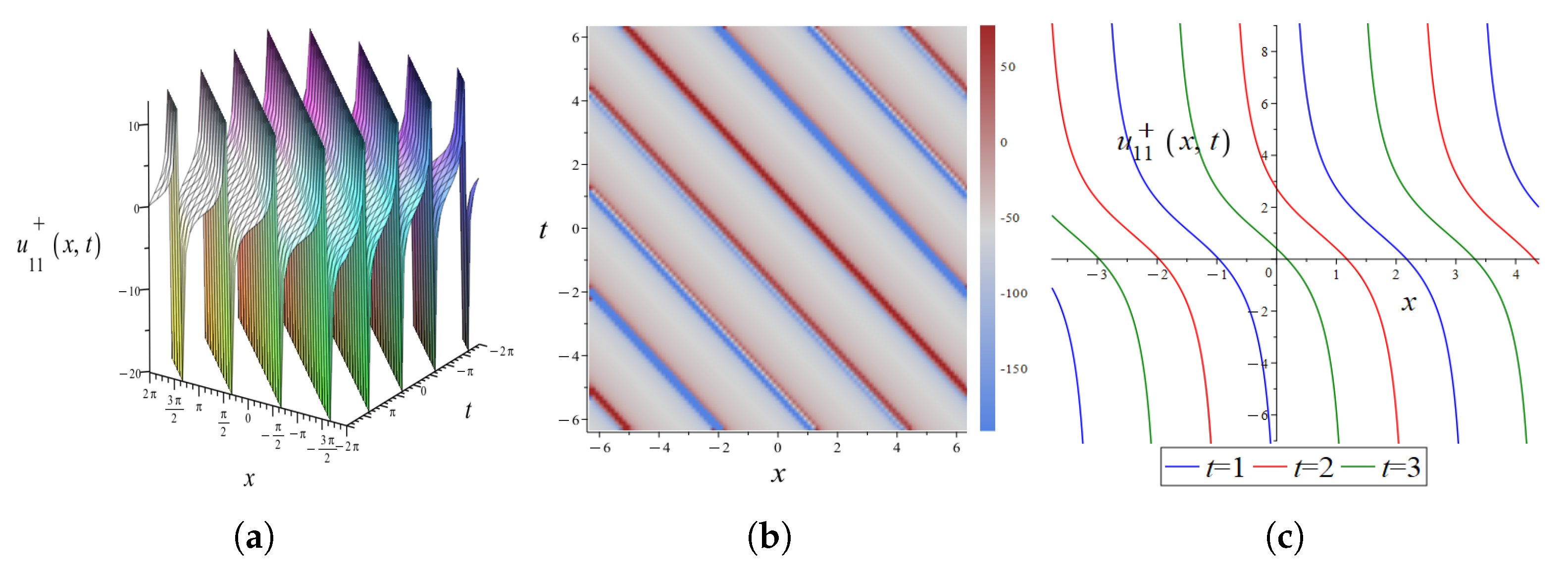
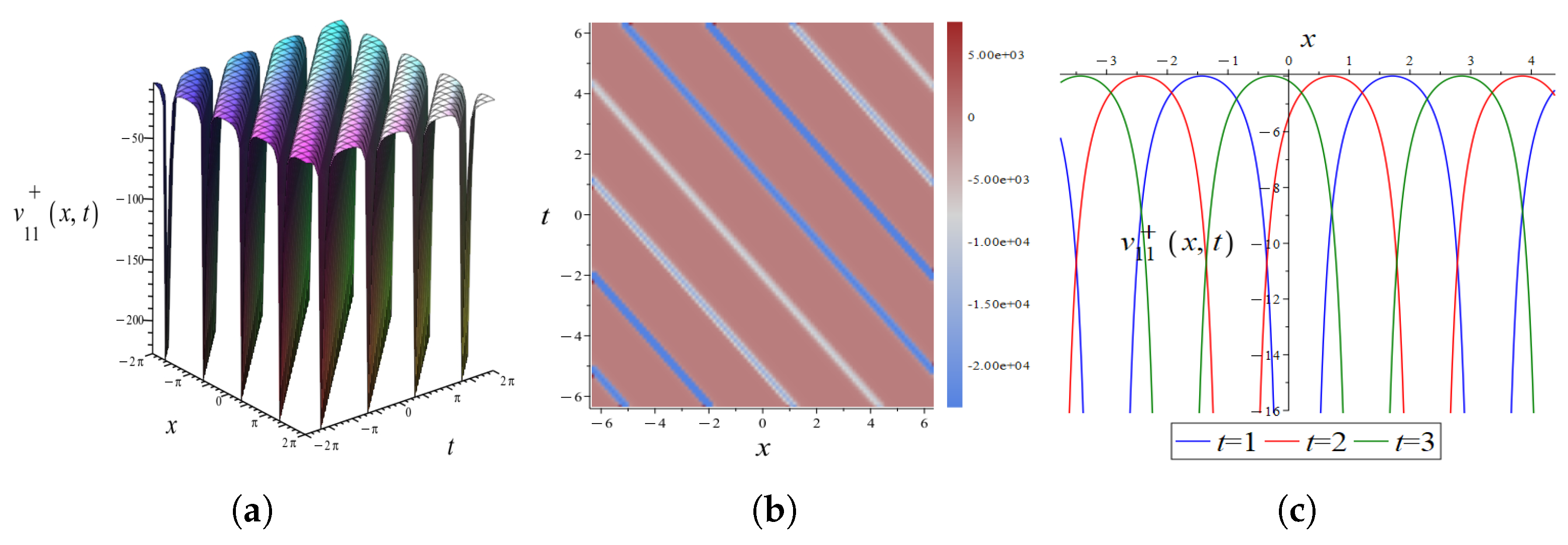
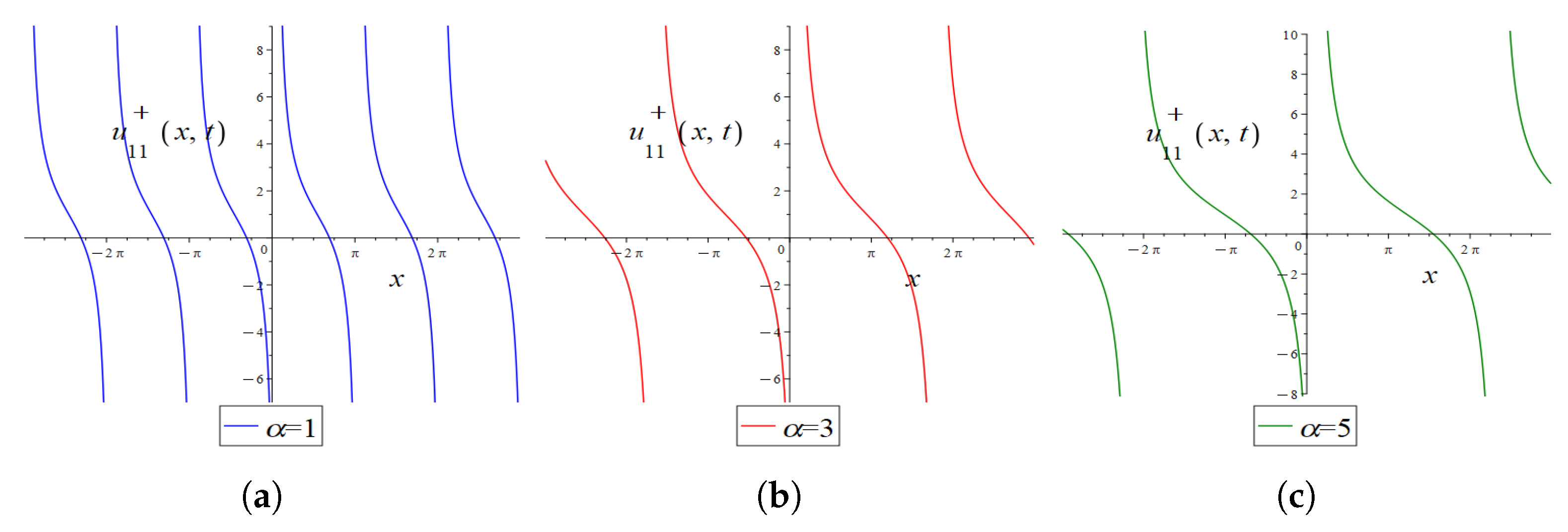
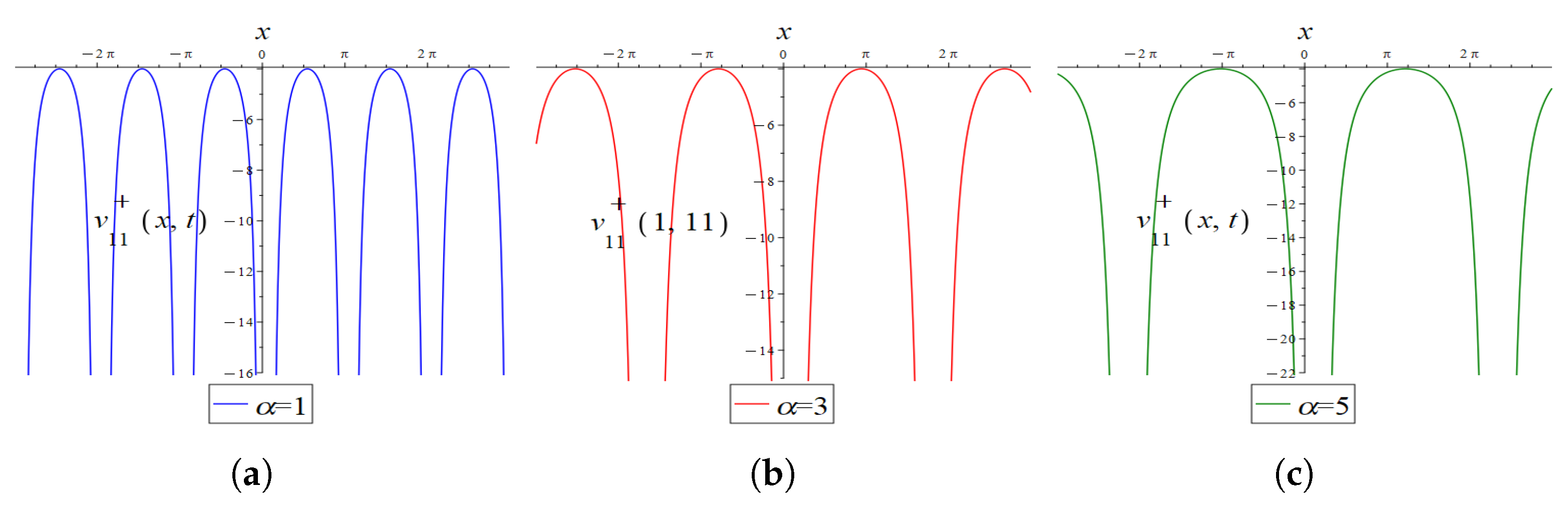
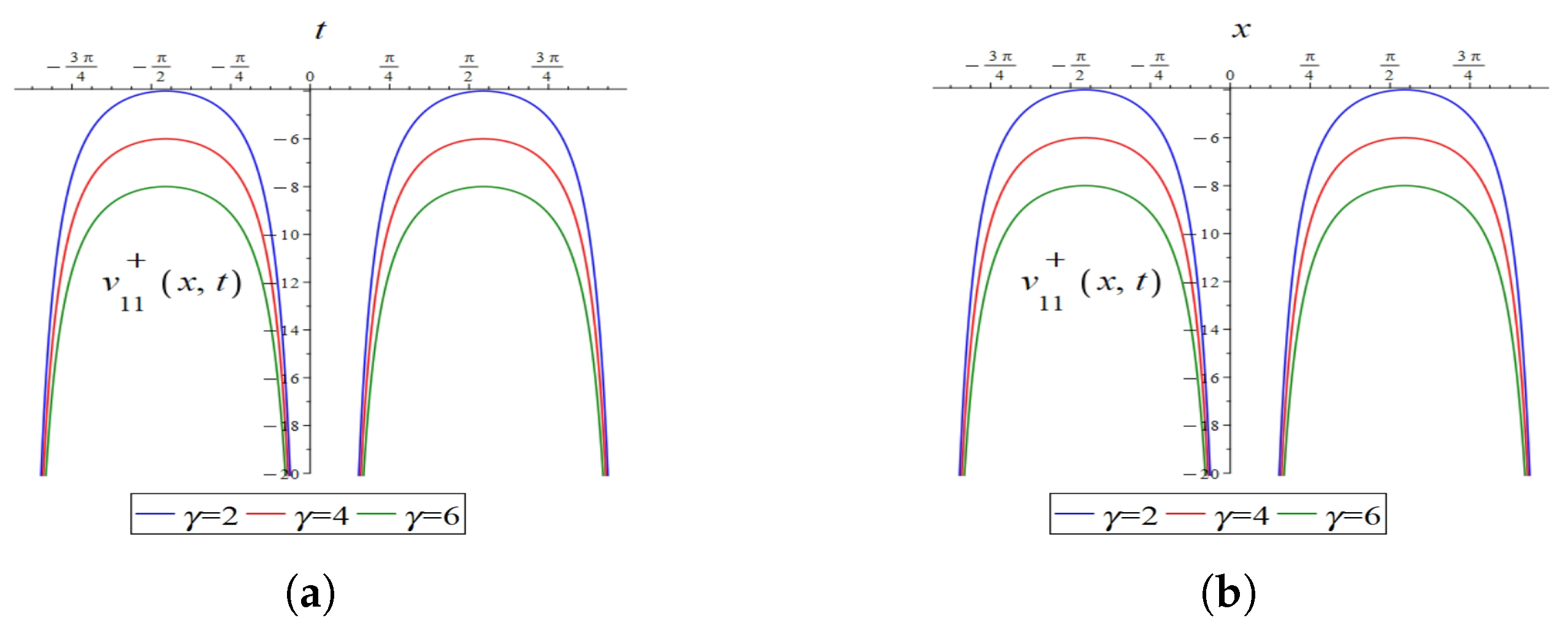
4.3. Graphical Interpretation of the Exact Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| gBBKW | generalized Boussinesq–Broer–Kaup–Whitham; |
| CRE | consistent Riccati expansion; |
| KdV | Korteweg–de Vries; |
| mKdV | modified Korteweg–de Vries; |
| NPDEs | nonlinear partial differential equations; |
| SSM | Sardar sub-equation method; |
| MSSM | modified Sardar sub-equation method; |
| KB | Kaup–Boussinesq; |
| WBK | Whitham–Broer–Kaup; |
| ODE | ordinary differential equation. |
References
- Kodama, Y. KP Solitons and the Grassmannians; Springer Briefs in Mathematical Physics; Springer: Singapore, 2017. [Google Scholar]
- Maleewong, M.; Grimshaw, R. Evolution of wind-generated shallow-water waves in the framework of a modified Kadomtsev-Petviashvili equation. Fluids 2025, 10, 61. [Google Scholar] [CrossRef]
- Thomas, D.B. Cosmological gravity on all scales: Simple equations, required conditions, and a framework for modified gravity. Phys. Rev. D 2020, 101, 123517. [Google Scholar] [CrossRef]
- Bernardo, H.; Franzmann, G. α′-Cosmology: Solutions and stability analysis. J. High Energy Phys. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Joseph, G.W.; Övgün, A. Cosmology with variable G and nonlinear electrodynamics. Indian J. Phys. 2022, 96, 1861–1866. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Nonlinear equations for symmetric massless higher spin fields in (A)dSd. Phys. Lett. B 2003, 567, 139–151. [Google Scholar] [CrossRef]
- Benci, V.; Fortunato, D. Variational Methods in Nonlinear Field Equations; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Cheemaa, N.; Seadawy, A.R.; Sugati, T.G.; Baleanu, D. Study of the dynamical nonlinear modified Korteweg–de Vries equation arising in plasma physics and its analytical wave solutions. Results Phys. 2020, 19, 103480. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel exact and approximate solutions to the family of the forced damped Kawahara equation and modeling strong nonlinear waves in a plasma. Chin. J. Phys. 2022, 77, 2454–2471. [Google Scholar] [CrossRef]
- Xie, X.Y.; Meng, G.Q. Collisions between the dark solitons for a nonlinear system in the geophysical fluid. Chaos Soliton. Fract. 2018, 107, 143–145. [Google Scholar] [CrossRef]
- Panoiu, N.C.; Sha, W.E.I.; Lei, D.Y.; Li, G.C. Nonlinear optics in plasmonic nanostructures. J. Opt. 2018, 20, 083001. [Google Scholar] [CrossRef]
- Wen, X.; Gong, Z.; Li, D. Nonlinear optics of two-dimensional transition metal dichalcogenides. InfoMat 2019, 1, 317–337. [Google Scholar] [CrossRef]
- Johnson, R.S. Application of the ideas and techniques of classical fluid mechanics to some problems in physical oceanography. Philos. Trans. R. Soc. A 2018, 376, 20170092. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhang, Y.F. Residual symmetries and Bäcklund transformations of (2+1)-dimensional strongly coupled Burgers system. Adv. Math. Phys. 2020, 2020, 6821690. [Google Scholar] [CrossRef]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2+1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Younis, M.; Ali, I.; Althobaiti, S.; Mahmoud, S.F. Soliton solutions, Painleve analysis and conservation laws for a nonlinear evolution equation. Results Phys. 2021, 23, 103999. [Google Scholar] [CrossRef]
- Yuan, F.; He, J.S.; Cheng, Y. Exact solutions of a (2+1)-dimensional extended shallow water wave equation. Chinese Phys. B 2019, 28, 237–244. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Chen, J.; Guo, Q. Construction of higher-order smooth positons and breather positons via Hirota’s bilinear method. Nonlinear Dynam. 2021, 105, 2611–2618. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, Z. The derivative nonlinear Schrödinger equation with zero/nonzero boundary conditions: Inverse scattering transforms and N-double-pole solutions. J. Nonlinear Sci. 2020, 30, 3089–3127. [Google Scholar] [CrossRef]
- Xin, X.; Liu, Y.; Xia, Y.; Liu, H. Integrability, Darboux transformation and exact solutions for nonlocal couplings of AKNS equations. Appl. Math. Lett. 2021, 119, 107209. [Google Scholar] [CrossRef]
- Wang, X.; He, J.S. Darboux transformation and general soliton solutions for the reverse space-time nonlocal short pulse equation. Phys. D 2023, 446, 133639. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhang, Y.F. A kind of nonisospectral and isospectral integrable couplings and their Hamiltonian systems. Commun. Nonlinear Sci. 2021, 99, 105822. [Google Scholar] [CrossRef]
- Liu, W.H.; Zhang, Y.F. Optimal systems, similarity reductions and new conservation laws for the classical Boussinesq–Burgers system. Eur. Phys. J. Plus 2020, 135, 1–11. [Google Scholar] [CrossRef]
- Benoudina, N.; Zhang, Y.; Khalique, C.M. Lie symmetry analysis, optimal system, new solitary wave solutions and conservation laws of the Pavlov equation. Commun. Nonlinear Sci. 2021, 94, 105560. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhang, Y.F. Application of Riemann–Hilbert method to an extended coupled nonlinear Schrödinger equations. Comput. Appl. Math. 2023, 420, 114812. [Google Scholar] [CrossRef]
- Wu, J. Riemann–Hilbert approach and soliton analysis of a novel nonlocal reverse-time nonlinear Schrödinger equation. Nonlinear Dynam. 2024, 112, 4749–4760. [Google Scholar] [CrossRef]
- Yin, Y.H.; Lü, X.; Ma, W.X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dynam. 2022, 108, 4181–4194. [Google Scholar] [CrossRef]
- Dong, S.; Lan, Z.Z.; Gao, B.; Shen, Y.J. Bäcklund transformation and multi-soliton solutions for the discrete Korteweg–de Vries equation. Appl. Math. Lett. 2022, 125, 107747. [Google Scholar] [CrossRef]
- Lou, S.Y. Residual symmetries and Bäcklund transformations. arXiv 2013, arXiv:1308.1140. [Google Scholar]
- Lou, S.Y. Consistent Riccati expansion and solvability. arXiv 2013, arXiv:1308.5891. [Google Scholar]
- Lou, S.Y. Consistent Riccati expansion for integrable systems. Stud. Appl. Math. 2015, 134, 372–402. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J. Soliton molecules, nonlocal symmetry and CRE method of the KdV equation with higher-order corrections. Phys. Scr. 2020, 95, 075202. [Google Scholar] [CrossRef]
- Song, J.F.; Hu, Y.H.; Ma, Z.Y. Bäcklund transformation and CRE solvability for the negative-order modified KdV equation. Nonlinear Dynam. 2017, 90, 575–580. [Google Scholar] [CrossRef]
- Ren, B.; Lin, J.; Liu, P. Soliton molecules and the CRE method in the extended mKdV equation. Commun. Theor. Phys. 2020, 72, 55005. [Google Scholar] [CrossRef]
- Liu, P.; Cheng, J.; Ren, B.; Yang, J.R. Bäcklund transformations, consistent Riccati expansion solvability, and soliton–cnoidal interaction wave solutions of Kadomtsev–Petviashvili equation. Chin. Phys. B 2020, 29, 020201. [Google Scholar] [CrossRef]
- Sheng, Q.; Wo, W. Symmetry analysis and interaction solutions for the (2+1)-dimensional Kaup–Kupershmidt system. Appl. Math. Lett. 2016, 58, 165–171. [Google Scholar] [CrossRef]
- Liu, X.Z.; Yu, J.; Lou, Z.M.; Cao, Q.J. Residual symmetry reduction and consistent Riccati expansion of the generalized kaup-kupershmidt equation. Commun. Theor. Phys. 2016, 69, 625–630. [Google Scholar] [CrossRef]
- Cheng, W.; Li, B. CRE Solvability, Exact Soliton-Cnoidal Wave Interaction Solutions, and Nonlocal Symmetry for the Modified Boussinesq Equation. Adv. Math. Phys. 2016, 2016, 4874392. [Google Scholar] [CrossRef]
- Zhao, Z.; Han, B. Nonlocal symmetry and explicit solutions from the CRE method of the Boussinesq equation. Eur. Phys. J. Plus 2018, 133, 1–9. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Akinyemi, L.; Akpan, U.; Veeresha, P.; Rezazadeh, H.; Inc, M. Computational techniques to study the dynamics of generalized unstable nonlinear Schrödinger equation. J. Ocean Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Murad, M.A.S.; Ismael, H.F.; Sulaiman, T.A. Various exact solutions to the time-fractional nonlinear Schrödinger equation via the new modified Sardar sub-equation method. Phys. Scr. 2024, 99, 085252. [Google Scholar] [CrossRef]
- Ahmad, J.; Hameed, M.; Mustafa, Z.; Rehman, S.U. Soliton patterns in the truncated M-fractional resonant nonlinear Schrödinger equation via modified Sardar sub-equation method. J. Opt. 2024, 1–22. [Google Scholar] [CrossRef]
- Kamel, N.M.; Ahmed, H.M.; Rabie, W.B. Retrieval of soliton solutions for 4th-order (2+1)-dimensional Schrödinger equation with higher-order odd and even terms by modified Sardar sub-equation method. Ain. Shams. Eng. J. 2024, 15, 102808. [Google Scholar] [CrossRef]
- Hamid, I.; Kumar, S. Newly formed solitary wave solutions and other solitons to the (3+1)-dimensional mKdV–ZK equation utilizing a new modified Sardar sub-equation approach. Mod. Phys. Lett. B 2024, 39, 2550027. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Ocean shallow-water studies on a generalized Boussinesq-Broer-Kaup-Whitham system: Painlevé analysis and similarity reductions. Chaos Soliton. Fract. 2023, 169, 113214. [Google Scholar] [CrossRef]
- Fan, E. Multiple travelling wave solutions of nonlinear evolution equations using a unified algebraic method. J. Phys. A 2002, 35, 6853. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Tharwat, M.M.; Abdelkawy, M.A. Integrable system modelling shallow water waves: Kaup–Boussinesq shallow water system. Indian J. Phys. 2013, 87, 665–671. [Google Scholar] [CrossRef]
- Congy, T.; Ivanov, S.K.; Kamchatnov, A.M.; Pavloff, N. Evolution of initial discontinuities in the Riemann problem for the Kaup-Boussinesq equation with positive dispersion. Chaos 2017, 27, 083107. [Google Scholar] [CrossRef]
- Wei, L.; Ding, X.F. Using symbolic computation to construct travelling wave solutions to nonlinear partial differential equations. Chin. Phys. 2004, 13, 1639. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, B. Non-local symmetry, interaction solutions and conservation laws of the (1+1)-dimensional Wu-Zhang equation. Pramana-J. Phys. 2021, 95, 129. [Google Scholar] [CrossRef]
- Fan, E.; Hon, Y.C. A series of travelling wave solutions for two variant Boussinesq equations in shallow water waves. Chaos Soliton. Fract. 2003, 15, 559–566. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, R.K. Exact solutions of a variant Boussinesq system. Int. J. Eng. Sci. 2006, 44, 1256–1268. [Google Scholar] [CrossRef]
- Fei, J.; Ma, Z.; Cao, W. Residual symmetries and interaction solutions for the Whitham-Broer-Kaup equation. Nonlinear Dynam. 2017, 88, 395–402. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, K.L. Variational principles for fractal Whitham–Broer–Kaup equations in shallow water. Fractals 2021, 29, 2150028. [Google Scholar] [CrossRef]
- Kupershmidt, B.A. Mathematics of dispersive water waves. Commun. Math. Phys. 1985, 99, 51–73. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.E. Darboux transformations of classical Boussinesq system and its multi-soliton solutions. Phys. Lett. A 2001, 284, 253–258. [Google Scholar] [CrossRef]
- Rahioui, M.; El Kinani, E.H.; Ouhadan, A. Nonlocal residual symmetries, N-th Bäcklund transformations and exact interaction solutions for a generalized Broer–Kaup–Kupershmidt system. Z. Angew. Math. Phys. 2024, 75, 37. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Zhao, Z.; Han, B. Residual symmetry, Bäcklund transformation and CRE solvability of a (2+1)-dimensional nonlinear system. Nonlinear Dynam. 2018, 94, 461–474. [Google Scholar] [CrossRef]
- Liu, Y.; Li, B. Nonlocal symmetry and exact solutions of the (2+1)-dimensional Gardner equation. Chin. J. Phys. 2016, 54, 718–723. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Yang, S.; Fang, Y.; Liu, M. Solitons, Cnoidal Waves and Nonlinear Effects in Oceanic Shallow Water Waves. Fractal Fract. 2025, 9, 305. https://doi.org/10.3390/fractalfract9050305
Dong H, Yang S, Fang Y, Liu M. Solitons, Cnoidal Waves and Nonlinear Effects in Oceanic Shallow Water Waves. Fractal and Fractional. 2025; 9(5):305. https://doi.org/10.3390/fractalfract9050305
Chicago/Turabian StyleDong, Huanhe, Shengfang Yang, Yong Fang, and Mingshuo Liu. 2025. "Solitons, Cnoidal Waves and Nonlinear Effects in Oceanic Shallow Water Waves" Fractal and Fractional 9, no. 5: 305. https://doi.org/10.3390/fractalfract9050305
APA StyleDong, H., Yang, S., Fang, Y., & Liu, M. (2025). Solitons, Cnoidal Waves and Nonlinear Effects in Oceanic Shallow Water Waves. Fractal and Fractional, 9(5), 305. https://doi.org/10.3390/fractalfract9050305





