Design of Non-Standard Finite Difference and Dynamical Consistent Approximation of Campylobacteriosis Epidemic Model with Memory Effects
Abstract
1. Introduction
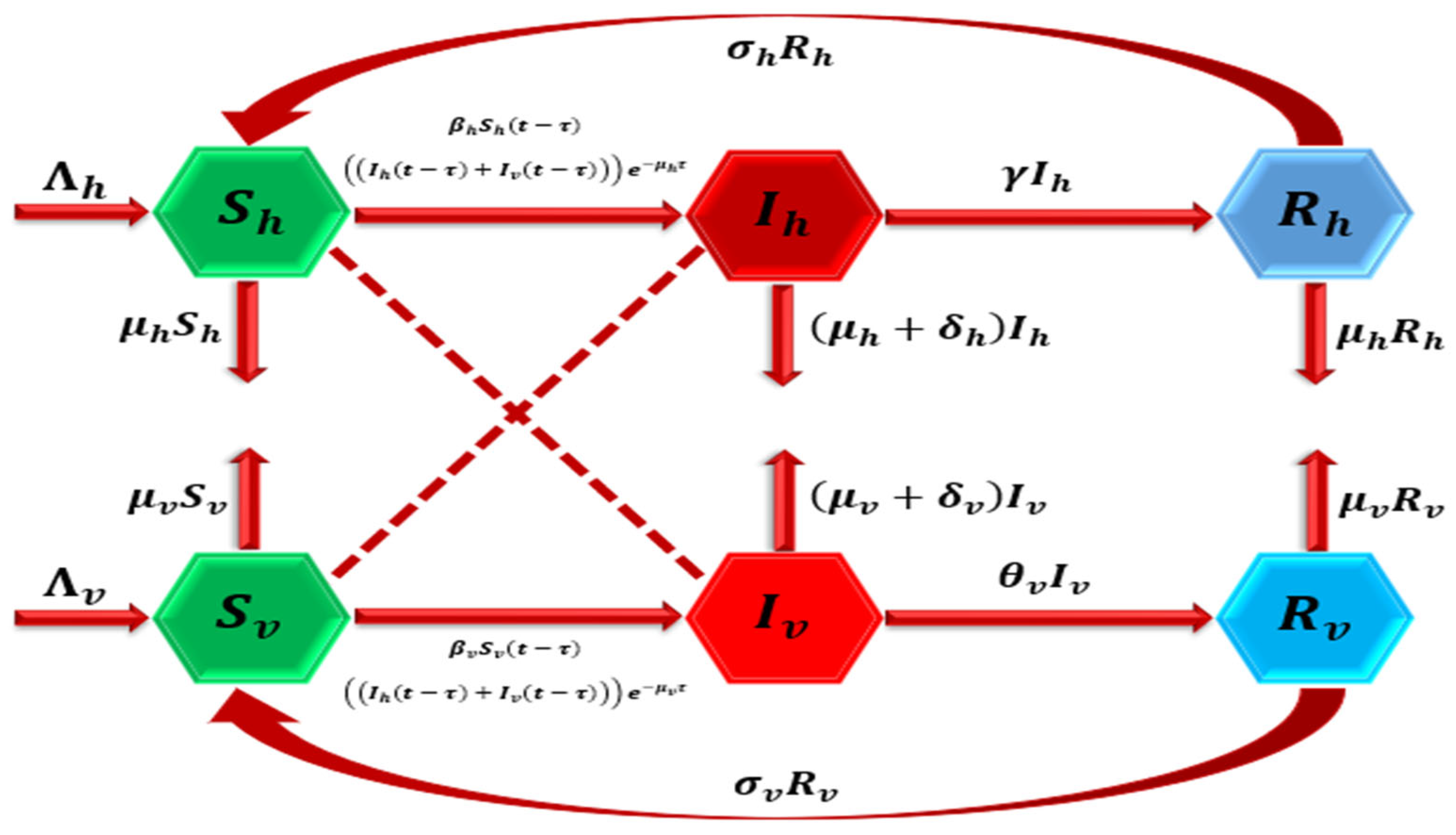
2. Model Formulation
2.1. Existence and Uniqueness of the Stochastic Fractional Delayed Model
2.2. Model Equilibria and Reproduction Number
2.3. Extinction and Persistence of the Stochastic Fractional Delayed Model
3. Sensitivity Analysis
4. Stochastic Fractional Delayed GL-NSFD Method
5. Positivity and Boundedness of Stochastic Fractional Delayed GL-NSFD
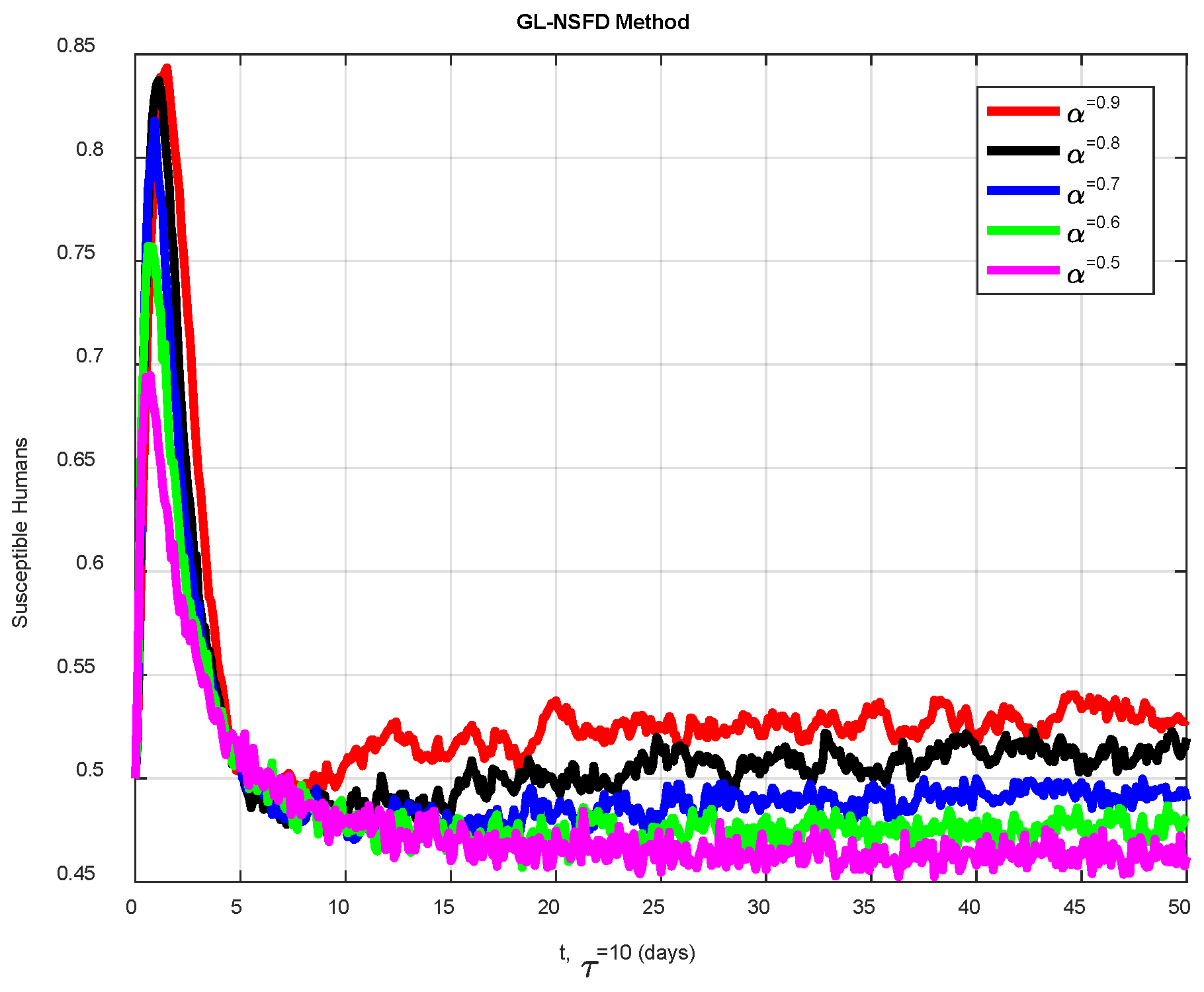
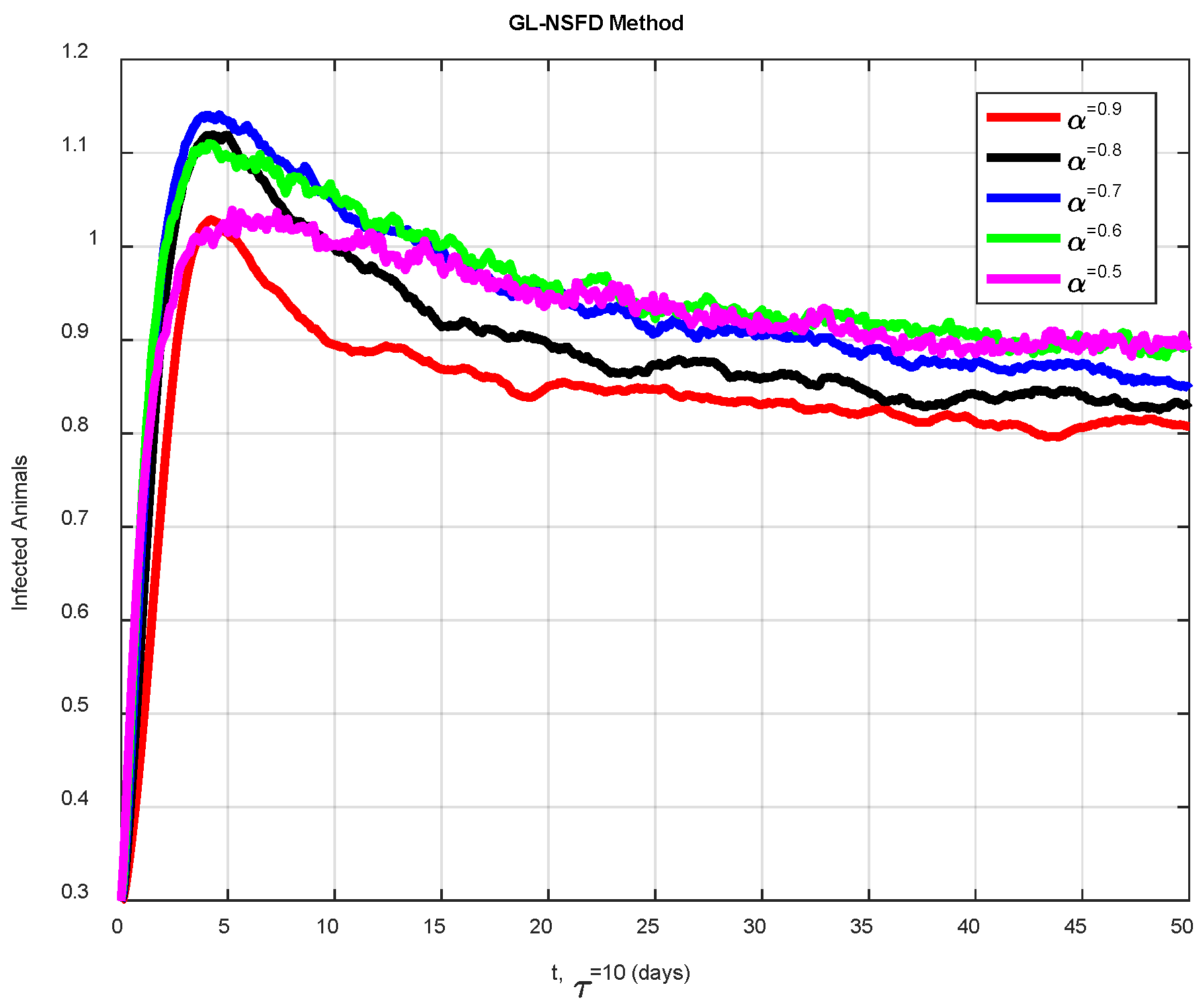
6. Numerical Simulations
Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osman, S.; Togbenon, H.A.; Otoo, D. Modelling the dynamics of campylobacteriosis using non finite difference approach with optimal control. Comput. Math. Methods Med. 2020, 2020, 8843299. [Google Scholar] [CrossRef]
- Chuma, F.M.; Ngailo, E.K. Mathematical analysis of campylobacteriosis disease model in human with saturated incidence rate and treatment. Math. Open 2024, 3, 2350011. [Google Scholar] [CrossRef]
- Iacono, G.L.; Cook, A.J.C.; Derks, G.; Fleming, L.E.; French, N.; Gillingham, E.L.; Villeta, L.C.G.; Heaviside, C.; La Ragione, R.M.; Leonardi, G.; et al. A mathematical, classical stratification modeling approach to disentangling the impact of weather on infectious diseases: A case study using spatio-temporally disaggregated Campylobacter surveillance data for England and Wales. PLoS Comput. Biol. 2024, 20, e1011714. [Google Scholar] [CrossRef] [PubMed]
- Dzianach, P.A.; Dykes, G.A.; Strachan, N.J.; Forbes, K.J.; Pérez-Reche, F.J. Unveiling the Mechanisms for Campylobacter jejuni Biofilm Formation Using a Stochastic Mathematical Model. Hygiene 2024, 4, 326–345. [Google Scholar] [CrossRef]
- Carvalho, D.; Chitolina, G.Z.; Wilsmann, D.E.; Lucca, V.; Emery, B.D.D.; Borges, K.A.; Furian, T.Q.; Santos, L.R.D.; Moraes, H.L.D.S.; Nascimento, V.P.D. Development of Predictive Modeling for Removal of Multispecies Biofilms of Salmonella Enteritidis, Escherichia coli, and Campylobacter jejuni from Poultry Slaughterhouse Surfaces. Foods 2024, 13, 1703. [Google Scholar] [CrossRef] [PubMed]
- Holmes, J. Understanding How Mutability Facilitates Survival of Alternating Selection and Bottlenecks by the Major Food-Borne Pathogen Campylobacter jejuni. Ph.D. Dissertation, University of Leicester, Leicester, UK, 2024. [Google Scholar]
- Sahin, O.; Pang, J.; Pavlovic, N.; Tang, Y.; Adiguzel, M.C.; Wang, C.; Zhang, Q. A Longitudinal Study on Campylobacter in Conventionally Reared Commercial Broiler Flocks in the United States: Prevalence and Genetic Diversity. Avian Dis. 2024, 67, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Braga, P.F.D.S. Enhancing the control of Campylobacter jejuni in a Theragnostic Approach: FTIR-ATR Combined with Artificial Intelligence, Binding-Peptides, and the Use of Chicken Embryos as an In Vivo Model. Ph.D. Thesis, Universidade Federal de Uberlândia, Uberlândia, Brazil, 2024. [Google Scholar]
- Sinha, R.; LeVeque, R.M.; Callahan, S.M.; Chatterjee, S.; Stopnisek, N.; Kuipel, M.; Johnson, J.G.; DiRita, V.J. Gut metabolite L-lactate supports Campylobacter jejuni population expansion during acute infection. Proc. Natl. Acad. Sci. USA 2024, 121, e2316540120. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, M.A.; Azam, F.; Alam, P. Deciphering Campylobacter jejuni DsbA1 protein dynamics in the presence of anti-virulent compounds: A multi-pronged computer-aided approach. J. Biomol. Struct. Dyn. 2024, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Knipper, A.D.; Plaza-Rodríguez, C.; Filter, M.; Wulsten, I.F.; Stingl, K.; Crease, T. Modeling the survival of Campylobacter jejuni in raw milk considering the viable but non-culturable cells (VBNC). J. Food Saf. 2023, 43, e13077. [Google Scholar] [CrossRef]
- Brinch, M.L.; Hald, T.; Wainaina, L.; Merlotti, A.; Remondini, D.; Henri, C.; Njage, P.M.K. Comparison of source attribution methodologies for human campylobacteriosis. Pathogens 2023, 12, 786. [Google Scholar] [CrossRef] [PubMed]
- Soto-Beltrán, M.; Lee, B.G.; Amézquita-López, B.A.; Quiñones, B. Overview of methodologies for the culturing, recovery and detection of Campylobacter. Int. J. Environ. Health Res. 2023, 33, 307–323. [Google Scholar] [CrossRef] [PubMed]
- Said, Y.; Singh, D.; Sebu, C.; Poolman, M. A novel algorithm to calculate elementary modes: Analysis of Campylobacter jejuni metabolism. Biosystems 2023, 234, 105047. [Google Scholar] [CrossRef] [PubMed]
- Myintzaw, P.; Jaiswal, A.K.; Jaiswal, S. A review on campylobacteriosis associated with poultry meat consumption. Food Rev. Int. 2023, 39, 2107–2121. [Google Scholar] [CrossRef]
- Bodie, A.R.; Rothrock Jr, M.J.; Ricke, S.C. Comparison of optical density-based growth kinetics for pure culture Campylobacter jejuni, coli and lari grown in blood-free Bolton broth. J. Environ. Sci. Health Part B 2023, 58, 671–678. [Google Scholar] [CrossRef] [PubMed]
- Rousou, X.; Furuya-Kanamori, L.; Kostoulas, P.; Doi, S.A. Diagnostic accuracy of multiplex nucleic acid amplification tests for Campylobacter infection: A systematic review and meta-analysis. Pathog. Glob. Health 2023, 117, 259–272. [Google Scholar] [CrossRef] [PubMed]
- Hendrickson, S.M.; Thomas, A.; Raué, H.P.; Prongay, K.; Haertel, A.J.; Rhoades, N.S.; Slifka, J.F.; Gao, L.; Quintel, B.K.; Amanna, I.J.; et al. Campylobacter vaccination reduces diarrheal disease and infant growth stunting among rhesus macaques. Nat. Commun. 2023, 14, 3806. [Google Scholar] [CrossRef] [PubMed]
- Knipper, A.D.; Göhlich, S.; Stingl, K.; Ghoreishi, N.; Fischer-Tenhagen, C.; Bandick, N.; Tenhagen, B.A.; Crease, T. Longitudinal study for the detection and quantification of Campylobacter spp. in dairy cows during milking and in the dairy farm environment. Foods 2023, 12, 1639. [Google Scholar] [CrossRef] [PubMed]
- Kingsbury, J.M.; Horn, B.; Armstrong, B.; Midwinter, A.; Biggs, P.; Callander, M.; Mulqueen, K.; Brooks, M.; van der Logt, P.; Biggs, R. The impact of primary and secondary processing steps on Campylobacter concentrations on chicken carcasses and portions. Food Microbiol. 2023, 110, 104168. [Google Scholar] [CrossRef] [PubMed]
- Sene, N. Analysis of the stochastic model for predicting the novel coronavirus disease. Adv. Differ. Equ. 2020, 2020, 568. [Google Scholar] [CrossRef] [PubMed]





| Parameters | Signs |
|---|---|
| Positive | |
| Positive | |
| Negative | |
| Negative | |
| Negative |
| Parameters | Values |
|---|---|
| Parameters | Values | Source [1] |
|---|---|---|
| Estimated | ||
| Estimated | ||
| Fitted | ||
| Fitted | ||
| Fitted | ||
| Estimated | ||
| Estimated | ||
| Fitted | ||
| Estimated | ||
| Fitted | ||
| 0.1 | Estimated | |
| 0.001 | Fitted | |
| Fitted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Minhós, F.; Shafique, U.; Fadhal, E.; Alfwzan, W.F. Design of Non-Standard Finite Difference and Dynamical Consistent Approximation of Campylobacteriosis Epidemic Model with Memory Effects. Fractal Fract. 2025, 9, 358. https://doi.org/10.3390/fractalfract9060358
Raza A, Minhós F, Shafique U, Fadhal E, Alfwzan WF. Design of Non-Standard Finite Difference and Dynamical Consistent Approximation of Campylobacteriosis Epidemic Model with Memory Effects. Fractal and Fractional. 2025; 9(6):358. https://doi.org/10.3390/fractalfract9060358
Chicago/Turabian StyleRaza, Ali, Feliz Minhós, Umar Shafique, Emad Fadhal, and Wafa F. Alfwzan. 2025. "Design of Non-Standard Finite Difference and Dynamical Consistent Approximation of Campylobacteriosis Epidemic Model with Memory Effects" Fractal and Fractional 9, no. 6: 358. https://doi.org/10.3390/fractalfract9060358
APA StyleRaza, A., Minhós, F., Shafique, U., Fadhal, E., & Alfwzan, W. F. (2025). Design of Non-Standard Finite Difference and Dynamical Consistent Approximation of Campylobacteriosis Epidemic Model with Memory Effects. Fractal and Fractional, 9(6), 358. https://doi.org/10.3390/fractalfract9060358








