Dynamical Analysis of Mpox Disease with Environmental Effects
Abstract
1. Introduction
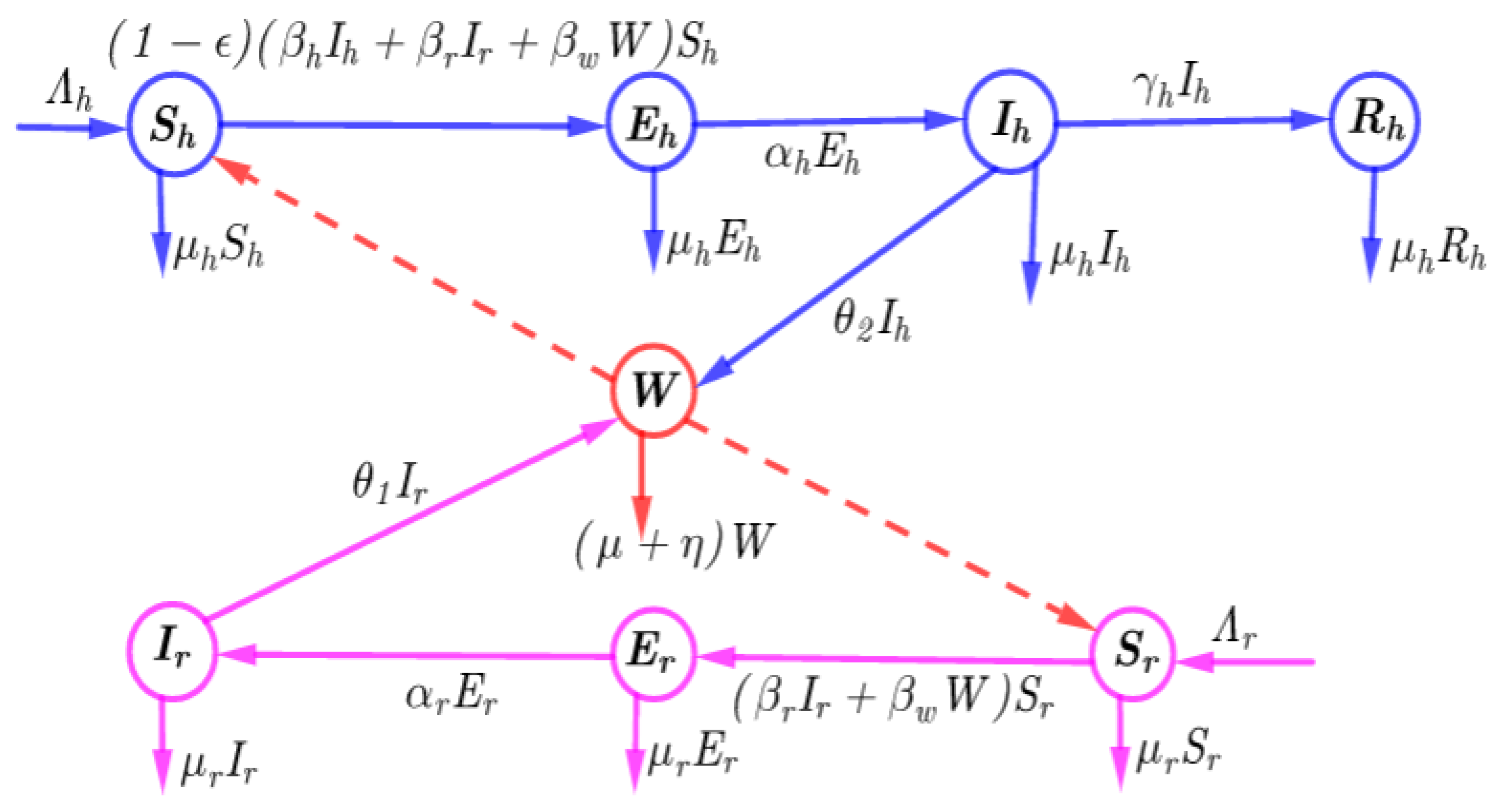
2. Model Formulation
3. Model Analysis
3.1. Preliminaries on the Caputo Fractional Calculus
3.2. The Existence and Uniqueness of the Solution
3.3. The Numerical Scheme of System (3) in Caputo Fractional Derivatives
4. Basic Properties
4.1. The Positivity of the Solutions
4.2. The Boundedness of the Model Solution
4.3. The Basic Reproduction Number and the Existence of Equilibria
5. Results and Discussion
5.1. Estimation of the Model Parameters
- n denotes the number of monthly reported real data on monkeypox for 29 months;
- is the observed number of infectious human cases at month k;
- is the model-predicted number of infectious human cases at month k.
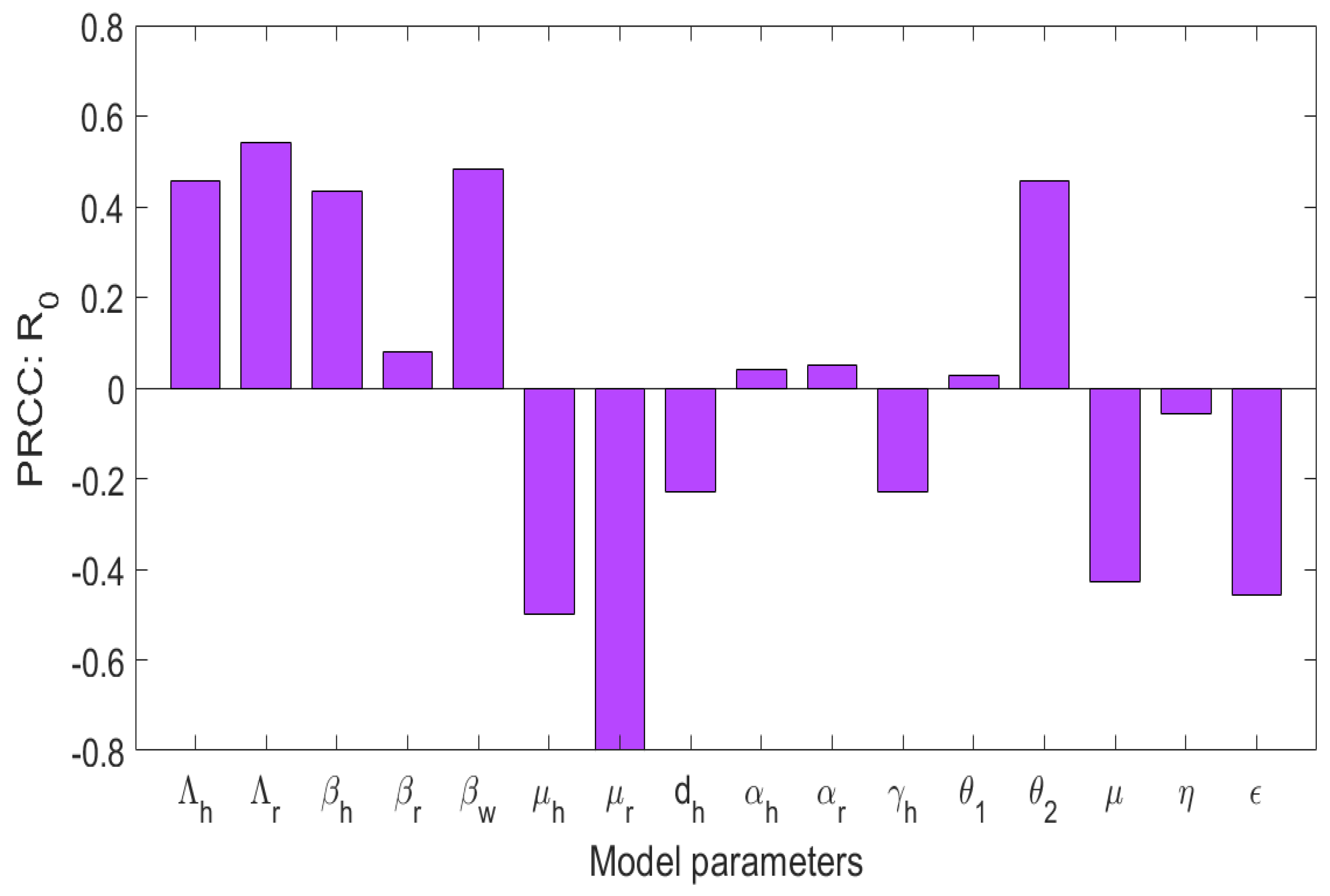
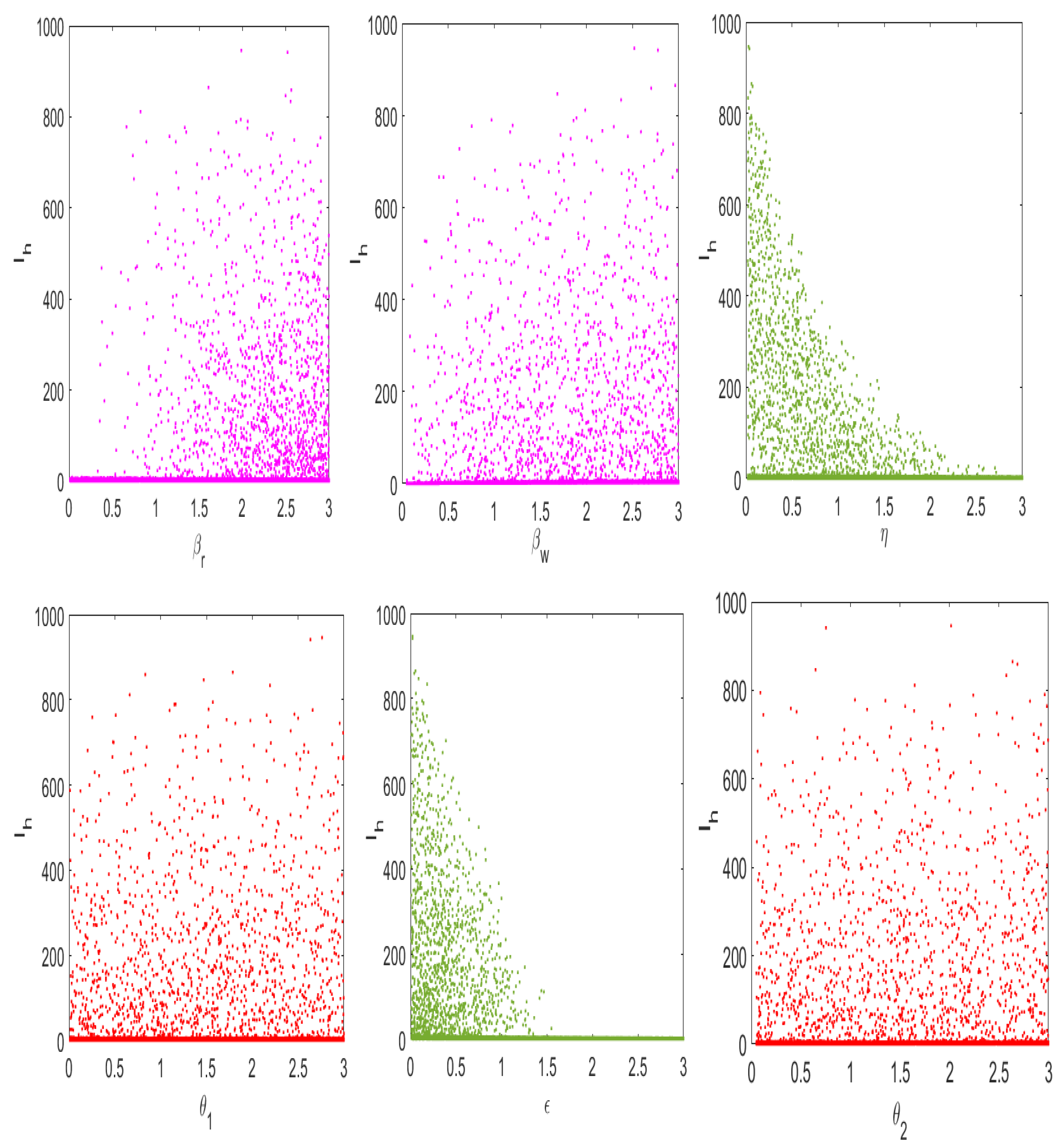
5.2. The Sensitivity Analysis
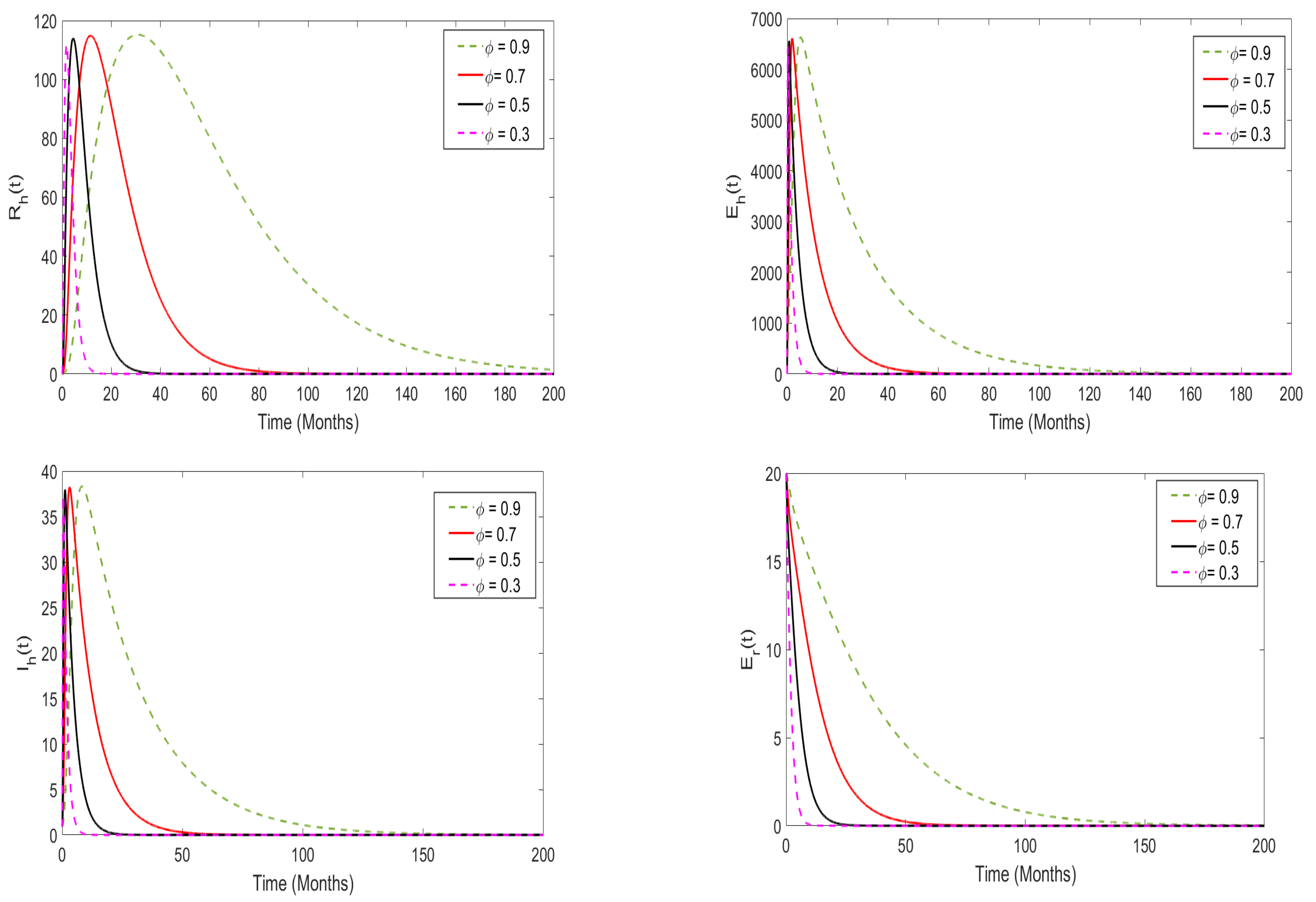
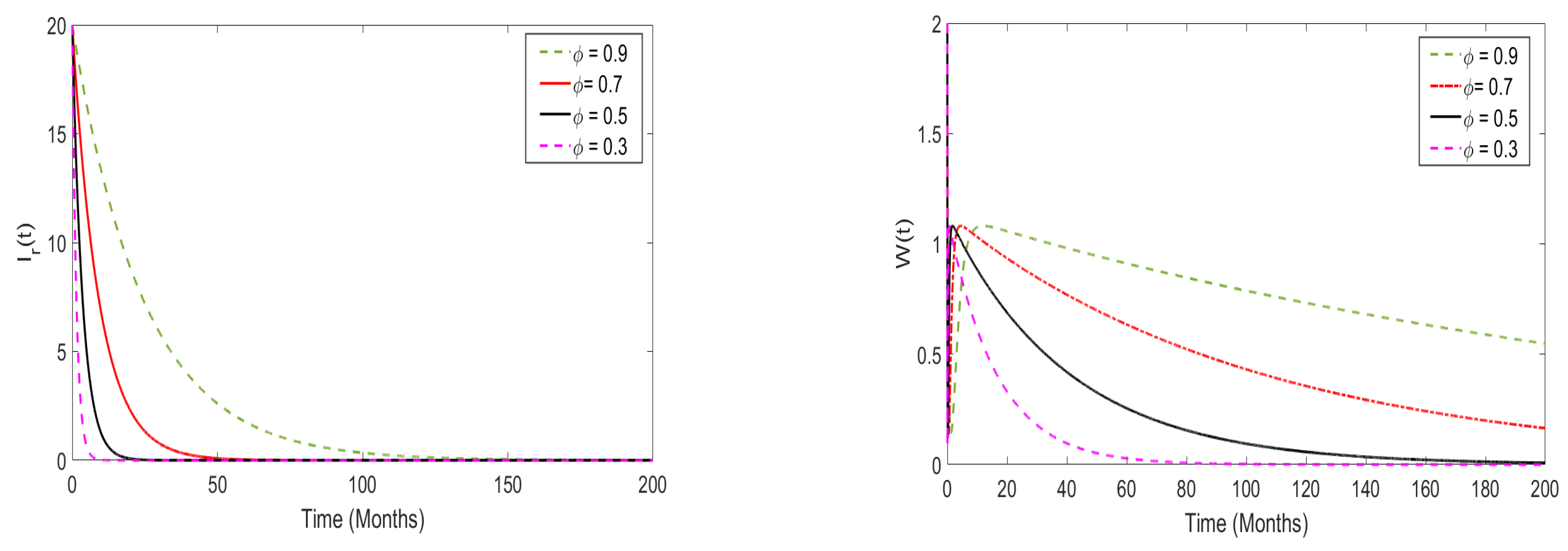
5.3. The Role of Memory Effects on the Disease Dynamics
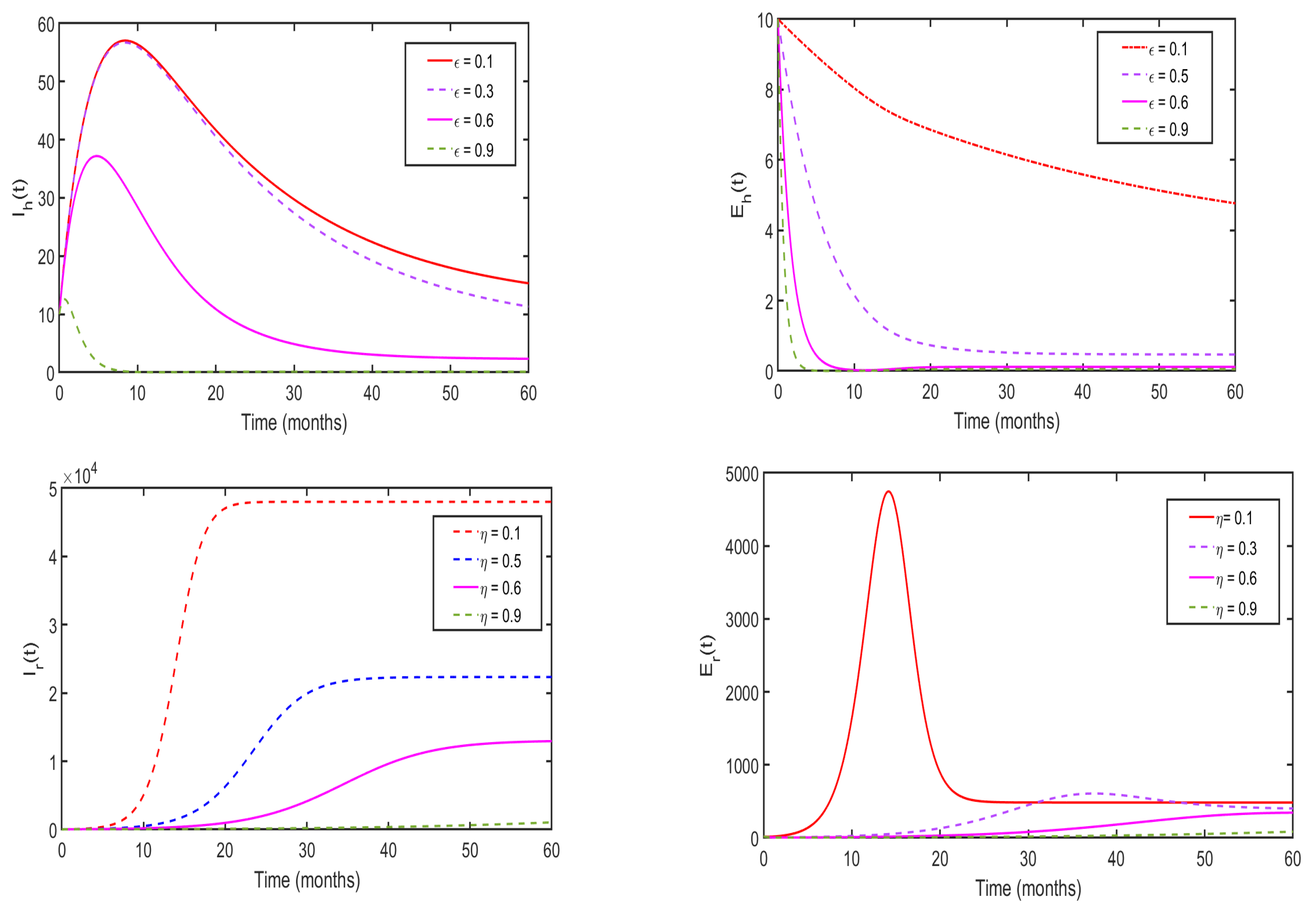
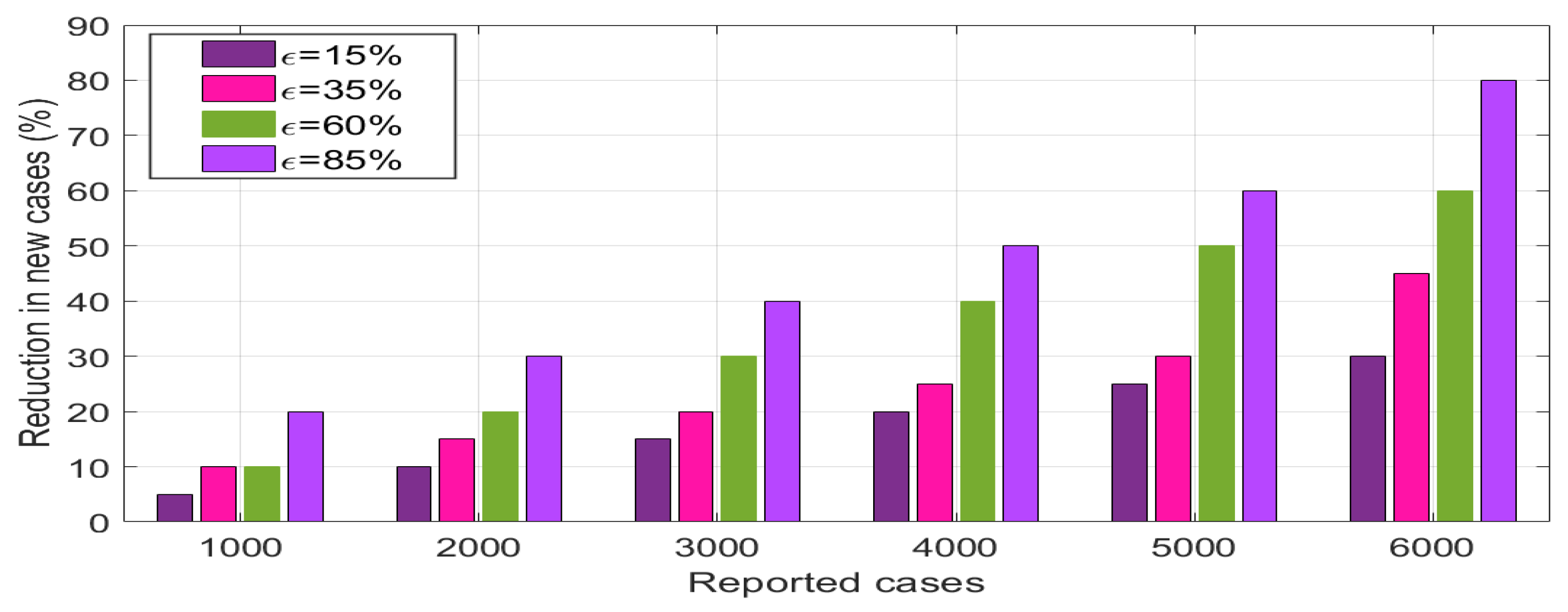
5.4. Effects of Environmental Sanitation and Human Awareness on the Disease Dynamics
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hatami, H.; Jamshidi, P.; Arbabi, M.; Safavi-Naini, S.A.A.; Farokh, P.; Izadi-Jorshari, G.; Mohammadzadeh, B.; Nasiri, M.J.; Zandi, M.; Nayebzade, A. Demographic, epidemiologic, and clinical characteristics of human monkeypox disease pre-and post-2022 outbreaks: A systematic review and meta-analysis. Biomedicines 2023, 11, 957. [Google Scholar] [CrossRef] [PubMed]
- Banuet-Martinez, M.; Yang, Y.; Jafari, B.; Kaur, A.; Butt, Z.A.; Chen, H.H.; Yanushkevich, S.; Moyles, I.R.; Heffernan, J.M.; Korosec, C.S. Monkeypox: A review of epidemiological modelling studies and how modelling has led to mechanistic insigh. Epidemiol. Infect. 2023, 151, e121. [Google Scholar] [CrossRef] [PubMed]
- El-Mesady, A.; Elsonbaty, A.; Adel, W. On nonlinear dynamics of a fractional order monkeypox virus model. Chaos Solitons Fractals 2022, 164, 112716. [Google Scholar] [CrossRef] [PubMed]
- Farman, M.; Akgül, A.; Garg, H.; Baleanu, D.; Hincal, E.; Shahzeen, S. Mathematical analysis and dynamical transmission of monkeypox virus model with fractional operator. Expert Syst. 2025, 42, e13475. [Google Scholar] [CrossRef]
- Alakunle, E.; Moens, U.; Nchinda, G.; Okeke Malachy, I. Monkeypox virus in Nigeria: Infection biology, epidemiology, and evolution. Viruses 2020, 12, 1257. [Google Scholar] [CrossRef]
- Mandja, B.-A.M.; Brembilla, A.; Handschumacher, P.; Bompangue, D.; Gonzalez, J.-P.; Muyembe, J.-J.; Mauny, F. Temporal and spatial dynamics of monkeypox in Democratic Republic of Congo, 2000–2015. EcoHealth 2019, 16, 476–487. [Google Scholar] [CrossRef]
- Ayeh, M.A.; Cofie, K.; Mensah, G.S.; Amo-Kodieh, F.; Kyeremeh, P. Monkeypox Infection: Risk Assessment and Clinical Outcomes Among Immunocompromised Populations in Sub-Saharan Africa:: A Systematic Review and Meta-analysis. Ghana J. Nurs. Midwifery 2024, 1, 107–124. [Google Scholar] [CrossRef]
- Di Gennaro, F.; Veronese, N.; Marotta, C.; Shin, J.I.; Koyanagi, A.; Silenzi, A.; Antunes, M.; Saracino, A.; Bavaro, D.F.; Soysal, P. Human monkeypox: A comprehensive narrative review and analysis of the public health implications. Microorganisms 2022, 10, 1633. [Google Scholar] [CrossRef]
- Chaix, E.; Boni, M.; Guillier, L.; Bertagnoli, S.; Mailles, A.; Collignon, C.; Kooh, P.; Ferraris, O.; Martin-Latil, S.; Manuguerra, J.-C. Risk of Monkeypox virus (MPXV) transmission through the handling and consumption of food. Microb. Risk Anal. 2022, 22, 100237. [Google Scholar] [CrossRef]
- Lusekelo, E.; Helikumi, M.; Kuznetsov, D.; Mushayabasa, S. Dynamic modelling and optimal control analysis of a fractional order chikungunya disease model with temperature effects. Results Control Optim. 2023, 10, 100206. [Google Scholar] [CrossRef]
- Mckenzie, H.W.; Jin, Y.; Jacobsen, J.; Lewis Mark, A. R_0 analysis of a spatiotemporal model for a stream population. SIAM J. Appl. Dyn. Syst. 2012, 11, 567–596. [Google Scholar] [CrossRef]
- Peter, O.J.; Abidemi, A.; Ojo, M.M.; Ayoola Tawakalt, A. Mathematical model and analysis of monkeypox with control strategies. Eur. Phys. J. Plus 2023, 138, 242. [Google Scholar] [CrossRef]
- Peter, O.J.; Madubueze, C.E.; Ojo, M.M.; Oguntolu, F.A.; Ayoola Tawakalt, A. Modeling and optimal control of monkeypox with cost-effective strategies. Model. Earth Syst. Environ. 2023, 9, 1989–2007. [Google Scholar] [CrossRef]
- El Mansouri, A.; Smouni, I.; Khajji, B.; Labzai, A.; Belam, M. Mathematical modeling and optimal control strategy for the monkeypox epidemic. Math. Model. Comput. 2023, 10, 944–955. [Google Scholar] [CrossRef]
- Okongo, W.; Okelo Abonyo, J.; Kioi, D.; Moore, S.E.; Nnaemeka Aguegboh, S. Mathematical modeling and optimal control analysis of Monkeypox virus in contaminated environment. Model. Earth Syst. Environ. 2024, 10, 3969–3994. [Google Scholar] [CrossRef]
- Soni, K.; Sinha, A.K. Modeling and stability analysis of the transmission dynamics of monkeypox with control intervention. Partial Differ. Equations Appl. Math. 2024, 10, 100730. [Google Scholar] [CrossRef]
- Musafir, R.R.; Suryanto, A.; Darti, I. Optimal control of a fractional-order monkeypox epidemic model with vaccination and rodents culling. Results Control Optim. 2024, 14, 100381. [Google Scholar] [CrossRef]
- Peter, O.J.; Kumar, S.; Kumari, N.; Oguntolu, F.A.; Oshinubi, K.; Musa, R. Transmission dynamics of Monkeypox virus: A mathematical modelling approach. Model. Earth Syst. Environ. 2022, 8, 3423–3434. [Google Scholar] [CrossRef]
- Adepoju, O.A.; Ibrahim, H.O. An optimal control model for monkeypox transmission dynamics with vaccination and immunity loss following recovery. Healthc. Anal. 2024, 6, 100355. [Google Scholar] [CrossRef]
- Alshehri, A.; Ullah, S. Optimal control analysis of Monkeypox disease with the impact of environmental transmission. Aims Math. 2023, 8, 16926–16960. [Google Scholar] [CrossRef]
- Rashid, S.; Bariq, A.; Ali, I.; Sultana, S.; Siddiqa, A.; Elagan Sayed, K. Dynamic analysis and optimal control of a hybrid fractional monkeypox disease model in terms of external factors. Sci. Rep. 2025, 15, 2944. [Google Scholar] [CrossRef]
- Adel, W.; Elsonbaty, A.; Aldurayhim, A.; El-Mesady, A. Investigating the dynamics of a novel fractional-order monkeypox epidemic model with optimal control. Alex. Eng. J. 2023, 73, 519–542. [Google Scholar] [CrossRef]
- Musafir, R.R.; Suryanto, A.; Darti, I. Stability analysis of a fractional-order monkeypox epidemic model with quarantine and hospitalization. J. Biosaf. Biosecurity 2024, 6, 34–50. [Google Scholar] [CrossRef]
- ul Rehman, A.; Singh, R.; Abdeljawad, T.; Okyere, E.; Guran, L. Modeling, analysis and numerical solution to malaria fractional model with temporary immunity and relapse. Adv. Differ. Equ. 2021, 2021, 390. [Google Scholar] [CrossRef]
- Ahmad, Y.U.; Andrawus, J.; Ado, A.; Maigoro, Y.A.; Yusuf, A.; Althobaiti, S.; Mustapha, U.T. Mathematical modeling and analysis of human-to-human monkeypox virus transmission with post-exposure vaccination. Model. Earth Syst. Environ. 2024, 10, 2711–2731. [Google Scholar] [CrossRef]
- Yuan, P.; Tan, Y.; Yang, L.; Aruffo, E.; Ogden, N.H.; Bélair, J.; Arino, J.; Heffernan, J.; Watmough, J.; Carabin, H. Modeling vaccination and control strategies for outbreaks of monkeypox at gatherings. Front. Public Health 2022, 10, 1026489. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Farid, S.; Ullah, S.; Altanji, M.; Nawaz, R.; Wondimagegnhu Teklu, S. Mathematical assessment of monkeypox disease with the impact of vaccination using a fractional epidemiological modeling approach. Sci. Rep. 2023, 13, 13550. [Google Scholar] [CrossRef]
- Addai, E.; Ngungu, M.; Omoloye, M.A.; Marinda, E. Modelling the impact of vaccination and environmental transmission on the dynamics of monkeypox virus under Caputo operator. Math. Biosci. Eng. 2023, 20, 10174–10199. [Google Scholar] [CrossRef]
- Venkatesh, A.; Manivel, M.; Arunkumar, K.; Prakash Raj, M.; Shyamsunder Purohit, S.D. A fractional mathematical model for vaccinated humans with the impairment of Monkeypox transmission. Eur. Phys. J. Spec. Top. 2024, 1–21. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Musa, S.S.; Inc, M. Modeling the role of public health intervention measures in halting the transmission of monkeypox virus. AIMS Math. 2023, 8, 14142–14166. [Google Scholar] [CrossRef]
- Biswas, A.S.; Aslam, B.H.; Tiwari, P.K. Mathematical modeling of a novel fractional-order monkeypox model using the Atangana–Baleanu derivative. Phys. Fluids 2023, 35, 11. [Google Scholar] [CrossRef]
- Yaga, S.J. Modeling Monkeypox Epidemics: Thresholds, Temporal Dynamics, and Waning Immunity from Smallpox Vaccination. medRxiv 2025. [Google Scholar] [CrossRef]
- Spath, T.; Brunner-Ziegler, S.; Stamm, T.; Thalhammer, F.; Kundi, M.; Purkhauser, K.; Handisurya, A. Modeling the protective effect of previous compulsory smallpox vaccination against human monkeypox infection: From hypothesis to a worst-case scenario. Int. J. Infect. Dis. 2022, 124, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Helikumi, M.; Bisaga, T.; Makau, K.A.; Mhlanga, A. Modeling the Impact of Human Awareness and Insecticide Use on Malaria Control: A Fractional-Order Approach. Mathematics 2024, 12, 3607. [Google Scholar] [CrossRef]
- Helikumi, M.; Mushayabasa, S. Mathematical modeling of trypanosomiasis control strategies in communities where human, cattle and wildlife interact. Anim. Dis. 2023, 3, 25. [Google Scholar] [CrossRef]
- Khan, A.; Sabbar, Y.; Din, A. Stochastic modeling of the Monkeypox 2022 epidemic with cross-infection hypothesis in a highly disturbed environment. Math. Biosci. Eng. 2022, 19, 13560–13581. [Google Scholar] [CrossRef]
- Brand, S.P.C.; Cavallaro, M.; Cumming, F.; Turner, C.; Florence, I.; Blomquist, P.; Hilton, J.; Guzman-Rincon, L.M.; House, T.; Nokes, D.J. The role of vaccination and public awareness in forecasts of Mpox incidence in the United Kingdom. Nat. Commun. 2023, 14, 4100. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Latha, V.P.; Rihan, F.A. A Fractional-Order Model for Zika Virus Infection with Multiple Delays. Complexity 2019, 1, 4178073. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Batiha, I.M.; Abubaker, A.A.; Jebril, I.H.; Al-Shaikh, S.B.; Matarneh, K.; Almuzini, M. A Mathematical Study on a Fractional-Order SEIR Mpox Model: Analysis and Vaccination Influence. Algorithms 2023, 16, 418. [Google Scholar] [CrossRef]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Ravichandran, C. A review of fractional order epidemic models for life sciences problems: Past, present and future. Alex. Eng. J. 2024, 95, 283–305. [Google Scholar] [CrossRef]
- Lusekelo, E.; Helikumi, M.; Kuznetsov, D.; Mushayabasa, S. Quantifying the effects of temperature and predation on the growth of Aedes mosquito population. Model. Earth Syst. Environ. 2023, 9, 3193–3206. [Google Scholar] [CrossRef]
- Helikumi, M.; Lolika Paride, O. Global dynamics of fractional-order model for malaria disease transmission. Asian Res. J. Math. 2022, 18, 82–110. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Dieg, CA, USA, 1999. [Google Scholar]
- Delavari, H.; Baleanu, D.; Sadati, J. Stability analysis of Caputo fractional-order nonlinear systems revisited. Nonlinear Dyn. 2012, 67, 2433–2439. [Google Scholar] [CrossRef]
- Molla, J.; Sekkak, I.; Mundo Ortiz, A.; Moyles, I.; Nasri, B. Mathematical modeling of mpox: A scoping review. ONE Health 2023, 16, 100540. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Vargas-De-León, C. Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent, Part II. Geophys. J. R. Astr. Soc. 1967, 13, 529–539, Reprinted in Fract. Calc. Appl. Anal. 2008, 11, 4–14. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010; p. 247. [Google Scholar]
- van-den Driessche, P.; Watmough, J. Reproduction number and sub-threshold endemic equilibria for compartment models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Shuai, Z.; Heesterbeek, J.A.P.; van den Driessche, P. Extending the type reproduction number to infectious disease control targeting contact between types. J. Math. Biol. 2013, 67, 1067–1082. [Google Scholar] [CrossRef]
- LaSalle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Bhunu, C.P.; Mushayabasa, S. Modelling the transmission dynamics of pox-like infections. IAENG Int. J. 2011, 41, 141–149. [Google Scholar]
- World Health Organization (WHO). Monkeypox: Public Health Advice for Gay, Bisexual and Other Men Who Have Sex with Men; World Health Organization: Geneva, Switzerland, 2022; Available online: https://www.who.int/news-room/questions-and-answers/item/monkeypox (accessed on 25 April 2025).
- Centers for Disease Control and Prevention (CDC). Preventing Mpox; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2024. Available online: https://www.cdc.gov/mpox/prevention/index.html (accessed on 25 April 2025).







| Symbol | Definition | Value | Units | Source |
|---|---|---|---|---|
| disease transmission from human to human | 0.00006 | year−1 | [53] | |
| disease transmission from rodent to human | 0.0001 | year−1 | [18,53] | |
| disease transmission from the environment to humans | 0.027 | year−1 | [18,53] | |
| natural mortality rate of humans | year−1 | [53] | ||
| natural mortality rate of rodents | year−1 | [18,53] | ||
| progression rate of humans from incubation to infectiousness | 0.2 | year−1 | [18] | |
| progression rate of rodents from incubation to infectiousness | 0.7 | year−1 | [18] | |
| recovery rate of infected individuals | year−1 | [18] | ||
| new recruitment of humans | year−1 | [18,53] | ||
| new recruitment of rodents | year−1 | [18,53] | ||
| rate of human awareness | year−1 | fitted | ||
| rate of use of environmental sanitation | year−1 | fitted | ||
| natural decay of the virus in the environment | 0.0939 | year−1 | [18] | |
| rate of virus shedding into the environment from rodents | 50 mL | year−1 | fitted | |
| rate of virus shedding into the environment from humans | 20 mL | year−1 | fitted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helikumi, M.; Ojija, F.; Mhlanga, A. Dynamical Analysis of Mpox Disease with Environmental Effects. Fractal Fract. 2025, 9, 356. https://doi.org/10.3390/fractalfract9060356
Helikumi M, Ojija F, Mhlanga A. Dynamical Analysis of Mpox Disease with Environmental Effects. Fractal and Fractional. 2025; 9(6):356. https://doi.org/10.3390/fractalfract9060356
Chicago/Turabian StyleHelikumi, Mlyashimbi, Fredrick Ojija, and Adquate Mhlanga. 2025. "Dynamical Analysis of Mpox Disease with Environmental Effects" Fractal and Fractional 9, no. 6: 356. https://doi.org/10.3390/fractalfract9060356
APA StyleHelikumi, M., Ojija, F., & Mhlanga, A. (2025). Dynamical Analysis of Mpox Disease with Environmental Effects. Fractal and Fractional, 9(6), 356. https://doi.org/10.3390/fractalfract9060356






