A Non-Standard Finite Difference Scheme for Time-Fractional Singularly Perturbed Convection–Diffusion Problems
Abstract
1. Introduction
- Time-fractional singularly perturbed convection–diffusion models play a crucial role in modeling anomalous transport phenomena in biological systems. They are particularly effective in capturing subdiffusive behavior observed in complex environments such as cellular interiors. These models account for memory effects and accurately represent sharp concentration gradients, making them highly suitable for simulating processes like drug diffusion through tissues and intracellular signaling pathways.
- Time-fractional singularly perturbed convection–diffusion equations are applied to model heat and mass transfer in advanced materials exhibiting memory-dependent behavior. They provide a more accurate representation of transport processes in materials like polymers and viscoelastic composites.
- In porous media, time-fractional models effectively capture anomalous diffusion arising from the heterogeneous structure of material. They are especially valuable for simulating groundwater flow and contaminant transport, where conventional models often fail to reflect the intricate and non-uniform nature of the underlying flow dynamics.
- (i)
- It produces oscillation-free solutions on a uniform mesh.
- (ii)
- It delivers more accurate results than traditional methods.
- (iii)
- It maintains convergence order even for very small values of .
- (iv)
- It is unconditionally stable and exhibits parameter-uniform convergence.
2. Some Preliminaries
3. Numerical Scheme
3.1. Temporal Discretization
3.2. Space Discretization
3.2.1. Derivation of NSFD Scheme
3.2.2. Full Discrete Scheme
4. Convergence Estimates
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers, 3rd ed.; McGraw-Hill Book Co.: New York, NY, USA, 1978. [Google Scholar]
- Nayfeh, A.H. Introduction to Perturbation Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- O’Malley, R.E., Jr. Introduction to Singular Perturbations, 3rd ed.; Harcourt Brace Jovanovich: New York, NY, USA, 1974. [Google Scholar]
- Clavero, C.; Jorge, J.C.; Lisbona, F.J. A uniformly convergent scheme on a nonuniform mesh for convection-diffusion parabolic problems. J. Comput. Appl. Math. 2003, 154, 415–429. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Gupta, V.; Awasthi, A. A uniformly convergent B-spline collocation method on a nonuniform mesh for singularly perturbed one-dimensional time-dependent linear convection-diffusion problem. J. Comput. Appl. Math. 2008, 220, 271–289. [Google Scholar] [CrossRef]
- Clavero, C.; Gracia, J.L.; Stynes, M. A simpler analysis of a hybrid numerical method for time-dependent convection-diffusion problems. J. Comput. Appl. Math. 2011, 235, 5240–5248. [Google Scholar] [CrossRef]
- Yüzbasıa, S.; Sahin, N. Numerical solutions of singularly perturbed one-dimensional parabolic convection–diffusion problems by the Bessel collocation method. Appl. Math. Comput. 2013, 220, 305–315. [Google Scholar]
- Clavero, C.; Gracia, J.L. A high order HODIE finite difference scheme for 1D parabolic singularly perturbed reaction-diffusion problems. Appl. Math. Comput. 2012, 218, 5067–5080. [Google Scholar] [CrossRef]
- Bansal, K.; Sharma, K.K. Parameter uniform numerical scheme for time dependent singularly perturbed convection-diffusion-reaction problems with general shift arguments. Numer. Algorithms 2017, 75, 113–145. [Google Scholar] [CrossRef]
- Chang, A.; Sun, H.G.; Zheng, C.; Lu, B.; Lu, C.; Ma, R.; Zhang, Y. A time fractional convection–diffusion equation to model gas transport through heterogeneous soil and gas reservoirs. Physica A 2018, 502, 356–369. [Google Scholar] [CrossRef]
- Pavlenko, I.; Ochowiak, M.; Włodarczak, S.; Krupińska, A.; Matuszak, M. Parameter identification of the fractional-Order mathematical model for convective mass transfer in a porous medium. Membranes 2023, 13, 819. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press, Inc.: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; p. 523. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press, Inc.: Boca Raton, FL, USA, 2015. [Google Scholar]
- Cai, M.; Li, C. Theory and Numerical Approximations of Fractional Integrals and Derivatives; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2020; p. 317. [Google Scholar]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2017, 225, 1533–1552. [Google Scholar] [CrossRef]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Choudhary, R.; Singh, S.; Kumar, D. A second-order numerical scheme for the time-fractional partial differential equations with a time delay. Comput. Appl. Math. 2017, 41, 28. [Google Scholar] [CrossRef]
- Soori, Z.; Aminataei, A. A new approximation to Caputo-type fractional diffusion and advection equations on non-uniform meshes. Appl. Numer. Math. 2019, 144, 21–41. [Google Scholar] [CrossRef]
- Gracia, J.L.; O’Riordan, E.; Stynes, M. Convergence in positive time for a finite difference method applied to a fractional convection-diffusion problem. Comput. Methods Appl. Math. 2023, 18, 33–42. [Google Scholar] [CrossRef]
- Gao, G.-h.; Sun, Z.-z.; Zhang, H.-w. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Roul, P.; Sundar, S. Novel numerical methods based on graded, adaptive and uniform meshes for a time-fractional advection-diffusion equation subjected to weakly singular solution. Numer. Algorithms 2025, 98, 531–561. [Google Scholar] [CrossRef]
- Kopteva, N. Error analysis of an L2-type method on graded meshes for a fractional-order parabolic problem. Math. Comp. 2021, 90, 327. [Google Scholar] [CrossRef]
- Kumar, K.; P, P.C.; Vigo-Aguiar, J. Numerical solution of time-fractional singularly perturbed convection-diffusion problems with a delay in time. Math. Methods Appl. Sci. 2021, 44, 3080–3097. [Google Scholar] [CrossRef]
- Kumie, H.G.; Tirunehi, A.A.; Derese, G.A. Crank–Nicolson method for solving time-fractional singularly perturbed delay partial differential equations. Res. Math. 2024, 11, 2293373. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Gupta, V. A robust uniformly convergent finite difference scheme for the time-fractional singularly perturbed convection-diffusion problem. Comput. Math. Appl. 2023, 137, 126–146. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Gupta, V.; Dubey, S. A robust higher-order finite difference technique for a time-fractional singularly perturbed problem. Math. Comput. Simul. 2024, 215, 43–68. [Google Scholar] [CrossRef]
- Aniley, W.T.; Duressa, G.F. Uniformly convergent numerical method for time-fractional convection–diffusion equation with variable coefficients. Partial Differ. Equ. Appl. Math. 2023, 8, 100592. [Google Scholar] [CrossRef]
- Tiruneh, A.A.; Kumie, H.G.; Derese, G.A. Singularly perturbed time-fractional convection–diffusion equations via exponential fitted operator scheme. Partial Differ. Equ. Appl. Math. 2024, 11, 100873. [Google Scholar] [CrossRef]
- Aniley, W.T.; Duressa, G.F. A novel exponentially fitted finite-difference method for time-fractional singularly perturbed convection-diffusion problems with variable coefficients. Front. Appl. Math. Stat. 2025, 11, 1541766. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Roos, H.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations, 2nd ed.; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ladyzhenskaia, O.A.; Solonnikov, V.A.; Ural’tseva, N.N. Linear and Quasi-Linear Equations of Parabolic Type, 23rd ed.; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations, 3rd ed.; World Scientific Publishing Co.: River Edge, NJ, USA, 1994. [Google Scholar]
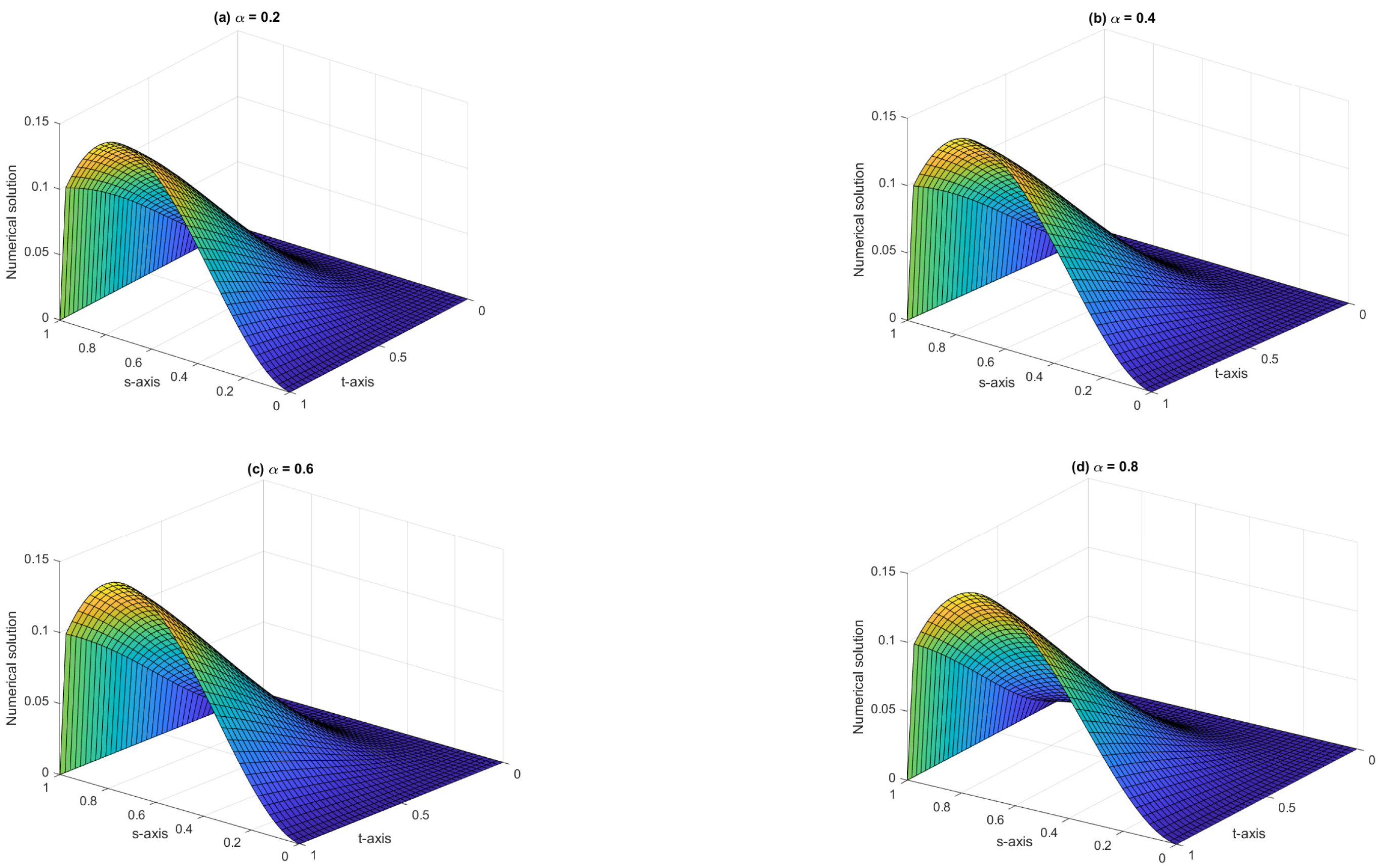
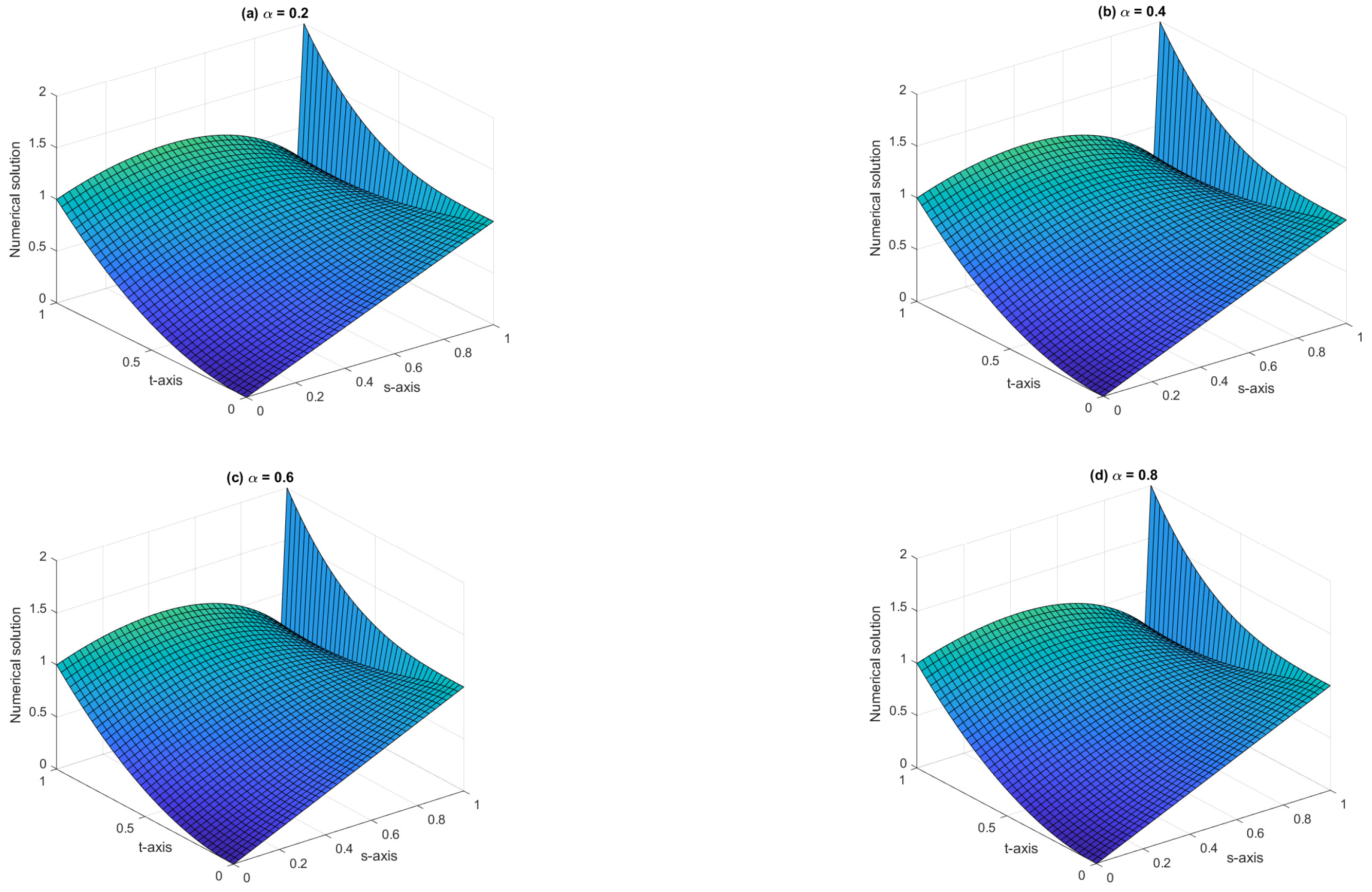
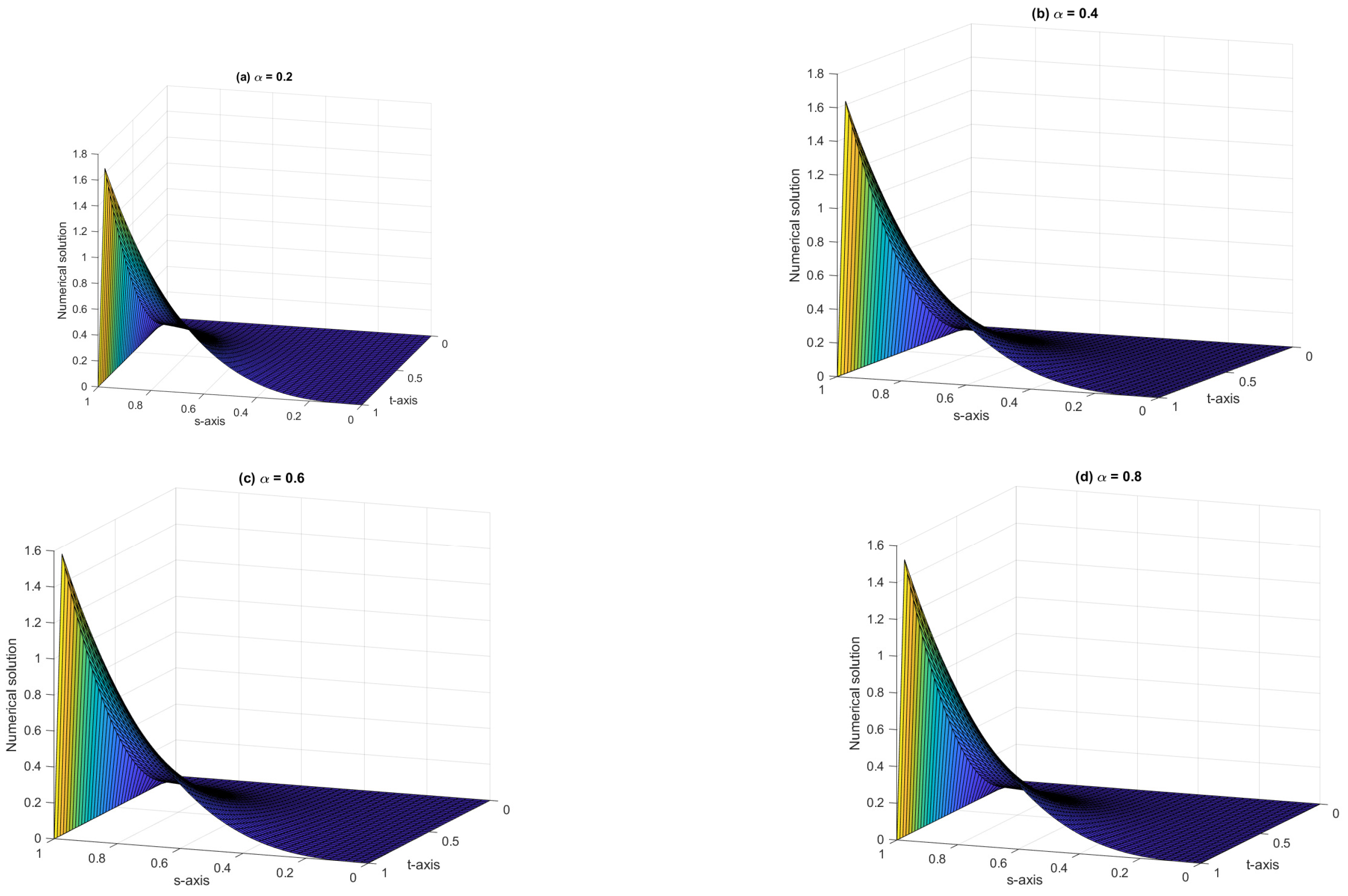

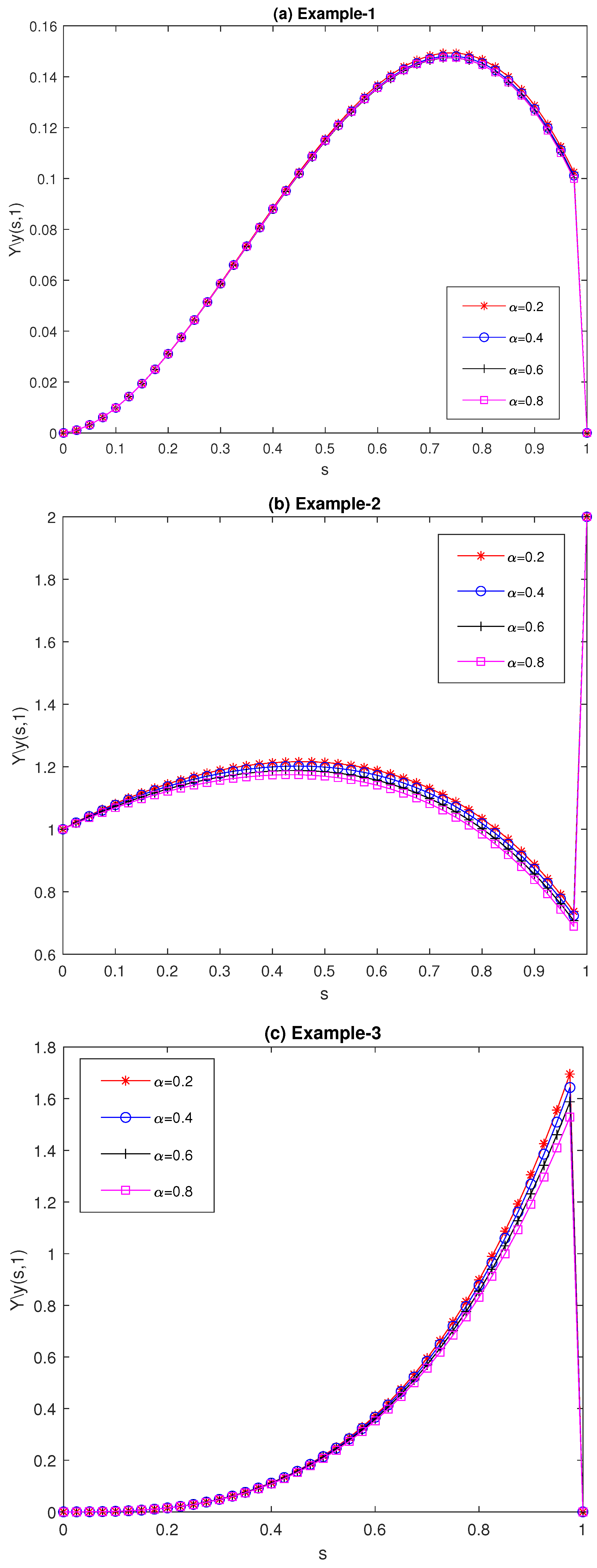
| ↓ | Er | Roc | Er | Roc | Er | Roc |
|---|---|---|---|---|---|---|
| − | − | − |
| ↓ | M = 20 | M = 40 | M = 80 | M = 160 | M = 320 |
|---|---|---|---|---|---|
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| - | |||||
| - |
| Sahoo [26] | Present Method | Sahoo [26] | Present Method | |
|---|---|---|---|---|
| /(N,M) | (32, 32) | (32, 32) | (64, 64) | (64, 64) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| ↓ | Er | Roc | Er | Roc | Er | Roc |
|---|---|---|---|---|---|---|
| − | − | − |
| ↓ | M = 20 | M = 40 | M = 80 | M = 160 | M = 320 |
|---|---|---|---|---|---|
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| - | |||||
| - |
| Sahoo [26] | Present Method | Sahoo [26] | Present Method | |
|---|---|---|---|---|
| /(N,M) | (32, 32) | (32, 32) | (64, 64) | (64, 64) |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| ↓ | Er | Roc | Er | Roc | Er | Roc |
|---|---|---|---|---|---|---|
| − | − | − |
| ↓ | M = 20 | M = 40 | M = 80 | M = 160 | M = 320 |
|---|---|---|---|---|---|
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| - | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| - | |||||
| - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podila, P.C.; Mishra, R.; Ramos, H. A Non-Standard Finite Difference Scheme for Time-Fractional Singularly Perturbed Convection–Diffusion Problems. Fractal Fract. 2025, 9, 333. https://doi.org/10.3390/fractalfract9060333
Podila PC, Mishra R, Ramos H. A Non-Standard Finite Difference Scheme for Time-Fractional Singularly Perturbed Convection–Diffusion Problems. Fractal and Fractional. 2025; 9(6):333. https://doi.org/10.3390/fractalfract9060333
Chicago/Turabian StylePodila, Pramod Chakravarthy, Rahul Mishra, and Higinio Ramos. 2025. "A Non-Standard Finite Difference Scheme for Time-Fractional Singularly Perturbed Convection–Diffusion Problems" Fractal and Fractional 9, no. 6: 333. https://doi.org/10.3390/fractalfract9060333
APA StylePodila, P. C., Mishra, R., & Ramos, H. (2025). A Non-Standard Finite Difference Scheme for Time-Fractional Singularly Perturbed Convection–Diffusion Problems. Fractal and Fractional, 9(6), 333. https://doi.org/10.3390/fractalfract9060333








