Remarks on the Relationship Between Fractal Dimensions and Convergence Speed

Abstract

This paper conducts an in-depth investigation into the fundamental relationship between the fractal dimensions and convergence properties of mathematical sequences. By concentrating on three representative classes of sequences, namely, the factorial-decay, logarithmic-decay, and factorial–exponential types, a comprehensive framework is established to link their geometric characteristics with asymptotic behavior. This study makes two significant contributions to the field of fractal analysis. Firstly, a unified methodology is developed for the calculation of multiple fractal dimensions, including the Box, Hausdorff, Packing, and Assouad dimensions, of discrete sequences. This methodology reveals how these dimensional quantities jointly describe the structures of sequences, providing a more comprehensive understanding of their geometric properties. Secondly, it is demonstrated that different fractal dimensions play distinct yet complementary roles in regulating convergence rates. Specifically, the Box dimension determines the global convergence properties of sequences, while the Assouad dimension characterizes the local constraints on the speed of convergence. The theoretical results presented herein offer novel insights into the inherent connection between geometric complexity and analytical behavior within sequence spaces. These findings have immediate and far-reaching implications for various applications that demand precise control over convergence properties, such as numerical algorithm design and signal processing. Notably, the identification of dimension-based convergence criteria provides practical and effective tools for the analysis of sequence behavior in both pure mathematical research and applied fields.

1. Introductions and Preliminaries

Historically, researchers have extensively studied sets and functions characterized by classical calculus, predominantly focusing on smooth and well-behaved objects. In contrast, less smooth and irregular sets and functions have often been overlooked, dismissed as exceptions, or regarded as mathematical curiosities [1]. However, these “non-smooth objects” frequently offer more accurate and realistic representations of numerous natural phenomena, such as the intricate patterns of snowflakes, the rugged outlines of coastlines, and the complexities of other irregular geometries. Traditional Euclidean frameworks are inadequate for capturing such complexities, and these objects thus require specialized tools and perspectives for their study.

Over the past few decades, scholars have made significant progress in systematically exploring and rigorously describing these irregular structures within well-defined mathematical frameworks, as evidenced by foundational works [2,3,4]. Among these advancements, fractal geometry has emerged as a powerful and general framework for the analysis and comprehension of these complex and irregular sets. By transcending the limitations of traditional geometry, fractal geometry has become indispensable in various scientific and mathematical domains.

The concept of the fractal dimension lies at the core of fractal geometry, serving as a fundamental tool for quantifying and analyzing the structural properties of fractals. This concept has found applications in a broad spectrum of disciplines, including mathematics, healthcare [5], and earth sciences [6]. Beyond its theoretical significance, the fractal dimension has become crucial in analyzing real-world data structures, where convergence properties directly affect computational efficiency, such as the following:

(1) Signal Processing: In electroencephalogram (EEG) signal analysis, the Box dimension of time-series data correlates with signal regularity, facilitating the development of noise reduction algorithms [7,8].

(2) Material Science: The convergence rate of fractal aggregates influences the mechanical properties of porous materials. Rapid convergence (low Box dimension) indicates a uniform pore distribution [9].

(3) Financial Modeling: High-frequency trading data often exhibit fractal patterns. Understanding the relationships between dimensions and convergence helps optimize risk assessment models [10].

Our study establishes connections among these domains by rigorously linking sequence convergence to fractal dimensions, providing a unified framework for quantifying complexity in applied systems. Among the various types of fractal dimensions, the Hausdorff dimension and the Box dimension [1,11,12,13] are of particular significance. This paper aims to conduct an in-depth exploration of fractal dimensions by examining their definitions, exploring their unique properties, and highlighting their diverse applications. Notably, the work of Koçak and Azcan [14] has provided valuable insights into convergent sequences of real numbers, presenting representative examples of sequences with and without a Box dimension of 0, as summarized below.

Proposition 1

([14]). Let ${\mathbb{N}}^{\ast }$ denote the set of positive integers. Then, we have the following statements.

(1) $\left\{{\displaystyle \frac{1}{ln(n+1)}}\right|n\in {\mathbb{N}}^{\ast }\}$ has the Box dimension 1;

(2) For $\alpha >0,\left\{{\displaystyle \frac{1}{n^{\alpha }}}\right|n\in {\mathbb{N}}^{\ast }\}$ has the Box dimension ${\displaystyle \frac{1}{1+\alpha }};$

(3) For $0<r<1,\left\{r^n\right|n\in {\mathbb{N}}^{\ast }\}$ has the Box dimension 0.

It is well known that

$$\underset{n\to +\infty }{lim}{\displaystyle \frac{lnn}{n^k}}=0$$

and

$$\underset{n\to +\infty }{lim}{\displaystyle \frac{n^k}{k^n}}=0$$

for all $k>1.$ Furthermore, Proposition 1 indicates that the Box dimension can, to a certain degree, characterize the convergence rate of a sequence. Evidently, the convergence speeds of the aforementioned sequences are correlated with their fractal dimensions. Inspired by this correlation, a natural conjecture arises: whether there exist more complex point arrays whose Box dimensions can assume any value within the interval $[0,1].$ Additionally, this conjecture prompts further investigations into the relationships between other fractal dimensions, such as the Hausdorff dimension and the Assouad dimension, and the convergence properties of sequences. For a sequence that converges monotonically to 0, an additional hypothesis is proposed: there may be an intimate connection between the Box dimension and the convergence rate of the series constructed from its terms. This potential relationship could offer novel perspectives on the interaction between fractal dimensions and sequence behavior, thereby enhancing our comprehension of fractal structures in both numerical and geometric contexts. The recent research by Brown et al. [15] has deepened the theoretical understanding of fractal dimensions in sequence spaces, while Luukkainen [16] has elucidated the pivotal role of the Assouad dimension in the analysis of irregular sets. Our study integrates these approaches, bridging the existing research gaps.

To derive the conclusion, we first introduce the definitions of the following three dimensions.

Definition 1

([1]). Let $\Lambda (\ne \varnothing )$ be any bounded subset of ${\mathbb{R}}^n(n\in {\mathbb{N}}^{\ast }).$ Let $N_{\delta }\left(\Lambda \right)$ be the smallest number of cubes of side δ that intersect $\Lambda .$ Then, the lower and upper Box dimensions of Λ are defined as, respectively,

$${\underline{dim}}_B\left(\Lambda \right)=\underset{\delta \to 0^{+}}{\underline{lim}}{\displaystyle \frac{log{N}_{\delta }\left(\Lambda \right)}{-log\delta }}$$

and

$${\overline{dim}}_B\left(\Lambda \right)=\underset{\delta \to 0^{+}}{\overline{lim}}{\displaystyle \frac{log{N}_{\delta }\left(\Lambda \right)}{-log\delta }}.$$

If the above two are equal, we refer to the common value as the Box dimension

$${dim}_B\left(\Lambda \right)=\underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{log{N}_{\delta }\left(\Lambda \right)}{-log\delta }}.$$

$N_{\delta }\left(\Lambda \right)$ is any of the following five numbers:

(1) The least number of closed spheres of radius δ covering Λ;

(2) The least number of cubes of side δ covering Λ;

(3) The least number of cubes of the number of δ-net cubes intersecting Λ;

(4) The least number of sets of diameter a covering Λ at most δ;

(5) The greatest number of mutually non-intersecting spheres of radius δ with the center on Λ.

The definitions of ${\underline{dim}}_B\left(\Lambda \right)$ and ${\overline{dim}}_B\left(\Lambda \right)$, respectively, quantify the scaling behavior of the minimal covering number $N_{\delta }\left(\Lambda \right)$ as the box size δ approaches 0. The Box dimension captures the geometric complexity of a set Λ and is constrained by the embedding space. Specifically, in ${\mathbb{R}}^n$, the Box dimension satisfies the relationship

$$0\le {\underline{dim}}_B\left(\Lambda \right)\le {\overline{dim}}_B\left(\Lambda \right)\le n.$$

Remark 1.

$0\le {\underline{dim}}_B\left(\Lambda \right)\le {\overline{dim}}_B\left(\Lambda \right)\le 1\mathrm{when}n=1.$

This reflects the fact that, in ${\mathbb{R}}^1$, any set can have at most the complexity of a one-dimensional structure.

Definition 2

([1]). Let a Borel set $F\subseteq {\mathbb{R}}^n$ be as follows. For $s\ge 0$ and $\delta >0,$ define

$$\begin{array}{c}\hfill {\mathcal{H}}_{\delta }^s\left(F\right)=inf\left\{\sum _{i=1}^{\infty }{\left|U_i\right|}^s:\left\{U_i\right\}\mathrm{is}\mathrm{a}\delta -\mathrm{cover}\mathrm{of}\mathrm{F}\right\}\end{array},$$

where $\left|U\right|=sup\left\{\right|x-y|:x,y\in U\}$ denotes the diameter of a nonempty set U and the infimum is taken over all countable collections $\left\{U_i\right\}$ of sets for which $F\subset \bigcup _{i=1}^{\infty }{U}_i$ and $0<|U_i|\le \delta .$ As δ decreases, ${\mathcal{H}}_{\delta }^s\left(F\right)$ can not decrease and therefore it has a limit (possibly infinite) as $\delta \to 0^{+};$ define

$${\mathcal{H}}^s\left(F\right)=\underset{\delta \to 0^{+}}{lim}{\mathcal{H}}_{\delta }^s\left(F\right).$$

The quantity ${\mathcal{H}}^s\left(F\right)$ is known as the s-dimensional Hausdorff measure of F. For a given F, there is a value ${dim}_H\left(F\right)$ for which ${\mathcal{H}}^s\left(F\right)=\infty$ for $s<{dim}_H\left(F\right)$ and ${\mathcal{H}}^s\left(F\right)=0$ for $s>{dim}_H\left(F\right).$ The Hausdorff dimension ${dim}_H\left(F\right)$ is defined to be this value, that is,

$${dim}_H\left(F\right)=inf\{s:{\mathcal{H}}^s\left(F\right)=0\}=sup\{s:{\mathcal{H}}^s\left(F\right)=\infty \}.$$

Definition 3

([1]). For $s⩾0$ and $\delta >0,$ let

$${\mathcal{P}}_{\delta }^s\left(F\right)=sup\left\{\sum _i{\left|B_i\right|}^s:\left\{B_i\right\}\mathit{is}\mathit{a}\mathit{collection}\mathit{of}\mathit{disjoint}\mathit{balls}\mathit{of}\mathit{radii}\mathit{at}\mathit{most}\delta \mathit{with}\mathit{centers}\mathit{in}F\right\}.$$

Since ${\mathcal{P}}_{\delta }^s\left(F\right)$ decreases with $\delta ,$ the limit

$${\mathcal{P}}_0^s\left(F\right)=\underset{\delta \to 0^{+}}{lim}{\mathcal{P}}_{\delta }^s\left(F\right)$$

exists. By considering countable dense sets, it is easy to see that ${\mathcal{P}}_0^s\left(F\right)$ is not a measure. Hence, we modify the definition to

$${\mathcal{P}}^s\left(F\right)=inf\left\{\sum _i{\mathcal{P}}_0^s\left(F_i\right):F\subset \bigcup _{i=1}^{\infty }{F}_i\right\}.$$

It may be shown that ${\mathcal{P}}^s\left(F\right)$ is a measure on ${\mathbb{R}}^n,$ known as the s-dimensional Packing measure. We define the Packing dimension in the natural way:

$${dim}_{\mathrm{P}}\left(F\right)=sup\{s:{\mathcal{P}}^s\left(F\right)=\infty \}=inf\{s:{\mathcal{P}}^s\left(F\right)=0\}.$$

The Hausdorff dimension and the Packing dimension, both measure-based, quantify a set’s geometric complexity through its scaling behavior. While the Hausdorff dimension focuses on fine details and the Packing dimension provides an upper bound on density, both primarily reflect global properties. In contrast, the Assouad dimension emphasizes local scaling, capturing the worst-case density across all scales, making it well suited for sets with non-uniform structures.

Definition 4

([17]). The Assouad dimension of a nonempty set $F\subseteq {\mathbb{R}}^d$ is defined by

$$\begin{array}{cc}\hfill {dim}_A\left(F\right)& =inf\{\alpha :\mathit{there}\mathit{exists}\mathrm{a}\mathit{constant}c>0\mathit{such}\mathit{that},\hfill \\ & \mathit{for}\mathit{all}0<r<R\mathrm{and}x\in F,N_r\left(B(x,R)\cap F\right)⩽c{\left({\displaystyle \frac{R}{r}}\right)}^{\alpha }\}.\hfill \end{array}$$

At the end of this section, certain notations throughout the present paper have been illustrated as follows.

(1) $\mathbb{Z}$ denotes the set of integers.

(2) ${\mathbb{N}}^{\ast }$ denotes the set of positive integers.

(3) $\mathbb{R}$ denotes the real numbers.

(4) For the set of all $\left\{a_n\right|n\in {\mathbb{N}}^{\ast }\}$ and $\left\{b_n\right|n\in {\mathbb{N}}^{\ast }\},$$a_n\sim b_n$ represents $\underset{n\to \infty }{lim}{\displaystyle \frac{a_n}{b_n}}=1.$

(5) For any sequence ${\left\{u_n\right\}}_{n=1}^{\infty },$ and any $a\in \mathbb{R},u_n\searrow a$ indicates $\underset{n\to \infty }{lim}{u}_n=a$ and $u_n>u_{n+1}$ for all $n\in {\mathbb{N}}^{\ast }$, while $u_n\nearrow a$ means $\underset{n\to \infty }{lim}{u}_n=a$ and $u_n<u_{n+1}$ for all $n\in {\mathbb{N}}^{\ast }.$

(6) The floor function, denoted as $\lfloor x\rfloor ,$ is defined as the greatest integer less than or equal to $x.$ Formally, this is as follows:

$$\lfloor x\rfloor =max\{n\in \mathbb{Z}\mid n\le x\}.$$

The ceiling function, denoted as $\lceil x\rceil$, is defined as the smallest integer greater than or equal to $x.$ Formally, this is as follows:

$$\lceil x\rceil =min\{n\in \mathbb{Z}\mid n\ge x\}.$$

2. Main Results

In this section, we will discuss the Box dimension, the Hausdorff dimension, the Packing dimension, and the Assouad dimension of three sequences, providing detailed calculations or proofs for each.

2.1. The Box Dimension

For discrete point sets, the Box dimension is typically greater than 0, reflecting the sparse distribution of points in space. The Box dimension of most sequences requires explicit calculation. Below, we present the detailed computation process for the Box dimension of three specific sequences.

Theorem 1.

$\Omega =\left\{{\displaystyle \frac{1}{n!}}|n\in {\mathbb{N}}^{\ast }\right\}$ has the Box dimension 0.

Proof of Theorem 1. 

Let $0<\delta <{\displaystyle \frac{1}{2}}$ and k be the integer satisfying ${\delta }_{k+1}\le \delta <{\delta }_k,$ where ${\delta }_k={\displaystyle \frac{1}{(k-1)!}}-{\displaystyle \frac{1}{k!}}={\displaystyle \frac{k-1}{k!}}$ and ${\delta }_{k+1}={\displaystyle \frac{1}{k!}}-{\displaystyle \frac{1}{(k+1)!}}={\displaystyle \frac{k}{(k+1)!}}$. Due to

$${\displaystyle \frac{k+1}{k}}\delta \ge {\displaystyle \frac{k+1}{k}}{\delta }_{k+1}={\displaystyle \frac{1}{k!}},$$

we observe that $\lceil {\displaystyle \frac{k+1}{k}}\rceil$ intervals of length $\delta$ cover $\left[0,{\displaystyle \frac{1}{k!}}\right],$ leaving $k-1$ points of $\Omega$, which can be covered by another $k-1$ intervals. Thus, $N_{\delta }\left(\Omega \right)\le {\displaystyle \frac{1}{k}}+k$ and

$${\displaystyle \frac{ln{N}_{\delta }\left(\Omega \right)}{-ln\delta }}\le {\displaystyle \frac{ln\left(\frac{1}{k}+k\right)}{-ln{\delta }_k}}={\displaystyle \frac{ln(1+k^2)-lnk}{ln\frac{k!}{k-1}}}.$$

(1)

According to the Stirling’s formula,

$$k!\sim \sqrt{2\pi k}{\left({\displaystyle \frac{k}{e}}\right)}^k,k\to +\infty ,$$

it holds

$${\displaystyle \frac{ln(1+k^2)-lnk}{ln\frac{k!}{k-1}}}\sim {\displaystyle \frac{ln(1+k^2)-lnk}{\frac{1}{2}ln\sqrt{2\pi }+\frac{1}{2}lnk+klnk-k-ln(k-1)}},k\to +\infty .$$

(2)

Note that

$$\underset{k\to +\infty }{lim}{\displaystyle \frac{ln(1+k^2)-lnk}{\frac{1}{2}ln\sqrt{2\pi }+\frac{1}{2}lnk+klnk-k-ln(k-1)}}=0.$$

(3)

It is obvious that $k\to +\infty$ is equivalent to $\delta \to 0^{+}.$ By combing Equations (1)–(3), we obtain

$${\overline{dim}}_B\left(\Omega \right)\le 0.$$

In addition, since $\Omega$ is a point set, we can obtain

$${\underline{dim}}_B\left(\Omega \right)\ge 0$$

in Remark 1. That is,

$${dim}_B\left(\Omega \right)=0.$$

□

Theorem 2.

For $a>1,\Psi =\left\{{\displaystyle \frac{1}{{ln}^{a}n}}|n\in {\mathbb{N}}^{\ast }\right\}$ has the Box dimension 1.

Proof of Theorem 2. 

Let $0<\delta <{\displaystyle \frac{1}{{ln}^{a}2}}-{\displaystyle \frac{1}{{ln}^{a}3}}$ and k be the integer satisfying ${\delta }_{k+1}\le \delta <{\delta }_k,$ where ${\delta }_k={\displaystyle \frac{1}{{ln}^a(k-1)}}-{\displaystyle \frac{1}{{ln}^{a}k}}$ and ${\delta }_{k+1}={\displaystyle \frac{1}{{ln}^{a}k}}-{\displaystyle \frac{1}{{ln}^a(k+1)}}.$ If $\left|U\right|<\delta ,$ then U can cover at most one of the points in the set $\left\{{\displaystyle \frac{1}{{ln}^{a}2}},{\displaystyle \frac{1}{{ln}^{a}3}},\cdots ,{\displaystyle \frac{1}{{ln}^{a}k}}\right\}$ since the distance between any pair of these points is at least

$${\displaystyle \frac{1}{{ln}^a(k-1)}}-{\displaystyle \frac{1}{{ln}^{a}k}}>\delta .$$

Consequently, at least $k-1$ sets of diameter $\delta$ are required to cover $\Psi ,$ namely, $N_{\delta }\left(\Psi \right)\ge k-1.$ Thus,

$${\displaystyle \frac{ln{N}_{\delta }\left(\Psi \right)}{-ln\delta }}\ge {\displaystyle \frac{ln(k-1)}{-ln{\delta }_{k+1}}}={\displaystyle \frac{ln(k-1)}{-ln\left[\frac{1}{{ln}^{a}k}-\frac{1}{{ln}^a(k+1)}\right]}}.$$

(4)

Note that

$$ln(k-1)\sim lnk\sim ln(k+1),k\to +\infty ,$$

(5)

$${\displaystyle \frac{1}{{ln}^a(k+1)}}-{\displaystyle \frac{1}{{ln}^{a}k}}\to 0,k\to +\infty .$$

Further, the Taylor expansion gives

$${\displaystyle \frac{1}{{ln}^a(k+1)}}-{\displaystyle \frac{1}{{ln}^{a}k}}\sim {\displaystyle \frac{1}{k}}·{\displaystyle \frac{a}{{ln}^{a+1}k}},k\to +\infty .$$

(6)

Thus, the logarithmic term in the denominator can be approximated as

$$-ln\left({\displaystyle \frac{a}{k{ln}^{a+1}k}}\right)=lnk-lna+(a+1)lnlnk.$$

(7)

It is obvious that $k\to +\infty$ is equivalent to $\delta \to 0^{+}.$ By combing Equations (4)–(7), we obtain

$${\underline{dim}}_B\left(\Psi \right)\ge 1.$$

In addition, since $\Psi$ is a point set, we know that

$${\overline{dim}}_B\left(\Psi \right)\le 1$$

in Remark 1. That is,

$${dim}_B\left(\Psi \right)=1.$$

□

Theorem 3.

$\chi =\left\{{\displaystyle \frac{e^n·n!}{n^{n+p}}}\right|n\in {\mathbb{N}}^{\ast }\}$ has the Box dimension ${\displaystyle \frac{1}{p+\frac{1}{2}}}$.

Proof of Theorem 3. 

Let $0<\delta <{\displaystyle \frac{1}{p+\frac{1}{2}}}$ and k be the integer satisfying ${\delta }_{k+1}\le \delta <{\delta }_k,$ where ${\delta }_k={\displaystyle \frac{e^{k-1}·(k-1)!}{{(k-1)}^{k-1+p}}}-{\displaystyle \frac{e^k·k!}{k^{k+p}}}$ and ${\delta }_{k+1}={\displaystyle \frac{e^k·k!}{k^{k+p}}}-{\displaystyle \frac{e^{k+1}·(k+1)!}{{(k+1)}^{k+1+p}}}.$ We prove ${dim}_B\left(\chi \right)={\displaystyle \frac{1}{p+\frac{1}{2}}}$ in two parts.

On one hand, if $\left|U\right|<\delta ,$ then U can cover at most one of the points $\left\{e,{\displaystyle \frac{2e^2}{2^{2+p}}},\cdots ,{\displaystyle \frac{e^k·k!}{k^{k+p}}}\right\}$ since the distance between any pair of these points is at least

$${\displaystyle \frac{e^{k-1}·(k-1)!}{{(k-1)}^{k-1+p}}}-{\displaystyle \frac{e^k·k!}{k^{k+p}}}>\delta .$$

Consequently, at least k sets of diameter $\delta$ are required to cover $\chi ,$ namely, $N_{\delta }\left(\chi \right)\ge k.$ Thus,

$${\displaystyle \frac{ln{N}_{\delta }\left(\chi \right)}{-ln\delta }}\ge {\displaystyle \frac{lnk}{-ln{\delta }_{k+1}}}={\displaystyle \frac{lnk}{-ln\left[\frac{e^k·k!}{k^{k+p}}-\frac{e^{k+1}·(k+1)!}{{(k+1)}^{k+1+p}}\right]}}.$$

(8)

Applying Stirling’s formula $k!\sim \sqrt{2\pi k}{\left({\displaystyle \frac{k}{e}}\right)}^k$ to ${\delta }_{k+1}$, we obtain the following:

$${\displaystyle \frac{e^k·k!}{k^{k+p}}}\sim \sqrt{2\pi }{k}^{{\displaystyle \frac{1}{2}}-p},k\to +\infty ,$$

(9)

$${\displaystyle \frac{e^{k+1}·(k+1)!}{{(k+1)}^{k+1+p}}}\sim \sqrt{2\pi }{(k+1)}^{{\displaystyle \frac{1}{2}}-p},k\to +\infty .$$

(10)

For large k, the difference in Equation (8) behaves as

$${\delta }_{k+1}\sim \sqrt{2\pi }\left[k^{{\displaystyle \frac{1}{2}}-p}-{(k+1)}^{{\displaystyle \frac{1}{2}}-p}\right].$$

(11)

Using the first-order Taylor expansion ${(k+1)}^{{\displaystyle \frac{1}{2}}-p}\approx k^{{\displaystyle \frac{1}{2}}-p}+\left({\displaystyle \frac{1}{2}}-p\right)k^{-{\displaystyle \frac{1}{2}}-p}$, we obtain

$${\delta }_{k+1}\sim \sqrt{2\pi }\left(p-{\displaystyle \frac{1}{2}}\right)k^{-{\displaystyle \frac{1}{2}}-p}.$$

(12)

Substituting Equation (12) into Equation (8), we obtain the following:

$${\displaystyle \frac{lnk}{-ln{\delta }_{k+1}}}\sim {\displaystyle \frac{lnk}{-ln\left[\sqrt{2\pi }\left(p-\frac{1}{2}\right)k^{-\frac{1}{2}-p}\right]}}\to {\displaystyle \frac{1}{p+\frac{1}{2}}}\mathrm{as}k\to \infty .$$

This proves

$${dim}_B\left(\chi \right)\ge {\displaystyle \frac{1}{p+\frac{1}{2}}}.$$

On the other hand, by combing Equation (9) and Equation (11), we can obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{1-{\left(1+\frac{1}{k}\right)}^{\frac{1}{2}-p}}}·\delta & \ge {\displaystyle \frac{1}{1-{\left(1+\frac{1}{k}\right)}^{\frac{1}{2}-p}}}·{\delta }_{k+1}\hfill \\ \hfill & \sim {\displaystyle \frac{e^{k}k!}{k^{k+p}}}.\hfill \end{array}$$

(13)

So, the interval $[0,{\displaystyle \frac{e^{k}k!}{k^{k+p}}}]$ can be fully covered using scaling factor

$${\displaystyle \frac{1}{1-{\left(1+\frac{1}{k}\right)}^{\frac{1}{2}-p}}}·\delta .$$

The remaining $k-1$ discrete points each require one $\delta$-cover. Thus, the total covering number satisfies

$$N_{\delta }\left(\chi \right)\le ⌈{\displaystyle \frac{1}{1-{(1+\frac{1}{k})}^{\frac{1}{2}-p}}}⌉+k-1.$$

So, we can obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{ln{N}_{\delta }\left(\chi \right)}{-ln\delta }}& \le {\displaystyle \frac{ln\left[\frac{2}{\left|\frac{1}{2}-p\right|k^{-1}}+k\right]}{-ln\left(\sqrt{2\pi }|p-\frac{1}{2}|k^{-\frac{1}{2}-p}\right)}}\hfill \\ \hfill & \sim {\displaystyle \frac{lnk}{(\frac{1}{2}+p)lnk}}(\mathrm{dominant}\mathrm{term}\mathrm{analysis})\hfill \\ \hfill & \to {\displaystyle \frac{1}{p+\frac{1}{2}}}\mathrm{as}k\to \infty \hfill \end{array}$$

(14)

Equation (13) and Equation (14) establish the upper bound

$${\overline{dim}}_B\left(\chi \right)\le {\displaystyle \frac{1}{p+\frac{1}{2}}}$$

Combining with the lower bound result from the first part, we conclude

$${dim}_B\left(\chi \right)={\displaystyle \frac{1}{p+\frac{1}{2}}}$$

□

Building upon this, we can determine the convergence or divergence of each sequence based on the Box dimension [10]. Furthermore, the corresponding parameter ranges for these behaviors can also be established.

Remark 2

([10]). Since ${dim}_B\left(\Omega \right)=0<{\displaystyle \frac{1}{2}}$ and ${dim}_B\left(\Psi \right)=1>{\displaystyle \frac{1}{2}},$ the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{1}{n!}}$ converges and the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{1}{{ln}^{a}n}}(a>1)$ diverges. Likewise, for the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{e^n·n!}{n^{n+p}}},$ if $p>{\displaystyle \frac{3}{2}},$ then ${dim}_B\left(\chi \right)<{\displaystyle \frac{1}{2}}$ so that the series converges. If ${\displaystyle \frac{1}{2}}<p<{\displaystyle \frac{3}{2}},$ then ${dim}_B\left(\chi \right)>{\displaystyle \frac{1}{2}}$ so that the series diverges.

The relationship between the Box dimension and the convergence or divergence of a series, as illustrated above, provides a foundation for exploring more complex cases. In particular, staggered series exhibit distinct behaviors that can be analyzed under similar dimensional criteria. This leads to the following observation.

Remark 3.

For the staggered series ${\displaystyle \sum _{n=1}^{\infty }}{(-1)}^n{a}_n,$ let $\Gamma =\left\{{(-1)}^n{a}_n\right|n\in {\mathbb{N}}^{\ast }\}.$ We obtain that ${dim}_B\left(\Gamma \right)$ is between 0 and 1 if it satisfies the following conditions [10]:

(1) There is an $N\in {\mathbb{N}}^{\ast }$ such that $a_n\searrow 0$ and $a_n-a_{n+1}\searrow 0$ for all $n\ge N;$

(2) $\sum _{n=1}^{\infty }{(-1)}^n{a}_n$ converges.

2.2. The Hausdorff Dimension and the Packing Dimension

Compared to the Box dimension, the Hausdorff dimension and the Packing dimension are more rigorous, placing greater emphasis on the fine structure of a set. However, discrete point sets lack complex geometric structures. Therefore, we can directly apply the following lemmas to arrive at the same conclusion.

Lemma 1

([1]). (Countable stability.) If $F_1,F_2,\cdots ,F_n,\cdots$ is a (countable) sequence of sets, for $i\in {\mathbb{N}}^{\ast },$ then

$${dim}_H\left(\bigcup _{i=1}^{\infty }{F}_i\right)=\underset{1⩽i<\infty }{sup}\left\{{dim}_H{F}_i\right\}.$$

Lemma 2

([1]). (Countable set.) If F is countable, then ${dim}_{H}F=0;$ for $i\in {\mathbb{N}}^{\ast },$ if $F_i$ is a single point, then ${dim}_H{F}_i=0.$ Thus, it follows from Lemma 1 that ${dim}_H\left(\bigcup _{i=1}^{\infty }{F}_i\right)=0.$

For the above $\Omega ,\Psi ,\chi ,$ we have

$${dim}_H\left(\Omega \right)={dim}_H\left(\Psi \right)={dim}_H\left(\chi \right)=0$$

by Lemma 2. In addition, the Packing measure and the Packing dimension have the properties of the Hausdorff measure and the Hausdorff dimension [1]; thus, we can also obtain

$${dim}_P\left(\Omega \right)={dim}_P\left(\Psi \right)={dim}_P\left(\chi \right)=0.$$

2.3. The Assouad Dimension

Definition 5.

A sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ satisfies Property T if there is the following:

(i) 

$\exists N\in {\mathbb{N}}^{\ast }$ such that $a_n\searrow 0$ and $a_n-a_{n+1}\searrow 0$ for $n\ge N$ (monotonicity);

(ii) 

$\underset{n\to \infty }{lim}{\displaystyle \frac{a_{n-1}}{a_n}}=1$ (asymptotic ratio condition);

(iii) 

$\underset{n\to \infty }{lim}{\displaystyle \frac{a_n-a_{n+1}}{a_{n+1}-a_{n+2}}}=1$ (uniform difference decay).

Theorem 4.

For any sequence $F={\left\{u_n\right\}}_{n=1}^{\infty }$ with Property T:

(1)

${dim}_A\left(F\right)=1$ reflects the maximal local density variation;

(2)

For $\Omega =\left\{{\displaystyle \frac{1}{n!}}\right\}$ (lacking Property T), ${dim}_A\left(\Omega \right)=0$ due to the following:

$${\displaystyle \frac{{\Omega }_{n-1}}{{\Omega }_n}}=n\to \infty \mathrm{and}{\displaystyle \frac{{\Omega }_n-{\Omega }_{n+1}}{{\Omega }_{n+1}-{\Omega }_{n+2}}}={\displaystyle \frac{n+2}{n}}\to 1$$

Proof. 

Part (1): ${dim}_A\left(F\right)=1$ for Property T sequences

For fixed k, set $x_k=0$, $R_k=u_k$, and $r_k=u_k-u_{k+1}$. By Property T(iii), $r_k/u_{k+1}\to 0$. The number of $r_k$-balls needed to cover $B(0,R_k)\cap F$ satisfies the following:

$$N_{r_k}\ge {\displaystyle \frac{u_k}{2r_k}}={\displaystyle \frac{1}{2\left(1-\frac{u_{k+1}}{u_k}\right)}}\sim {\displaystyle \frac{1}{2\left(1-e^{-1}\right)}}·{\displaystyle \frac{R_k}{r_k}}$$

using Property T(ii) that $u_{k+1}/u_k\to e^{-1}$. From Definition 4, this implies ${dim}_A\left(F\right)\ge 1$. The upper bound ${dim}_A\left(F\right)\le 1$ follows from ${dim}_A\le {dim}_B=1.$ Part (2): ${dim}_A\left(\Omega \right)=0.$

For ${\Omega }_k={\displaystyle \frac{1}{k!}}$, we have

$${\displaystyle \frac{{\Omega }_{k-1}}{{\Omega }_k}}=k\to \infty$$

violating Property T(ii). The gaps satisfy

$${\displaystyle \frac{{\Omega }_k-{\Omega }_{k+1}}{{\Omega }_{k+1}-{\Omega }_{k+2}}}={\displaystyle \frac{k+2}{k}}\to 1$$

For $R={\displaystyle \frac{1}{m!}}$ and $r={\displaystyle \frac{1}{(m+1)!}},$

$$N_r\left(B(0,R)\right)\le m\mathrm{but}{\left({\displaystyle \frac{R}{r}}\right)}^{\alpha }={(m+1)}^{\alpha }\to \infty \forall \alpha >0$$

Thus, no $\alpha >0$ satisfies the Assouad condition.

□

For the above $\Psi$ and $\chi$ with the property $T,$ we have ${dim}_A\left(\Psi \right)={dim}_A\left(\chi \right)=1.$ For $\Omega$ lacking property T, ${dim}_A\left(\Omega \right)=0.$ Alternatively, is it possible to construct or identify a sequence whose Box dimension is 0 while the Assouad dimension reaches 1? This intriguing question invites further exploration into the intricate relationships between these dimensional measures.

3. Graphs and Numerical Results

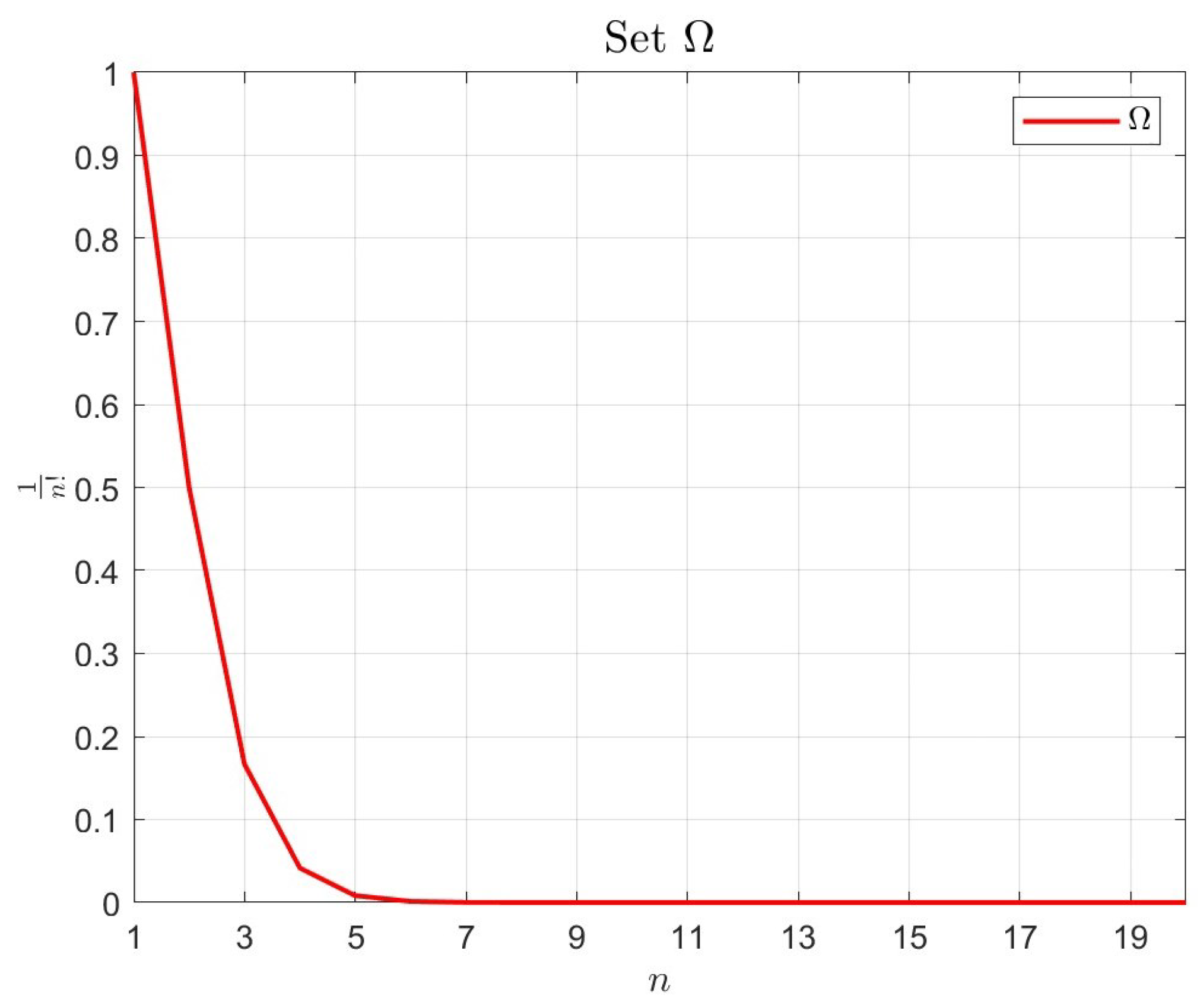
Figure 1 demonstrates the characteristic exponential decay of the sequence $\Omega$ as n increases. The values exhibit a sharp decline for $n\le 5$, followed by rapid convergence toward zero when $n>5$. This accelerated convergence stems from the factorial denominator’s growth rate, which dominates polynomial and exponential scaling. The fractal dimension analysis reveals that the Hausdorff dimension, the Packing dimension, and the Box dimension all equal zero (${dim}_H\left(\Omega \right)={dim}_P\left(\Omega \right)={dim}_B\left(\Omega \right)=0$), indicating an absence of fractal structure at any scale. Notably, the Assouad dimension ${dim}_A\left(\Omega \right)=0$ confirms the sequence’s ultra-sparse local configuration, consistent with its super-exponential convergence properties established in Theorem [17]. This complete dimensional collapse underscores the sequence’s significance in numerical analysis where accelerated convergence is paramount.

Figure 2 presents the parametric decay behavior of sequence $\Psi$, where the convergence rate varies systematically with parameter a. At $a=1.5$, the sequence displays gradual decay, maintaining relatively high values for small n. Progressive increases to $a=2,2.5,3,$ and $3.5$ yield successively steeper convergence profiles, particularly noticeable in the asymptotic regime. This parametric dependence reflects the growing dominance of the logarithmic denominator ${ln}^{a}n$ at large n. Dimensional analysis reveals a fundamental dichotomy: while the Hausdorff and Packing dimensions vanish (${dim}_H\left(\Psi \right)={dim}_P\left(\Psi \right)=0$) and the Box dimension reaches unity (${dim}_B\left(\Psi \right)=1$), the Assouad dimension ${dim}_A\left(\Psi \right)=1$ (Theorem [17]) indicates maximal local density fluctuations. This dimensional contrast between global linearity and local clustering explains the sequence’s constrained convergence rate despite its simple one-dimensional global structure, a consequence of its preservation of Property T.

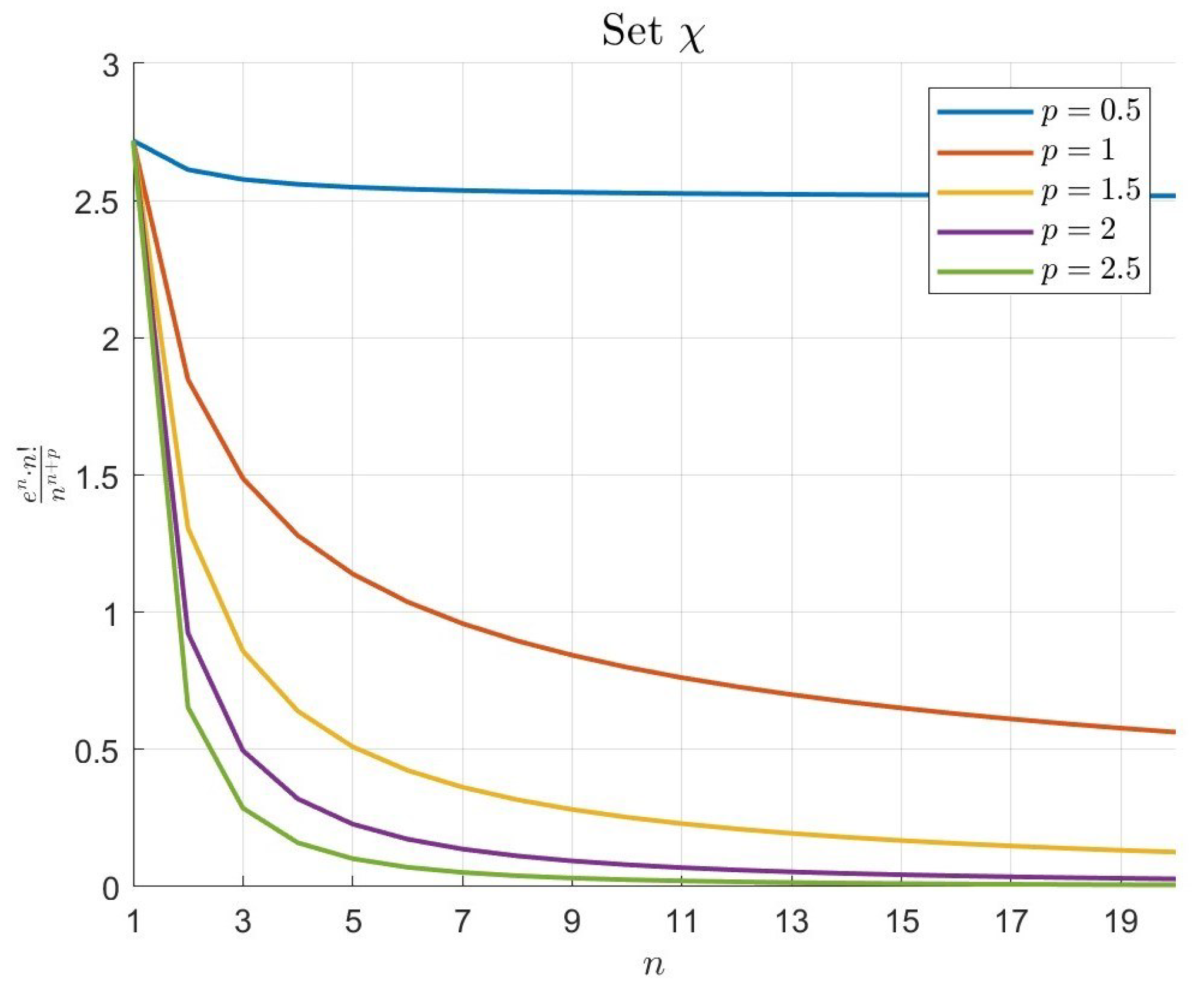
The sequence $\chi$ in Figure 3 exhibits dual-phase behavior characterized by initial growth followed by asymptotic decay. For small n, the factorial and exponential terms dominate, producing rapid initial growth. However, the denominator $n^{n+p}$ eventually governs the asymptotic behavior, inducing convergence to zero. Larger values of parameter p accelerate this decay, producing sharper convergence profiles. The Box dimension ${dim}_B\left(\chi \right)=1/(p+{\displaystyle \frac{1}{2}})$ quantifies how p modulates the global distribution density, with higher values yielding more compact configurations. Remarkably, the Assouad dimension remains fixed at ${dim}_A\left(\chi \right)=1$ (Theorem [17]), demonstrating robust local clustering properties inherent to sequences satisfying Property T. This dimensional combination positions $\chi$ as intermediate between $\Omega$ and $\Psi$ in convergence speed—its global structure (quantified by the Box dimension) is more complex than $\Omega$ but simpler than $\Psi$, while its local behavior (characterized by the Assouad dimension) maintains the constrained clustering that limits convergence rates.

Our dimensional analysis reveals fundamental relationships between geometric structure and convergence behavior. The factorial sequence $\Omega$ (Figure 1) exhibits complete dimensional collapse, with all four dimensions equaling zero, corresponding to its ultra-sparse configuration. The logarithmic sequence $\Psi$ (Figure 2) displays dimensional dichotomy: zero-valued Hausdorff and Packing dimensions, unit Box dimension, and unit Assouad dimension, reflecting its hybrid global–local structure. The factorial–exponential sequence $\chi$ (Figure 3) demonstrates parametric dimensional control, where p modulates the Box dimension while the Assouad dimension remains fixed. The Assouad dimension proves particularly valuable for explaining why sequences with similar global structures (e.g., $\Psi$ and $\chi$) exhibit different convergence behaviors due to their distinct local density properties.

Several important caveats should be noted. First, these conclusions assume strictly monotonic sequences with discrete sampling. Extension to non-monotonic or continuous cases may require additional dimensional analysis. Second, the observed dimensional relationships hold for the specific sequence classes studied; generalization to broader function spaces warrants further investigation. Nevertheless, the consistent correlation between the Assouad dimension and local convergence constraints suggests this measure provides robust insights across diverse mathematical contexts. Collectively, the combined examination of the Hausdorff dimension, the Packing dimension, the Box dimension, and the Assouad dimension establishes a comprehensive framework for analyzing how multiscale geometric properties govern sequence convergence.

4. Conclusions and Further Research

4.1. The Fractal Dimension Aggregation

This is

Table 1. Aggregation.

N	The Hausdorff Dimension	The Packing Dimension	The Box Dimension	The Assouad Dimension
$\Omega =\left\{{\displaystyle \frac{1}{n!}}|n\in {\mathbb{N}}^{\ast }\right\}$	0	0	0	0
$a>1,\Psi =\left\{{\displaystyle \frac{1}{{ln}^{a}n}}|n\in {\mathbb{N}}^{\ast }\right\}$	0	0	1	1
$\chi =\{{\displaystyle \frac{e^n·n!}{n^{n+p}}},n\in {\mathbb{N}}^{\ast }\}$	0	0	${\displaystyle \frac{1}{p+\frac{1}{2}}}$	1

: Aggregation, in which we want to show the aggregation of the fractal dimensions of the above three-point columns.

4.2. The Relationship

Our investigation of sequence convergence rates builds upon the quantitative framework established in [18], extending their metric characterization through fractal dimensional analysis. The following definition formalizes our measure of convergence speed:

Definition 6.

For a convergent series ${\sum }_{n=1}^{\infty }{a}_n$, the convergence coefficient $\Phi \left(a_n\right)={\displaystyle \frac{a_n}{a_{n+1}}}$ quantifies the rate of convergence. Larger values of $\Phi \left(n\right)$ correspond to the faster convergence of ${\sum }_{n=1}^{\infty }{a}_n$.

Consider the three canonical series formed by our studied sequences:

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{n!}},\sum _{n=1}^{\infty }{\displaystyle \frac{1}{{ln}^{a}n}}(a>1),\mathrm{and}\sum _{n=1}^{\infty }{\displaystyle \frac{e^n·n!}{n^{n+p}}}\end{array}$$

corresponding to $\Omega$, $\Psi$, and $\chi$, respectively. Our analysis reveals the following hierarchy of convergence rates:

$$\begin{array}{c}\hfill \Phi \left(\Psi \right)<\Phi \left(\chi \right)<\Phi \left(\Omega \right)\end{array}$$

with corresponding Box dimensions satisfying the following:

$$\begin{array}{c}\hfill {dim}_B\left(\Omega \right)=0<{dim}_B\left(\chi \right)={\displaystyle \frac{1}{p+\frac{1}{2}}}<{dim}_B\left(\Psi \right)=1\end{array}$$

This inverse relationship between the Box dimension and convergence rate demonstrates that sparser sequences (lower ${dim}_B$) exhibit faster convergence.

The Assouad dimension provides deeper insight into local convergence constraints. For sequences with ${dim}_A=1$ (including $\Psi$ and $\chi$, which satisfy Property T), the local density structure bounds the convergence rate:

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim\; sup}\Phi \left(u_n\right)\le e\end{array}$$

This bound reflects linear clustering behavior that maintains a consistent point density across scales. Conversely, sequences with ${dim}_A=0$ (such as $\Omega =\{1/n!\}$) display super-sparse distributions with unbounded convergence rates:

$$\begin{array}{c}\hfill \Phi \left({\Omega }_n\right)=n\to \infty \end{array}$$

enabling convergence faster than any exponential scale.

The Assouad dimension thus classifies convergence behavior into two distinct regimes:

• Systems with ${dim}_A=1$ exhibit constrained dynamics ($\Phi \le e$);
• Systems with ${dim}_A=0$ demonstrate unconstrained divergence ($\Phi \to \infty$).

This dichotomy reveals how geometric constraints at local scales govern asymptotic behavior.

The Box dimension and Assouad dimension offer complementary perspectives:

• The Box dimension measures global sparsity, with ${dim}_B\left(\Omega \right)=0$ and ${dim}_B\left(\Psi \right)=1$ representing extremal cases;
• The Assouad dimension characterizes local density fluctuations and their impact on convergence.

Their combined use provides a complete dimensional framework:

• The Box dimension determines series convergence (global criterion);
• The Assouad dimension governs the limiting convergence speed (local refinement).

While these results hold for our studied sequence classes, their universal applicability to all monotonically decreasing sequences requires further investigation. Potential exceptions may exist in edge cases or under different boundary conditions. Future work should include the following:

• Examine non-monotonic sequences;
• Investigate sequences with intermediate Assouad dimensions ($0<{dim}_A<1$);
• Develop theoretical bounds for more general function classes.

Such investigations would further refine our understanding of the dimensional–convergence relationship.

5. Potential Applications

The established relationship between fractal dimensions and sequence convergence speed opens new avenues for scientific computing and data analysis:

1.

Convergence Diagnostics for Numerical Algorithms

• Sequences with ${dim}_B<0.5$ and ${dim}_A=0$ (e.g., $\Omega =\left\{{\displaystyle \frac{1}{n!}}\right\}$) exhibit ultra-fast convergence, ideal for testing high-precision summation algorithms.
• Sequences with ${dim}_B=1$ and ${dim}_A=1$ (e.g., $\Psi =\left\{{\displaystyle \frac{1}{{ln}^{a}n}}\right\}$) serve as critical cases for analyzing boundary convergence in Monte Carlo simulations.

2.

Fractal-Based Signal Processing

• EEG Denoising: Signals (${dim}_B\approx 0$) are distinguished from noise (${dim}_B\approx 1$) using the criteria from Section 2.
• Financial Time Series: The Assouad dimension identifies transitions between clustered (${dim}_A=1$) and sparse (${dim}_A=0$) market regimes.

3.

Materials Science Characterization

• Porous material analysis: The ${dim}_B\left(\chi \right)={\displaystyle \frac{1}{p+\frac{1}{2}}}$ relationship parallels pore-size distribution measurements.
• Fracture surface evaluation: ${dim}_A=0$ sequences model brittle fractures; ${dim}_A=1$ describes ductile fractures.

4.

Computational Complexity Optimization

• Algorithm Design: Auto-tune precision by monitoring residual sequence’s Box dimension.
• Data Compression: Apply factorial-based encoding to ${dim}_A=0$ sequences.