Analysis of Large Membrane Vibrations Using Fractional Calculus

Abstract

The study of vibration equations of large membranes is crucial in various scientific and engineering fields. Analyzing the vibration equations of bridges, roofs, and spacecraft structures helps in designing structures that resist excessive oscillations and potential failures. Aircraft wings, parachutes, and satellite components often behave like large membranes. Understanding their vibration characteristics is essential for stability, efficiency, and durability. Studying large membrane vibration involves solving partial differential equations and eigenvalue problems, contributing to advancements in numerical methods and computational physics. In this paper, the Elzaki transformation decomposition method and the Shehu transformation decomposition method, along with inverse Elzaki and inverse Shehu transformations, are used to investigate the fractional vibration equation of a large membrane. The solutions are obtained in terms of Mittag–Leffler functions.

1. Introduction

Investigating the Vibration Equation is both challenging and essential for various applications, as many modern devices, such as microphones and audio systems, rely on membranes, making it crucial to study their physics and wave propagation [1,2,3,4]. In bioengineering, physiological tissues are often modeled as membranes, and the human hearing system is understood through the physical properties of the eardrum’s Vibration Equation. A deep understanding of membrane vibrations is vital for designing assistive devices for deaf people. Additionally, the vibration equation of a large membrane serves as a fundamental mathematical model describing two-dimensional wave propagation, playing a crucial role in fields such as acoustics, engineering, biomedical science, and astrophysics [5,6,7,8]. Mastering membrane vibrations enables the development of efficient systems in musical instruments, aerospace structures, and medical devices [9,10,11]. In recent years, fractional calculus has been viewed as an effective approach to modeling real-world scenarios with high precision and efficiency [12,13,14,15,16]. Fractional calculus [17,18,19] has emerged as a valuable tool for modeling complex and anomalous phenomena in various scientific and engineering fields.

Here, the time-fractional derivatives are included in the following equation. We have examined large membrane vibrations involving fractional derivatives in this article [20].

$${\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}=c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right), 1<\gamma \le 2$$

with initial conditions (IC)

$$h\left(v,0\right)=h_1\left(v\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_u\left(v,0\right)=c\left(h_2\left(v\right)\right),$$

where $D_u^{\gamma }h\left(v,u\right)$ represents the Liouville–Caputo fractional derivatives of a function $h\left(v,u\right)$ that describes the displacement of finding a particle at the point in time $u,$ and $c$ indicates the wave velocity of the free vibration.

Advancements in computational methods have also played a crucial role in the growing adoption of large membrane vibration equations involving fractional derivatives. The fractional vibration equation was investigated by using various methods such as $q$ homotopy analysis transform method [20], Laplace decomposition method [20], Yang transform decomposition method [21], Yang transform perturbation method [21], Sumudu transform perturbation method [15], residual power series method [22], Operational matrix method [23], and so on.

Adomian decomposition method (ADM) is a semi-analytical technique first introduced by George Adomian [24]. The Elzaki transform (ET) and the ADM are used to create the Elzaki transformation decomposition method (ETDM). ETDM is one of the simple and efficient techniques for resolving fractional partial differential equations. Laplace and Sumudu transformations are modified in the ET. Differential equations having constant or non-constant coefficients can sometimes be solved using ET rather than Laplace or Sumudu transformations [25,26,27]. With the use of ET, researchers have been able to solve a variety of problems, including the Navier-Stokes equations [28], heat-like equations [29], advection equation [30], hyperbolic equations [30], and Fisher’s equations [30]. The Shehu transformation decomposition method (STDM) is a combination of the Shehu transform (ST) and the ADM. The ST, which researchers frequently use for fractional-order differential equations [31,32,33,34], has recently attracted the attention of researchers. STDM has fewer variables than other analytical techniques, and due to the lack of discretion or linearization, it is the recommended method. Using the STDM and ETDM, we have examined the large membrane vibration equation with fractional derivative in the current article.

The structure of this paper is as follows. In Section 2, some basic features of fractional calculus related to the titled problems have been represented. Section 3 contains the methodology. Convergence analysis of these methods is developed in Section 4. Three example problems are included to validate the effectiveness and exactness of the proposed method in Section 5. A comparison of obtained results has been discussed in Section 6. Finally, the conclusion section is included in Section 7.

2. Preliminaries

The essential fractional calculus, the Elzaki transform, and the Shehu transform concepts that will be used throughout this study have been discussed in this part.

Definition 1.

The fractional Riemann Liouville integral operator of a function $h$ is given as [35,36,37]

$$J^{\alpha }h\left(u\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\displaystyle {\int }_0^u{\left(u-\eta \right)}^{\alpha -1}h\left(\eta \right)d\eta ,}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha >0,\hspace{0.17em}\hspace{0.17em}u>0$$

and $J^{0}h\left(u\right)=h\left(u\right)$.

Definition 2.

The Caputo fractional derivatives of a function $h$ are presented as [38,39,40].

$$D^{\alpha }h\left(u\right)=J^{k-\alpha }{D}^{k}h\left(u\right)=\left\{\begin{array}{l}{\displaystyle \frac{1}{\mathsf{\Gamma }\left(k-\alpha \right)}}{\displaystyle \underset{0}{\overset{u}{\int }}\frac{h^{\left(k\right)}\left(\eta \right)d\eta }{{\left(u-\eta \right)}^{\alpha +1-k}},\hspace{0.17em}\hspace{0.17em}k-1\hspace{0.17em}\hspace{0.17em}<\alpha <k,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k\in N}\\ {\displaystyle \frac{d^k}{d{u}^k}}h\left(u\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha =k,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k\in N\end{array}\right.$$

Definition 3.

The Mittag–Leffler (1902–1905) functions $E_{\gamma }$ and $E_{\gamma ,\eta }$, defined by the power series [36,41].

$$E_{\gamma }\left(u\right)={\displaystyle \sum _{k=0}^{\infty }\frac{u^k}{\mathsf{\Gamma }\left(k\gamma +1\right)}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{E}_{\gamma ,\eta }\left(u\right)={\displaystyle \sum _{k=0}^{\infty }\frac{u^k}{\mathsf{\Gamma }\left(k\gamma +\eta \right)}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma ,\eta >0$$

Definition 4.

For $u\in \left(0,\infty \right)$, the Elzaki transform of $h\left(u\right)$ is given by [29,42].

$$E\left(h\left(u\right)\right)=H\left(s\right)=s{\displaystyle {\int }_0^{\infty }h\left(u\right)}{e}^{-{\displaystyle \frac{1}{s}}u}du$$

Some of the useful Elzaki transforms which are applied in this paper, are as follows:

For $E\left(h_1\left(u\right)\right)=H_1\left(s\right)$ and $E\left(h_2\left(u\right)\right)=H_2\left(s\right)$

$$E\left[h_1\left(u\right)+h_2\left(u\right)\right]=H_1\left(s\right)+H_2\left(s\right),$$

$$E\left[h^{\left(k\right)}\left(u\right)\right]={\displaystyle \frac{H\left(s\right)}{s^k}}-{\displaystyle \sum _{n=0}^{k-1}{s}^{2-k+n}{h}^n\left(0\right)},$$

$$E\left[u^k\right]=k!\hspace{0.17em}{s}^{k+2},\hspace{0.17em}\hspace{0.17em}k\in N,$$

$$E\left\{e^{-cu}\right\}={\displaystyle \frac{s^2}{1+cs}},$$

$$E\left\{\sin \left(cu\right)\right\}={\displaystyle \frac{c{s}^3}{1+c^2{s}^2}},$$

Lemma 1

([26,42]). Let $B\left(s\right)$ be the Laplace transform of $h\left(u\right)$, then Elzaki transform $H\left(s\right)$ is defined as $H\left(s\right)=s\hspace{0.17em}B\left({\displaystyle \frac{1}{s}}\right)$.

Lemma 2

([42,43]). The Elzaki transform of Caputo fractional derivatives of order $\gamma$ can be obtained in the form of $E\left[D^{\gamma }h\left(u\right)\right]={\displaystyle \frac{H\left(s\right)}{s^{\gamma }}}-{\displaystyle \sum _{n=0}^{k-1}{s}^{n-\gamma +2}{h}^{\left(n\right)}\left(0\right)};\hspace{0.17em}\hspace{0.17em}k-1<\gamma \le k,\hspace{0.17em}k\in N.$

Definition 5

([25,42]). If we consider $H\left(s\right)$ is the Elzaki transform of function $h\left(u\right)$ then the inverse of $H\left(s\right)$ is $h\left(u\right)$ such that $E^{-1}\left[H\left(s\right)\right]=h\left(u\right);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall u>0$.

Definition 6.

The Shehu transform for the function $h\left(u\right)$ is defined as [44],

$$S\left(h\left(u\right)\right)=H\left(s,\sigma \right)={\displaystyle {\int }_0^{\infty }h\left(u\right)\hspace{0.17em}\hspace{0.17em}}{e}^{{\displaystyle \frac{-su}{\sigma }}}du\hspace{0.17em};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sigma >0,s>0,u\ge 0.$$

Some of the useful Shehu transforms which are applied in this paper, are as follows:

$$\mathrm{For} S\left(h_1\left(u\right)\right)=H_1\left(s,\sigma \right) \mathrm{and} S\left(h_2\left(u\right)\right)=H_2\left(s,\sigma \right)$$

$$S\left[A{h}_1\left(u\right)+B{h}_2\left(u\right)\right]=A{H}_1\left(s,\sigma \right)+B{H}_2\left(s,\sigma \right),$$

where $A$ and $B$ are constants.

$$S\left(1\right)={\displaystyle \frac{\sigma }{s}},$$

$$S\left(u\right)={\displaystyle \frac{{\sigma }^2}{s^2}},$$

$$S\left(e^{bu}\right)={\displaystyle \frac{\sigma }{s-b\sigma }},$$

$$S\left(\sin \left(bu\right)\right)={\displaystyle \frac{b{\sigma }^2}{s^2+b^2{\sigma }^2}},$$

$$S\left(\cos \left(bu\right)\right)={\displaystyle \frac{\sigma \hspace{0.17em}s}{s^2+b^2{\sigma }^2}},$$

$$S\left({\displaystyle \frac{u^k}{k!}}\right)={\left({\displaystyle \frac{\sigma }{s}}\right)}^{k+1}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}k=0,1,2,\dots \hspace{0.17em}\hspace{0.17em}\hspace{0.17em},$$

$$S\left\{h^{\left(k\right)}\left(u\right)\right\}={\displaystyle \frac{s^k}{{\sigma }^k}}H\left(s,\sigma \right)-{{\displaystyle \sum _{l=0}^{k-1}\left(\frac{s}{\sigma }\right)}}^{k-l-1}{h}^{\left(l\right)}\left(0\right).$$

Lemma 4.

The Shehu transform of Caputo fractional derivatives of order $\gamma$ is expressed as [45]

$$S\left\{h^{\left(\gamma \right)}\left(u\right)\right\}={\displaystyle \frac{s^{\gamma }}{{\sigma }^{\gamma }}}H\left(s,\sigma \right)-{{\displaystyle \sum _{l=0}^{k-1}\left(\frac{s}{\sigma }\right)}}^{\gamma -l-1}{h}^{\left(l\right)}\left(0\right);0<\gamma \le k.$$

Definition 7

([46]). If we consider $H\left(s,\sigma \right)$ is the Shehu transform for a function $h\left(u\right)$ then the inverse of $H\left(s,\sigma \right)$ is $h\left(u\right)$ such that $S^{-1}\left[H\left(s,\sigma \right)\right]=h\left(u\right);\hspace{0.17em}\forall u\ge 0$

alternatively,

$$h\left(u\right)=S^{-1}\left[H\left(s,\sigma \right)\right]={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\int }_{\psi -i\infty }^{\psi +i\infty }\frac{e^{-\frac{su}{\sigma }}}{\sigma }H\left(s,\sigma \right)ds}.$$

Lemma 5

([46]). If $S^{-1}\left[H_1\left(s,\sigma \right)\right]=h_1\left(u\right)$ and $S^{-1}\left[H_2\left(s,\sigma \right)\right]=h_2\left(u\right)$,

then

$$\begin{array}{l}{S}^{-1}\left[A{H}_1\left(s,\sigma \right)+B{H}_2\left(s,\sigma \right)\right]\\ =A{S}^{-1}\left[H_1\left(s,\sigma \right)\right]+B{S}^{-1}\left[H_2\left(s,\sigma \right)\right]\\ =A{h}_1\left(u\right)+B{h}_2\left(u\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}.\end{array}$$

where $A$ and $B$ are constants.

3. Methodology

The fractional partial differential equation problem of the vibration equation of a large membrane is considered as the following:

$${\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}=c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)$$

(1)

with IC:

$$h\left(v,0\right)=h_1\left(v\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_u\left(v,0\right)=c\left(h_2\left(v\right)\right),$$

(2)

where $h\left(v,u\right)$ stand for displacement and $c$ for free vibration wave velocity.

3.1. Case 1 (ETDM)

ET technique for Caputo fractional derivatives is applied to Equation (1) and gives

$$E\left({\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}\right)=E\left[c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)\right].$$

This gives

$${\displaystyle \frac{E\left(h\left(v,u\right)\right)}{s^{\gamma }}}-{\displaystyle \sum _{n=0}^1{s}^{n-\gamma +2}{h}^{\left(n\right)}\left(v,0\right)}=E\left[c^2\left(h_{vv}+{\displaystyle \frac{1}{v}}{h}_v\right)\right]$$

(3)

Multiplying $s^{\gamma }$ on both sides of Equation (3), we have

$$E\left(h\left(v,u\right)\right)=s^{2}h\left(v,0\right)+s^3{h}_u\left(v,0\right)+s^{\gamma }{c}^2\left[E\left(h_{vv}+{\displaystyle \frac{1}{v}}{h}_v\right)\right]$$

(4)

Applying inverse of ET on both sides of Equation (4) yields

$$h\left(v,u\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)+E^{-1}\left(s^{\gamma }{c}^{2}E\left(h_{vv}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \frac{1}{v}}{h}_v\right)\right)$$

(5)

The ETDM represents the solution as an infinite series of components as

$$h\left(v,u\right)={\displaystyle \sum _{k=0}^{\infty }{h}_k^{\left(E\right)}\left(v,u\right)}$$

(6)

By substituting Equation (6) in Equation (5), one gets

$${\displaystyle \sum _{k=0}^{\infty }{h}_k^{\left(E\right)}}\left(v,u\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)+E^{-1}\left(s^{\gamma }{c}^2\left(E{\left({\displaystyle \sum _{k=0}^{\infty }{h}_k^{\left(E\right)}\left(v,u\right)}\right)}_{vv}+{\displaystyle \frac{1}{v}}{\left({\displaystyle \sum _{k=0}^{\infty }{h}_k^{\left(E\right)}\left(v,u\right)}\right)}_v\right)\right)$$

(7)

By comparing both sides of Equation (7), we have

$$h_0^{\left(E\right)}\left(v,u\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)$$

(8)

$$h_n^{\left(E\right)}\left(v,u\right)=E^{-1}\left(s^{\gamma }{c}^2\left(E{\left(h_{n-1}^{\left(E\right)}\left(v,u\right)\right)}_{vv}+{\displaystyle \frac{1}{v}}{\left(h_{n-1}^{\left(E\right)}\left(v,u\right)\right)}_v\right)\right)\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\ge 1$$

(9)

From Equations (8) and (9), we can determine the components $h_k^{\left(E\right)}\left(v,u\right)$ and hence, the series solution of $h\left(v,u\right)$ in Equation (6) can be obtained for the $k$ term approximant as ${Z_k}^{\left(E\right)}\left(v,u\right)={\displaystyle \sum _{n=0}^k{h}_n^{\left(E\right)}\left(v,u\right).}$

3.2. Case 2 (STDM)

The ST procedure for Caputo fractional derivatives is applied to Equation (1) and gives

$$S\left({\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}\right)=S\left(c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<\gamma \le 2$$

This gives

$${\displaystyle \frac{s^{\gamma }}{{\sigma }^{\gamma }}}H\left(s,\sigma \right)-{\left({\displaystyle \frac{s}{\sigma }}\right)}^{\gamma -1}h\left(v,0\right)-{\left({\displaystyle \frac{s}{\sigma }}\right)}^{\gamma -2}{h}_u\left(v,0\right)=S\left(c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)\right)$$

(10)

Multiplying ${\displaystyle \frac{{\sigma }^{\gamma }}{s^{\gamma }}}$ on both sides of Equation (10), we have

$$H\left(s,\sigma \right)=\left({\displaystyle \frac{\sigma }{s}}\right)h_1\left(v\right)+{\left({\displaystyle \frac{\sigma }{s}}\right)}^{2}c{h}_2\left(v\right)+{\left({\displaystyle \frac{\sigma }{s}}\right)}^{\gamma }{c}^2\left(S\left(h_{vv}+{\displaystyle \frac{1}{v}}{h}_v\right)\right)$$

(11)

Applying inverse of ST on both sides of Equation (11) yields

$$h\left(v,u\right)=h_1\left(v\right)+c{h}_2\left(v\right)u+S^{-1}\left({\left({\displaystyle \frac{\sigma }{s}}\right)}^{\gamma }{c}^2\left(S\left(h_{vv}+{\displaystyle \frac{1}{v}}{h}_v\right)\right)\right)$$

The STDM represents the solution as an infinite series of components as

$$h\left(v,u\right)={\displaystyle \sum _{K=0}^{\infty }{h}_k^{\left(S\right)}\left(v,u\right)}$$

(12)

By substituting Equation (12) in Equation (11), we get

$${\displaystyle \sum _{k=0}^{\infty }{h}_k^{\left(S\right)}\left(v,u\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)+S^{-1}\left({\left(\frac{\sigma }{s}\right)}^{\gamma }{c}^2\left(S\left({\left({\displaystyle \sum _{K=0}^{\infty }{h}_k^{\left(S\right)}}\left(v,u\right)\right)}_{vv}+\frac{1}{v}{\left({\displaystyle \sum _{K=0}^{\infty }{h}_k^{\left(S\right)}}\left(v,u\right)\right)}_v\right)\right)\right)}$$

(13)

By comparing both sides of Equation (13), we have

$$h_0^{\left(S\right)}\left(v,u\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)$$

(14)

$$h_n^{\left(S\right)}\left(v,u\right)=S^{-1}\left({\left({\displaystyle \frac{\sigma }{s}}\right)}^{\gamma }{c}^2\left(S{\left(h_{n-1}^{\left(S\right)}\left(v,u\right)\right)}_{vv}+{\displaystyle \frac{1}{v}}{\left(h_{n-1}^{\left(S\right)}\left(v,u\right)\right)}_v\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n\ge 1$$

(15)

From Equations (14) and (15), we can determine the components $h_k^{\left(S\right)}\left(v,u\right)$ and hence, the series solution of $h\left(v,u\right)$ in Equation (12) can be obtained for the $k$ term approximant as ${Z_k}^{\left(S\right)}\left(v,u\right)={\displaystyle \sum _{n=0}^k{h}_n^{\left(S\right)}\left(v,u\right).}$

4. Convergence Analysis

The fractional Klein Gordan equation’s uniqueness and convergence of the solution using NTDM and STDM are provided in [47]; accordingly, in this section, we illustrate the uniqueness and convergence of the solution of the fractional vibration equation of large membrane by using ETDM and STDM.

Uniqueness and Convergence of ETDM and STDM for Large Membrane of Vibration Equation

Assume $\left|L\left(h\left(v,u\right)\right)-L\left(h^{*}\left(v,u\right)\right)\right|<\omega \left|h\left(v,u\right)-h^{*}\left(v,u\right)\right|,\forall \hspace{0.17em}\hspace{0.17em}h\left(v,u\right),h^{*}\left(v,u\right)\in C\left[I\right]$, where $C\left[I\right]$ denotes continuous function on $I$ and $L$ specify the linear operator, i.e., $L\left(h\left(v,u\right)\right)=h{\left(v,u\right)}_{vv}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \frac{1}{v}}h{\left(v,u\right)}_v$.

Theorem 1.

Uniqueness of the ETDM solution of Equation (6) occurs when $0<\omega {\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}<1$.

Proof. 

Let us take a Banach space $\left(C\left[I\right],\hspace{0.17em}‖\hspace{0.17em}.\hspace{0.17em}‖\right)$ for all continuous function on $I$ with the norm $‖\hspace{0.17em}.\hspace{0.17em}‖$. Let $F:C\left[I\right]\to C\left[I\right]$ is a mapping such that

$$F\left(h\right)=h_1\left(v\right)+uc\left(h_2\left(v\right)\right)+E^{-1}\left(s^{\gamma }{c}^{2}E\left(h_{vv}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \frac{1}{v}}{h}_v\right)\right)$$

$$\begin{array}{l}‖F\left(h\right)-F\left(h^{*}\right)‖=\underset{u,v\in I}{\max }\left|E^{-1}\left(s^{\gamma }{c}^{2}E\left(L\left(h\left(v,u\right)\right)\right)\right)-E^{-1}\left(s^{\gamma }{c}^{2}E\left(L\left(h^{*}\left(v,u\right)\right)\right)\right)\right|\\ =\underset{u,v\in I}{\max }\left|{\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}{c}^2\left(L\left(h\left(v,u\right)\right)-L\left(h^{*}\left(v,u\right)\right)\right)\right|\\ \le c^2\omega {\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}‖h-h^{*}‖\\ <c^2‖h-h^{*}‖\end{array}$$

Hence, ETDM solution of Equation (6) is unique. □

Theorem 2.

The ETDM solution of Equation (6) is convergent when $0<c^2\omega {\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}<1$.

Proof. 

Let us take a Banach space $\left(C\left[I\right],\hspace{0.17em}‖\hspace{0.17em}.\hspace{0.17em}‖\right)$ for all continuous function $I$ with the norm $‖\hspace{0.17em}.\hspace{0.17em}‖$. For $Z_f^{\left(E\right)},Z_g^{\left(E\right)}\in C\left[I\right]$ and $f,g\in N,f\ge g$,

$$\begin{array}{l}‖Z_f^{\left(E\right)}-Z_g^{\left(E\right)}‖\\ =\underset{u,v\in I}{\max }\left|Z_f^{\left(E\right)}\left(v,u\right)-Z_g^{\left(E\right)}\left(v,u\right)\right|\\ =\underset{u,v\in I}{\max }\left|{\displaystyle \sum _{k=g+1}^f{h}_k^{\left(E\right)}\left(v,u\right)}\right|\\ =\underset{u,v\in I}{\max }\left|{\displaystyle \sum _{k=g+1}^f{E}^{-1}\left(s^{\gamma }{c}^2\left(E\left(L\left(h_{k-1}^{\left(E\right)}\left(v,u\right)\right)\right)\right)\right)}\right|\\ =\underset{u,v\in I}{\max }\left|E^{-1}\left(s^{\gamma }{c}^2\left(E\left({\displaystyle \sum _{k=g+1}^{f}L\left(h_{k-1}^{\left(E\right)}\left(v,u\right)\right)}\right)\right)\right)\right|\\ \underset{u,v\in I}{=\max }\left|E^{-1}\left(s^{\gamma }{c}^2\left(E\left({\displaystyle \sum _{k=g}^{f-1}L\left(h_k^{\left(E\right)}\left(v,u\right)\right)}\right)\right)\right)\right|\\ =\underset{u,v\in I}{\max }\left|E^{-1}\left(s^{\gamma }{c}^2\left(E\left({\displaystyle \sum _{k=0}^{f-1}L\left(h_k^{\left(E\right)}\left(v,u\right)\right)}-{\displaystyle \sum _{k=0}^{g-1}L\left(h_k^{\left(E\right)}\left(v,u\right)\right)}\right)\right)\right)\right|\\ =\underset{u,v\in I}{\max }\left|E^{-1}\left(s^{\gamma }{c}^2\left(E\left(L\left(Z_{f-1}^{\left(E\right)}\left(v,u\right)\right)-L\left(Z_{g-1}^{\left(E\right)}\left(v,u\right)\right)\right)\right)\right)\right|\\ <\underset{u,v\in I}{\max }\left|\omega \hspace{0.17em}{c}^2{\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}\left(Z_{f-1}^{\left(E\right)}\left(v,u\right)-Z_{g-1}^{\left(E\right)}\left(v,u\right)\right)\right|\\ <\omega \hspace{0.17em}{c}^2{\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}‖Z_{f-1}^{\left(E\right)}-Z_{g-1}^{\left(E\right)}‖\end{array}$$

If $f=g+1$,

$$‖Z_{g+1}^{\left(E\right)}-Z_g^{\left(E\right)}‖<\omega \hspace{0.17em}{c}^2{\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}‖Z_g^{\left(E\right)}-Z_{g-1}^{\left(E\right)}‖$$

Let $b=\omega \hspace{0.17em}{c}^2{\displaystyle \frac{u^{\gamma -2}}{\mathsf{\Gamma }\left(\gamma -1\right)}}$

$$‖Z_{g+1}^{\left(E\right)}-Z_g^{\left(E\right)}‖<b\hspace{0.17em}‖Z_g^{\left(E\right)}-Z_{g-1}^{\left(E\right)}‖<b^2\hspace{0.17em}‖Z_{g-1}^{\left(E\right)}-Z_{g-2}^{\left(E\right)}‖<\cdots <b^g\hspace{0.17em}‖Z_1^{\left(E\right)}-Z_0^{\left(E\right)}‖$$

$$\begin{array}{l}‖Z_f^{\left(E\right)}-Z_g^{\left(E\right)}‖\\ =‖\left(Z_f^{\left(E\right)}-Z_{f-1}^{\left(E\right)}\right)+\left(Z_{f-1}^{\left(E\right)}-Z_{f-2}^{\left(E\right)}\right)+\cdots \cdots +\left(Z_{g+1}^{\left(E\right)}-Z_g^{\left(E\right)}\right)‖\\ \le ‖Z_f^{\left(E\right)}-Z_{f-1}^{\left(E\right)}‖+‖Z_{f-1}^{\left(E\right)}-Z_{f-2}^{\left(E\right)}‖+\cdots \cdots +‖Z_{g+1}^{\left(E\right)}-Z_g^{\left(E\right)}‖\\ <\left(b^{f-1}+b^{f-2}+\cdots \cdots +b^g\right)\hspace{0.17em}‖Z_1^{\left(E\right)}-Z_0^{\left(E\right)}‖\\ \le b^g{\displaystyle \frac{\left(1-b^{f-g}\right)}{\left(1-b\right)}}‖h_1^{\left(E\right)}‖\\ <b^g{\displaystyle \frac{1}{\left(1-b\right)}}‖h_1^{\left(E\right)}‖\end{array}$$

As $g\to \infty ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{b}^g\to 0$. Therefore, $‖Z_f^{\left(E\right)}-Z_g^{\left(E\right)}‖\to 0,$ when $g\to \infty$.

$\therefore$ The sequence $\left\{Z_k^{\left(E\right)}\right\}$ is a Cauchy sequence in Banach space $\left(C\left[I\right],‖\hspace{0.17em}.\hspace{0.17em}‖\right)$, and hence it is convergent. □

Theorem 3.

The STDM solution of Equation (12) is unique when $0<\omega {\displaystyle \frac{u^{\gamma -1}}{\mathsf{\Gamma }\left(\gamma \right)}}<1$.

Proof. 

Since this proof is similar to Theorem 1, it was omitted. □

Theorem 4.

The STDM solution of Equation (12) is convergent when $0<c^2\omega {\displaystyle \frac{u^{\gamma -1}}{\mathsf{\Gamma }\left(\gamma \right)}}<1$.

Proof. 

Since this proof is similar to Theorem 2, it was omitted. □

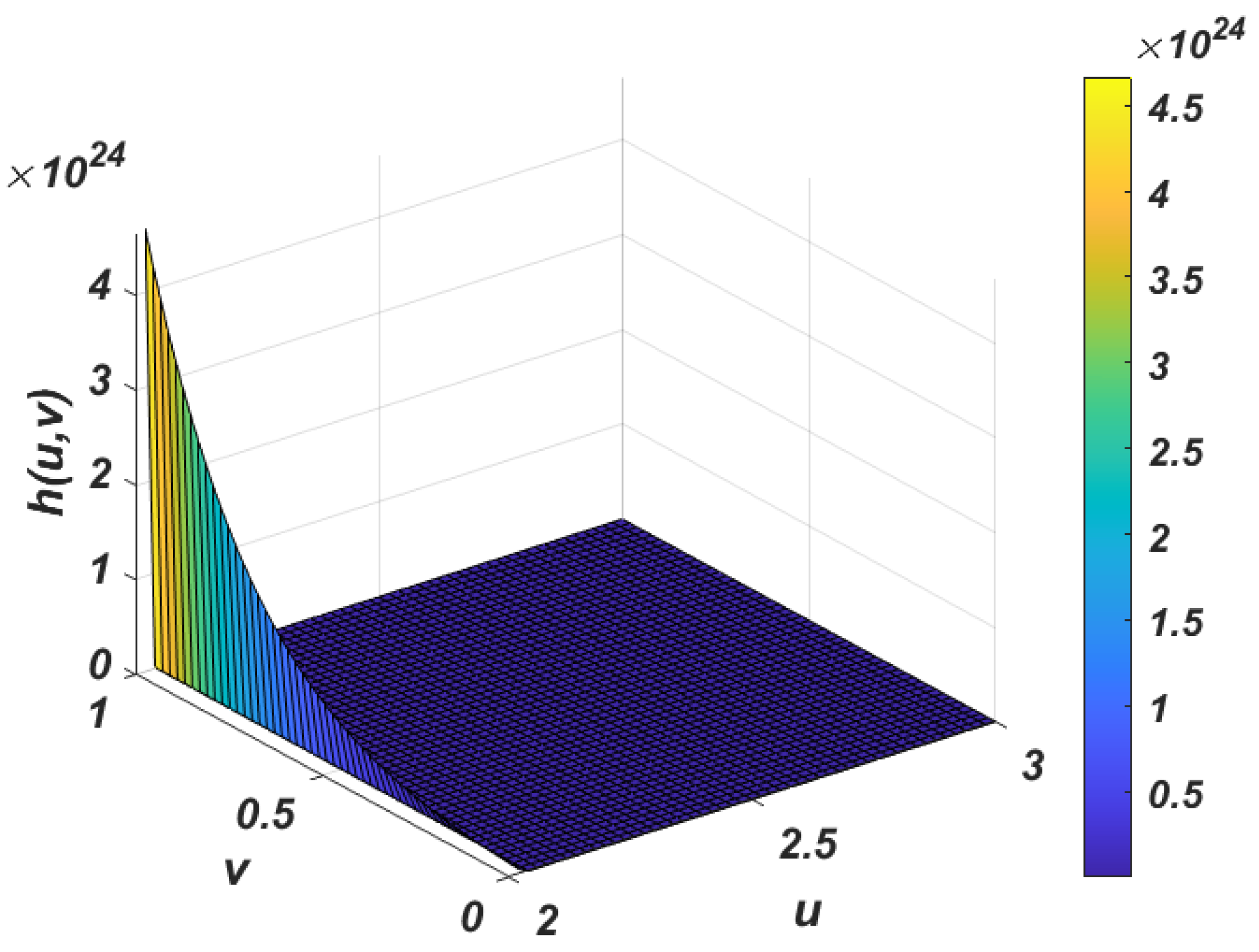
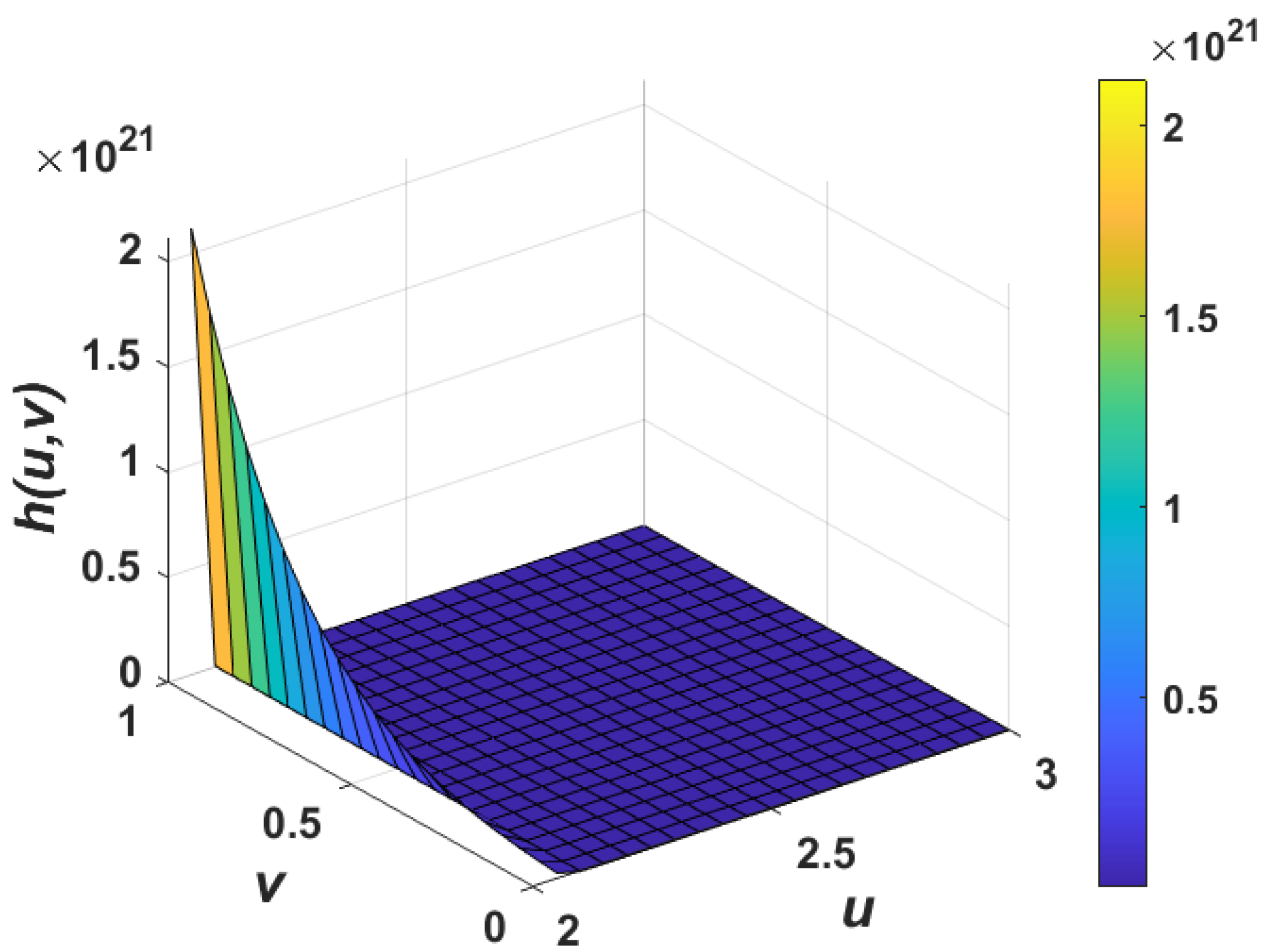
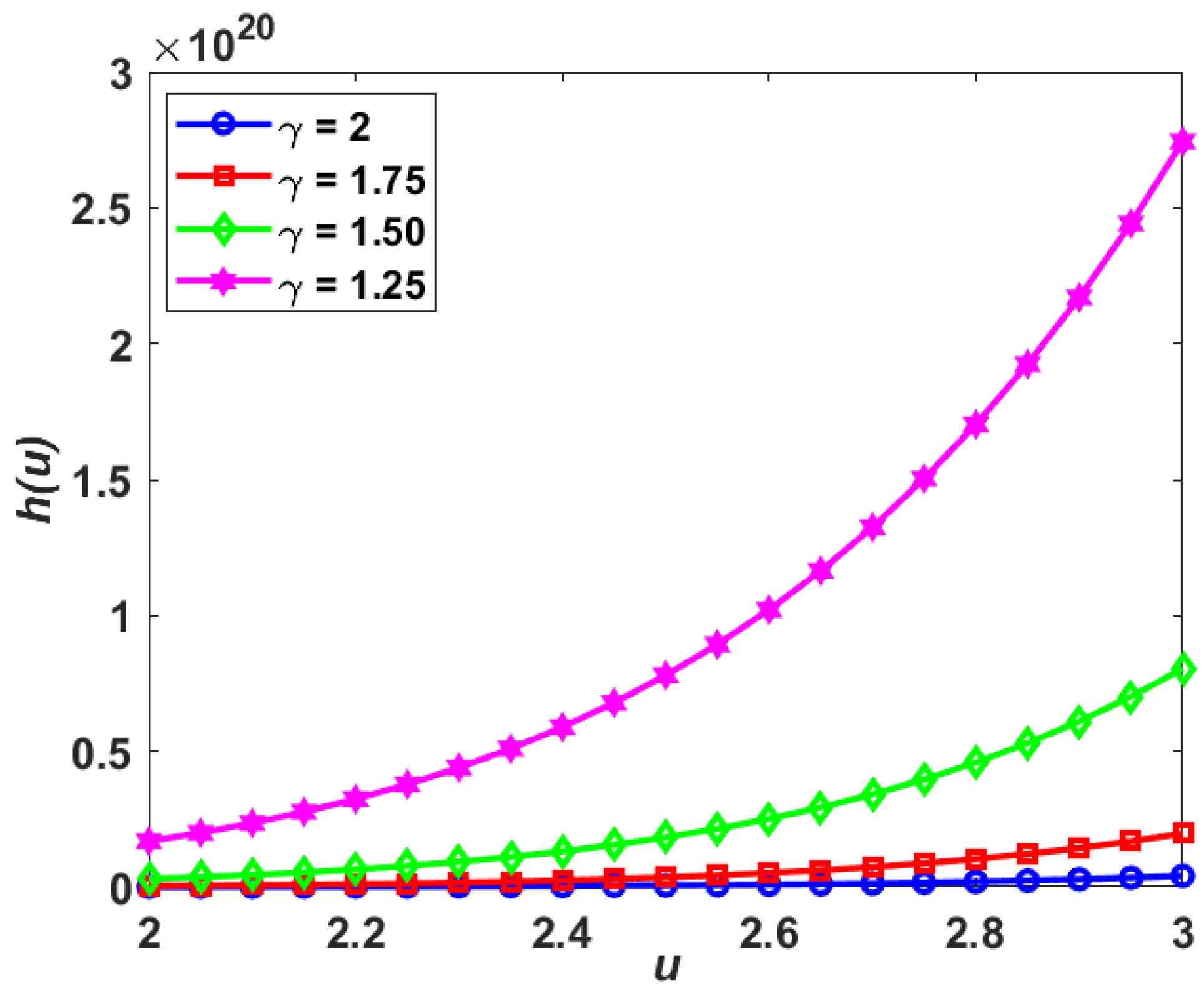
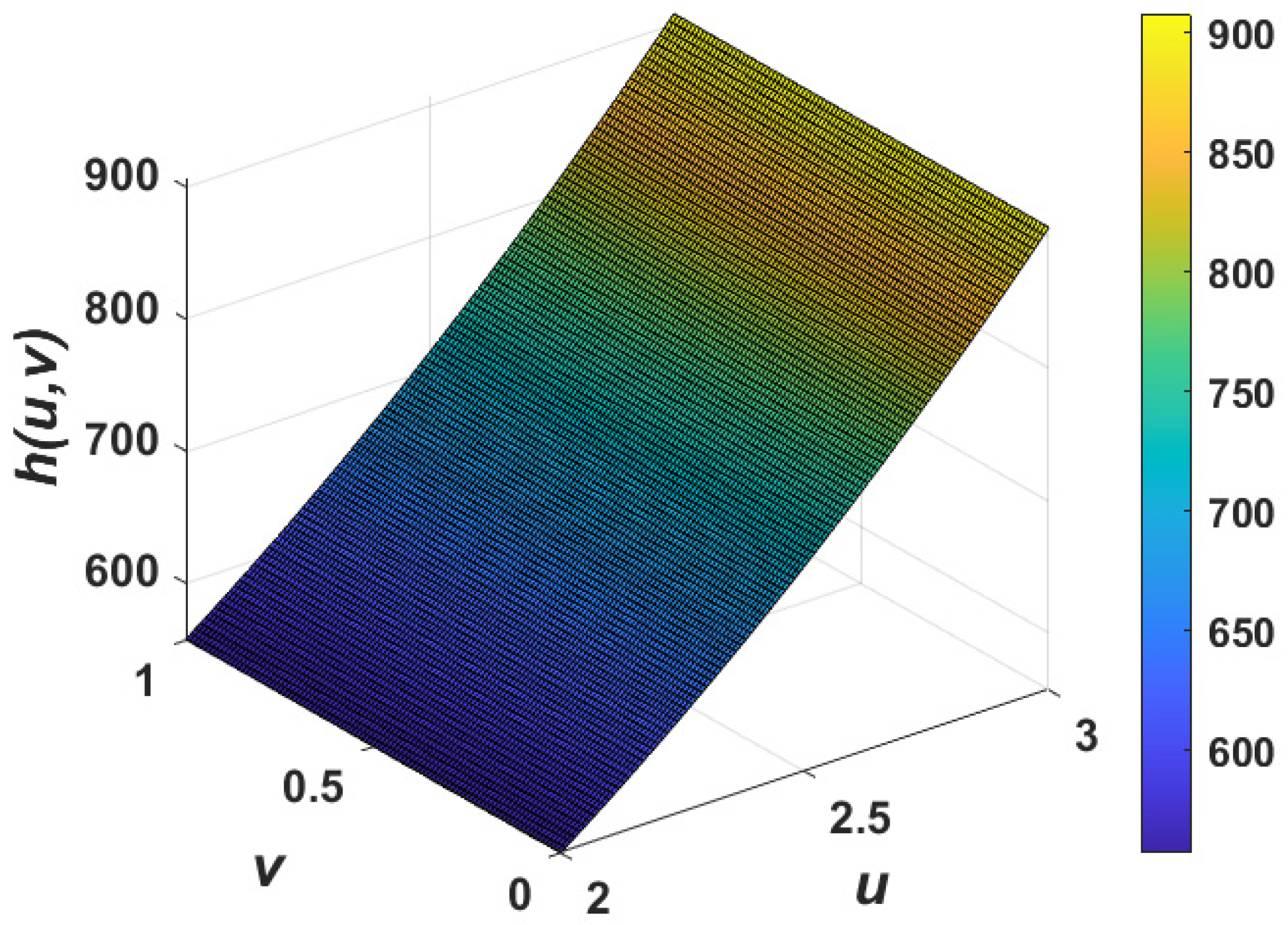
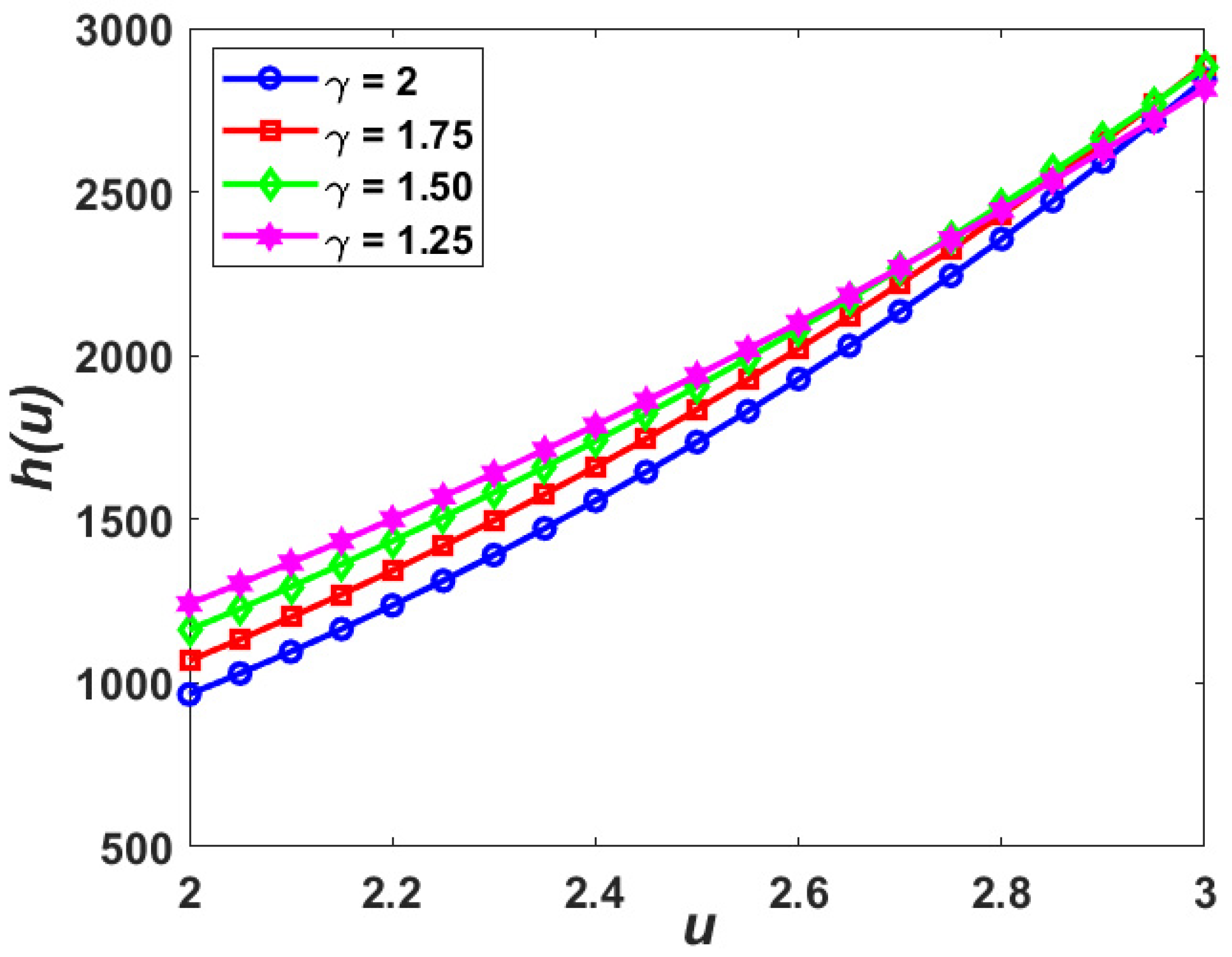
5. Numerical Examples

This section comprises various numerical experiments to acquire an approximation of the solution to the vibration equations of large membranes comprising fractional derivative Equations (1) and (2). The adaptability of STDM and ETDM are shown by the computational results, which are used to assess the method’s correctness in comparison to precise and/or computational results from earlier studies. The outcomes of our techniques implementation showcase that they are very competitive and that they are simple to use.

5.1. Example 1

Consider the following vibration equation of a large membrane with fractional derivative [20,22]

$${\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}=c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)$$

with IC:

$$h\left(v,0\right)=v^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_u\left(v,0\right)=cv$$

By employing ETDM, we get

$$h_0^{\left(E\right)}\left(v,u\right)=v^2+ucv$$

$$h_1^{\left(E\right)}\left(v,u\right)=4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(E\right)}\left(v,u\right)={\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}$$

We obtain ETDM solution by incorporating $h_0^{\left(E\right)}\left(v,u\right),h_1^{\left(E\right)}\left(v,u\right),\cdots ,$ in Equation (6) as

$$\begin{array}{l}h\left(v,u\right)=v^2+ucv+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^7}{v^5}}{\displaystyle \frac{u^{3\gamma +1}}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^9}{v^7}}{\displaystyle \frac{u^{4\gamma +1}}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \\ =v^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+ucv\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \right)\\ =v^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+ucv\hspace{0.17em}{E}_{\gamma ,2}\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right)\end{array}$$

where $T^k={\left[1.3.5.\cdots \cdots .\left(2k-3\right)\right]}^2$.

The solution obtained by the proposed method is found to be exactly as that of [22].

On the other hand, by employing STDM, we have,

$$h_0^{\left(S\right)}\left(v,u\right)=v^2+ucv$$

$$h_1^{\left(S\right)}\left(v,u\right)=4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(S\right)}\left(v,u\right)={\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}$$

STDM solution is obtained by incorporating $h_0^{\left(S\right)}\left(v,u\right),h_1^{\left(S\right)}\left(v,u\right),\cdots ,$ in Equation (12) as

$$\begin{array}{l}h\left(v,u\right)=v^2+ucv+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^7}{v^5}}{\displaystyle \frac{u^{3\gamma +1}}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^9}{v^7}}{\displaystyle \frac{u^{4\gamma +1}}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \\ =v^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+ucv\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \right)\\ =v^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+ucv\hspace{0.17em}{E}_{\gamma ,2}\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right),\end{array}$$

where $T^k={\left[1.3.5.\cdots \cdots .\left(2k-3\right)\right]}^2$.

It is found that the solution produced by the suggested approach is identical to that of [22].

5.2. Example 2

Next, consider the following large membrane of vibration equation involving fractional [20,22].

$${\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}=c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)$$

with IC:

$$h\left(v,0\right)=v,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_u\left(v,0\right)=cv$$

From ETDM, we get

$$h_0^{\left(E\right)}\left(v,u\right)=v+ucv$$

$$h_1^{\left(E\right)}\left(v,u\right)={\displaystyle \frac{c^2}{v}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(E\right)}\left(v,u\right)={\displaystyle \frac{c^4}{v^3}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}$$

ETDM solution then may be obtained by incorporating $h_0^{\left(E\right)}\left(v,u\right),h_1^{\left(E\right)}\left(v,u\right),\cdots ,$ in Equation (6) as

$$\begin{array}{l}h\left(v,u\right)=v+ucv+{\displaystyle \frac{c^2}{v}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^3}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}9{\displaystyle \frac{c^6}{v^5}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +1\right)}}+9{\displaystyle \frac{c^7}{v^5}}{\displaystyle \frac{u^{3\gamma +1}}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^7}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +1\right)}}+225{\displaystyle \frac{c^9}{v^7}}{\displaystyle \frac{u^{4\gamma +1}}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \\ =v\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +1\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +1\right)}}+\cdots \right)\\ +ucv\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \right)\\ =v\hspace{0.17em}{E}_{\gamma }\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right)+ucv\hspace{0.17em}{E}_{\gamma ,2}\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right)\end{array}$$

where $T^k={\left[1.3.5.\cdots \cdots .\left(2k-3\right)\right]}^{.2}.$

The solution obtained by the proposed method is found to be exactly as that of [22].

For STDM, we have

$$h_0^{\left(S\right)}\left(v,u\right)=v+ucv$$

$$h_1^{\left(S\right)}\left(v,u\right)={\displaystyle \frac{c^2}{v}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(S\right)}\left(v,u\right)={\displaystyle \frac{c^4}{v^3}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}$$

Finally, the STDM solution is found by incorporating $h_0^{\left(S\right)}\left(v,u\right),h_1^{\left(S\right)}\left(v,u\right),\cdots ,$ in Equation (12)

$$\begin{array}{l}h\left(v,u\right)=v+ucv+{\displaystyle \frac{c^2}{v}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^3}{v}}{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^3}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+{\displaystyle \frac{c^5}{v^3}}{\displaystyle \frac{u^{2\gamma +1}}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}9{\displaystyle \frac{c^6}{v^5}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +1\right)}}+9{\displaystyle \frac{c^7}{v^5}}{\displaystyle \frac{u^{3\gamma +1}}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^7}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +1\right)}}+225{\displaystyle \frac{c^9}{v^7}}{\displaystyle \frac{u^{4\gamma +1}}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \\ =v\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +1\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +1\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +1\right)}}+\cdots \right)\\ +ucv\left(1+{\displaystyle \frac{c^2}{v^2}}{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +2\right)}}+{\displaystyle \frac{c^4}{v^4}}{\displaystyle \frac{u^{2\gamma }}{\mathsf{\Gamma }\left(2\gamma +2\right)}}+9{\displaystyle \frac{c^6}{v^6}}{\displaystyle \frac{u^{3\gamma }}{\mathsf{\Gamma }\left(3\gamma +2\right)}}+225{\displaystyle \frac{c^8}{v^8}}{\displaystyle \frac{u^{4\gamma }}{\mathsf{\Gamma }\left(4\gamma +2\right)}}+\cdots \right)\\ =v\hspace{0.17em}{E}_{\gamma }\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right)+ucv\hspace{0.17em}{E}_{\gamma ,2}\left({\displaystyle \frac{c^2}{v^2}}T{u}^{\gamma }\right),\end{array}$$

where $T^k={\left[1.3.5.\cdots \cdots .\left(2k-3\right)\right]}^2$.

It is found that the solution produced by the suggested approach is identical to that of [22].

5.3. Example 3

Finally, let us consider the following large membrane of vibration equation [20,22]

$${\displaystyle \frac{{\partial }^{\gamma }h}{\partial u^{\gamma }}}=c^2\left({\displaystyle \frac{{\partial }^{2}h}{\partial v^2}}+{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial h}{\partial v}}\right)$$

with IC:

$$h\left(v,0\right)=v^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{h}_u\left(v,0\right)=c{v}^2$$

Using ETDM, one may write

$$h_0^{\left(E\right)}\left(v,u\right)=v^2+uc{v}^2$$

$$h_1^{\left(E\right)}\left(v,u\right)=4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(E\right)}\left(v,u\right)=0$$

Correspondingly, the ETDM solution will be obtained by introducing $h_0^{\left(E\right)}\left(v,u\right),\hspace{0.17em}\hspace{0.17em}{h}_1^{\left(E\right)}\left(v,u\right),\cdots ,$ in Equation (6)

$$\begin{array}{l}h\left(v,u\right)=v^2+uc{v}^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+0+\cdots \\ =v^2+uc{v}^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}\end{array}$$

It is found that the solution produced by the suggested approach is identical to that of [22].

Further, by employing STDM, we have

$$h_0^{\left(S\right)}\left(v,u\right)=v^2+uc{v}^2$$

$$h_1^{\left(S\right)}\left(v,u\right)=4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}$$

$$h_2^{\left(S\right)}\left(v,u\right)=0$$

Similarly from STDM, the solution will be obtained by incorporating $h_0^{\left(S\right)}\left(v,u\right),h_1^{\left(S\right)}\left(v,u\right),\cdots ,$ in Equation (12)

$$\begin{array}{l}h\left(v,u\right)=v^2+uc{v}^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}+0+\cdots \\ =v^2+uc{v}^2+4c^2{\displaystyle \frac{u^{\gamma }}{\mathsf{\Gamma }\left(\gamma +1\right)}}+4c^3{\displaystyle \frac{u^{\gamma +1}}{\mathsf{\Gamma }\left(\gamma +2\right)}}\end{array}$$

It is found that the solution produced by the suggested approach is identical to that of [22].

6. Numerical Results and Discussion

This section determines displacement $h\left(v,u\right)$ for various values of time $u$ and fractional time derivative $\gamma$ for the above three different examples in

Table 1. Comparative analysis among LDM [20], RPSM [22], solution by ETDM and STDM for $h\left(v,u\right)$ at different values of $u$ and $\gamma$ when $c=5$ and $v=6$ for example 1.

$\mathit{u}$	$\mathit{\gamma }$	${\mathit{h}}_{\mathit{L}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{R}\mathit{P}\mathit{S}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$
0.2	1.5	48.8406	48.8415	48.8415	48.8415
	2	44.0278	44.0278	44.0278	44.0278
0.4	1.5	67.6701	67.6820	67.6829	67.6829
	2	56.2234	56.2235	56.2234	56.2234
0.6	1.5	90.7471	90.7980	90.8153	90.8153
	2	72.7599	72.7598	72.7599	72.7599
0.8	1.5	117.5902	117.6890	117.8195	117.8195
	2	93.8217	93.8205	93.8216	93.8216
1	1.5	148.1551	148.0990	148.7224	148.7224
	2	119.6163	119.6060	119.6150	119.6150

,

Table 2. Comparative analysis among termwise solution of ETDM and STDM for $h\left(v,u\right)$ at different values of $\gamma$ and $u$ when $c=5$ and $v=6$ for example 1.

$\mathit{u}$	$\mathit{\gamma }$	1st Term		2nd Term		3rd Term		4th Term
		${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$
0.2	1.5	48.8404	48.8404	48.8414	48.8414	48.8415	48.8415	48.8415	48.8415
	2	44.0277	44.0277	44.0278	44.0278	44.0278	44.0278	44.0278	44.0278
0.4	1.5	67.6650	67.6650	67.6804	67.6804	67.6824	67.6824	67.6829	67.6829
	2	56.2222	56.2222	56.2234	56.2234	56.2234	56.2234	56.2234	56.2234
0.6	1.5	90.7096	90.7096	90.7877	90.7877	90.8066	90.8066	90.8153	90.8153
	2	72.7500	72.7500	72.7593	72.7893	72.7598	72.7598	72.7599	72.7599
0.8	1.5	117.4152	117.4152	117.6621	117.6621	117.7542	117.7542	117.8195	117.8195
	2	93.7777	93.7777	93.8172	93.8172	93.8210	93.8210	93.8216	93.8216
1	1.5	147.4940	147.4940	148.0968	148.0968	148.4109	148.4109	148.7224	148.7224
	2	119.4722	119.4722	119.5927	119.5927	119.6107	119.6107	119.6150	119.6150

and

Table 3. Comparative analysis among solutions of ETDM and STDM for $h\left(v,u\right)$ at different values of $\gamma$ and $u$ when $c=5$ and $v=6$ for example 1, example 2, and example 3.

$\mathit{u}$	$\mathit{\gamma }$	Example 1		Example 2		Example 3
		${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{E}\mathit{T}\mathit{D}\mathit{M}}$	${\mathit{h}}_{\mathit{S}\mathit{T}\mathit{D}\mathit{M}}$
0.2	1.5	48.8415	48.8415	12.3976	12.3976	81.4197	81.4197
	2	44.0278	44.0278	12.1113	12.1113	74.6667	74.6667
0.4	1.5	67.6829	67.6829	19.4835	19.4835	142.2552	142.2552
	2	56.2234	56.2234	18.5600	18.5600	121.3333	121.3333
0.6	1.5	90.8153	90.8153	27.4697	27.4697	220.9154	220.9154
	2	72.7599	72.7599	25.5268	25.5268	180.0000	180.0000
0.8	1.5	117.8195	117.8195	36.7233	36.7233	319.9498	319.9498
	2	93.8216	93.8216	33.2122	33.2122	254.6667	254.6667
1	1.5	148.7224	148.7224	47.8953	47.8953	441.6758	441.6758
	2	119.6150	119.6150	41.8518	41.8518	349.3333	349.3333

and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 which are discussed below. Table 1, for example 1, shows that for c = 5, $v$ = 6, and various values of u and $\gamma$ present methods are in excellent agreement with the existing methods, i.e., LDM [20] and RPSM [22]. Similarly, by taking the same values of $c$, $v$, $u$, and $\gamma$ as previously, term-wise solutions of vibration equation of large membrane with fractional derivative derived by ETDM and STDM, for example 1, are shown in Table 2. For $c$ = 5 and $v$ = 6, solutions of example 1, 2, and 3 for various values of $u$ and $\gamma$ are depicted in Table 3. Figure 1, Figure 3, and Figure 6 show that for $c$ = 5, displacement increases with the increase of $v$ and $u$. Figure 2, Figure 4, and Figure 6 show that for $v$ = 3 and $c$ = 5, displacement increases with the increase of $u$, whereas displacement decreases with the increase of $\gamma$. It has also been observed that the rate of change of displacement is higher when $h_1\left(v\right)$ and $h_2\left(v\right)$ are nonlinear than when $h_1\left(v\right)$ and $h_2\left(v\right)$ are linear. It comes from the observation that example 3 exhibits a higher rate of change of displacement than the other two examples. All the figures in this section are presented for STDM solutions. Similarly, the figures can be generated for ETDM solutions.

7. Conclusions

The new modification of the decomposition method is a powerful tool that makes it easy to obtain analytical solutions for fractional differential equations. The main aim of this article is to provide a series of solutions to the differential equations of fractional order. In this article, ETDM and STDM are successfully implemented to examine the large membrane vibration equation involving fractional derivatives. The presented approach provides an efficient way of solving these kinds of vibration problems with fractional derivatives. Three example problems are addressed in order to validate and test the efficacy of the proposed method. The illustrative examples show that the method is easy to use and is an effective tool for solving fractional partial differential equations. Thus, it is concluded that ETDM and STDM are quite useful, convenient, and powerful analytical methods to find the solution to the fractional problems arising in mathematics and engineering. The superiority of these methods lies in their ability to provide faster convergence, reduced computational complexity, and explicit analytical solutions compared to conventional methods such as LDM, HAM, and RPSM, which often struggle with iterative complexity and convergence issues. Furthermore, unlike numerical techniques that introduce discretization errors, ETDM and STDM yield solutions in terms of Mittag–Leffler functions, ensuring a more accurate representation of long-memory and nonlocal effects in fractional-order systems.