Fractional-Order Modeling and Control of HBCS-MG in Off-Grid State
Abstract
1. Introduction
- A simplified equivalent circuit for a fractional-order inductor is proposed, which greatly reduces the computational complexity of its parameters.
- The existing studies on inverters are all concentrated on the fractional-order modeling and control of grid-connected inverters, this paper considered fractional-order characteristics of the resistive-inductive load in off-grid conditions.
- Based on the double fractional-order PI controller, the transfer function between the inverter port voltage and the load voltage is derived so as to establish the complete fractional state-space mathematical model of the system in dq coordinates.
- The impact of the fractional-order variation of the fractional-order PI controllers and the fractional elements on system performance in the frequency domain and time domain is described in detail, laying the foundation for optimizing system control.
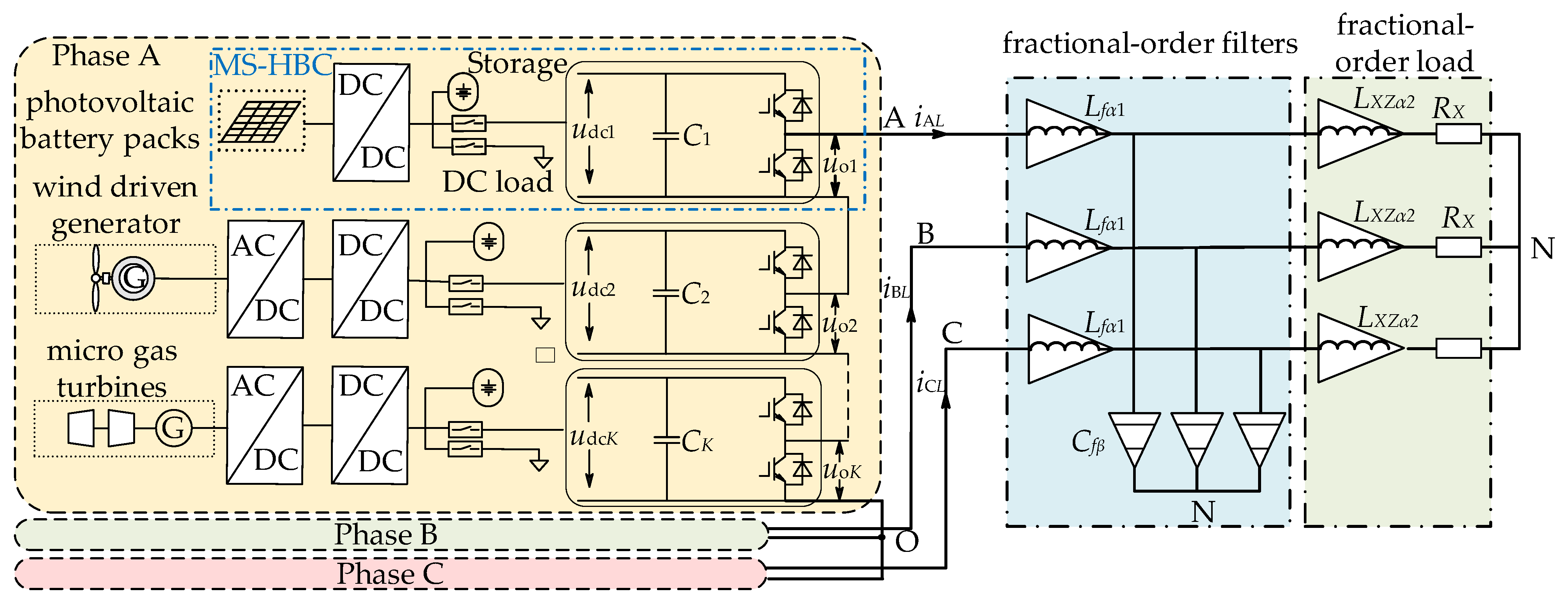
2. HBCS-MG System Structure and Fractional Mathematical Model
2.1. HBCS-MG System Structure
2.2. Equivalent Circuit of the Fractional Element
2.3. Fractional-Order Equivalent Circuit of the System
2.4. Fractional-Order Mathematical Model of the System in Rotating Coordinates
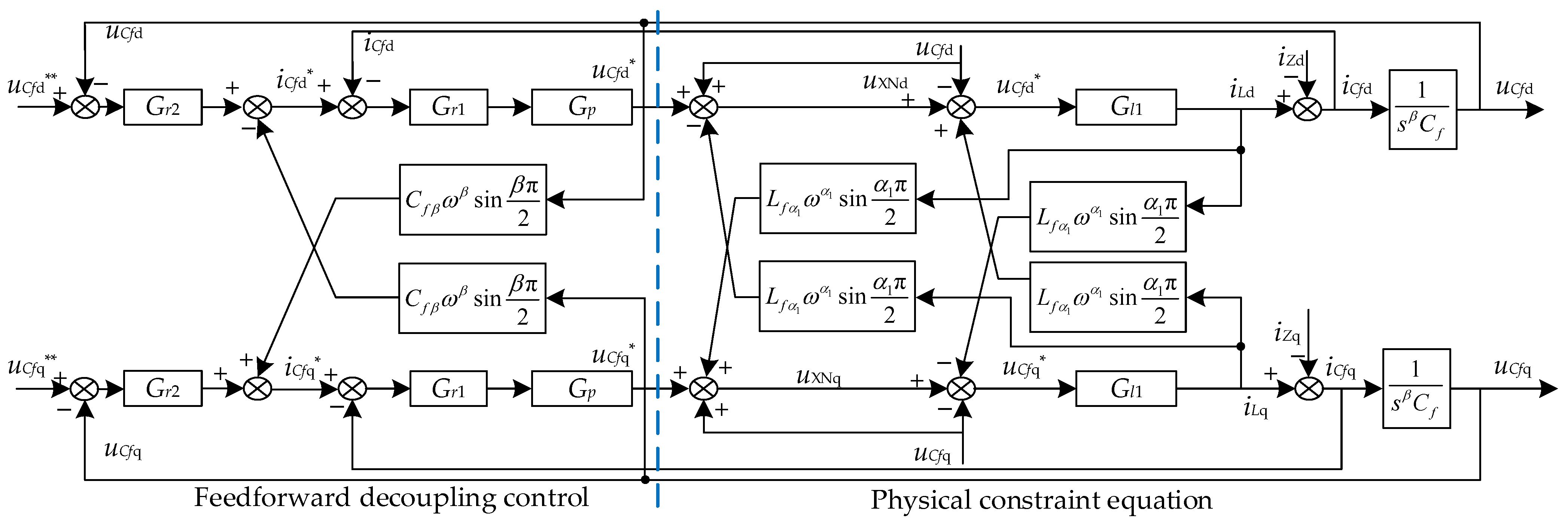
3. Fractional-Order Double-Closed-Loop Control of the System
3.1. Fractional-Order Decoupling Control
3.2. Transfer Function of the Fractional-Order Double-Closed-Loop Control System
4. Effect of the Fractional-Order Controller on System Performance
4.1. Amplitude-Frequency Characteristics of αrk Variation with the Outer-Loop Opened
4.2. Characterization of the System Step Response as αrk Varies
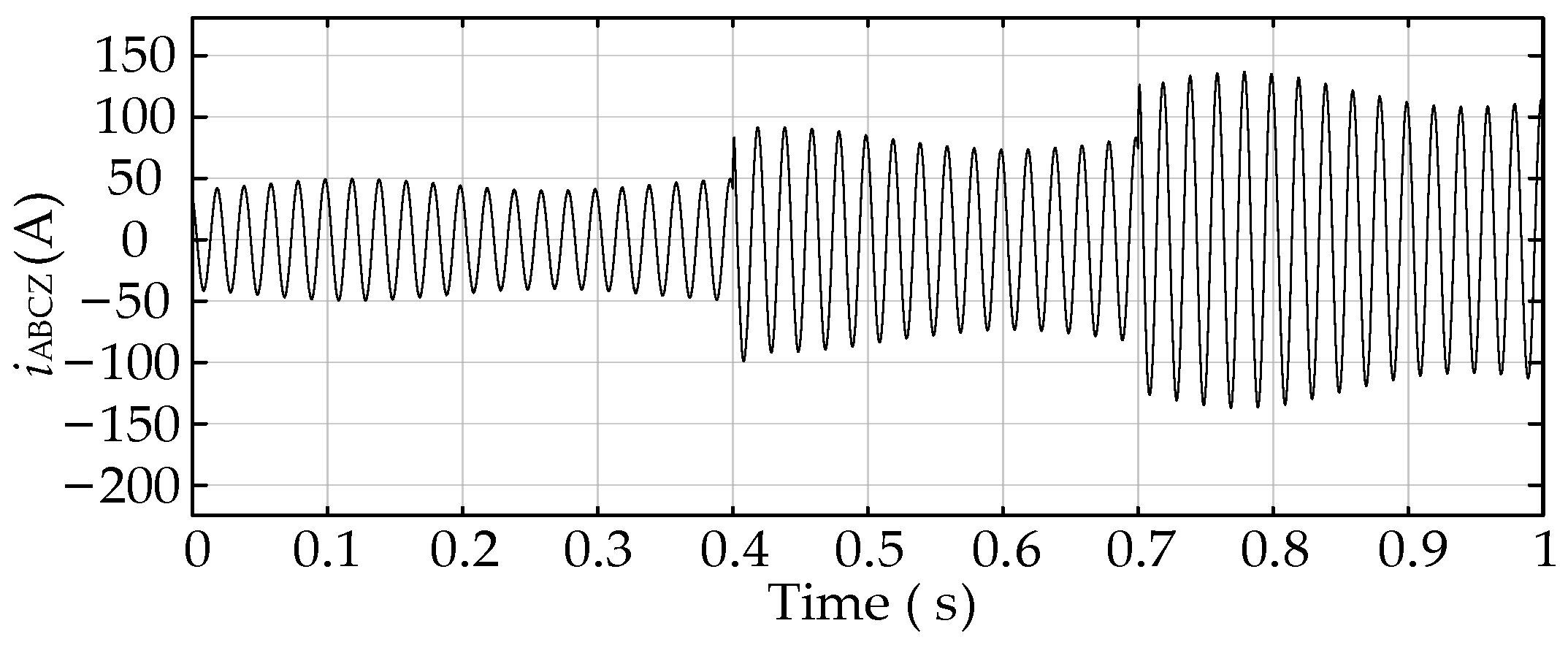
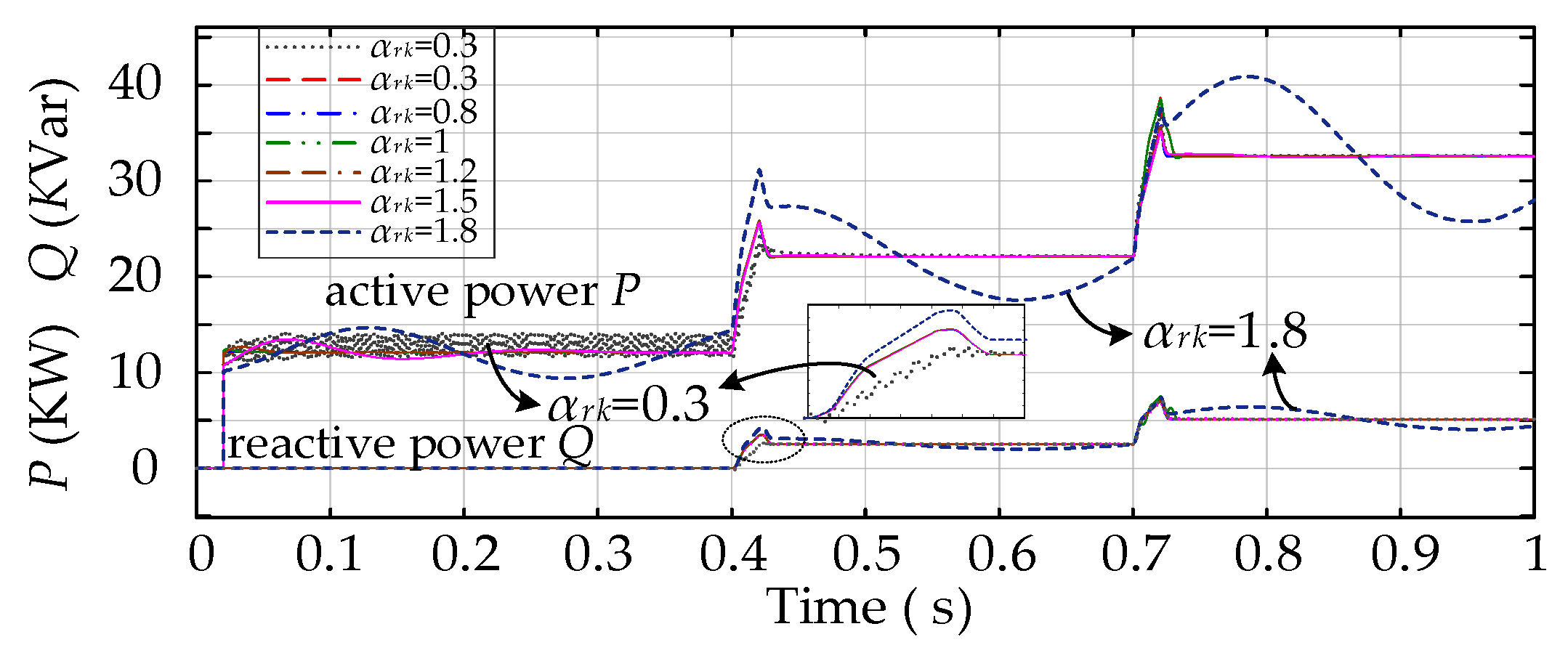
4.3. Electrical Characterization of the System as αrk Changes
5. Effect of the Fractional-Order of the Fractance Element on System Performance
5.1. Effect of Changing α1 on System Performance
5.1.1. Amplitude-Frequency Characteristics of α1 Variation with the Outer-Loop Opened
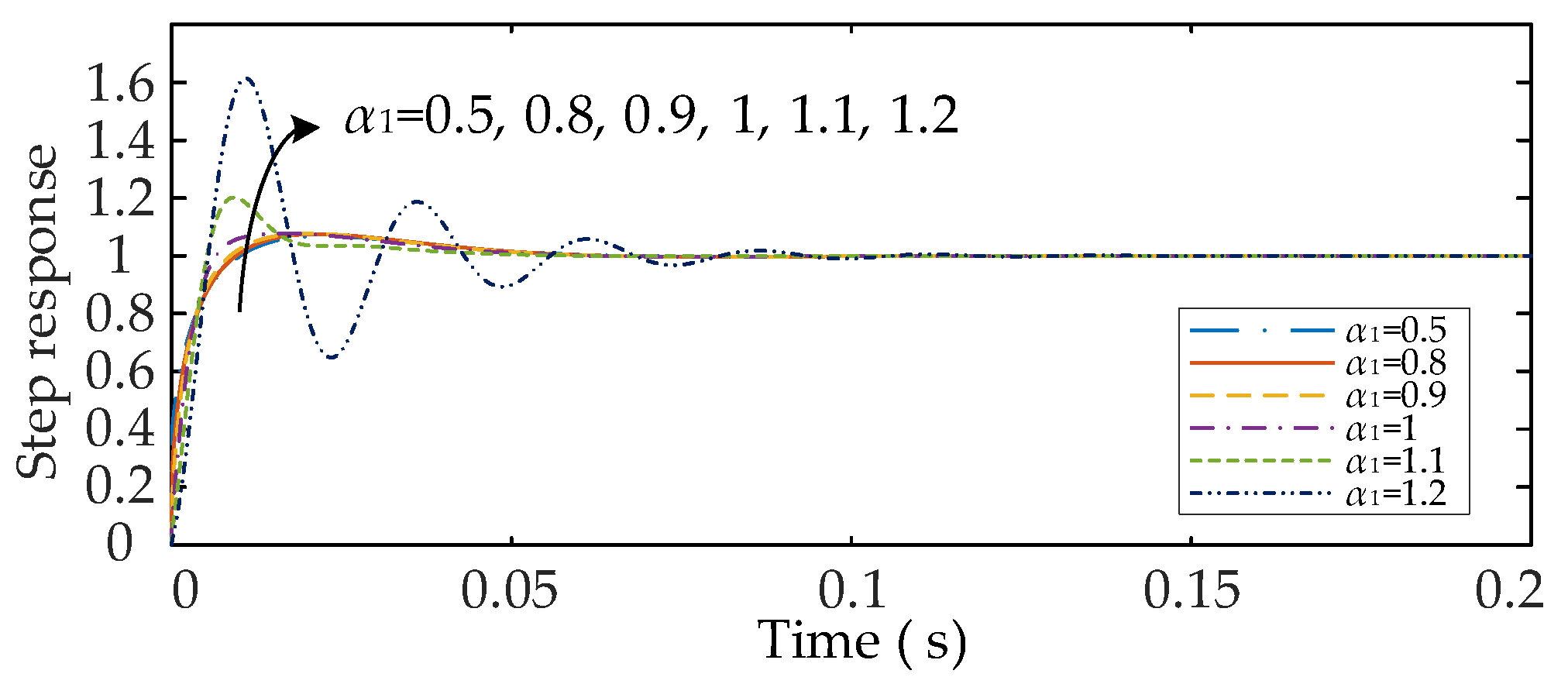
5.1.2. Effect of Changing α1 on the Dynamic Response Characteristics of the System
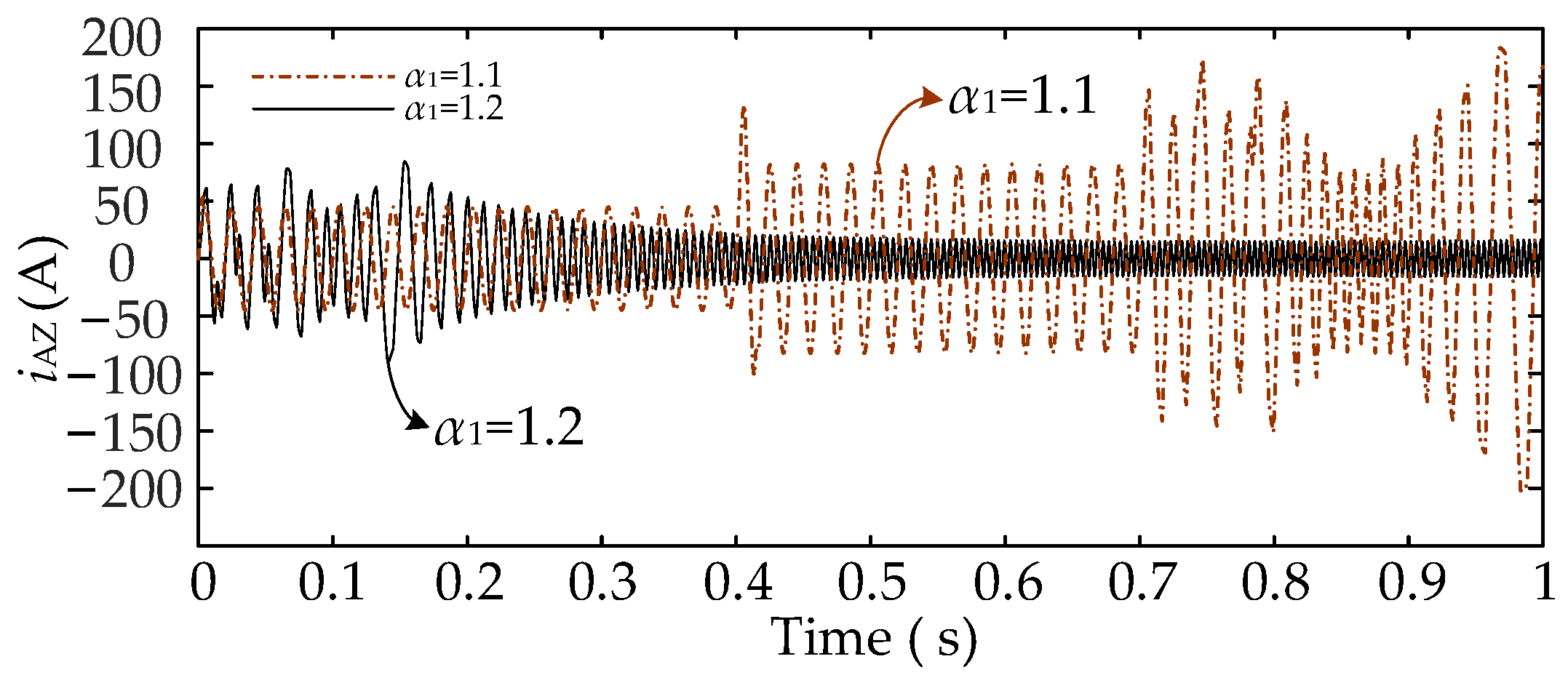
5.1.3. Electrical Characterization of the System as α1 Change
5.2. Effect of Changing β on System Performance
5.2.1. Amplitude-Frequency Characteristics of β Variation with the Outer-Loop Opened
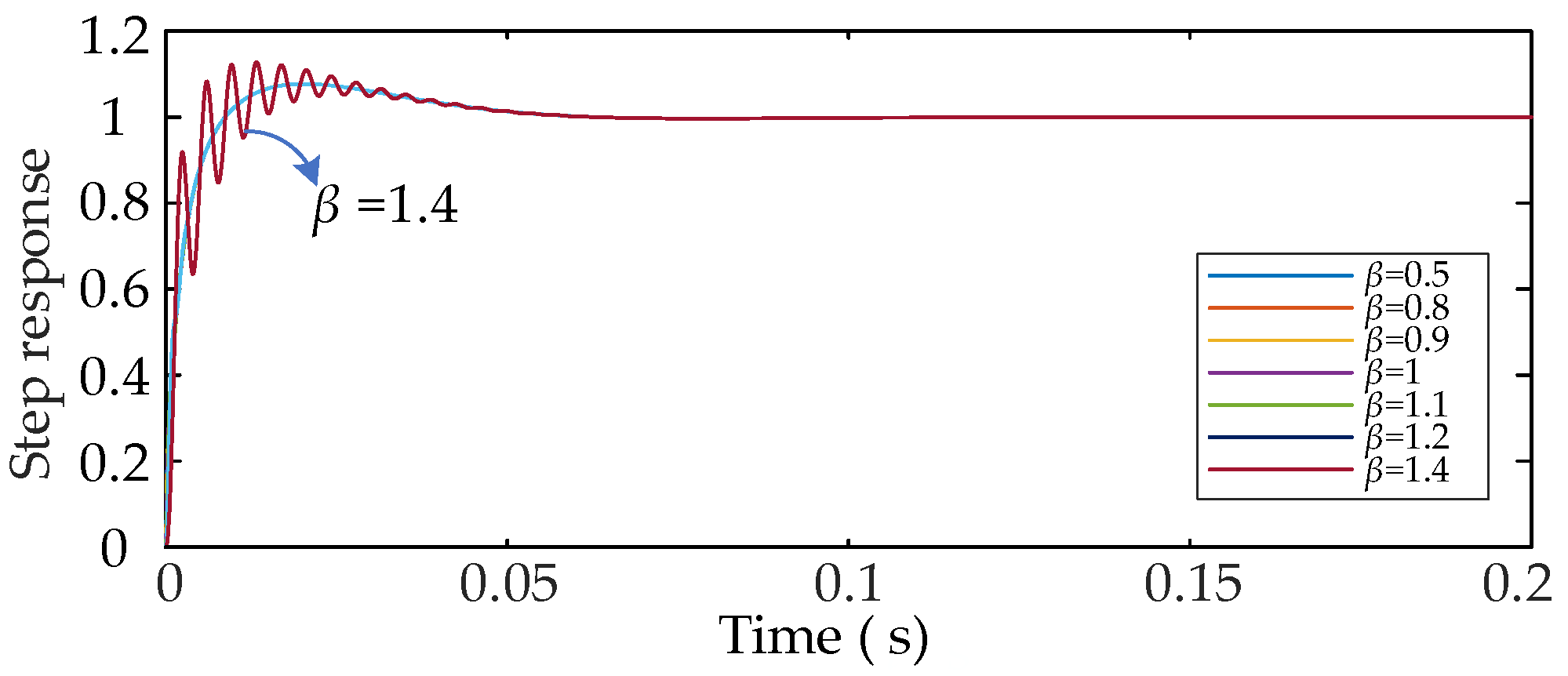
5.2.2. Effect of Changing β on the Dynamic Response Characteristics of the System
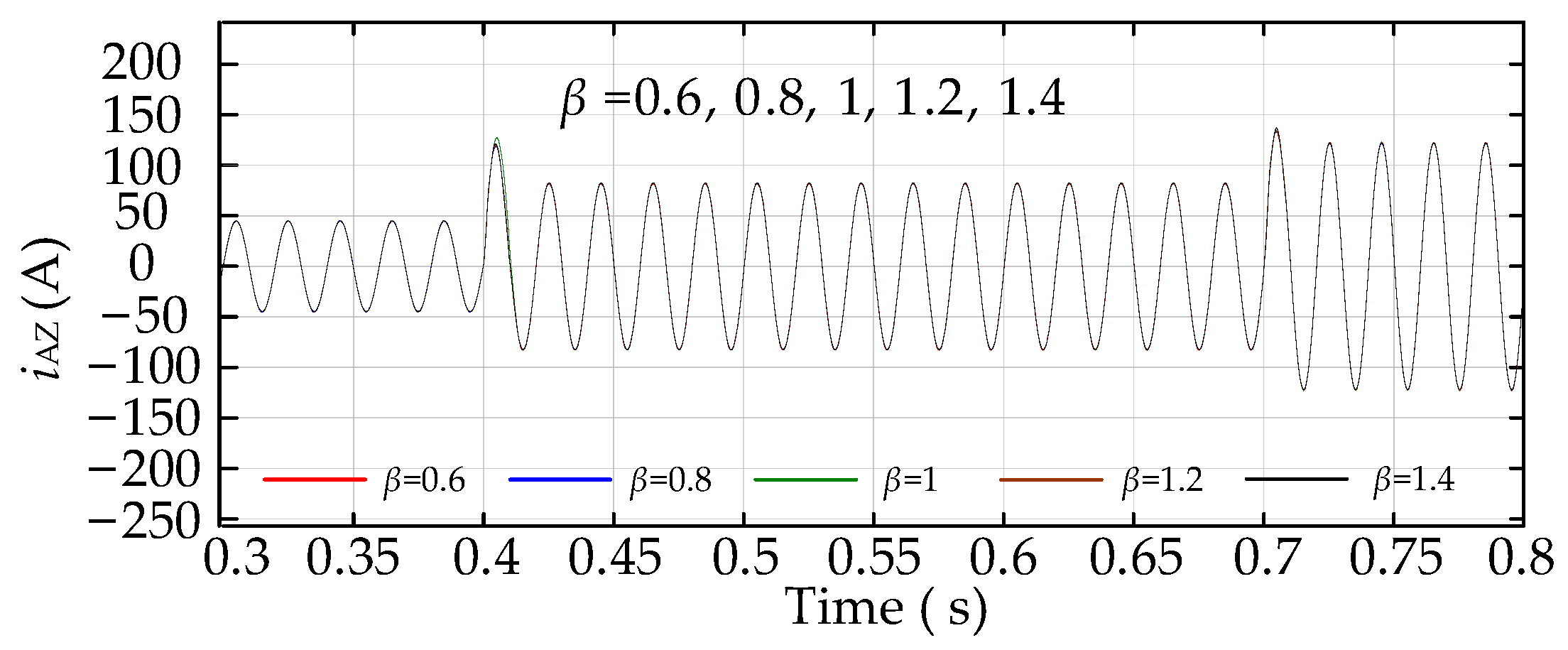
5.2.3. Electrical Characterization of the System as β Vary
5.3. Effect of Changing α2 on System Performance
5.3.1. Amplitude-Frequency Characteristics of α2 Variation with the Outer Loop Opened
5.3.2. Effect of Changing α2 on the Dynamic Response Characteristics of the System
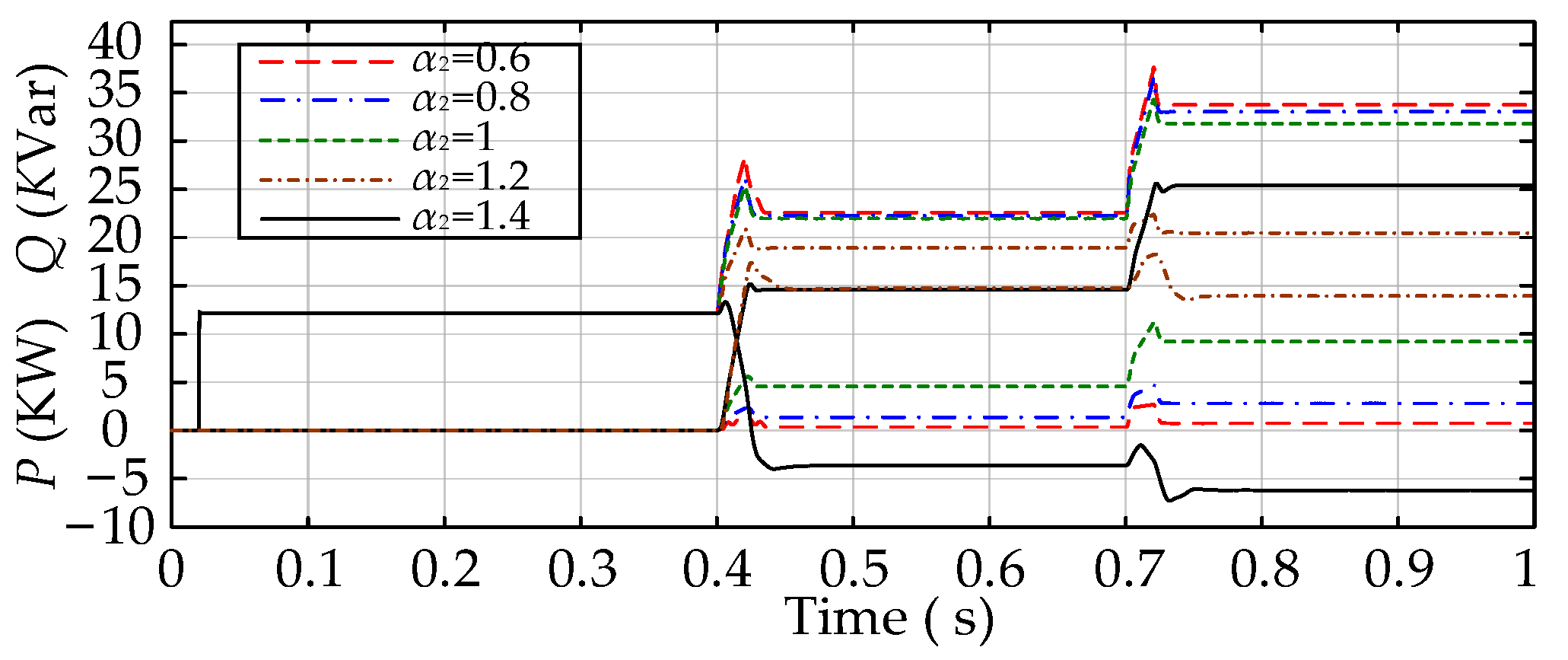
5.3.3. Electrical Characterization of the System as α2 Varies
6. Conclusions
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HBCS-MG | Half-bridge converter series microgrid |
| FOPI | Fractional-order PI |
| SMSI-MG | Microgrid with series micro-source inverters |
| MMC-MG | Modular multilevel converter half-bridge series microgrid |
| WECS | Wind energy conversion system |
| HESG | Hybrid excitation synchronous generator |
| FOVSR | Fractional-order voltage source PWM rectifier |
| MS-HBC | Micro-source half-bridge converter |
| VSG | Virtual synchronous generator |
| THD | Total harmonic distortion |
Appendix A
References
- Hou, N.; Ding, L.; Gunawardena, P.; Wang, T.H.; Zhang, Y.; Li, Y.W. A Partial Power Processing Structure Embedding Renewable Energy Source and Energy Storage Element for Islanded DC Microgrid. IEEE Trans. Power Electron. 2020, 36, 2499–2504. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Song, M.L.; Shen, Z.Y. The evolution of renewable energy and its impact on carbon reduction in China. Energy 2021, 237, 121639. [Google Scholar] [CrossRef]
- Severino, B.; Strunz, K. Enhancing transient stability of DC microgrid by enlarging the region of attraction through nonlinear polynomial droop control. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 4388–4401. [Google Scholar] [CrossRef]
- Li, D.S.; Sun, Q.Y.; Wang, R.; Sui, Z. Transient Stability Analysis and Enhancement of Inverter-Based Microgrid Considering Current Limitation. IEEE Trans. Power Electron. 2025, 40, 2429–2441. [Google Scholar] [CrossRef]
- Hu, J.F.; Shan, Y.H.; Yang, Y.; Parisio, A.; Li, Y.; Amjady, N. Economic Model Predictive Control for Microgrid Optimization: A Review. IEEE Trans. Smart Grid 2024, 15, 472–484. [Google Scholar] [CrossRef]
- Wang, X.G.; Ding, Y.J.; Li, J.J.; Guo, Y.J. Characteristics analysis of micro-source half-bridge converter series Y-connection based microgrid systems. J. Power Electron. 2023, 23, 1483–1495. [Google Scholar] [CrossRef]
- Wang, X.G.; Li, J.J.; Guo, Q.; Wang, H.L.; Ding, Y.J. Parameter design of half-bridge converter series Y-connection microgrid grid-connected filter based on improved PSO-LSSVM. Int. Trans. Electr. Energy Syst. 2023, 2023, 9534004. [Google Scholar] [CrossRef]
- Yu, D.H.; Liao, X.Z.; Wang, Y. Modeling and analysis of Caputo–Fabrizio definition-based fractional-order boost converter with inductive loads. Fractal Fract. 2024, 8, 81. [Google Scholar] [CrossRef]
- Govind, D.; Suryawanshi, H.M.; Nachankar, P.P.; Narayana, C.L.; Singhal, A. Fractional-order LC filter modeling, implementation, and analysis for distributed power generation system. Int. J. Circuit Theory Appl. 2023, 51, 4565–4583. [Google Scholar] [CrossRef]
- El-Khazali, R. Fractional-order LCαL filter-based grid connected PV systems. In Proceedings of the 2019 IEEE 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019; pp. 533–536. [Google Scholar]
- Kashfi, R.; Balochian, S.; Alishahi, M. Design of a optimal robust adaptive neural network-based fractional-order PID controller for H-bridge single-phase inverter. Appl. Soft Comput. 2024, 166, 112142. [Google Scholar] [CrossRef]
- Zhao, C.N.; Jiang, M.R.; Huang, Y.Q. Formal verification of fractional-order PID control systems using higher-order logic. Fractal Fract. 2022, 6, 485. [Google Scholar] [CrossRef]
- Tumari, M.Z.M.; Ahmad, M.A.; Rashid, M.I.M. A fractional order PID tuning tool for automatic voltage regulator using marine predators algorithm. Energy Rep. 2023, 9, 416–421. [Google Scholar] [CrossRef]
- Krishna, P.S.; Rao, P.V.G.K. Fractional-order PID controller for blood pressure regulation using genetic algorithm. Biomed. Signal Process. Control 2024, 88, 105564. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Calgan, H.; Demirtas, M. Fractional-Order sliding mode control of a 4D memristive chaotic system. J. Vib. Control 2023, 30, 7–8. [Google Scholar] [CrossRef]
- Mseddi, A.; Dhouib, B.; Zdiri, M.A.; Alaas, Z.; Naifar, O.; Guesmi, T.; Alshammari, B.M.; Alqunun, K. Exploring the Potential of Hybrid Excitation Synchronous Generators in Wind Energy: A Comprehensive Analysis and Overview. Process 2024, 12, 1186. [Google Scholar] [CrossRef]
- Mseddi, A.; Wali, K.; Abid, A.; Naifar, O.; Rhaima, M.; Mchiri, L. Advanced modeling and control of wind conversion systems based on hybrid generators using fractional order controllers. Asian J. Control 2024, 26, 1103–1119. [Google Scholar] [CrossRef]
- Mohamed, A.T.; Mahmoud, F.M.; Swief, R.A.; Said, L.A.; Radwan, A.G. Optimal fractional-order PI with DC-DC converter and PV system. Ain Shams Eng. J. 2021, 12, 1895–1906. [Google Scholar] [CrossRef]
- Fang, S.C.; Wang, X.G. Modeling and analysis method of fractional-order buck-boost converter. Int. J. Circuit Theory Appl. 2020, 48, 1493–1510. [Google Scholar] [CrossRef]
- Chen, Y.F.; Wang, X.; Zhang, B.; Xie, F.; Chen, S. Differences between Riemann-Liouville and Caputo calculus definitions in analyzing fractional boost converter with discontinuous-conduction-mode operation. Int. J. Circuit Theory Appl. 2024, 52, 4164–4183. [Google Scholar] [CrossRef]
- Yang, N.N.; Wu, C.J.; Jia, R.; Liu, C.X. Modeling and characteristics analysis for a buck-boost converter in pseudo-continuous conduction mode based on fractional calculus. Math. Probl. Eng. 2016, 2016, 6835910. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, X.C.; Meng, X.R.; Qin, J.B.; Liu, H. Modeling and analysis of a single-phase fractional-order voltage source pulse width modulation rectifier. J. Power Sources 2020, 497, 228821. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, X.C.; Liu, H.; Meng, X.R. Fractional-order modeling and analysis of a three-phase voltage source PWM rectifier. IEEE Access 2020, 8, 13507–13515. [Google Scholar] [CrossRef]
- Lei, Y.; Xiong, H.J.; Lei, D.M. Fractional order PID control strategy for modular multilevel converters. In Proceedings of the 2017 International Conference on Industrial Informatics—Computing Technology, Intelligent Technology, Industrial Information Integration (ICIICII), Wuhan, China, 2–3 December 2017; pp. 223–226. [Google Scholar]
- Wang, X.G.; Cai, J.H. Grid-Connected inverter based on a resonance-free fractional-order LCL filter. Fractal Fract. 2022, 6, 374. [Google Scholar] [CrossRef]
- Li, X.C.; Luo, X.L.; Hou, L.L.; Xu, J.H. Research on grid-side control of wind power generation based on fractional LCL filter. Acta Energ. Sol. Sin. 2022, 43, 383–391. [Google Scholar] [CrossRef]
- Li, X.C.; Hou, L.L.; Luo, X.L.; Xu, J.H. Research on fractional modeling and controller design of three-phase inverter grid-connected system. Acta Energ. Sol. Sin. 2023, 44, 415–424. [Google Scholar] [CrossRef]
- Liao, X.Z. Fractional Modelling and Analysis of Fractional Order RLC Circuit Systems; China Science Publishing & Media Ltd. (CSPM): Beijing, China, 2023; pp. 18–27. [Google Scholar]
- Li, B.B.; Yang, R.F.; Xu, D.D.; Wang, G.L.; Wang, W.; Xu, D.G. Analysis of the phase-shifted carrier modulation for modular Multilevel converters. IEEE Trans. Power Electron. 2015, 30, 297–310. [Google Scholar] [CrossRef]















| d | 1 | 2 | 3 | 4 | 5 | R0/Ω | L0/mH | |
|---|---|---|---|---|---|---|---|---|
| Ri/Ω | 47.7 | 931.4 | 1.8 × 104 | 3.4 × 105 | 1.2 × 107 | 5 | / | |
| Ci/μF | 5.8 | 1.2 | 24.6 | 50.8 | 56.7 | |||
| Ri/Ω | 1.26 | 0.07 | 3.9 × 10−3 | 2.1 × 10−4 | 1.2 × 10−5 | / | 1.99 | |
| Li/mH | 0.75 | 1.04 | 1.44 | 1.98 | 2.78 |
| E | 170 V | Time/s Load | 0–0.4 Z1 | 0.4–0.7 Z2 | 0.7–1 Z3 |
|---|---|---|---|---|---|
| Lf | 5 mH | RX/Ω | 4 | 2.1 | 1.4 |
| Cf | 20 μF | LXZ/mH | 0 | 1.4 | 1.3 |
| Proportionality Coefficient | Integral Coefficient | |
|---|---|---|
| Inner-loop PI controller | kp1 = 3 | ki1 = 500 |
| Outer-loop PI controller | kp2 = 2 | ki2 = 500 |
| αr2 αr1 | 0.3 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 |
|---|---|---|---|---|---|---|---|
| 0.3 | −16.3 | −1.0 | Inf | Inf | Inf | Inf | −34.7 |
| 0.5 | −1.1 | 15.1 | Inf | Inf | Inf | Inf | −20.1 |
| 0.8 | Inf | Inf | Inf | Inf | Inf | −18.7 | −7.0 |
| 1 | Inf | Inf | Inf | Inf | Inf | −8.1 | 0.0 |
| 1.2 | Inf | Inf | Inf | Inf | −10.3 | 0.3 | 6.7 |
| 1.5 | Inf | Inf | −23.3 | −12.6 | −3.6 | 8.4 | 17.5 |
| 1.8 | −38.9 | −24.5 | −11.9 | −5.1 | 1.1 | 10.7 | 25.3 |
| αr2 αr1 | 0.3 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 |
|---|---|---|---|---|---|---|---|
| 0.3 | −15.0 | −1.5 | 33.7 | 36.5 | 36.8 | 36.9 | 36.9 |
| 0.5 | −1.3 | 59.2 | 99.2 | 112.1 | 117.7 | 119.3 | 119.4 |
| 0.8 | 22.0 | 107.9 | 83.8 | 82.8 | 92.3 | 114.7 | 119.5 |
| 1 | 23.6 | 115.9 | 91.9 | 67.9 | 53.1 | 47.0 | −0.3 |
| 1.2 | 23.7 | 118.4 | 105.7 | 67.7 | 32.5 | −1.3 | −45.9 |
| 1.5 | 23.8 | 119.0 | 114.8 | 92.9 | 22.5 | −38.9 | −85.1 |
| 1.8 | 23.8 | 119.0 | 116.1 | 105.1 | −15.6 | −79.5 | −122.1 |
| αr2 αr1 | 0.5 | 0.7 | 0.8 | 1 | 1.2 | 1.5 | Trends |
|---|---|---|---|---|---|---|---|
| 0.5 | 1.03 | 1.064 | 1.058 | 1.023 | 1.023 | 1.028 | ↑↓↑ |
| 0.7 | 1.047 | 1.111 | 1.105 | 1.089 | 1.075 | 1.068 | ↑↓ |
| 0.8 | 1.035 | 1.095 | 1.116 | 1.131 | 1.125 | 1.10.7 | ↑↓ |
| 1 | 1.011 | 1.055 | 1.089 | 1.189 | 1.245 | 1.246 | ↑ |
| 1.2 | 1.013 | 1.043 | 1.077 | 1.196 | 1.331 | 1.44 | ↑ |
| 1.5 | 1.017 | 1.039 | 1.061 | 1.152 | 1.333 | NaN | ↑ |
| 1.8 | 1.02 | 1.04 | 1.055 | 1.111 | 1.25 | NaN | ↑ |
| trends | ↑↓↑ | ↑↓ | ↑↓ | ↑↓ | ↑ | ↑ |
| αr2 αr1 | 0.5 | 0.7 | 0.8 | 1 | 1.2 | 1.5 | Trends |
|---|---|---|---|---|---|---|---|
| 0.5 | 0.0008 | 0.0014 | 0.0019 | 0.0058 | 0.0183 | 0.0502 | ↑ |
| 0.7 | 0.0014 | 0.0026 | 0.0037 | 0.0078 | 0.0174 | 0.0453 | ↑ |
| 0.8 | 0.0019 | 0.0036 | 0.0051 | 0.0104 | 0.0196 | 0.045 | ↑ |
| 1 | 0.0099 | 0.0078 | 0.0101 | 0.0178 | 0.0178 | 0.053 | ↑ |
| 1.2 | 0.0249 | 0.0203 | 0.0202 | 0.0279 | 0.0279 | 0.0713 | ↑ |
| 1.5 | 0.064 | 0.0543 | 0.0507 | 0.0504 | 0.0504 | 2.9071 | ↓↑ |
| 1.8 | 0.1287 | 0.113 | 0.106 | 0.0944 | 0.0944 | 2.7238 | ↓↑ |
| trends | ↑ | ↑ | ↑ | ↑ | ↓↑ | ↓↑ |
| αr2 αr1 | 0.5 | 0.7 | 0.8 | 1 | 1.2 | 1.5 | Trends |
|---|---|---|---|---|---|---|---|
| 0.5 | 0.0014 | 0.0029 | 0.004 | 0.009 | 0.0248 | 0.2324 | ↑ |
| 0.7 | 0.0027 | 0.0056 | 0.0084 | 0.0194 | 0.1079 | 0.222 | ↑ |
| 0.8 | 0.0034 | 0.0085 | 0.0123 | 0.0463 | 0.104 | 0.2176 | ↑ |
| 1 | 0.002 | 0.0205 | 0.0252 | 0.0773 | 0.1159 | 0.3892 | ↑ |
| 1.2 | 0.0055 | 0.1528 | 0.1518 | 0.1276 | 0.2744 | 1.5546 | ↑ |
| 1.5 | 0.064 | 0.2865 | 0.278 | 0.2615 | 0.6758 | NaN | ↑ |
| 1.8 | 0.502 | 0.4849 | 0.8499 | 1.1981 | 3 | NaN | ↑ |
| trends | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ |
| αr1 | 0.4 | 0.6 | 0.8 | 1.2 | 1.4 | 1.8 | |
|---|---|---|---|---|---|---|---|
| up/V | 0 s | 180.5 | 180.5 | 180.3 | 180.5 | 179.1 | 179.4 |
| 0.4 s | 185.8 | 192.7 | 185.2 | 185.3 | 185.5 | 185.5 | |
| 0.7 s | 195.1 | 187.5 | 187.9 | 195.4 | 189.1 | 188.9 | |
| Z1 | uw/V THD | 180 1.27% | 180 0.76% | 180 0.74% | 180 0.74% | 180 0.75% | 180 0.76% |
| Z2 | uw/V THD | 180 3.45% | 180 3.47% | 180 3.49% | 180 3.49% | 180 3.49% | 180 3.49% |
| Z3 | uw/V THD | 180 3.58% | 180 3.59% | 180 3.58% | 180 3.58% | 180 3.61% | 180 3.61% |
| αrk | 0.3 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | |
|---|---|---|---|---|---|---|---|---|
| up/V | 0.4 s | unstable | 186 | 185.2 | 185.6 | 186.6 | 186.6 | 205.2 |
| 0.7 s | 187.8 | 195 | 187.9 | 196.4 | 190.7 | 189.4 | 195.3 | |
| Z1 | uw/V THD | 184.3 126% | 180 1.63% | 180 0.76% | 180 0.73% | 180 0.73% | 178.9 1.19% | unstable 5.33% |
| Z2 | uw/V THD | 180.4 3.57% | 180 3.45% | 180 3.47% | 180 3.5% | 180 3.5% | 179.9 3.51% | unstable 5.24% |
| Z3 | uw/V THD | 180.1 3.86% | 180 3.58% | 180 3.59% | 179.9 3.66% | 180 3.65% | 179.9 3.69% | unstable 5.73% |
| 0.5 | 0.8 | 1 | 1.1 | 1.2 | 1.5 | |
|---|---|---|---|---|---|---|
| h/(dB) | Inf | Inf | Inf | Inf | 80 | 30 |
| γ/(deg) | 120 | 112 | 95 | 73 | 37 | −125 |
| ωx/(rad/s) | NaN | NaN | NaN | NaN | 2.5 × 105 | 600/3.8 × 104 |
| ωc/(rad/s) | 338 | 304 | 299 | 299 | 265 | 57 |
| α2 | 0.6 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | |
|---|---|---|---|---|---|---|---|
| up/V | 0.4 s | 185.3 | 185.3 | 185.2 | 183.1 | 192.9 | Unstable |
| 0.7 s | 186.6 | 186.8 | 187.9 | 191.1 | 201 | ||
| Z1 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | |
| THD | 24.1% | 1.8% | 0.76% | 0.32% | 0.17% | ||
| Z2 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | |
| THD | 111.2% | 26.3% | 3.47% | 1.57% | 1.15% | ||
| Z3 Steady-state | uw/V | 179.4 | 180 | 180 | 180 | NaN | |
| THD | 110.8% | 25.3% | 3.59% | 2.07% | 112% |
| β | 0.5 | 0.8 | 1 | 1.1 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|
| h/(dB) | Inf | Inf | Inf | 16.4 | 6.8 | −14.2 |
| γ/(deg) | 83.9 | 83.8 | 83.6 | 83.5 | 83.5 | −55.4 |
| ωx/(rad/s) | NaN | NaN | NaN | 9.1 × 103 | 4.6 × 103 | 1.7 × 103 |
| ωc/(rad/s) | 609 | 610 | 613 | 618 | 628 | 1.9 × 103 |
| β | 0.6 | 0.8 | 0.9 | 1 | 1.2 | 1.4 | |
|---|---|---|---|---|---|---|---|
| up/V | 0.4 s | 184.7 | 185.2 | 185.2 | 186.3 | 185.4 | 186 |
| 0.7 s | 187.7 | 187.9 | 187.9 | 187.9 | 188.1 | 188.6 | |
| Z1 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | 180 0.17% |
| THD | 0.83% | 0.76% | 0.67% | 0.46% | 0.28% | ||
| Z2 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | 180 0.21% |
| THD | 27.4% | 3.47% | 1.63% | 1.52% | 0.29% | ||
| Z3 Steady-state | uw/V | 179.4 | 180 | 180 | 180 | 180 | 180 0.4% |
| THD | 2.5e3% | 3.59% | 2.09% | 1.5% | 0.5% |
| α2 | 0.5 | 0.8 | 1 | 1.1 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|
| h/(dB) | Inf | Inf | Inf | Inf | Inf | Inf |
| γ/(deg) | 103.1 | 104.5 | 107.7 | 84.2 | 70.3 | 69 |
| ωx/(rad/s) | NaN | NaN | NaN | NaN | NaN | NaN |
| ωc/(rad/s) | 299.6 | 299.5 | 293.8 | 1.8 × 104 | 1.7 × 104 | 1.5 × 104 |
| α2 | 0.6 | 0.8 | 0.9 | 1 | 1.2 | 1.4 | |
|---|---|---|---|---|---|---|---|
| up/V | 0.4 s | 190.5 | 185 | 185.2 | 185.1 | 183.1 | |
| 0.7 s | 188.7 | 188.2 | 187.9 | 187.5 | 187.3 | ||
| Z1 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | 180 0.76% |
| THD | 0.77% | 0.75% | 0.76% | 0.75% | 0.75% | ||
| Z2 Steady-state | uw/V | 180 | 180 | 180 | 180 | 180 | Unstable |
| THD | 27.4% | 1.93% | 3.47% | 4.79% | 6.34% | ||
| Z3 Steady-state | uw/V | 179.4 | 180 | 180 | 180 | 180 | |
| THD | 2.5e3% | 2.01% | 3.59% | 5.09% | 9.54% |
| Z1 | Z2 | Z3 | ||||
|---|---|---|---|---|---|---|
| Variable | Stable Range | Optimum/ THD | Stable Range | Optimum/ THD | Stable Range | Optimum/ THD |
| αrk | 0.5–1.2 | 1/0.73% | 0.3–1.5 | 0.5/3.45% | 0.3–1.5 | 0.5/3.58% |
| α1 | 0.7–1.1 | 1.1/0.17% | 0.9–1.1 | 1.1/1.15% | 0.9–1 | 1/2.07% |
| β | 0.6–1.4 | 1.4/0.17% | 0.8–1.4 | 1.4/0.21% | 0.8–1.4 | 1.4/0.4% |
| α2 | 0.6–1.4 | Same | 0.8–1.1 | 0.8/1.93% | 0.8–1 | 0.8/2.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Wang, X.; Zhao, L.; Wang, H.; Li, J. Fractional-Order Modeling and Control of HBCS-MG in Off-Grid State. Fractal Fract. 2025, 9, 202. https://doi.org/10.3390/fractalfract9040202
Ding Y, Wang X, Zhao L, Wang H, Li J. Fractional-Order Modeling and Control of HBCS-MG in Off-Grid State. Fractal and Fractional. 2025; 9(4):202. https://doi.org/10.3390/fractalfract9040202
Chicago/Turabian StyleDing, Yingjie, Xinggui Wang, Lingxia Zhao, Hailiang Wang, and Jinjian Li. 2025. "Fractional-Order Modeling and Control of HBCS-MG in Off-Grid State" Fractal and Fractional 9, no. 4: 202. https://doi.org/10.3390/fractalfract9040202
APA StyleDing, Y., Wang, X., Zhao, L., Wang, H., & Li, J. (2025). Fractional-Order Modeling and Control of HBCS-MG in Off-Grid State. Fractal and Fractional, 9(4), 202. https://doi.org/10.3390/fractalfract9040202






