Fractional-Order Modeling and Identification for Dual-Inertia Servo Inverter Systems with Lightweight Flexible Shaft or Coupling

Abstract

To effectively mitigate resonance in dual-inertia servo inverter systems with a lightweight flexible shaft or coupling, the precise modeling of the dual-mass mechanism is essential. This paper proposes a fractional-order modeling and identification methodology tailored for a dual-mass loading permanent magnet synchronous motor (PMSM) servo inverter system. By extending the traditional integer-order model to a more precise fractional-order one, the accuracy of resonance capture can be enhanced within the dual-inertia mechanism. Model parameters are identified using an output error approach combined with the Levenberg–Marquardt (LM) algorithm for fractional-order identification. To validate the effectiveness of this proposed methodology, a PMSM servo inverter experimental platform was developed, and identification experiments were conducted on this platform. The experimental results demonstrate that the proposed fractional-order modeling and parameter identification method significantly improves the system characterization accuracy of the dual-inertia servo inverter system.

1. Introduction

Permanent magnet synchronous motor (PMSM) servo systems are widely employed across diverse industrial applications, such as machine tools, industrial robots, and large optical telescopes. These applications demand excellent dynamic response and precise positioning capabilities [1]. In these systems, reducers or coupling connectors are typically required to connect the servo motor with the load to deliver the necessary torque. However, since these transmission components do not behave as ideal rigid bodies, resonance phenomena can occur during operation. This results in a typical dual-inertia servo system [2]. When operating within this resonant environment, system accuracy may be compromised, and there is potential for metal fatigue, which poses significant safety risks [3].

To address the resonance issue, it is essential to acquire an accurate model of the dual-inertia servo system in order to design appropriate controllers [4], such as notch filters [5,6] or feedback compensators [7]. An inaccurate model not only fails to suppress resonance but may also induce more severe vibrations [8]. The acquisition of the dual-inertia system model can be divided into two steps, namely, modeling and identification. Typically, the modeling and identification methods for dual-inertia servo inverter systems can be categorized into parametric and non-parametric ones.

Among these methods, the non-parametric one does not require a priori knowledge of the system structure, offering broad adaptability and theoretically being applicable to any system [9]. This method conducts the modeling and identification steps simultaneously. Reference [10] utilized a system modeling and identification method based on the least squares technique combined with balanced truncation to identify the model of a dual-inertia system. Reference [11] adopted a modeling method based on impulse response and the Hankel matrix in the field of linear systems and effectively identified the model of the antenna servo system with flexible characteristics. Reference [12] substituted the traditional fast Fourier transform method with the Welch method for power spectrum analysis using input and output data, thereby obtaining the frequency-domain response. Subsequently, the nonlinear least squares algorithm was applied to fit the resonant and anti-resonant frequencies of the system, achieving high identification accuracy. This type of modeling method does not rely on the system a priori knowledge. However, the model structure obtained by non-parametric methods may have certain differences from the theoretical model structure, and extracting the model parameters from it may be somewhat challenging. For example, it may encounter challenges in distinguishing resonant components when dealing with more complex systems.

The parameter modeling and identification method estimates unknown parameters in the model by fitting input and output data. So, this method needs to model the system first and then identify it. Since this method initially acquires a system model, the architecture of the final identified model can be predetermined. Consequently, this approach facilitates controller design. To date, there have been many studies on parameter modeling and identification of dual-inertia system. According to Reference [9], the key parameters that require identification for a dual-inertia system model primarily encompass the rotational inertia of the load, the rigidity coefficient of the transmission mechanism, and the damping coefficient, etc. In Reference [13], in the speed loop control mode, accurate values for the motor’s rotational inertia and damping coefficient were obtained through the application of a low-frequency sinusoidal excitation signal followed by half-cycle integration. However, these methods have a relatively limited scope of application due to constraints in the model’s expressive ability, often resulting in models that lack sufficient precision. Currently, these methods predominantly employ integer-order models. Meanwhile, it has been demonstrated that the dual-inertia system exhibits nonlinear characteristics [14], which cannot be adequately captured by traditional integer-order models. Therefore, it is necessary to utilize a model that more closely approximates the actual system for parameter identification.

Fractional-order calculus, as a critical component of mathematical theory, has demonstrated distinct advantages in the modeling of various systems, including power electronic systems [15,16], battery charge and discharge control systems [17], robotic system [18], and many other systems [19,20]. Similarly, fractional-order modeling also has many applications in mechanical and electrical motor control. A previous study [21] demonstrates the application of a fractional-order system in modeling industrial process systems with large inertia and time delay. Based on the analysis of actual industrial process data, the advantages of the proposed fractional-order model and its corresponding system identification method for industrial processes with large inertia and time delay are verified. Another study [22] integrated the electromagnetic and mechanical components of a permanent magnet synchronous motor (PMSM), developed a fractional-order modeling and identification method for the PMSM servo system, and experimentally validated the superiority of the fractional-order model in the PMSM servo system. As mentioned above, it is difficult for integer-order models to fully express dual-inertia systems, but fractional-order models can solve these problems well [23]. Fractional-order operators, as generalizations of integer-order operators, significantly enhance the expressive capability of traditional models in control theory. Moreover, since integer-order operators are special cases of fractional-order operators, the set of fractional-order system models inherently encompasses all possible integer-order models. Consequently, parameter identification results obtained using fractional-order models are expected to be at least as accurate as, if not superior to, those derived from integer-order models.

Considering the limitations inherent in existing identification methods, this paper introduces a fractional-order modeling and identification methodology specifically designed for a dual-inertia permanent magnet synchronous motor (PMSM) servo inverter system. By extending from the conventional integer-order model to a more accurate fractional-order one, the precision of resonance capture within the dual-inertia system is notably enhanced. Then, the model parameters are estimated using an output error method integrated with the Levenberg–Marquardt (LM) algorithm, tailored for fractional-order parameter identification. The proposed method primarily focuses on the modeling and identification of the mechanical components in the dual-inertia system, while the electromagnetic component is treated as an idealized proportional element. The experimental results confirm that the proposed fractional-order modeling and parameter identification approach significantly improves the accuracy of system characterization in dual-inertia servo inverter systems. And this model and method will provide fundamental support for further application of fractional-order control-related theories in resonance suppression. This modeling and identification method can enhance the modeling accuracy of complex dual-inertia systems, such as harmonic gear motors with flexible couplings and rope-driven mechanical joints. The key contributions of this paper can be summarized as follows:

(1)

The structural composition of the dual-inertia system and the mechanisms underlying resonance generation were investigated. The principle of fractional-order calculus was introduced to extend the current model of the dual-inertia system from the integer-order one to the fractional-order one.

(2)

A model identification approach for the dual-inertia servo system in the time domain was developed, ensuring the effectiveness of the fractional-order dual-inertia servo model.

(3)

Experiments involving the dual-inertia servo model and the identification algorithm were carried out on the test platform. The proposed method and model were evaluated against the existing integer-order model. It was verified that the proposed fractional-order servo model has higher accuracy than the integer-order one.

This paper is organized as follows. Section 2 analyzes the integer-order model and the fractional-order extended model of the dual-inertia servo system and calculates the integer-order realization of the fractional-order model. Section 3 analyzes the fractional-order identification method based on time-domain error and the LM algorithm to obtain the unknown parameters in the fractional-order model. Section 4 outlines the verification of the proposed model and method on the experimental platform. Section 5 summarizes this paper.

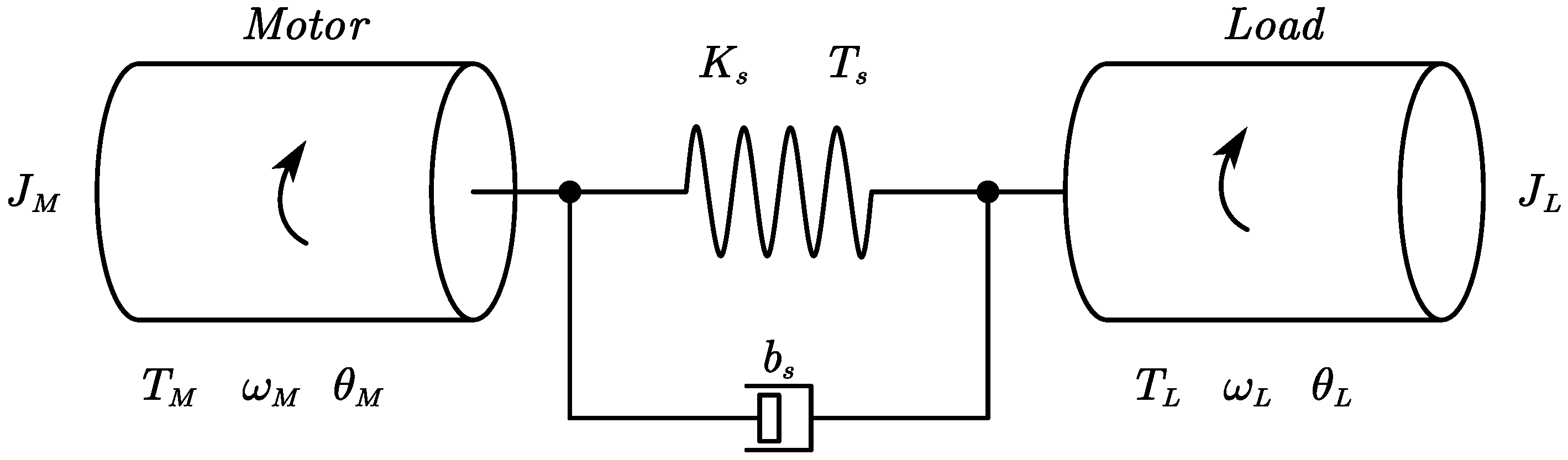
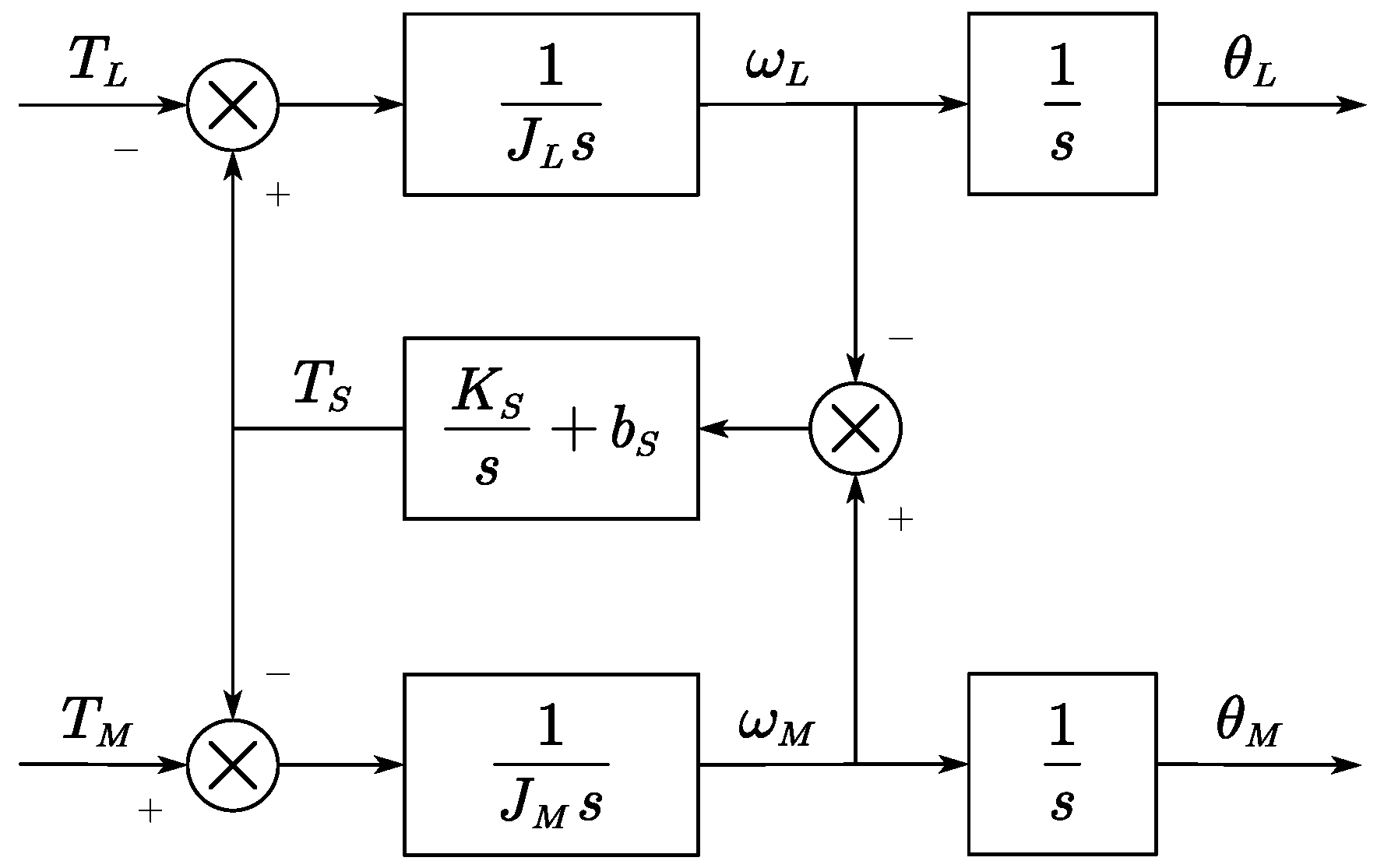
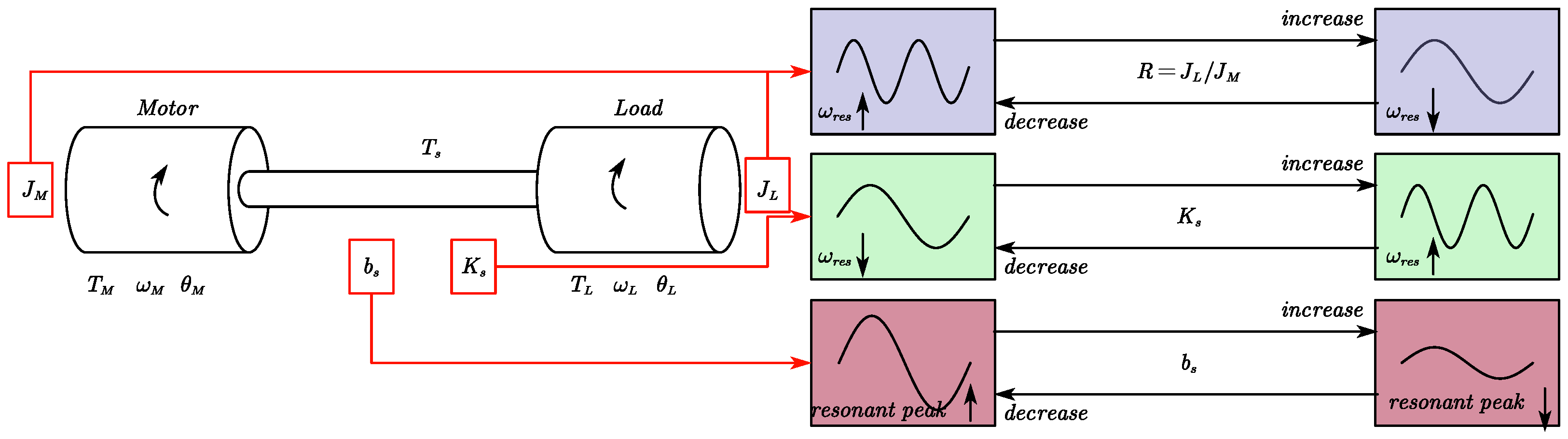
2. The Fractional-Order Modeling of Dual-Inertia Servo Inverter Systems

2.1. Integer-Order Dual-Inertia Servo System Model

The servo drive system typically constitutes a canonical dual-inertia system, wherein the flexible coupling components may include synchronous belts, elastic shafts, or other mechanical structures. The dual-inertia system diagram is shown in Figure 1. The motor is the input of the system and is responsible for generating the driving torque. The spring and damper in the middle are the equivalent simplification of the flexible connection components. The load is the mechanically equivalent structure connected behind the coupling.

In Figure 1, $J_M$ and $J_L$ represent the moments of inertia of the motor and the load, respectively. ${\omega }_M$ and ${\omega }_L$ denote the angular velocities of the motor and the load, while $T_M$ and $T_L$ represent the output torque of the motor and the torque experienced by the load, respectively. $T_s$ signifies the torsional torque resulting from the angular discrepancy between the motor and the load. Additionally, $K_s$ and $b_s$ are the stiffness coefficient and damping coefficient of the coupling connector.

Based on the above mechanical structure, the dynamics equation can be listed as follows.

$$\left\{\begin{array}{c}{J}_M\dot{{\omega }_M}=T_M-T_s\hfill \\ J_L\dot{{\omega }_L}=T_s-T_L\hfill \\ T_s=K_s({\theta }_M-{\theta }_L)+b_s({\omega }_M-{\omega }_L)\hfill \end{array}\right.$$

(1)

The result can be formed as space state equation as shown below:

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\omega }_M(t)\\ {\omega }_L(t)\\ T_s(t)\end{array}\right]=\left[\begin{array}{ccc}-{\displaystyle \frac{b_s}{J_M}}& {\displaystyle \frac{b_s}{J_M}}& -{\displaystyle \frac{1}{J_M}}\\ {\displaystyle \frac{b_s}{J_L}}& -{\displaystyle \frac{b_s}{J_L}}& {\displaystyle \frac{1}{J_L}}\\ K_s& -K_s& 0\end{array}\right]\left[\begin{array}{c}{\omega }_M(t)\\ {\omega }_L(t)\\ T_s(t)\end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{1}{J_M}}\\ 0\\ 0\end{array}\right]\left[T_M(t)\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{1}{J_L}}\\ 0\end{array}\right]\left[T_L(t)\right]$$

(2)

Taking practical applications into consideration, the system’s load end speed ${\omega }_L$ is typically the output, while the motor torque $T_M$ is the system input. The load torque $T_L$ is the disturbance input. Based on the structure of Equation (2), the dual-inertia model structure diagram is shown in Figure 2.

According to the above block diagram, the following transfer functions can be conducted.

$$\left\{\begin{array}{c}{G}_{ME}(s)={\displaystyle \frac{{\omega }_M(s)}{T_M(s)}}={\displaystyle \frac{1}{(J_M+J_L)s}}{\displaystyle \frac{J_L{s}^2+b_{s}s+K_s}{J_P{s}^2+b_{s}s+K_s}}\hfill \\ G_{LE}(s)={\displaystyle \frac{{\omega }_L(s)}{T_M(s)}}={\displaystyle \frac{1}{(J_M+J_L)s}}{\displaystyle \frac{b_{s}s+K_s}{J_P{s}^2+b_{s}s+K_s}}\hfill \\ J_P={\displaystyle \frac{J_M·J_L}{J_M+J_L}}\hfill \end{array}\right.$$

(3)

where $G_{ME}(s)$ is the transfer function with $T_M(s)$ as the input and ${\omega }_M(s)$ as the output. $G_{LE}(s)$ is the transfer function with $T_M(s)$ as the input and ${\omega }_L(s)$ as the output.

Obviously, this system is more complex than the rigid-body model. Compared to the purely rigid-body system, it has two additional zeroes and poles. The pole part is the additional second-order oscillation part, and the zero part is the first- or second-order differential part.

To simplify the system, the structure of the transfer function $G_{ME}(s)$ from motor torque to motor speed can be decomposed into rigid links and resonant parts as the following equations:

$$G_I(s)={\displaystyle \frac{1}{(J_M+J_L)s}},G_P(s)={\displaystyle \frac{J_L{s}^2+b_{s}s+K_s}{J_P{s}^2+b_{s}s+K_s}}$$

(4)

where $G_I(s)$ represents the transfer function of the rigid part, and $G_P(s)$ represents the transfer function of the resonance part. The resonance model $G_P(s)$ can be transformed into the standard form as follows.

$$\begin{array}{c}{G}_P(s)={\displaystyle \frac{J_L{s}^2+b_{s}s+K_s}{J_P{s}^2+b_{s}s+K_s}}={\displaystyle \frac{J_L}{J_P}}{\displaystyle \frac{{(\frac{s}{{\omega }_z})}^2+2{\zeta }_z\frac{s}{{\omega }_z}+1}{{(\frac{s}{{\omega }_p})}^2+2{\zeta }_p\frac{s}{{\omega }_p}+1}}·{({\displaystyle \frac{{\omega }_z}{{\omega }_p}})}^2\hfill \\ {\omega }_p=\sqrt{{\displaystyle \frac{K_s}{J_P}}}{\zeta }_p=\sqrt{{\displaystyle \frac{b_s^2}{4K_s{J}_P}}}\hfill \\ {\omega }_z=\sqrt{{\displaystyle \frac{K_s}{J_L}}}{\zeta }_p=\sqrt{{\displaystyle \frac{b_s^2}{4K_s{J}_L}}}\hfill \\ {\displaystyle \frac{{\omega }_p}{{\omega }_z}}=\sqrt{1+{\displaystyle \frac{J_L}{J_L}}}=\sqrt{1+R}\hfill \end{array}$$

(5)

where ${\omega }_p$ and ${\omega }_z$ are the resonant and anti-resonant frequencies of the system, ${\zeta }_p$ and ${\zeta }_z$ are the corresponding damping coefficients, and $R=J_L/J_M$ is the ratio of rotational inertia.

Then, based on the frequency characteristics of the second-order inertial part and the second-order differential part, the resonant frequency ${\omega }_{res}$ and the anti-resonant frequency ${\omega }_{ares}$ can be calculated as follows:

$$\begin{array}{c}{\omega }_{res}={\omega }_p\sqrt{1-{\zeta }_p^2}\hfill \\ {\omega }_{ares}={\omega }_z\sqrt{1-{\zeta }_z^2}\hfill \end{array}$$

(6)

If the damping coefficient $b_s\ll 4K_s{J}_P$ and $b_s\ll 4K_s{J}_L$, then it should be reasonable to assume that ${\omega }_p$ is approximately equal to resonant frequency ${\omega }_{res}$, and ${\omega }_z$ is approximately equal to the anti-resonant frequency ${\omega }_{ares}$.

By analyzing the frequency-domain characteristic curve of the resonant part in Figure 3, it can be seen that there is a resonant peak and an anti-resonant peak. When the input signal is close to the resonant frequency, the system amplitude response increases, causing a resonance phenomenon.

And from Equations (5) and (6), the resonant frequency ${\omega }_{res}$ and the anti-resonant frequency ${\omega }_{ares}$ rises when stiffness coefficient $K_s$ increases. In addition, as the damping coefficient $b_s$ increases, the resonant peak of the system decreases, while the anti-resonant peak increases. When the inertia ratio R increases, the system’s resonant peak rises, while the anti-resonant peak drops. The frequency gap between the two widens. Figure 4 is a schematic diagram illustrating the influence of parameters on resonance.

In practical systems, frictional damping is also present. Define $K_L$ as the load damping coefficient. To further enhance the dual-inertia model, the model structure in Figure 2 can be improved to that shown in Figure 5a. The state-space equation of the system is as follows:

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{\omega }_M(t)\\ {\omega }_L(t)\\ T_s(t)\end{array}\right]=\left[\begin{array}{ccc}-{\displaystyle \frac{b_s}{J_M}}& {\displaystyle \frac{b_s}{J_M}}& -{\displaystyle \frac{1}{J_M}}\\ {\displaystyle \frac{b_s}{J_L}}& -{\displaystyle \frac{b_s+K_L}{J_L}}& {\displaystyle \frac{1}{J_L}}\\ K_s& -K_s& 0\end{array}\right]\left[\begin{array}{c}{\omega }_M(t)\\ {\omega }_L(t)\\ T_s(t)\end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{1}{J_M}}\\ 0\\ 0\end{array}\right]\left[T_M(t)\right]+\left[\begin{array}{c}0\\ -{\displaystyle \frac{1}{J_L}}\\ 0\end{array}\right]\left[T_L(t)\right]$$

(7)

Converting Equation (7) into a transfer function yields the following result:

$$\begin{array}{c}{G}_{ME}(s)={\displaystyle \frac{{\omega }_M(s)}{T_M(s)}}={\displaystyle \frac{J_L{s}^2+(b_s+K_L)s+K_s}{K_s{K}_L+J_L{K}_{s}s+J_M{K}_{s}s+b_s{K}_{L}s+J_L{J}_M{s}^3+J_L{b}_s{s}^2+J_M{b}_s{s}^2+J_M{K}_L{s}^2}}\hfill \\ G_{LE}(s)={\displaystyle \frac{{\omega }_L(s)}{T_M(s)}}={\displaystyle \frac{b_{s}s+K_s}{K_s{K}_L+J_L{K}_{s}s+J_M{K}_{s}s+b_s{K}_{L}s+J_L{J}_M{s}^3+J_L{b}_s{s}^2+J_M{b}_s{s}^2+J_M{K}_L{s}^2}}\hfill \end{array}$$

(8)

It can be seen that all the polynomial coefficients in the denominator of the system’s transfer function are greater than zero. Given that the inertia, damping, and elasticity coefficients of the original system parameters are positive real numbers, the system cannot possess poles with real parts greater than zero. Consequently, all poles of the system are located in the left half of the s-plane, ensuring the stability of the system.

2.2. Fractional-Order Dual-Inertia Servo System Model

In practical systems, the characteristics of transmission mechanisms deviate from ideal characteristics, particularly in flexible part. They contain some nonlinear properties that are not reflected in Figure 1. The ideal dual-inertia system model could not describe the transmission behavior accurate enough. So, it is difficult to meet the model accuracy criteria in application scenarios with high performance requirements. Therefore, in this subsection, fractional-order operators is introduced to improve the modeling accuracy for the above-mentioned model as Figure 5b. Fractional-order integral operators can expand integer-order models to fractional-order ones and effectively improve the model’s capability for fitting the characteristics of flexible parts. Especially for couplings or shaft components made of multi-molecular materials [24], their characteristics are highly suitable for description using fractional-order models. Furthermore, based on the findings presented in the study [22], the mechanical component of the motor is preferably modeled using a fractional-order operator. Since integer-order systems can also be represented as fractional-order systems of order 1, the application scope of this fractional-order system is not narrowed.

Fractional-order operators are not easy to implement in practice and generally need to be discretized and approximated. Commonly used fractional discretization methods include the Oustaloup filter [23], impulse response invariant discretization [25], Carlson method [26] and Matsuda–Fujii filter [26,27]. Among them, the Oustaloup method allows for the selection of interested frequency bands. Moreover, its structure can be easily written into a state space equation, which helps to reduce the calculation amount of identification. Therefore, fractional-order integrator $1/s^{\lambda }$ in the model uses the Oustaloup filter as the method of approximation to the integer-order system. Assuming that the frequency band to be approximated is $({\omega }_b,{\omega }_h)$, where ${\omega }_b$ is the lower limit of the frequency band and ${\omega }_h$ is the upper limit of the frequency band, the selection of this frequency band should be sufficient to cover the frequencies of the various characteristics of the mechanical system. Assuming that the order of the cascade filter is $2N+1$, in general, the selected filter frequency band contains 1 more octave, and its order needs to be increased by 1–2 orders [28]. Then, the fractional integrals in the system can be expanded into the following equation.

$${\displaystyle \frac{1}{s^{\lambda }}}={\displaystyle \frac{1}{s}}{s}^{1-\lambda }={\displaystyle \frac{1}{s}}{G}_f(s)={\displaystyle \frac{1}{s}}{\omega }_h^{1-\lambda }\prod _{i=-N}^N{\displaystyle \frac{s+{\omega }_i^{\prime }}{s+{\omega }_i}}$$

(9)

where $G_f(s)$ is the Oustaloup filter of fractional-order differential operator $s^{1-\lambda }$, and ${\omega }_i^{\prime }$ and ${\omega }_i$ are as follows.

$$\begin{array}{c}{\omega }_i^{\prime }={\omega }_b{({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{{\displaystyle \frac{i+N+0.5\lambda }{2N+1}}}\hfill \\ {\omega }_i={\omega }_b{({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{{\displaystyle \frac{i+N+1-0.5\lambda }{2N+1}}}\hfill \end{array}$$

(10)

In order to simplify the calculation, define $t=i+N+1$, and Equation (9) can be changed as follows:

$${\displaystyle \frac{1}{s^{\lambda }}}={\displaystyle \frac{{\omega }_h^{1-\lambda }}{s}}\prod _{t=1}^{2N+1}{\displaystyle \frac{1+s/{\omega }_t^{\prime }}{1+s/{\omega }_t}}\prod _{t=1}^{2N+1}{\displaystyle \frac{{\omega }_t^{\prime }}{{\omega }_t}}$$

(11)

where ${\omega }_t^{\prime }$ and ${\omega }_t$ are as follows:

$$\begin{array}{c}{\omega }_t^{\prime }={\omega }_b{({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{{\displaystyle \frac{t-1+0.5\lambda }{2N+1}}}\hfill \\ {\omega }_t={\omega }_b{({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{{\displaystyle \frac{t-0.5\lambda }{2N+1}}}\hfill \end{array}$$

(12)

To simplify the formula above, define $G_{\lambda }$ and $C_{\lambda }$ as follows:

$$\begin{array}{c}{G}_{\lambda }={\omega }_h^{1-\lambda }\hfill \\ C_{\lambda }=\prod _{t=1}^{2N+1}{\displaystyle \frac{{\omega }_t^{\prime }}{{\omega }_t}}={({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{\lambda -1}\hfill \end{array}$$

(13)

Equation (11) can be rewritten as follows:

$${\displaystyle \frac{1}{s^{\lambda }}}={\displaystyle \frac{G_{\lambda }{C}_{\lambda }}{s}}\prod _{t=1}^{2N+1}{\displaystyle \frac{1+s/{\omega }_t^{\prime }}{1+s/{\omega }_t}}$$

(14)

So, the fractional-order part can be transformed into the structure shown in Figure 6.

The input signal of the fractional-order part is defined as $u^{\ast }$, and the output signal is defined as $y^{\ast }$. According to Equation (14), the fractional-order part has a total of $2N+2$ state variables, which are defined as $x_1^{\ast },x_2^{\ast },\cdots ,x_{2N+2}^{\ast }$. Then, the model of the fractional-order part can be approximated as follows.

$$\begin{array}{c}s{x}_1^{\ast }(s)=G_{\lambda }{u}^{\ast }(s)\hfill \\ {\displaystyle \frac{x_{k+1}^{\ast }(s)}{x_k^{\ast }(s)}}={\displaystyle \frac{1+s/{\omega }_k^{\prime }}{1+s/{\omega }_k}},1\le k\le 2N+1\hfill \end{array}$$

(15)

Define $\alpha ={\displaystyle \frac{{\omega }_k}{{\omega }_k^{\ast }}}={({\displaystyle \frac{{\omega }_h}{{\omega }_b}})}^{{\displaystyle \frac{1-\lambda }{2N+1}}}$. Then, Equation (15) can be written as follows:

$$s{x}_{k+1}^{\ast }(s)-\alpha s{x}_k^{\ast }(s)={\omega }_k{x}_k^{\ast }(s)-{\omega }_k{x}_{k+1}^{\ast }(s)$$

(16)

The system output $y^{\ast }$ can be written as follows:

$$y^{\ast }(s)=C_{\lambda }{x}_{2N+2}^{\ast }(s)$$

(17)

Based on the above calculation, the equation can be obtained as follows:

$$\begin{array}{c}\dot{x_1^{\ast }}=G_{\lambda }{u}^{\ast }\hfill \\ \dot{x_2^{\ast }}-\alpha \dot{x_1^{\ast }}={\omega }_1{x}_1^{\ast }-{\omega }_1{x}_2^{\ast }\hfill \\ \dot{x_3^{\ast }}-\alpha \dot{x_2^{\ast }}={\omega }_2{x}_2^{\ast }-{\omega }_2{x}_3^{\ast }\hfill \\ ⋮\hfill \\ \dot{x_{2N+2}^{\ast }}-\alpha \dot{x_{2N+1}^{\ast }}={\omega }_{2N+1}{x}_{2N+1}^{\ast }-{\omega }_{2N+1}{x}_{2N+2}^{\ast }\hfill \\ y^{\ast }=C_{\lambda }{x}_{2N+2}^{\ast }\hfill \end{array}$$

(18)

Subsequently, an individual fractional integral can be expressed in the form of the following state-space equation.

$$\left\{\begin{array}{c}{M}^{\prime }\dot{x^{\ast }}=A^{\prime }{x}^{\ast }+B^{\prime }{u}^{\ast }\hfill \\ y^{\ast }=C^{\ast }{x}^{\ast }\hfill \end{array}\right.$$

(19)

where

$$M^{\prime }=\left[\begin{array}{cccccc}1& 0& 0& \cdots & 0& 0\\ -\alpha & 1& 0& \cdots & 0& 0\\ 0& -\alpha & 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & -\alpha & 1\end{array}\right],B^{\prime }=\left[\begin{array}{c}{G}_{\lambda }\\ 0\\ 0\\ ⋮\\ 0\\ 0\end{array}\right],C^{\ast }={\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ 0\\ C_{\lambda }\end{array}\right]}^T$$

(20)

$$A^{\prime }=\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ {\omega }_1& -{\omega }_1& 0& \cdots & 0& 0\\ 0& {\omega }_2& -{\omega }_2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & -{\omega }_{2N}& 0\\ 0& 0& 0& \cdots & {\omega }_{2N+1}& -{\omega }_{2N+1}\end{array}\right],x^{\ast }=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ ⋮\\ x_{2N+1}\\ x_{2N+2}\end{array}\right]$$

(21)

Define $A^{\ast }$ and $B^{\ast }$ as follows:

$$\begin{array}{c}{A}^{\ast }=M^{\prime -1}{A}^{\prime }\hfill \\ B^{\ast }=M^{\prime -1}{B}^{\prime }\hfill \end{array}$$

(22)

The state space equation of the flexible part can be obtained as follows:

$$\left\{\begin{array}{c}\dot{x^{\ast }}=A^{\ast }{x}^{\ast }+B^{\ast }{u}^{\ast }\hfill \\ y^{\ast }=C^{\ast }{x}^{\ast }\hfill \end{array}\right.$$

(23)

In order to distinguish the parameters of the three fractional-order integrations in the system, we add the suffix n to the parameters of Equations (19)–(23). $n=1,2,3$, represent the parameters and state variables of the flexible link, the driving inertia link, and the load inertia link, respectively. According to the structure of the dual-inertia servo system in Figure 5b and Figure 6 and the result of Equation (23), the following equation can be obtained.

$$\left\{\begin{array}{c}{M}^{″}\dot{x}=A^{″}x+B^{″}u\hfill \\ y=Cx\hfill \end{array}\right.$$

(24)

where

$$M^{″}=\left[\begin{array}{ccc}{M}_1^{\prime }& 0& 0\\ 0& M_2^{\prime }& 0\\ 0& 0& M_3^{\prime }\end{array}\right]=\left[\begin{array}{ccccccccc}1& 0& 0& \cdots & 0& 0& \cdots & 0& 0\\ -{\alpha }_1& 1& 0& \cdots & 0& 0& \cdots & 0& 0\\ 0& -{\alpha }_1& 1& \cdots & 0& 0& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& \cdots & 0& 0\\ 0& 0& 0& \cdots & -{\alpha }_2& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮\\ 0& 0& 0& \cdots & 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 0& \cdots & -{\alpha }_3& 1\end{array}\right]$$

(25)

$$B^{″}=\left[\begin{array}{c}0\\ ⋮\\ 0\\ C_{\lambda 2}{G}_{\lambda 2}/J_M\\ ⋮\\ 0\\ 0\\ ⋮\\ 0\end{array}\right],C={\left[\begin{array}{c}0\\ ⋮\\ 0\\ 0\\ ⋮\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]}^T$$

(26)

$$A^{″}=\left[\begin{array}{ccccccccc}& & 0& 0& \cdots & K_s{G}_{\lambda 1}{C}_{\lambda 1}& 0& \cdots & -K_s{G}_{\lambda 1}{C}_{\lambda 1}\\ & A_1^{\prime }& & ⋮& & ⋮& ⋮& & ⋮\\ & & & 0& \cdots & 0& 0& \cdots & 0\\ 0& \cdots & -G_{\lambda 2}{C}_{\lambda 2}/J_M& & & -G_{\lambda 2}{C}_{\lambda 2}{b}_s/J_M& 0& \cdots & G_{\lambda 2}{C}_{\lambda 2}{b}_s/J_M\\ ⋮& & ⋮& & A_2^{\prime }& & ⋮& & ⋮\\ 0& \cdots & 0& & & & 0& \cdots & 0\\ 0& \cdots & G_{\lambda 3}{C}_{\lambda 3}/J_L& 0& \cdots & G_{\lambda 3}{C}_{\lambda 3}{b}_s/J_L& & & -G_{\lambda 2}{C}_{\lambda 2}(b_s/J_L+K_L/J_L)\\ ⋮& & ⋮& ⋮& & ⋮& & A_3^{\prime }& \\ 0& \cdots & 0& 0& \cdots & 0& & & \end{array}\right]$$

(27)

Define A and B as follows:

$$\begin{array}{c}A={M^{″}}^{-1}{A}^{″}\hfill \\ B={M^{″}}^{-1}{B}^{″}\hfill \end{array}$$

(28)

The state space equation of the flexible link can be obtained:

$$\left\{\begin{array}{c}\dot{x}=Ax+Bu\hfill \\ y=Cx\hfill \end{array}\right.$$

(29)

At this point, the fractional-order expression and integer-order approximate realization of the dual-inertia servo system are obtained.

3. Identification for Dual-Inertia Servo Inverter Systems

In order to obtain the parameters of the above model, it is necessary to design an optimization algorithm to realize the identification. Common optimization algorithms include the Newton method, the Gauss–Newton method, and the gradient descent method, etc. Given that the LM algorithm demonstrates superior stability compared to other algorithms while maintaining relatively simple computations and faster convergence speeds, it was selected as the method for parameter identification [29]. According to the analysis in Section 2, to obtain the system model, parameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, $K_s$, $b_s$, $J_M$, $J_L$, and $K_L$ need to be identified. Firstly, the parameter vector $\theta$ to be identified is defined as follows:

$$\theta =\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\\ {\theta }_4\\ {\theta }_5\\ {\theta }_6\\ {\theta }_7\\ {\theta }_8\end{array}\right]=\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ {\lambda }_3\\ K_s\\ b_S\\ J_M\\ J_L\\ K_L\end{array}\right]$$

(30)

The parameter identification result of $\theta$ is defined as follows:

$\widehat{\theta }$, $\widehat{\theta }={\left[\begin{array}{cccccccc}\widehat{{\theta }_1}& \widehat{{\theta }_2}& \widehat{{\theta }_3}& \widehat{{\theta }_4}& \widehat{{\theta }_5}& \widehat{{\theta }_6}& \widehat{{\theta }_7}& \widehat{{\theta }_8}\end{array}\right]}^T$

Define the collected data input as $\mathbf{u}$ and output as $\mathbf{y}$. And $u_k$ and $y_k$ represent the data collected at the $k^{th}$ moment. n is the number of collected data points.

$$\begin{array}{c}\mathbf{u}=\left[\begin{array}{cccccc}{u}_1& u_2& \cdots & u_k& \cdots & u_n\end{array}\right]\hfill \\ \mathbf{y}=\left[\begin{array}{cccccc}{y}_1& y_2& \cdots & y_k& \cdots & y_n\end{array}\right]\hfill \end{array}$$

(31)

In this paper, the unknown parameters in fractional model of dual-inertia system are identified based on time-domain output error and the LM algorithm. The block diagram of this method is shown in Figure 7.

In Figure 7, $\widehat{y_k}$ is the output of the estimation model, ${\epsilon }_k$ is the error between the estimated output and the actual output, J is the square difference of the output error, and $\widehat{\theta }$ is the estimated value of the parameter.

$${\epsilon }_k=y_k-\widehat{y_K}(\widehat{\theta })$$

(32)

$$J=\sum _{k=1}^n{\epsilon }_k^2=\sum _{k=1}^n{[y_k-\widehat{y_K}(\widehat{\theta })]}^2$$

(33)

The state space Equation (29) is written in the form of a function.

$$\widehat{y_k}(\widehat{\theta })=f({\mathbf{x}}^k,\widehat{\theta })$$

(34)

where ${\mathbf{x}}^k$ represents the state value x at the $k^{th}$ moment.

$${\mathbf{x}}^k={\left[\begin{array}{cccc}{x}_1^k& x_2^k& \cdots & x_{6N+6}^k\end{array}\right]}^T$$

(35)

The parameter estimate after i iterations is defined as ${\widehat{\theta }}^i$.

$${\widehat{\theta }}^i={\left[\begin{array}{cccc}{\widehat{{\theta }_1}}^i& {\widehat{{\theta }_2}}^i& \cdots & {\widehat{{\theta }_8}}^i\end{array}\right]}^T$$

(36)

The function $f({\mathbf{x}}^k,\widehat{\theta })$ is expanded by Taylor expansion.

$$f({\mathbf{x}}^k,\widehat{\theta })=f({\mathbf{x}}^k,{\widehat{\theta }}^i)+[\sum _{j=1}^8(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i){\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,\widehat{\theta })]+\cdots +{\displaystyle \frac{1}{n!}}[\sum _{j=1}^8{(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i)}^n{\displaystyle \frac{{\partial }^n}{{\partial \widehat{{\theta }_j}}^n}}f({\mathbf{x}}^k,\widehat{\theta })]+\cdots$$

(37)

Ignoring the higher-order remainder, J can be expressed as the following equation.

$$J\approx \sum _{k=1}^n{\{y_k-f({\mathbf{x}}^k,{\widehat{\theta }}^i)+[\sum _{j=1}^8(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i){\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,\widehat{\theta })]\}}^2$$

(38)

In order to obtain the minimum value of J, the derivative of the above equation is calculated. And let the derivative be equal to 0.

$$\begin{array}{c}-2\sum _{k=1}^n\{[y_k-f(x^k,{\widehat{\theta }}^i)-\sum _{j=1}^8(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i){\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)]{\displaystyle \frac{\partial }{\partial \widehat{{\theta }_1}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\}=0\\ -2\sum _{k=1}^n\{[y_k-f(x^k,{\widehat{\theta }}^i)-\sum _{j=1}^8(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i){\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)]{\displaystyle \frac{\partial }{\partial \widehat{{\theta }_2}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\}=0\\ ⋮\\ -2\sum _{k=1}^n\{[y_k-f(x^k,{\widehat{\theta }}^i)-\sum _{j=1}^8(\widehat{{\theta }_j}-{\widehat{{\theta }_j}}^i){\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)]{\displaystyle \frac{\partial }{\partial \widehat{{\theta }_6}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\}=0\end{array}$$

(39)

The output sensitivity function is defined as ${\sigma }_{\widehat{y},\widehat{\theta }}^i(k)$ as shown in the following equation.

$${\sigma }_{\widehat{y},\widehat{\theta }}^i(k)={\displaystyle \frac{d}{d\widehat{\theta }}}f(x^k,{\widehat{\theta }}^i)=\left[\begin{array}{c}{\displaystyle \frac{\partial }{\partial \widehat{{\theta }_1}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\\ {\displaystyle \frac{\partial }{\partial \widehat{{\theta }_2}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\\ ⋮\\ {\displaystyle \frac{\partial }{\partial \widehat{{\theta }_8}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)\end{array}\right]$$

(40)

The output sensitivity function for the parameter ${\sigma }_{\widehat{y},\widehat{{\theta }_j}}^i(k)$ is as follows

$${\sigma }_{\widehat{y},\widehat{{\theta }_j}}^i(k)={\displaystyle \frac{\partial }{\partial \widehat{{\theta }_j}}}f({\mathbf{x}}^k,{\widehat{\theta }}^i)$$

(41)

The following equation can be obtained.

$$\sum _{k=1}^n\left[\begin{array}{cccc}{\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k)& {\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k)& \cdots & {\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k)\\ {\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k)& {\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k)& \cdots & {\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k)\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k)& {\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k)& \cdots & {\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k){\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k)\end{array}\right]\left[\begin{array}{c}\widehat{{\theta }_1}-{\widehat{{\theta }_1}}^i\\ \widehat{{\theta }_2}-{\widehat{{\theta }_2}}^i\\ ⋮\\ \widehat{{\theta }_8}-{\widehat{{\theta }_8}}^i\end{array}\right]=\left[\begin{array}{c}{\epsilon }_k{\sigma }_{\widehat{y},\widehat{{\theta }_1}}^i(k)\\ {\epsilon }_k{\sigma }_{\widehat{y},\widehat{{\theta }_2}}^i(k)\\ ⋮\\ {\epsilon }_k{\sigma }_{\widehat{y},\widehat{{\theta }_8}}^i(k)\end{array}\right]$$

(42)

The following equation can be obtained.

$$\sum _{k=1}^n\{[{\sigma }_{\widehat{y},\widehat{\theta }}^i(k)]{[{\sigma }_{\widehat{y},\widehat{\theta }}^i(k)]}^T\}(\widehat{\theta }-{\widehat{\theta }}^i)=\sum _{k=1}^n({\epsilon }_k{\sigma }_{\widehat{y},\widehat{\theta }}^i(k))$$

(43)

The derivative of the state variable value with respect to $\widehat{\theta }$ iteration is defined as the state sensitivity ${\sigma }_{x,\widehat{\theta }}^i$ after the $i^{th}$.

$${\sigma }_{x,\widehat{\theta }}^i={\displaystyle \frac{d}{d\widehat{\theta }}}x({\widehat{\theta }}^i)=\left[\begin{array}{cccc}{\sigma }_{x,{\widehat{\theta }}_1}^i& {\sigma }_{x,{\widehat{\theta }}_2}^i& \cdots & {\sigma }_{x,{\widehat{\theta }}_8}^i\end{array}\right]$$

(44)

Then, the expression of the state sensitivity function ${\sigma }_{x,{\widehat{\theta }}_j}^i$ of the function for parameter ${\widehat{\theta }}_j$ is as follows.

$${\sigma }_{x,{\widehat{\theta }}_j}^i={\left[\begin{array}{cccc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}{x}_1({\widehat{\theta }}^i)& {\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}{x}_2({\widehat{\theta }}^i)& \cdots & {\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}{x}_{6N+6}({\widehat{\theta }}^i)\end{array}\right]}^T$$

(45)

where $j=1,2,3$.

The estimated system can be expressed as follows:

$$\left\{\begin{array}{c}\dot{x}(\widehat{\theta })=A(\widehat{\theta })x(\widehat{\theta })+B(\widehat{\theta })u(\widehat{\theta })\hfill \\ y(\widehat{\theta })=C(\widehat{\theta })x(\widehat{\theta })\hfill \end{array}\right.$$

(46)

Take the partial derivative of the above equation.

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}\dot{x}(\widehat{\theta })={\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}A(\widehat{\theta })x(\widehat{\theta })+A(\widehat{\theta }){\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}x(\widehat{\theta })+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}B(\widehat{\theta })u(\widehat{\theta })\hfill \\ y(\widehat{\theta })={\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}C(\widehat{\theta })x(\widehat{\theta })+C(\widehat{\theta }){\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_j}}x(\widehat{\theta })\hfill \end{array}\right.$$

(47)

The output sensitivity function of the three parameters can be obtained as follows:

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_1}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_1}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_1}}A({\widehat{\theta }}^i)& {\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_1}}B({\widehat{\theta }}^i)\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_1}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_1}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_1}}C({\widehat{\theta }}^i)& 0\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \end{array}\right.$$

(48)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_2}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_2}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_2}}A({\widehat{\theta }}^i)& {\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_2}}B({\widehat{\theta }}^i)\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_2}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_2}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_2}}C({\widehat{\theta }}^i)& 0\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \end{array}\right.$$

(49)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_3}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_3}^i+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_3}}A({\widehat{\theta }}^i)x({\widehat{\theta }}^i)\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_3}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_3}^i\hfill \end{array}\right.$$

(50)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_4}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_4}^i+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_4}}A({\widehat{\theta }}^i)x({\widehat{\theta }}^i)\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_4}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_4}^i\hfill \end{array}\right.$$

(51)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_5}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_5}^i+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_5}}A({\widehat{\theta }}^i)x({\widehat{\theta }}^i)\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_5}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_5}^i\hfill \end{array}\right.$$

(52)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_6}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_6}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_6}}A({\widehat{\theta }}^i)& {\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_6}}B({\widehat{\theta }}^i)\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_6}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_6}^i+\left[\begin{array}{cc}{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_6}}C({\widehat{\theta }}^i)& 0\end{array}\right]\left[\begin{array}{c}x({\widehat{\theta }}^i)\\ u\end{array}\right]\hfill \end{array}\right.$$

(53)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_7}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_7}^i+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_7}}A({\widehat{\theta }}^i)x({\widehat{\theta }}^i)\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_7}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_7}^i\hfill \end{array}\right.$$

(54)

$$\left\{\begin{array}{c}{\dot{\sigma }}_{x,{\widehat{\theta }}_8}^i=A({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_8}^i+{\displaystyle \frac{\partial }{\partial {\widehat{\theta }}_8}}A({\widehat{\theta }}^i)x({\widehat{\theta }}^i)\hfill \\ {\dot{\sigma }}_{y,{\widehat{\theta }}_8}^i=C({\widehat{\theta }}^i){\sigma }_{x,{\widehat{\theta }}_8}^i\hfill \end{array}\right.$$

(55)

So, the Jacobi matrix $J_{\theta }^i$ and the Hessen matrix $H_{\theta }^i$ are obtained.

$$\begin{array}{c}{J}_{\theta }^i=\sum _{k=1}^n({\epsilon }_k{\sigma }_{\widehat{y},\widehat{\theta }}^i(k))\hfill \\ H_{\theta }^i=\sum _{k=1}^n\{[{\sigma }_{\widehat{y},\widehat{\theta }}^i(k)]{[{\sigma }_{\widehat{y},\widehat{\theta }}^i(k)]}^T\}\hfill \end{array}$$

(56)

In order to ensure that the matrix is invertible, the matrix $(H_{\theta }^i+\mu I)$ is used instead of the Hessen matrix $H_{\theta }^i$. $\mu$ is the damping coefficient, and I is the identity matrix. The LM algorithm is actually a method that lies between the Gauss–Newton method and the gradient descent method. And the coefficient $\mu$ is a parameter that controls the degree to which this method approaches either of the above methods.

In practical operation, in order to achieve rapid convergence and avoid becoming trapped in a local optimum, the initial values of the optimized parameters can be set as the nominal values of the parameters in integer order.

We obtained the calculation results required by the LM optimization algorithm.

4. Experimental Demonstration

4.1. Experimental Setup

To validate the accuracy of the proposed fractional-order model for the dual-inertia servo inverter system, an experimental setup was constructed. This setup comprises a power supply, two motor drivers, a coupling connector, a drive motor, a load motor, and a host computer as illustrated in Figure 8. In this setup, the motors adopted are permanent magnet synchronous motors, and the coupling is made of thermoplastic polyurethane rubber shown in Figure 9. The load motor is employed to simulate operational loads, while the coupling connector between the drive motor and the load motor demonstrates the flexible characteristics inherent in dual-inertia servo systems. The parameters of this experimental platform are detailed in

Table 1. System parameter settings.

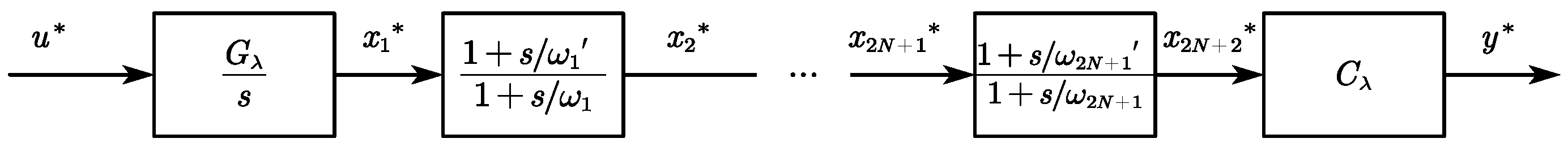
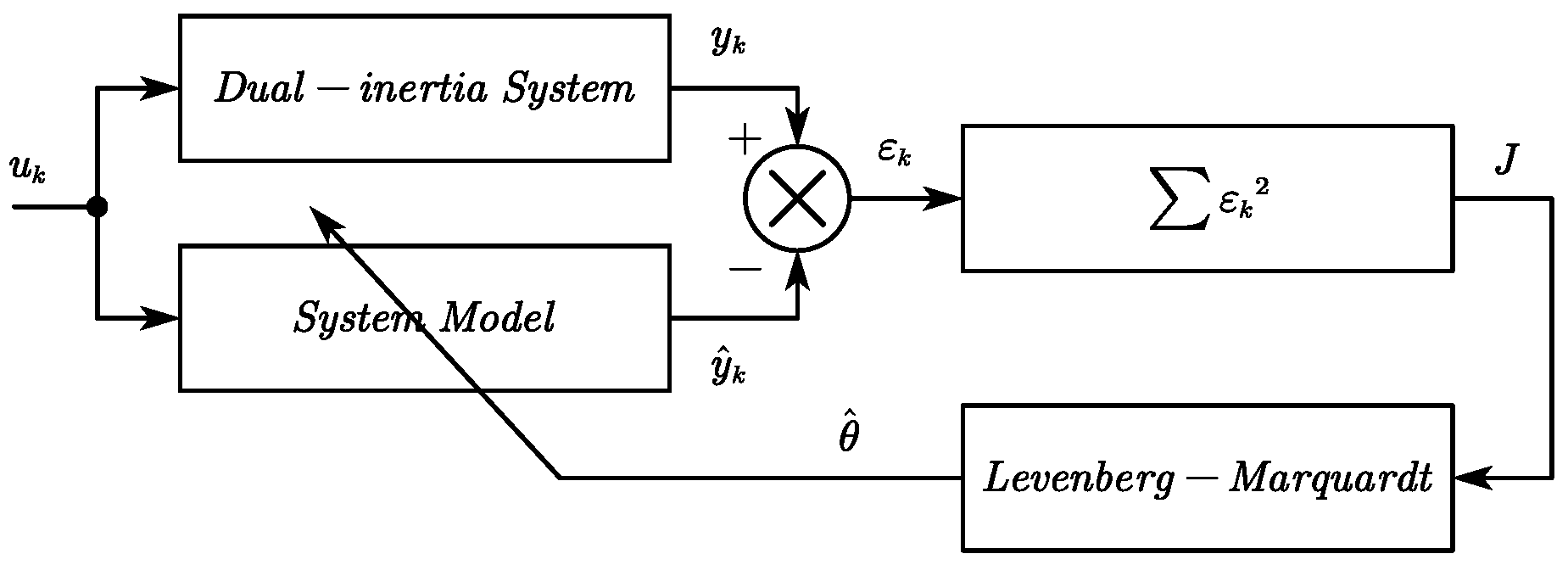
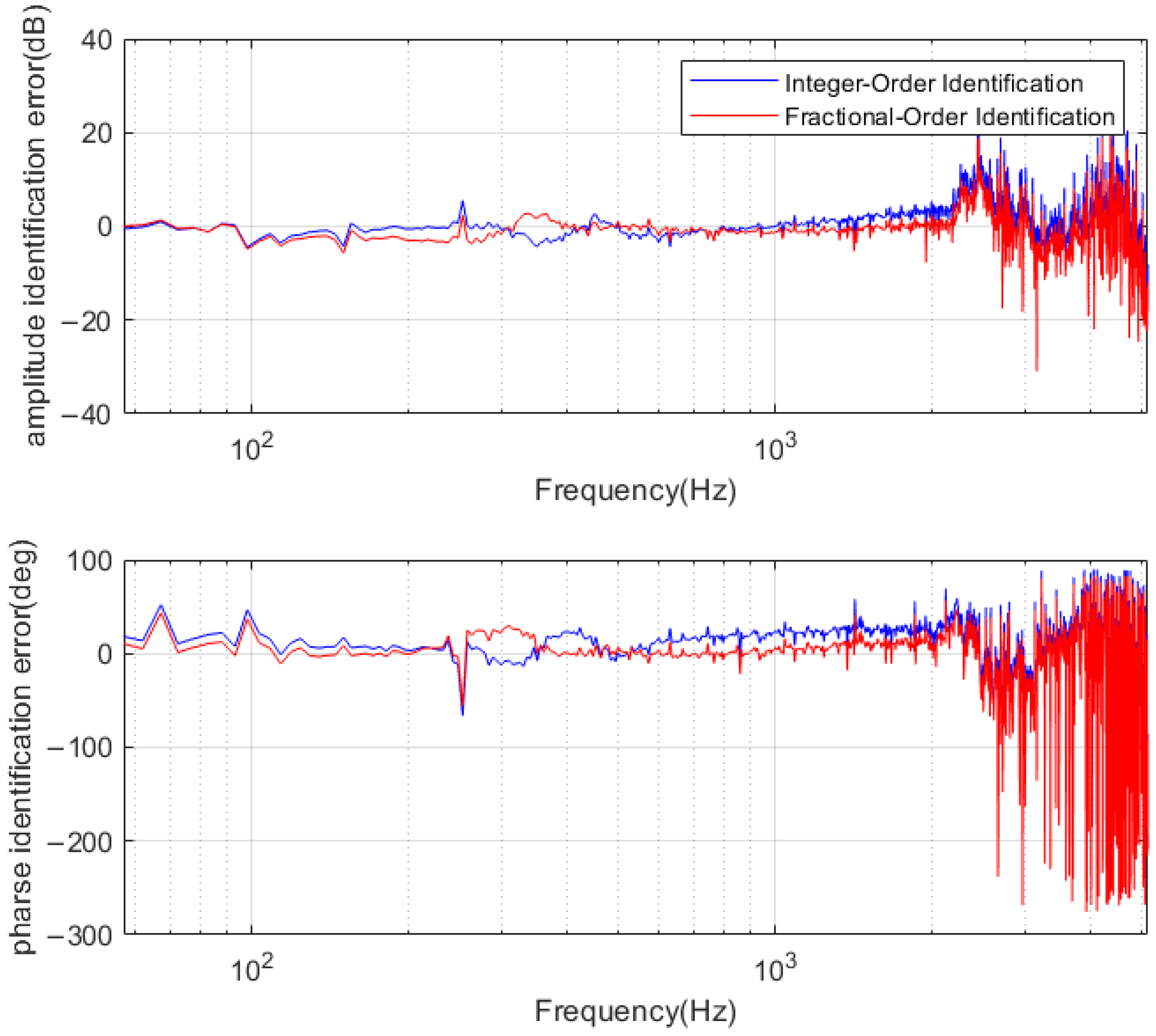
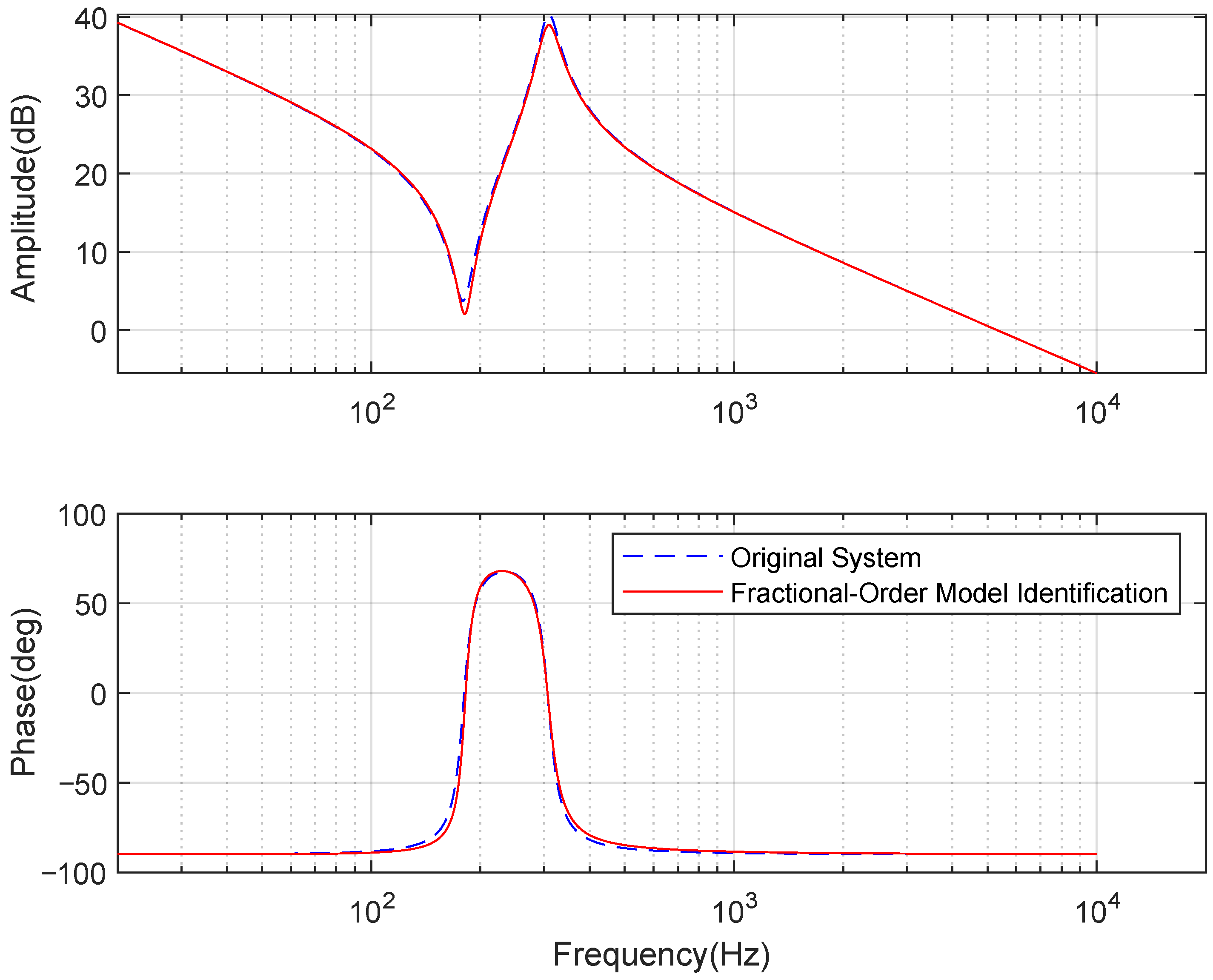
Parameter	Nominal Value
Speed loop bandwidth	30 Hz
Current loop bandwidth	2000 Hz
Motor power of drive motor	400 W
Motor power of load motor	400 W
Nominal speed of drive motor	3000 r/min
Nominal speed of load motor	3000 r/min
Nominal torque of drive motor	1.27 N·m
Nominal torque of load motor	1.27 N·m
Inertia of drive motor	6.80 × 10−5 kg·m2
Inertia of load motor	6.80 × 10−5 kg·m2
Diameter of the coupling	20 mm
Length of the coupling	30 mm
Data sampling frequency	16 kHz

.

4.2. Experimental Data Collection

This experiment required the collection of the input activate signal, the output signal, and other related signals of the servo system. The output signal (rotational speed) of the system was collected by the encoder at the end of the motor, while the input signal (current) was collected by the sampling resistor in the motor driver. The experiment for data collection in the open loop is simple to operate and implement. However, the open-loop speed system is unstable and prone to safety hazards. Therefore, the closed-loop data collection for identification was adopted; that is, the activate input signal and the related output signals were collected when the servo system was in the closed-loop operation of the speed loop.

The specific process of data collection in the experimental test in this study is shown in Figure 10. Proportional Integral (PI) Controllers were adopted as the original current loop and speed loop controllers of the experimental platform, and the parameter tuning methods are described in [30]. To mitigate the potential non-linear effects arising from the motor’s electromagnetic component, it is necessary to initially input a step signal, ensuring that the motor operates under normal operating conditions. Subsequently, the procedures of signal injection and data acquisition can be executed. The specific collection steps are as follows: Firstly, a step signal was input to the servo system to enable the servo system operate under the normal reference tracking conditions [31]. After the system is stable, the activate signal of the servo system was superimposed to start the identification. Then, the q-axis current data $i_q^{\ast }$ and the rotational speed data ${\omega }_m$ were collected and saved.

In terms of the selection of activate signals, the energy spectrum of the signal should be as wide as possible and evenly distributed. Theoretically, white noise is the most ideal activate signal, but due to its difficulty in implementation, it is difficult to directly apply it in engineering. In contrast, although the pseudo-random binary sequence (PRBS) does not have as ideal a spectral characteristic as white noise, it has good autocorrelation and is easy to implement in digital systems. Moreover, by adjusting the sequence length, sampling frequency, and amplitude of the PRBS, activate signals with different performance characteristics can be flexibly generated to meet the actual engineering requirements [32]. Thus, the PRBS was used as the activate signal.

The data collected in the experiment are shown in Figure 11.

4.3. Parameter Identification

The frequency response of the actual dual-inertia servo inverter system is in Figure 12, where the frequency responses of the fractional-order model and the integer-order model obtained by the same LM method are compared with the result of the actual dual-inertia servo inverter system. The the detailed comparison is shown in

Table 2. Experimental results of main parameters.

Parameter	Integer-Order Model	Fractional-Order Model
${\lambda }_1$	1	0.955
${\lambda }_2$	1	1.382
${\lambda }_3$	1	1.057
$J_M$ (kg·m2)	$5.67\times {10}^{-5}$	$2.62\times {10}^{-6}$
$J_L$ (kg·m2)	$4.71\times {10}^{-5}$	$5.58\times {10}^{-5}$
$K_S$ (N/rad)	224	225
$b_s$ (N/rad/s)	0.0113	0.0555
$K_L$ (N/rad/s)	0.0084	0.0098

, which lists the results of the order of the integrator in the flexible part ${\lambda }_1$, order of the integrator in the drive and load parts ${\lambda }_2$ and ${\lambda }_3$, moments of inertia of the motor and the load $J_M$ and $J_L$, stiffness coefficient of the coupling connector $K_s$, damping coefficient of the coupling connector $b_s$, and load damping coefficient $K_L$ obtained by different models.

From Figure 12, it can be seen that the phase–frequency curve of the fractional-order model is closer to the actual dual-inertia servo inverter system than that of the integer-order model, while the amplitude–frequency curves differ little from each other. Consequently, these findings indicate that the fractional-order model provides a superior representation of the actual system.

Figure 13 shows the response amplitude errors and phase errors of the two methods in the frequency domain. Here, the error is quantified as the discrepancy between the result of parameter identification and the result obtained from power spectrum estimation. Moreover, by excluding the high-frequency component with much noise (above 2500 Hz), the squared sum of the frequency-domain response errors was computed, and the results are presented in

Table 3. Squared sum of the frequency-domain response errors.

	Integer-Order Identification	Fractional-Order Identification
Sum of squared amplitude errors (dB2)	$9.5478\times {10}^3$	$4.8188\times {10}^3$
Sum of squared phase errors (deg2)	$2.9704\times {10}^6$	$1.2364\times {10}^5$

. Obviously, whether from the perspective of amplitude–frequency response or phase-frequency response, the error of the fractional-order model is smaller. The fractional-order model is superior to the integer-order model.

The time-domain response output results of the system using different models are compared as shown in Figure 14. The sum of the response error’s squares in time domain was calculated, and the results are shown in

Table 4. Squared sum of the time-domain response errors.

	Integer-Order Identification	Fractional-Order Identification
Sum of squared speed errors (RPM2)	$5.114\times {10}^6$	$4.877\times {10}^6$

.

From Table 4, it is evident that the time-domain response of the fractional-order model exhibits greater proximity to the actual values compared to the integer-order model, thereby demonstrating higher accuracy. Consequently, the fractional-order model yields superior identification results.

4.4. Noise Sensitivity Test

In order to test the influence of noise on the proposed identification method, a simulation platform based on MATLAB R2021a/Simulink was set up to simulate the sampling process of the actual system as Figure 15. Then, noise with a variance of 0.5 was inserted into the system output signal. Next, identification processing of the collected data was carried out. The results in the frequency domain and time domain are shown in Figure 16 and Figure 17.

Obviously, the influence of noise on system identification is not significant.

Overall, the proposed fractional-order modeling and identification method has the following characteristics:

(1)

The results in Figure 13 and Table 3 indicate that the fractional-order model and its identification method proposed in this paper demonstrate certain advantages over the traditional integer-order models in terms of frequency-domain performance.

(2)

The results in Figure 14 and Table 4 indicate that the aforementioned method also has advantages in the time domain.

(3)

Figure 16 and Figure 17 show that this method is hardly affected by sampling noise.

5. Conclusions

To achieve a more accurate dual-inertia model and parameters, this paper introduces a fractional-order dual-inertia model along with a corresponding parameter identification method. This approach generalizes the conventional integer-order dual-inertia model to a fractional-order one, thereby enhancing the model’s descriptive capability while preserving its relative simplicity. Consequently, the modeling accuracy is significantly improved. Subsequently, based on the proposed fractional-order dual-inertia model, an optimized parameter identification strategy is formulated. This strategy employs the system’s time-domain error for sampling and utilizes the Levenberg–Marquardt (LM) algorithm for optimization calculations to derive optimal design parameters. The experimental results demonstrate that the fractional-order model and the associated identification strategy presented in this paper provide superior system modeling accuracy compared to traditional integer-order models. The identification model is more precise in the frequency domain compared to the integer one, and the output error under input excitation conditions are notably reduced. Based on the research results of this paper, the next step of work will focus on the enhanced fractional-order dual-inertia model, aiming to design more reasonable control strategies and resonance suppression methods.